应力-应变全曲线
应力-应变曲线
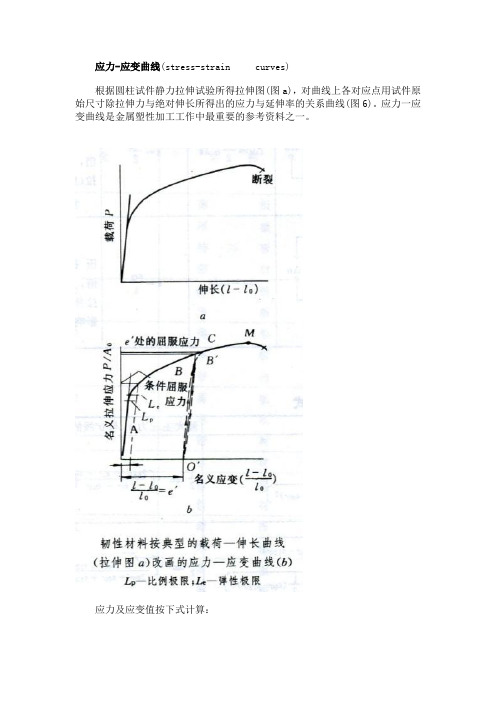
应力-应变曲线(stress-strain curves)根据圆柱试件静力拉伸试验所得拉伸图(图a),对曲线上各对应点用试件原始尺寸除拉伸力与绝对伸长所得出的应力与延伸率的关系曲线(图6)。
应力一应变曲线是金属塑性加工工作中最重要的参考资料之一。
应力及应变值按下式计算:式中σi 表示拉伸图上任意点的应力值,δi为i点的延伸率,Pi及Δli为该点的拉力与绝对伸长值,F0及l为试件的断面积和计算长度。
试件受拉伸时,先产生弹性变形,这时应力应变成比例,当出现二者不能保持线性关系的点时,表示材料已屈服而将发生塑性变形,这时的应力定义为屈服应力或流变应力,用σs表示,其求法见屈服点。
拉伸时当试件计算长度上的均匀变形阶段结束而产生细颈时,变形将集中在细颈部分。
出现细颈前材料所能承受的应力名为强度极限或抗拉强度,用σb表示σb =Pmax/F式中Pmax为拉伸图上所记录的最大载荷值。
试件出现细颈后很快即断裂,断裂应力σfσf =Pf/Tf式中Pf 是断裂时的拉力,Ff是断口面积。
试件拉断时的延伸率δf(%)或断面收缩率ψ(%)是表示材料可承受最大塑性变形能力的指标:矾一牮×100(4)£fPf=盐≯×100(5)』’0式中厶和Ff是将断开的试件对合后测定的试件长度和断口处的面积。
抗拉强度靠及延伸率d或断面收缩率妒是材料性能的两个基本指标,在工程上有着广泛的应用。
屈服应力民(或乱:)是金属塑性加工时变形体开始产生塑性变形所必需的最小应力,它是计算变形力的一个重要参数。
应力-应变曲线表征材料受外力作用时的行为。
材料受力后即发生弹性变形,这时应力应变呈简单的线性关系,继续增加作用力至一定大小后材料将出现塑性变形,以后变形与应力的关系复杂,当塑性变形至一定程度以后,试件破断则变形过程终结。
所以任何变形过程均包括弹性变形、塑性变形及破断3个典型阶段。
金属的塑性加工过程处于弹性变形与破断二者之间。
首先要创造一定的应力状态条件使金属能发生塑性变形,其次是安排一个使塑性变形尽可能大又不致发生破坏的热力学条件。
简述岩石典型的全应力-应变曲线的四个阶段

简述岩石典型的全应力-应变曲线的四个
阶段
岩石典型的全应力-应变曲线是指岩石在受到外力作用下,受力和变形关系的一种变化过程,一般情况下是由四个阶段构成的。
第一阶段是岩石的弹性阶段,也称为线性弹性阶段。
在这个阶段,岩石的弹性模量比较大,当受到外力作用时,岩石的变形量比较小,变形量与外力之间有着线性的关系,这个阶段是岩石变形最小的一个阶段。
第二阶段是岩石的塑性阶段,也称为非线性弹性阶段。
在这个阶段,岩石的弹性模量比较小,当受到外力作用时,岩石的变形量会明显增加,变形量与外力之间没有线性的关系,这个阶段是岩石变形最大的一个阶段。
第三阶段是岩石的稳定阶段,在这个阶段,岩石的变形量不再增加,变形量与外力之间也没有明显的关系,这个阶段是岩石变形的最稳定阶段。
最后一阶段是岩石的恢复阶段,这个阶段是岩石变形最大的一个阶段,也是岩石变形过程中最重要的一个阶段。
在这个阶段,岩石被外力作用后,会出现微小的变形,但是变形量会随着外力的减小而逐渐减小,最终变形量恢复到未受力前的状态。
以上就是岩石典型的全应力-应变曲线的四个阶段,它们是线性弹性阶段、非线性弹性阶段、稳定阶段和恢复阶段。
这四个阶段在岩石变形的过程中起着十分重要的作用,可以帮助我们更好地了解岩石的变形特性,从而更好地利用岩石。
应力-应变曲线
混凝土是一种复合建筑材料,内部组成结构非常复杂。
它是由二相体所组成,即粗细骨料被水泥浆所包裹,靠水泥浆的粘接力,使骨料相互粘接成为整体。
如果考虑到带气泡和毛细孔隙的存在,混凝土实际是一种三相体的混合物,不能认为是连续的整体。
[2]1. 普通高强度混凝土只能测出压应力-应变曲线的上升段,因为混凝土一旦出现出裂缝,承力系统在加压过程中积累的大量弹性能突然急剧释放,使得裂缝迅速扩展,试件即刻发生破坏,无法测得应力-应变曲线的下降段。
[1]2. 拟合本文的高强混凝土和纤维与混杂纤维增强高强混凝土的受压本构方程的参数结果图3和图4为掺杂了纤维与混杂纤维的纤维增强高强混凝土的压缩应力一应变全曲线,由曲线可以看出,纤维与混杂纤维增强高强混凝土则能够准确地测出完整的压应力.应变曲线.纤维增强高强混凝土和混杂纤维增强高强混凝土的这两种曲线具有相同的形状啪,都由三段组成:线性上升阶段、初裂点以后的非线性上升阶段、峰值点以后的缓慢下降阶段.[2]3.[3]再生混凝土设计强度等级为C20,C25,C30,C40,再生骨料取代率100%。
标准棱柱体试件150mm*150mm*300mm,28天强度测试结果。
“等应力循环加卸载试验方法”测定再生混凝土的应力-应变全曲线,即每次加载至预定应力后再卸载至零,再次进行加载,多次循环后达不到预定应力而自动转向包络线时,进行下一级预定应力的加载。
再生粗骨料来源的地域性和差异性使再生骨料及再生混凝土的力学性能有较大差别。
4.通过对普通混凝土和高强混凝土在单轴收压时的应力应变分析发现,混凝土的弹性模量随混凝土的强度的提高而提高,混凝土弹性段的范围随混凝土强度的提高而增大,混凝土应力应变曲线的下降段,随混凝土强度的提高而越来越陡,混凝土的峰值应变与混凝土的抗压强度无正比关系。
图2给出了各组混凝土试件的平均应力应变曲线,从图中可以看出A1-A5试件的曲线为完整的圆滑曲线。
A6,A7由于混凝土试件强度较高实验设备刚度不够,当σc>f c 后,试验机释放的能量迅速传到周围的4个钢柱上,从而引起混凝土突然破坏,所以曲线只有上升段没有下降段,A1-A7试件的应力应变曲线的上升段是相似的,但下降段的曲线形状差别较大。
混凝土应力-应变全曲线的试验研究

混凝土应力-应变全曲线的试验研究
混凝土是建筑工程中常用的材料之一,因其具有良好的承载能力
和耐久性,混凝土的应力-应变关系的研究对于了解混凝土性能具有重
要意义。
本文旨在通过试验研究混凝土的应力-应变全曲线。
试验方法:选取典型的混凝土材料进行试验,采用万能试验机对
其进行拉伸试验,记录其载荷与变形的关系,从而得到应力-应变曲线。
试验结果:试验得到的混凝土应力-应变曲线可分为三段,即线
性段、弯曲段和残余强度段。
其中线性段为混凝土的弹性阶段,应变
与应力成正比,弯曲段为混凝土的塑性变形阶段,应变增大速度逐渐
减缓,应力也逐渐减小,残余强度段为混凝土的破坏阶段,应变增大
较快,应力快速下降。
结论:通过试验可以得出,混凝土的应力-应变关系是复杂的非
线性关系,混凝土在不同阶段表现出不同的性能,加强混凝土的质量
控制,可以有效提高其承载能力和使用寿命。
应力 应变 曲线

应力应变曲线
应力-应变曲线描述了材料在受到外部力作用下的应力和应变之间的关系。
应力(stress)指的是材料在单位面积上受到的力的大小,通常以强度(N/m^2)作为单位。
应力-应变曲线的横轴通常表示材料的应变(strain),应变指的是材料在受到力后产生的形变程度,通常以长度的相对变化或者角度的相对变化表示。
应力-应变曲线通常可以分为四个阶段:
1. 弹性阶段(Elastic region):当材料受到小应力时,材料会表现出弹性行为,即应变与应力成正比。
在这个阶段,应力增加时材料会发生形变,但一旦外力消失,材料会恢复到原来的形状。
2. 屈服阶段(Yield Point):当材料受到足够大的应力时,材料会超过其弹性限度,开始发生可见的形变。
这个阶段的应力-应变曲线通常表现为一个明显的曲线,材料开始变得塑性。
3. 塑性阶段(Plastic region):在这个阶段,材料受到的应力继续增加,但应变的增加速度逐渐减慢。
材料开始发生不可逆的塑性变形。
4. 断裂阶段(Fracture point):当材料受到过大的应力时,材料会发生断裂,即完全失去其机械性能。
应力-应变曲线的形状和材料的性质,结构和处理方式等因素密切相关。
不同材料(如金属、塑料、陶瓷等)的应力-应变曲线会有所不同,也受到温度、湿度等环境条件的影响。
这在工程设计和材料选择中具有重要的意义,可以帮助工程师评估材料的强度、延展性、可塑性和抗断裂性等性能。
混凝土受压应力-应变全曲线方程(描述)

混凝土受压应力-应变全曲线方程混凝土受压应力-应变全曲线方程混凝土的应力-应变关系是钢筋混凝土构件强度计算、超静定结构内力分析、结构延性计算和钢筋混凝土有限元分析的基础,几十年来,人们作了广泛的努力,研究混凝土受压应力-应变关系的非线性性质,探讨应力与应变之间合理的数学表达式,1942年,Whitney 通过混凝土圆柱体轴压试验,提出了混凝土受压完整的应力应变全曲线数学表达式,得出了混凝土脆性破坏主要是由于试验机刚度不足造成的重要结论,这一结论于1948年由Ramaley 和Mchenry 的试验研究再次证实,1962年,Barnard 在专门设计的具有较好刚性且能控制应变速度的试验机上,试验了一批棱柱体试件以及试件两靖被放大的圆柱体试件,试验再次证明,混凝土的突然破坏并非混凝土固有特性,而是试验条件的结果,即混凝土的脆性破坏可用刚性试验机予以防止,后来由很多学者(如M.Sagin ,P.T.Wang ,过镇海等)所进行的试验,都证明混凝土受压应力-应变曲线确实有下降段存在,那么混凝土受压应力与应变间的数学关系在下降段也必然存在,研究这一数学关系的工作一刻也没有停止。
钢筋混凝土结构是目前使用最为广泛的一种结构形式。
但是,对钢筋混凝土的力学性能还不能说已经有了全面的掌握。
近年来,随着有限元数值方法的发展和计算机技术的进步,人们已经可以利用钢筋混凝土有限元分析方法对混凝土结构作比较精确的分析了。
由于混凝土材料性质的复杂性,对混凝土结构进行有限元分析还存在不少困难,其中符合实际的混凝土应力应变全曲线的确定就是一个重要的方面。
1、混凝土单轴受压全曲线的几何特点经过对混凝土单轴受压变形的大量试验大家一致公认混凝土单轴受压变过程的应力应变全曲线的形状有一定的特征。
典型的曲线如图1所示,图中采用无量纲坐标。
sc c E E N f y x 0,,===σεε 式中,c f 为混凝土抗压强度;c ε为与c f 对应的峰值应变;0E 为混凝土的初始弹性模量;s E 为峰值应力处的割线模量。
常用混凝土受压应力_应变曲线的比较和应用
常用混凝土受压应力—应变曲线的比较及应用摘要:为了对受弯截面进行弹塑性分析及其他研究,在对各种混凝土受压应力应变曲线研究的基础上,总结出了四种常用曲线,这些曲线已经被广泛应用。
对四种常用曲线进行简介,并指出了它们的适用范围及优缺点。
在进行受弯截面弹塑性分析时,介绍了运用四种常用曲线对其受力性能进行分析的计算模式,并且运用实际案例进行受弯截面弹塑性分析,方便工程师们参考和借鉴。
关键词:混凝土;受压应力应变曲线;本构关系;受弯截面0 引言混凝土受压应力—应变曲线是其最基本的本构关系,又是多轴本构模型的基础,在钢筋混凝土结构的非线件分析中,例如构件的截面刚度、截面极限应力分布、承载力和延性、超静定结构的内力和全过程分析等过程中,它是不可或缺的物理方程,对计算结果的准确性起决定性作用。
近年来,国内外学者对其进行了大量的研究及改进,已有数十条曲线表达式,其中部分具有代表性的表达式已经被各国规范采纳。
常用的表达式包括我国《混凝土结构设计规范》(GB50010-2010)、CEB-FIP Model Code(1990)、清华过镇海以及美国学者Hognestad 建议的混凝土受压应力应变关系,在已有研究的基础上,本文将对各个表达式在实际运用中的情况进行比较,并且通过实际算例运用这些表达式进行受弯截面弹塑性分析,从而为工程师们在实际应用时提供参考和借鉴。
1 常用混凝土受压应力—应变曲线比较至今已有不少学者提出了多种混凝土受压应力应变曲线,常用的表达式采用两类,一类是采用上升段与下降段采用统一曲线的方程,一类是采用上升段与下降段不一样的方程。
1.1 中国规范我国《混凝土结构设计规范》(GB50010-2010)采用的模式为德国人R üsch1960年提出的二次抛物线加水平直线,如图1-1所示。
上升阶段的应力应变关系式为:)(])(2[02000ε≤εεε-εε⨯σ=σ (1-1)A 点为二次抛物线的顶点,应力为0σ,是压应力的最大值,A 点的压应变为0ε。
应力-应变曲线
应力-应变曲线
四、强度
1.强度是指金属材料抵抗塑性变形和断裂的能力。 2.强度特性指标主要是指屈服强度和抗拉强度。 (1)屈服强度:当材料受外力作用产生0.2%残余变形的应力,作为 该材料的屈服强度。
式中:
——材料屈服时的最小载荷, ;
——试件的原始横截面面积,;—源自屈服强度, 。应力-应变曲线
(4)强化:材料经过屈服点后,其变形抗力增大,这种现象称为强化。
应力-应变曲线
五、塑性
1.塑性:金属材料受力后在断裂之前产生塑性变形的能力。
2.塑性指标
(1)断后伸长率:
式中: ——试件拉断后的长度, ;
——试件的原始长度,
。
(2)断面收缩率:
式中: ——试件的原始横截面面积, mm2 ; ——试件拉断处的横截面面积,mm2 。
图1-6 卸荷曲线
应力-应变曲线
三、弹性
1.弹性的定义:具有弹性变形特性的材料能够发生弹性变形而不发生永久 变形的能力,称为弹性。
2.弹性模量 (1)表示引起单位应变所需的应力的大小。 (2)工程上常用弹性模量作为衡量材料刚度的指标,E越大,刚度越好。 (3)刚度是材料抵抗弹性变形的能力。 (4)材料在一定外力作用下,弹性变形越大,刚度越小,反之,其刚度 越大。 (5)弹性极限是试件在最大弹性变形时材料所承受的应力。
四、强度
(2)屈服:应力没有增加,但试件变形仍自动增长的现象称为屈服。 (3)抗拉强度:材料在断裂前所能承受的最大应力称为抗拉强度。 当应力达到抗拉强度时,试件某一部分的横截面积显著缩小。试件的变形 主要集中在该处,故抗拉强度通常被作为零件因断裂失效的设计依据。
式中: ——材料在屈服阶段后所能抵抗的最大力, ; ——试件的原始横截面面积, ; ——抗拉强度, 。
阐述岩石的应力应变全过程曲线
阐述岩石的应力应变全过程曲线应力-应变全过程曲线是研究岩石力学特性的重要指标之一。
它可以描述岩石在不同应力作用下的应变变化规律,揭示岩石的变形、破裂和失稳等行为。
岩石的应力-应变全过程曲线通常包括弹性阶段、屈服阶段、塑性阶段和破坏阶段。
首先是岩石的弹性阶段。
在这个阶段,岩石在外力作用下发生应变,但在去除外力后,能够完全恢复到初始状态,没有残余应变。
这是因为岩石在弹性阶段内,岩石的分子、原子间只发生了位置的微小位移,没有发生断裂或滑动。
岩石的弹性本性可以用胡克定律来描述,即应力与应变之间存在线性关系。
胡克定律表达为σ = Eε,其中σ为应力,E为弹性模量,ε为应变。
弹性模量是岩石抵抗变形的能力的物理量,它反映了岩石的刚性。
在这个阶段,应力-应变曲线呈现出线性关系,岩石的应力呈现出线性递增的趋势。
随着应力的增加,岩石进入屈服阶段。
在这个阶段,岩石开始发生塑性变形,即应力作用下,岩石发生了不可逆的应变。
当外力减小或去除时,岩石会有残余应变。
在这个阶段,应力-应变曲线的斜率减小,表明岩石的刚性有所降低。
接下来是岩石的塑性阶段。
在这个阶段,岩石的应力继续增加,而应变较为显著。
岩石逐渐失去了弹性,产生了更大的变形。
在这个阶段,岩石的应力-应变曲线呈现出韧性变形的特点,应力增加速率逐渐降低。
最后是岩石的破坏阶段。
当岩石的应力继续增加到一定程度时,岩石无法再承受外力的作用而发生破裂。
在这个阶段,岩石的破裂韧性降低,应力-应变曲线呈现出明显的下降趋势。
岩石的破坏通常伴随着岩石断裂带的形成,断裂带中存在裂纹和剪切面。
岩石的应力-应变全过程曲线对岩石力学性质的研究具有重要的意义。
它可以用来评价岩石的强度、变形能力以及抗破裂能力。
通过分析和比较不同岩石的应力-应变全过程曲线,可以对岩石的力学性质进行定量描述和比较,为地质工程设计和岩石工程地质问题的解决提供依据。
此外,岩石的应力-应变全过程曲线还可以用于岩石的动态力学特性研究,例如岩石的动态强度和岩石的动态断裂特性。
混凝土基本力学性能二
c
fc
混凝土棱柱体抗压强度和峰值应变的比 值,即峰值割线模量(N/mm2)。
αa=a1,规范称之为曲线上升段参数。 物理意义:混凝土的初始切线模量与峰值割线模量之比E0/Ep; 几何意义:曲线的初始斜率和峰点割线斜率之比。 上升段曲线方程为:
x 1
y a x (3 2 a ) x ( a 2) x
x 1
解得:
x y d ( x 1) 2 x
⑷
u 1 (1 2 d 1 4 d ) c 2 d
分析或验算结构构件时,混凝土的单轴压应变不宜超过值εu。
按上述公式计算随混凝土抗压强度而变化的各项参数值,经 整理后如表。 混凝土单轴受压应力-应变曲线的参数值
0 u
x 1
c fc
y 1 (1 x) n y 1
取
c x 0
y
c
fc
曲线方程可改写为 式中各参数都随混凝 土的立方体抗压强度 标准值fcu,k而变化,计 算公式为:
cu 1 x 0
1 n 2 ( f cu 50) ≯2.0 60 0 0.002 0.5( f cu 50) 10 6
≮0.002
≯0.0033
u 0.0033 ( f cu 50) 10 6
上升段:
0
c n c f c [1 (1 ) ] 0
70
C80
60
下降段: 0 u
c fc
50
C60
40
1 n 2 ( f cu 50) ≯2.0 60 0 0.002 0.5( f cu 50) 10 6
⑷
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
混凝土的受压应力-应变曲线方程是其最基本的本构关系, 又是多轴本构模型的基础。在钢筋混凝土结构的非线性分析中, 是不可或缺的物理方程,对计算结果的准确性起决定性作用。
1.3.1 试验方法
棱柱体抗压试验若应用普通液压式材料试验机加载,可获 得应力应变曲线的上升段。但试件在达到最大承载力后急速破 裂,量测不到有效的下降段曲线。
第1章 基本力学性能
1.1 材料组成和材性特点 1.2 抗压强度 1.3 受压应力—应变全曲线 1.4 抗拉强度和变形 1.5 抗剪强度和变形
1.3 受压应力-应变全曲线
混凝土受压应力-应变全曲线包括上升段和下降段,是其力 学性能的全面宏观反应:
◆曲线峰点处的最大应力即棱柱体抗压强度,相应的应变为峰值 应变εp ; ◆曲线的(割线或切线)斜率为其弹性(变形)模量,初始斜率 即初始弹性模量Ec ; ◆下降段表明其峰值应力后的残余强度;曲线的形状和曲线下的 面积反映了其塑性变形的能力,等等。
上升段理论曲线随参数αa的变化: αa>3,曲线局部y>1,
显然违背试验结果; 1.1<αa<1.5,曲线的初始
段(x<0.3)内有拐点,单 曲度不明显,在y≤0.5~0.6范 围内接近一直线;
αa<1.1,上升段曲线上 拐点明显,与混凝土材性不 符。
下降段曲线方程为: αd下降段参数
对参数取αa 和αd 赋予不等的数值,可得变化的理论曲线。
对于曲线的上升段和下降段,有的用统一方程,有的则 给出分段公式。其中比较简单、实用的曲线形式如图。
我国《规范》采用曲线方程为: 上升段曲线方程为:
αa:曲线上升段参数。 物理意义:
何意义:
⑶
曲线的初始斜率和峰点割线斜率之比。
由数学条件2的不等式,可得αa值的范围:
1.3.2 全曲线方程
混凝土受压应力-应变全曲线、及图像化的本构关系,是研 究和分析混凝土结构和构件受理性能的主要变形依据,为此需 要建立相应的数学模型。
将混凝土受压应力-应变全曲线用无量纲坐标表示:
绘制峰点坐标为(1,1) 的标准曲线如图,曲线形状有 一定差别,但具有一致的几何 特性,可用数学条件描述。
原因:试验机的刚度不足。
要获得稳定的应力-应变全曲线,必须控制混凝土试件缓慢 地变形和破坏。有两类试验方法:
①应用电液伺服阀控制的刚性试验机直接进行试件等应变 速度加载;
②在普通液压试验机上附加刚性元件,使试验装置的总体 刚度超过试件下降段的最大线刚度,就可防止混凝土的急速破 坏。
按上述方法实测的混凝土棱柱体受压应力-应变全曲线如图。
其几何特征的数学描述如下: 这些几何特征与混凝土的受压变形和破坏过程(见
前)完全对应.具有明确的物理意义。
下降段曲线可无限延长,收敛 于横坐标轴,但不相交。
为了准确地拟合 混凝土的受压应力应变试验曲线,各国 研究人员提出了多种 数学函数形式的曲线 方程,如:多项式、 指数式、三角函数、 有理分式、分段式等。
