4聚合物的分子量和分子量分布详解
第四章 聚合物的分子量和分子量分布解析

• 4.1.1聚合物分子量的多分散性
–聚合物分子量具有两个特点:
聚合物分子量比低分子大几个数量级,一般在 103 ~107之间。 除了有限的几种蛋白质高分子外,聚合物分子 量是不均一的,具有多分散性。
因此,确切地描述聚合物的分子量应给出给出分子 量的统计平均值和试样的分子量分布。
例如:设聚合物总质量m,总物质的量n,
第i种分子的分子量为Mi,物质的量为ni,质量为 mi在整个试样中的摩尔分数为xi,质量分数wi, 则:
ni n; mi m
i
ni n
xi ;
i
mi m
wi
分子量
间隔不
xi 1;
wi 1
断减小
i
i
0 n(M )dM n, 0 m(M )dM m
0 x(M )dM 1, 0 w(M )dM 1
Schulz-Flory 最可几分布
Schulz分布
Poisson分布
(2)模型分布
Gaussian 分布
Wesslau 对数 正态分布
Schulz-Zimm 分布函数
Tung 分布函数
• 多分散系数:Polydispersity coefficient
Mw 或 MZ
Mn
Mw
α=1,分子呈单分散 (α=1.03~1.05近似为单分散);
– 另一方面,聚合物的分子量和分子量分布又可作为 加工过程中各种工艺条件选择的依据,如加工温度、 成型压力等的确定。
• 4.1聚合物分子量的统计意义
– 4.1.1聚合物分子量的多分散性 – 4.1.2统计平均分子量 – 4.1.3分子量分布宽度 – 4.1.4聚合物的分子量分布函数
第四章 聚合物的分子量和分子量分布

• 4.1聚合物分子量的统计意义
– – – – – – – – – – – 4.1.1聚合物分子量的多分散性 4.1.2统计平均分子量 4.1.3分子量分布宽度 4.1.4聚合物的分子量分布函数 4.2.1端基分析 4.2.2沸点升高和冰点降低(依数性) 4.2.3气相渗透法 4.2.4渗透压法 4.2.5光散射法 4.2.6质谱法 4.2.7黏度法
α=1,分子呈单分散 (α=1.03~1.05近似为单分散); α=2,缩聚产物; α=3~5,自由基产物; α=25~30,有支化(PE)
第二节 聚合物分子量的测定方法
• 绝对法:实验得到的数据可以分别计算出分 子的质量和摩尔质量而不需要有关聚合物结 构的假设; • 等价法:只要知道高分子的化学结构(即端 基结构和每个分子上端基的数目),就可以 通过端基测定计算高分子的摩尔质量; • 相对法:依赖于溶质的化学结构、物理形态 以及溶质-溶剂之间的相互作用。但是,该 法需要用其他绝对法进行校准。
– 按质量的统计平均分子量,定义为:
Mw
2 n M i i
n M
i i
i
i
m M m
i i i i
i
wi M i
i
用连续函数表示:
Mn
M ( M )dM m(M )dM
0 m 0
0
M w ( M )dM
Mw
n M n M
i i i i
2 i
第四章 聚合物的分子量和 分子量分布
聚合物的分子量与分子量分布对其使用 性能和加工性能的影响
– 聚合物的分子量和分子量分布对使用性能,加工性 能有很大影响。如机械强度、韧性以及成型加工过 程都与分子量有关。 – 一般来说材料的性能随着分子量提高而提高,但是 分子量太高,又给加工带来困难。所以选用某种聚 合物进行加工,需先知道其分子量以及分子量分布。 – 另一方面,聚合物的分子量和分子量分布又可作为 加工过程中各种工艺条件选择的依据,如加工温度、 成型压力等的确定。
高分子物理第四章 聚合物的分子量与分子量分布

分子量分布宽度
第四章
聚合物的分子量与分子量分布
分子量分布宽度
分布宽度指数
n M Mn
2
2
n
Mw Mn 1 M n
2
w M Mw
2
M
2 n
2 w
Mz 1 M w
Mw
Mn
Mz
Mw
通过实验分别测定若 干不同浓度溶液的渗 透压π,用π/c对c作图 将得到一条直线,直 线的截距可以求得分 子量 M ,斜率可以求 得A2
第四章
聚合物的分子量与分子量分布
例
某种聚合物溶解于两种溶剂 A和B中,渗透压π和浓度c的关系
如图所示: (1)当浓度c→0时,从纵轴上的截距能得到什么? (2)从曲线A的初始直线段的斜率能得到什么? (3)B是良溶剂还是劣溶剂?
w
i
i
1
mi ni M i
分子量的 离散分布
第四章
聚合物的分子量与分子量分布
聚合物的分子量
间断函数变为连续函数,则得到
分子量的 微分分布
第四章
聚合物的分子量与分子量分布
聚合物的分子量
聚合物分子量积分分布函数
分子量的 积分分布
第四章
聚合物的分子量与分子量分布
聚合物的分子量
微分分布函数与积分分布函数之间的关系
大粒子Zimm图
第四章
聚合物的分子量与分子量分布
聚合物分子量的测定方法
粘度法-粘均分子量
液体在流动时,在其分子间产生内摩擦的性质,称为液体的黏 性,粘度是表征液体流动时受内摩擦的大小。 高分子的 分子量影响 其在溶液中 的形态,进 而会影响其 溶液粘度。 第四章 聚合物的分子量与分子量分布
第四章聚合物的分子量和分子量分布解读

M
n
a1 b
1 1 b
M
w
a
1
b
1
1 b
M
z
a1
b
1
2 b
d.Scholz-Zimm分布
wM
yh
rh
1
1
M
h
e
ym
四.分级数据与平均分子量
若原试样的归一化重量分布 wM
0 wM dM 1
M
2
e
bMdM
b2
2 b3
2 b
M w2 Mn
,为定值。
wM 的峰位分子量:
dwM dM
b2
e bM
bM e bM
b2 e bM 1 bM
从
d
wM
dM
0
:
wM 的峰位分子量为:
1 b
M
n
b.对数正态分布函数
wM 1
M
z
1
N
i
M
i
4
N
i
M
3 i
W
i
M
i
3
W
i
M
i
2
粘均分子量:
M
W
i
M
i
1
这里的是指Mark-Houvink方程:
K M
中的 值。当 1 时,
M M w
0.5 1
平均分子量的通式:
聚合物的分子量和分子量分布习题及解答
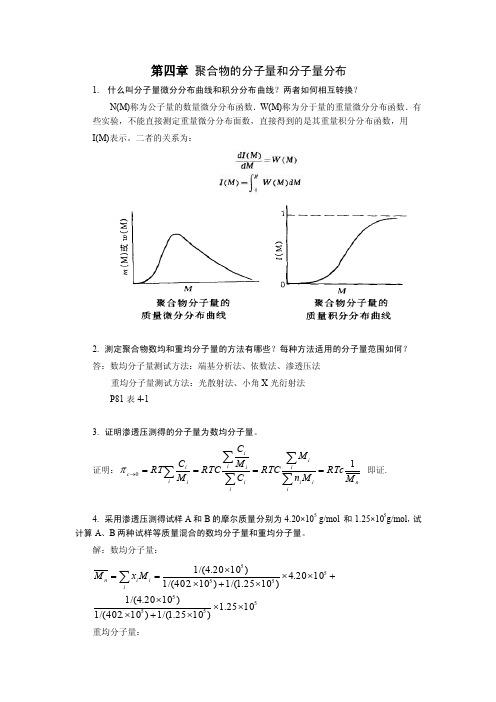
第四章 聚合物的分子量和分子量分布1. 什么叫分子量微分分布曲线和积分分布曲线?两者如何相互转换?N(M)称为公子量的数量微分分布函数.W(M)称为分于量的重量微分分布函数.有些实验,不能直接测定重量微分分布面数,直接得到的是其重量积分分布函数,用 I(M)表示。
二者的关系为:2. 测定聚合物数均和重均分子量的方法有哪些?每种方法适用的分子量范围如何? 答:数均分子量测试方法:端基分析法、依数法、渗透压法重均分子量测试方法:光散射法、小角X 光衍射法P81表4-13. 证明渗透压测得的分子量为数均分子量。
证明:n ii i i i i i i i i i ii c M RTc M n M RTC C M C RTC M C RT 10====∑∑∑∑∑→π 即证.4. 采用渗透压测得试样A 和B 的摩尔质量分别为4.20×105 g/mol 和1.25×105g/mol ,试计算A 、B 两种试样等质量混合的数均分子量和重均分子量。
解:数均分子量:555555551025.1)1025.1/(1)10.402/(1)1020.4/(11020.4)1025.1/(1)10.402/(1)1020.4/(1⨯⨯⨯+⨯⨯+⨯⨯⨯+⨯⨯==∑ii i n M x M重均分子量:55510725.21025.15.01020.45.0⨯=⨯⨯+⨯⨯==∑i ii M M ωω5.35℃时,,环已烷为聚苯乙烯(无规立构)的θ溶剂。
现将300mg 聚苯已烯(ρ=1.05 g/cm 3,n M =1.5×105)于 35℃溶于环己烷中,试计算:(1)第二维利系数A z ;(2)溶液的渗透压。
6.某聚苯乙烯试样经分级后得到5个级分。
用光散射法测定了各级分的重均分子量,用粘度法(22℃、二氯乙烷溶剂)测定了各级分的特性粘度,结果如下所示: 试计算Mark -Houwink 方程[η]=KM α中的两个参数K 和α。
高分子物理 第4章 聚合物的分子量和分子量分布

第四章
聚合物的分子量及分布是聚合物最基本的参数之一。 聚合物的许多性质与分子量有关: 如: 熔体粘度 弹性模量 耐热性 抗拉强度 冲击强度 成型性
“高分子溶液 ”是测定聚合物分子量和分子量分布重 要 的理论基础。
化学化工学院
第四章
高聚物性质与分子量及其分布的关系 1. 拉伸强度和冲击强度
与样品中低分子量部分有较大关系
第四章
则以上的量之间存在下列关系:
ni n 总物质的量
i
m
i
i
m 总质量
ni Xi n
摩尔分数
mi wi m
质量分数
X
i
i
1
w
i
i
1
化学化工学院
第四章
n(M)或x(M)
M
图4-1 聚合物分子量的 数量微分分布曲线
m(M)或w(M)
M
图4-2 聚合物分子量的 质量微分分布曲线
第四章
平均分子量 方法
佛点升高,冰点降低, 气相渗透,等温蒸馏
类型
分子量范围/(g/mol)
Mn
A
E A
<104
102~3104 5103~106
Mn Mn
Mn
端基分析 膜渗透法
电子显微镜
平衡沉降 光散射法
密度梯度中的平衡沉降
A
A A
>5105
102~106 >102
Mw
Mw Mw
A
A A
>5104
★ 第 四 章
第二节 聚合物分子量的测定方法
一、端基分析
1)链末端带有化学定量分析可确定的基团; 2)酸碱滴定法测定末端基团的数目,高分子链的数目; 3)端基分析法计算聚合物数均分子量。
聚合物的分子量及其分布.

Mw / Mn
分子量分布情况 均一分布 分布较窄 分布较宽
• 分子量分布是影响聚合物性能的因素之一 分子量过高 分子量低 聚合物强度增加 聚合物强度降低 加工成型时塑化困难 易于加工
不同用途的聚合物应有其合适的分子量分布
M = Wi M ia
1
a
Ni M Ni M i
M
a 1 i
1
a
• 其中α 为常数,若α =1,则 = ,一 般情况下,0.5<α <0.9。相对而言,粘均分子 量较接近质均分子量。
MW
例:假定某聚合物试样中含有相对分子质量分别为10000和 100000。 (1)、以等摩尔比相混; (2)、以1%和99%的质量分数相混。 、 试分别求混合物的、。 HI M
W Ni M i Mn N Ni
(2)质均分子量
• 对聚合物的稀溶液用 光散射方法测定的是 质均分子量,等于分 子量乘上相应质量分 数的加合。
M W= Wi M i
i 1
Wi M i W
i
2 N M i i
N M
i
i
(3)粘均分子量
• 用聚合物稀溶液的特性粘度测定得到。
Mn n( M 10 M 20 ) Xn *
Mn n(M10 M 20 ) DP* (M10 M 20 ) DP* M0
①对一种单体均聚合
结构单元=重复单元
Xn= n =DP
Mn n M 0 Xn.M 0 或 Mn n M 0 DP M 0
第四章 聚合物分子量及分子量分布

毛细管粘度计测定聚合物粘度
泊肃叶方程:
PR 4t
8lV
m
t 、 t0 时刻: r ( At B / t ) 0 0 0 0
稀溶液情况下:
( At B / t )
当液体的流速较大时:
简化为:
ghR 4 t
8lV
V 8lt
乌式粘度计
r
t t0
无规线团散射公式:
1 cos 2 Kc 1 8 2 h (1 sin 2 ......) 2 A2 c 2 9 ( ) 2 2 R M
实验测定值进一步修订:
2
1 cos 2 Kc 1 8 2 h (1 sin 2 ......) ) 2 A2 c 2sin R M 9 ( ) 2 2
n2 ( M M n ) 2 n M n (d 1)
2 w w 2 n 2 w
( M M ) M
2
(d 1)
8
2 2 >0) 多分散试样,d>1或 n >0 ( w
7
2 单分散试样,d=1或 n2 w 0
第二节
合成高聚物中d的典型区间
粘度比(相对粘度): r
-1、面积为1厘米2
时两层液体间的内摩擦力,称为液体的粘度
牛顿流体:粘度不随剪切力和剪切速率而改变的液体
r 随溶液浓度的增加而增加
粘度相对增量(增比粘度): sp
r 0
高分子稀溶液为牛顿流体(理想状况)
粘度随剪切应力变化而变化 非牛顿流体 粘度与时间有关 ……
高聚物 阴离子聚合“活性”聚合物 加成聚合物(双基终止) 加成聚合物(歧化终止)或缩聚物 高转化率烯类聚合物 自动加速生成的聚合物 配位聚合物 支化聚合物 d 1.01~1.05 1.5 2.0 2~ 5 5~10 8~30 20~50
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Characteristics of polymer molecular weights
高分子的分子量的特点
• 分子量非常大,范围 从10,000到1,000,000 g/mol, 甚至更大。
• 小分子的分子量是固定的,除了有限的几种蛋白质 高分子外,聚合物分子量是不固定的,分子量的大 小主要依赖于聚合方法。
高分子专业:
金属专业:
平均每个专业多少人?
210人
60人
无机非金属专业: 30人
210 60 30(总人数) 100 111 (专业个数)
Number average 数均
210 * 210 210 60 30
60 30 * 60 * 30 210 60 30 210 60 30 Weight average 重均
mi ni M i
数均分子量:按物 质的量统计平均分 子量 重均分子量:按质 量统计平均分子量
Mn
n M n
i i i i
i
Ni M i
i
Mw
mi M i
i
m
i
2 n M i i
i
n M
i i
i
i
Wi M i
i
Method of weighting 权重法
• 大部分高分子的分子量具有多分散性,可以看做包 含很多组分的混合物。
• 分子量分布是聚合物最基本的结构参数之一,它对于 高分子材料加工条件的控制均有重要意义: • ①高分子材料加工条件的控制
如:熔体强度与弹性与样品中高分子量部分有较大关系
• ②高分子材料使用性质
如:拉伸强度和冲击强度与样品中低分子量部分有较大关系
Mn
i
20
10
10 30 10 20 10 10 104 20 104 10 10 10
10 302 10 202 10 102 Mw 104 23.3 104 ni M i 10 30 10 20 10 10
Z均分子量:按Z量的统计平均分子量
Z量的定义:级分重量单根分子量,即
Z i Wi M i
Mz
3 N M i i 2 N M i i i i
2 w M i i
w M
i i
i
i
数均:
-点
重均:
-面
Z均:
-体
Example:
ni
nM n
i i
10
10
10
Mi(×10-4) 30
10 303 10 203 10 103 4 4 Mz 10 25.7 10 2 2 2 2 n M 10 30 10 20 10 10 i i
3 n M i i
2 n M i i
黏均分子量:用稀溶液黏度法测得的平均分子量
M
N iM i i N iM i i
涂料中主要用作添加剂;
CH3 Si CH3 O
n
硅油——分子量很低的聚硅氧烷,是粘度从0.65×10-3~1000Pa·s的液体,
硅树脂——分子量为700~5000,具有分支结构和多羟基的聚硅氧烷,可
进一步固化成立体网状结构,是涂料中重要的成膜物质。
硅橡胶——平均相对分子质量在40万~80万的高相对分子质量线形聚硅氧
Polymer Physics
高分子物理
4 Polymer molecular weights and molecular weight distribution
高分子的分子量和 分子量分布
高分子与小分子性能比较
Polymer
高分子
Liquid, solid
Monomer
小分子
Gas, liquid, solid
i i i i i i i
i
M wi M i i
• ③溶液性质
如:溶液粘度与样品中高分子量部分有较大关系
• ④聚合反应机理
4.1 聚合物分子量的统计意义
4.1.1 聚合物分子量的多分散性 聚合物分子量特点:
分子链个数
1)分子量大;
2)多分散性。
以间断函数表示
分子量
以连续函数表示
M
0
n( M )dM n
m( M )dM m
n(M)为聚合物分子量按数量的分布函数
特点:高强度、高 模量、强的韧性, 强度与木材、水泥 甚至钢材可比,韧 性和弹性不亚于棉、 麻、毛和天然橡胶
特点:机械强度 和韧性很低,韧 性差,工程使用 价值不高
分子量达到一定值后(临界分子量)高分子材料才具有机械强度 m 极性聚合物 m 非极性聚合物 l 临界聚合度40 临界聚合度80
Strength
1
1/
Mn
n M n
i i i i
i
m mi mi M i i Mi i
i
m
i
1 wi / M i
i
M
w i 分子量可以看作 = -1粘均分子量的特例
Mw
m M w M m
Polar
Nonpolar
分子量过高,强度达到极限,但熔体 粘度过大,加工困难
Molecular Weight 纤维 分子量分布宜窄 塑料与橡胶 分子量分布宜适当放宽,以提高加工性能;
大分子量组分提高强度,小分子量组分起增塑作用
分子量不同时应用不同
聚二甲基硅氧烷 Polydimethyl silioxane PDMS
样品a:可纺性很差; 样品b:有所改善;
5 10 15 M×10-4
样品c:由于分子量15~20万的大分子所占的比例较大, 可纺性很好。
4.1.2 统计平均分子量
假定某高分子试样中含有若干种分子量不相等的分子, 该种分子的总质量为m,总摩尔数为n,种类序数用i表示, 第i种分子的质量为mi ,摩尔数为ni,分子量为Mi ,在整 个试样中的质量分数为Wi,摩尔分数为Ni。
m(M)为聚合物分子量按质量的分布函数
0
0
x( M )dM 1
w( M )dM 1
x(M)为聚合物分子量按数量分数的分布函数,或称 归一化数量分布函数。
0
w(M)为聚合物分子量按质量分数的分布函数,或称 归一化质量分布函数。
聚丙烯腈试样的纺丝性能
(三种Mw相同的试样)
M(W)
a
c b
