探索数学实验 1
北师大版数学四年级上册 数学好玩(1) 滴水实验

一个没有拧紧的水龙头, 一年会滴多少水呢?
设计滴水实验,推算出一个没拧紧的水龙头 一年大约会浪费多少水。
活设动计任方务案 1.设计什么实验可以解决这个问题呢?
我想用盛满水的纸杯扎个眼 代替水龙头,看一看这个纸 杯平均1分漏掉多少水。
再算一算1时、1天、 1年……
活设动计任方务案 2.小组讨论,设计具体的实验方案。
数学好玩
第1课时 滴水实验
水资源是一种可再生资源,但并不是取之不尽 用之不竭的。预计到2025年,世界上将会有30 亿人面临缺水,40个国家和地区淡水严重不足, 水资源短缺已经成为制约经济发展和人们生产 生活的重要因素。
水龙头在滴水,多浪费啊! 我们用完水后要随手关紧 水龙头!
活活动动任任务
做个实验,试一试。
活交动流任反务思 3.读一读,想一想。
节约
浪费
(1)读了上面的资料,你有什么感想?
(2)请留心观察生活,在你身边有哪些浪费水的现象? 你知道哪些节约用水的好方法?
活交动流任反务思 3.读一读,想一想。
节约
浪费
(1)节约用水,从我做起,从节约每一滴水做起。
(2)洗菜的水、养鱼的水可以用来浇花;洗衣服水 可以用来冲马桶。
活自动我任评务价 在这次活动中,我的表现是(请把每项 后面的☆涂上颜色,涂满5个为做得最好的):
设计实验方案合理可行。 得到的实验数据合理可信。 小组分工合理,积极参与活动。 能用得到的数据解决问题。 能积极与同伴进行交流。
这节课有什么收获呢? 节约用水,从我做起,从一点一滴做起!
观察自己家的用水情况,看看平时父母 在生活中是怎样节约用水的。收集起来和大 家交流,并把好的方法告诉自己的家长。
我们组实验了两次才成功。 可以多测量几次,然后算平均数。
数学建模实验雨中漫步1

数学实验作业雨中漫步系部:数学系专业:s10数学教育学号:103103011013姓名:张鹏飞实验目的:1.生活中的我们常常会遇到下雨而没带雨具的时刻,我们在那时会有很多选择,其中之一就是淋雨,往往好多人会在雨中快走或奔跑而使自己身体淋雨量最小化,但往往很多人会感觉到淋雨量并不会因为快走或奔跑而减少多少,反而有时候淋雨量倒有所增加,淋雨量和速度等有关参数的关系如何,是否人走得越快雨淋得越少2.运用matlab软件实验内容:给定的降雨条件下,分别建立相应的数学模型,分析人体在雨中行走时淋雨多少与行走速度、降雨方向等因素的关系。
其中文中所涉及到的降雨量是指从天空降落到地面上的雨水,未经蒸发、渗透、流失而在水面上积聚的水层深度,它可以直观地表示降雨的多少。
淋雨量,是指人在雨中行走时全身所接收到得雨的体积,可表示为单位时间单位面积上淋雨的多少与接收雨的面积和淋雨时间的乘积。
1,设降雨淋遍全身不考虑雨的方向,经简化假设得人淋雨面积为前后左右及头顶面积之和。
2,雨迎面吹来,雨线方向与行走方向在同一平面,人淋雨面积为前方和头顶面积之和。
因各个方向上降雨速度分量不同,故分别计算头顶和前方的淋雨量后相加即为总的淋雨量。
据此可列出总淋雨量v时,淋W与行走速度v之间的函数关系。
分析表明当行走速度为m ax雨量最少。
3,雨从背面吹来,雨线与行走方向在同一平面内,人淋雨量与人和雨相对速度有关。
列出函数关系式分析并求解。
实验准备: matlab软件绘图,从网上查找各种资料a---长方体的长单位:米b---长方体的宽单位:米c---长方体的厚度单位:米Q---淋雨量单位:升v---人行走的速度单位:米每秒D---路程单位:米I---降雨强度单位:厘米每小时P---雨滴的密度单位:u---雨滴下落的速度单位:米每秒θ---雨迎面吹来时与人体的夹角α---与从后面吹来与人体的夹角实验步骤:在给定的降雨条件下,分别建立相应的数学模型,分析人体在雨中行走时淋雨多少与行走速度、降雨方向等因素的关系。
数学实验报告 (1)

(1)参数方程:z=2^2^/2^2^sin y x y x ++(-8<=x<=8,-8<=y<=8) (2)程序:[X,Y]=meshgrid(-8::8);r=sqrt(x.^2+y.^2)+eps;Z=sin(r)./r;Mesh(x,y,z)Axis square(3)程序的输出结果:3:球面,椭球面,双叶双曲面,单叶双曲面1球面: (4):参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕcos *sin *sin *cos *sin *R z R y R x 0π<=θ<2* 0<=ϕ<π (5)程序:u=[0:pi/60:2*pi];v=[0:pi/60:pi];[U,V]=meshgrid(u,v);R=3;X=R*sin(v).*cos(u);Y=R*sin(v).*sin(u);Z=R*cos(v);Surf(x,y,z);axis equal;(3)程序输出结果:2椭球面: (1)参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕcos *sin *sin *cos *sin *c z b y a x 0<=θ<2*π 0<=ϕ<=π (2)程序:ezsurf(‘3*sin(u)*cos(v) ,’3*sin(u)*sin(v)’,’1*cos(u)’,[0,pi,0,2*pi]);(3)程序的输出结果:3单叶双曲面: (1)参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕtan sin *sec *cos *sec *z a y a x 0<=θ<2*π -π/2<ϕ<π/2 (2)程序:ezsurf(‘3*sec(u)*cos(v),’3*sec(u)*sin(v)’,’5*tan(u)’,[-pi/2,pi/2,0,2*pi]);axis auto(3)输出程序结果:4双叶双曲面: (1)参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕsec *sin *tan *cos *tan *c z b y a x 0<=θ<2*π -π<ϕ<3*π/2,ϕ≠π/2(2)程序:ezsurf(‘3*tan(u)*cos(v)’,’3*tan(u)*sin(v)’,’5*sec(u)’,[-pi/2,3*pi/2,0,2*pi]);axis auto(4) (3)输出程序结果:抛物螺线: (1)参数方程:⎪⎩⎪⎨⎧===2^*sin **cos **t c z t t b y t t a x 0<T<+∞ (2)程序:ezplot3(‘2*t*cos(t)’,’2*t*sin(t)’,’t.^2/3’,[0,50]);(3)输出程序结果:(5)马鞍面: (1)参数方程:z=x^2/9-y^2/4 (-25<=x<=25,-25<=y<=25)(2)程序:[X,Y]=meshgrid(-25:1:25);Z=X.^2/9-Y.^2/4;Surf(X,Y,Z)Title(‘马鞍面’)grid off(3)输出程序结果:(6)黎曼函数:(1)程序:n=100;x=[];y=[];k=1;for q=2:nfor p=1:q-1if gcd(q,p)==1 %利用函数gcd(m,n)可求m和n的最大公约数x(k)=p/q;y(k)=1/q;k=k+1;endendendplot(x,y,’.b’); axis([0,1,0,1])(2)程序输出结果:。
数学实验中班幼儿通过实验探索数学的奥秘

数学实验中班幼儿通过实验探索数学的奥秘在幼儿教育中,数学教学一直是一个重要的课程内容。
而为了提高幼儿对数学的兴趣和理解能力,教师们不断探索着不同的教学方法和实践活动。
其中,数学实验被广泛运用于幼儿园的教学中。
本文将详细探讨数学实验在幼儿教育中的重要性,并通过具体实例,说明幼儿通过实验可以深入理解数学的奥秘。
首先,数学实验作为一种活动形式,能够激发幼儿的探索欲望和好奇心。
实验本身就是一种发现和探索的过程,通过自己动手去做实验,幼儿能够亲身体验数学的乐趣和神奇之处,从而培养对数学知识的兴趣。
例如,在幼儿园的数学活动中,可以设计一个简单的实验,让幼儿用水果进行数数或者测量,他们会通过实际操作感受到数字、重量、大小等数学概念,从而激发他们对数学的兴趣。
其次,数学实验能够帮助幼儿掌握数学知识和解决问题的能力。
通过实践操作,幼儿能够深入理解数学中的抽象概念和运算规律。
例如,在幼儿园的几何教学中,可以设计一个实验,让幼儿利用积木搭建不同形状的房子,并观察其特点。
通过此实验,幼儿可以亲身体会到不同形状的房子有不同的特点,从而理解几何学中形状的定义,并能够运用这些知识解决与形状相关的问题。
此外,数学实验还能够培养幼儿的观察力和实践能力。
在实验中,幼儿需要通过观察和实践来获取数据和结论。
而培养幼儿的观察力和实践能力是数学教育的重要目标之一。
例如,在幼儿园的量的教学中,可以设计一个实验,让幼儿通过多次实验,观察和比较容器中液体的多少,并思考导致液体多少变化的因素。
通过这个实验,幼儿可以培养观察和实践的能力,同时也能够对容量的概念有更深入的理解。
最后,数学实验有助于培养幼儿的团队合作和创造能力。
在实验中,幼儿需要与小组成员一起合作,共同完成实验任务。
通过合作,幼儿可以学会相互配合和倾听他人的意见,培养良好的团队合作意识。
而在实验中,幼儿还能够发挥自己的创造力,尝试不同的方法和思路,从而解决实验中遇到的问题。
综上所述,数学实验作为一种重要的幼儿教学方法,对于幼儿的数学学习有着积极的影响。
数学实验1-3章习题答案
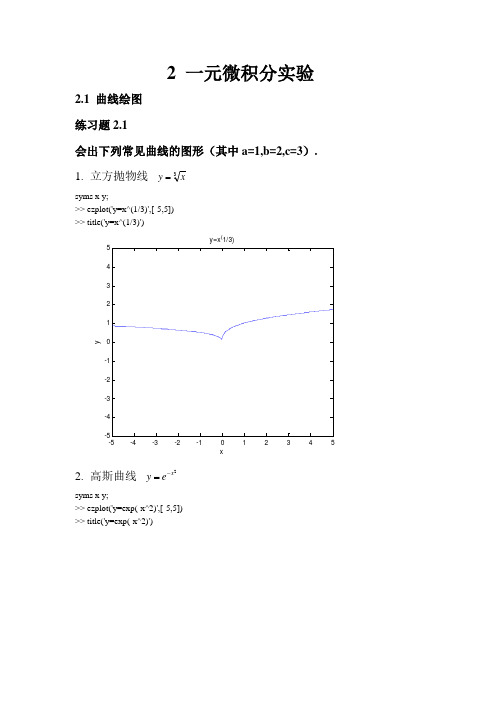
ans =
18.3287
函数的单调区间为:
(1)单调递增区间:-2<x<-1.5326 -0.7315<x<0以及1.5951<x<2;
(2)单调递减区间:-1.5326<x<-0.7315以及0<x<1.5951.
(2)
函数的图形为:
clear
>> fplot('3*x^5-20*x^3+10',[-3,3])
ans =
-3
最值2:
x=1:0.1:3;
>> y=3.*x.^5-20.*x.^3+10;
>> [m k]=max(y)
m =
199
k =
21
>> x(k)
ans =
3
驻点1及相应的二阶导数值:
clear
>> syms x y
>> y=3*x^5-20*x^3+10;
>> yxx=diff(y,x,2);
>> grid on
f=inline('100*acos(1-1/200*(r^2))+r^2*acos(1/20*r)-10*sqrt(r^2-1/400*r^4)-50*pi','r');
>> y=fzero(f,12)
y =
11.5873
3.求解下列非线性方程组在远点附近的根:
clear
>> syms x y z
>> [x y z]=solve('9*x^2+36*y^2+4*z^2-36','x^2-2*y^2-20*z','16*x-x^3-2*y^2-16*z^2',x,y,z)
数学好玩 第1课时 滴水实验(Word教案)2023-2024学年四年级数学上册同步备课(北师大版)

数学好玩第1课时滴水实验(Word教案)2023-2024学年四年级数学上册同步备课(北师大版)一、教学目标1. 让学生通过观察和操作,理解滴水实验的基本原理,感受数学与生活的紧密联系。
2. 培养学生的观察能力、动手操作能力和逻辑思维能力。
3. 引导学生运用数学知识解决实际问题,增强学生的数学应用意识。
二、教学内容1. 滴水实验的基本原理和操作方法2. 通过滴水实验,认识时间和速度的关系3. 利用滴水实验解决实际问题三、教学重难点1. 教学重点:滴水实验的基本原理和操作方法,时间和速度的关系2. 教学难点:利用滴水实验解决实际问题四、教学准备1. 教具:滴水实验装置、计时器、尺子、水杯等2. 学具:滴水实验装置、计时器、尺子、水杯等五、教学过程1. 导入新课通过提问方式引导学生回顾上一节课的内容,引出本节课的主题——滴水实验。
2. 探究活动(1)介绍滴水实验装置,引导学生观察和操作,了解滴水实验的基本原理。
(2)学生分组进行滴水实验,记录实验数据,如滴水时间、水滴下落的高度等。
(3)分析实验数据,引导学生发现时间和速度的关系。
3. 拓展应用(1)引导学生运用滴水实验的知识,解决实际问题,如计算物体下落的高度、预测物体落地的时间等。
(2)学生分组讨论,分享解决问题的方法和结果。
4. 总结反馈(1)教师引导学生总结本节课的学习内容,梳理滴水实验的基本原理和操作方法。
(2)学生分享自己的学习收获和感悟。
六、课后作业1. 完成课后练习题,巩固滴水实验的知识。
2. 尝试运用滴水实验的知识解决生活中的实际问题,并记录下来。
七、板书设计1. 板书滴水实验的基本原理和操作方法。
2. 板书时间和速度的关系。
八、教学反思1. 本节课的教学目标是否达到,学生的参与度和学习效果如何。
2. 教学过程中的重难点是否讲解清楚,学生是否掌握。
3. 教学方法是否得当,是否有利于培养学生的观察能力、动手操作能力和逻辑思维能力。
4. 课后作业的设置是否合理,能否帮助学生巩固所学知识。
幼儿大班数学教案:探索与实验

幼儿大班数学教案:探索与实验作为幼儿教育的一部分,数学教育在幼儿园中也扮演着非常重要的角色。
幼儿期是儿童认知和思维发展中的关键时期,儿童的数学学习也开始呈现出越来越明显的特点。
为了培养幼儿趣味盎然的数学学习兴趣和认知能力,许多幼儿教育者将数学教育视为幼儿园教育的核心部分。
本文将以数字和形状探索的实验性学习为例,探讨一种基于幼儿探索和实验,以强化幼儿数学学习兴趣为目的的数学教育的教案设计。
一、引言幼儿时期,孩子们的认知和学习能力处于发展的初级阶段,数学教育应尽可能考虑到幼儿认知和思维发展的趋势。
在这个阶段,幼儿的数学概念相对较简单,我们可以利用他们的天性去发掘、探索和理解数学知识。
幼儿课程的时间较短,需要让幼儿感受到数学学习的乐趣。
我们提倡以实验和探索为核心的数学教育,这种方法能够刺激幼儿的好奇心和求知欲,激发幼儿对数学的兴趣。
实验就是为了寻求新的知识和策略,而探索则是为了发现和认识新的领域和结构。
在这种学习环境中,幼儿们会发现无限的施展空间,并能通过“玩”来获得有趣的经验和知识。
二、教案的目标本教案的目标是:通过实验和探索,激发幼儿学习数学的兴趣,帮助幼儿掌握数字和形状的概念,培养他们的数学思维和判断力,并增强幼儿的观察能力、记忆力和空间想象力。
三、教学计划3.1 活动介绍:数字和形状探索实验这个活动的主要目的是让幼儿们通过实验和探索,深化他们对数字和形状的认知。
3.2 教学目标1. 培养幼儿的思维能力和掌握数字和形状的概念。
2. 增强幼儿的观察能力。
3. 培养幼儿判断和推理能力。
4. 增强幼儿的空间想象力。
5. 学会用简单的方式对数字进行加减法运算。
3.3 教学准备材料:彩色图形卡片,数字卡片,纸板,笔,彩色计数杆,同形状不同颜色的积木3.4 活动步骤步骤一:认识数字教师将数字卡片放在地上,让幼儿用脚或手指指向不同的数字,与教师一同朗读出来。
幼儿们可以在教师的帮助下,制定数字的顺序和大小,各自试图说出自己能说出的最大或最小的数字,以加强记忆与理解数字的概念。
小学生数学实验100例

小学生数学实验100例第1篇:我的数学小实验的日记今天中午,为了能把筷子体积测得更准确,我叫爸爸从化学室拿了一个细长的量筒,刻度单位更小,每个单位只有1立方厘米。
此时,我似乎感觉到了胜利在向我招手,真可谓万事具备,只差动手实验了。
首先,我用铅笔在一次筷子上划了一道分界线,将筷子平均分成两段,并用水浸泡,以免筷子在测定过程中洗水。
随后,将筷子入量筒中,并用滴管将水滴入量筒中,让量筒内的水涨到筷子的分界线上,记下量筒内的水位刻度(38毫升)后,将筷子从量筒内取出,再记下量筒内的水位刻度(34.5毫升),前后两次水位刻度之差就是这一部分筷子的体积,即3.5立方厘米。
用同样的方法,我又测量了筷子另一部分的体积是5立方厘米,两次测定结果相加得到这双筷子的体积为8.5立方厘米。
当我得到这个结果时,我兴奋地叫了,此时的我是多么自豪、多么骄傲啊!接着,我又按每人一天使用3双计算出了我们学校(1500人)及全国(12亿)一年消耗的一次*筷子量,分别是13.96立方米和11169000立方米。
结果使我大吃一惊,每年竟有这么多的木料做成一次筷子被浪费了,真是太可惜!在此,我呼吁在校的同学,不!是全国,也不!应该是全世界的每个人都不要再使用一次筷子了,只有这样,才能保护好我们的森林资源,使我们共有的地球环境更加美好,让地球上的每一个人呼吸到干净、清新的空气。
第2篇:我的小实验数学日记下午放学时,班主任老师给我们布置了一道家庭作业,要求大家想办法测算一次筷子的体积,并用数学日记的形式将测算过程记录下来。
这道家庭作业,表面上是一次数学实践活动,实际可能寓意更深,因为一次筷子的使用与环保有关,一回到家,我就静静地坐在书桌前思考这个问题。
一次*筷子的形状是一个不规则的立体图形,怎样才能测算出它的体积呢?我思来想去,一会儿抓耳挠腮,一会儿摇,终于,有了一点眉目。
我可以将一次筷子放入装满水的容器中,这样容器中的水就会溢出来,溢出水的多少不就是筷子的体积吗?可是筷子比水轻,会浮在水面上,又该怎么办呢?可不可以用石头或胶布之类的东西将筷子固定住呢?我想应该是可以的,但这些办法测定起来又都太麻烦了,要是有更简便的方法该多好啊!经过冥思苦想,我终于自豪的笑了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
非线性迭代一、实验背景与实验目的迭代是数学研究中的一个非常重要的工具,通过函数或向量函数由初始结点生成迭代结点列,也可通过函数或向量函数由初值(向量)生成迭代数列或向量列。
蛛网图也是一个有用的数学工具,可以帮助理解通过一元函数由初值生成的迭代数列的敛散性,也帮助理解平衡点(两平面曲线交点)的稳定性。
本实验在Mathematica 平台上首先利用蛛网图和迭代数列研究不动点的类型;其次通过蛛网图和迭代数列研究Logistic 映射,探索周期点的性质、认识混沌现象;第三通过迭代数列或向量列求解方程(组)而寻求有效的求解方法;最后,利用结点迭代探索分形的性质。
二、实验材料2.1迭代序列与不动点给定实数域上光滑的实值函数)(x f 以及初值0x ,定义数列)(1n n x f x =+, ,2,1,0=n (2.2.1)}{n x 称为)(x f 的一个迭代序列。
函数的迭代是数学研究中的一个非常重要的思想工具,利用迭代序列可以研究函数)(x f 的不动点。
对函数的迭代过程,我们可以用几何图象来直观地显示它——“蜘蛛网”。
运行下列Mathematica 程序:Clear[f]f[x_] := (25*x - 85)/(x + 3); (实验时需改变函数) Solve[f[x]==x , x] (求出函数的不动点)g1=Plot[f[x], {x, -10, 20}, PlotStyle -> RGBColor[1, 0, 0], DisplayFunction -> Identity];g2=Plot[x, {x, -10, 10}, PlotStyle -> RGBColor[0, 1, 0], DisplayFunction -> Identity]; x0=5.5; r = {};r0=Graphics[{RGBColor[0, 0, 1], Line[{{x0, 0}, {x0, x0}}]}]; For[i = 1, i <= 100, i++,r=Append[r, Graphics[{RGBColor[0, 0, 1], Line[{{x0, x0},{x0, f[x0]}, {f[x0], f[x0]}}] }]]; x0=f[x0] ];Show[g1, g2, r, r0, PlotRange -> {-1, 20}, (PlotRange 控制图形上下范围) DisplayFunction -> $DisplayFunction] x[0]=x0;x[i_]:=f[x[i-1]]; (定义序列) t=Table[x[i],{i,1,10}]//N ListPlot[t] (散点图)观察蜘蛛网通过改变初值,你能得出什么结论?如果只需迭代n 次产生相应的序列,用下列Mathematica 程序: Iterate[f_,x0_,n_Integer]:=Module[{ t={},temp= x0},AppendTo[t,temp]; For[i=1,i <= n, i++,temp= f[temp]; AppendTo[t,temp]]; tf[x_]:= (x+ 2/x)/2; Iterate[f,0.7,10]设()x f 是一个定义在实数域上的实值函数,如果存在u 使得()u u f =,则称u 为()x f 的不动点。
我们用u u →表示这件事。
如果所有附近的点在选代过程中都趋向于某个不动点,则该不动点称为吸引点,有时也称该不动点是稳定的。
如果所有附近的点在选代过程中都远离它而去,则该不动点称为排斥点,有时也称该不动点是不稳定的。
如果21)(u u f =,32)(u u f =,…,1)(u u f k =且k j uu ji ,,2,1,=≠,则ku u u ,,,21 形成一个k 循环,用121u u u u k →→→→ 记这个事实。
1u 称为一个k 周期点,k u u u ,,,21 称为一个周期轨道。
显然,不动点就是周期为1的周期点。
类似于不动点,如果所有附近的点在迭代过程中都趋向于某个周期点,则该周期点称为吸引点;如果所有附近的点在迭代过程中都远离它而去,则该周期点称为排斥点。
如果点u 最终落于某个循环之中,则称它是一个预周期点。
例如,l 是1)(2-=x x f 的预周期点。
三、实验方案3.1迭代序列与不动点首先对函数38525+-=x x y 研究不动点,需要 (1)对Plot 中{x,-10,20}可改为{x,-50,50};对PlotRange 中{ -1,20}可改为{-50,50};(2)x0=5.5中5.5分别改为-30,-20,-5,-3.001,-2.999,-1,0,1,1.5,2.5,4,4.5,4.9,4.999,5,5.1,5.001,6,10,16,17,18,20,30;(3)对t=Table[x[i],{i,1,10}]//N 中10分别改为100,200,500,1000; 运行程序后观察蛛网图与散点图!一看数列是否收敛?如收敛,极限是多少?收敛速度是快是慢?二看蛛网图中的轨道是否趋于平衡点?与平衡点处曲线的斜率有没有关系?三看初值对结果有没有影响?其次,分别就x x f sin )(=,1)(+-=x x f 等函数利用(2.2.1)做迭代序列}{n x ,观察蛛网图中的轨道是否趋于平衡点和序列的收敛性。
四、实验过程与结果4.1 迭代序列与不动点实验一:稳定点为5、17 图像为:-10-551015510152046851015202530结果分析:从图像上观察到,数列收敛于一个常数实验二:对Plot 中{x,-10,20}可改为{x,-50,50}; 对PlotRange 中{-1,20}可改为{-50,50}, 稳定点为5、17图像为:-20-1010203040-40-20204046851015202530结果分析:数列收敛到17,收敛速度慢,蛛网图中的轨道趋于平衡点,与平衡点处曲线斜率有关。
实验三:x0=5.5中5.5分别改为-30,-20,-5,-3.001,-2.999,-1,0,1,1.5,2.5,4,4.5,4.9,4.999,5,5.1,5.001,6,10,16,17,18,20,30;x0=5.5-20-1010203040-40-20204046851015202530x0=-30-202040-40-20204046817171717x0=-20-202040-40-20204046817171717x0=-5-20-10102030-40-20204046817171717x0=-3.001-20-10102030-40-20204046851015202530x0=-2.999-202040-40-20204051015202530x0=-1-202040-40-202040468171717x0=0-202040-40-20204046817171717x0=1-202040-40-20204046817171717x0=1.5-202040-40-20204051015202530x0=2.5-20-10102030-40-20204046851015202530x0=4-20-10102030-40-20204046817171717x0=4.5-202040-40-20204046851015202530x0=4.9-202040-40-20204051015202530x0=4.999-202040-40-20204046851015202530x0=5-5510-40-202040468246810x0=5.1-20-1010203040-40-20204046851015202530x0=5.001-20-1010203040-40-20204051015202530x0=6-20-1010203040-40-20204046817171717x0=10-20-1010203040-40-20204046817171717x0=16-20-1010203040-40-20204046817171717x0=17-20-1010203040-40-20204051015202530x0=18-20-1010203040-40-20204046851015202530x0=20-20-1010203040-40-202040468171717x0=30-20-1010203040-40-20204046817171717结果分析:从对蛛网图与散点图的观察发现,数列收敛到17,收敛速度慢,蛛网图中的轨道趋于平衡点,与平衡点处曲线的斜率逐渐相近,初始值对结果没影响。
实验四:对t=Table[x[i],{i,1,10}]//N 中10分别改为100,200,500,1000;改为100-20-1010203040-40-2020402040608017171717改为200-20-1010203040-40-2020405010015017171717结果分析:从对蛛网图与散点图的观察发现,数列收敛且收敛速度快,蛛网图中的轨道趋于平衡点,初始值对结果没有影响。
