LTI系统的单位冲激响应.ppt
合集下载
连续时间LTI系统的冲激响应

A (t) + 3B (t) B '(t) 2 (t) '(t)
解得A= -1, B =1
h(t) e3tu(t) (t)
可见冲激响应的形式要根据微分方程情况设定
2. 冲激响应的求解
连续时间LTI系统的冲激响应h(t)满足微分方程
h(n)(t)
a h (n1) n 1
(t)
a h ' (t) 1
a n 1h (n1) (t)
a h ' (t) 1
a 0h ( t )
bm (m) (t)
b m 1 ( m 1 ) ( t )
b 1
'(t)
b (t) 0
2. 冲激响应的求解
[例] 某线性时不变系统的微分方程为y'(t) 3y(t) 2x(t), t 0 试求系统的冲激响应h(t)。
i1
j0
由微分方程的特征根确定u(t)前的指数形式。
由微分方程 (t)的最高阶导数与h(t)的最高阶导数确定 (j)(t)项。
连续时间LTI系统的冲激响应
谢谢
本课程所引用的一些素材为主讲老师多年的教学积累,来 源于多种媒体及同事、同行、朋友的交流,难以一一注明出处, 特此说明并表示感谢!
a 0h ( t )
bm
(m)
(t)
b
b 1
'(t) b0 ( t )
(1) 当 n>m 时(假设特征根为不等实根)
n
h(t) ( Kiesit )u(t)
i1
(2) 当nm 时, h(t)应含有冲激及其高阶导数
n
mn
h(t) ( Kiesit )u(t) Aj ( j) (t)
i1
解得A= -1, B =1
h(t) e3tu(t) (t)
可见冲激响应的形式要根据微分方程情况设定
2. 冲激响应的求解
连续时间LTI系统的冲激响应h(t)满足微分方程
h(n)(t)
a h (n1) n 1
(t)
a h ' (t) 1
a n 1h (n1) (t)
a h ' (t) 1
a 0h ( t )
bm (m) (t)
b m 1 ( m 1 ) ( t )
b 1
'(t)
b (t) 0
2. 冲激响应的求解
[例] 某线性时不变系统的微分方程为y'(t) 3y(t) 2x(t), t 0 试求系统的冲激响应h(t)。
i1
j0
由微分方程的特征根确定u(t)前的指数形式。
由微分方程 (t)的最高阶导数与h(t)的最高阶导数确定 (j)(t)项。
连续时间LTI系统的冲激响应
谢谢
本课程所引用的一些素材为主讲老师多年的教学积累,来 源于多种媒体及同事、同行、朋友的交流,难以一一注明出处, 特此说明并表示感谢!
a 0h ( t )
bm
(m)
(t)
b
b 1
'(t) b0 ( t )
(1) 当 n>m 时(假设特征根为不等实根)
n
h(t) ( Kiesit )u(t)
i1
(2) 当nm 时, h(t)应含有冲激及其高阶导数
n
mn
h(t) ( Kiesit )u(t) Aj ( j) (t)
i1
§2.5 冲激响应和阶跃响应ppt课件

e t
H
r t
u t
H
g t
返回
三.冲激响应的求解方法
1. 冲激响应的数学模型
对于线性时不变系统,可以用高阶微分方程表示为:
n n 1 d r ( t) d r ( t) d r ( t) C C C C r ( t) 0 1 n 1 n n n 1 d t d t d t m m 1 d e ( t) d e ( t) d e ( t) E E E E e ( t) 0 1 m 1 m m m 1 d t d t d t
方法2:奇异函数项相平衡法
设特征根为简单根(无重根的单根),则:
当n > m 时,ht 不含 t 及其各阶导数,其解的形式为: n a it h ( t) A u ( t) ie 1 i 当n m 时,h t 中应包含 t ,其解的形式为:
齐次方程
冲激 t 在 t 0时转为系统的储能(由 vC (0 )体现), t >0时,在非零初始条件下齐次方程的解,即为原系统 的冲激响应。
求解
1 特征方程 RC a 1 0 特征根 a RC t
v ( t ) A e u ( t ) C
RC
t> 0 时的解
2.求解方法
方法1:冲激函数匹配法:首先求出 0 ~ 0跳变值,由于 冲激响应为零状态响应,则h(n)(0-)=0,所以 h(n)(0+)=跳变值;t 0时, t 及其导数均为零,
因而方程式右端的自由项恒等于零,其解的形式
为微分方程的齐次解 ,即: h( t ) Ai ea t
dt
H
r t
u t
H
g t
返回
三.冲激响应的求解方法
1. 冲激响应的数学模型
对于线性时不变系统,可以用高阶微分方程表示为:
n n 1 d r ( t) d r ( t) d r ( t) C C C C r ( t) 0 1 n 1 n n n 1 d t d t d t m m 1 d e ( t) d e ( t) d e ( t) E E E E e ( t) 0 1 m 1 m m m 1 d t d t d t
方法2:奇异函数项相平衡法
设特征根为简单根(无重根的单根),则:
当n > m 时,ht 不含 t 及其各阶导数,其解的形式为: n a it h ( t) A u ( t) ie 1 i 当n m 时,h t 中应包含 t ,其解的形式为:
齐次方程
冲激 t 在 t 0时转为系统的储能(由 vC (0 )体现), t >0时,在非零初始条件下齐次方程的解,即为原系统 的冲激响应。
求解
1 特征方程 RC a 1 0 特征根 a RC t
v ( t ) A e u ( t ) C
RC
t> 0 时的解
2.求解方法
方法1:冲激函数匹配法:首先求出 0 ~ 0跳变值,由于 冲激响应为零状态响应,则h(n)(0-)=0,所以 h(n)(0+)=跳变值;t 0时, t 及其导数均为零,
因而方程式右端的自由项恒等于零,其解的形式
为微分方程的齐次解 ,即: h( t ) Ai ea t
dt
信号与系统 双语 奥本海姆 第二章PPT课件

10
Chapter 2 §2.3 卷积的计算 1. 由定义计算卷积积分
例2.6 xte au tt,a0htut
2. 图解法 例2.7 求下列两信号的卷积
xt 1 , 0tT ht
0 , 其余t 3. 利用卷积积分的运算性质求解
LTI Systems
yt
t , 0t2T 0 , 其余t
11
Chapter 2
in Terms of impulses
Example 2
3 xn
2
1
1 01 2
n
xknk
x n x 1 n 1 x 0 n x 1 n 1
xnxknk k 4
Chapter 2
LTI Systems
§2.1.2 The Discrete-Time Unit Impulse Responses and the
LTI Systems
§2.3 Properties of LTI Systems
xt ht ytxtht
xn hn ynxnhn
LTI系统的特性可由单位冲激响应完全描述
Example 2.9 ① LTI system
h n
1
0
n0,1 otherwise
② Nonlinear System
③ Time-variant System
a y n x n x n 1 2 aytco s3 txt
b y n m x n ,x a n 1 x b ytetxt 12
Chapter 2
LTI Systems
§2.3.1 Properties of Convolution Integral and Convolution Sum 1. The Commutative Property (交换律)
系统的单位冲激响应与单位样值响应

求系数Ci,cj
例1:求齐次解: r"(t) 5r' (t) 6r(t) e(t)
解:该微分方程的特征方程为: 2 5 6 0 解得特征根: 1 2,2 3
齐次解为: rn (t) c1e2t c2e3t
例3:求齐次解: r"(t) 4r' (t) 4r(t) e(t)
解: 2 4 4 0 1,2 2 二重根
rn (t) c1te2t c2e2t
例4:方程为: r"(t) 3r' (t) 2r(t) e' (t) 2e(t)
若激励为: e(t) t 2 求其特解 rf(t).
r 查表2-3-1得对应的特征解为: f (t) A2t 2 A1t A0 rf" (t),rf' (t),rf (t) e' (t), e(t) 代入原微分方程得:
解:特征根为 1 1, 2 2
零输入状态响应
零输入响应: rZi (t) CZi1et CZi2e2t r(0) 1, r'0 1 代入原方程
rZi (0) CZi1 CZi2 1
r
' Zi
(0)
CZi1
2CZi 2
1
CZi1 CZi 2
t=0时 初值代入: r(0) c1 c2 2 1
r'(0) c1 2c2 2 1 c1 1, c2 2
全解: r(t) et 2e2t t 2 2t 2 t 0
解题思路: 1 齐次解:其形式与激励e(t)无关,仅依赖于系统 本身特征――>自由响应或固有响应,系数ci,cj 与激励有关.
34连续时间LTI系统的冲激响应

=
3u(
)
2e
3(t
)u
(t
)d
详细求解见后
= 2(1 e3t )u(t)
卷积法求解yzs (t)的思路
(1) 将任意信号分解为单位冲激信号的线性组合 (2) 求出单位冲激信号作用在系统上的响应
—— 单位冲激响应h(t) (3) 利用线性时不变系统的特性,即可求出任意信号x(t)激励
1. 冲激响应的定义
若描述连续时间LTI系统的常系数线性微分方程为
y(n) (t) an1 y(n1) (t) L a1 y '(t) a0 y(t)
bm x(m)
(t)
b x(m1) m1
(t)
L
b1x ' (t) b0x(t)
则连续时间LTI系统的冲激响应h(t)应满足
北京交通大学 信号处理课程组
连续时间LTI系统的冲激响应
系统完全响应 = 零输入响应 + 零状态响应
系统的零状态响应 当系统的零状态响应是当系统的初始状态为零时,
由系统的外部激励 x(t) 而产生的响应,用表示yzs (t)。
连续时间LTI系统的冲激响应
假设单位冲激信号d (t)作用在系统上的冲激响应为h(t)
d (t)
系统
h(t)
零状态
而任意信号x(t) 都可以分解为单位冲激信号的线性组合,
即
x(t) x( ) d (t )d
零状态响应
yzs (t)
x( ) h(t )d
x(t) h(t)
即 yzs (t)为输入激励 x(t)与系统的冲激响应 h (t)的卷积积分。
第二章LTI系统的时域分析ppt课件

注意:为方便起见,对单一零状态系统进行讨论时常常仅用y(t)代表yf(t)。
y( t ) a0 y当( tf)(t b)0f (t()t )时 h( t ) a0h( t ) b0 ( t )
2、h(t)的求解方法 (1) 利用阶跃响应与冲激响应的关系求解
此方法适用于简单电路,前提是阶跃响应g(t)简单易求。
y( t ) yh( t ) yp( t )
1、齐次解yh(t)
y( n )( t ) an1 y( n1 )( t ) a1 y( t ) a0 y( t ) 0
特征方程
的解
n n1 a1 a0 0
➢ 齐次微分方程的特征根:特征方程的 n 个根λi (i=1,2,…,n) ; ➢ 齐次解yh(t)的函数形式由特征根确定;
零状态 系统
y f ( t ) h( t )
yf(t)= g(t)
➢ 零状态系统:在激励 f(t) 的作用下将产生零状态响应yf(t);
➢ 如果激励是单位冲激信号δ(t),产生的响应称为单位冲激响应,用h(t)表示。 ➢ 如果激励是单位阶跃信号ε(t),产生的响应称为单位阶跃响应,用g(t)表示。
n
m
ai y(k i) bj f (k j)
i0
j0
(an 1, m n)
差分方程的经典解分为齐次解yh(k)和特解yp(k)。
y(k) yh (k) yp (k)
1、差分方程的齐次解
n阶前向齐次差分方程 y(k n) an1y(k n 1) a1y(k 1) a0 y(k) 0
i1
y( t
)
yh( t
)
yp( t
)
C
1e
C2 t
ie
§2-6 LTI系统的单位冲激响应
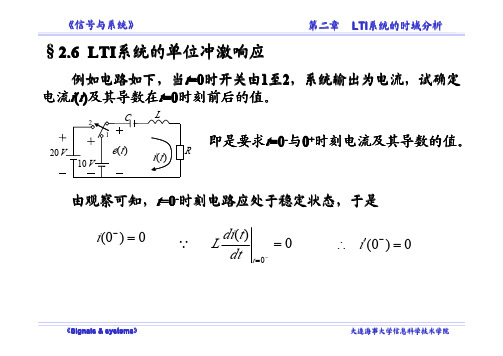
h′(t ) + 2h(t ) = δ(t )
⑴ 求特征根,确定齐次通解。
α+2=0
α = −2
−2 t
hh (t ) = Ae u (t )
⑵ 确定特解,并确定t=0+时刻的初始条件。 比较以上方程两边可见, ′(t ) 中应有强度为1的冲激,而 h(t )中 h 没有冲激存在,否则h′(t ) 中将有冲激的导数出现。因此,h(t ) 中没 有特解出现。
第二章
LTI系统的时域分析 LTI系统的时域分析
⑶ 确定齐次解中的待定系数,求出系统的单位冲激响应。
hh (0 + ) = B0 = −1 = A
所以
h(t ) = h p (t ) + hh (t )
= δ(t ) − e −2t u (t )
一般的,对于如下形式的微分方程
N k =0 M k =0
《Signals & systems》 systems》 大连海事大学信息科学技术学院
《信号与系统》 信号与系统》
第二章
LTI系统的时域分析 LTI系统的时域分析
所以
h(t ) = hh (t ) = Ae u (t )
因为
0+ 0+
−2 t
h (0 + ) =
−∞
∫ h′(t )dt
=
−∞
∫ δ(t )dt = 1
所以
A1 = 2
A2 = −1
h(t ) = ( 2e − t − e −2t )u (t )
《Signals & systems》 systems》 大连海事大学信息科学技术学院
《信号与系统》 信号与系统》
§2-3 LTI系统的单位冲激响应
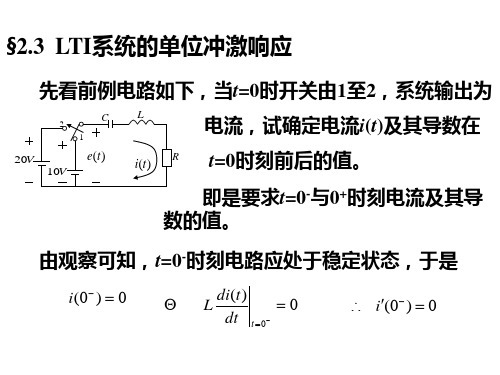
B0Δu=- Δu表示在t=0时刻系统由于冲激作用引起的跳变,
跳变值B0= -1 。它是在单位冲激信号的作用下,系统在 t=0+时刻建立起来的状态。利用此状态可以确定齐次响应 中的待定系数。
⑶ 确定齐次解中的待定系数,求出系统的单位冲激响
应。
hh (0 ) B0 1 A
所以
h(t) hp (t) hh (t)
2
3
2
3
(n) [ 3 (1)n1 4 (1)n1]u(n 1) 22 33
(n) [3(1)n 4(1)n ]u(
)1
A2
(
1) 3
1
2 A1
3A2
0
所以
h(0) A1 A2 1 A1 3 A2 2
h(n) [3(1)n 2(1)n ]u(n)
2
3
(n) [3(1)n 2(1)n ]u(n 1)
2
3
例如:已知系统差分方程,求系统的单位样值响应h(n)。
h(0) 1 5 h(1) 1 h(2) 1
6
6
当n=1
当n=2
h(1) 0 5 h(0) 1 h(1) 5
6
6
6
h(2) 0 5 h(1) 1 h(0) 19
6
6
36
同样,在大多数情况下不易得到封闭的解。
解法二:由因果性与零状态条件,通过迭代求得一组初始 条件,进而求n>0时的零输入响应。
y(n) 5 y(n 1) 1 y(n 2) x(n) x(n 1)
6
6
解、此时以上方程可以写成
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
所以 B1 1 B0 3B1 3
由此得到t=0+时刻的条件:
B0 0
h(0 ) B0 0
h(0 ) B1 1
⑶ 确定齐次解中的待定系数,求出系统的单位冲激响 应。
h(0 ) 1 A1 A2
h(0 ) 0 A1 2A2 A1 2 A2 1
所以
h(t) (2et e2t )u(t)
所以
h(t) hp (t) hh (t)
(t) e2tu(t)
一般的,对于如下形式的微分方程
N
M
ak y(k) (t) bk x(k) (t)
k 0
k 0
当N>M,单位冲激响应中只有自由响应;当N≤M,则还 有受迫响应分量:冲激和冲激的各阶导数。
例如 设系统方程如下,试求系统的单位冲激响应h(t)。 y(t) 3y(t) 2y(t) x(t) 3x(t)
§2.3 LTI系统的单位冲激响应
先看前例电路如下,当t=0时开关由1至2,系统输出为
C
L
2
1
电流,试确定电流i(t)及其导数在
20V
e(t)
10V
i(t) R
t=0时刻前后的值。
即是要求t=0-与0+时刻电流及其导 数的值。
由观察可知,t=0-时刻电路应处于稳定状态,于是
i(0 ) 0
di(t)
二、离散时间系统的单位样值响应
(n) 零状态系统 h(n)
单位样值响应h(n)是系统在零状态时,由单位样值信 号作用之下产生的响应。因此,它是一个零状态响应。
同样,单位样值信号δ(n)仅在n=0时刻等于1,其它时 刻δ(n)=0,因此系统在n>0时的响应是零输入响应。
因为是差分方程的时域求解,除了有类似于以上单位 冲激响应求解的方法外,还可以用迭代法求解响应。
于是在t=0时刻,系统的特解 hp (t) (t)
B0Δu=- Δu表示在t=0时刻系统由于冲激作用引起的跳变,
跳变值B0= -1 。它是在单位冲激信号的作用下,系统在 t=0+时刻建立起来的状态。利用此状态可以确定齐次响应 中的待定系数。
⑶ 确定齐次解中的待定系数,求出系统的单位冲激响
应。
hh (0 ) B0 1 A
比较以上方程两边可设:在t=0时刻
h(t) B1(t) B0(t) 于是在t=0时刻
h(t) B1(t) B0u 将这两式代入以上方程
B1(t) B0(t) 2B1(t) (t) (t)
即有
B1(t) (B0 2B1)(t) (t) (t)
B1 1 B0 2B1 1
B0 1
解:此时方程应为 h(t) 3h(t) 2h(t) (t) 3(t)
⑴ 求特征根,确定齐次通解。
2 3 2 0
பைடு நூலகம்
1 1 2 2
所以t>0时 h(t) A1et A2e2t
或表示为: h(t) ( A1et A2e2t )u(t)
⑵ 确定特解,并确定t=0+时刻的初始条件。 比较以上方程两边可设:在t=0时刻 h(t) B1(t) B0(t)
L
0
dt t0
i(0 ) 0
当t=0+时刻,由于电感电流不会突变,于是
i(0 ) 0
di(t)
L
10
dt t0
i(0 ) 10 L
可见,在当t=0时刻的前后,电路中状态发生了跳变。
由前所讲已知,当-∞<t<∞时系统方程为
d 2i(t) R di(t) 1
10
dt 2
L
dt
i(t) (t)
例如、设系统方程如下,试求系统的单位冲激响应h(t)。
⑴ y(t) 2y(t) x(t) ⑵ y(t) 2y(t) x(t) x(t)
1/解:此时方程应为
h(t) 2h(t) (t)
⑴ 求特征根,确定齐次通解。
20
2
hh (t) Ae2tu(t) ⑵ 确定特解,并确定t=0+时刻的初始条件。
LC
L
即系统方程的右边出现冲激信号,t=0时刻的条件会发生 跳变。
一、单位冲激响应
(t) 零状态系统 h(t)
单位冲激响应h(t)是系统在零状态时,由单位冲激作用 之下产生的输出响应。因此,它是一个零状态响应。
h(t) hh (t) hp (t) 但是,单位冲激信号δ(t)仅在t=0时刻不等于0,当t>0时 δ(t)=0,因此系统在t>0时的响应是零输入响应的形式。 因此,在时域求解的情况下,hp(t)与t=0+时条件的确定 成了h(t)求解的关键。
6
6
考虑到系统是因果的和零状态的,当n=0
h(0) 1 5 h(1) 1 h(2) 1
6
6
当n=1
当n=2
h(1) 0 5 h(0) 1 h(1) 5
6
6
6
h(2) 0 5 h(1) 1 h(0) 19
6
6
36
同样,在大多数情况下不易得到封闭的解。
下面还是通过举例,说明单位样值相应的求解。
例如:已知系统差分方程,求系统的单位样值响应h(n)。
y(n) 5 y(n 1) 1 y(n 2) x(n)
6
6
解、此时以上方程可以写成
h(n) 5 h(n 1) 1 h(n 2) (n)
6
6
解法一(迭代法):将方程写成如下形式
h(n) (n) 5 h(n 1) 1 h(n 2)
比较以上方程两边可见,h(t) 中应有强度为1的冲激, 而 h(t) 中没有冲激存在,否则 h(t) 中将有冲激的导数出 现。因此,h(t) 中没有特解出现。
所以
h(t) hh (t) Ae2tu(t)
因为
0
0
h(0 ) h(t)dt (t)dt 1
⑶ 由t=0+时刻的初始条件,确定待定系数。
所以
h(0 ) 1 A
h(t) e2tu(t)
对于低阶方程的另一种解法是,将含待定系数的h(t) 代入方程,然后使方程两边相等以确定待定系数。
2/解:此时方程应为 h(t) 2h(t) (t) (t)
⑴ 求特征根,确定齐次通解。
20
2
hh (t) Ae2tu(t)
⑵ 确定特解,并确定t=0+时刻的初始条件。
于是在t=0时刻 h(t) B1(t) B0u
h(t) B1u 由此得到,h(t)中特解等于0;将以上三式代入以下方程
h(t) 3h(t) 2h(t) (t) 3(t)
B1(t) B0(t) 3B1(t) (t) 3(t) B1(t) (B0 3B1)(t) (t) 3(t)
