ARCH模型介绍
使用ARCH模型进行金融计算

使用ARCH模型进行金融计算ARCH模型是金融领域中常用的一种计量经济学方法,用于分析和预测金融时间序列数据的波动性。
ARCH模型的全称是自回归条件异方差模型(Autoregressive Conditional Heteroskedasticity Model),它能够捕捉到金融市场中的波动性聚集现象,帮助投资者更好地理解和应对市场风险。
首先,ARCH模型的基本思想是,金融市场中的价格和收益率并不是随机波动的,而是存在一定的波动性聚集现象。
也就是说,市场的波动性在某个时期内可能会比其他时期更高或更低。
ARCH模型通过引入条件异方差的概念,能够对这种波动性聚集进行建模。
ARCH模型的核心是条件异方差,即波动性的方差是与过去的波动性有关的。
在ARCH模型中,通过引入滞后期的平方误差项来捕捉波动性的变化。
具体来说,ARCH模型可以表示为:σt^2 = α0 + α1ε(t-1)^2 + α2ε(t-2)^2 + ... + αpε(t-p)^2其中,σt^2表示第t期的条件异方差,ε(t-i)表示第t-i期的误差项,α0、α1、α2...αp是模型的参数,p是滞后期数。
ARCH模型的核心思想是,过去的波动性会对当前的波动性产生影响,通过对过去波动性的建模,可以更好地预测未来的波动性。
ARCH模型的应用范围非常广泛,包括股票、债券、汇率、商品等金融市场中的各种时间序列数据。
例如,在股票市场中,投资者可以利用ARCH模型对股票的波动性进行建模,从而制定更合理的投资策略。
在外汇市场中,投资者可以利用ARCH模型对汇率的波动性进行预测,从而进行有效的风险管理。
此外,ARCH模型还可以与其他模型相结合,进行更复杂的金融计算。
例如,可以将ARCH模型与随机游走模型相结合,构建GARCH模型(GeneralizedARCH Model),从而更准确地描述金融市场中的波动性聚集现象。
GARCH模型在金融风险管理、期权定价等领域有着广泛的应用。
ARCH学习总结

ARCH 学习1. ARCH 模型 定义:均值方程t t ε= ~..t i i d ν 2()0()1t t E E νν== 01at j t jj h ααε-==+∑ 特性:A.无条件均值 B.条件均值 C.无条件方差 D.条件方差高铁梅版本总结自回归条件异方差(Autoregressive Conditional Heteroscedasticity Model , ARCH)模型是特别用来建立条件方差模型并对其进行预测的。
自相关的问题是时间序列数据所特有,而异方差性是横截面数据的特点,但时间序列同样也存在异方差特征,在金融数据上这一特征很明显。
为了刻画这种相关性,恩格尔提出自回归条件异方差(ARCH)模型。
ARCH 的主要思想是时刻 t 的ut 的方差(= σ2 t )依赖于时刻(t -1)的扰动项平方的大小,即依赖于 û2t - 1 。
ARCH 模型如果 ut 的均值为零,对 y t 取基于(t -1)时刻的信息的期望,即Et -1(yt ),有如下的关系: 即第一个方程式为均值方程。
假设在时刻 ( t -1 ) 所有信息已知的条件下,扰动项 ut 的条件分布是:~ 也就是,ut 遵循以0为均值,(α0+α1u 2t-1 )为方差的正态分布。
由于(6.1.7)中 ut 的方差依赖于前期的平方扰动项,我们称它为ARCH(1)过程: 通常用极大似然估计得到参数γ0, γ1, γ2, ⋯⋯, γk , α0, α1的有效估计。
容易加以推广,ARCH (p )过程可以写为: (6.1.8) 这时方差方程中的(p +1)个参数α0, α1, α2, ⋯⋯, αp 也要和回归模型中的参数γ0, γ1, γ2, ⋯⋯, γk 一样,利用极大似然估计法进行估计。
如果(6.1.8)中方差不存在异方差,则02)var(ασ==t t u即: 相应的检验,对(6.1.8)建立方程,如果显著为0,即不存在异方差,否则存在异方差,等价于存在ARCH 效应。
arch模型的原理 -回复

arch模型的原理-回复ARCH模型,即自回归条件异方差模型(Autoregressive Conditional Heteroskedasticity Model),是为了捕捉时间序列数据中异方差(heteroskedasticity)现象而生的一种经济计量模型。
在本文中,将一步一步回答“ARCH模型的原理”。
第一步,我们先了解什么是异方差。
异方差是指时间序列数据中,随着时间的推移,序列的方差出现明显变化的情况。
在金融市场,股票价格或金融资产的收益率常常呈现出异方差现象,即在某些时期波动较小,而在其他时期波动较大。
这种异方差现象对于风险度量和预测模型的构建都有很大的影响。
第二步,ARCH模型的基本思想是通过引入时间序列自己的过去序列的方差来解释序列的异方差现象。
也就是说,ARCH模型假设时间序列数据的方差是由过去的误差平方项决定的。
如果过去的方差较大,那么未来的方差也会较大;反之,如果过去的方差较小,那么未来的方差也会较小。
第三步,ARCH模型的具体形式是通过引入一个滞后期数的误差项平方的线性组合来表示方差的变化。
以ARCH(p)模型为例,其表达式为:σ^2_t = α_0 + α_1 * ε^2_(t-1) + α_2 * ε^2_(t-2) + ... + α_p * ε^2_(t-p)其中,σ^2_t表示时间t的方差,α_0为常数项,α_i(i=1,2,...,p)为参数,ε_t(t=1,2,...,p)为误差项。
在ARCH(p)模型中,根据过去p期的误差项平方的线性组合来估计当前时间的方差。
第四步,ARCH模型的参数估计可以使用最大似然估计法(Maximum Likelihood Estimation,简称MLE)进行。
MLE的思想是找到一组参数值,使得模型产生的数据的概率最大化。
对于ARCH模型,我们需要对误差项的平方进行参数估计,然后利用MLE来求解最优的参数。
第五步,ARCH模型的估计和预测过程需要进行模型检验。
arch模型
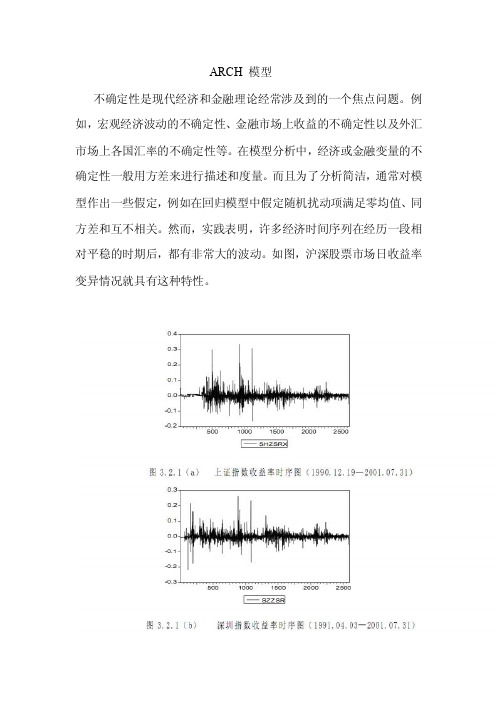
ARCH 模型不确定性是现代经济和金融理论经常涉及到的一个焦点问题。
例如,宏观经济波动的不确定性、金融市场上收益的不确定性以及外汇市场上各国汇率的不确定性等。
在模型分析中,经济或金融变量的不确定性一般用方差来进行描述和度量。
而且为了分析简洁,通常对模型作出一些假定,例如在回归模型中假定随机扰动项满足零均值、同方差和互不相关。
然而,实践表明,许多经济时间序列在经历一段相对平稳的时期后,都有非常大的波动。
如图,沪深股票市场日收益率变异情况就具有这种特性。
在这种情况下,同方差假定是不恰当的。
在这种情况下,人们关心的是如何预测序列的条件方差。
例如,作为资产持有者,他既关心收益率的预测值,同时也关心持有期内方差的大小。
如果一位投资者计划在第 t 时期买入某项资产,在第 t+1 时期售出,则无条件方差(即方差的长期预测值)对他来讲就不重要了。
对于这一类问题,可以使用自回归条件异方差模型 (autoregressive conditiona heteroskedastic model ,简称 ARCH 模型)来进行分析。
最早的 ARCH 模型是由 Robert Engle 于 1982 年建立的,因此它的发展历史不长。
但是,这种模型及其各种推广形式已被广泛应用于经济和金融数据序列的分析,ARCH 模型族已成为研究经济变量变异聚类特性的有效工具。
第一节 ARCH 模型的概念与性质 1、ARCH 过程ARCH 模型的一般性定义如下。
假设时间序列{}t y 服从如下回归模型:'t t ty x u ξ=+(8.1.1)其中 t x 是外生变量向量,它可以包含被解释变量的滞后项,ξ是回归参数向量。
如果扰动项序列{}t u 满足:11|~(0,)(,,)t t t t t t q u N h h h u u ---Ω= (8.1.2)其中:11122{,',,'}t t t t t y x y x -----Ω= 为t 时期以前的信息集。
金融计量经济第三讲ARCH模型的理论与应用

讨论课内容
• 1、利用证券市场指数数据分析股票市场的 衰减系数; • 2、非对称ARCH模型—TARCH和EGARCH模型的应用
练习,可采用自回归模型和单指数模型; • 3、准备讨论课内容,分小组,每组最多3人,讨论较前沿 的金融计量应用论文,最好是外文文献,若有思想较好的 个人作品也可。课堂讨论时间每组30分钟左右,听课的同 学可提问。请在二周后上报小组成员名单及分工。 • 1和2需要将分析结果做成文挡,电邮给老师(下周前)。 • Zhujin@
• (*)和(**)有何区别? • 此方法可以用于期货价格、自由汇率等时间序列 的计算,不同问题结果分析时有所侧重。
不同阶段的时间序列的结果(当堂演算): • 从1991年3月到95年12月:衰减系数>1,不符 合GARCH模型的要求; • 从95年12月到98年12月,衰减系数=0.92; • 98年12月到今,衰减系数=0.97
H0 : 1 2 q 0; H1 : i 0,1 i q
ht 0 1 t 1 q t q t (3.6)
例3.1:开放式基金与股价指数因果 关系分析
• 选指数型基金一家,上证180指数为解释变 量,讨论之间是否有ARCH特征。
时间序列分析上机练习参考
• 有用的时间序列数据:各市场中的股价指数、行 业指数、个股价格、成交量;开放式基金或封闭 式基金净值与价格,开放式基金规模;期货价格、 持仓量、交易量;外汇交易价格;CPI;GDP; 其它金融时间序列; • 练习目的:掌握并熟练ADF检验、单整与协整检 验、EMC、Granger因果检验、ARCH系列应用 • 建模参考:A、B市场关联性、基金与股价指数的 关联性、购买力平价模型、股价与CPI或GDP的 关系,基金规模与股价或净值的关系等; • 选择一些建模主题,寻找数据,进行各项检验及 回归分析。Βιβλιοθήκη 第三节 其它ARCH类模型
arch效应一元回归模型

arch效应一元回归模型arch效应是指在金融市场中存在的时间序列的波动率聚集性现象。
在金融市场中,价格的波动性是投资者非常关注的一个指标,因为波动率的变化会对投资决策产生重要影响。
arch效应的提出为我们解释金融市场中价格波动性的聚集性提供了一个重要的理论框架。
arch模型是用来描述金融市场中的波动性聚集性现象的一种经济学模型。
它是由罗伯特·恩格尔(Robert F. Engle)于1982年提出的,因此也被称为“恩格尔的arch模型”。
arch模型是一种条件异方差模型,它假设金融时间序列的波动率是与其历史波动率相关的。
在arch模型中,波动率被认为是时间序列中的一个随机变量,它的变化是受到历史波动率的影响的。
arch模型可以用来对金融市场中的价格波动性进行建模和预测。
在arch模型中,条件异方差被认为是一个滞后变量的函数,它可以通过对历史波动率的估计来预测未来的波动率。
arch模型的核心思想是,当前的波动率与过去的波动率有关,较高的波动率往往会导致未来较高的波动率,较低的波动率会导致未来较低的波动率。
arch 模型可以帮助我们理解金融市场中的波动率聚集性现象,并对未来的波动率进行预测。
arch模型的估计方法主要有两种,一种是最大似然估计法,另一种是广义最小二乘法。
最大似然估计法是通过最大化似然函数来估计模型的参数,而广义最小二乘法是通过最小化模型的加权残差平方和来估计模型的参数。
这两种方法在实际应用中都有一定的优缺点,选择哪种方法要根据实际情况来决定。
arch模型在金融领域中有着广泛的应用。
它可以用来对金融市场中的风险进行度量和管理,可以帮助投资者进行风险控制和资产配置。
arch模型还可以用来对金融市场中的波动率进行预测,帮助投资者做出更准确的投资决策。
此外,arch模型还可以用来对金融市场中的高频数据进行建模和分析,以及对金融市场中的异常波动进行检测和解释。
尽管arch模型在金融领域中有着广泛的应用,但它也存在一些局限性。
arch

2 t −1
可以看出, 的条件分布是正态的, 可以看出, ε t 的条件分布是正态的,但其条件方差是过 去平方误差的线性函数,是随时间而变化的函数。 而变化的函数 去平方误差的线性函数,是随时间而变化的函数。
5
RCH模型 (二)ARCH模型 RCH
ARCH类模型一般由两个方程组成 ARCH类模型一般由两个方程组成 ( ) 条件均值方程: 如 AR(p)模型
16
(三)扩展的ARCH模型 扩展的ARCH模型 ARCH
1.指数的GARCH模型 GARCH模型 1.指数的GARCH模型— E( Exponential )GARCH模型 指数的GARCH模型 ε t = ht vt 其中, 独立同分布, ),t 其中,{ vt}独立同分布,且 vt ~N(0,1), = 1, 独立同分布 ( , ), , 有下面的形式: 2,.......,T。并设条件方差 ht 有下面的形式: , , 。 p q ε t −i ε t −i log(ht ) = α 0 + ∑θ j log ht − j + ∑ α i + ϕi ht −i ht −i j =1 i =1
计算标准化残差序列( ˆ 计算标准化残差序列( vt )的JB统计量 统计量 模型判定 AIC SC
10
4. 预测 的值, 只要知道参数 a 0 , a1 ,...... ,a q 的值,就可以在 2 ε t2−q , (t — 1)时刻,利用给定的数据 ε t −1 ,...… , )时刻, 2 在时刻t的条件方差 预测 ε t 在时刻 的条件方差 σ t 。
18
3. TARCH模型 模型 TARCH(Threshold ARCH)模型最先由 ( ( )模型最先由Zakoian( 1990)提出,它具有如下形式的条件方差 )提出,
第7章、ARCH模型和GARCH模型

第7章、ARCH模型和GARCH模型研究内容:研究随时间而变化的风险。
(回忆:Markowitz均值-方差投资组合选择模型怎样度量资产的风险)本章模型与以前所学的异方差的不同之处:随机扰动项的无条件方差虽然是常数,但是条件方差是按规律变动的量。
波动率的聚类性(volatility clustering):一段时间内,随机扰动项的波动的幅度较大,而另外一定时间内,波动的幅度较小。
如图,§1、ARCH 模型1、条件方差多元线性回归模型:条件方差或者波动率(Condition variance ,volatility )定义为 其中1t ψ-是信息集。
2、ARCH 模型的定义Engle (1982)提出ARCH 模型(autoregressive conditional heteroskedasticity ,自回归条件异方差)。
ARCH(q)模型:t t t y βε=+x (1)t ε的无条件方差是常数,但是其条件分布为22211t t q t qσωαεαε--=+++ (2) 其中1t ψ-是信息集。
方程(1)是均值方程(mean equation )✓ 2t σ:条件方差,含义是基于过去信息的一期预测方差方程(2)是条件方差方程(conditional variance equation ),由二项组成 ✓ 常数ω✓ ARCH 项2t i ε-:滞后的残差平方习题: 方程(2)给出了t ε的条件方差,请计算t ε的无条件方差。
证明:利用方差分解公式:Var(X) = Var Y [E(X|Y)] + E Y [Var(X|Y)]由于21|(0,)t t t N εψσ-,所以条件均值为0,条件方差为2t σ。
那么,推出1var()1t qωεαα=---,说明1(0,)1tqN ωεαα---3、ARCH 模型的平稳性条件在ARCH(1)模型中,观察参数α的含义: 当1α→时,var()t ε→∞ 当0α→时,退化为传统情形,(0,)tN εωARCH 模型的平稳性条件:1i α∑<(这样才得到有限的方差)4、ARCH效应检验ARCH LM Test:拉格朗日乘数检验建立辅助回归方程此处e是回归残差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ARCH模型介绍
σ_t^2=α_0+α_1*ε_(t-1)^2+α_2*ε_(t-2)^2+...+α_p*ε_(t-p)^2
其中,σ_t^2表示在t时刻的波动性,α_0表示常数项,
α_1,α_2,...,α_p是ARCH模型的参数,ε_t-1,ε_t-2,...,ε_t-p是
t时刻的残差。
ARCH模型最重要的特点是它能够捕捉到波动性的聚集,即高波动性
的时期往往会持续一段时间,而低波动性的时期也会持续一段时间。
这是
因为ARCH模型中的参数可以控制波动性的趋势和持续性。
当参数值较大时,波动性的变化会更加剧烈;当参数值较小时,波动性的变化会更加平缓。
ARCH模型在金融领域特别受到关注,因为金融市场的波动性非常重要。
通过使用ARCH模型,我们可以对金融市场的波动性进行建模和预测。
例如,可以利用ARCH模型来估计股票价格的波动性,进而对股票的风险
进行评估。
此外,ARCH模型还可以用于进行对冲策略的设计,以便在市
场波动性较高时降低风险。
除了ARCH模型,还有一种更广义的模型叫做GARCH模型,即广义自
回归条件异方差模型。
GARCH模型在ARCH模型的基础上增加了过去时刻
波动性的指数加权平均项。
这允许GARCH模型能够更好地捕捉到波动性的
长期记忆特性。
GARCH模型的一般形式可以表示为:
σ_t^2=α_0+α_1*ε_(t-1)^2+α_2*ε_(t-2)^2+...+α_p*ε_(t-p)^2+β_1*σ_(t-1)^2+β_2*σ_(t-2)^2+...+β_q*σ_(t-q)^2
其中,σ_t^2表示在t时刻的波动性,α_0表示常数项,
α_1,α_2,...,α_p是ARCH模型的参数,β_1,β_2,...,β_q是GARCH 模型的参数,ε_t-1,ε_t-2,...,ε_t-p是t时刻的残差,σ_t-
1,σ_t-2,...,σ_t-q是t时刻的波动性。
GARCH模型在金融领域的应用更为广泛,因为它可以更准确地描述金融市场中的波动性。
总结起来,ARCH模型是一种用于描述时间序列数据中波动性的统计模型。
它通过引入一个异方差因素,将当前时刻的波动性与过去时刻的残差的平方相关联。
ARCH模型的核心思想是波动性的聚集,它可以用于对金融市场的波动性进行建模和预测。
另外,GARCH模型是ARCH模型的扩展形式,可以更好地捕捉到波动性的长期记忆特性。
GARCH模型在金融领域应用广泛,可用于风险评估和对冲策略设计。
