1.2 同位角、内错角、同旁内角
合集下载
同位角、内错角、同旁内角 优秀教学课件ppt

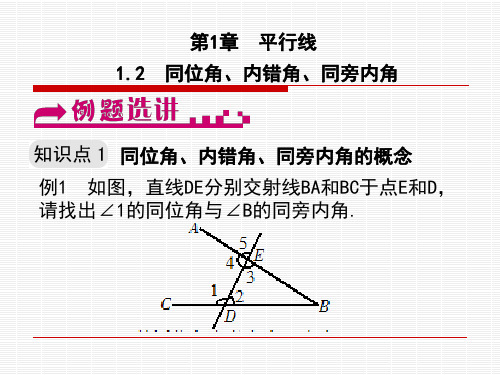
例1:如图,直线DE截直线AB,AC,构成8个角。
指出所有的同位角、内错角和同旁内角。
D
21 34
B
A
∠2和∠5
截线
∠3和∠6
同位角 ∠4和∠7
58
E
67
∠1和∠8
C
内错角 ∠4和∠5 ∠1和∠6
被截线
同旁内角 ∠1和∠5 ∠4和∠6
∠A与∠5? ∠A与∠4? ∠A与∠8? ∠A与∠7?
例2、如图,∠α与∠C,∠β与∠B 是哪两条直线被哪一条直线所截成的什么 角?
那么∠1与∠5是一对什么角?(同旁内角)
∠4与∠5呢? (内错角)
练习2
DA
1 4
5
E
23 F
B
C
(3)哪两条直线被哪一条直线所截,
∠2与∠5是同位角? (直线AB和CD被直线EF所截)
例3、如图:直线DE交∠ABC的边BA于 点 F. 如果内错角∠1与∠2相等,那么同 位角∠1与∠4相等,同旁内角∠1与∠3互 补.请说明理由.
截线的两旁
同旁内角 被截直线之间
截线的同旁
如图:两只手的食子和拇指在同一平面内,它 们构成的一对角可以看成是什么角?类似地,你 还能用两只手的手指构成同位角和同旁内角吗?
角。 (4)∠2与∠4是A__B_和_A_F_被BC所截构成的_同__位_
角。
练习2
DA
1 4
5
E
23
F
B
C
(1)如果把图看成是直线AB,EF被直线CD所截,
那么∠1与∠2是一对什么角? (同位角)
∠3与∠4呢? (内错角) ∠ 2与∠4呢? (同旁内角)
练习2
DA
1 4
1.2 同位角、内错角、同旁内角
解:(1)内错角,同旁内角,同位角. (2)∠1=∠2,∠1与∠3互补,理由见“分 析”. 注意点:同位角、内错角、同旁内角都是指角 的位置关系,与角的大小是否相等无关. 在三 种角的识别过程中,只能是两条直线被第三条 直线所截,不能出现与第四条直线有关的角. 错题展示
例1 如图,下列判断: (1)∠A与∠1是同位角; (2)∠A与∠B是同旁内角; (3)∠4与∠1是内错角; (4)∠1与∠3是同位角. 其中正确的说法有( A. 1个 C. 3个 错答:A或B或D. B. 2个 D. 4个
)
正答:C
错因:没有认真理解同位角、内错角、同旁内 角的概念,不能在复杂图形中辨认这三类角, 从而产生错误. (1)(2)(3)是正确的, (4)是错误的.
例2 如图,图中有______________对内错角.
错答:2
正答:4 错因:分类讨论不清,与∠D是内错角的有 ∠DAG和∠FCD;与∠B是内错角的有∠HAB和 ∠ECB.
同位角、内错角、同旁内角的识别 例2 下列图形中,∠1与∠2不是同位角的是 ( )
解:C 注意点:判断是否为同位角、内错角、同旁内角 的前提条件是这两个角必须有一条边在同一直线 上.
同位角、内错角、同旁内角的综合应用
例3 如图,直线DE,BC被直线AB所截.
(1)∠1与∠2,∠1与∠3,∠1与∠4各是什么 关系的角? (2)如果∠1=∠4,那么∠1和∠2相等吗?∠1 和∠3互补吗?为什么?
分析: (1)认准第三条直线是AB,从角所处的位置来 判断. ∠1与∠2在直线DE,BC之间且在直线AB 的两侧,是内错角. ∠1与∠3在直线DE,BC之 间且在直线AB的同侧,是同旁内角. ∠1与∠4 在直线DE,BC的同一侧,且在直线AB的同一侧 ,是同位角. ( 2) ∵∠1=∠4(已知),∠2=∠4(对顶角相等) , ∴∠1=∠2. ∵∠2+∠3=180°(平角的定义), ∴∠1+∠3=180°,∴∠1与∠3互补.
1.2 同位角、内错角、同旁内角精美课件ppt

1.2 同位角、内错角、同旁内角
课内练习 1 已知直线 l1 , l2 ,l3 ,l4 (如图).
(1)当哪两条直线被哪条直线所截时,∠l与∠3 是同位角?当哪两条 直线被哪条直线所 截时,∠1与∠4是 内错角?
1.2 同位角、内错角、同旁内角
解: l1 ,l2 被l3 所截时, ∠1与∠3为同位角; l3 ,l4被l1 所截时, ∠1与∠4是内错角.
2 燕子风筝的骨架如图所示. (1)∠1与∠5是一对什么角?
如果∠1=∠6=45°,那么 ∠5等于多少度?根据什么? ∠5与∠1相等吗?
解: ∠1与∠5是一对内错角,∠5=45°,根据对顶角相等,∠1=∠5.
1.2 同位角、内错角、同旁内角
(2)∠2与∠3是一对什么角?如果∠2=∠4=45°, 那么∠3等于多少度? 根据什么?∠2+∠3 等于多少度?
1.2 同位角、内错角、同旁内角
例 如图,直线DE交∠ABC的边BA于点F.如果 内错角∠1与∠2相等,那么同位角∠1与∠4相 等,同旁内角∠1与∠3互补,请说明理由.
1.2 同位角、内错角、同旁内角
解:∵∠2与∠4是对顶角, ∴∠2=∠4. 已知∠1=∠2, ∴∠1=∠4. ∵∠2与∠3互为补角, ∴∠2+∠3=180°. ∴∠1+∠3=180°. 即∠1与∠3互补.
1.2 同位角、内错角、同旁内角
2 ∠3与∠5分别位于第三条直线l3的异侧,并 且都在两条直线l1与l2之间, 这样的一对角叫做内错角 (alternate interior angles).
1.2 同位角、内错角、同旁内角
3 ∠3与∠6都在第三条直线l3的同旁,并且在 直线l1与l2之间,这样 的一对角叫做同旁内角 (same-side interior angles).
1.2同位角,内错角,同旁内角

3.同旁内角呢?4.它们组成什么样的字母形状呢?
以表格形式进行归纳总结(见ppt)
(5)例题讲解
例1:如图:请指出图中的同位角,内错角及同旁内角。
1. 其中:∠1与∠5;∠4与∠6是直线和直线被直线所截得到的同旁内角。此时三线构成了个角。此时,同位角有:,内错角有:。
2.其中:∠1与∠A是直线和直线被直线所截得到的同旁内角。此时三线构成了_______个角。此时,同位角有:,内错角有:。
课题
1.2同位角,内错角,同旁内角
主备
孙伟伟
教学
目标
知识与技能
1.理解同位角、内错角、同旁内角的概念;
2.能够在图中找出两条直线被三条直线所截所形成的同位角、内错角、同旁内角
3.会根据“关系角”确定“三线”。
过程与方法
通过应用与日常生活的一些含有“三角”的图形联系,抽象到几何图形,培养学生看图和识图能力,由较复杂的图形中分解出简单的、基本图形的能力。
情感、态度与价值观
在训练过程中,不断提高学生排除变式图形中的非本质现象。
教学重难点
重点:同位角、内错角、同旁内角的概念
难点:在较复杂的图形中辨认同位角、内错角、同旁内角.
集体备课
个性备课
一:教学目标
1.理解同位角、内错角、同旁内角的概念;
2.能够在图中找出两条直线被三条直线所截所形成的同位角、内错角、同旁内角
3.其中:∠5与∠A是直线和直线被直线所截得到的同旁内角。此时三线构成了______个角。此时,同位角有:,内错角有:。
看图填空
(1)若ED,BC被AB所截,则∠1与是同位角。
(2)若ED,BC被AF所截,则∠3与是内错角。
(3)∠1与∠3是AB和AF被所截构成的角。
以表格形式进行归纳总结(见ppt)
(5)例题讲解
例1:如图:请指出图中的同位角,内错角及同旁内角。
1. 其中:∠1与∠5;∠4与∠6是直线和直线被直线所截得到的同旁内角。此时三线构成了个角。此时,同位角有:,内错角有:。
2.其中:∠1与∠A是直线和直线被直线所截得到的同旁内角。此时三线构成了_______个角。此时,同位角有:,内错角有:。
课题
1.2同位角,内错角,同旁内角
主备
孙伟伟
教学
目标
知识与技能
1.理解同位角、内错角、同旁内角的概念;
2.能够在图中找出两条直线被三条直线所截所形成的同位角、内错角、同旁内角
3.会根据“关系角”确定“三线”。
过程与方法
通过应用与日常生活的一些含有“三角”的图形联系,抽象到几何图形,培养学生看图和识图能力,由较复杂的图形中分解出简单的、基本图形的能力。
情感、态度与价值观
在训练过程中,不断提高学生排除变式图形中的非本质现象。
教学重难点
重点:同位角、内错角、同旁内角的概念
难点:在较复杂的图形中辨认同位角、内错角、同旁内角.
集体备课
个性备课
一:教学目标
1.理解同位角、内错角、同旁内角的概念;
2.能够在图中找出两条直线被三条直线所截所形成的同位角、内错角、同旁内角
3.其中:∠5与∠A是直线和直线被直线所截得到的同旁内角。此时三线构成了______个角。此时,同位角有:,内错角有:。
看图填空
(1)若ED,BC被AB所截,则∠1与是同位角。
(2)若ED,BC被AF所截,则∠3与是内错角。
(3)∠1与∠3是AB和AF被所截构成的角。
1.2_同位角内错角同旁内角

如图:两只手的食子和拇 指在同一平面内,它们构 成的一对角可以看成是什 么角?类似地,你还能用 两只手的手指构成同位角 和同旁内角吗?
小 结
1、这节课研究的是两条直线被第三条直线所截形成的不同顶点 处的两个角之间的位置关系,即同位角、内错角、同旁内角。
2、同位角、内错角、同旁内角的特点:
与被截直线的关系
内错角:∠3与∠5;
∠4与∠6.
8
同旁内角: ∠4与∠5; ∠3与∠6.
l4 已知直线 l1 ,l 2 , l3 ,(如图) . (1)当哪条直线被哪两条直线所截时, 1与 3 是同位角?当哪两条直线被哪 l1 条直线所截时1与 4是内错角? l2 (2)请说出图中一对同位角、一对内 错角、一对同旁内角,并分别说明是 哪两条直线被哪条直线所截而成的.
∠4与∠5是一对内错角.
直线AB,CD被直线EF所截
2.看图填空: (1)若ED,BF被AB所截, 则∠ 1与 ∠2 是同位角;
B E 1 3 2
A
D 4 F C
(2)若ED,BC被AF所截, 则∠3与 ∠4 是内错角;
(3)∠1与∠3是AB和AF被 ED 所截 构成的 内错 角; (4)∠2 与∠4是 AB 和 AF BC所截构成的 同位 角。 被
C 3
D
2
2
2
2
B
2
2
C
课内练习
1.(1)如果把图看成是直线AB,EF被 直线CD所截,那么∠1与∠2是一对什 么角?∠3与∠4呢?∠2与∠4呢?
A 1 4 E 5 2 3 F
∠1与∠2是一对同位角,
∠3与∠4是一对内错角, ∠2与∠4是一对同旁内角.
D
(2)如果把图看成是直线 CD,EF被直线AB所截, B C 那么∠1与∠5是一对什么 角?∠4与∠5呢? (3) 哪两条直线被哪一条直线 ∠1与∠5是一对同旁内角, 所截, ∠ 2与∠ 5是同位角
1.2--同位角内错-角同旁内角

.
13
例2
如图:直线DE交∠ABC的边BA于点 F. 如果内错角∠1与∠2相等,那么你能 找出图中其它相等的角吗?请说明理由。
同位角∠1与∠4相等
有互补的角吗?
D
同旁内角∠1与∠3互补
A F4E 23
1
B
C
如图:两只手的食子和拇 指在同一平面内,它们构 成的一对角可以看成是什 么角?类似地,你还能用 两只手的手指构成同位角 和同旁内角吗?
同位角
同位角
12
(4)
同位角
2 1 (5)
ba
1
2
c
(6)
同位角
1 2 (7)
1
2 (8)
内错角
.
1
1
2
2
(9)
(10)
同旁内角
8
2、下列各图中 1与 2哪些是同位角?哪些不是?
1 2
()
1
1 2
()
1
2 ()
2
()
.
9
例1 如图,直线DE截AB,AC,构成8个角。指出
所有的同位角、内错角和同旁内角。 1.若DE,AB被AC所截呢?
2.若DE,AC被AB所截呢?
关键:要先分 清哪两条直线 被哪一条直线 所截
D
21
34
A
58
67 E
B
C
课堂练习:
1、如图,(1)1和4是直线__A_B__与直线_C_D__被直线__B_D___
所截形成的___内__错__角___。
(2)2和 3是直线__A_D__与直线_B_C__被直线__B_D___所截形成
∠1与∠2是一对同位角,
∠3与∠4是一对内错角,
1.2__同位角、内错角、同旁内角
C 7
3
E 1 5 2
D
B
内错角是
Z 形状
4
A 8 7
6
5
4 2
活动3 认识同旁内角
⑴观察∠2、∠5与截线、被截直线有哪些位置关系? C 7 4 A 8 2 6 3 E 1 5
D
B
两条直线被第三条直线所截构成的八个角中,位于截 线的同一侧,被截直线的内侧的角,称为同旁内角.
活动3 认识同旁内角
⑵图中还有其它的同旁内角吗?若有,请你找出来.
c
4
1
2
3
4
a
⑴
⑵
活动5 巩固练习
AB CD BD 2、如图,(1)1和 4是直线_____与直线____被直线______ 内错角 所截形成的__________。
AD BC BD (2) 2和 3是直线_____与直线____被直线______所截形成 内错角 的_________。
请找出图中所有的同位角、内错角和同旁内角。
说能出你这节课的收获和体验让大家
与你分享吗?
活动6 课堂小结与作业
小结: 1.同位角是 F 形状 2.内错角是 Z 形状 3.同旁内角是 C 形状 作业: 作业本2
同位角、内错角和同旁内角的结构特征:
l3
2 1 3 4 6 5 7 8
l1
l2
能力挑战: 看图填空
A E
2 1 3
D
4
B
F
C
(1)若ED,BF被AB所截, ∠2 则∠1与_____是同位角。
能力挑战: 看图填空
A E
2 1 3
D
4
B
F
C
(2)若ED,BC被AF所截, ∠4 则∠3与_____是内错角。
(完整版)1.2同位角内错角同旁内角
义务教育课程标准实验教科书浙教版 (七年级下)
观察 如图:1、怎样描述这三条直线 的位置关系?
直线AB、CD被第三条直线EF所截
2、在两个交点处形
成几个角?这些角有
哪些与我们学过的有
关?
A
截线
E
21
B
34
65
C
78 D
被截线
F
观察 问题1:观察∠1与∠5的位置关系
同位角:①在截线EF的同旁
②在被截线AB、CD的同侧
他们的公共边
图形结构形如字母“F”,叫作“F”型
下列各图中 1与 2 哪些是同位角?哪些不是?
1 2
() 1
2 ()
1 2
() 1 2
()
探索交流
1、图中的角是那类角? 内错角 2、他们有何共同特征? 组成∠1和∠2的边中,截线是
他们的公共边
图形结构形如字母“Z”,叫作“Z”型
1 探索交流
1、图中的角是那类角? 同旁内角 2、他们有何共同特征?组成∠1和∠2的边中,截线是
他们的公共边
图形结构形如字母“U”,叫作“U”型
E
A
21 34
B
65 D
C
78
F
截线 被截线
同位角 同旁 同侧
内错角 异侧 之间
同旁内角 同旁 之间
结构特征
F Z U
如图:两只手的食子和拇指在同一平面内,它 们构成的一对角可以看成是什么角?
你还能用两只手的手指构成同位角和同旁内角吗?
看图填空:
作业导练最后一题
A
(1)若ED,BF被AB所截,
则∠ 1与 ∠2 是同位角; (2)若ED,BC被AF所截,
E1
观察 如图:1、怎样描述这三条直线 的位置关系?
直线AB、CD被第三条直线EF所截
2、在两个交点处形
成几个角?这些角有
哪些与我们学过的有
关?
A
截线
E
21
B
34
65
C
78 D
被截线
F
观察 问题1:观察∠1与∠5的位置关系
同位角:①在截线EF的同旁
②在被截线AB、CD的同侧
他们的公共边
图形结构形如字母“F”,叫作“F”型
下列各图中 1与 2 哪些是同位角?哪些不是?
1 2
() 1
2 ()
1 2
() 1 2
()
探索交流
1、图中的角是那类角? 内错角 2、他们有何共同特征? 组成∠1和∠2的边中,截线是
他们的公共边
图形结构形如字母“Z”,叫作“Z”型
1 探索交流
1、图中的角是那类角? 同旁内角 2、他们有何共同特征?组成∠1和∠2的边中,截线是
他们的公共边
图形结构形如字母“U”,叫作“U”型
E
A
21 34
B
65 D
C
78
F
截线 被截线
同位角 同旁 同侧
内错角 异侧 之间
同旁内角 同旁 之间
结构特征
F Z U
如图:两只手的食子和拇指在同一平面内,它 们构成的一对角可以看成是什么角?
你还能用两只手的手指构成同位角和同旁内角吗?
看图填空:
作业导练最后一题
A
(1)若ED,BF被AB所截,
则∠ 1与 ∠2 是同位角; (2)若ED,BC被AF所截,
E1
同位角内错角同旁内角
1.2 同位角,内错角,同旁内角
一、创设情景
1.1 同位角,内错角,同旁内角
平面上,两条直线有相交和平 行两种位置关系.
1.1 同位角,内错角,同旁内角
l
a
直线a、b被直线l所截.
b
1.1 同位角,内错角,同旁内角
直线a、b被直线l所截,有几对对 顶角,它们分别是哪些角?
b
α
有4对对顶角, ∠2与∠4,∠5与∠7,∠6 与∠8, ∠1和∠3分别是对顶角.
l
1
2
3 4
56 87
二、探索交流 1 观察交流
l
12
b
3 4
从直线 l 来看,∠1与∠5处于哪个位置? 5 6
∠1与∠5处于直线 l 的同一侧. α
87
对于直线a、b,∠1与∠5又处于哪个位置?
1
∠1与∠5都处于直线a、b的同一方.
这样的一对角( ∠1与∠5 )就是同位角. 5
图中的同位角还有哪些?
学校与游乐场所在的角 形成一(同位角 )角
学校与超市所在的角形 成一对( 同旁内角 )角
学校与飞机场所在的角 形成一对( 内错角 )角
游乐 场
超市 学校 学
解放路
马 人飞机场
鞍 民
池 路
路
六、例题精讲
例2 如图,直线DE交∠ABC的边BA于点 F,如果∠1=∠2,那么:
F
①同位角∠1和∠4相等,
②同旁内角∠1和∠3互补。
b
这样的一对角( ∠4与∠6 )就是内错角
l
12 3
4
56 87
图中的内错角还有哪些? 内错角还有∠3与∠5.
4
6
(Z型)
三、类比交流 变式图形:图中的∠1与∠2都是内错角.
一、创设情景
1.1 同位角,内错角,同旁内角
平面上,两条直线有相交和平 行两种位置关系.
1.1 同位角,内错角,同旁内角
l
a
直线a、b被直线l所截.
b
1.1 同位角,内错角,同旁内角
直线a、b被直线l所截,有几对对 顶角,它们分别是哪些角?
b
α
有4对对顶角, ∠2与∠4,∠5与∠7,∠6 与∠8, ∠1和∠3分别是对顶角.
l
1
2
3 4
56 87
二、探索交流 1 观察交流
l
12
b
3 4
从直线 l 来看,∠1与∠5处于哪个位置? 5 6
∠1与∠5处于直线 l 的同一侧. α
87
对于直线a、b,∠1与∠5又处于哪个位置?
1
∠1与∠5都处于直线a、b的同一方.
这样的一对角( ∠1与∠5 )就是同位角. 5
图中的同位角还有哪些?
学校与游乐场所在的角 形成一(同位角 )角
学校与超市所在的角形 成一对( 同旁内角 )角
学校与飞机场所在的角 形成一对( 内错角 )角
游乐 场
超市 学校 学
解放路
马 人飞机场
鞍 民
池 路
路
六、例题精讲
例2 如图,直线DE交∠ABC的边BA于点 F,如果∠1=∠2,那么:
F
①同位角∠1和∠4相等,
②同旁内角∠1和∠3互补。
b
这样的一对角( ∠4与∠6 )就是内错角
l
12 3
4
56 87
图中的内错角还有哪些? 内错角还有∠3与∠5.
4
6
(Z型)
三、类比交流 变式图形:图中的∠1与∠2都是内错角.
1.2 同位角、内错角、同旁内角(新浙教版)
∴∠1+∠3=180°
课堂练习:
AB 与直线___ 1、如图,(1) 1和 4 是直线____ CD 被直 内错角 BD 所截形成的_________ 线_____ 。
(2) 2和 3 是直线____ AD 与直线___ BC 被直线____ BD 所
A 内错角 。 截形成的________ A 1 1 B 3 3 2 2 C (2) B D 4 4 (1) 1 4 D
总结
与两直 线的位 置关系 同位 两直线 角 同侧
与截线的位置 关系 截线同侧 截线异侧
基本图 形
图形结构 特征 “F ”
内错 两直线 角 之间
同旁 两直线 内角 之间
“Z”
“n ”
截线的同侧
六、挑战极限
如图,平行直线AB、CD与相交直线EF 、GH相交,图中的 同旁内角共有( )对 A 4对 B E 8对 C G 12 对 D 16对
游乐 场 超市 学校 学 解 放 路
马
飞机场 人
民 路
鞍 池
路
课内练习
1.(1)如果把图看成是直线AB,EF被 直线CD所截,那么∠1与∠2是一对什 么角?∠3与∠4呢?∠2与∠4呢?
D
∠1与∠2是一对同位角,
∠3与∠4是一对内错角, ∠2与∠4是一对同旁内角.
A 1
4
E 5
2
3
F
(2)如果把图看成是直线C B C D,EF被直线AB所截, (3)哪两条直线被哪一条直 那么∠1与∠5是一对什么 线所截,∠2与∠5是同位角 角?∠4与∠5呢?
A C
B D
H
F
∠1与∠5是一对同旁内角, ∠4与∠5是一对内错角. 直线AB,CD被直线EF所截
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关键: 分清截线 和被截线
D
2 3 4 1
A
5 6
8 7
E C
B
A
(2)∠A与∠8是哪两条直线被第 3条直线所截的一对内错角? D (AB与DE 被AC所截的内错角与∠5是一对什么角?哪两条直线 被第三条直线所截的一对角? (AB与DE 被AC所截,是同旁内角) ∠A与∠6呢? (AB与DE 被AC所截,是同位角) 归纳:两个角若有一边在同一直线上,这条直 线就是截线,其余两边所在的直线是两被截线。
同旁
“F” “Z” “U”
两侧
同旁
1.2 同位角、内错角、同旁内角
三 线 八 角
a
2
1(
) 3 6 7 4 5 ( ) 8
截线
c
b
任意的两个角之间有哪些位置关 系呢?被截线
}
不同顶点上的两个角之间有哪些位置 关系呢?
例1 如图,直线AB,AC被直线DE所截,构成8个
角。指出所有的同位角、内错角和同旁内角。
(1)若DE,AC被AB所截呢?
练习: 第7页课内练习1,2
例2、 如图 直线DE交∠ABC的边AB于点F。
如果内错角∠1与∠2相等,那么同位角∠1与∠4
相等,同旁内角∠1与∠3互补。请说明理由。
F
练习: 第8页作业题3
本课你有什么收获呢?
与被截 线的位 置关系 同位 角 内错 角 同旁 内角 同侧 之间 之间 与截线的位置 关系 基本图 形 图形结构 特征
