分段函数的拐点
中考知识点分段函数

中考知识点分段函数一、定义域和值域分段函数的定义域和值域是由各个分段的定义域和值域确定的。
以函数f(x) = { x+3, x<0 2x, x>=0 } 为例,其定义域为整个实数集,值域为 (-∞, +∞)。
二、分段函数的图像对于分段函数,要根据每个分段的函数表达式来绘制图像。
以函数f(x) = { x+3, x<0 2x, x>=0} 为例,在x<0时,图像是一条斜率为1的直线,过原点,并且在x=0处有一个开口向上的拐点。
三、分段函数的连续性分段函数在分段点处可能不连续,需要通过计算极限来确定。
以函数f(x) = { x+3, x<0 2x, x>=0} 为例,分段点x=0处的左极限等于0,右极限等于0,与f(0)=0相符,因此该分段函数在x=0处连续。
四、分段函数的性质1. 分段函数的奇偶性由各个分段的奇偶性决定。
以函数f(x) = { x+3, x<0 2x, x>=0 } 为例,第一段函数x+3是奇函数,第二段函数2x是偶函数,所以整个分段函数为奇函数。
2. 分段函数的单调性由各个分段的单调性决定。
以函数f(x) = { x+3, x<0 2x, x>=0 } 为例,第一段函数x+3是递增函数,第二段函数2x也是递增函数,所以整个分段函数是递增函数。
3. 分段函数的最大值和最小值在每个分段函数的最大值和最小值中取得。
以函数f(x) = { x+3, x<0 2x, x>=0 } 为例,在第一段函数中,最小值为3,最大值不存在;在第二段函数中,最小值不存在,最大值也不存在。
四、分段函数的应用1. 分段函数可以描述现实生活中的一些问题,如电话费计费等。
以电话费计费为例,某通信公司的计费标准为:前50分钟,每分钟0.5元;超过50分钟,每分钟0.3元。
假设通话时长为x分钟,对应的通话费用为函数f(x) = { 0.5x,x<=50 0.3(x-50)+25, x>50 }。
考研数学 知识结构思维导图(数二)
1.分离变量,物以类聚人以群分 2.y'在等式左侧,右侧应写成乘积形式
一阶微分方程的求解
齐次型
y'=f(y/x)
对x求导
1/y'=f(x/y)
对y求导
换元后分离变量,交换x和y的地位
一阶线性型(或可换元为它)
y'+p(x)y=q(x) 伯努利方程
y'+p(x)y=q(x)的特殊形式
伯努利方程可理解为一 阶线性方程的普遍形式
符号函数 抽象函数
复合函数
偏导函数
换元法
一元函数积分换元法 二元函数积分换元法
应用
面积
1.积分变化口诀:后积先定限,限内画直 线,先交先下限,后交写上限;
2.注意对称性得0的应用可以极大地化简计 算
微分方程
可分离变量
y'=f(x).g(y)
分离变量
y'=f(ax+by+c)
换元后再分离变量
一般一层积分不易处理,化成两层积分,在交换 积分次序
分部积分法
换序型
反常积分的计算
研究对象
常规题型取绝对值时取值范围
曲线平移时相关符号不同取值范围所对应的面积
切线综合
函数列综合
题型总结
在平面极坐标系中,如果极径ρ随极角θ的 增加而成比例增加(或减少),这样的动
点所形成的轨迹叫做螺线。
阿基米德螺旋线
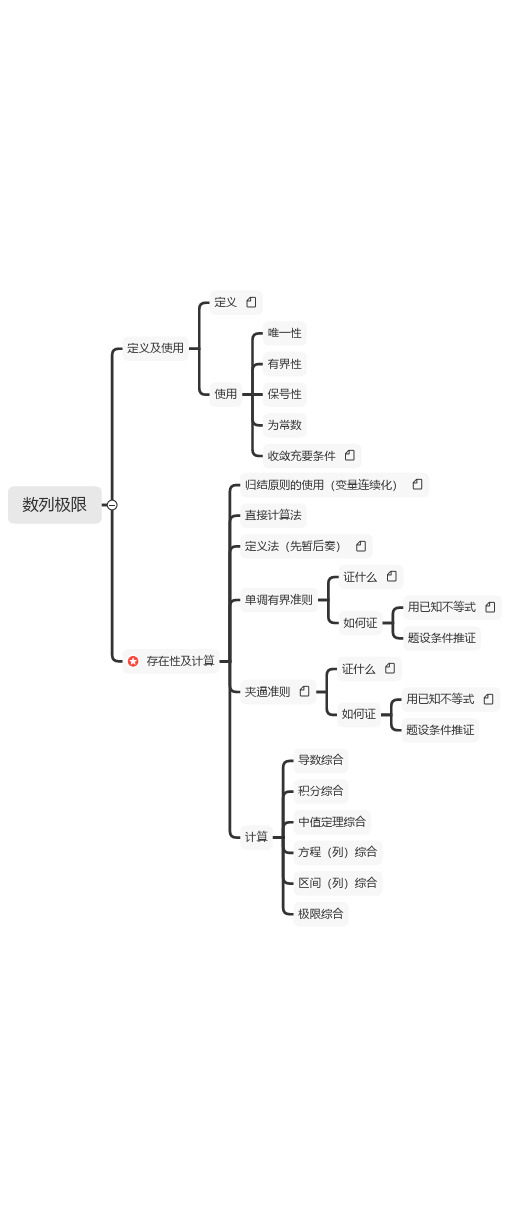
数列极限
定义
定义及使用
唯一性 有界性
使用
保号性
为常数
收敛充要条件
归结原则的使用(变量连续化)
直接计算法
定义法(先暂后奏)
国开电大-高等数学基础-第1-4次作业答案

高等数学基础第一次作业第1章 函数第2章 极限与连续(一) 单项选择题⒈下列各函数对中,(C )中的两个函数相等.A. 2)()(x x f =,x x g =)( B. 2)(x x f =,x x g =)(C. 3ln )(x x f =,x x g ln 3)(= D. 1)(+=x x f ,11)(2--=x x x g分析:判断函数相等的两个条件(1)对应法则相同(2)定义域相同A 、2()f x x ==,定义域{}|0x x ≥;x x g =)(,定义域为R定义域不同,所以函数不相等;B 、()f x x ==,x x g =)(对应法则不同,所以函数不相等;C 、3()ln 3ln f x x x ==,定义域为{}|0x x >,x x g ln 3)(=,定义域为{}|0x x > 所以两个函数相等D 、1)(+=x x f ,定义域为R ;21()11x g x x x -==+-,定义域为{}|,1x x R x ∈≠ 定义域不同,所以两函数不等。
故选C⒉设函数)(x f 的定义域为),(+∞-∞,则函数)()(x f x f -+的图形关于(C )对称. A. 坐标原点 B. x 轴 C. y 轴 D. x y = 分析:奇函数,()()f x f x -=-,关于原点对称偶函数,()()f x f x -=,关于y 轴对称()y f x =与它的反函数()1y f x -=关于y x =对称,奇函数与偶函数的前提是定义域关于原点对称设()()()g x f x f x =+-,则()()()()g x f x f x g x -=-+= 所以()()()g x f x f x =+-为偶函数,即图形关于y 轴对称故选C⒊下列函数中为奇函数是(B ).A. )1ln(2x y += B. x x y cos =C. 2xx a a y -+= D. )1ln(x y +=分析:A 、()()()()22ln(1)ln 1y x x xy x -=+-=+=,为偶函数B 、()()()cos cos y x x x x x y x -=--=-=-,为奇函数 或者x 为奇函数,cosx 为偶函数,奇偶函数乘积仍为奇函数C 、()()2x xa a y x y x -+-==,所以为偶函数 D 、()ln(1)y x x -=-,非奇非偶函数故选B⒋下列函数中为基本初等函数是(C ). A. 1+=x y B. x y -= C. 2xy = D. ⎩⎨⎧≥<-=0,10,1x x y 分析:六种基本初等函数(1) y c =(常值)———常值函数(2) ,y x αα=为常数——幂函数 (3) ()0,1x y a a a =>≠———指数函数 (4) ()log 0,1a y x a a =>≠———对数函数(5) sin ,cos ,tan ,cot y x y x y x y x ====——三角函数(6) [][]sin ,1,1,cos ,1,1,tan ,cot y arc x y arc x y arc x y arc x=-=-==——反三角函数分段函数不是基本初等函数,故D 选项不对 对照比较选C⒌下列极限存计算不正确的是(D ).A. 12lim 22=+∞→x x x B. 0)1ln(lim 0=+→x x C. 0sin lim =∞→x x x D. 01sin lim =∞→xx x分析:A 、已知()1lim 00n x n x→∞=>2222222211lim lim lim 1222101x x x x x x x x x x x →∞→∞→∞====++++ B 、0limln(1)ln(10)0x x →+=+=初等函数在期定义域内是连续的C 、sin 1limlim sin 0x x x x xx →∞→∞==x →∞时,1x是无穷小量,sin x 是有界函数,无穷小量×有界函数仍是无穷小量D 、1sin1lim sin lim1x x x x x x→∞→∞=,令10,t x x =→→∞,则原式0sin lim 1t t t →== 故选D⒍当0→x 时,变量(C )是无穷小量. A.x x sin B. x1C. xx 1sinD. 2)ln(+x 分析;()lim 0x af x →=,则称()f x 为x a →时的无穷小量A 、0sin lim1x xx →=,重要极限B 、01lim x x→=∞,无穷大量C 、01lim sin 0x x x →=,无穷小量x ×有界函数1sin x 仍为无穷小量D 、()0limln(2)=ln 0+2ln 2x x →+=故选C⒎若函数)(x f 在点0x 满足(A ),则)(x f 在点0x 连续。
找界点 划区界——高中化学中的分段函数问题归类例析

故 加 稀 硝 酸 后 剩 余 金 属 及 溶 液 中 出 现 的 离 子 组 合
应 有 表 1 1 示 的六 种 情 况 : — 所
表 1 1 —
1 2 3
(5 ) 故从第 一个 拐点处开始 , 16g , 表示 AlO 。 ( H) 达到最
大量 , 一 1 第 二 个 拐 点 处 B S 4达 到 最 大 量 , f 5mI , aO
一
2 L. 0m
三 、 式 盐 一 正 盐 型 酸
Fe C e ’ u F ‘ CU F 2 e+ F 2 Cu Cu e 2
这种类 型常有二 氧化碳参加反应. 【 2 (0 2年 , 海 高考题 ) 足量 C ) 通 入 例 】 20 上 将 ( 2 KO 和 C ( H a OH) 的混合稀溶液 中, 。 生成 沉淀 的物 质的 量 () 和通人 C 2 积( 的关 系正确 的是 ( O 体 ) ) .
数 的题 型 归 纳 于 下 .
一
沉
淀
质 量
\
) mL 2 ] /
A 沉
淀 ቤተ መጻሕፍቲ ባይዱ
) mL 2 ] /
B
、
氧 化 还 原 型
质 量
\
即根据物质的还 原性 或氧化性 顺序分段 讨论 , 如 例
在 F 、 u粉 的 混 合 物 中 加稀 硝 酸 , 得 什 么 成 分 ? 由 于 eC 可 硝 酸 是 一 种 强 氧 化 剂 , 两 种 金 属 都 能 被 氧 化 , 为 还 这 因
中学 教 学 参 考
复 习指津
找 界 点
— —
划 区 界
高 中化学 中的分段 函数 问题 9类例析 5 -
matlab拟合分段函数

matlab拟合分段函数在MATLAB中,拟合分段函数可以通过多种方法实现。
这里将介绍两种主要方法:分段线性拟合和分段多项式拟合。
1.分段线性拟合:分段线性拟合是将整个函数区间分成多个小区间,在每个小区间内使用线性函数进行拟合。
这种方法适用于函数在不同区间内的变化趋势不同的情况。
首先,我们需要定义函数的分段点。
假设我们的函数在x=0、x=1和x=2处有拐点,我们可以按照以下方式定义这些分段点:xdata = [0, 1, 2];接下来,我们需要给出函数在每个区间内的取值,这些值可以通过观察得到或通过其他方法计算得出。
假设我们的函数在这些分段点处的取值分别为:ydata = [1, 4, 2];现在,我们可以使用polyfit函数进行分段线性拟合:p = polyfit(xdata, ydata, 1);这里的1表示我们要拟合的线性函数的阶数。
我们还可以使用polyval函数来计算拟合得到的函数在任意点的取值:x=0:0.1:2;y = polyval(p, x);最后,我们可以使用plot函数将原始数据点和拟合得到的分段线性函数画在同一张图上,以进行比较:figureplot(x, y, 'r-', xdata, ydata, 'bo')legend('分段线性函数', '原始数据点')2.分段多项式拟合:分段多项式拟合是将整个函数区间分成多个小区间,在每个小区间内使用不同的多项式函数进行拟合。
这种方法适用于函数在不同区间内的曲线特征不同的情况。
和分段线性拟合类似,我们需要首先定义分段点和函数在这些分段点处的取值:xdata = [0, 1, 2];ydata = [1, 4, 2];然后,我们可以使用polyfit函数进行分段多项式拟合:p = polyfit(xdata, ydata, n);这里的n表示我们要拟合的多项式函数的阶数。
拐点(数学用语)—搜狗百科

拐点(数学用语)—搜狗百科可以这样通俗的理解拐点,即在a点的左右f''(x)的正负发生变化的点,f''(a)异号(由正变负或由负变正)或者不存在。
在数学领域是指,凸曲线与凹曲线的连接点。
拐点定义(根据高等数学同济7版上册第147页)一般的,设y=f(x)在区间I上连续,x0是I的内点(除端点外的I 内的点)。
如果曲线y=f(x)在经过点(x0,f(x0))时,曲线的凹凸性改变了,那么就称点(x0,f(x0))为这曲线的拐点。
凹的充分条件:若曲线y=f(x)(a≤x≤b)的一段,位于其任意一点的切线之上(或之下),则称这个可微分的函数y=f(x)的图形于闭区间[a,b]上是凹(或对应地,凸)的。
在假设二阶导函数f'(x)存在的情况下,当a0[或对应地f'(x)<0]成立,为图形是凹(或对应地,凸)的充分条件。
拐点的必要条件:设f(x)在(a,b)内二阶可导,x0∈(a,b),若(x0,f(x0))是曲线y=f(x)的一个拐点,则f‘’(x0)=0。
拐点的充分条件:设f(x)在(a,b)内二阶可导,x0∈(a,b),则f‘’(x0)=0,若在x0两侧附近f‘’(x0)异号,则点(x0,f(x0))为曲线的拐点。
否则(即f‘’(x0)保持同号,(x0,f(x0))不是拐点。
当函数图像上的某点使函数的二阶导数为零,且三阶导数不为零时,这点即为函数的拐点。
若函数y=f(x)在c点可导,且在点c一侧是凸,另一侧是凹,则称c是函数y=f(x)的拐点。
另外,如果c是拐点,必然有f''(c)=0或者f''(c)不存在;反之则不成立;比如,f(x)=x^4,有f''(0)=0,但f''(x)=12x^2在整个定义域内恒大于0,所以0不是函数f(x)=x^4的拐点,且整个函数在R上是凹的。
拐点的求法(摘录自高等数学同济5版上册第149页)可以按下列步骤来判断区间I上的连续曲线y=f(x)的拐点:⑴求f''(x);⑵令f''(x)=0,解出此方程在区间I内的实根,并求出在区间I内f''(x)不存在的点;⑶对于⑵中求出的每一个实根或二阶导数不存在的点x0,检查f''(x)在x0左右两侧邻近的符号,那么当两侧的符号相反时,点(x0,f(x0))是拐点,当两侧的符号相同时,点(x0,f(x0))不是拐点。
函数拐点的定义

函数拐点的定义在数学中,函数拐点是指函数图像的一个特殊点,其前后的函数趋势明显不同。
形式上,如果函数f(x)在点x0处发生拐弯,则存在一个实数k,使得f(x)在x0处的导数存在,且导数的值等于k。
由于函数图像的拐点是由导数的变化引起的,因此拐点也被称为导数拐点。
在数学分析中,函数拐点可以用来分析函数的性质,如单调性、凹凸性等。
1. 函数拐点的定义在数学中,函数拐点是指函数图像的一个特殊点,其前后的函数趋势明显不同。
形式上,如果函数f(x)在点x0处发生拐弯,则存在一个实数k,使得f(x)在x0处的导数存在,且导数的值等于k。
由于函数图像的拐点是由导数的变化引起的,因此拐点也被称为导数拐点。
具体来说,函数f(x)在点x0处发生拐点,当且仅当存在一个实数k,使得f(x)在x0处的导数存在,且导数的值等于k。
这意味着,如果函数f(x)在x0处的导数存在,则函数f(x)在x0处的导数的取值必须是一个定值。
如果函数f(x)在x0处的导数不存在,则函数f(x)在x0处并不存在拐点。
在实际应用中,函数拐点可以用来分析函数的性质,如单调性、凹凸性等。
例如,如果函数f(x)在x0处存在拐点,则可以判断函数f(x)在x0处的单调性,即函数f(x)在x0处是单调递增还是单调递减。
此外,函数拐点还可以用来判断函数f(x)在x0处的凹凸性,即函数f(x)在x0处是凸出还是凹陷。
通常来说,如果函数f(x)在x0处存在拐点,且函数f(x)在x0处的导数大于0,则函数f(x)在x0处是凸出的;如果函数f(x)在x0处存在拐点,且函数f(x)在x0处的导数小于0,则函数f(x)在x0处是凹陷的。
另外,函数拐点还可以用来分析函数的单调性和凹凸性的变化。
例如,如果函数f(x)在x0处存在拐点,且函数f(x)在x0处的导数变化由正变为负,则可以判断函数f(x)在x0处由单调递增变为单调递减;如果函数f(x)在x0处存在拐点,且函数f(x)在x0处的导数变化由负变为正,则可以判断函数f(x)在x0处由单调递减变为单调递增。
教材回归(七)分段函数的应用

分段函数与数学建模的关系
THANKS
感谢您的观看。
根据定积分的定义,需要将积分区间分成若干个子区间,并在每个子区间上分别计算积分。
分段函数的反常积分
类似于定积分,反常积分也需要根据分段函数在各区间上的表达式分别进行计算。
分段函数的原函数
为了计算分段函数的定积分,需要先找到分段函数的原函数。
积分在解决实际问题中的应用
积分可以用来解决各种实际问题,如计算面积、体积等。
收益管理
在酒店、航空和物流等行业,分段函数被用于预测和管理收益,例如根据预订数量和价格水平来调整价格。
分段函数可以用于描述弹性材料在不同应力水平下的行为,例如弹性模量、泊松比等。
弹性力学
热传导
电磁学
在热传导过程中,分段函数可以用于描述温度在不同时间和空间位置的变化。
在电磁学中,分段函数可以用于描述电流、电压和电阻在不同条件下的变化。
教材回归(七)分段函数的应用
目录
分段函数的定义与性质 分段函数的实际应用 分段函数的图像分析 分段函数的解析解法 分段函数在微积分中的应用 分段函数与其他数学概念的关系
01
CHAPTER
分段函数的定义与性质
分段函数是一个函数,它在不同的区间上由不同的函数表达式定义。
定义
分段函数 $f(x) = begin{cases} x + 1, & x < 0 x, & 0 leq x < 1 2x, & x geq 1 end{cases}$
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分段函数的拐点
分段函数是高中数学课程中的一大重点内容,而其中分段函数的拐点是一个非常重要的概念。
在本文中,我们将会深入探讨分段函数的拐点,包括其定义、性质、求解以及相关例题。
一、定义
拐点,又称拐角点,是指函数图像发生突变的点。
在分段函数中,当两条直线的斜率不同时,函数图像就会出现一个弯曲的拐点。
可以用导数的方法来求出函数的拐点。
二、性质
1. 拐点处函数的导数变化
我们知道,函数的导数是函数的变化率。
因此,当函数的导数发生突变时,函数图像就会出现拐点。
在拐点左边,函数导数增加,而在拐点右边,函数导数减少。
2. 拐点处函数的二阶导数为零
当函数的二阶导数为零时,就会出现拐点。
因此,求出函数的二阶导数并且令其等于零,就可以求出函数的拐点。
3. 函数的极值点可能也是拐点
函数的极值点可能也是拐点。
当函数的极值点和拐点重合时,函数的图像在此处有一个非常尖锐的弯曲。
三、求解方法
1. 导数法
在函数图像上,找到两条直线的交点,即为拐点。
由于函数的导数是函数变化率的表现,我们可以通过求导数来确定函数的拐点。
具体来说,先求出函数的导数,然后求出导数的导数,即函数的二阶导数。
令二阶导数等于零,解出方程,就可以求出函数的拐点。
2. 自变量法
自变量法是另一种常用的求解分段函数拐点的方法。
具体来说,我们可以分别求出函数的两个段的自变量,然后求解这两个自变
量之间的交点。
这个交点,即为函数的拐点。
四、例题
考虑以下分段函数:
$f(x)=\begin{cases} x^2 & x\leq 2 \\ 2x-2 & x > 2 \end{cases}$
首先,我们需要求出函数的导数:
$f'(x)=\begin{cases} 2x & x < 2 \\ 2 & x > 2 \end{cases}$
然后,我们需要求出函数的二阶导数:
$f''(x)=\begin{cases} 2 & x < 2 \\ 0 & x > 2 \end{cases}$
令$f''(x)=0$,解得$x=2$。
因此,$x=2$是函数的拐点。
另一个例题:
考虑以下分段函数:
$f(x)=\begin{cases} x^3+3x^2-10x-24 & x\leq 1 \\ x^2+x-2 & x > 1 \end{cases}$
首先,我们需要求出函数的导数:
$f'(x)=\begin{cases} 3x^2+6x-10 & x < 1 \\ 2x+1 & x > 1
\end{cases}$
然后,我们需要求出函数的二阶导数:
$f''(x)=\begin{cases} 6x+6 & x < 1 \\ 2 & x > 1 \end{cases}$
令$f''(x)=0$,解得$x=-1$。
但是,$x=-1$不在函数的定义域内,因此不能是函数的拐点。
同样的,$x=1$也不能是函数的拐点,因
为在此处函数的导数并不连续。
因此,这个分段函数不具有拐点。
五、结论
分段函数的拐点是函数图像发生突变的点。
拐点处函数的导数变化,函数的二阶导数为零。
我们可以用导数法或者自变量法来求解分段函数的拐点。
在求解拐点的时候,一定要注意函数的定义域和导数的连续性。
