贾俊平第四版统计学-第七章参数估计练习题
统计学贾俊平第四版第七章课后答案目前最全

7.1从一个标准差为5的总体中抽出一个容量为40的样本,样本均值为25。
(1) 样本均值的抽样标准差x σ等于多少?(2) 在95%的置信水平下,允许误差是多少?解:已知总体标准差σ=5,样本容量n =40,为大样本,样本均值x =25, (1)样本均值的抽样标准差x σ=n σ=405=0.7906 (2)已知置信水平1-α=95%,得 α/2Z =1.96, 于是,允许误差是E =nα/2σZ =1.96×0.7906=1.5496。
7.2 某快餐店想要估计每位顾客午餐的平均花费金额。
在为期3周的时间里选取49名顾客组成了一个简单随机样本。
(1)假定总体标准差为15元,求样本均值的抽样标准误差。
x nσ=49==2.143 (2)在95%的置信水平下,求边际误差。
x x t σ∆=⋅,由于是大样本抽样,因此样本均值服从正态分布,因此概率度t=2z α 因此,x x t σ∆=⋅2x z ασ=⋅0.025x z σ=⋅=1.96×2.143=4.2 (3)如果样本均值为120元,求总体均值 的95%的置信区间。
置信区间为:(),x x x x -∆+∆=()120 4.2,120 4.2-+=(115.8,124.2) 7.37.4 从总体中抽取一个n=100的简单随机样本,得到x =81,s=12。
要求:大样本,样本均值服从正态分布:2,xN n σμ⎛⎫ ⎪⎝⎭或2,s xN n μ⎛⎫⎪⎝⎭置信区间为:2x z x z n n αα⎛-+ ⎝n 100=1.2 (1)构建μ的90%的置信区间。
2z α=0.05z =1.645,置信区间为:()81 1.645 1.2,81 1.645 1.2-⨯+⨯=(79.03,82.97)(2)构建μ的95%的置信区间。
2z α=0.025z =1.96,置信区间为:()81 1.96 1.2,81 1.96 1.2-⨯+⨯=(78.65,83.35)(3)构建μ的99%的置信区间。
贾俊平《统计学》复习笔记课后习题详解及典型题详解(参数估计)【圣才出品】

∧
定义:点估计是用样本统计量θ的某个取值直接作为总体参数 θ 的估计值。 局限性:一个点估计值的可靠性是由它的抽样标准误差来衡量的,这表明一个具体的点 估计值无法给出估计的可靠性的度量,因此不能完全依赖于一个点估计值,而应围绕点估计 值构造总体参数的一个区间。 (2)区间估计 区间估计的基本思想:在点估计的基础上,给出总体参数估计的一个区间范围,该区间 通常由样本统计量加减估计误差得到。进行区间估计时,根据样本统计量的抽样分布能够对 样本统计量与总体参数的接近程度给出一个概率度量。 置信区间:在区间估计中,由样本统计量所构造的总体参数的估计区间。
著性水平表示区间估计的不可靠概率。置信度愈大(即估计的可靠性愈大),则置信区间相
应也愈大(即估计准确性愈小)。
3.评价估计量的标准
2 / 57
圣才电子书
(1)无偏性
十万种考研考证电子书、题库视频学习平台
指估计量抽样分布的数学期望等于被估计的总体参数。
∧
∧
∧
设总体参数为 θ,所选择的估计量为θ,若有 E(θ)=θ,则称θ为 θ 的无偏估计量。
1 / 57
圣才电子书 十万种考研考证电子书、题库视频学习平台
置信下限:置信区间的最小值。
置信上限:置信区间的最大值。
置信水平(也称为置信度或置信系数):将构造置信区间的步骤重复多次,置信区间中
包含总体参数真值的次数所占的比例。
∧
∧
区间估计的数学定义:若用两个统计量θ1(x1,x2,…,xn)和θ2(x1,x2,…,xn)
存在“可能包含”或“可能不包含”的问题。
③在实际问题中,进行估计时往往只抽取一个样本,此时所构造的是与该样本相联系的
统计学课后习题答案(第四版)贾俊平(第4、5、7、10章)

《统计学》第四版 第四章练习题答案众数:M o =1O;中位数:中位数位置=n+1/2=5.5 , M e =10 ;平均数:(2) Q L 位置=n/4=2.5, Q L =4+7/2=5.5 ; Q u 位置=3n/4=7.5 , Q u =12(4) 4.2 和 M O =23。
将原始数据排序后,计算中位数的位置为:中位数位置=n+1/2=13,第13个位置上的数值为23,所以中位数为 M e =23(2)Q L 位置=n/4=6.25, Q L ==19 ; Q u 位置=3n/4=18.75,Q u =26.5茎 叶 频数 5 5 1 6 6 7 8 3 71 3 4 8 85(3)第一种排队方式: 离散程度大于第二种排队方式。
(4 )选方法二,因为第二种排队方式的平均等待时间较短,且离散程度小于第一种排队方 式。
_ Z X i4.4 ( 1)X8223/30=274.14.1 ( 1 ) 二X i X =n96.9,6 102' (X i-X ) _156.4 42n -1, 9由于平均数小于中位数和众数,所以汽车销售量为左偏分布。
(1)从表中数据可以看出,年龄出现频数最多的是 19和23,故有个众数,即 M O =19(3)⑶平均数-A =600/25=24,标准差—(XLX)\ n —1210626.6525-1n(4) 偏态系数SK=1.08,峰态系数K=0.77(5) 分析:从众数、中位数和平均数来看,网民年龄在 23-24岁的人数占多数。
由于标准差较大,说明网民年龄之间有较大差异。
从偏态系数来看,年龄分布为右偏,由于偏态系数 1,所以,偏斜程度很大。
由于峰态系数为正值,所以为尖峰分布。
(1)茎叶图如下: 大于 4.3 —2'(X 一 X ) 4.080.714nn -1■ 8由于两种排队方式的平均数不同,所以用离散系数进行比较。
(2) X 二一^ =63/9=7, S = ■■n中位数位置=n+1/2=15.5 , M e=272+273/2=272.5(2) Q L位置=n/4=7.5, Q L==(258+261)/2=259.5 ; Q u 位置=3n/4=22.5 , Q u=(284+291)/2=287.5' (^-X ^ /3002-7 = 21.17 I n —1 \ 30—12100 +3000 +15004.5 (1)甲企业的平均成本=总成本/总产量=-2100 3000---- + ----- 15 20乙企业的平均成本=总成本/总产量=3255150015006255=18.293255 1500 1500 342____ + _____ + _____152030原因:尽管两个企业的单位成本相同, 但单位成本较低的产品在乙企业的产量中所占比重较 大,因此拉低了总平均成本。
统计学贾俊平_第四版课后习题答案
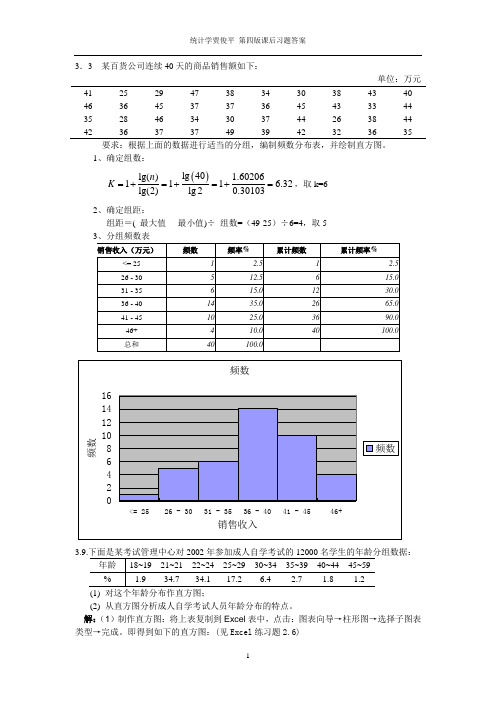
3.3 某百货公司连续40天的商品销售额如下:单位:万元41 25 29 47 38 34 30 38 43 40 46 36 45 37 37 36 45 43 33 44 35 28 46 34 30 37 44 26 38 44 42363737493942323635要求:根据上面的数据进行适当的分组,编制频数分布表,并绘制直方图。
1、确定组数: ()l g 40l g () 1.60206111 6.32l g (2)l g 20.30103n K =+=+=+=,取k=62、确定组距:组距=( 最大值 - 最小值)÷ 组数=(49-25)÷6=4,取5(1) 对这个年龄分布作直方图;(2) 从直方图分析成人自学考试人员年龄分布的特点。
解:(1)制作直方图:将上表复制到Excel 表中,点击:图表向导→柱形图→选择子图表类型→完成。
即得到如下的直方图:(见Excel 练习题2.6)(2)年龄分布的特点:自学考试人员年龄的分布为右偏。
解:(1)根据上面的数据,画出两个班考试成绩的对比条形图和环形图。
3.14 已知1995—2004年我国的国内生产总值数据如下(按当年价格计算):要求:(2)绘制第一、二、三产业国内生产总值的线图。
4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下:2 4 7 10 10 10 12 12 14 15要求:(1)计算汽车销售量的众数、中位数和平均数。
(2)根据定义公式计算四分位数。
(3)计算销售量的标准差。
(4)说明汽车销售量分布的特征。
解:Statistics汽车销售数量N Valid 10Missing 0Mean 9.60Median 10.00Mode 10Std. Deviation 4.169Percentiles 25 6.2550 10.0075 12.50种是所有颐客都进入一个等待队列:另—种是顾客在三千业务窗口处列队3排等待。
统计学贾俊平_第四版课后习题答案第七章

7.11 (1) 解:已知n=50,1a -=0.9522,ss x z xz nn a aæö-×+×ç÷èø=81.822981.8229101.491.966,101.491.9665050æö-´+´ç÷èø= (100.89,101.91)(2)解:已知n=50,1a -=0.95,2z a =00.0225z =1.96,样本比率p=(50-5)/50=0.9 则食品合格率的95%的置信区间:()()2211,p p p p p zp z nna aæö--ç÷-×+×ç÷èø=()()0.910.90.910.90.9 1.91.966,0.9 1.91.9665050æö---´+´ç÷èø=(0.8168,0.9832)7.22 (1)由题知,该题为大样本,方差已知,则有21m m -的95%的置信区间为:176.12100201001696.1)2325()(2221212/21±=+´±-=+±-n s n s z x x a即(0.824,3.176)(2m m -的95%的置信区间为:()()64.42112212212/21±=÷÷øöççèæ+-+±-n n s n ntxxpa 即(—2.64,6.64) (3)由题知,该题为小样本,方差不同, 则有21m m -的95%的置信区间为:()()64.42112212212/21±=÷÷øöççèæ+-+±-n n s n n tx x p a 即(—2.64,6.64) (4)由题知,该题为小样本,样本量不等,方差相等,则合并估计量为()()713128524211212222112==-+-+-=n n s n s n s p 则有21m m -的95%的置信区间为:()()02.42112212212/21±=÷÷øöççèæ+-+±-n n s n n tx x p a 即(—2.02,6.02) ,2z a =00.0225z =1.96。
统计学(第四版)袁卫 庞皓 贾俊平 杨灿 统计学 第七章练习题参考解答

STATISTICS
单击练此习处题编第部辑七分母章版参标考题解样答式
练习题7.1
1. 设销售收入 为自变量,销售成本 为因变量。现已根据某百货
公司某年12个月的有关资料计算出以下数据:(单位:万元)
(xt x)2 425053.73 x 647.88
(yt y)2 262855.25
F (k 1, n k) F0.05 (1, 26) 2.91
F=17.70503 F0.05 (1, 26) 2.91
所以y和 联合起来对最终消费有显著影响,即回归方 程整体上是显著的。
练习题7.7
下表给出y对x2和x3回归的结果:
离差来源
平方和(SS) 自由度(df)
由F=58.20479,大于临界值 F0.05 (4 1, 22 4) 3.16 ,
说明模型在整体上是显著的。
练习题7.5
为进一步研究前期的消费对本期消费的影响,准备拟合以下
形式的消费函数: ct 1 yt 2ct1 ut
式中:ct 为t 期的消费;ct1 为 t-1期的消费;yt 为国民总收入。
t 2 (n 2) t0.025 (10) 2.2281 t 245.71875 t0.025 (8) 2.2281
H0 : 0 ,检验说明x对y有显著影响.
(4) 假定下年1月销售收入为800万元,利用拟合的回归方 程预测其销售成本,并给出置信度为95%的预测区间
y 549.8
(xt x)(yt y) 334229.09
(1)拟合简单线性回归方程,并对方程中回归系数的经济意义作 出解释。
统计学第七章、第八章课后题答案
统计学复习笔记第七章参数估计一、思考题1.解释估计量和估计值在参数估计中,用来估计总体参数的统计量称为估计量。
估计量也是随机变量。
如样本均值,样本比例、样本方差等。
根据一个具体的样本计算出来的估计量的数值称为估计值。
2.简述评价估计量好坏的标准(1)无偏性:是指估计量抽样分布的期望值等于被估计的总体参数。
(2)有效性:是指估计量的方差尽可能小。
对同一总体参数的两个无偏估计量,有更小方差的估计量更有效。
(3)—致性:是指随着样本量的增大,点估计量的值越来越接近被估总体的参数。
3.怎样理解置信区间在区间估计中,由样本统计量所构造的总体参数的估计区间称为置信区间。
置信区间的论述是由区间和置信度两部分组成。
有些新闻媒体报道一些调查结果只给出百分比和误差(即置信区间),并不说明置信度,也不给出被调查的人数,这是不负责的表现。
因为降低置信度可以使置信区间变窄(显得“精确”),有误导读者之嫌。
在公布调查结果时给出被调查人数是负责任的表现。
这样则可以由此推算出置信度(由后面给出的公式),反之亦然。
4.解释95%的置信区间的含义是什么置信区间95%仅仅描述用来构造该区间上下界的统计量(是随机的)覆盖总体参数的概率。
也就是说,无穷次重复抽样所得到的所有区间中有95% (的区间)包含参数。
不要认为由某一样本数据得到总体参数的某一个95%置信区间,就以为该区间以0.95的概率覆盖总体参数。
5.简述样本量与置信水平、总体方差、估计误差的关系。
1.估计总体均值时样本量n为其中:E22.样本量n与置信水平1- a、总体方差•:、估计误差E之间的关系为与置信水平成正比,在其他条件不变的情况下,置信水平越大,所 需要的样本量越大;与总体方差成正比,总体的差异越大,所要求的样本量也越大; 与与总体方差成正比,样本量与估计误差的平方成反比,即可以接 受的估计误差的平方越大,所需的样本量越小。
二、练习题1. 从一个标准差为5的总体中采用重复抽样方法抽出一个样本 量为40的样本,样本均值为25。
贾俊平第四版统计学-第七章参数估计练习题
第七章参数估计练习题一.选择题1.估计量的含义是指()A.用来估计总体参数的统计量的名称B.用来估计总体参数的统计量的具体数值C.总体参数的名称D.总体参数的具体取值2.一个95%的置信区间是指()A.总体参数有95%的概率落在这一区间内B.总体参数有5%的概率未落在这一区间内C. 在用同样方法构造的总体参数的多个区间中,有95%的区间包含该总体参数。
D.在用同样方法构造的总体参数的多个区间中,有95%的区间不包含该总体参数。
3.95%的置信水平是指()A.总体参数落在一个特定的样本所构造的区间内的概率是95%B.在用同样方法构造的总体参数的多个区间中,包含总体参数的区间比例为95%C.总体参数落在一个特定的样本所构造的区间内的概率是5%D.在用同样方法构造的总体参数的多个区间中,包含总体参数的区间比例为5%4.根据一个具体的样本求出的总体均值的95%的置信区间()A.以95%的概率包含总体均值B.有5%的可能性包含总体均值C.一定包含总体均值D.要么包含总体均值,要么不包含总体均值5. 当样本量一定时,置信区间的宽度()A.随着置信水平的增大而减小B. .随着置信水平的增大而增大C.与置信水平的大小无关 D。
与置信水平的平方成反比6.当置信水平一定时,置信区间的宽度()A.随着样本量的增大而减小B. .随着样本量的增大而增大C.与样本量的大小无关 D。
与样本量的平方根成正比7.在参数估计中,要求通过样本的统计量来估计总体参数,评价统计量的标准之一是使它与总体参数的离差越小越好。
这种评价标准称为()A.无偏性 B. 有效性 C. 一致性 D. 充分性8. 置信水平(1-α)表达了置信区间的()A.准确性 B. 精确性 C. 显著性 D. 可靠性9. 在总体均值和总体比例的区间估计中,边际误差由()A.置信水平决定 B. 统计量的抽样标准差确定C. 置信水平和统计量的抽样标准差D. 统计量的抽样方差确定10. 当正态总体的方差未知,且为小样本条件下,估计总体均值使用的分布是()A.正态分布B. t分布C.χ2 分布D. F分布11. 当正态总体的方差未知,且为大样本条件下,估计总体均值使用的分布是()A.正态分布B. t分布C.χ2 分布D. F分布12. 当正态总体的方差已知时,且为小样本条件下,估计总体均值使用的分布是()A.正态分布B. t分布C.χ2 分布D. F分布13. 当正态总体的方差已知时,且为大样本条件下,估计总体均值使用的分布是()A.正态分布B. t分布C.χ2 分布D. F分布14. 对于非正态总体,在大样本条件下,估计总体均值使用的分布是()A.正态分布B. t分布C.χ2 分布D. F分布15.对于非正态总体,在大样本条件下,总体均值在(1-α)置信水平下的置信区间可以写为()A.B.C.D.16.正态总体方差已知时,在小样本条件下,总体均值在(1-α)置信水平下的置信区间可以写为()A.B.C.D.17.正态总体方差未知时,在小样本条件下,总体均值在(1-α)置信水平下的置信区间可以写为()A.B.C.D.18. 在进行区间估计时,若要求的置信水平为90%,则其相应的临界值为()A.1.65B.1.96C.2.58D. 1.519.在其他条件相同的条件下,95%的置信区间比90%的置信区间()A.要宽B.要窄C.相同D. 可能宽也可能窄20.指出下面的说法哪一个是正确的()A.置信水平越大,估计的可靠性越大B. 置信水平越大,估计的可靠性越小C. 置信水平越小,估计的可靠性越大 D. 置信水平的大小与估计的可靠性无关21. 指出下面的说法哪一个是正确的()A.样本量越大,样本均值的抽样标准误差就越小B. 样本量越大,样本均值的抽样标准误差就越大C. 样本量越小,样本均值的抽样标准误差就越小D.样本均值的抽样标准误差与样本量无关22. 一项调查表明,有33%的被调查者认为她们所在的公司十分适合女性工作。
贾俊平《统计学》章节题库(含考研真题)(参数估计)【圣才出品】
近,样本标准差也与总体标准差逐渐接近,所以 S 是 σ 的一致估计。由于随机变量分布函
数形式未知,所以无法知道 S 是否是 σ 的最大似然估计,B 项错误。
1 / 51
圣才电子书 十万种考研考证电子书、题库视频学习平台
2.在参数估计中,要求通过样本的统计量来估计总体参数,评价统计量的标准之一是 使它与总体参数的离差越小越好。这种评价标准称为( )。[山东大学 2015 研]
(3)欲在缩小估计区间宽度的同时,提高置信度,唯一途径为( )。 A.以样本标准差替代总体标准差 B.减少样本容量 C.以样本中位数替代样本均值
5 / 51
圣才电子书
D.增加样本容量
十万种考研考证电子书、题库视频学习平台
【答案】D
【解析】由(1)题解析中的公式可知,置信度提高,区间宽度随之扩大,要在缩小估
A.无偏性 B.有效性 C.一致性 D.充分性 【答案】B 【解析】有效性是指对同一总体参数的无偏估计量,有更小标准差的估计量更有效,即 估计量与总体参数的离差越小越好。
3.一项研究表明,大公司的女性管理人员与小公司的女性管理人员颇为相似。该项研 究抽取了两个独立的随机样本,小公司抽取 86 名女性经理,大公司抽取 91 名女性经理, 根据若干个与工作有关的变量做了比较,其中所提出的一个问题是“如果有机会的话,你是 否会改变所从事的工作?”小公司的 86 名经理中有 65 人作了否定回答,大公司的 91 名经 理中有 51 人作了否定回答。两组女性经理中有机会改变工作的比例之差的 95%的置信区间 为( )。[山东大学 2015 研]
A.0.195±0.017 B.0.195±0.117 C.0.195±0.127 D.0.195±0.137 【答案】D
统计学贾俊平第7章 参数估计
7.1 7.2 7.3 7.4
参数估计
参数估计的一般问题 一个总体参数的区间估计 两个总体参数的区间估计 样本容量的确定
1
All rights reserved
1
引例
美国《华尔街日报》2011年4月21日发表题为《盖 洛普发现,中国民众生活艰难》
盖洛普民意调查所布的2010年全球幸福度调查结果表 明,只有12%的中国人认为自己“生活美满”。多达 71%的答问者说,他们生活”艰难”。17%的人说自己 的生活”苦不堪言” 与此相比,只有38%的美国人说自己生活艰难,有多达 59%的答问者认为自己生活美满。即便考虑到中国房价 失控和食品价格持续上涨的因素,仍无法理解为什么 将近四分之三的中国人认为自己生活艰难
5
All rights reserved
分类表
6
All rights reserved
进一步讨论
Results are based on face-to-face and telephone interviews with approximately 1,000 adults, aged 15 and older, conducted between 2005 and 2009 in 155 countries. For results based on the total samples, one can say with 95% confidence that the maximum margin of sampling error ranges from ±2.1 percentage points in China to ±5.8 percentage points in Zambia. The margin of error reflects the influence of data weighting. In addition to sampling error, question wording and practical difficulties in conducting surveys can introduce error or bias into the findings of public opinion polls.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章参数估计练习题
一.选择题
1.估计量的含义是指()
A.用来估计总体参数的统计量的名称
B.用来估计总体参数的统计量的具体数值
C.总体参数的名称
D.总体参数的具体取值
2.一个95%的置信区间是指()
A.总体参数有95%的概率落在这一区间内
B.总体参数有5%的概率未落在这一区间内
C. 在用同样方法构造的总体参数的多个区间中,有95%的区间包含该总体参数。
D.在用同样方法构造的总体参数的多个区间中,有95%的区间不包含该总体参数。
3.95%的置信水平是指()
A.总体参数落在一个特定的样本所构造的区间内的概率是95%
B.在用同样方法构造的总体参数的多个区间中,包含总体参数的区间比例为95%
C.总体参数落在一个特定的样本所构造的区间内的概率是5%
D.在用同样方法构造的总体参数的多个区间中,包含总体参数的区间比例为5%
4.根据一个具体的样本求出的总体均值的95%的置信区间()
A.以95%的概率包含总体均值
B.有5%的可能性包含总体均值
C.一定包含总体均值
D.要么包含总体均值,要么不包含总体均值
5. 当样本量一定时,置信区间的宽度()
A.随着置信水平的增大而减小
B. .随着置信水平的增大而增大
C.与置信水平的大小无关D。
与置信水平的平方成反比
6.当置信水平一定时,置信区间的宽度()
A.随着样本量的增大而减小
B. .随着样本量的增大而增大
C.与样本量的大小无关D。
与样本量的平方根成正比
7.在参数估计中,要求通过样本的统计量来估计总体参数,评价统计量的标准之一是使它与总体参数的离差越小越好。
这种评价标准称为()
A.无偏性 B. 有效性 C. 一致性D. 充分性
8. 置信水平(1-α)表达了置信区间的()
A.准确性 B. 精确性 C. 显著性 D. 可靠性
9. 在总体均值和总体比例的区间估计中,边际误差由()
A.置信水平决定 B. 统计量的抽样标准差确定
C. 置信水平和统计量的抽样标准差
D. 统计量的抽样方差确定
10. 当正态总体的方差未知,且为小样本条件下,估计总体均值使用的分布是()
A.正态分布
B. t分布
C.χ2分布
D. F分布
11. 当正态总体的方差未知,且为大样本条件下,估计总体均值使用的分布是()
A.正态分布
B. t 分布
C.χ2 分布
D. F 分布
12. 当正态总体的方差已知时,且为小样本条件下,估计总体均值使用的分布是( )
A.正态分布
B. t 分布
C.χ2 分布
D. F 分布
13. 当正态总体的方差已知时,且为大样本条件下,估计总体均值使用的分布是( )
A.正态分布
B. t 分布
C.χ2 分布
D. F 分布
14. 对于非正态总体,在大样本条件下,估计总体均值使用的分布是( )
A.正态分布
B. t 分布
C.χ2 分布
D. F 分布
15.对于非正态总体,在大样本条件下,总体均值在(1-α)置信水平下的置信区间可以写为( ) A. n z x 22/σα± B. n z x 22/σα± C. n z x σα2/± D. n
s z x 22/α± 16.正态总体方差已知时,在小样本条件下,总体均值在(1-α)置信水平下的置信区间可以写为( ) A. n z x 22/σα± B. n s t x 2/α± C. n z x σα2/± D. n
s z x 22/α± 17.正态总体方差未知时,在小样本条件下,总体均值在(1-α)置信水平下的置信区间可以写为( ) A. n z x 22/σα± B. n s t x 2/α± C. n z x σα2/± D. n
s z x 22/α± 18. 在进行区间估计时,若要求的置信水平为90%,则其相应的临界值为( )
A.1.65
B.1.96
C.2.58
D. 1.5
19.在其他条件相同的条件下,95%的置信区间比90%的置信区间( )
A.要宽
B.要窄
C.相同
D. 可能宽也可能窄
20.指出下面的说法哪一个是正确的( )
A.置信水平越大,估计的可靠性越大
B. 置信水平越大,估计的可靠性越小
C. 置信水平越小,估计的可靠性越大
D. 置信水平的大小与估计的可靠性无关
21. 指出下面的说法哪一个是正确的( )
A.样本量越大,样本均值的抽样标准误差就越小
B. 样本量越大,样本均值的抽样标准误差就越大
C. 样本量越小,样本均值的抽样标准误差就越小
D.样本均值的抽样标准误差与样本量无关
22. 一项调查表明,有33%的被调查者认为她们所在的公司十分适合女性工作。
假定总体比例为33%,取边际误差分别为10%,5%,2%,1%,在建立总体比例95%的置信区间时,随着边际误差的减少,样本量会( )
A.减少
B. 增大
C. 可能减少也可能增大
D. 不变
二.填空题
1.若从一总体中抽取一个样本,样本容量为n,其95%的置信区间为(a, b),则其样本均值
为_________, 若总体方差已知,则该总体方差为_____________________。
若总体方差未知,且样本量为15,则其样本均值为______,样本方差为_____________________。
若总体方差未知,且样本量为30,则其样本均值为______,样本方差为_____________________。
若增加样本容量置信区间会变_____________________。
2.一总体服从正态分布,并且方差已知。
从其中抽取的一样本容量为25,在95%的置信水
平下区间估计的边际误差为15,那么总体标准差是_____________________。
3.一总体方差已知,对总体均值进行区间估计时,所用的样本容量为150。
当要求边际误
差从30减少到20,置信水平不变,则样本容量应取_____________________。
4.根据以往的经验,某乡农户的年收入分布曲线是一个严重偏斜的非对称曲线。
现随机抽
取25户进行调查,他们的户均年收入为13200元。
为了估计该乡农户的户均年收入,能否根据上述数据求得一个置信度为95%的置信区间?给出回答,并说明理由__________________________________________________________________________。
5.某企业根据对顾客随机抽样的样本信息推断:对本企业产品表示满意的顾客比例的95%
的置信水平的置信区间是(56%,64%)。
试判断下列说法正确与否。
(1)总体比例的95%的置信水平的置信区间是(56%,64%)。
______________ (2)总体真实比例有95%的可能落在(56%,64%)中。
______________
(3)区间(56%,64%)有95%的概率包含了总体真实比例。
______________
(4)在100次抽样得到的100个置信区间中,约有95个覆盖了总体真实比例。
_____ 6.有50个调查者分别对同一个正态总体进行抽样,样本容量都是100,总体方差未知。
它
们分别根据各自的样本数据得到总体均值的一个置信度90%的置信区间。
试问:
(1)这些置信区间中应该大约有_______________区间会覆盖总体均值。
(2)这些置信区间的中心相同吗?给出回答,并说明理由__________________________________________________________________。
(3)这些置信区间的宽度完全相同吗?给出回答,并说明理由__________________________________________________________________。
三.计算题
1.为了解某银行营业厅办理某业务的办事效率,调查人员观察了该银行营业厅办理该业务的柜台办理每笔业务的时间,随机记录了16名客户办理业务的时间,测得平均办理时间为12分钟,样本标准差为4.1分钟,假定办理该业务的时间服从正态分布,则:
(1)此银行办理该业务的平均时间的置信水平为95%的区间估计是什么?
(2)若样本容量为40,而观测的数据的样本均值和样本标准差不变,则置信水平为95%的置信区间是什么?
2.据一次抽样调查表明,居民每日平均读报时间的95%的置信区间为[2.2,
3.4]小时,问该次抽样样本平均读报时间x是多少?若样本容量为100,则样本标准差是多少?若想将边际误差降为0.4小时,那么在相同的置信水平下,样本容量应该为多少?
3.一家调查公司进行一项调查,其目的是为了了解某市电信营业厅大客户对该电信的服务的满意情况。
调查人员随机访问了30名去该电信营业厅办理业务的大客户,发现受访的大客户中有9名认为营业厅现在的服务质量比两年前好。
试在95%的置信水平下对大客户中认
为营业厅现在的服务质量比两年前好的比例进行区间估计。
4.为了确定某大学学生配戴眼镜的比例,调查人员欲对该大学的学生进行抽样调查。
而根据以往的调查结果表明,该大学有75%的学生配戴眼镜。
则对于边际误差E分别为5%,10%,置信水平都为95%,抽取的样本量各为多少合适?。
