第7章 统计学参数估计
7 参数估计
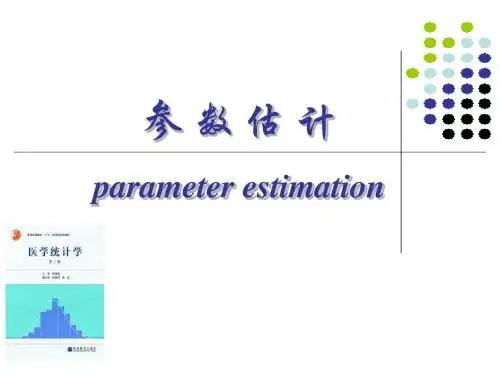
3个抽样实验结果图示
均数
均数
5. 15 5. 36 5. 57 5. 77 5. 98 6. 19
频数 100 150 200 250 300 350 400 450 50 0
n = 30; SX = 0.0920
均数
3. 71 3. 92 4. 12 4. 33 4. 54 4. 74 4. 95 5. 15 5. 36 5. 57 5. 77 5. 98 6. 19
t= X −µ X −µ = SX S/ n t变 换
σX
N(0,1) 0 t(ν) (
X
0
t 分布与正态分布的比较
t 分布:形状与 分布:形状与N(0,1)相似, 相似, 相似 分布中间较小, 但t分布中间较小,两侧较大。 分布中间较小 两侧较大。
随着v增大, 分布逼近 随着 增大,t分布逼近 增大 分布逼近N(0,1); ; v ∞时,t分布演变成 时 分布演变成 分布演变成N(0,1)。 。
参数估计
parameter estimation
统计学
统计描述
统计推断
参数估计
假设检验
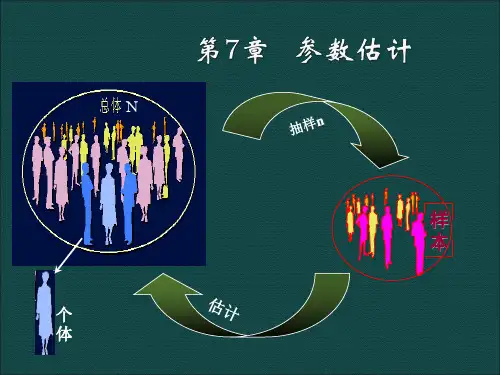
总体、 总体、个体和样本
总体(population):调查研究的事物或现象的全体 个体(item unit):组成总体的每个元素 样本(sample):从总体中所抽取的部分个体 样本容量(sample size):样本中所含个体的数量
总体参数
µ、σ、π
可信区间(confidence interval, CI) 可信区间
可信区间
均 数
率
方差
σ2 未知
σ2 已知
总体均数的估计
点估计: 点估计:point estimation 区间估计: 区间估计:interval estimation 样本统计量 点估计) (点估计)
贾俊平《统计学》(第7版)考点归纳和课后习题详解(含考研真题)(第7章 参数估计)【圣才出品】

第7章参数估计7.1 考点归纳【知识框架】【考点提示】(1)置信区间的含义理解(选择题、简答题考点);(2)估计量的三个评价标准(判断题、填空题、简答题考点);(3)区间估计的步骤(简答题考点)、总体参数的区间估计选择恰当的统计量(计算题考点);(4)必要样本容量的影响因素、计算(简答题、计算题考点)。
【核心考点】考点一:参数估计的基本原理1.置信区间(1)置信水平为95%的置信区间的含义:用某种方法构造的所有区间中有95%的区间包含总体参数的真值。
(2)置信度愈高(即估计的可靠性愈高),则置信区间相应也愈宽(即估计准确性愈低)。
(3)置信区间的特点:置信区间受样本影响,具有随机性,总体参数的真值是固定的。
一个特定的置信区间“总是包含”或“绝对不包含”参数的真值,不存在“以多大的概率包含总体参数”的问题。
2.评价估计量的标准(1)无偏性:估计量抽样分布的期望值等于被估计的总体参数,即E(θ∧)=θ。
(2)有效性:估计量的方差尽可能小。
(3)一致性:随着样本量的增大,估计量的值越来越接近被估计总体的参数。
【提示】本考点常见考查方式:①直接考查置信水平为95%的置信区间的含义;②置信度、估计可靠性、置信区间的关系及应用;③置信区间的特点;④给出估计量的具体含义,判断体现了什么标准;⑤直接回答估计量的三个评价标准及具体含义(简答题)。
考点二:一个总体参数的区间估计表7-1 一个总体参数的区间估计【总结】一个总体参数的估计及所使用的分布见图7-1:图7-1 一个总体参数的估计及所使用的分布【真题精选】设总体X~N(μ,σ2),σ2已知,样本容量和置信水平固定,对不同的样本观测值,μ的置信区间的长度()。
[对外经济贸易大学2018研]A.变长B .变短C .保持不变D .不能确定 【答案】C【解析】在正态总体方差已知的条件下,μ的置信区间为/2x z ±ασ所以置信区间长度为/22Z α,当样本容量和置信水平固定时,置信区间长度保持不变。
第7章参数估计
x 1 0
f P 1-p
x
xf f
1 p 0 (1 p) p (1 p)
p
2 (x x)2 f (1 p)2 p (0 p)2 (1 p)
f
p (1 p)
似然函数常简记为L或 L 1,2, ,k
未知参数的函数。
38
若有 ˆi (x1, x2,..., xn ) i 1, 2, k 使得
L x1, x2,..., xn;ˆ1, ˆ 2,
, ˆ k
max L (1 ,2 , ,k )
x1, x2,..., xn; 1, 2,
, k
则 ˆi (X1, X2,..., Xn) 为参数θi的极大似然估计量。
中选出一个使样本观察值出现的概率为最大的 ˆ 作
为θ的估计量。
称 ˆ 为θ 的极大似然估计量。
37
2.似然函数的数学表达式
设X1,X2,…Xn是取自总体X的一个样本,样本的联合密度 (连续型)或联合分布律 (离散型)为 :
f (x; 1,2 , , k )
定义似然函数为:
n
L L x1,..., xn; 1, 2, , k f xi; 1, 2, , k i 1 x1, x2 ,..., xn 给定的样本观察值
§7.1.4抽样误差
1.误差:调查结果与实际值之间的差异 抽样调查中的误差
登记性误差(非抽样误差) 误差代表性误差随系机统误误差差((抽非样抽误样差误)差)
2.抽样误差—由于抽样的随机性而产生的 样本指标对总体指标的代表性误差。抽样误 差可以计算并加以控制,但不可以避免。
统计学第五版课后练答案(7-8章)

第七章 参数估计7.1 (1)x σ==(2)2x z α∆= 1.96=1.54957.2 某快餐店想要估计每位顾客午餐的平均花费金额。
在为期3周的时间里选取49名顾客组成了一个简单随机样本。
(1)假定总体标准差为15元,求样本均值的抽样标准误差。
x σ==(2)在95%的置信水平下,求估计误差。
x x t σ∆=⋅,由于是大样本抽样,因此样本均值服从正态分布,因此概率度t=2z α 因此,x x t σ∆=⋅2x z ασ=⋅0.025x z σ=⋅=1.96×2.143=4.2 (3)如果样本均值为120元,求总体均值 的95%的置信区间。
置信区间为:2x z x z αα⎛-+ ⎝=()120 4.2,120 4.2-+=(115.8,124.2)7.322x z x z αα⎛-+ ⎝=104560±(87818.856,121301.144) 7.4 从总体中抽取一个n=100的简单随机样本,得到x =81,s=12。
要求:大样本,样本均值服从正态分布:2,x N n σμ⎛⎫ ⎪⎝⎭ 或2,s x N n μ⎛⎫⎪⎝⎭置信区间为:22x z x z αα⎛-+ ⎝=1.2 (1)构建μ的90%的置信区间。
2z α=0.05z =1.645,置信区间为:()81 1.645 1.2,81 1.645 1.2-⨯+⨯=(79.03,82.97)(2)构建μ的95%的置信区间。
2z α=0.025z =1.96,置信区间为:()81 1.96 1.2,81 1.96 1.2-⨯+⨯=(78.65,83.35)(3)构建μ的99%的置信区间。
2z α=0.005z =2.576,置信区间为:()81 2.576 1.2,81 2.576 1.2-⨯+⨯=(77.91,84.09)7.5 (1)2x z α±=25 1.96±=(24.114,25.886)(2)2x z α±119.6 2.326±=(113.184,126.016)(3)2x z α± 3.419 1.645±(3.136,3.702)7.6 (1)2x z α±=8900 1.96±=(8646.965,9153.035)(2)2x z α±8900 1.96±=(8734.35,9065.65)(3)2x z α±8900 1.645±=(8761.395,9038.605)(4)2x z α±8900 2.58±=(8681.95,9118.05)7.7 某大学为了解学生每天上网的时间,在全校7 500名学生中采取重复抽样方法随机抽取36人,调解:(1)样本均值x =3.32,样本标准差s=1.611α-=0.9,t=2z α=0.05z =1.645,x z α± 3.32 1.645±=(2.88,3.76)1α-=0.95,t=z α=0.025z =1.96,x z α± 3.32 1.96±(2.79,3.85)1α-=0.99,t=z α=0.005z =2.576,2x z α± 3.32 2.76±(2.63,4.01)7.82x t α±=10 2.365±7.9 某居民小区为研究职工上班从家里到单位的距离,抽取了由16个人组成的一个随机样本,他们到单位的距离(单位:km)分别是:10 3 14 86 9 12 117 5 1015 9 16 13 2假定总体服从正态分布,求职工上班从家里到单位平均距离的95%的置信区间。
第7章 统计学 参数估计 练习题

第7章参数估计练习题一、填空题(共10题,每题2分,共计20分)1.参数估计就就是用_______ __去估计_______ __。
2、点估计就就是用_______ __得某个取值直接作为总体参数得_______ __。
3.区间估计就是在_______ __得基础上,给出总体参数估计得一个区间范围,该区间通常由样本统计量加减_______ __得到。
4、如果将构造置信区间得步骤重复多次,置信区间中包含总体参数真值得次数所占得比例称为_______ __,也成为_______ __。
5.当样本量给定时,置信区间得宽度随着置信系数得增大而_______ __;当置信水平固定时,置信区间得宽度随着样本量得增大而_______ __。
6、评价估计量得标准包含无偏性、_______ __与_______ __。
7、在参数估计中,总就是希望提高估计得可靠程度,但在一定得样本量下,要提高估计得可靠程度,就会_______ __置信区间得宽度;如要缩小置信区间得宽度,又不降低置信程度,就要_______ __样本量。
8、估计总体均值置信区间时得估计误差受总体标准差、_______ __与_______ __得影响。
9、估计方差未知得正态总体均值置信区间用公式_______ __;当样本容量大于等于30时,可以用近似公式_______ __。
10、估计正态总体方差得置信区间时,用_____ __分布,公式为______ __。
二、选择题(共10题,每题1分,共计10分)1.根据一个具体得样本求出得总体均值得95%得置信区间 ( )。
A.以95%得概率包含总体均值B.有5%得可能性包含总体均值C.一定包含总体均值D、要么包含总体均值,要么不包含总体均值2.估计量得含义就是指( )。
A、用来估计总体参数得统计量得名称B 、 用来估计总体参数得统计量得具体数值C 、 总体参数得名称D 、 总体参数得具体数值3. 总体均值得置信区间等于样本均值加减边际误差,其中边际误差等于所要求置信水平得临界值乘以( )。
概率论与数理统计-参数估计

第七章 参数估计
例:
引言
设总体 X 是服从参数为 的指数分布,其中参数
未 知 ,
0 .X1 ,,
X
是总体
n
X
的一个样本,
我们的任务是根据样本,来估计 的取值,从
而估计总体的分布.
这 是 一 个 参 数 估 计 问 题.
第七章 参数估计
§1 点估计 §2 估计量的评选标准 §3 区间估计
第七章 参数估计 §1 点估计
2
令
A1
A2
, (
2
1)
.
第七章 参数估计
例6(续)
解此方程组,得
§1 点估计
ˆ
A1 2 A2 A12
,
ˆ
A2
A1 A12
.
ˆ X 2 ,
即
B2
ˆ X .
B2
其中 B2
1 n
n i 1
Xi X
2 为样本的二阶中心矩.
第七章 参数估计(第二十二讲) 三、 极大似然法
§1 点估计
1
第七章 参数估计
例6(续)
EX 2 x 2 f
x dx x 2
x 1e x dx
0
§1 点估计
2 2 x ( e 2)1 x dx
2 0 2
2 2
1 2
1
2
因此有
EX
,
EX
2
1 .
⑵ 在不引起混淆的情况下,我们统称估计量
与估计值为未知参数 的估计.
第七章 参数估计
二、 矩估计法
§1 点估计
设X为连续型随机变量,其概率密度为
f ( x;1 ,, k ), X为离散型随机变量,其分布列为
统计学第七章参数估计
单击添加文本具体内容
参数估计
假设检验
描述统计
推断统计
参数估计在统计方法中的地位
统计方法
统计推断的过程
总体
总体均值、比例、方差等
样本统计量 如:样本均值、比例、方差
样本
§7.1 参数估计的一般问题
单击此处添加文本具体内容,简明扼要地阐述你的观点
一、估计量和估计值
参数估计(Parameter Estimation) ,用样本估计量估计总体估计值。
一个总体参数的区间估计
总体参数
符号表示
样本统计量
均值
比例
方差
第一章节
总体均值的区间估计 (正态总体、2已知,或非正态总体、大样本)
总体均值的区间估计 (大样本)
假定条件 总体服从正态分布,且方差(2) 未知 如果不是正态分布,可由正态分布来近似 (n 30) 使用正态分布统计量 z 总体均值 在1- 置信水平下的置信区间为
(1)估计量:用来估计总体参数的样本统计量。如:样本算术平均数、样本中位数、样本标准差、样本方差等。 例如: 样本均值就是总体均值 的一个估计量 (2)参数用 表示,估计量用 表示 (3)估计值:估计参数时计算出来的统计量的具体值 如果样本均值 x =80,则80就是的估计值
矩估计法
最小二乘法
换句话说,做出校全体女大学生身高均数为163.0 -- 164.5cm的结论,说对的概率是95%,说错的概率是5%;做出校全体女大学生身高均数为162.7 – 164.7cm的结论,说对的概率是99%,说错的概率是1%。
3、置信区间与置信水平
(1 - ) 区间包含了 的区间未包含
a /2
A
B
的抽样分布
统计学第七章、第八章课后题答案
统计学复习笔记第七章 参数估计一、 思考题1. 解释估计量和估计值在参数估计中,用来估计总体参数的统计量称为估计量。
估计量也是随机变量。
如样本均值,样本比例、样本方差等。
根据一个具体的样本计算出来的估计量的数值称为估计值。
2. 简述评价估计量好坏的标准(1)无偏性:是指估计量抽样分布的期望值等于被估计的总体参数。
(2)有效性:是指估计量的方差尽可能小。
对同一总体参数的两个无偏估计量,有更小方差的估计量更有效。
(3)一致性:是指随着样本量的增大,点估计量的值越来越接近被估总体的参数。
3. 怎样理解置信区间在区间估计中,由样本统计量所构造的总体参数的估计区间称为置信区间。
置信区间的论述是由区间和置信度两部分组成。
有些新闻媒体报道一些调查结果只给出百分比和误差(即置信区间),并不说明置信度,也不给出被调查的人数,这是不负责的表现。
因为降低置信度可以使置信区间变窄(显得“精确”),有误导读者之嫌。
在公布调查结果时给出被调查人数是负责任的表现。
这样则可以由此推算出置信度(由后面给出的公式),反之亦然。
4. 解释95%的置信区间的含义是什么置信区间95%仅仅描述用来构造该区间上下界的统计量(是随机的)覆盖总体参数的概率。
也就是说,无穷次重复抽样所得到的所有区间中有95%(的区间)包含参数。
不要认为由某一样本数据得到总体参数的某一个95%置信区间,就以为该区间以0.95的概率覆盖总体参数。
5. 简述样本量与置信水平、总体方差、估计误差的关系。
1. 估计总体均值时样本量n 为2. 样本量n 与置信水平1-α、总体方差、估计误差E 之间的关系为 其中: 2222α2222)(E z n σα=n z E σα2=▪ 与置信水平成正比,在其他条件不变的情况下,置信水平越大,所需要的样本量越大;▪ 与总体方差成正比,总体的差异越大,所要求的样本量也越大;▪ 与与总体方差成正比,样本量与估计误差的平方成反比,即可以接受的估计误差的平方越大,所需的样本量越小。
07心理统计学-第七章 参数估计
犯错误的概率,常用α(或p)表示。则1-α为置信 度。(显著性水平越高表示的是α值越小,即犯错误的可
能性越低) α为预先设定的临界点,常用的如.05、.01、.001;p 为检验计算所得的实际(犯错误)概率。
第一节 点估计、区间估计与标准误
三、区间估计与标准误
3、区间估计的原理与标准误
转换成比率为
p
n
p, SE p
n
pq n
同理可得公式7-17。自习[例7-12、例7-13]
1、从某地区抽样调查400人,得到每月人均文化消费为 160元。已知该地区文化消费的总体标准差为40元。试 问该地区的每月人均文化消费额。(α=.05,总体呈正态
分布)
2、上题中总体方差未知,已知Sn-1=44元。 3、已知某中学一次数学考试成绩的分布为正态分布,总 体标准差为5。从总体中随机抽取16名学生,计算得平 均数为81、标准差为Sn=6。试问该次考试中全体考生成 绩平均数的95%置信区间。 4、上题中总体方差未知,样本容量改为17人。 5、假定智商服从正态分布。随机抽取10名我班学生测 得智商分别为98、102、105、105、109、111、117、 123、124、126(可计算得M=112,Sn≈9.4),试以95% 的置信区间估计我班全体的智商平均数。 返回
值表,求tα /2(df)。
5、计算置信区间CI。
σ2已知,区间为M-Zα /2 SE <μ< M+Zα /2 SE;
σ2未知,区间为M-tα /2(df)SE <μ< M+tα /2(df)SE。
6、对置信区间进行解释。
二、σ2已知,对μ的区间估计(Z分布,例7-1 & 2) 三、σ2未知,对μ的区间估计(t分布,例7-3 & 4)
统计学参数估计PPT课件
在应用参数估计时,需要注意样本的代表性、数据的准确性和可靠性等问题, 以保证估计的准确性和可靠性。
对未来研究的建议
01
进一步探讨参数估计的理论基础
可以进一步探讨参数估计的理论基础,如大数定律和中心极限定理等,
以更好地理解和掌握参数估计的方法和原理。
02
探索新的估计方法
随着统计学的发展,可以探索新的参数估计方法,以提高估计的准确性
指导决策
评估效果
基于参数估计结果,制定科学合理的 决策。
利用参数估计,评估政策、项目等实 施效果。
预测未来
通过参数估计,预测未来的趋势和变 化。
02
参数估计的基本概念
点估计
定义
点估计是用一个单一的数值来估 计未知参数的值。
举例
在调查某班级学生的平均身高时, 我们可能使用所有学生身高的总 和除以人数来估计平均身高,这 里的总和除以人数就是点估计。
最小二乘法的缺点是假设误差项独立 同分布,且对异常值敏感,可能影响 估计的稳定性。
最小二乘法的优点是简单易行,适用 于线性回归模型,且具有优良的统计 性质。
贝叶斯估计法
贝叶斯估计法是一种基于贝叶 斯定理的参数估计方法,通过 将先验信息与样本数据相结合 来估计参数。
贝叶斯估计法的优点是能够综 合考虑先验信息和样本数据, 给出更加准确的参数估计。
高维数据的参数估计问题
1 2 3
高维数据对参数估计的影响
随着数据维度的增加,参数估计的复杂度和难度 也会相应增加,容易出现维度诅咒等问题。
高维数据参数估计的方法
针对高维数据,可以采用降维、特征选择、贝叶 斯推断等方法进行参数估计,以降低维度对估计 的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:总体服从正态分布,方差已知,置信度为95% 则z0.025=1.96,
x Z
2
7.48 1.96 0.06 7.48 0.024 7.456
n
25
x Z
2
7.48 1.96 0.06 7.48 0.024 7.504
n
25
在置信度为95%水平下,金属棒的平均长度在 7.456~7.504厘米之间。
解 : 已 知 2=1800000 , =0.05 , Z/2=1.96,E=500
107.5
95.0
108.8
115.6
100.0
123.5
102.0
101.6
102.2
116.6
95.4
97.8
108.6
105.0
136.8
102.8
101.5
98.4
93.3
解:已知n=25,1-=95% ,根据样本数据计算得
s2 =93.21
2置信度为95%的置信区间为
2
2
(n
1)
2 0.025
1.正态总体,方差已知或非正态总体、大样本
样本均值 X~N(μ,σ2/n)
z x ~ N (0,1) / n
总体均值μ在1-α的置信水平下的置信区间为
x Z
2
n
【例】某厂成批生产某种金属棒,其长度服从
正态分布,标准差为0.06厘米,对一个由25 根棒组成的随机样本进行了测量,平均长度为
7.48厘米,求这批金属棒平均长度μ的置信度 为95%的置信区间。
假设我们是盟军手下 负责解决这个问题的统计 人员。制造出来的坦克总 数肯定大于等于记录的最 大编号。为了找到它比最 大编号大多少,我们先找 到被缴获坦克编号的平均 值,并认为这个值是全部 编号的中点。因此样本均 值乘以2就是总数的一个 估计;当然要特别假设缴 获的坦克代表了所有坦克 的一个随机样本。
置信区间为:
x Z
2
s 40 1.645 n
5 40 1.37 36
则投保人平均年龄在90%的置信度下的
置信区间为38.63岁-41.37岁。
3. 正态总体、方差未知、小样本
用样本方差s2代替总体方差σ2
样本均值经标准化处理后服从自由度为
(n-1)的t分布
t x ~ t(n 1)
s/ n
总体均值μ在1-α的置信水平下的置信区间为
【例】某大学从该校学生中随机抽取100人, 调查到他们平均每天参加体育锻炼的时间为 26分钟。试以95%的置信水平估计该大学 全体学生平均每天参加体育锻炼的时间(已 知总体方差为36分钟)。
解:虽然总体分布未知,但总体方差已知,
样本量充分大, x=26, =6,n=100, Z
/2=1.96
x Z 2
3. 一致性
随着样本量的增大,点估计量的值越来越接 近被估总体的参数。
7.2 一个总体参数的区间估计
7.2.1 总体均值的区间估计
总体均值的置信区间=样本均值±边际误差
• 总体是否为正态分布 • 总体方差是否已知 • 样本是大样本还是小样本
1.正态总体,方差已知或非正态总体、大样本 2.分布未知,方差未知,大样本 3.正态总体,方差未知,小样本
N的另一个点估计公式是: N=m(1+1/k)-1 , 其中m是缴获到的最大的坦克编号,k是被俘虏坦 克个数。假如你俘虏了10 辆坦克,其中最大编 号是50,那么坦克总数的一个估计是 (1+1/10)50-1=54。此处我们认为坦克的实际 数略大于最大编号。
从战后发现的德军记录来看,盟军的估计值非 常接近所生产的坦克的真实值。记录仍然表明统 计估计比通常通过其他情报方式作出估计要大大 接近于真实数目。统计学家们做得比间谍们更漂 亮!
解:已知n=100,zα/2 =1.96, p=42/100=0.42
p1 p
0.421 0.42
p z / 2
0.42 1.96 n
100
0.42 0.097
因此,该校找到工作的应届毕业生中女 同学的比例为0.323-0.517
【例】某企业在一项关于职工流动原因的
研究中,从该企业前职工的总体中随机 选取了200人组成一个样本。在对其进 行访问时,有140人说他们离开该企业 是由于同管理人员不能融洽相处。试对
第7章 参数估计
统计方法
描述统计
推断统计
参数估计
假设检验
7.1 参数估计
1. 用样本统计量去估计总体参数。
2. 估计量——用来估计总体参数的统计量 估计值——一个具体样本计算出的统计 量的数值
参数估计的方法
点估计
区间估计
二战中的点估计—
德军有多少辆坦克?
二战期间,盟军非常想知
道德军总共制造了多少辆坦克。 德国人在制造坦克时是墨守成规 的,他们把坦克从1开始进行了 连续编号。在战争过程中,盟军 缴获了一些敌军坦克,并记录了 它们的生产编号。那么怎样利用 这些号码来估计坦克总数呢?在 这个问题中,总体参数是未知的 坦克总数N,而缴获坦克的编号则 是样本。
x t
2
s n
【例】某时装店的管理人员想估计其顾客的平均
年龄,随机抽取了16位顾客进行了调查,得到 样本均值为32岁,样本标准差为8岁,假定顾客 的年龄近似服从正态分布,求该店全部顾客平均
年龄在置信度为95%的置信区间。
解:因为总体近似服从正态分布,方差未知, 所抽样本为小样本,则总体均值的置信区间为
x Z
2
s n
【例】一家保险公司收集到由36位投保人组成 的随机样本,他们的平均年龄为40岁,标准差 为5岁,求这家保险公司的所有投保人的平均 年龄在90%的置信水平下的置信区间。
解:总体的分布未知,总体方差也未知,但所抽
样本容量36为大样本,因此,求总体均值的 置信区间可用样本标准差代替总体标准差
小样本
大样本
2已知
2已知
Z分布
Z分布
Z分布
2未知
2未知
Z分布
t分布
方差 2分布
7.3 样本量的确定
样本量、置信水平、置信区间三者的关系
样本量
不变 不变 扩大 扩大
置信水平
提高 降低 不变 提高
置信区间
扩大 缩小 缩小 不变
估计总体均值时样本量的确定
总体均值的置信区间为
x Z
2
n
边际误差
E Z
2
包含总体参数真值的置信区间占所有置信区间 的比例。常用1-α表示置信水平。
a. 总体参数的真值是未知的、固定的,构造出的 置信区间可能包含真值,也可能不包含真值;
b. 设置信水平为95%,则说明有95%的置信区间 包含总体真值,有5%的置信区间不包含总体真值。
练习题
1. 一个95%的置信区间是指( )
ห้องสมุดไป่ตู้
s
8
x t0.025(161)
32 2.131 32 4.262 27.738
n
16
x t0.025(161)
s 32 2.131 n
8 32 4.262 36.262 16
因此,有95%的把握估计全部顾客平均年龄在 27.738至36.262之间。
不同情况下总体均值的区间估计
当总体比例π已知时,总体比例π在1-α置信水 平下的置信区间为:
p z / 2
(1 )
n
实际情况中,π值是未知的,要被估计 的,所以需要用样本比例p来代替π,则 总体比例的置信区间为:
p(1 p)
p z / 2
n
【例】某所大学想要了解应届毕业生在大四找 到工作的学生中女生所占的比例,随机抽取了 100名找到工作的应届毕业生,其中42人为女 生。试以95%的置信水平估计该校找到工作的 应届毕业生中女同学的比例的置信区间。
常用置信水平的临界值(Zα/2值)
置信水平
90% 95% 99%
α
0.10 0.05 0.01
α/2
0.05 0.025 0.005
Zα/2
1.645 1.96 2.58
评价估计量的标准
1. 无偏性
∧
E(θ) =θ
2. 有效性
对同一总体参数的两个无偏估计量,标准差 越小的估计量估计效果越好,称估计量越有效。
n , x Z 2
n
26 1.96
6 ,26 1.96 100
6 100
24.824,27.176
在95%的置信水平下估计大学生平均 每 天 参 加 锻 炼 的 时 间 在 24.824 ~ 27.176 分钟之间。
2. 方差未知,大样本(n≥30)
总体均值μ在1-α的置信水平下的置信区间为
【例】某超市想要估计每个顾客平均每次购物
花费的金额。根据过去的经验,标准差大约
为120元,现要以95%的置信水平去估计每 个顾客平均购物金额的置信区间,并要求边
际误差不超过20元,应抽取多少个顾客作 为样本?
解:已知=120(元),Z/2=1.96,E=20(元)
应抽取的样本容量为
n
Z2 2 2
由于这种原因而离开该企业的人员的真 正比例构造95%的置信区间。
解:已知 n=200 ,p =0.7 , np =140>5,
n(1- p)=60>5,= 0.95,Z/2=1.96
pˆ Z 2
pˆ (1 pˆ ) n
0.7 1.96 0.7(1 0.7) 200
0.636,0.764
我们可以95%的概率保证该企业职工由 于同管理人员不能融洽相处而离开的比 例在63.6%~76.4%之间
(24)
39.3641
2 1
2
(n
1)
