棱柱
棱柱分类及分类的依据

棱柱分类及分类的依据一、基于底面的形状的分类:1. 正棱柱:底面是一个正多边形,且底面的边与棱柱的侧面垂直。
2. 正多棱柱:底面是一个正多边形,但底面的边与棱柱的侧面不垂直。
3. 不规则棱柱:底面是一个不规则的多边形。
二、基于侧面的形状的分类:1. 直棱柱:侧面是由底面上的点和底面外的点直接相连而成的线段。
2. 斜棱柱:侧面是由底面上的点和底面外的点通过折线连接而成的。
三、基于棱柱的高度的分类:1. 高棱柱:棱柱的高度较大。
2. 矮棱柱:棱柱的高度较小。
以上是根据棱柱的不同特点进行的分类,每种分类都有其独特的特点和应用场景。
正棱柱是最常见的一种棱柱,它具有对称性,可以在建筑、几何学等领域得到广泛应用。
正多棱柱相对于正棱柱而言,其底面的边与侧面的夹角不是90度,因此具有一些特殊的性质和应用。
不规则棱柱则更加灵活多样,可以根据具体需求进行设计和制作。
直棱柱是最简单的一种棱柱,其侧面是由底面上的点和底面外的点直接相连而成的线段,形状规整,适用于一些简单的结构和装饰。
而斜棱柱则更加复杂,可以在一些特殊的场景中发挥作用,比如设计斜坡、楼梯等。
根据棱柱的高度进行分类主要是为了区分不同尺寸的棱柱。
高棱柱适用于一些需要较大空间的场景,如大型建筑物的支撑结构、储物柜等。
而矮棱柱则更加灵活轻便,适用于一些空间有限的场景,如家居装饰、小型建筑物的支撑结构等。
除了以上的分类依据,我们还可以根据底面的边数、侧面的棱数等进行更加详细的分类。
不同的分类依据可以根据实际需求进行选择和应用,以满足不同场景的要求。
棱柱作为一种常见的立体图形,具有丰富的分类和应用。
通过对棱柱的分类及分类依据的探讨,我们可以更好地理解和应用棱柱,为实际问题的解决提供更多的思路和方法。
希望本文能够帮助读者对棱柱的分类有一个清晰的认识。
棱柱
棱柱的性质
1. 侧棱都相等,侧面是平行四边形; 2. 两个底面与平行于底面的截面是全等的多边形; 3. 过不相邻的两条侧棱的截面是平行四边形
常见四棱柱:
底面是平行 侧棱与底面 • 四棱柱 四边形 平行六面体 垂直 直平行
棱柱的概念
1、我们常见的一些物体,例如三棱 镜,方砖以及螺杆的头部,它们都 呈棱柱形状,如图:
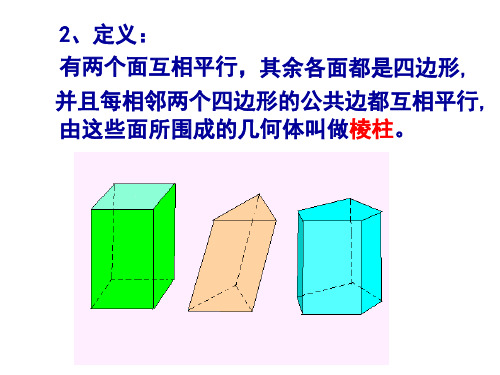
2、定义: 有两个面互相平行,其余各面都是四边形, 并且每相邻两个四边形的公共边都互相平行, 由这些面所围成的几何体叫做棱柱。
有关棱柱的几个名称
两个互相平行的面叫做棱柱的底面, 其余各面叫做棱柱的侧面。 两个面的公共边叫做棱柱的棱,其中 两个侧面的公共边叫做棱柱的侧棱。 侧面与底面的公共顶点叫做棱柱的顶 点,不在同一个面上的两个顶点的连 线叫做棱柱的对角线。两个底面的距 离叫做棱柱的高。
则
cos cos cos 2
2 2 2
例1
下列命题正确的是( D )
A1 B1 A B
C1
A.有两个面平行 , 其余各面都是 四边形的几何体叫棱柱. B. 有两个面平行 , 其余各面都是 平行四边形的几何体叫棱柱.
C. 有两个侧面是矩形的棱柱是直 棱柱. D. 有两个相邻侧面垂直于底面的 棱柱是直棱柱.
ACB 90 ,E为BB 的中点, A1 DE 90 1
Байду номын сангаас
求二面角 C A1 E D 的大小。
A1 B1
F
C1
A D B
E
C
例4 正三棱柱ABC A1 B1C1的底面边长为 a ,在侧 a 棱 BB1上截取 BD ,在侧棱 CC1 上截取CE a ,
棱柱的认识与计算

棱柱的认识与计算棱柱是一种常见的几何体,它具有多个平行的底面,以及与底面平行的侧面连接这些底面。
在本文中,我们将介绍棱柱的基本概念,包括它的特征、计算公式以及一些实际应用。
一、棱柱的定义与特征棱柱是一种立体几何体,它由两个相似的多边形底面和连接这些底面的矩形侧面构成。
棱柱的底面通常是正多边形,而侧面是长方形。
棱柱的特征包括:1. 底面:棱柱有两个平行的多边形底面,它们具有相同的形状和大小;2. 侧面:棱柱的侧面是若干个矩形,它们连接底面的对应顶点,并且与底面平行;3. 高度:棱柱的高度是连接两个底面中心的线段。
二、棱柱的计算公式1. 底面积:棱柱的底面积可以通过计算底面的面积得到。
如果底面是正多边形,则可以使用相应的公式计算面积。
2. 侧面积:棱柱的侧面积等于侧面的面积之和。
由于棱柱的侧面是矩形,因此可以使用矩形的面积公式计算。
3. 总表面积:棱柱的总表面积是指包括底面和侧面的所有面积之和。
可以通过计算底面积和侧面积然后求和得到。
4. 体积:棱柱的体积可以通过计算底面积再乘以高度得到。
即体积= 底面积 ×高度。
三、棱柱的实际应用1. 容器储存:棱柱形状的容器广泛应用于工业生产和日常生活中的液体和颗粒物体的储存。
在设计容器大小和容积时,需要准确计算棱柱的体积。
2. 建筑结构:柱体是建筑中常见的结构形式,例如柱子和立柱。
了解棱柱的属性和计算公式可以帮助工程师进行设计和施工。
3. 几何问题:在数学学科中,经常涉及到棱柱的计算问题,例如棱柱体积的计算,棱柱与其他几何体的相互关系等。
综上所述,棱柱是一种具有特定特征和计算方法的立体几何体。
通过了解棱柱的定义、特征以及计算公式,我们可以更好地理解和应用它在实际生活和学科中的意义。
无论是在工程建筑、数学学科还是其他领域,棱柱都扮演着重要的角色。
我们应该掌握对它的理解与运用。
棱柱
棱柱的表示法
1、用表示底面各顶点的字母来表示棱柱,
如:棱柱ABCDE- A1B1C1D1E1 2、用表示一条对角线端点的两个字母表示,
如:棱柱AC1
A1
E1 D1
B1
C1
A B
的洞口常筑有弧塔或烟囱,而当潮水将至,它们会躲入洞中并用泥团堵住洞口。 粘土招潮蟹(学名:Uca argillicola)最大的特征是雄蟹具有一对大小悬殊的螯,摆在前胸的大螯像是武士的盾牌。它会做出舞动大螯的动作,这个被称为“招潮”的动作,目的是威吓敌人或是求偶。此外,该蟹还有一对火柴棒般突出的眼睛,非常特别。它
E DCΒιβλιοθήκη 棱柱的分类 1、按侧棱与底面的关系分为: 1) 侧棱不垂直于底面的棱柱叫做斜棱柱。 2)侧棱垂直于底面的棱柱叫做直棱柱。
底面是正多边形的直棱柱叫做正棱柱。
•
;/ 嗨热线网
分布于朝鲜西岸、日本、澳大利亚、新喀里多尼亚、新加坡、加里曼丹岛、菲律宾、台湾岛以及中国大陆的广东、福建、浙江、山东等地,生活环境为海水,多见穴居于港湾中的沼泽泥滩上。 [3] 喜欢栖息在较为泥泞的沼泽,多位于红树林附近,会筑火山形或称烟 囱状的洞口,生性喜欢隐密,挥动大螯的动作缓慢,一有风吹草动会快速地奔回洞穴内躲藏。喜欢吃泥土中的有机质。也喜欢和邻居玩换房子游戏,如果邻居不换,就用抢的。 弧边招潮蟹的活动随潮水的涨落有一定的规律,高潮时则停于洞底,退潮后则到海滩上活动、取食、修补洞穴,最后则占领洞穴,准备交配。洞穴是招潮蟹生活的中心,在洞穴里既可以避免水陆各类捕食者的侵袭,又可以避免潮水浸淹或太阳直射。 [4] 弧边招潮蟹靠视觉和听觉接受通讯、联络、警告的信号。实现社会性聚集行为。以沉积物为食,能吞食泥沙,摄取其中的有机物,将不可食的部分吐出。它们取食藻类和其他有机物。它们用小螯刮取淤泥土表面的小颗粒送进嘴巴,这些小颗粒含有很多的碎屑 、藻类、细菌、以及其它的微生物,送入口中后,即被体内吸收。口中有一个特别的器官,可以将食物分类和过滤,不能利用的残渣再由小螯取出置于地面,集中形成人们所看到的小土球,称之为“拟粪”,有别于真正通过消化道从肛门排出的粪便。雌雄蟹
棱柱与棱锥的概念与计算

棱柱与棱锥的概念与计算在几何学中,棱柱和棱锥是两个常见的三维几何体。
它们具有不同的形状和特点,并且在计算其面积和体积时需要使用不同的公式。
一、棱柱的概念与计算棱柱是一种具有两个相等且平行的底面的几何体。
其侧面由若干个矩形组成,而底面则是由相等的多边形构成。
棱柱的名字通常根据底面的形状来命名,例如正方形棱柱、长方形棱柱等。
棱柱的计算主要涉及到面积和体积的计算。
下面将介绍一些常用的计算公式。
1. 底面积(B):棱柱的底面积可以根据底面的形状来计算。
例如,正方形底面的棱柱的底面积可以用公式B = 边长^2来计算。
2. 侧面积(S):棱柱的侧面积是指所有侧面的总和。
对于矩形侧面,可以用长乘以宽来计算。
因此,棱柱的侧面积可以用公式S = 周长 ×高来计算。
3. 总面积(A):棱柱的总面积是指所有面积的总和。
可以用底面积加上两倍的侧面积来计算。
公式为A = 2B + S。
4. 体积(V):棱柱的体积可以通过将底面积乘以高来计算。
因此,公式为V = B ×高。
二、棱锥的概念与计算棱锥是一种具有一个底面和一个顶点的几何体。
棱锥的侧面由多个三角形组成,而底面则可以是不规则的多边形。
和棱柱一样,棱锥的名字也通常根据底面的形状来命名,例如正三角锥、正四边锥等。
棱锥的计算也涉及到面积和体积的计算。
下面介绍一些常用的计算公式。
1. 底面积(B):棱锥的底面积可以根据底面的形状来计算。
例如,正三角形底面的棱锥的底面积可以使用公式B = (边长 ×高) / 2来计算。
2. 侧面积(S):棱锥的侧面积是指所有侧面的总和。
对于三角形侧面,可以使用海伦公式来计算面积,然后将其累加。
因此,棱锥的侧面积可以用公式S = ∑(边长 ×半周长)来计算。
3. 总面积(A):棱锥的总面积是指底面积加上所有侧面积的总和。
公式为A = B + S。
4. 体积(V):棱锥的体积可以通过将底面积乘以高再除以3来计算。
棱柱的知识点总结

棱柱的知识点总结棱柱的性质:1. 顶点和边的关系:棱柱有两个底面和若干个侧面,每个顶点都与若干个侧面的交点,并且与两个底面的交点。
顶点的个数等于棱柱的顶面个数和底面个数之和。
2. 棱柱的表面积和体积:棱柱的表面积等于底面积加上所有侧面积的总和,棱柱的体积等于底面积乘以高。
3. 棱柱的对称性:直棱柱在面对对角线对称和旋转180度对称的情况下,依然可以保持不变。
斜棱柱和正棱柱也有类似的对称性。
4. 棱柱的平行四边形关系:侧面都是平行四边形意味着棱柱的对边相等,且相对的对边平行。
在学习棱柱的过程中,我们还要掌握以下几个重要的知识点:1. 垂直棱柱、斜棱柱和正棱柱的特点和区别。
2. 棱柱的体积计算公式和表面积计算公式。
3. 棱柱的侧面展开图的绘制。
4. 棱柱的空间图形。
5. 棱柱的空间视图和投影。
垂直棱柱、斜棱柱和正棱柱的特点和区别:垂直棱柱:底面和顶面是平行的,并且相互垂直,侧面是平行四边形,也可以是矩形或者正方形。
垂直棱柱有很多例子,比如正方体、长方体等。
斜棱柱:底面和顶面不是平行的,侧面是平行四边形或者矩形。
斜棱柱的侧面和底面可以有不同的倾斜角度,所以斜棱柱有很多种不同的情况。
正棱柱:底面和顶面是平行的,侧面是等腰梯形。
正棱柱是一种特殊的棱柱,它具有独特的性质和特点。
对于垂直棱柱、斜棱柱和正棱柱,我们要掌握它们的特点和区别,以便能够正确识别和分类各种类型的棱柱。
棱柱的体积计算公式和表面积计算公式:棱柱的体积计算公式:V = 底面积 × 高棱柱的表面积计算公式:S = 2×底面积 + 侧面积在计算棱柱的体积和表面积时,我们要根据公式给出的参数,先计算出底面积和侧面积,然后代入公式求得棱柱的体积和表面积。
棱柱的侧面展开图的绘制:侧面展开图是指将棱柱的侧面展开平铺在平面上的图形,一般用来计算棱柱的表面积。
在绘制侧面展开图时,我们要根据棱柱的侧面形状和大小,将侧面展开成一个平面图形,然后根据展开图计算侧面积。
棱柱的性质及判定归纳
棱柱的性质及判定归纳
棱柱的定义
棱柱是一种几何体,具有以下特点:
- 该几何体由两个平行的多边形构成,上下底面多边形相等;
- 侧面是连接对应顶点的线段,形成一系列平行四边形;
- 侧面线段的长度相等。
棱柱的性质
棱柱具有以下性质:
1. 底面:棱柱的底面是多边形,其形状由具体的棱柱决定;
2. 侧面:棱柱的侧面是平行四边形,每个平行四边形的对边相等;
3. 顶点:棱柱的顶点是多边形的顶点以及侧面线段的连接点;
4. 高度:棱柱的高度是侧面线段的长度,垂直于底面的距离;
5. 表面积:棱柱的表面积可以计算底面和侧面积之和;
6. 体积:棱柱的体积可以计算底面的面积乘以高度。
棱柱的判定归纳
棱柱可以根据不同情况进行判定:
1. 如果底面是正多边形,并且侧边长度相等,则该棱柱为正棱柱;
2. 如果底面是任意多边形,并且侧边长度相等,则该棱柱为斜
棱柱;
3. 如果底面是圆形,并且侧边长度相等,则该棱柱为圆柱;
4. 如果底面既不是正多边形也不是圆形,并且侧边长度不相等,则该几何体不是棱柱。
希望以上内容对您有所帮助。
棱柱
下列几何体都是棱柱,它们有什么共 同性质?
D1
C1 B1 A1
C1 B1 C A
A1
A1 B1
E1 C1 E
D1
D A B
C A
B
D B C
1、棱柱的概念
如果一个多面体有两个面互相平 行, 其余每相邻两个面的交线互相 平行,这样的多面体叫做棱柱。 两个互相平行的面叫做 棱柱的底
作业:习题七
P 52. 2. 3.5
《 优化设计》p47 强化训 练①②③④
斜三棱柱、 直四棱柱、
正五棱柱
4.棱柱集合、斜棱柱集合、直棱柱集合、 正棱柱集合之间存在怎样的包含关系?
棱柱集合 直棱柱集合 斜棱柱 集合 正棱柱 集合
4、棱柱的性质
动画 (1)侧棱都相等,侧面是平行四边形。直棱柱的各个侧 面都是矩形;正棱柱的各个侧面都是全等的矩形。 动画 (2)两个底面与平行底面的平面的截面是全等的多边形。 〔3)不相邻的两条侧棱的截面是平行四边形。 动画
面,简称底; 其余各面叫做棱柱的侧面;
Hale Waihona Puke 思考:有两个面互相平行,其余各面都是平行四 边形的几何体是棱柱吗? 答:不一定。如右图所示,不是棱柱。
棱柱的表示法
1 .用平行的两底面多边形的字母表示棱柱,如:棱柱 ABCD- A1B1C1D1 2 .用表示一条对角线端点的两个字母表示,如:棱柱 A C1 D1 A1 B1 C1
C1
A1
A1 B1 B1
E1 C1 E
D1
D A B
C
A
C
A
B B C
D
棱柱的棱的概念
棱柱的棱的概念棱柱是一种几何形状,具有特定的几何属性。
在数学和几何学中,棱柱是一种多边形的立体扩展形状,由两个平行并且相等的多边形底面以及它们之间的侧面构成。
棱柱是一种特殊的多面体,其侧面是由多边形组成,而底面是相同的多边形。
棱柱的名称来源于它具有的特定特征,即其侧面是直线段的集合,这些直线段是多边形的边。
这些直线段被称为棱,因此棱柱是由多边形构成的棱所围成的立体。
一个棱柱通常由以下几部分构成:底面、顶面、侧面、轴、母线和棱。
底面和顶面是平行的、相似的多边形,它们的边与棱柱的轴垂直。
侧面是连接底面和顶面的矩形或平行四边形,它们的形状与底面和顶面相同。
棱是指连接底面和顶面相对顶点的直线段。
轴是连接底面和顶面中心的直线段,母线是连接底面和顶面对应边中点的直线段。
棱柱可以分为不同类型,根据其底面和侧面的形状,如正棱柱和斜棱柱。
正棱柱是底面和顶面都是正多边形的棱柱,而斜棱柱则是底面和顶面是任意多边形的棱柱。
此外,棱柱还可以根据其顶点的形状而被命名为正四棱柱、正六棱柱等。
棱柱的体积可以通过数学公式进行计算,其体积等于底面积乘以棱柱的高。
底面积可以通过底面的面积公式进行计算,高可以通过连接棱柱底面和顶面的垂直距离来确定。
棱柱的表面积也可以通过数学公式进行计算,其表面积等于底面积加上所有侧面的总面积。
棱柱作为一种几何形状,在现实生活中有着广泛的应用。
例如,建筑中的柱子、筒仓中的储粮筒和工业中的储气罐等都可以看作是棱柱的实际应用。
此外,在工程学、建筑学和设计学中,研究人员还经常通过对棱柱形状的研究来进行创新设计和工程计算。
总之,棱柱是一种具有特定特征和属性的几何形状。
它由底面、顶面、侧面、轴、母线和棱组成,可以分为不同类型。
棱柱在现实生活中有着广泛的应用,具有重要的理论和实际意义。
通过对棱柱的研究和应用,我们可以更好地理解和利用这一几何形状,为实际生活和科学研究带来更多的启发和帮助。
(完整版)棱柱基本知识点总结
(完整版)棱柱基本知识点总结棱柱基本知识点总结
1. 定义:
棱柱是一种由底面形状相同的平面多边形和连接底面对应顶点
的线段构成的立体图形。
2. 特征:
- 底面:棱柱的底面是一个多边形,通常为三角形、四边形或
多边形。
- 侧面:棱柱的侧面由连接底面对应顶点的线段构成,形成棱。
- 高度:棱柱的高度是底面与顶面之间的距离。
- 顶面:棱柱的顶面与底面形状相同,并且平行于底面。
3. 公式:
- 表面积:棱柱的表面积可以通过计算底面的面积及侧面的面
积求得。
- 底面面积的计算公式根据底面形状而定,如三角形底面可用
海伦公式计算。
- 侧面的面积可以通过计算侧面的高度与底面周长之积得到。
- 体积:棱柱的体积可以通过计算底面的面积与高度的乘积求得。
4. 命名:
- 根据底面形状的不同,棱柱可以分为三角柱、四边柱、五边柱等。
- 当棱柱的高度与底面的边垂直时,可以称为垂直棱柱。
5. 应用:
- 棱柱广泛应用于建筑、制造业、数学等领域。
- 在建筑中,棱柱形状的建筑物可以提供强大的结构支撑。
- 在制造业中,棱柱形状的零件可以提供稳定的组装平面。
- 在数学中,棱柱是几何形体的一种基本结构,具有丰富的性质和变化。
以上是对棱柱基本知识点的简要总结,希望对您有所帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)
⑷
棱柱的定义
注:本节所说的多 边形包括它的内部
由一个平面多边形上各点沿同一方向移动相同的距离形成的几何体.
棱柱的元素
顶点
底面 侧面 侧棱
①底面 ②侧面 ③侧棱
平移起止位置的两个面叫做棱柱的底面.
多边形的边平移所形成的面叫做棱柱的侧面. 相邻两侧面的公共边叫做棱柱的侧棱.
√
) ) )
( (
√
(
× ×
√
)
)
(5) 如果棱柱有两个相邻侧面是矩形, 那么它是直棱柱.- - - - (
一个棱柱是正四棱柱的条件是( D ) A . 底面是正方形,有两个侧面是矩形; B . 底面是正方形,有两个侧面垂直于底面;
C . 底面是菱形,且每一个顶点处有两条棱互相垂直;
D . 底面是正方形,每个侧面都是全等矩形.
A' O'
D B
面
C
O A
多面体分类:
按多面体面数分类,
如四面体、五面体、六面体等.
把多面体的任何一个面伸展为平面, 如果所有其他各面都在这个平面的同侧, 这样的多面体叫做凸多面体.
V
C
α
D A E B
高中主要研究凸多面体,本节课学习棱柱.
合作探究
下图中的物体具有什么样的共同的结构特 征?
棱柱的结构特征
B C
20 15
15
10
B
5 10 20
A
A
小结
一.多面体 二.棱柱
1.棱柱的概念 2.棱柱的表示 3.棱柱的性质 4.棱柱的分类 5.特殊的四棱柱
(B) C B F D E A (C)C A B D F E
(D)它们之间不都存在包含关系.
E
判断下列命题是否正确:
(1)直棱柱的侧棱长与高相等; - (2)直棱柱的侧面及过不相邻的两条 侧棱的截面都是矩形;- - - (3)正棱柱的侧面是正方形;- (4)如果棱柱有一个侧面是矩形, 那么它是直棱柱;- - - - - - (
D C
理解棱柱的定义
①过BC的截面截去长方体的一角, 截去的几何体是不是棱柱,余下的几 何体是不是棱柱?
答:都是棱柱.
理解棱柱的定义
②观察右边的棱柱,共有多少对平 行平面?能作为棱柱的底面的有几对?
答:四对平行平面;只有一对可以作为棱柱的底 面.
1、按侧棱与底面是否垂直可分为: 1) 侧棱不垂直于底的棱柱叫做斜棱柱
底面是矩形且侧 棱垂直与底面 底面是平行四边形
高与底面边长相等
四棱柱→长方体→正四棱柱→正方体
底面是正方形
底面是平行四边形 四棱柱 侧棱垂直于底面
平行六面体 侧棱垂直于底面
直四棱柱
直平行 六面体
底面是平行四边形
棱相等
正方体
正四棱柱
底面是正方形
长方体
底面是矩形
已知集合 A={正方体},B={长方体},C={正四 棱柱},D={平行六面体},E={四棱柱},F={直 平行六面体},则( B ) (A)A B C F D
侧面与底面的公共顶点叫做棱柱的顶点.
④顶点
棱柱的表示法
(1) .用平行的两底面多边形的字母表示棱柱,如: 棱柱ABCDE-A1B1C1D1E1 (2).用表示一条对角线端点的两个字母表示, 如:棱柱AC1
D1
A1 D A B1 C1 A1 C C B C1
A1
B1 B1 E A B
E1
D1
C1
B
A
E’ F’ A’ D’
B’
C’
E F A
D C B
2)侧棱垂直于底的棱柱叫做直棱柱
3) 底面是正多边形的直棱柱叫做正棱柱
2、按底面的边数分为:棱柱的底面可以是三角形、 四边形、五边形、……把这样的棱柱分别叫做三棱 柱、四棱柱、五棱柱、……
三棱柱
四棱柱
五棱柱
六棱柱
注:这两种分类彼此可渗透,例如斜三棱柱,直四棱柱, 正五棱柱等.
思考:棱柱集合、斜棱柱集合、直棱柱集合、 正棱柱集合之间存在怎样的包含关系? 棱柱
正棱柱 斜棱柱
直棱柱
观察下列棱柱并思考:棱柱具备哪些性质?
D1 A1 B1
C1 A1
C1
A1 B1 B1
E1
C1 E
D1
D A B
C A
C A B B
D C
1. 侧棱都相等,侧面是平行四边形;
2. 两个底面与平行于底面的截面是全等的多边形;
特殊的四棱柱
四棱柱:底面为四边形的棱柱. 平行六面体:底面是平行四边形的四棱柱; 直平行六面体:侧棱与底面垂直的平行六面体; 长方体:底面是矩形的直平行六面体; 正四棱柱:底面为正方形的直平行六面体; 正方体:棱长都相等的长方体.
将下列几何体按范围大到小进行排序: 四棱柱 长方体 正四棱柱 正方体
3. 过不相邻的两条侧棱的截面是平行四边形
问题1:有两个面互相平行,其余各面都 是四边形的几何体一定是棱柱吗? 答:不一定是.如右图所示,不是棱柱.
问题2:有两个面互相平行,其余各面都是 平行四边形的几何体一定是棱柱吗?
答:不一定是.如右图所示,不是棱柱. 问题3:有两个面互相平行,其余各面都是四边 形,并且每相邻两个四边形的公共边都互相平 行,由这些面所围成的几何体一定是棱柱吗? 答:一定是.
1.1.2棱柱、棱锥和棱台 的结构特征
问题1:观察下面的实物图片, 这些图片中的物 体具有怎样的形状?属于哪种空间几何体?
问题2:观察上述空间几何体,分析它的结构特征, 打算把上述几何体分成几类?
问题3:如何定义多面体与旋转体呢?
食盐晶体
明矾晶体
石膏晶体
多面体
由若干个平面多边形围成 的几何体叫做多面体.
小结
一.多面体 二.棱柱
1.棱柱的概念 2.棱柱的表示 3.棱柱的性质 4.棱柱的分类 5.特殊的四棱柱
6.棱柱的练习
已知:长方体AC’ 中,B’D是一条对角线。
求证:B’D 2 = AB 2 +BC 2 +BB’ 2 证明:连结BD ∵B’B⊥BD ∴B’D 2 =BD 2+BB’ 2 又 BD 2 =AB 2 +AD 2 =AB 2 +BC 2 ∴B’D 2 = AB 2 +BC 2 +BB’ 2
A’ D
A D’
C’
B’ C
B
定理:长方体一条对角线的长的平方等于一个顶点 上三条棱的长的平方和. 灯
6.棱柱的练习
如图,长方体的长为15cm,宽为10cm,高为20cm, 点B到点C的距离为5cm,一只蚂蚁如果要沿着长 方体的表面从A点爬到B点,需要爬行的最短距离 是多少?
B C
20 15
A
10
6.棱柱的练习
如图,长方体的长为15cm,宽为10cm,高为20cm, 点B到点C的距离为5cm,一只蚂蚁如果要沿着长 方体的表面从A点爬到B点,需要爬行的最短距离 是多少?
B C
20 15
A
10
6.棱柱的练习
如图,长方体的长为15cm,宽为10cm,高为20cm, 点B到点C的距离为5cm,一只蚂蚁如果要沿着长 方体的表面从A点爬到B点,需要爬行的最短距离 是多少?
D1 A1 B1
C1
顶点 棱
围成多面体的各个多边形 叫做多面体的面.
相邻两个面的公共边 叫做多面体的棱. 棱与棱的公共点 叫做多面体的顶点.
D
面
C B
A
A′
O′平面多 边形围成的几何体.
顶点 棱
A D1 A1 B1
C1
旋转体
由一个平面图形 绕它所在平面内的一 条直线旋转所形成的 旋转轴 封闭几何体.
