6、简谐振动、单自由度系统与频响函数解析
第1章 单自由度系统振动

例:杠杆系统
杠杆是不计质量的刚体
l3
l2
l1
m1 k1
x
k
2
m
2
求:
系统对于坐标 x 的等效质量和等效刚度
• 阻尼自由振动
前面的自由振动都没有考虑运动中阻力的影响,实际系统的 机械能不可能守恒,因为总存在着各种各样的阻力。振动中 将阻力称为阻尼,例如摩擦阻尼,电磁阻尼,介质阻尼和结 构阻尼。尽管已经提出了许多数学上描述阻尼的方法,但是 实际系统中阻尼的物理本质仍然极难确定。 最常用的一种阻尼力学模型是粘性阻尼。在流体中低速运动 或沿润滑表面滑动的物体,通常就认为受到粘性阻尼。
粘性阻尼力与相对速度称正比,即:
Pd cv
c:为粘性阻尼系数,或阻尼系数
单位: N s / m 建立平衡位置,并受力分析 动力学方程: 或写为:
k m
c 0
kx cx
x
m
kx 0 m x cx
2 0 x 0 2 x 0 x
固有频率
c 2 km
• 能量法
对于不计阻尼即认为没有能量损失的单自由度系统,也可以 利用能量守恒原理建立自由振动的微分方程,或直接求出系 统的固有频率。 无阻尼系统为保守系统,其机械能守恒,即动能 T 和势能 V 之和保持不变 ,即:
或:
T V const
d T V 0 dt
弹簧质量系统 动能: 势能:
max 0 x max x
0
k m mt
若忽略 mt ,则0 增大
• 等效质量和等效刚度
方法1:
选定广义位移坐标后,将系统得动能、势能写成如下形式: 1 1 2 T Mex V Ke x2 2 2
单自由度振动系统

n
x0
sin n t
系统总响应
振动系统总的响应=上述两部分响应之和
x x1 x2 x0 cos nt
n
x0
sin nt
叠加性是线性系统的重要特征
数字特征
A ——振幅,振动物体离开静平衡位置的最 大位移 ——圆频率 n T ——振动周期,旋转矢量转动一周 ( 2 ),振动物体的位移值也就重复一次, 振动周期:振动重复一次所需要的时间间隔 f ——振动频率,单位时间内完成的振动的 次数
总动能: Ts Tm 1 1 lx 2 1 mx 2 1 m 1 l x 2 T 23 2 2 3
系统微分方程
系统的势能:
由: 微分方程:
1 2 U kx 2
d T U 0 dt
1 x m l kx 0 3
例三
如右图,弹簧 在静平衡位置 长度为 l ,单 位长度的质量 为 ,求系统 的固有频率。
基本假设
假设系统的变形是线性的,即当弹簧下段 的位移为 x 的时候,在距离弹簧上端 u 的截 u 面振幅为 l x ,假定系统的速度分布也满足 线性要求(在端点处显然成立)
0
0
设质量块的位移为 x ,速度为 x ,
1 f T
固有特性
n
k m
m T 2 n k 2
1 n 1 f T 2 2 k m
可见,上述三个量都由振动系统的参数确定,而 与初始条件无关,是系统的固有特性,因而又称 作:固有圆频率、固有周期和固有频率
系统的初始条件只决定振动的振幅和初相位
系统参数对振动特性的影响
汽车振动分析之 单自由度

B 1 2 2 2 B0 (1 ) (2 )
振幅放大因子 动力放大系数
在不同的ξ值时,放大因子β,相位角θ与频率比λ的关 系图如下
Your site here
LOGO
λ
幅频响应曲 线
相频响应曲 线
Your site here
LOGO
B 1 B0 (1 2 ) 2 (2 ) 2
2.阻尼使系统振动的振幅按几何级数衰减。 相邻两个振幅之比为
Ai enTd Ai 1
式中η —减幅系数; n—衰减系数。 工程上,为应用方便起见,常用对数减幅系数δ 代替减 幅系数η ,即
ln nTd
Your site here
LOGO
综上所述,有阻尼系统是否作自由振动的条件为
x2 (t )
B0 sin(t ) (1 ) (2 )
2 2 2
Your site here
LOGO
简谐激励下的强迫振动稳态响应解为:
x 2 (t )
B0 sin( t )
2 2
(1 ) (2 )
2
强迫振动稳态响应的基本特点:
1、系统在简谐激励的作用下,其强迫振动稳态响应是简谐振动, 振动的频率与激励频率相同。 2、强迫振动稳态响应的相位比激励的相位滞后
激振力方向改变太快,振动物 体由于惯性来不及跟随。系统 的振幅B主要取决于系统的惯性 。 称为惯性控制区。
相位差 θ 接近 π ,即在高频范围 内位移与激振力接近反向
Your site here
LOGO
B 1 B0 (1 2 ) 2 (2 ) 2
3、频率比
p
1 B B0
第二章单自由度系统自由振动)

三、单自由度系统在简谐激励作用下的受迫振动 1、简谐激励下的受迫振动响应及频谱分析 2、受迫振动的复数求解法--单位谐函数法 3、支座简谐激励(位移激励)引起的振动与被动隔振 4、偏心质量(力激励)引起的振动与主动隔振 5、测振传感器的原理
正弦型激励 周期激励 任意激励
k
kx m x
m
F(t)
mx kx F0 sin t
p2 k m
x p2x F0 sin t
第一章 概论
一、振动及其研究的问题 1、振动 2、振动研究的问题 振动隔离 在线控制 工具开发 动态性能分析 模态分析
第一章 概论
二、振动分类及研究振动的一般方法 1、振动分类:振动分析、振动环境预测、系统识别 2、研究振动的一般方法 (1)理论分析方法
建立系统的力学模型、建立运动方程、求解方程得到响应 (2)实验研究方法 (3)理论与实验相结合的方法
②旋转矢量表示法
③复数表示法
z Acos(t ) iAsin(t )
z Aei(t )
eit cost i sin t eit cost i sin t
x Im( Aei(t) ) Asin(t )
x
iAei(t )
振幅
A
x02
x0 p
2
初相位
arctan px0
x0
固有圆频率 p k m
(rad/s)
固有频率 f p 1 k
2 2 m
(HZ)
固有周期 T 1 2 m (s)
f
k
例题2.7 某仪器中一元件为等截面悬臂梁,梁的质 量可忽略。在梁的自由端由磁铁吸住两个集中质量 m1、m2。梁在静止时,断电使m2突然释放,求随 后m1的振动。
工程振动名词术语大全(中英文),没见过这么全的

工程振动名词术语大全(中英文),没见过这么全的1 振动信号的时域、频域描述振动过程 (Vibration Process)简谐振动 (Harmonic Vibration)周期振动 (Periodic Vibration)准周期振动 (Ouasi-periodic Vibration)瞬态过程 (Transient Process)随机振动过程 (Random Vibration Process)各态历经过程 (Ergodic Process)确定性过程 (Deterministic Process)振幅 (Amplitude)相位 (Phase)初相位 (Initial Phase)频率 (Frequency)角频率 (Angular Frequency)周期 (Period)复数振动 (Complex Vibration)复数振幅 (Complex Amplitude)峰值 (Peak-value)平均绝对值 (Average Absolute Value)有效值 (Effective Value,RMS Value)均值 (Mean Value,Average Value)傅里叶级数 (FS,Fourier Series)傅里叶变换 (FT,Fourier Transform)傅里叶逆变换 (IFT,Inverse Fourier Transform)离散谱 (Discrete Spectrum)连续谱 (Continuous Spectrum)傅里叶谱 (Fourier Spectrum)线性谱 (Linear Spectrum)幅值谱 (Amplitude Spectrum)相位谱 (Phase Spectrum)均方值 (Mean Square Value)方差 (Variance)协方差 (Covariance)自协方差函数 (Auto-covariance Function)互协方差函数 (Cross-covariance Function)自相关函数 (Auto-correlation Function)互相关函数 (Cross-correlation Function)标准偏差 (Standard Deviation)相对标准偏差 (Relative Standard Deviation)概率 (Probability)概率分布 (Probability Distribution)高斯概率分布 (Gaussian Probability Distribution) 概率密度 (Probability Density)集合平均 (Ensemble Average)时间平均 (Time Average)功率谱密度 (PSD,Power Spectrum Density)自功率谱密度 (Auto-spectral Density)互功率谱密度 (Cross-spectral Density)均方根谱密度 (RMS Spectral Density)能量谱密度 (ESD,Energy Spectrum Density)相干函数 (Coherence Function)帕斯瓦尔定理 (Parseval''s Theorem)维纳,辛钦公式 (Wiener-Khinchin Formula)2 振动系统的固有特性、激励与响应振动系统 (Vibration System)激励 (Excitation)响应 (Response)单自由度系统 (Single Degree-Of-Freedom System) 多自由度系统 (Multi-Degree-Of- Freedom System) 离散化系统 (Discrete System)连续体系统 (Continuous System)刚度系数 (Stiffness Coefficient)自由振动 (Free Vibration)自由响应 (Free Response)强迫振动 (Forced Vibration)强迫响应 (Forced Response)初始条件 (Initial Condition)固有频率 (Natural Frequency)阻尼比 (Damping Ratio)衰减指数 (Damping Exponent)阻尼固有频率 (Damped Natural Frequency)对数减幅系数 (Logarithmic Decrement)主频率 (Principal Frequency)无阻尼模态频率 (Undamped Modal Frequency)模态 (Mode)主振动 (Principal Vibration)振型 (Mode Shape)振型矢量 (Vector Of Mode Shape)模态矢量 (Modal Vector)正交性 (Orthogonality)展开定理 (Expansion Theorem)主质量 (Principal Mass)模态质量 (Modal Mass)主刚度 (Principal Stiffness)模态刚度 (Modal Stiffness)正则化 (Normalization)振型矩阵 (Matrix Of Modal Shape)主坐标 (Principal Coordinates)模态坐标 (Modal Coordinates)模态分析 (Modal Analysis)模态阻尼比 (Modal Damping Ratio)频响函数 (Frequency Response Function)幅频特性 (Amplitude-frequency Characteristics)相频特性 (Phase frequency Characteristics)共振 (Resonance)半功率点 (Half power Points)波德图(Bodé Plot)动力放大系数 (Dynamical Magnification Factor)单位脉冲 (Unit Impulse)冲激响应函数 (Impulse Response Function)杜哈美积分(Duhamel’s Integral)卷积积分 (Convolution Integral)卷积定理 (Convolution Theorem)特征矩阵 (Characteristic Matrix)阻抗矩阵 (Impedance Matrix)频响函数矩阵 (Matrix Of Frequency Response Function) 导纳矩阵 (Mobility Matrix)冲击响应谱 (Shock Response Spectrum)冲击激励 (Shock Excitation)冲击响应 (Shock Response)冲击初始响应谱 (Initial Shock Response Spectrum)冲击剩余响应谱 (Residual Shock Response Spectrum) 冲击最大响应谱 (Maximum Shock Response Spectrum) 冲击响应谱分析 (Shock Response Spectrum Analysis)3 模态试验分析机械阻抗 (Mechanical Impedance)位移阻抗 (Displacement Impedance)速度阻抗 (Velocity Impedance)加速度阻抗 (Acceleration Impedance)机械导纳 (Mechanical Mobility)位移导纳 (Displacement Mobility)速度导纳 (Velocity Mobility)加速度导纳 (Acceleration Mobility)驱动点导纳 (Driving Point Mobility)跨点导纳 (Cross Mobility)传递函数 (Transfer Function)拉普拉斯变换 (Laplace Transform)传递函数矩阵 (Matrix Of Transfer Function)频响函数 (FRF,Frequency Response Function)频响函数矩阵 (Matrix Of FRF)实模态 (Normal Mode)复模态 (Complex Mode)模态参数 (Modal Parameter)模态频率 (Modal Frequency)模态阻尼比 (Modal Damping Ratio)模态振型 (Modal Shape)模态质量 (Modal Mass)模态刚度 (Modal Stiffness)模态阻力系数 (Modal Damping Coefficient)模态阻抗 (Modal Impedance)模态导纳 (Modal Mobility)模态损耗因子 (Modal Loss Factor)比例粘性阻尼 (Proportional Viscous Damping)非比例粘性阻尼 (Non-proportional Viscous Damping)结构阻尼 (Structural Damping,Hysteretic Damping)复频率 (Complex Frequency)复振型 (Complex Modal Shape)留数 (Residue)极点 (Pole)零点 (Zero)复留数 (Complex Residue)随机激励 (Random Excitation)伪随机激励 (Pseudo Random Excitation)猝发随机激励 (Burst Random Excitation)稳态正弦激励 (Steady State Sine Excitation)正弦扫描激励 (Sweeping Sine Excitation)锤击激励 (Impact Excitation)频响函数的H1 估计 (FRF Estimate by H1)频响函数的H2 估计 (FRF Estimate by H2)频响函数的H3 估计 (FRF Estimate by H3)单模态曲线拟合法 (Single-mode Curve Fitting Method)多模态曲线拟合法 (Multi-mode Curve Fitting Method)模态圆 (Mode Circle)剩余模态 (Residual Mode)幅频峰值法 (Peak Value Method)实频-虚频峰值法 (Peak Real/Imaginary Method)圆拟合法 (Circle Fitting Method)加权最小二乘拟合法 (Weighting Least Squares Fitting method) 复指数拟合法 (Complex Exponential Fitting method)4 传感器测量系统传感器测量系统 (Transducer Measuring System)传感器 (Transducer)振动传感器 (Vibration Transducer)机械接收 (Mechanical Reception)机电变换 (Electro-mechanical Conversion)测量电路 (Measuring Circuit)惯性式传感器 (Inertial Transducer,Seismic Transducer) 相对式传感器 (Relative Transducer)电感式传感器 (Inductive Transducer)应变式传感器 (Strain Gauge Transducer)电动力传感器 (Electro-dynamic Transducer)压电式传感器 (Piezoelectric Transducer)压阻式传感器 (Piezoresistive Transducer)电涡流式传感器 (Eddy Current Transducer)伺服式传感器 (Servo Transducer)灵敏度 (Sensitivity)复数灵敏度 (Complex Sensitivity)分辨率 (Resolution)频率范围 (Frequency Range)线性范围 (Linear Range)频率上限 (Upper Limit Frequency)频率下限 (Lower Limit Frequency)静态响应 (Static Response)零频率响应 (Zero Frequency Response)动态范围 (Dynamic Range)幅值上限 Upper Limit Amplitude)幅值下限 (Lower Limit Amplitude)最大可测振级 (Max.Detectable Vibration Level)最小可测振级 (Min.Detectable Vibration Level)信噪比 (S/N Ratio)振动诺模图 (Vibration Nomogram)相移 (Phase Shift)波形畸变 (Wave-shape Distortion)比例相移 (Proportional Phase Shift)惯性传感器的稳态响应(Steady Response Of Inertial Transducer)惯性传感器的稳击响应 (Shock Response Of Inertial Transducer) 位移计型的频响特性(Frequency Response Characteristics Vibrometer)加速度计型的频响特性(Frequency Response Characteristics Accelerometer)幅频特性曲线 (Amplitude-frequency Curve)相频特性曲线 (Phase-frequency Curve)固定安装共振频率 (Mounted Resonance Frequency)安装刚度 (Mounted Stiffness)有限高频效应 (Effect Of Limited High Frequency)有限低频效应 (Effect Of Limited Low Frequency)电动式变换 (Electro-dynamic Conversion)磁感应强度 (Magnetic Induction, Magnetic Flux Density)磁通 (Magnetic Flux)磁隙 (Magnetic Gap)电磁力 (Electro-magnetic Force)相对式速度传 (Relative Velocity Transducer)惯性式速度传感器 (Inertial Velocity Transducer)速度灵敏度 (Velocity Sensitivity)电涡流阻尼 (Eddy-current Damping)无源微(积)分电路 (Passive Differential (Integrate) Circuit)有源微(积)分电路 (Active Differential (Integrate) Circuit)运算放大器 (Operational Amplifier)时间常数 (Time Constant)比例运算 (Scaling)积分运算 (Integration)微分运算 (Differentiation)高通滤波电路 (High-pass Filter Circuit)低通滤波电路 (Low-pass Filter Circuit)截止频率 (Cut-off Frequency)压电效应 (Piezoelectric Effect)压电陶瓷 (Piezoelectric Ceramic)压电常数 (Piezoelectric Constant)极化 (Polarization)压电式加速度传感器 (Piezoelectric Acceleration Transducer) 中心压缩式 (Center Compression Accelerometer)三角剪切式 (Delta Shear Accelerometer)压电方程 (Piezoelectric Equation)压电石英 (Piezoelectric Quartz)电荷等效电路 (Charge Equivalent Circuit)电压等效电路 (Voltage Equivalent Circuit)电荷灵敏度 (Charge Sensitivity)电压灵敏度 (Voltage Sensitivity)电荷放大器 (Charge Amplifier)适调放大环节 (Conditional Amplifier Section)归一化 (Uniformization)电荷放大器增益 (Gain Of Charge Amplifier)测量系统灵敏度 (Sensitivity Of Measuring System)底部应变灵敏度 (Base Strain Sensitivity)横向灵敏度 (Transverse Sensitivity)地回路 (Ground Loop)力传感器 (Force Transducer)力传感器灵敏度 (Sensitivity Of Force Transducer)电涡流 (Eddy Current)前置器 (Proximitor)间隙-电压曲线 (Voltage vs Gap Curve)间隙-电压灵敏度 (Voltage vs Gap Sensitivity)压阻效应 (Piezoresistive Effect)轴向压阻系数 (Axial Piezoresistive Coefficient)横向压阻系数 (Transverse Piezoresistive Coefficient)压阻常数 (Piezoresistive Constant)单晶硅 (Monocrystalline Silicon)应变灵敏度 (Strain Sensitivity)固态压阻式加速度传感器(Solid State Piezoresistive Accelerometer)体型压阻式加速度传感器(Bulk Type Piezoresistive Accelerometer)力平衡式传感器 (Force Balance Transducer)电动力常数 (Electro-dynamic Constant)机电耦合系统 (Electro-mechanical Coupling System)5 检测仪表、激励设备及校准装置时间基准信号 (Time Base Signal)李萨茹图 (Lissojous Curve)数字频率计 (Digital Frequency Meter)便携式测振表 (Portable Vibrometer)有效值电压表 (RMS Value Voltmeter)峰值电压表 (Peak-value Voltmeter)平均绝对值检波电路 (Average Absolute Value Detector)峰值检波电路 (Peak-value Detector)准有效值检波电路 (Quasi RMS Value Detector)真有效值检波电路 (True RMS Value Detector)直流数字电压表 (DVM,DC Digital Voltmeter)数字式测振表 (Digital Vibrometer)A/D 转换器 (A/D Converter)D/A 转换器 (D/A Converter)相位计 (Phase Meter)电子记录仪 (Lever Recorder)光线示波器 (Oscillograph)振子 (Galvonometer)磁带记录仪 (Magnetic Tape Recorder)DR 方式(直接记录式) (Direct Recorder)FM 方式(频率调制式) (Frequency Modulation)失真度 (Distortion)机械式激振器 (Mechanical Exciter)机械式振动台 (Mechanical Shaker)离心式激振器 (Centrifugal Exciter)电动力式振动台 (Electro-dynamic Shaker)电动力式激振器 (Electro-dynamic Exciter)液压式振动台 (Hydraulic Shaker)液压式激振器 (Hydraulic Exciter)电液放大器 (Electro-hydraulic Amplifier)磁吸式激振器 (Magnetic Pulling Exciter)涡流式激振器 (Eddy Current Exciter)压电激振片 (Piezoelectric Exciting Elements)冲击力锤 (Impact Hammer)冲击试验台 (Shock Testing Machine)激振控制技术 (Excitation Control Technique)波形再现 (Wave Reproduction)压缩技术 (Compression Technique)均衡技术 (Equalization Technique)交越频率 (Crossover Frequency)综合技术 (Synthesis Technique)校准 (Calibration)分部校准 (Calibration for Components in system) 系统校准 (Calibration for Over-all System)模拟传感器 (Simulated Transducer)静态校准 (Static Calibration)简谐激励校准 (Harmonic Excitation Calibration)绝对校准 (Absolute Calibration)相对校准 (Relative Calibration)比较校准 (Comparison Calibration)标准振动台 (Standard Vibration Exciter)读数显微镜法 (Microscope-streak Method)光栅板法 (Ronchi Ruling Method)光学干涉条纹计数法 (Optical Interferometer Fringe Counting Method)光学干涉条纹消失法(Optical Interferometer Fringe Disappearance Method)背靠背安装 (Back-to-back Mounting)互易校准法 (Reciprocity Calibration)共振梁 (Resonant Bar)冲击校准 (Impact Exciting Calibration)摆锤冲击校准 (Ballistic Pendulum Calibration)落锤冲击校准 (Drop Test Calibration)振动和冲击标准 (Vibration and Shock Standard)迈克尔逊干涉仪 (Michelson Interferometer)摩尔干涉图象 (Moire Fringe)参考传感器 (Reference Transducer)6 频率分析及数字信号处理带通滤波器 (Band-pass Filter)半功率带宽 (Half-power Bandwidth)3 dB 带宽 (3 dB Bandwidth)等效噪声带宽 (Effective Noise Bandwidth)恒带宽 (Constant Bandwidth)恒百分比带宽 (Constant Percentage Bandwidth)1/N 倍频程滤波器 (1/N Octave Filter)形状因子 (Shape Factor)截止频率 (Cut-off Frequency)中心频率 (Centre Frequency)模拟滤波器 (Analog Filter)数字滤波器 (Digital Filter)跟踪滤波器 (Tracking Filter)外差式频率分析仪 (Heterodyne Frequency Analyzer) 逐级式频率分析仪 (Stepped Frequency Analyzer)扫描式频率分析仪 (Sweeping Filter Analyzer)混频器 (Mixer)RC 平均 (RC Averaging)平均时间 (Averaging Time)扫描速度 (Sweeping Speed)滤波器响应时间 (Filter Response Time)离散傅里叶变换 (DFT,Discrete Fourier Transform) 快速傅里叶变换 (FFT,Fast Fourier Transform)抽样频率 (Sampling Frequency)抽样间隔 (Sampling Interval)抽样定理 (Sampling Theorem)抗混滤波 (Anti-aliasing Filter)泄漏 (Leakage)加窗 (Windowing)窗函数 (Window Function)截断 (Truncation)频率混淆 (Frequency Aliasing)乃奎斯特频率 (Nyquist Frequency)矩形窗 (Rectangular Window)汉宁窗 (Hanning Window)凯塞-贝塞尔窗 (Kaiser-Bessel Window)平顶窗 (Flat-top Window)平均 (Averaging)线性平均 (Linear Averaging)指数平均 (Exponential Averaging)峰值保持平均 (Peak-hold Averaging)时域平均 (Time-domain Averaging)谱平均 (Spectrum Averaging)重叠平均 (Overlap Averaging)栅栏效应 (Picket Fence Effect)吉卜斯效应 (Gibbs Effect)基带频谱分析 (Base-band Spectral Analysis)选带频谱分析 (Band Selectable Sp4ctralAnalysis)细化 (Zoom)数字移频 (Digital Frequency Shift)抽样率缩减 (Sampling Rate Reduction)功率谱估计 (Power Spectrum Estimate)相关函数估计 (Correlation Estimate)频响函数估计 (Frequency Response Function Estimate) 相干函数估计 (Coherence Function Estimate)冲激响应函数估计 (Impulse Response Function Estimate) 倒频谱 (Cepstrum)功率倒频谱 (Power Cepstrum)幅值倒频谱 (Amplitude Cepstrum)倒频率 (Quefrency)7 旋转机械的振动测试及状态监测状态监测 (Condition Monitoring)故障诊断 (Fault Diagnosis)转子 (Rotor)转手支承系统 (Rotor-Support System)振动故障 (Vibration Fault)轴振动 (Shaft Vibration)径向振动 (Radial Vibration)基频振动 (Fundamental Frequency Vibration)基频检测 (Fundamental Frequency Component Detecting) 键相信号 (Key-phase Signal)正峰相位 (+Peak Phase)高点 (High Spot)光电传感器 (Optical Transducer)同相分量 (In-phase Component)正交分量 (Quadrature Component)跟踪滤波 (Tracking Filter)波德图 (Bode Plot)极坐标图 (Polar Plot)临界转速 (Critical Speed)不平衡响应 (Unbalance Response)残余振幅 (Residual Amplitude)方位角 (Attitude Angle)轴心轨迹 (Shaft Centerline Orbit)正进动 (Forward Precession)同步正进动 (Synchronous Forward Precession)反进动 (Backward Precession)正向涡动 (Forward Whirl)反向涡动 (Backward Whirl)油膜涡动 (Oil Whirl)油膜振荡 (Oil Whip)轴心平均位置 (Average Shaft Centerline Position)复合探头 (Dual Probe)振摆信号 (Runout Signal)电学振摆 (Electrical Runout)机械振摆 (Mechanical Runout)慢滚动向量 (Slow Roll Vector)振摆补偿 (Runout Compensation)故障频率特征 (Frequency Characteristics Of Fault) 重力临界 (Gravity Critical)对中 (Alignment)双刚度转子 (Dual Stiffness Rotor)啮合频率 (Gear-mesh Frequency)间入简谐分量 (Interharmonic Component)边带振动 (Side-band Vibration)三维频谱图 (Three Dimensional Spectral Plot)瀑布图 (Waterfall Plot)级联图 (Cascade Plot)阶次跟踪 (Order Tracking)阶次跟踪倍乘器 (Order Tracking Multiplier)监测系统 (Monitoring System)适调放大器 (Conditional Amplifier)趋势分析 (Trend Analysis)倒频谱分析 (Cepstrum Analysis)直方图 (Histogram)确认矩阵 (Confirmation Matrix)通频幅值 (Over-all Amplitude)幅值谱 (Amplitude Spectrum)相位谱 (Phase Spectrum)报警限 (Alarm Level)。
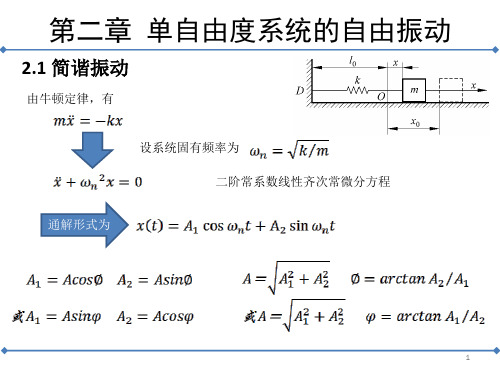
第二章 单自由度系统的自由振动
35
第二章 单自由度系统的自由振动
方程的特征根为: 讨论在阻尼比ξ取值不同时,微分方程解 (1)小阻尼情况,即ξ<1:
此时特征方程的根:
的性质。
微分方程的解为:
设:
,考虑初始条件t=0时,有
,
,将其
代入微分方程的解中,有
t=0时
求解 得到
36
第二章 单自由度系统的自由振动
为:
T
1
•
m(l )2
2
U 1 k(a)2
2
平衡位置时: kas mgl
d
1 2
ml 2
•
2
1 2
k
(a
)
2
0
dt
••
k
(a)2
0
ml
n
a l
k m
T
2 n
2l
a
m k
22
第二章 单自由度系统的自由振动
2.3 瑞利法
8
第二章 单自由度系统的自由振动
例题讲解3 重物落下,与简支梁做完全非弹性碰撞
梁长 L,抗弯刚度 EJ m
h
l/2
0
l/2
求: 梁的自由振动频率和最大挠度
第二章 单自由度系统的自由振动
解: 取平衡位置 以梁承受重物时的静平衡位 置为坐标原点建立坐标系
静变形 由材料力学 : mgl3
48EJ
1 2
m2
(
l2 l1
x)2
1 2
第二章单自由度系统自由振动)
(1)等效刚度
通常用能量法求复杂系统的等效刚度,即按实际系统要转化的弹簧 的弹性势能与等效系统弹簧势能相等的原则来求系统的等效刚度。
1、单自由度系统及其振动微分方程建立 (1)单自由度振动系统
(2)单自由度系统振动方程的建立方法 ①牛顿第二定律或达朗贝尔原理
f m&x& f m&x& 0 M J&& M J&& 0
例题2-1 (教材例题2.10) 建立如图所示振动系统的振动微分方程。
ml&x&
若动能达到最大Tm ax时取势能为0,则动能为0时,势能必取得最大值U m ax
Tm
ax=U
m
,可由此得到固有频率
ax
例题:求圆轴圆盘扭振系统的振动固有频率
T 1 m(l)2
2
U 1 k(a)2
2
d [1 m(l)2 1 k(a)2 ] 0
dt 2
2
可得 + k ( a )2 0
例题2-3
meq J m1r 2 m2 R2 keq (k1 k3 )r 2 (k2 k4 )R2
例题2-4 (教材例题2.4)
例题2-5 (教材例题2.5)
me
m
L
3
mA
J
mvb2 a2
1 3
msb2
例题2-6 (教材例题2.3、2.6) 求轴向轴转化的单轴系的等效刚度和等效旋转质量
单自由度系统在简谐激励作用下的受迫震动读后感
三 单自由度系统在简谐激励作用下的受迫震动读后感这一章讲的是单自由度系统受到简谐荷载或者简谐位移作用时, 系统的位移时间函数求解与应用, 可以把此章节分为三部分。
系统对简谐力的响应表达式:无阻尼系统在受简谐荷载作用时, 可以算得其位移时间方程的表达式:t rk F t B t A t u θωωsin 1/sin cos )(20-++= 当初始条件给定时, 比如说如果初始位移 和初始速度 , 该以得出:)sin (sin 1/)(20t r t rk F t u ωθ--= 由这个表达式可以看出当r=1时, 即激励的频率与系统的固有频率相同时, 系统的位移无限大, 这种现象称之为共振, 这时结构会冲破约束, 导致破坏。
阻尼系统在受简谐激励作用时, 通过解微分方程, 可以得出其位移时间表达式:222)2()1()sin()sin cos ()(ξϕθωωξωr r t u t B t A e t u st D D t +--++=-由于阻尼的存在, 初始自由振动和伴随自由振动都含有一个振幅衰减因子, 故经过一段时间之后系统的振动将趋于稳定, 工程上比较关心稳态解, 即原方程的特解, 即:222)2()1()sin()(ξϕθr r t u t u st +--=从该试可以得出稳态阶段的振幅, 将振幅与静态位移ust 作比, 可以得到系统的动力放大系数D 。
计算阻尼比的方法:共振放大法: 我们可以通过测出r=1时的D 的值, 计算出系统的阻尼比, 因为当r=1时, , 但是该方法不太实用, 求静位移时可能出现问题, 因为典型的简谐震动加载体系是不能再零频率是工作的。
带宽法:通过测得 最大振幅处(共振时的振幅)时的对应两个频率, 然后通过计算可以得到系统阻尼比, 该方法避免开了测系统静位移, 比共振法适用。
每周能量损失法: 由于系统的阻尼, 系统就会有能量的耗散, 因为在稳态阶段, 系统每周的运动方式是相同, 为周期函数, 故在稳态阶段, 在一个周期里, 外力对结构做的功等于系统耗散的能量。
于开平-结构动力学第二讲
(2) 阻尼力的功:
Wd A cos t dt c 2 / 1 cos 2 t cA2 2 dt 0 2 1 2 1 2 2 2 / cA2 2 cA cos 2 t dt 0 2 2
5 稳态响应振幅和相位
5.2 初始相位角 根据初相位角表达式
2 tg 1 2
可以画出初相位角随频率比的变化曲线,简称相频曲线:
在共振点,不管阻尼比多大,初相位角均为90度。
6 稳态响应复数解法及频响函数
之前将外载荷假设为正弦形式,其运动控制方程为:
������������ሷ 1 + ������������ሶ 1 + ������������1 = ������0 sin������������ 简谐激励的另一种典型形式为余弦形式,其运动控制方程写作: ������������ሷ 2 + ������ ������ሶ 2 + ������������2 = ������0 cos������������ (2) (1)
o o o
o
1 2 Fo A sin Fo A sin 2
6 稳态响应复数解法及频响函数
令方程特解为������ ������ = ������������ ������ ������������������ ,代入运动控制方程得: (−������2 ������������������ + ������������������������������ + ������������������ )������ ������������������ = ������0 ������ ������������������ 方程对任意时刻t恒等,则方程两边指数函数������ ������������������ 前系数相等,由此可得: ������������ = ������0 ������ − ������������ 2 + ������������������
第二章-(第1节)单自由度系统的自由振动
tan 1
ωn x0 x 0
(2.1-11)
2.1 简谐振动
弹簧悬挂的物体沿铅锤方向的振动
当振动系统为静平衡时弹簧在 重力mg的作用下将有静伸长
s
mg k
(2.1-12)
在重力与弹簧力的作用下,
物体的运动微分方程为
mx mg k(s x) (2.1-13)
因为mg=ks,上式仍可简化为
mx kx
波变化。
2.1 简谐振动
振动周期
振动重复一次所需要的时间间隔,称之为振
动周期。 在简谐振动的情况下,每经过一个周期,相
位就增加2,因此
[n(t+T)+]-(nt+)=2
故有
T 2 n
(2.1-9)
实际上T代表发生一次完整运动所需要的时间
,周期通常以秒(s)计。
2.1 简谐振动
振动频率
在单位秒时间内振动重复的次数,称为振动 频率,一般用f 表示。
解:取偏角为坐标。从平衡位
置出发,以逆时针方向为正,锤的
切向加速度为 ,l故 有运动微分方
程为
ml2 mgl sin
假定角不大,可令sin,则
上式简化为 g 0
l
图 2.1-5
2.1 简谐振动
例题:列写振动微分方程求系统的周期(例2.1-2)
故
n2
g l
则振动周期为
T 2 2 l
n
g
2.1 简谐振动
或
② x(t) Asin(nt )
(2.1-7)
式中常数A和(=/2-)分别称为振幅和相角。方程(2.1-
7)说明该系统以固有频率n作简谐振动。
2.1 简谐振动 简谐振动的定义及矢量表示
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1x
a v
0.5
t
2
4
6
8
10
12
14
-0.5
-1
常数A和 的确定
x Acos(t ) v dx Asin(t )
dt
由初始条件:
x0 Acos v0 A sin
A=
x02
v0
2
tg v0 x0
说明:
(1) 一般来说 的取值 在-π和π(或0和2π)之 间;
对数衰减率
A1
A3
AK t
A2
A4
AK 1
A Ae K
0t
1 2
0TD1
1 2
A Ae e e K 1
0
(
t
TD1 2
)
ln
ln
AK AK 1
1 2
TD1
1 2
2 2
单自由度系统的强迫振动
运动方程为:mx bx kx F0 sint
m
k o x
微分dd2t方2x程特征2 x 0
k
m
解
d2x + ω2x = 0 dt 2
可得
位 移 x A cos( t ) 振动方程
速 度 v dx A sin(t ) A cos(t )
dt
2
加速度 a dv A 2 cos(t ) A 2 cos(t )
临界阻尼状态几种初始条件 曲线
小阻尼状态
当 1时,系统为小阻尼状态,
方程特征根为两个不等实根, 方程解为:
x Ae0t cos 1 20t
小阻尼状态下系统的响应曲线
可见,小阻尼状态下,系统的自由
响应按照具有固定频率的谐波振荡,
但是谐波的幅值按照指数规律衰减。
小阻尼情况下的阻尼比计算
结论:
(1)单自由度无阻尼系统的自由振动是以正弦或余弦函数表示 的,故称为简谐振动。 (2)自由振动的角频率即系统的固有频率仅由系统本身参数确 定,与外界激励、初始条件无关。
k
m
(3)自由振动的振幅A和初相角φ由初始条件所确定。
单自由度系统
单自由度系统的阻尼自由振动
k
b
mx
mx bx kx 0
A2e
)e 2 10t
0t
可见,大阻尼状态下,系统的自由
响应按照指数规律衰减,逐渐向平
衡位置靠近,解中的常数A1和A
由
2
系统的初始状态决定。
临界阻尼状态
当 1时,系统为临界阻尼状态,
方程特征根为两个重根,方 程解为:
x ( A1 A2t)e0t
可见,临界阻尼状态下,系统的自 由响应也是按照指数规律衰减,逐 渐向平衡位置靠近,解中的常数A1 和A2由系统的初始状态决定。
惯性测量原理—摆系统
右图所示惯性系统的运动方程为:
m&x& cx& kx mX&& 经过拉普拉斯变换后有(不考虑负号):
,
x X
s2
s2 20s 02
其中,0
k m
c
2 mk
对于不同的0和,系统表现出不同
的性质。
位移摆
当 1, 0时
有
x X
1,在自振
频率以上,呈现
位移平坦特性摆
体称为位移摆。
即摆体和外界振
动位移成正比。
幅 频 特 性 曲 线 (自 振 频 率 1Hz, 阻 尼 比 0.707) 1.5
1
0.5
0
-2
-1
0
1
2
3
10
10
10
10
10
10
幅 频 特 性 曲 线 ( 自 振 频 率 1Hz, 阻 尼 比 0.707) 200
(q 02 2) 2)2 4 202
2
A2
(02
(q 02 2) 2)2 4 2022
0D 1 20
有阻尼强迫振动的解:
x2
(02
(q 02 2) 2)2 42022
sint
(02
(q 02 2) 2)2 42022
cont
x2 Asin(t )
A
A12
A22
q / 02
(1
2 02
)2
4 22 02
arctg
A2 A1
arctg(202 02 )
A
1
(1 u2 )2 4u2 2
xst
xst
u
0
1
,为动力放大系数
(1 u2 )2 4u2 2
F0 sint
x 20 x
02 x
F0 m
sin t
q sin t
方程的解为:
x
x1
x
,
2
x1为阻尼自由振动项;
x
为阻尼强迫振动项
2
x1 e(0t C1 cos0Dt C2 sin 0Dt)
x2 A1 sint A2 cost
A1
(02
150
100
50
0
-2
-1
0
1
2
3
10
10
10
10
10
10
速度摆
当 ? 1,在0附近
有x sX
1,以自振
x 10-3 3
幅 频 特 性 曲 线 ( 自 振 频 率 1Hz, 阻 尼 比 30)
2
1
频率为中心,呈现
0 10-4
10-2
100
102
104
速度平坦特性摆
幅 频 特 性 曲 线 ( 自 振 频 率 1Hz, 阻 尼 比 30) 100
0
k m
x 20x 02x 0 b
2 mk
r1,2 0 0 2 1
x A1er1t A2er2t
0 :无阻尼固有角频率
:阻尼常数
大阻尼状态
当 1时,系统为大(过)阻尼
状态,方程特征根为两个不等实 根,方程解为:
x (A1e
2 10t
体称为位移摆。即 50
0
摆体和外界振动速 -50
度成正比。
-100
10-4
10-2
100
102
104
加速度摆
当 1,在0以下
有x s2X
1,在自振
频率为以下,呈现
加速度平坦特性,
摆体称为加速度摆。
即摆体和外界振动
加速度成正比。
x 10-6 幅 频 特 性 曲 线 ( 自 振 频 率 100Hz, 阻 尼 比 0.707) 3
2
1
0
100
101
102
103
104
105
幅 频 特 性 曲 线 ( 自 振 频 率 100Hz, 阻 尼 比 0.707) 0
-50
-100
-150
-200
100
101102103Fra bibliotek104
105
简谐振动
以无阻尼自由振动的弹簧振子为例得出普遍结论:
由 F ma kx
运动学特征
a k x 2 x
