保守力及其性质
第四章动和能

∑Ai
注意: 功是过程量,与路径有关。 ★ 注意: 1. 功是过程量,与路径有关。 2. 功是标量,但有正负。 功是标量,但有正负。
⑵ 万有引力的功
质点之间在引力作用下相对运动时, 所在处为原点, 质点之间在引力作用下相对运动时,以 M 所在处为原点,M 的方向为矢径的正方向。 指向 m 的方向为矢径的正方向。m 受的引力方向与矢径方向 相反。 相反。 b Mm b rb A = a F ⋅ dr = ∫r − G 3 r ⋅ dr 引 a
R+ h R+ h
R
R
R
GMm
r
2
ˆ r ) ⋅ dr
o
R
GMmh = −GMm ∫ = R( R + h) r
R+ h 2
dr
例2、 质量为 2 kg 的质点在力 、
F =12 t i (SI)
的作用下,从静止出发, 轴正向作直线运动。 的作用下,从静止出发,沿x轴正向作直线运动。 轴正向作直线运动 求前三秒内该力所作的功。 求前三秒内该力所作的功。 一维运动可以用标量) 解:(一维运动可以用标量) :(一维运动可以用标量
外力的功之和内力的功之和系统末动能系统初动能所有外力对质点系做的功和内力对质点系做的功之和等于质点系总动能的增量
第四章
动和能
§1. 功和功率
一. 功 ⑴ 恒力的功 恒力沿直线做的功: 恒力沿直线做的功: 单位: J 单位:
F
θ
M M
F
∆r
A = F cosθ ∆ r = F ⋅ ∆r (点乘积,标量积 点乘积, 点乘积 标量积)
A外 + A内 = E − E = 系统总动能增量
Kb Ka
保守力的性质

保守力的性质假设作用力F为保守力,则它满足以下三个等价的充分必要条件:1、F的旋度是零:∇×F=02、对于任意简单闭合路径C,所做的机械功W是零:W=F∙d rc=03、作用力F是某位势Φ的梯度:F=−∇Φ数学证明1⇒2:设定C为任意简单闭合路径。
思考边界为C的任意曲面S。
斯托克斯定理阐明∇×F S ∙d a=F∙d rc假设F的旋度等于零,方程左边为零,则机械功W是零。
所以,第二个条件是正确的。
2⇒3:假设,对于任意简单闭合路径C,所做的机械功W是零,则保守力所做于粒子的机械功,独立于路径的选择。
设定函数Φx=−F∙d rxo其中,o和x分别是特定的原点和空间内任意一点。
根据微积分基本定理,F x=−∇Φx所以,第三个条件是正确的。
3⇒1:假设第三个条件是正确的。
思考下述方程:∇×F=−∇×∇Φ=−ð2Φðyðz−ð2Φðzðyx−ð2Φðzðx−ð2Φðxðzy−ð2Φðxðy−ð2Φðyðxz=0所以,第一个条件是正确的。
总结,这三个条件是等价的。
由于符合第二个条件就等于通过保守力的闭合路径考试。
所以,只要满足上述三个条件的任何一条件,施加于粒子的作用力就是保守力。
大地测量学复习资料(考试必备)

⼤地测量学复习资料(考试必备)1.垂线同总地球椭球(或参考椭球)法线构成的⾓度称为绝对(或相对)垂线偏差2.以春分点作为基本参考点,由春分点周⽇视运动确定的时间,称为恒星时3.以真太阳作为基本参考点,由其周⽇视运动确定的时间,称为真太阳时。
⼀个真太阳⽇就是真太阳连续两次经过某地的上中天(上⼦午圈)所经历的时间。
4.以格林尼治平⼦夜为零时起算的平太阳时称为世界时5.原⼦时是⼀种以原⼦谐振信号周期为标准6.归算:就是把地⾯观测元素加⼊某些改正,使之成为椭球⾯上相应元素。
7.把以垂线为依据的地⾯观测的⽔平⽅向值归算到以法线为依据的⽅向值⽽加的改正定义为垂线偏差改正7.⼤地线椭球上两点间的最短程曲线。
8.设椭球⾯上P点的⼤地经度L,在此⼦午⾯上以椭圆中⼼O为原点建⽴地⼼纬度坐标系; 以椭球长半径a为半径作辅助圆,延长P2P与辅助圆相交P1点,则OP1与x 轴夹⾓称为P点的归化纬度u。
9.仪器加常数改正因测距仪、反光镜的安置中⼼与测距中⼼不⼀致⽽产⽣的距离改正,称仪器加常数改正,包括测距仪加常数和反光镜加常数。
10.因测距仪的基准频率等因素产⽣的尺度参数成为乘常数。
11.基本分划与辅助分划相差⼀个常数301.55cm,称为基辅差,⼜称尺常数12.控制⽹可靠性:控制⽹能够发现观测值中存在的粗差和抵抗残存粗差对平差的影响13.M是椭球⾯上⼀点,MN是过M的⼦午线,S为连接MP的⼤地线长,A为⼤地线在M点的⽅位⾓。
以M为极点;MN为极轴;P点极坐标为(S, A)⼀点定位,如果选择⼤地原点:则⼤地原点的坐标为:多点定位,采⽤⼴义弧度测量⽅程1954年北京坐标系可以认为是前苏联1942年坐标系的延伸。
它的原点不在北京,⽽在前苏联的普尔科沃。
相应的椭球为克拉索夫斯基椭球。
1954年北京坐标系的缺限:①椭球参数有较⼤误差。
②参考椭球⾯与我国⼤地⽔准⾯存在着⾃西向东明显的系统性的倾斜,在东部地区⼤地⽔准⾯差距最⼤达+68m。
静电场力做功与路径无关静电场力是保守力(精)

国际单位制(SI制)单位为:焦耳/库仑 记作: J C1 也称为: 伏特 (Volt,V) 1J C1 1V
二、点电荷的电场的电势 ~用场强分布和电势的定义直接积分。
p E
E
q
4 0r 2
rˆ
r
q
V
v v E dl
r
p
电场所做的功为:
A r rA r
r
L
q0
r E
r
qg
rr '
dl
dr
r
rB
B
W
B
dW
A
rB rA
q0q dr
40r 2
q0q
4 0
1 ( rA
1 rB
)
②对于由多个静止点电荷组成的系统或静止的连续带
电体,可看成是由无数电荷元组成的点电荷系。
vv v
v
由场强叠加原理: E E1 E2 L En
q
4 0 r
2
dr
q
4 0 r
•电势的正负与源电荷q正负有关
①正点电荷周围的场电势为正,离电荷越远,电 势越低。
②负点电荷周围的场电势为负,离电荷越远,电 势越高。
•场强总是从电势高处指向电势低处。
三、电势的叠加原理 由场强叠加原理和电势的定义,直接得出电势叠加原理。
表述:一个电荷系的电场中,任一点的电势等于每一个 带电体单独存在时在该点所产生电势的代数和。
一般,场源电荷有限分布:选 V 0
场源电荷无限分布:不选 V 0
许多实际问题中选 V地球 0
2. 叠加法
①将带电体划分为电荷元 dq
2.5 动能定理和功能原理

结论:
成对 保守内力功 特点:只取决于相互作
用质点的始末相对位置,是始末位置的函数。
§2.5 动能定理和功能原理 第二章 质点动力学
4. 成对保守内力 作功特点
《大学物理》教程
讨论
一对
m' m m' m W1 W2 ( G ) ( G ) 万有引力作功 rA rB
ACB
A
D
C
B
Fc dr Fc dr
BDA
Fc dr Fc dr
ACB
ADB
0
§2.5 动能定理和功能原理
始末位置 相同
第二章 质点动力学
3. 成对力作功
《大学物理》教程
有人问:
力是一种 相互作用 力总是成对 出现,满足 牛三律 这对力作功 有特点吗?
§2.5 动能定理和功能原理 第二章 质点动力学
1. 质点 的动能定理
《大学物理》教程
b
a
1 1 2 2 F dr mvb mva 2 2
定义功(过程量):力对空间的累积量
W
① 元功:
b
a
F dr
dW F dr ② 功率:单位时间内作的功 P F v dt dt
xb
xa
1 2 1 2 kxdx kxa kxb 2 2
小结: 弹簧力做功与路径无关,只与运动 起点和终点的位置有关。
§2.5 动能定理和功能原理 第二章 质点动力学
《大学物理》教程
讨论
定义式法 求功的计算举例
例3 万有引力做功 以 m 2 为参考系
a m
r (t ) F
浅议物理学中的保守力和势能

浅议物理学中的保守力和势能【摘要】保守力和势能在物理学中扮演着重要的角色。
保守力是指不依赖路径的力,其所做的功与路径无关。
势能则是对保守力的一种描述,是可用于确定力学系统状态的函数。
保守力和势能之间存在着密切的关系,一般通过势能函数来确定。
根据保守力和势能的关系,我们可以推导出机械能守恒定律,即在只受保守力的情况下,力学系统的机械能保持不变。
保守力和非保守力的区别在于是否可以用势能来描述。
保守力和势能的重要性体现在它们对力学系统的描述和分析中起到了关键作用,而在物理学中也有着广泛的应用。
为了更深入地理解和探索保守力和势能,未来的研究方向可能会集中在更复杂系统下的运用和拓展。
【关键词】保守力、势能、物理学、性质、关系、确定、守恒定律、区别、重要性、应用、未来研究方向。
1. 引言1.1 保守力的基本概念保守力是物理学中一个非常重要的概念,它在描述物体运动和相互作用过程中起着至关重要的作用。
保守力是一种在物体运动中所做的功与路径无关的力,即对于沿着任意闭合路径作功的保守力,总是零。
这意味着保守力对物体的位移所做的功只依赖于起点和终点,而与具体路径无关。
保守力的基本概念包括以下几个要点:1. 保守力与势能的关系:保守力可以用势能来描述和计算。
势能是对物体在某个力场中位置所储存的能量,而保守力则是通过势能的梯度来定义和推导的。
具体来说,对于一个保守力F,其对应的势能函数为U,满足F = -∇U。
这里的负号表示力是势能的负梯度方向,即力的方向指向势能减小的方向。
2. 势能的引入:为了便于描述和计算保守力对物体的作用,我们引入了势能这一概念。
势能可以是位置的函数,也可以是速度和其他物理量的函数。
通过引入势能,我们可以将关于保守力的问题转化为寻找势能函数和利用势能函数进行计算的问题。
保守力的基本概念包括了与势能的关系和势能的引入。
这些概念在物理学中有着广泛的应用和重要性,对于解决各种运动和相互作用问题都起着至关重要的作用。
理论力学复习题

理论力学复习题一、 填空1、质点沿空间曲线232()(32)(24)r t t i t j t t K =++−+− 运动在2t S =时,质点的速度V =__________________;加速度a = __________________,速度大小为V =__________________;加速度大小为a =__________________。
2、质量为m 的质点运动规律为j t i t a r ωωsin cos +=,式中a 、b ,ω均为常数,则质点的轨道道方程为 ,质点从(a ,0)运动到(b ,0),在这一过程中动量的增量=ΔP,动能的增量Δ=K E 。
3、已知点的运动方程为t R y t R x ωωcos ,sin ==,其中R ,W 为常量,点的运动轨迹为__________________,速度为v =__________________,加速度a =__________________。
4、在极坐标中,其径向和横向单位矢量j ,i 的时间导数分别为=dti d =dtj d 。
5、质点的运动速度为(1)kt V A e −=−,其中A ,K 均为常数。
当0t =时质点位于坐标的原点,则质点的运动方程为__________________;加速度为__________________。
6、某质点运动方程为r=e at,θ=bt;该质点径向速率V r =_____________,横向速率V=________________;径向加速度的值αr =________________,横向加速度的值αθ=_______________,加速度的值α=________________。
7、在自然坐标系中,切向加速度ιa 和法向加速度n a 的计算公式为ιa =___________,n a =________________;8、在极坐标中加速度的两个分量为(1)__________________,(2)__________________。
保守力和势能
一对力所作的总功的只取决于两质点的相对运动;
一对力做功的代数和与参考系的选择无关;
5
什么条件下, 一对内力做功为零?
v
m
M
f
s s
C
f
v
N
C
N
Af Af 0
作用点无相对位移
AN AN 0
相互作用力与相对位移垂直
6
功的大小与参照系有关
功的单位为焦耳 功率(power) 功率:单位时间内力对物体所作的功 平均功率
yb ya
W mgdy mg( yb ya ) mg( ya yb )
重力是保守力。重力的功等于重力势能增量 的负值。重力势能以地面为零势能点。
y dy a p o
12
dr dx
W mg( yb ya ) =-EP 为势能增量
dr
b
EP mgdy mg(0 y) mgy
P
C
y
R
.
o
m
F
解:
F F0 xi F0 yj
r
x
0
dr dxi dyj
2R
r xi yj
2 A F d r F0 x d x F0 y d y 2F0 R
0 0
8
练习2 如图 M =2kg , k =200N m , s = 0.2m , g ≈ 10ms
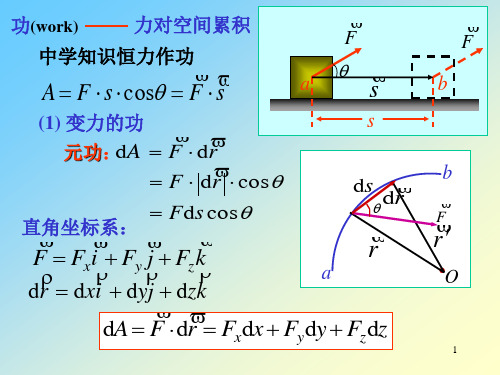
功(work)
力对空间累积
中学知识恒力作功
F
a
F
A F s cos F s
s
s
ds
dr
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
保守力及其性质
曹瑞廷
随着“应试教育”向素质教育模式的转轨,高考也由知识立意向能力立意转化,中学物理教学的要求已经变得越来越高了。
中学物理的教学过程中,让学生掌握获取知识的方法、拓宽思维的深度和广度,是教学中的一个重要任务。
特别是高三复习中,教师应对每个知识点的来龙去脉,对每个知识点的发生、发展过程,预以足够的重视,做到以新型的行为交往模式,使学生摆脱机械的知识接受器的学习模式,开启思维的通道,把前后知识联系起来,找到某些知识点的共同点,达到复习、巩固、提高能力的目的。
在中学物理中,力可以按效果或性质来分类,在高三复习中,我们可以引导学生研究重力、电场力、万有引力、分子力、弹簧的弹力、核力等,从中可以发现这些力有一个共同的特点,即力所做的功仅仅依赖于受力质点的始末位置,与质点经过的路径无关。
我们把具有这种性质的力称为保守力。
而像摩擦力等则不具有上述特点,称为非保守力。
一、保守力做功与路径无关,只跟起点和终点的位置有关的证明
1、重力的功
h1的A点自由下落到高度为h2的B点,
再水平移到C点。
物体在水平移动过程中,
重力对物体并不做功,所以在整个过程
中,重力对物体所做的功,就等于物体由A点自由下落到B点的过程中重力所做的功。
W G=mgh1-mgh2
如果让这个物体沿着斜面AC滑下,从原来高度为h1的A点滑到高度为h2的C点,物体沿斜面滑下的距离是S,重力所做的功是:
W G=mgsinθS=mg△h=mgh1-mgh2
我们看到,物体由起点A到终点C,不论沿折线ABC,还是沿着斜面
AC,重力所做的功仍然是:
W G=mgh1-mgh2
这就是说,重力对物体所做的功只跟起点和终点的位置有关,而跟物体
运动的路径无关。
2、静电场力的功
B、C三点,其中A的电势为U A,B、
C两点的电势分别为U B、U C且U B=U C。
设将电量为q的正电荷从A点移
到B点,再移到C点,在整个过程中
电场力做功为:
W=W AB+W BC=qEd+0=q(U A-U B)=qU A-qU B=qU A-qU C
如果让这个电荷沿斜线AC移动,电场力做功为
W=qEScosθ=qEd=qU A-qU C
可以证明,不论电荷q是正是负,不论沿斜线AC移动,还是沿着折线
ABC移动,电场力做的功总是相等的。
可以证明,这个电荷沿任一路径从A移到C,电场力做的功总为:
W=qEScosθ=qEd=qU A-qU C
同样可以证明,在非匀强电场中上述关系也是成立的。
这就是说,电场力对移动电荷所做的功只跟起点和终点的位置有关,与
移动的路径无关。
3、可以证明万有引力、分子力、弹簧的弹力与重力、电场力一样,
都具有共同的特点,即:保守力所做的功仅仅依赖于受力质点的始末位置,
与质点经过的路径无关。
二、保守力总是与一定形式的势能相对应
对保守力来说,若受力质点始末位置一定,则力所做的功便唯一确定,与路径无关。
这样就存在一个由相对位置决定的势能。
当质点由初始位置移到末位置时,势能的增量等于力所做功的负值。
即:力做的功等于势能的减少量。
公式表达为:
W=-△E p =-( Ep 2 –Ep 1) 或W = Ep 1 –Ep 2 三、 应用
例1:小球质量m=0.5kg ,由高度为H=20m 的高台上以初速度V 0=20m/s 与方向成θ=60°角斜向上抛出,若空气阻力不计,小球落地时速度多大?(g=10m/s 2)
解:小球运动中只受重力作用,根据动能定理:
2
02
12
2
1
νν
m m W G -
=
由于重力做的功等于重力势能增量的负值。
W G = mgH-0=mgH 所以
s m s m gH /3.28/2010220
22
2
0=⨯⨯+=
+=νν
例2:如图所示,一质量为m ,带电量为-q 的小物体,可在水平轨道OX 上运动,O 端有一与轨道垂直的固定墙。
轨道处于匀强电场中,场强大小为E ,方向沿OX 轴正
方向。
小物体以初速度
V 0从X 0点沿OX 轨道运动,运动时受到大小不变的摩擦力f 的作用,且f 〈qE ,设小物体与墙碰撞时不损失机械能,且电量保持不变,试求它在停止运动前所通过的总路程S 多大?
解:小物体在水平方向受到电场力和摩擦力的作用。
当它向左运动时,电场力向左而摩擦力向右,且电场力大于摩擦力,它做匀加速直线运动;当它向右运动时,电场力和摩擦力均向左,它做匀减速直线运动。
由上述分析可知,当它向左加速运动,遇到墙时发生碰撞,改变为向右做减速运动,直到速度减为零。
然后又向左加速运动,遇墙又碰撞,变为向右做减速运动,这样反复不止,但因存在摩擦力,向右运动的最大距离一次比一次小,直到为零。
由于电场力做功与路径无关,所以电场力做功为qEX 0 。
摩擦力做功与路径有关,因而摩擦力做功为μmgS 。
根据动能定理有:
2
2
10νμm mgS qEx
-
=-
整理得:
例3、两个分子甲和乙相距较远(此时它们之间的分子力可忽略),设甲固定不动,乙逐渐向甲靠近直到不能靠近的整个过程中,分子力对乙分子的做功情况是 。
两分子的势能变化情况是 。
解:根据分子力做功的特点,可知:先做正功,后做负功。
热能先减小后增大。
例4、水平放置的平行金属板A 、B 间形成匀强电场。
一带电油滴以初速度V 0从某一角度射入电场区,如图所示,已
知油滴的质量为m ,电量为+q 。
试求:(1)油滴进入电场区后做速度为V 0
f
m qEx
S 222
ν
+
=
的匀速直线运动且油滴始终未与A 板相碰,求该电场区场强大小和方向?(2)当油滴运动到距B 板h 处时,突然场强减为原来的三分之一,油滴打在B 板上的末速度为多大?
解:(1)因为匀速直线运动,所以油滴所受合力为零,即:
F 电= mg ∴场强方向向上 F 电 = qE ∴q
mg q F E ==
电
(2)当E ′= E/3 时,合力方向竖直向下,油滴做类平抛运动。
根据动能定理,得:
2
2
2
12131mV mV
qEh mgh -
=
-
整理以上两式,得:
gh
V V 3
42
0+
=
通过以上例题可以看出,在曲线运动中,这类力做功是无法用功的定义直接求出,而利用这类力做功等于势能的减少量可以很方便求出。
这样,不仅增加学生对这些知识点融会贯通,达到复习目的。
也使学生掌握了一种学习的方法,提高了学习的能力。
山西平阳机械厂中学。
