三视图小正方体个数口诀
由三视图确定小正方体的个数的方法

由三视图确定小正方体的个数的方法
通过三视图确定小正方体的个数是一种简单而有效的方法,可以用来解决许多复杂的几何问题。
三视图法是一种几何技术,它使用三个平面图来表示一个物体的形状,其中包括正视图、左视图和俯视图。
这三个视图是从不同的角度来看待物体的,可以清楚地显示出物体的三维形状。
例如,如果要确定小正方体的个数,可以使用三视图法。
首先,先找出三个视图,即正视图,左视图和俯视图,仔细观察每个视图中小正方体的位置,数数它们的个数。
然后,根据三个视图中小正方体的位置和数量,计算出小正方体的总数。
根据三视图法,可以通过观察三个视图来确定小正方体的总数,而不需要真正地计算它们的体积。
这一步骤非常实用,可以节省大量的时间和精力。
当然,在使用三视图法之前,需要先熟悉三视图的概念,然后根据实际情况,灵活地运用这一技术来解决实际问题。
只有掌握了这种几何方法,才能解决复杂的几何问题。
总之,三视图法是一种有效的几何方法,可以用来快速确定小正方体的个数。
它可以节省大量的时间和精力,因此被广泛应用于复杂的几何问题的解决中。
正方体1~6相对数字口诀

正方体1~6相对数字口诀《正方体1~6相对数字口诀一》小朋友们呀,听好这个口诀哟。
一是前面小脸蛋,二在后面把家安。
就像小娃娃,前面玩耍脸朝前,后面就有小靠山。
三在左边来站岗,四在右边把手牵。
这就好比是两个小伙伴,一左一右来作伴。
五在上面像屋顶,六在下面当地基。
就像盖房子,屋顶在上遮风雨,地基在下稳稳立。
这样去想正方体上的数字,是不是就很容易记住啦。
《正方体1~6相对数字口诀二》小宝贝们,记好这个口诀哦。
一像小旗迎风飘,它的对面是六呀,六就像个大口袋把小旗装。
二似小鸭嘎嘎叫,对面数字是五呀,五像秤钩把小鸭钓。
三像耳朵听四方,它的对面是四呢,四就像小旗的杆儿和耳朵靠。
想象着这些有趣的画面,正方体1到6相对的数字就不会搞混啦,就像记住自己家的小伙伴一样简单呢。
《正方体1~6相对数字口诀三》小朋友,来听口诀啦。
一像铅笔细又长,它的对面是六像口哨吹得响。
二像鸭子水中游,对面数字五像秤砣重悠悠。
三像耳朵能听话,对面的四像小旗风中挂。
正方体就像一个小屋子,1和6一个在屋顶一个在屋底,2和5一个在墙上一个在地上,3和4在两边像两个小卫士。
这样想呀,就容易把这些数字的相对关系记住喽。
《正方体1~6相对数字口诀四》孩子们呀,咱们来记口诀喽。
一呢就像小棒立起来,它的对面是六,六就像个大圆圈把小棒绕。
二就像弯弯的小月亮,对面的五像大大的烧饼。
三像小山坡,对面四像小树一棵。
就好像在一个小世界里,小棒和圆圈相对,月亮和烧饼相对,山坡和小树相对,正方体上的数字就这么有序地被记住啦,是不是很有趣呢?《正方体1~6相对数字口诀五》小同学啊,下面这个口诀很有用呢。
一是尖尖的小箭头,对面是六像个大皮球。
二像小鹅伸着脖,对面的五像大菠萝。
三像小山有棱角,对面四像小扇摇啊摇。
想象一下,箭头指着皮球,小鹅对着菠萝,小山靠着小扇,正方体的1到6相对数字就清晰地在脑海里啦,就像看动画一样好记呢。
《正方体1~6相对数字口诀六》小朋友们快来呀,口诀来喽。
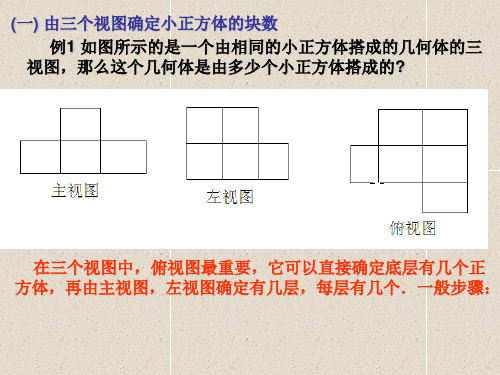
第3期利用三视图确定正方体的个数

第3期利用三视图确定正方体的个数三规则:主俯长对正、主左高平齐、俯左宽相等即:主视图和俯视图的长要相等主视图和左视图的高要相等左视图和俯视图的宽要相等。
应用如图表示某个由小正方体搭成的几何体的俯视图,俯视图无法表示该几何体的高度,用3代表右上角这个位置有3个立方体。
用2表示左上角这个位置有2个立方体,1表示右下角这个位置有1个立方体,此时,我们不但可以轻易地画出该几何体的其它两个视图,也可以得知该物体一共由1 2 3=6个小正方体组成.借助俯视图的这个功能,我们在确定一个几何体由多少个小正方体组成的时候,可以先画出俯视图,再根据主视图与左视图,确定俯视图各位置上的立方体的个数,从而快速找出正方体的个数.例1 如图是由一些相同的小正方体构成的立体图形的三视图,那么构成这个立体图形的小正方体有_______个解析第一步:从俯视图入手,结合主视图,从正面看过去,也就是从如下图的箭头方向看过去,可以确定的是俯视图最右侧只有一层,标上数字1,左边这列最高有两层,具体数目还不能确定第二步:结合左视图,从箭头方向看过去,右侧有两个一层的,所以马上可以确定如图两个位置的数量.由于左视图的最左侧最高有2个,所以,沿箭头方向看过去最左侧最高有2个,所以,俯视图的空白处应填2,如图,所以,一共有2 1 1 1=5个正方体.点拨:此立体图形的三视图都已知,所以俯视图结合主视图和左视图,容易明确个位置上的正方体的个数.例2 一个几何体由若干个大小相等的小立方体组成,下面分别是此几何体的主视图,和俯视图,该几何体至少是用错少个小立方块搭成的.解析此题已经存在俯视图,还是从俯视图出发考虑,因为主视图已经确定,如蓝色所示,右侧两个位置最高只有一个,所以填写数字1.而最左侧最高有两个,因为是最少是多少个,所以左侧三个位置,只要有一个位置是2个,其余都是1个即可,如图,有下面三种可能总数都为2 2 2=6个.此时顺便还可以求出最多有多少个.如图,只需要左侧最高都是2个即可,所以,最多有2 2 2 1 1=8个.点拨:此题已知主视图与俯视图,可利用主视图在俯视图的基础上填写添加数字,但由于左视图不确定,所以,可能有多种情况.例3 如图,一个几何体是由若干个小正方体堆积而成的,主视、左视图如下,要摆成这样的图形,至少需要多少块小正方形,最多需要多少块小正方体.解析此题没有俯视图,不妨尝试去画出俯视图,主视图和俯视图的长要相等左视图和俯视图的宽要相等.已知俯视图的长和和宽也不一定能完全确定俯视图的形状,但是可以确定俯视图最大可能是什么由题意,俯视图最大可能是首先算出几何体最多可能是多少个,再次基础上,减少正方体的个数,在主视图和左视图不变的前提下,看最少能剩下几个.结合主视图,从前面看俯视图,右侧两个最高是1,所以可以确定右侧两列的最多全是1结合左视图,从左边看俯视图,最上面行和最下面的行最高都是2,如图.最后确定左视图中间的,最高为1 .此时我们得出的小正方体最多可能是2 2 1 1 1 1 1 1 1=11个.如图,减少4个,不影响主视图再减少1个,不影响左视图不能再减少了,所以,此时的数量2 2 1 1=6即是最少需要的正方体个数.点拨:此题已知主视图与左视图,但是不知道俯视图,利用投影的原则,主视图和俯视图的长要相等,左视图和俯视图的宽要相等.尝试画出俯视图的最大可能,首先确定出几何体的最多可能的正方体的个数,在此基础上减少正方体的个数,但不改变主视图与俯视图,到最后不能再减少时,即可确定最少的可能的个数.《义务教育数学课程标准》指出,在数学课程中,应当注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想。
用三视图确定小正方体的块数的简便方法
(2)因为从俯视图可以确定底层有正方体,所以方格中的数字最
小为1,那么只要将每列上的数字留一个,其余的均改为1,这 样就可以确定最少需要的小正方体的块数.举两种情况如图:
321
321
111
32
11
32
32
11
11
所以这个几何体最多需要16块,最少需要10块
上主视图,左视图所看到的小正方体的最高层数.然后,在方 格纸中填入方格所在横,竖上的较小的数字(如果相同取相同的 数字),那么就可确定这个几何体所需最多的小正方体的块数.
(2)在方格纸中寻找所在横、竖方向上的数字一样的方格,取 相同的数字填人方格,这样就可以确定最少需要的小正方体 的块数.
22 3
格,则可得到这个几何体所需最多的小正方体的块数.
(2)因为从俯视图可以确定底层有正方体,所以方格中的数! 字最小为1,那么只要将每横上的数字留一个,其余的均改为1,
这样就可以确定最少需要的小正方体的块数.举两种情况,如
下图:
3
3
3
33
3
1
11
2 222
1
11
2 211
1
11
2ቤተ መጻሕፍቲ ባይዱ21
所以这个几何体最多需要11块,最少需要9块.
2 3
1
1
所以这个几何体最多需要19块,最 少需要8块.
2 13 2
在通过小正方体组合图形的三视图,确定组合图形中小正方 体的个数,在中考或竞赛中经常会遇到.解决这类问题如果没 有掌握正确的方法b呶仅依赖空间想象去解决,不仅思维难度 很大,还很容易出错.通过三视图确定组合图形的小正方体的 个数,关键是要弄清楚这个小正方体组合图形共有多少行、多 少列、每行每列中各有多少层,理清了这些行、列、层的数量, 再按照上面介绍的方法,小正方体的个数就迎刃而解了.
由三视图判断几何体或几何体组成的小正方体个数

由三视图判断小正方体个数问题通过小正方体组合图形的三视图,确定组合图形中小正方体的个数,在中考或竞赛中经常会遇到。
解决这类问题如果没有掌握正确的方法,仅仅依赖空间想象去解决,不仅思维难度很大,还很容易出错。
通过三视图计算组合图形的小正方体的个数,关键是要弄清楚这个小正方体组合图形共有多少行、多少列、每行每列中各有多少层,理清了这些行、列、层的数量,小正方体的个数就迎刃而解了.在三视图中,通过主视图、俯视图可以确定组合图形的列数;通过俯视图、左视图可以确定组合图形的行数;通过主视图、左视图可以确定行与列中的最高层数.以上方法可简要地概括为:“主俯看列,俯左看行,主左看层,分清行列层,计数不求人.”一、结果唯一的计数例1在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来,如图所示,则这堆正方体货箱共有()。
A.9箱B.10箱C.11箱D.12箱分析:由三视图可知,这堆货箱共有从前到后3行,从左到右3列。
由左视图:第一行均为1层,第二行最高2层,第三行最高3层;由主视图:第一列、第三列均为1层,第二列(中间列)最高为3层。
故第二行、第二列为2层,第三行第二列为3层,其余皆为1层。
各行、各列小正方体的个数如俯视图中所表示.这堆货箱共有3+1+1+2+1+1=9(箱)。
二、结果不唯一的计数例2(“希望杯”数学邀请赛试题)如图2,是由若干个(大于8个)大小相同的正方体组成的一个几何体的主视图和俯视图,则这个几何体的左视图不可能是()。
分析:由给出的主视图、俯视图可以看出,该几何体共有2行,3列。
第1列均为1层,第2列最高2层,第3列最高3层。
左视图为A时,第1行、第2行最高均为3层。
几何体中,第1列第1行为1层;第2列第1行、第2行均可为1层或2层,,但不能同时为1层;第3列两行均为3层。
此时,小正方体的个数如俯视图A所示,最少为1+2+1+3+3=10(个),最多为1+2+2+3+3=11个.左视图为B时,第一行均为1层,第二行最高为3层。
思维特训(十八) 由三视图巧算正方体个数

思维特训(十八)由三视图巧算正方体个数方法点津·在研究由小正方体搭成的几何体与其三视图的关系时,一般由实物图形可以唯一确定三视图,但反之却要分情况讨论.当条件给出几何体的三个视图或两个视图时,这个几何体不一定是确定的.俯视图确定几何体最底层正方体的个数,主视图和左视图确定几何体的层数、行数及列数.典题精练·类型一由给出的三种视图判断正方体的数量由三视图判断组成原几何体的小正方体的块数的一般解法:(1)数出主视图各列(竖为列)上正方形的个数,将数字分别填在俯视图所对应的列中;(2)再数出左视图各列上正方形的个数,将数字分别填在俯视图所对应的行(横为行)中;(3)在俯视图中的同一个小正方形中,前后两次数字相同的只取一个数,前后两次数字不同的取较小的数,最后将俯视图中各小正方形中的数字相加,所得结果就是组成原几何体的小正方体的总块数.1.由一些大小相同的小正方体组成的几何体的三视图如图18-Y-1所示,那么组成该几何体的小正方体有()图18-Y-1A.4个B.5个C.6个D.7个2.由若干个棱长相等的小正方体搭成的几何体的主视图、左视图、俯视图如图18-Y -2所示,则搭成这个几何体的小正方体有()图18-Y-2A.5个B.6个C.7个D.8个3.如图18-Y-3是由若干个大小相同的小正方体搭成的几何体的三视图,该几何体所用的小正方体的个数是()图18-Y-3A.6 B.4 C.3 D.24.一个几何体由多个完全相同的小正方体组成,它的三视图如图18-Y-4所示,那么组成这个几何体的小正方体的个数为()图18-Y-4A.2 B.3 C.5 D.105.几个棱长为1的小正方体组成的几何体的三视图如图18-Y-5所示,则这个几何体的体积是()图18-Y-5A.4 B.5 C.6 D.76.由完全相同的小立方块搭成的几何体的三视图如图18-Y-6所示,则组成该几何体共用了________个小立方块.图18-Y-6类型二由两种视图判断正方体的数量范围1.已知主视图、俯视图,判断小正方体的数量范围的步骤:在俯视图的方格中标上主视图所看到的小正方体的最高层数,将这些数字填入所在竖列上的每一个方格中,则可得到这个几何体所需最多的小正方体的块数;因为根据俯视图可以确定底层有多少个小正方体,所以方格中的数字最小为1,那么只要将每列上的数字留一个,最高层数不变,其余的均改为1,这样就可以确定最少需要的小正方体的块数.2.已知左视图、俯视图,判断小正方体的数量范围的步骤:在俯视图的方格中标上左视图所看到的小正方体的最高层数,其他步骤同上所述.7.用若干个大小相同的小正方体组合成的几何体的主视图和俯视图如图18-Y-7所示,则下面所给的四个选项中,不可能是这个几何体的左视图的是()图18-Y-7图18-Y-88.如图18-Y-9是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则搭成该几何体的小立方体的个数不可能是()图18-Y-9A.6 B.7 C.8 D.99.一个几何体是由若干个相同的小正方体组成的,其主视图和左视图如图18-Y-10所示,则这个几何体最多可由多少个这样的小正方体组成()图18-Y-10A.12个B.13个C.14个D.18个10.如图18-Y-11是由若干个完全相同的小正方体组成的一个几何体的主视图和左视图,则组成这个几何体的小正方体的个数是()图18-Y-11A.3或4或5 B.4或5C.5或6 D.6或711.用八个同样大小的小立方体搭成一个大立方体,如图18-Y-12①,得到的几何体的三视图如图②所示.若小明从八个小立方体中取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体的三视图仍是图②,则他取走的小立方体最多可以是________个.图18-Y-1212.用小正方体搭成一个几何体,使得其主视图、俯视图如图18-Y-13所示.这样的几何体只有一种吗?(1)它最多需要多少个小正方体?(2)它最少需要多少个小正方体?请分别画出这两种情况下该几何体的左视图.图18-Y-13详解详析1.C[解析] 解决这类问题要做到,一看俯视图,从左至右共有三列,从上到下共有三行;二看主视图,共有三列两行,第一列和第三列上分别只有一层,第二列上有两层,则俯视图中的一、三列上分别只有一个正方体,分别填1(如图①);三看左视图,共三列两行,第一列和第三列上分别只有一层,第二列上有两层,则俯视图中第一行只有一个正方体,填1,第二行有两个正方体,填2,第三行第二列只有一个正方体,填1,所以在俯视图中每个位置上小正方体的个数如图①所示,搭成这个几何体的小正方体的个数是1+2+1+1+1=6,故本题结果选C.相应的几何体如图②所示.2.B[解析] 综合三视图可知,2+1+1+1=5(个)小正方体,第二层应该有1个小正方体,因此搭成这个几何体的小正方体有5+1=6(个).故选B.3.A 4.C 5.B 6.77.C8.D9.B[解析] 主视图和左视图都为3列,可知该几何体的俯视图有三列三行,最多为3×3个正方形.由主视图可知在俯视图第1,3列的每个正方形内填2,第2列的每个正方形内填1;又由左视图可知,在俯视图的1,3行中(观察者需站在俯视图的左侧看)每个小正方形内都填入2,第2行填1,重叠交叉处数字取小,如图,故这个几何体最多由13个小正方体组成.故选B.10.A11.212.解:这样的几何体不止一种.(1)最多需要6+6+2=14(个)小正方体.左视图如图①.(2)最少需要4+4+2=10(个)小正方体.左视图如图②(左视图不唯一).。
【中考数学】“三视图”“小正方体个数”一篇搞定!

【中考数学】“三视图”“小正方体个数”一篇搞定!三视图常在选择题和填空题中考查,考查形式有:①判断几何体的三视图;②根据三视图求几何体的小正方体的个数;③由三视图还原几何体求其表面积。
常见几何体的展开图▼一对于三视图的判断可以分为两种类型具体方法如下:1.判断常见几何体的三视图主要是明确“主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等”,同时在画三视图时,看得见的部分的轮廓线画成实线,看不见的部分的轮廓线画成虚线;2.小正方块组成几何体视图的判断方法:(1)找准所判断视图的观察方向;(2)从视图的观察方向看几何体:①判断主视图时,从前往后看,几何体从左往右有x列,每一列最高有y层,对应到主视图中即有x列,每一列即有y个正方形,并注意每列中正方形的摆放位置;②判断左视图时,从左往右看,几何体从左往右有m列,每一列最高有n层,对应到左视图中即有m列,每一列即有n个正方形,并注意每列中正方形的摆放位置;③判断俯视图时,从上往下看,几何体从前往后有p行,每一行有q个,对应到俯视图即有p行,每行有q个,注意每行中正方形的摆放位置.二最多(最少)小正方体个数的计算1.当已知主视图和俯视图求最少需要小正方体个数时:最少需要小正方体个数=主视图中小正方体个数+俯视图中小正方体个数-主视图第一层小正方体个数;2.当已知主视图和俯视图求最多需要小正方体个数:主视图中第一列小正方体个数×俯视图中第一列小正方体个数+主视图中第二列小正方体个数×俯视图中第二列小正方体个数+…+主视图第n列小正方体个数×俯视图中第n列小正方体个数;3.当已知主视图和左视图求最多需要小正方体个数时:最多需要小正方体个数=主视图中第一行小正方体个数×左视图中第一行小正方体个数+主视图中第二行小正方体个数×左视图中第二行小正方体个数+…+主视图中第n行小正方体个数×左视图中第n行小正方体个数.。
由三视图-判断小正方体个数

由三视图,判断小正方体个数问题通过小正方体组合图形的三视图,确定组合图形中小正方体的个数,在中考或竞赛中经常会遇到。
解决这类问题如果没有掌握正确的方法,仅仅依赖空间想象去解决,不仅思维难度很大,还很容易出错。
通过三视图计算组合图形的小正方体的个数,关键是要弄清楚这个小正方体组合图形共有多少行、多少列、每行每列中各有多少层,理清了这些行、列、层的数量,小正方体的个数就迎刃而解了。
在三视图中,通过主视图、俯视图可以确定组合图形的列数;通过俯视图、左视图可以确定组合图形的行数;通过主视图、左视图可以确定行与列中的最高层数。
以上方法可简要地概括为:“主俯看列,俯左看行,主左看层,分清行列层,计数不求人。
”一、结果唯一的计数例1 在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来,如图所示,则这堆正方体货箱共有()。
A.9箱 B.10箱 C.11箱 D.12箱分析:由三视图可知,这堆货箱共有从前到后3行,从左到右3列。
由左视图:第一行均为1层,第二行最高2层,第三行最高3层;由主视图:第一列、第三列均为1层,第二列(中间列)最高为3层。
故第二行、第二列为2层,第三行第二列为3层,其余皆为1层。
各行、各列小正方体的个数如俯视图中所表示。
这堆货箱共有3+1+1+2+1+1=9(箱)。
二、结果不唯一的计数例2(“希望杯”数学邀请赛试题)如图2,是由若干个(大于8个)大小相同的正方体组成的一个几何体的主视图和俯视图,则这个几何体的左视图不可能是()。
分析:由给出的主视图、俯视图可以看出,该几何体共有2行,3列。
第1列均为1层,第2列最高2层,第3列最高3层。
左视图为A时,第1行、第2行最高均为3层。
几何体中,第1列第1行为1层;第2列第1行、第2行均可为1层或2层,,但不能同时为1层;第3列两行均为3层。
此时,小正方体的个数如俯视图A所示,最少为1+2+1+3+3=10(个),最多为1+2+2+3+3=11个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三视图小正方体个数口诀三视图求正方体个数口诀:主俯看列,俯左看行,主左看层。
前上看列,上右看行,前右看层。
前面看,上下左右都不变。
上面看,左右不变,前下后上。
右面看,上下不变,前左后右。
左面看,上下不变,前右后左。
一、三视图定义
三视图是观测者从上面、左面、正面三个不同角度观察同一个空间几何体而画出的图形。
将人的视线规定为平行投影线,然后正对着物体看过去,将所见物体的轮廓用正投影法绘制出来的图形称为视图。
一个物体有六个视图:从物体的前面向后面投射所得的视图称主视图(正视图)能反映物体的前面形状,从物体的上面向下面投射所得的视图称俯视图,能反映物体的上面形状。
从物体的左面向右面投射所得的视图称左视图(侧视图)能反映物体的左面形状,还有其它三个视图不是很常用。
三视图就是主视图(正视图)、俯视图、左视图(侧视图)的总称。
二、特点
一个视图只能反映物体的一个方位的形状,不能完整反映物体的结构形状。
三视图是从三个不同方向对同一个物体进行投射的结果,另外还有如剖面图、半剖面图等做为辅助,基本能完整的表达物体的结构。
