乘方的计算专题训练0,负指数,正指数专项练习30题(有答案)ok
乘方专项练习题

乘方专项练习题以下是乘方专项练习题集,共计1500字。
1. 计算下列乘方的值:(a) 2^3(b) 5^2(c) 10^02. 简化下列乘方表达式:(a) 8^2 * 8^4(b) (3^2)^3(c) (10^3)^2 / 10^53. 填写下表,给出相应乘方的值:-------------------------------------| 乘方表达式 | 值 |-------------------------------------| 4^3 | - || 7^2 | - || 2^0 | - || 9^1 | - |-------------------------------------4. 若 a = 2^3,b = 5^2,c = 7^2,则求下列乘方表达式的值:(a) a^2(b) b^3(c) c^05. 解决下列乘方方程,将 x 的值标明出来:(a) 3^(x+2) = 81(b) (2^3)^x = 2^126. 约化下列分式,其中 a,b 为正实数:(a) (a^2)^3 / (a^3)^2(b) (b^4)^2 / b^67. 计算下列乘方的结果,其中 x,y 为实数:(a) (x^2)^3(b) (xy^2)^4(c) (x^3y^2)^28. 计算并化简下列乘方表达式:(a) (2^3 * 2^4) / 2^2(b) (5^2)/(5^-3)(c) (x^6y^4)/(x^4y^3)9. 求下列乘方的结果,其中 n 为自然数:(a) (-2)^n(b) (-3)^n(c) (-4)^n10. 求下列乘方的结果,其中 m 为偶数,n 为奇数:(a) (-2)^m(b) (-5)^m(c) (-3)^n11. 解决下列的乘方不等式,并表示解集:(a) 2^(x+1) > 16(b) (1/2)^x > 1/812. 根据已知条件,应用指数法则化简下列乘方表达式:(a) (x^2)^3 * (x^2)^4(b) (2^3)^x * (2^4)^x13. 若 a = 5^3,b = 7^2,c = 2^4,则求下列乘方的结果:(a) a^2 * a^3(b) b^5 / b^2(c) (c^3)^214. 计算下列乘方的值,其中 x,y 为实数:(a) (xy)^2(b) (x^2)^3 * (xy)^4(c) (x^3y^2)^2 / (xy^3)^215. 在给定乘方的限制条件下,解决下列方程并求解集:(a) 3^(2x+1) = 9(b) (1/4)^(x-1) = 64以上为乘方专项练习题集。
最新零指数幂与负整数指数幂练习题及答案
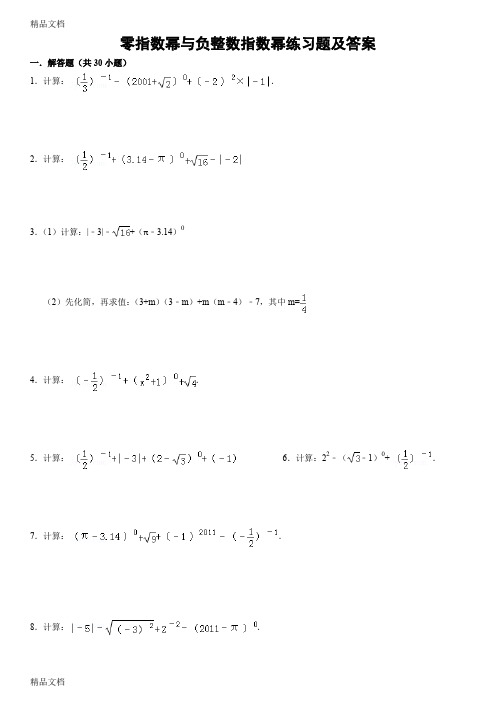
零指数幂与负整数指数幂练习题及答案一.解答题(共30小题)1.计算:.2.计算:3.(1)计算:|﹣3|﹣+(π﹣3.14)0(2)先化简,再求值:(3+m)(3﹣m)+m(m﹣4)﹣7,其中m=4.计算:.5.计算:6.计算:22﹣(﹣1)0+.7.计算:.8.计算:.9.(1)计算|﹣2|+(﹣1)0﹣()﹣1﹣(﹣1)2011(2)化简.10.计算:11.(1)计算:.(2)化简:求值.3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)],其中x=﹣,y=﹣3.12.(1)计算:23+﹣﹣;(2)解方程组:.13.计算:.14.(2009•重庆)计算:|﹣2|+()﹣1×(π﹣)0﹣+(﹣1)2.15.计算:﹣12+|﹣2|+()﹣1﹣5×(2009﹣π)016.计算:(﹣2)2+2×(﹣3)+()﹣117.(1)计算:()﹣1﹣++(﹣1)2009(2)解方程组:18.计算:|﹣|+(3.14﹣π)0+(﹣)2×()﹣219.计算﹣22+|4﹣7|+(﹣π)020.(1)计算:()2﹣(﹣3)+20(2)因式分解:a3﹣ab2.21.计算:﹣(﹣1)+|﹣2|+(π+3)0﹣.22.计算:+(﹣)0+(﹣1)3﹣|﹣1|.23.计算:.24.计算:22+(4﹣7)÷+()025.计算:26.计算:|﹣2|+﹣()﹣1+(3﹣π)027.计算:﹣1+(﹣2)3+|﹣3|﹣28.计算:(﹣1)2006+|﹣|﹣(2﹣)0﹣3.29.计算:.30.计算:零指数幂与负整数指数幂练习题及答案参考答案与试题解析一.解答题(共30小题)1.计算:.2.计算:3.(1)计算:|﹣3|﹣+(π﹣3.14)(2)先化简,再求值:(3+m)(3﹣m)+m(m﹣4)﹣7,其中m=×=14.计算:.5.计算:.6.计算:22﹣(﹣1)0+.7.计算:.8.计算:.9.(1)计算|﹣2|+(﹣1)0﹣()﹣1﹣(﹣1)2011(2)化简.﹣﹣(,10.计算:(11.(1)计算:.(2)化简:求值.3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)],其中x=﹣,y=﹣3.,×12.(1)计算:23+﹣﹣;(2)解方程组:.﹣;.故答案为﹣、13.计算:.14.(2009•重庆)计算:|﹣2|+()﹣1×(π﹣)0﹣+(﹣1)2.15.计算:﹣12+|﹣2|+()﹣1﹣5×(2009﹣π)0+|)+2.16.计算:(﹣2)2+2×(﹣3)+()﹣1))17.(1)计算:()﹣1﹣++(﹣1)2009(2)解方程组:∴原方程组的解为.18.计算:|﹣|+(3.14﹣π)0+(﹣)2×()﹣2.21.计算:﹣(﹣1)+|﹣2|+(π+3)﹣.﹣23.计算:.24.计算:22+(4﹣7)÷+()0÷(×+125.计算:26.计算:|﹣2|+﹣()﹣1+(3﹣π)027.计算:﹣1+(﹣2)3+|﹣3|﹣29.计算:.30.计算:+3+3﹣=3。
七年级下数学11零指数负指数 积幂的乘方学案练习题

知识点一:零指数幂的性质(重点)零指数幂的性质: 都等于1。
没有意义。
一般地,规定:=0a ( ) 1、下列运算正确的是( )A 0005.00= B ()52902=- C ()110=- D ()220-=-2、已知0≠x ,则下列式子不一定正确的是( )A ()120=-x B ()1202=+x C ()120=-x D 110=⎪⎭⎫⎝⎛x3、计算:⑴010 ⑵)0(0≠m m ⑶()03-π4、若==-x x ,则1658 。
知识点二:负整数指数幂(重点、难点)负整数指数幂: 的n -(p 是正整数)次幂,等于 。
n a -= (a ,n 是 )。
=-1a (0≠a ),即a a 与1- 。
1、下列计算正确的是( ) A ()1001.02=-- B 10001103=-- C 251512-=- D 33212a a =- 2、若()63--x 有意义,则x 的取值范围是( )A 3≠x B x >3 C x <3 D 无法确定3、计算:⑴210- ⑵32--)( ⑶()25.0-- ⑷()13-- ⑸141-⎪⎭⎫ ⎝⎛- ⑹()12---知识点三:把一个绝对值小于1的非零数表示为科学计数法用科学计数法可以把一个 表示成na 10⨯±的形式,其中 a ,n ,且n 的绝对值等于 (包括 )。
1、某种感冒病毒的直径约为0.000 000 12米,用科学计数法表示为 。
2、空气的单位体积质量是0.001 2393/cm g ,用科学计数法表示(结果保留三位有效数字)为 3/cm g 。
3、用科学计数法表示下列各数:-760 000= ; 0.000 000 061= ; 4、用小数表示3×102-,结果为( )A -0.03B -0.003C 0.03D 0.0035、将0.006 048用四舍五入法取近似值,保留两个有效数字,并用科学计数法表示出来为( ) A 3100.6-⨯ B 3106-⨯ C 3100.6⨯ D 3101.6-⨯练习1、在()()()()4372213131111x x x aa -=-÷-=-=-=--;;;中,其中正确的式子有( )A 1个B 2个C 3个D 4个 2、下列计算正确的是( ) A ()02.00=- B ()100011.03=- C 33310=÷- D ()044≠=÷a a a a 3、0.00898用科学计数法表示正确的是( )A 31098.8-⨯ B 4108.89-⨯ C 41098.8-⨯ D 410898.0-⨯4、若()120=-x ,则x 的取值范围是 ;若()23-+a 有意义,则a 为 。
乘方运算练习题及答案

乘方运算练习题及答案A、11个8连乘B、11乘以8C、8个11连乘D、8个别1相加、-3的值是A、-B、9C、-D、6、下列各对数中,数值相等的是 A、-与- B、-与 C、-与 D、与-3×2、下列说法中正确的是A、2表示2×3的积B、任何一个有理数的偶次幂是正数C、-3与互为相反数D、一个数的平方是5、下列各式运算结果为正数的是A、-2×B、×5C、×D、1-、如果一个有理数的平方等于,那么这个有理数等于 A、-B、2C、 D、2或-2、一个数的立方是它本身,那么这个数是 A、 0 B、0或1C、-1或1 D、0或1或-1、如果一个有理数的正偶次幂是非负数,那么这个数是 A、正数 B、负数C、非负数 D、任何有理数、-2××=A、 B、-C、-2D、210、两个有理数互为相反数,那么它们的n次幂的值A、相等B、不相等C、绝对值相等D、没有任何关系 11、一个有理数的平方是正数,则这个数的立方是 A、正数 B、负数C、正数或负数 D、奇数 12、2001924 24 423 24 4 6 223 2 2 2 223 3 3 242,这个数一定是3+2002÷?+2003的值等于A、0B、 1C、-1D、二、填空题?3?1、中指数为,底数为;4的底数是,指数是;的底数?2?65是,指数是,结果是;2、根据幂的意义,表示,-4表示;433、平方等于11的数是,立方等于的数是;4644、一个数的15次幂是负数,那么这个数的2003次幂是;、平方等于它本身的数是,立方等于它本身的数是;33?3??3?6、,,?? ;4447、??2?7?,??2?7?,??2?7?的大小关系用“<”号连接可表示为345338、如果a4??a4,那么a是;9、?1?2??2?3??3?42001?2002?? ;10、如果一个数的平方是它的相反数,那么这个数是;如果一个数的平方是它的倒数,那么这个数是;11、若?ab>0,则b 0 计算题23?1?1、2?、?1??2?43、??1?5、?23?6、?33?322220034、?1?31?3327、??2??22??28、4233?1?43??55??4?9、?262??321? 10、2??31??02?423??2?7?解答题1、按提示填写:2、有一张厚度是0.2毫米的纸,如果将它连续对折10次,那么它会有多厚?3、某种细菌在培养过程中,每半小时分裂一次,若这种细菌由1个分裂为16个,则这个过程要经过多长时间?4、你吃过“手拉面”吗?如果把一个面团拉开,然后对折,再拉开,再对折,??如此往复下去,对折10次,会拉出多少根面条?探究创新乐园 1、你能求出0.1252、若a是最大的负整数,求a2000101?8102的结果吗??a2001?a2002?a2003的值。
(完整版)指数与指数幂的运算习题(含答案),推荐文档

2 2 2 ⎝ ⎝ ⎭⎭指数与指数幂的运算 习题(含答案)一、单选题1.已知 x ,y 为正实数,则 A . 2lnx+lny =2lnx +2lny B . 2ln (x+y )=2lnx •2lny C . 2lnx•lny =2lnx +2lnyD . 2ln (xy )=2lnx •2lny12.化简[( ‒ 2)6]2 ‒ ( ‒ 1)0的结果为A . −9B . 7C . −10D . 93. 若 > 0,且 , 为整数,则下列各式中正确的是A . a m ÷ a n = anB . a m ⋅ a n = a mnC . () =+D . 1 ÷ a n = a 0 ‒ n4. 若 a >1,b >0,且 a b +a -b =2,则 a b -a -b 的值为( )A .B . 2 或-2C . -2D . 25.3‒ 27的值为(). A.9B. ‒ 9C.‒ 3D.3a 3x + a ‒ 3x26.若 = A . 2 ‒ 1 C . 2 + 1‒ 1,则 a x + a ‒ x 等于B . 2 ‒ 2 D . + 1log 3x , x > 0 ⎛ ⎛ 1 ⎫⎫7.已知函数 f (x )= { 2x , x ≤ 0,则 f f 9 ⎪⎪ 等于( )A . 4B . - 1 41C . -4D . 4 18.设 a = log 3,b = 20.3, c = log 2 ,则( )3A . a > b > cB . a > c > bC . c > a > b (1)9.设 y 1=40.9,y 2=80.48,y 3= 2 -1.5,则( ) A . y 3>y 1>y 2 B . y 2>y 1>y 3 C . y 1>y 2>y 3 D . y 1>y 3>y 2 10.有下列各式:D . b > a > c2 2n a n 3 x4+ y 36 (-5)2m ‒ 2n4 163 x3 x 227 - - ① = a ;②若 a ∈R ,则(a 2-a +1)0=1;4③ = x 3+ y ;④ 35 = .其中正确的个数是( ) A . 0 B . 1 C . 2D .311.化简(a 2-2+a -2)÷(a 2-a -2)的结果为( ) A . 1B . -1C .a 2 -1a 2 +1a 2 +1D .a 2 -112. 下列各式计算正确的是( )A . (-1)0=1B . 21a 2·a 2=a2 1 1 C . 43=8D . a 3÷ a - 3= a 313. 已知a m =4,a n =3,则 的值为( )2A.33B. 6 C . 2D . 2二、填空题化简 ⋅(x > 0) 的结果是.14.x ⋅ 15. 设函数 f (x ) = a x + (k -1)a -x + k 2 ( a > 0, a ≠ 1 )是定义域为 R 的奇函数.(1) 求 k 值;(2) 若 f (1) > 0 ,求使不等式 f (x 2 + x ) + f (t - 2x ) > 0 恒成立的t 的取值范围;(3)若 f (1) = 3 ,设 g (x ) = a 2x + a -2x - 2mf (x ) , g (x ) 在[1, +∞) 上的最小值为-1,2求m 的值.12⎛ 1 ⎫ - 16.计算: 83 ÷ ⎪ = .⎝ 4 ⎭ ⎛ 8 ⎫- 13 - ⎛ - 3 ⎫0+ =17. log 3 +⎝ 125 ⎪⎭ .⎝ 5 ⎪⎭2 518. (2a -3b 3 ) ⋅ (-3a -1b ) ÷ (4a -4b 3)(a > 0, b > 0) =.19.若2x + 2-x = 5 ,则8x + 8-x =.6 x23 a - 33 b- ⎛ 8 9 2 ( ‒ 8) (3) ;20. 0.064 13- - 1 ⎫0 + ⎡(-2)3 ⎤- 34 +16 ⎪ ⎣ ⎦⎝ ⎭- 34 + 0.0112 =⎛ 1 ⎫0 21. 计算: lg4 + lg25 + - ⎪ ⎝ ⎭=.22. 直线y = 2a 与函数 y = a x -1 (a > 0且a ≠ 1)的图象有且仅有两个公共点,则实数 a 的取值范围是.1 + log 12 - (0.7)0+ 0.25-1 =。
负数的乘方和加法练习题

负数的乘方和加法练习题一、负数的乘方1. 计算:(2)^32. 计算:(3)^43. 计算:(4)^54. 计算:(5)^65. 计算:(6)^26. 计算:(7)^37. 计算:(8)^48. 计算:(9)^59. 计算:(10)^610. 计算:(11)^2二、负数的加法1. 计算:(3) + (5)2. 计算:(4) + (7)3. 计算:(6) + (8)4. 计算:(9) + (10)5. 计算:(2) + (11)6. 计算:(5) + (12)7. 计算:(8) + (13)8. 计算:(10) + (14)9. 计算:(12) + (15)10. 计算:(14) + (16)三、负数的乘方和加法混合运算1. 计算:(2)^3 + (4)^22. 计算:(3)^4 + (5)^33. 计算:(4)^5 + (6)^44. 计算:(5)^6 + (7)^55. 计算:(6)^2 + (8)^36. 计算:(7)^3 + (9)^47. 计算:(8)^4 + (10)^58. 计算:(9)^5 + (11)^69. 计算:(10)^6 + (12)^210. 计算:(11)^2 + (13)^3四、应用题1. 某天的气温下降了5℃,接着又下降了3℃,求这天总共下降了多少℃。
2. 一辆汽车行驶过程中,速度先减少了20km/h,然后又减少了30km/h,求汽车总共减少了多少速度。
3. 小明有若干个糖果,先给了小红5个,又给了小华3个,求小明总共给了多少个糖果。
4. 一根绳子被剪成了三段,第一段比原长度减少了10cm,第二段比原长度减少了15cm,求这两段绳子总共减少了多少cm。
5. 一个水池里的水先减少了200升,然后又减少了300升,求水池里的水总共减少了多少升。
五、判断题1. (2)^2 的结果是 4。
()3. (4) + (4) 的结果是 8。
()4. (5)^2 + (5)^2 的结果是 0。
初二数学有理数的加减乘除以及乘方试题答案及解析
初二数学有理数的加减乘除以及乘方试题答案及解析1.计算: = .【答案】.【解析】针对有理数的乘方,零指数幂2个考点分别进行计算,然后根据实数的运算法则求得计算结果:.【考点】1.有理数的乘方;2.零指数幂.2.计算:(-2)2012×()2013=.【答案】.【解析】幂的乘方公式:(a m)n=a mn,由题,(-2)2012×()2013=(-2)2012×()2012×=(-×)2012×=.【考点】幂的乘方.3. PM2.5是指大气中直径小于或等于0.0000025m的颗粒物.将0.0000025用科学记数法可表示为 .【答案】【解析】科学记数法的表示方法:科学记数法的表示形式为,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.0.0000025=.【考点】科学记数法的表示方法点评:本题属于基础应用题,只需学生熟练掌握科学记数法的表示方法,即可完成.4.计算:=.【答案】-6【解析】有理数的乘法法则:两数相乘,同号得证,异号得负,并把绝对值相乘.=-6.【考点】有理数的乘法点评:本题属于基础应用题,只需学生熟练掌握有理数的乘法法则,即可完成.5.【解析】有理数的混合运算的顺序:先算乘方,再算乘除,最后算加减,同级运算按从左向右的顺序依次计算;有括号的先算括号里的.同时注意运算过程中可以运用运算律计算的要运用运算律简化计算.原式.【考点】有理数的混合运算点评:本题属于基础应用题,只需学生熟练掌握有理数的混合运算的顺序,即可完成.6.地球上七大洲的总面积约为149480000km2,该数请用科学计数法并保留3个有效数字表示为 .【答案】1.49×108【解析】科学计数法的表示方法。
有效数字的计算方法是:从左边第一个不是0的数字起,后面所有的数字都是有效数字.首先把这个数利用科学记数法表示,然后根据有效数字的确定条件,四舍五入即可求解解:149480000=1.49480000×108≈1.49×108(km2).故答案是:1.49×108km2【考点】科学计数法的表示方法点评:科学记数法的表示方法,以及用科学记数法表示的数的有效数字的确定方法7.1.0149精确到百分位的近似值为.【答案】1.01【解析】由题意精确到百分位就是对千分位四舍五入.1.0149精确到百分位的近似值为1.01.【考点】近似数与有效数字点评:本题属于基础应用题,只需学生熟练掌握四舍五入取近似数的方法,即可完成.8.用科学记数法表示:0.000258≈________________(保留两个有效数字).【答案】2.6×10-4【解析】有效数字的计算方法是:从左边第一个不是0的数字起,后面所有的数字都是有效数字.科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.【考点】本题考查的是科学记数法,近似数与有效数字点评:解答本题的关键是熟练掌握用科学记数法表示的数的有效数字只与前面的a有关,与10的多少次方无关.9.某种药品的说明书上,贴有如右所示的标签,一次服用这种药品的剂量x的范围是。
七年级的乘方题50道
七年级的乘方题50道一、基础计算类(1 20题)1. 计算:2^3解析:根据乘方的定义,2^3表示3个2相乘,即2×2×2 = 8。
2. 计算:(-3)^2解析:( 3)^2表示2个-3相乘,即(-3)×(-3)=9。
3. 计算:0^5解析:0的任何正整数次幂都为0,所以0^5=0。
4. 计算:1^10解析:1的任何次幂都为1,所以1^10=1。
5. 计算:(-1)^4解析:(-1)^4表示4个-1相乘,(-1)×(-1)×(-1)×(-1)=1。
6. 计算:3^2×2^2解析:先分别计算乘方,3^2=9,2^2=4,然后再相乘9×4 = 36。
7. 计算:(-2)^3÷2^2解析:(-2)^3=-8,2^2=4,则-8÷4=-2。
8. 计算:((1)/(2))^3解析:((1)/(2))^3=(1)/(2)×(1)/(2)×(1)/(2)=(1)/(8)。
9. 计算:(-(1)/(3))^2解析:(-(1)/(3))^2=(-(1)/(3))×(-(1)/(3))=(1)/(9)。
10. 计算:4^3-3^3解析:4^3=64,3^3=27,64 27=37。
11. 计算:(2×3)^2解析:先计算括号内的2×3 = 6,然后6^2=36。
12. 计算:(-2×3)^3解析:先计算括号内-2×3=-6,(-6)^3=(-6)×(-6)×(-6)= 216。
13. 计算:2^2+3^2-4^2解析:2^2=4,3^2=9,4^2=16,4 + 9-16=-3。
14. 计算:(-1)^5+1^6解析:(-1)^5=-1,1^6=1,-1 + 1=0。
15. 计算:5^2-2×5×3+3^2解析:根据完全平方公式(a b)^2=a^2-2ab + b^2,这里a = 5,b = 3,原式=(5 3)^2=4。
零指数、负指数、分式的计算-八年级数学下册期末解答压轴题必刷专题训练(华师大版)(解析版)
.
18.计算:
【答案】13
【详解】解:
19.计算
【答案】 ;
【详解】解:
20.计算: ;
【详解】解:原式
;
二、分式的化简求值
1.化简: .
【答案】
【详解】解:
.
2.先化简,再求值: ,其中 .
【答案】 ;1
【详解】解:
;
当 时,原式 .
3.先化简,再求值: ,其中 .
【答案】 ,1
【详解】解:
【答案】 ,
【详解】解:
,
由题意得: 、1、 ,当 时,原式 .
18.先化简: ,再选取一个合适a值代入计算.
【答案】 ; 时,原式的值为
【详解】解: ,
,
,
,
,
要使式子有意义, 可以取除 , 以外的任何数,
当 时,原式 .
19.先化简 ,然后在 范围内,选择一个合适的整数代入求值.
【答案】 ,10
【答案】1
【详解】
;
3.计算: .
【答案】
【详解】解:原式 ,
,
.
4.计算: .
【答案】
【详解】解:原式
.
5.计算: ;
【答案】 ;
【详解】解:
;
6.计算: .
【答案】
【详解】解:
.
7.计算:
【答案】
【详解】解
.
8.计算: ;
【答案】2
【详解】解:
.
9.计算: .
【答案】
【详解】解:原式
.
10.计算:
零指数、负指数、分式的计算
华师版八年级下册第一个解答题,通常有两个小题,第一个小题是与零指数和负指数有关的计算,第二个小题通常是分式的化简求值,计算在掌握方法的基础上,应该通过适当的练习达到熟练,本资源也适合其它版本相关章节。
六年级100道乘方练习题
六年级100道乘方练习题乘方运算在数学中起着重要的作用,是学习数学的基础知识之一。
为了帮助六年级学生巩固和提升乘方运算能力,本文设计了100道乘方练习题。
通过完成这些题目,希望学生能够熟练掌握乘方的概念和运算方法,并提高解决实际问题的能力。
1. 计算2³的值。
2. 计算5²的值。
3. 计算(-3)⁴的值。
4. 计算10⁰的值。
5. 计算4⁵的值。
6. 计算2⁸的值。
7. 计算8³的值。
8. 计算(1/2)²的值。
9. 计算(-4)⁷的值。
10. 计算0⁶的值。
练习题中涵盖了不同的乘方运算:包括正整数指数、负整数指数、0的零次方、零的乘方、分数指数等。
通过解答这些题目,学生能够理解乘方运算的规律,逐步掌握乘方运算的技巧。
11. 计算3² × 3³的值。
12. 计算4⁶ ÷ 4⁴的值。
13. 计算(2²)⁴的值。
14. 计算(3³)²的值。
15. 计算(5⁴)³的值。
16. 计算(2³)⁵的值。
17. 计算(1/2)⁴ × (1/2)³的值。
18. 计算(4⁵)² ÷ 4³的值。
19. 计算(-2)³ × (-2)⁵的值。
20. 计算(-3)⁶ ÷ (-3)²的值。
这些题目要求学生运用乘方的乘法和除法法则,将同底数的乘方进行合并或分解,巩固对乘方运算法则的理解。
21. 如果2的2次方等于x,求x的值。
22. 如果5的3次方等于y,求y的值。
23. 如果(-4)的4次方等于z,求z的值。
24. 如果10的0次方等于w,求w的值。
25. 如果3的5次方等于v,求v的值。
这些题目要求学生根据已知条件,解方程求解未知数,进一步培养学生的运算思维能力。
26. 如果2的a次方等于8,求a的值。
27. 如果x的b次方等于64,求b的值。
