1.3_线段的垂直平分线同步练习
1.3 线段的垂直平分线(原卷版)

第一单元第3课时线段的垂直平分线一、选择题1.如图,在Rt △ABC 中,∠B=90°,ED 是AC 的垂直平分线,交AC 于点D ,交BC 于点E .已知∠BAE=10°,则∠C 的度数为( )A .30°B .40°C .50°D .60°2.如图,在△ABC 中,DE 是边AB 的垂直平分线,BC=8cm ,AC=5cm ,则△ADC 的周长为( )A .14cmB .13cmC .11cmD .9cm3.如图,△ABC 中,BD 平分∠ABC ,BC 的中垂线交BC 于点E ,交BD 于点F ,连接CF .若∠A=60°,∠ABD=24°,则∠ACF 的度数为( )A .48°B .36°C .30°D .24°4.如图,已知直角三角形ABC 中,∠ACB=90°,E 为AB 上一点,且CE=EB ,ED ⊥CB 于D ,则下列结论中不一定成立的是( )A .AE=BEB .CE=21ABC .∠CEB=2∠AD .AC=21AB5.如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于()A、80°B、70°C、60°D、50°6.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为()A、6B、5C、4D、37.如图,直线CP是AB的中垂线且交AB于P,其中AP=2CP.甲、乙两人想在AB上取两点D、E,使得AD=DC=CE=EB,其作法如下:(甲)作∠ACP、∠BCP之角平分线,分别交AB于D、E,则D、E即为所求;(乙)作AC、BC之中垂线,分别交AB于D、E,则D、E即为所求.对于甲、乙两人的作法,下列判断何者正确()A、两人都正确B、两人都错误C、甲正确,乙错误D、甲错误,乙正确8.如图,在Rt△ABC中,∠C=90°,∠B=30°.AB的垂直平分线DE交AB于点D,交BC于点E,则下列结论不正确的是()A、AE=BEB、AC=BEC、CE=DED、∠CAE=∠B9.如图,AC=AD,BC=BD,则有()A、AB垂直平分CDB、CD垂直平分ABC、AB与CD互相垂直平分D、CD平分∠ACB10.如图,点P是△ABC内的一点,若PB=PC,则()A.点P在∠ABC的平分线上 B.点P在∠ACB的平分线上C.点P在边AB的垂直平分线上 D.点P在边BC的垂直平分线上二、填空题11.如图,ΔABC中,AB=AC,AB的垂直平分线交AC于P点.(1)若∠A=35°,则∠BPC=_____;(2)若AB=5 cm,BC=3 cm,则ΔPBC的周长=_____.12.如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC 的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为.13.如图:已知,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC与E,则△ADE的周长等于_________ .14.如图,△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于D,交AB于E,下述结论:(1)BD平分∠ABC;(2)AD=BD=BC;(3)△BDC的周长等于AB+BC;(4)D是AC中点.其中正确的命题序号是.三、解答题15.如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;(2)求证:BG2-GE2=EA2.16.如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.(1)若△CMN的周长为15cm,求AB的长;(2)若∠MFN=70°,求∠MCN的度数.。
八年级数学人教版上册同步练习 线段的垂直平分线的性质-八年级数学人教版(上)(解析版)

第十三章轴对称13.1.2线段的垂直平分线的性质一、选择题目:在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知线段AB和点C,D,且CA=CB,DA=DB,那么直线CD是线段AB的A.垂线B.平行线C.垂直平分线D.过中点的直线【答案】C2.点P是△ABC中边AB的垂直平分线上的点,则一定有A.PA=PB B.PA=PCC.PB=PC D.点P到∠ACB的两边的距离相等【答案】A【解析】∵点P在AB的垂直平分线上,∴PA=PB,故选A.3.下列说法错误的是A.E,D是线段AB的垂直平分线上的两点,则AD=BD,AE=BEB.若AD=BD,AE=BE,则直线DE是线段AB的垂直平分线C.若PA=PB,则点P在线段AB的垂直平分线上D.若PA=PB,则过点P的直线是线段AB的垂直平分线【答案】D【解析】A、∵E是线段AB的垂直平分线上的点,∴AE=BE.同理AD=BD.故A正确;B、若AD=BD,∴D在AB的垂直平分线上.同理E在AB的垂直平分线上.∴直线DE是线段AB的垂直平分线.故B正确;C、若PA=PB,则点P在线段AB的垂直平分线上,故C正确;D、若PA=PB,则点P在线段AB的垂直平分线上.但过点P的直线有无数条,不能确定过点P的直线是线段AB的垂直平分线.故D错误.故选D.4.关于线段的垂直平分线有以下说法:①一条线段的垂直平分线的垂足,也是这条线段的中点;②线段的垂直平分线是一条直线;③一条线段的垂直平分线是这条线段的唯一对称轴.其中,正确的说法有A.1个B.2个C.3个D.4个【答案】B5.如图,AC=AD,BC=BD,那么下列判断正确的是A.CD垂直平分AB B.AB垂直平分CDC.CD平分∠ACB D.∠ACB=∠ADB=90°【答案】B【解析】∵AC=AD,∴点A在线段CD的垂直平分线上,∵BC=BD,∴点B在线段CD的垂直平分线上,∴AB垂直平分CD.故选B.学科*网6.下面给出两个结论:①如图①,若PA=PB,QA=QB,则PQ垂直平分AB.②如图②,若点P到OA,OB的垂线段PC,PD相等,则OP平分∠AOB,其中A.只有①正确B.只有②正确C.①②都正确D.①②都不正确【答案】C7.如图,在Rt△ABC中,∠ACB=90°,BC的中垂线交斜边AB于D,图中相等的线段有A.1组B.2组C.3组D.4组【答案】D【解析】∵BC的中垂线交斜边AB于D,CD=BD,CE=BE,∴∠B=∠BCD,又∠A+∠B=90°,∠BCD+∠ACD=90°,∴∠A=∠ACD,∴AD=CD,∴AD=BD,共4组.故选D.学科*网二、填空题目:请将答案填在题中横线上.8.如图,已知AD是线段BC的垂直平分线,则AB=__________.【答案】AC【解析】∵AD是线段BC的垂直平分线,∴AB=AC,故答案为:AC.9.如图,AD⊥BC于D,BD=CD,则AB=AC,理由__________.【答案】线段的垂直平分线上的点到线段两端点的距离相等三、解答题:解答应写出文字说明、证明过程或演算步骤.10.如图所示,一辆汽车在笔直的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄,当汽车行驶到哪个位置时,与村庄M,N的距离相等.【解析】(1)连接MN;(2)作线段MN的垂直平分线l,交直线AB于C点,则C点即为所求.学科*网11.如图所示,AB=AC,BM=CM,直线AM是线段BC的垂直平分线吗?【解析】是.理由:∵AB=AC,BM=CM,∴点A、M都在线段BC的垂直平分线上.根据“两点确定一条直线”知,直线AM是线段BC的垂直平分线.12.如图,AB=AC,DB=DC,E是AD延长线上一点,求证:BE=CE.13.如图,已知AE=CE,BD⊥A C.求证:AB+CD=AD+BC.【解析】∵AE=CE,BD⊥AC,∴BD是线段AC的垂直平分线,∴AB=BC,AD=CD,∴AB+CD=AD+BC.学科*网14.(1)在△ABC中画出AB边的垂直平分线与BC边的垂直平分线.(2)设所画的两条垂直平分线相交于点O,则由点O在AB的垂直平分线上,可以知道哪两条线段相等?(3)由点O在BC的垂直平分线上,又可以得到什么结论?(4)由(2)与(3)的结论,在线段的相等关系方面,你有什么新的发现?请先用等式表示,再用文字加以叙述.祝福语祝你考试成功!。
2020年北师大版八年级下册课时训练:1.3 《线段的垂直平分线 》 含答案
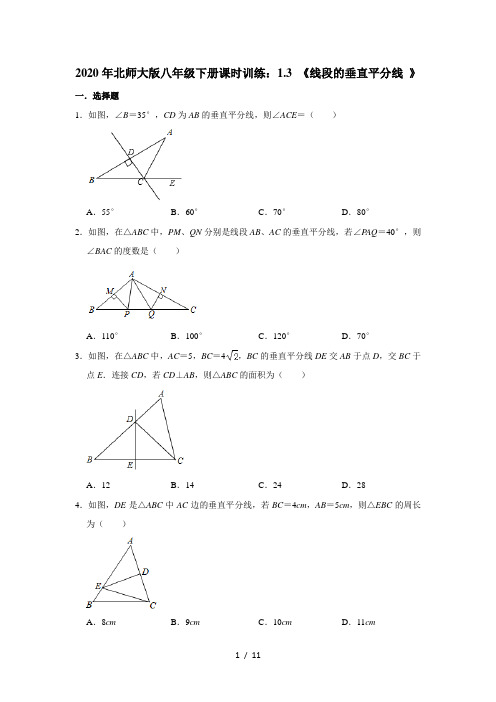
2020年北师大版八年级下册课时训练:1.3 《线段的垂直平分线》一.选择题1.如图,∠B=35°,CD为AB的垂直平分线,则∠ACE=()A.55°B.60°C.70°D.80°2.如图,在△ABC中,PM、QN分别是线段AB、AC的垂直平分线,若∠P AQ=40°,则∠BAC的度数是()A.110°B.100°C.120°D.70°3.如图,在△ABC中,AC=5,BC=4,BC的垂直平分线DE交AB于点D,交BC于点E.连接CD,若CD⊥AB,则△ABC的面积为()A.12B.14C.24D.284.如图,DE是△ABC中AC边的垂直平分线,若BC=4cm,AB=5cm,则△EBC的周长为()A.8cm B.9cm C.10cm D.11cm5.在国家精准扶贫政策的指导下,湖南龙山县有两个村庄P、Q种植了大量猕猴桃,现在正是丰收的季节.为了让猕猴桃通过互联网迅速销往各地,当地准备在两个村庄的公路m旁建立公用移动通信基站,要使基站到两个村庄的距离相等,基站应该建立在()A.A处B.B处C.C处D.D处6.如图,在△ABC中,∠ACD=20°,∠B=45°,BC的垂直平分线分别交AB、BC于点D、E,则∠A的度数是()A.60°B.65°C.70°D.75°7.如图,在△ABC中,AB=AC,AB的中垂线交AB于点D,交BC的延长线于点E,交AC于点F,若AB+BC=6,则△BCF的周长为()A.4.5B.5C.5.5D.68.如图,在△ABC中,BD平分∠ABC,E是BC的中点,过点E作BC的垂线交BD于点F,连结CF.若∠A=50°,∠ACF=40°,则∠CFD的度数为()A.30°B.45°C.55°D.60°二.填空题9.如图,DF垂直平分AB,EG垂直平分AC,若∠BAC=130°,则∠DAE=°.10.如图,在△ABC中,AC的垂直平分线DE分别交AC、AB于点D、E,若AB=7,BC =5,则△BCE的周长等于.11.如图,在△ABC中,点D在BC边上,DE垂直平分AC边,垂足为E,若∠B=70°,且AB+BD=BC,则∠BAC的度数为.12.如图,在△ABC中,BC=12,AB的垂直平分线EF交BC于点F,AC的垂直平分线MN交BC于点N,则△AFN的周长.13.如图,AD垂直平分BC于点D,EF垂直平分AB于点F,点E在AC上,BE+CE=20cm,则AB=.14.如图,在△ABC中,DE垂直平分AC,垂足为E,交BC于点D,AE=3cm,△ABD的周长为13cm,则△ABC的周长为cm.三.解答题15.如图,△ABC中,∠C=90°,DE垂直平分AB,若∠B=25°,求∠CAE的度数.16.如图,在钝角△ABC中,已知∠A=135°,边AB、AC的垂直平分线分别交BC于点D、E,交AB、AC于点F、G.若BD=12,CE=9.求DE的长度.17.如图,△ABC中AB、AC的垂直平分线分别交BC于E、N,若∠EAN=34°,求∠BAC 的度数.18.如图所示,在△ABC中,AB,AC的垂直平分线分别交BC于D,E,垂足分别是M,N.(1)若△ADE的周长为6,求BC的长;(2)若∠BAC=100°,求∠DAE的度数.19.如图,在△ABC中,∠C=90°,DE是AB的垂直平分线.(1)若AC=5,BC=7,求△ACD的周长;(2)若∠BAD:∠CAD=2:1,求∠B的度数.20.如图,△ABC中,∠ABC=30°,∠ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.(1)直接写出∠BAC的度数;(2)求∠DAF的度数,并注明推导依据;(3)若△DAF的周长为20,求BC的长.参考答案一.选择题1.解:∵CD为AB的垂直平分线,∴AC=BC,∴∠B=∠A=35°∴∠ACE=∠B+∠A=70°.故选:C.2.解:∵PM、QN分别是线段AB、AC的垂直平分线,∴P A=PB,QA=QC,∴∠P AB=∠B,∠QAC=∠C,∴∠P AB+∠QAC=∠B+∠C,∵∠P AB+∠B+∠P AQ+∠QAC+∠C=180°,∴∠P AB+∠QAC=70°,∴∠BAC=∠P AB+∠QAC+∠P AQ=110°,故选:A.3.解:∵CD⊥AB,∴∠CDB=∠CDA=90°,∵DE垂直平分BC,∴DB=DC,∴△BCD为等腰直角三角形,∴BD=CD=BC=×4=4,在Rt△ADC中,AD==3,∴AB=4+3=7,∴S△ABC=×CD×AB=×4×7=14.故选:B.4.解:∵DE是△ABC中AC边的垂直平分线,∴AE=CE,∴AE+BE=CE+BE=AB=5cm,∴△EBC的周长=BC+BE+CE=5+4=9(cm).5.解:基站应该建立在B处,故选:B.6.解:∵BC的垂直平分线分别交AB、BC于点D、E,∴BD=DC,∵∠B=45°,∴∠BCD=∠B=45°,∵∠ACD=20°,∴∠ACB=∠BCD+∠ACD=45°+25°=70°,∴∠A=180°﹣∠B﹣∠ACB=180°﹣70°﹣45°=65°,故选:B.7.解:∵DF为AB的垂直平分线,∴AF=BF,∴△BCF的周长=CF+BF+BC=CF+AF+BC=AC+BC,∵AB=AC,AB+BC=6,∴AC+BC=6,∴△BCF的周长为6.故选:D.8.解:∵BD平分∠ABC,∴∠ABD=∠CBD,设∠ABD=∠CBD=x°,则∠CFD=2x°,∵EF是BC的垂直平分线,∴BF=CF,∴∠FCB=∠CBD=x°,∵∠A=50°,∠ACF=40°,∴50°+40°+x°+2x°=180°,解得:x=30,∴∠CFD=2x°=60°,故选:D.9.解:∵∠BAC=130°,∴∠B+∠C=180°﹣130°=50°,∵DF垂直平分AB,EG垂直平分AC,∴DA=DB,EA=EC,∴∠DAB=∠B,∠EAC=∠C,∴∠DAB+∠EAC=∠B+∠C=50°,∴∠DAE=∠BAC﹣(∠B+∠C)=80°,故答案为:80.10.解:∵DE是AC的垂直平分线,∴EA=EC,∴△BCE的周长=BC+BE+EC=BC+BE+EA=BC+AB=12,故答案为:12.11.解:连接AD,∵DE垂直平分AC,∴AD=CD,∵AB+BD=BC=BD+CD,∴AB=CD,∴AB=AD,∴∠ADB=∠B=70°,∴∠C=∠ADB=35°,∴∠BAC=180°﹣∠B﹣∠C=75°,故答案为:75°.12.解:∵FE、NM分别为AB、AC的垂直平分线,∴F A=FB,NA=NC,∴△AFN的周长=AF+FN+NA=FB+FN+NC=BC=12,故答案为:12.13.解:∵EF垂直平分AB于点F,∴AE=BE,∵BE+CE=20cm,∴AE+CE=20cm,即AC=20cm,∵AD垂直平分BC于点D,∴AB=AC=20cm,故答案为:20cm.14.解:∵DE是边AC的垂直平分线,∴AD=CD,AE=EC,∵AE=3cm,△ABD的周长为13cm,∴AC=AE+EC=3+3=6(cm),△ABD的周长=AB+AD+BD=AB+CD+BD=AB+BC=13(cm),所以,△ABC的周长=AB+BC+AC=13+6=19(cm).故答案为:19.三.解答题15.解:∵DE垂直平分AB,∴EA=EB,∵∠B=25°,∴∠EAB=∠B=25°,∵∠C=90°,∴∠CAB=65°,∴∠CAE=65°﹣25°=40°.16.解:连接AD、AE,∵∠BAC=135°,∴∠B+∠C=45°,∵边AB、AC的垂直平分线分别交BC于点D、E,∴DA=DB=12,EA=EC=9,∴∠DAB=∠B,∠EAC=∠C,∴∠DAE=∠BAC﹣(∠DAB+∠EAC)=90°,由勾股定理得,DE==15.17.解:∵AB、AC的垂直平分线分别交BC于点E、N,∴AE=BE,AN=CN,∴∠BAE=∠B,∠CAN=∠C,∵∠AEN=∠BAE+∠B=2∠BAE,∠ANE=∠CAN+∠C=2∠CAN,∵∠EAN=34°,∴∠AEN+∠ANE=180°﹣∠EAN=146°,∴2∠BAE+2∠CAN=146°,∴∠BAE+∠CAN=73°,∴∠BAC=∠BAE+∠CAN+∠EAN=107°.18.解:(1)∵DM和EN分别垂直平分AB和AC,∴AD=BD,EA=EC,∵△ADE的周长为6,∴AD+DE+EA=6.∴BD+DE+EC=6,即BC=6;(2)∵DM和EN分别垂直平分AB和AC,∴AD=BD,EA=EC,∴∠B=∠BAD=∠ADE,∠C=∠EAC=∠AED.∵∠BAC=∠BAD+∠DAE+∠EAC=∠B+∠DAE+∠C=100°,∴∠B+∠C=100°﹣∠DAE,在△ADE中,∠DAE=180°﹣(∠ADE+∠AED)=180°﹣(2∠B+2∠C)∴∠DAE=180°﹣2(100°﹣∠DAE)∴∠DAE=20°.19.解:(1)∵DE是AB的垂直平分线,∴DA=DB,∴△ACD的周长=AC+CD+DA=AC+CD+DB+AC+CB=5+7=12;(2)∵DA=DB,∴∠BAD=∠B,设∠CAD=x,则∠BAD=∠B=2x,∵∠C=90°,∴∠CAB+∠B=90°,即x+2x+2x=90°,解得,x=18°,∴∠B=2x=36°.20.解:(1)∵∠ABC+∠ACB+∠BAC=180°,∴∠BAC=180°﹣30°﹣50°=100°;(2)∵DE是线段AB的垂直平分线,∴DA=DB,∴∠DAB=∠ABC=30°,同理可得,∠F AC=∠ACB=50°,∴∠DAF=∠BAC﹣∠DAB﹣∠F AC=100°﹣30°﹣50°=20°;(3)∵△DAF的周长为20,∴DA+DF+F A=20,由(2)可知,DA=DB,F A=FC,∴BC=DB+DF+FC=DA+DF+F A=20.11 / 11。
2021-2022学年北师大版八年级数学下册《1-3线段的垂直平分线》同步练习题(附答案)

2021-2022学年北师大版八年级数学下册《1-3线段的垂直平分线》同步练习题(附答案)1.到△ABC的三个顶点距离相等的点是△ABC的()A.三条角平分线的交点B.三边垂直平分线的交点C.三条高的交点D.三边中线的交点2.已知Rt△ABC,∠A=90°,AD=1,BD=3,AC上的点D在BC的垂直平分线上,则AC的长度为()A.6B.4C.5D.83.如图,点P是△ABC内的一点,若PB=PC,则()A.点P在∠ABC的平分线上B.点P在∠ACB的平分线上C.点P在边AB的垂直平分线上D.点P在边BC的垂直平分线上4.如图,在△ABC中,∠ACB=90°,DE垂直平分AB,垂足为D,如果∠A=30°,AB =6cm,那么CE等于()A.3cm B.2cm C.4cm D.cm5.如图,在△ABC中,∠C=90°,E是AB的中点,且DE⊥AB于点E,∠CAD:∠EAD =1:2,则∠B与∠BAC的度数为()A.30°,60°B.32°,58°C.36°,54°D.20°,70°6.如图,△ABC中,AB=AE,且AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,若△ABC周长为20,AC=8,则DC为()A.6B.8C.9D.107.如图,在△ABC中,BC=10,AB的中垂线交BC于D,AC的中垂线交BC于E,则△ADE的周长是()A.8B.10C.12D.148.如图,已知DE⊥BC,BE=EC,且AB=7、AC=8,则△ABD的周长等于()A.15B.20C.25D.309.如图,点D在△ABC的边BC上,且BC=BD+AD,则点D在线段()A.AB的垂直平分线上B.AC的垂直平分线上C.BC的垂直平分线上D.不能确定10.如图,在△ABC中,DE是AC的垂直平分线,AB=4,△ABD的周长为12,则BC=.11.如图,在△ABC中,∠B=40°,DE垂直平分AB,垂足为点E,交BD于点D,连接AD,则∠ADC的度数是.12.如图,在△ABC中,AC垂直平分线DE分别与BC、AC交于D、E,△ABD的周长是13,AE=5,△ABC的周长是.13.已知点P在线段AB的垂直平分线上,P A=4cm,则PB=cm.14.如图,在△ABC中,AD⊥BC于D,E是BC上一点,BD=DE,且点E在AC的垂直平分线上,若△ABE的周长为10,则DC=.15.如图所示,CD是AB的垂直平分线,若AC=2cm,BD=3cm,则四边形ACBD的周长是.16.如图,在△ABC中,边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,BD=5cm,则△ABD的周长是cm.17.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.若AB=5cm,BC=6cm,则AC=,DE=.18.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=60°,∠F AE=21°,则∠C=度.19.如图,点A为△PBC的三边垂直平分线的交点,且∠P=72°,则∠BAC=.20.如图,△ABC中,DE是边AC的垂直平分线,AE=2cm,△ABD的周长是8cm,则△ABC的周长是.21.如图△ABC中,DE是BC的垂直平分线,△ABD的周长为7cm,BE=2cm,则△ABC 的周长为cm.22.如图所示,在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E,若∠CAE=∠B+30°,则∠B=度.23.如图,△ABC中,AB的垂直平分线分别交AB,BC于点D,E,AC的垂直平分线分别交AC,BC于点F,G,连接AE,AG.(1)若△AEG的周长为10,求线段BC的长;(2)若∠BAC=104°,求∠EAG的度数.参考答案1.解:∵到三角形的一边的两端点距离相等的点在这边的垂直平分线上,∴到三角形三个顶点的距离都相等的点是这个三角形的三条边的垂直平分线的交点,故选:B.2.解:∵点D在BC的垂直平分线上,∴DB=DC=3∴AC=AD+CD=1+3=4.故选:B.3.解:∵PB=PC,∴P在线段BC的垂直平分线上,故选:D.4.解:∵在△ABC中,∠ACB=90°,∠A=30°,AB=6cm,∴BC=AB=3cm,∠ABC=90°﹣∠A=60°,∵DE垂直平分AB,∴BE=AE,∴∠ABE=∠A=30°,∴∠CBE=∠ABC﹣∠ABE=30°,∴CE=BC•tan30°=3×=3(cm).故选:A.5.解:设∠CAD=x,则∠EAD=2x,∵E是AB的中点,且DE⊥AB于点E,∴ED是AB的中垂线,∴AD=AB,∴∠DAB=∠DBA,∴x+2x+2x=90°,解得x=18°,∴∠B=2x=36°,∠CAB=90°﹣36°=54°.故选:C.6.解:∵△ABC周长为20,∴AB+BC+AC=20,∵AC=8,∴AB+BC=12,∵EF垂直平分AC,∴EA=EC,∵AB=AE,AD⊥BC,∴BD=DE,∴AB+BD=AE+DE=×(AB+BC)=6,∴DC=DE+EC=AE+DE=6,故选:A.7.解:∵AB的中垂线交BC于D,AC的中垂线交BC于E,∴DA=DB,EA=EC,∴△ADE的周长=AD+DE+EA=BD+DE+EC=BC=10,故选:B.8.解:∵DE⊥BC,BE=EC,∴DE是线段BC的垂直平分线,∴DB=DC,∴△ABD的周长=AB+AD+BD=AB+AD+CD=AB+AC=7+8=15,故选:A.9.解:∵BC=BD+AD=BD+CD∴AD=CD∴点D在AC的垂直平分线上.故选:B.10.解:∵DE是AC的垂直平分线,∴AD=DC,∴BC=BD+DC=BD+DA,∵AB=4,△ABD的周长为12,∴BC=12﹣4=8.故答案为:8.11.解:∵DE垂直平分AB,∴DA=DB,∴∠DAB=∠B=40°,∵∠ADC是△ADB的一个外角,∴∠ADC=∠DAB+∠B=80°,故答案为:80°.12.解:∵DE是线段AC的垂直平分线,∴DA=DC,AC=2AE=10,∵△ABD的周长是13,∴AB+BD+DA=13,∴AB+BD+DC=AB+BC=13,∴△ABC的周长=AB+BC+AC=23,故答案为:23.13.解:∵点P在线段AB的垂直平分线上,∴PB=P A,∵P A=4cm,∴PB=4cm.故答案为4cm.14.解:∵AD⊥BC于D,BD=DE,即AD垂直平分BE,∴AB=AE,∵△ABE的周长为10,∴AB+AE+BD+DE=10,∴AE+DE=5,∵点E在AC的垂直平分线上,∴EA=EC,∴DC=DE+EC=DE+AE=5.故答案为5.15.解:∵CD是AB的垂直平分线,AC=2cm,BD=3cm,∴AD=BD=3,AC=BC=2,∴四边形ACBD的周长=10cm.故答案为:10cm.16.解:∵DE是线段AB的垂直平分线,AE=3cm,BD=5cm,∴DA=DB=5(cm),AB=6(cm),∴△ABD的周长=BD+AD+AB=16(cm),故答案为:16.17.解:∵BC=6cm,∴BD=DC=3(cm),∵AD⊥BC,BD=DC,AB=5cm,∴AC=AB=5(cm),∵点C在AE的垂直平分线上,∴EC=AC=5(cm),∴DE=DC+EC=8(cm),故答案为:5cm;8cm.18.解:设∠C=x,∵DE是线段AC的垂直平分线,∴EA=EC,∴∠EAC=∠C=x,∴∠F AC=x+21°,∵AF平分∠BAC,∴∠BAF=∠F AC=x+21°,∴x+x+21°+x+21°+60°=180°,解得,x=26°,即∠C=x=26°,故答案为:26.19.解:∵A为△PBC三边垂直平分线的交点,∴点A是△PBC的外心,由圆周角定理得,∠BAC=2∠BPC=144°,故答案为:144°20.解:∵DE是AC的垂直平分线.∴AD=CD,AC=2AE=4cm.又∵△ABD的周长=AB+BD+AD=8cm.∴AB+BD+CD=8cm,即AB+BC=8cm.∴△ABC的周长=AB+BC+AC=8cm+4cm=12cm.故答案为:12cm21.解:∵DE是BC的垂直平分线,∴DB=DC,CE=BC=2,∵△ABD的周长为7cm,∴AB+AD+BD=AB+AD+CD=AB+AC=7,∴△ABC的周长=AB+AC+BC=11(cm),故答案为:11.22.解:∵DE垂直平分斜边AB,∴EA=EB,∴∠EAB=∠B,∴∠AEC=2∠B,∴∠B+30°+∠B+∠B=90°,解得,∠B=20°,故答案为2023.解:(1)∵DE垂直平分AB,GF垂直平分AC,∴EA=EB,GA=GC,∵△AEG的周长为10,∴AE+EG+AG=10,∴BC=BE+EG+GC=AE+EG+GC=10;(2)∵∠BAC=104°,∴∠B+∠C=180°﹣104°=76°,∵EA=EB,GA=GC,∴∠EAB=∠B,∠GAC=∠C,∴∠EAB+∠GAC=∠B+∠C=76°,∴∠EAG=∠BAC﹣(∠EAB+∠GAC)=104°﹣76°=28°.。
1.3 线段的垂直平分线 (1)

37.(2020 秋•雁塔区校级期末)如图,在△ABC 中,∠BAC=90°,BE 平分∠ABC,AM ⊥BC 于点 M 交 BE 于点 G,AD 平分∠MAC,交 BC 于点 D,交 BE 于点 F.求证:线段 BF 垂直平分线段 AD.
38.(2020 秋•虎林市期末)如图,△ABC 中,∠BAC=80°,若 MP 和 NQ 分别垂直平分 AB 和 AC. (1)求∠PAQ 的度数. (2)若△APQ 周长为 12,BC 长为 8,求 PQ 的长.
第 5页(共 13页)
与 BC 的交点,连接 AD.若 CD=2,BD=4,则 AC 的长为( )
A.4
B.3
C.2 3
D. 3
21.(2020 秋•滦州市期末)如图,在△ABC 中,∠ACD=20°,∠B=45°,BC 的垂直平
分线分别交 AB、BC 于点 D、E,则∠A 的度数是( )
A.60°
41.(2019 秋•晋江市期末)如图,在△ABC 中,点 E 是 BC 边上的一点,连接 AE,BD 垂
第 10页(共 13页)
直平分 AE,垂足为 F,交 AC 于点 D,连接 DE (1)若△ABC 的周长为 18,△DEC 的周长为 6,求 AB 的长; (2)若∠ABC=29°,∠C=47°,求∠CDE 度数.
AC 于 D,交 BC 于 E,D 为垂足,CE=10 cm,则 AB=( )
A.4 cm
B.5
C.6 cm
D.不能确定
3.(2020 秋•九龙坡区期中)如图,在△ABC 中,AB 边的中垂线 DE,分别与 AB、AC 边交
于点 D、E 两点,BC 边的中垂线 FG,分别与 BC、AC 边交于点 F、G 两点,连接 BE、
八年级数学下册《线段的垂直平分线》同步练习1(含答案)

1.3 线段的垂直平分线一、判断题1.如图(1),OC=OD直线AB是线段CD的垂直平分线2.如图(1),射成OE为线段CD的垂直平分线3.如图(2),直线AB的垂直平分线是直线CD4.如图(3),PA=PB,P′A=P′B,则直线PP′是线段AB的垂直平分线(1)(2)(3)二、填空题1.如右图,已知直线MN是线段AB的垂直平分线,垂足为D,点P是MN 上一点,若AB=10 cm,则BD=__________cm;若PA=10 cm,则PB=__________cm;此时,PD=__________cm.2.如左下图,在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABD 的周长是12 cm,AC=5cm,则AB+BD+AD=_____cm;AB+BD+DC=________cm;△ABC的周长是______cm.3.如右上图,在Rt△ABC中,∠C=90°,∠B=15°,DE是AB的中垂线,垂足为D,交BC于E,BE=5,则AE=_______,∠AEC=________,AC=________ .4.已知线段AB及一点P,PA=PB=3cm,则点P在__________上.5.如果P是线段AB的垂直平分线上一点,且PB=6cm,则PA=__________cm.6.如图(1),P是线段AB垂直平分线上一点,M为线段AB上异于A,B 的点,则PA,PB,PM的大小关系是PA__________PB______PM.7.如图(2),在△ABC中,∠C=90°,∠A=30°,BD平分∠ABC交BC于D,则点D在__________上.(1)(2)(3)8.如图(3),BC是等腰△ABC和等腰△DBC的公共底,则直线AD必是_____的垂直平分线.三、选择题1.下列各图形中,是轴对称图形的有多少个()①等腰三角形②等边三角形③点④角⑤两个全等三角形A.1个B.2个C.3个D.4个2.如左下图,AC=AD,BC=BD,则()A.CD垂直平分ADB.AB垂直平分CDC.CD平分∠ACBD.以上结论均不对3.如右上图,△ABC中,AB的垂直平分线交AC于D,如果AC=5 cm,BC=4cm,那么△DBC的周长是()A.6 cmB.7 cmC.8 cmD.9 cm4.如果三角形三条边的中垂线的交点在三角形的外部,那么,这个三角形是()A.直角三角形B.锐角三角形C.钝角三角形D.等边三角形四、解答题如右图,P是∠AOB的平分线OM上任意一点,PE⊥CA于E,PF⊥OB于F,连结EF.求证:OP垂直平分EF.参考答案一、1.× 2. × 3.× 4.√ 二、1.5 10 53 2.12 12 17 3.5 30° 2154.线段AB 的垂直平分线5.66.= >7.线段AB 的垂直平分线 8.线段BC三、1.D 2.B 3.D 4.C四、证明:∵PE ⊥OA 于E ,DF ⊥OB 于F ∴∠PEO=90°=∠PFO ∴在△PEO 和△PFO 中,⎪⎩⎪⎨⎧=∠=∠∠=∠OP OP FOP EOP PFO PEO ∴△PEO ≌△PFO ,∴PE=PF ,EO=FO ∴O 、P 在EF 的中垂线上, ∴OP 垂直平分EF.。
1.3 线段的垂直平分线(含答案)-
1.3 线段的垂直平分线练习【同步达纲练习】一、判断(4分×6=24分)( )1.三角形两边的垂直平分线交点在三角形一边上,则该三角形为等边三角形.( )2.到三角形三顶点距离相等的点在三角形内.( )3.到三角形距离三边相等的点是三条中垂线的交点.( )4.四边形ABCD 中共有一点P ,使PA=PB=PC=PD ,则∠A+∠C=180°.( )5.和线段两端距离相等的点只有线段的中点.( )6.和线段两端相等的点不一定在线段上.二、选择题(5分×6=30分)1.到三角形三个顶点距离相等的是( )A.三条中线交点B.三条高的交点C.三条角平分线的交点D.三条中垂线的交点2.线段AB 外有两点C ,D(在AB 同侧)使CA=CB ,DA=DB ,∠ADB=80°, ∠CAD=10°,则∠ACB=( )A.90°B.100°C.110°D.120°3.BD 为CE 的中垂线,A 在CB 延长线上,∠C=34°,则∠ABE=( )A.17°B.34°C.68°D.136°4.O 为△ABC 三边中垂线的交点,则O 称为△ABC 的( )A.外心B.内心C.垂心D.重心5.若三角形一边中垂线过另一边中点,则该三角形必为( )A .钝角三角形 B.锐角三角形C.直角三角形D.等腰三角形6. 如图,△ABC 中,∠ACB=90°, ∠A=30°AC 的中垂线交AC 于E.交AB 于D ,则图中60°的角共有( )A .6个 B.5个 C.4个 D3个三、填空(5分×6=30分)1.△ABC 中,AB=AC ,P 为形内一点,PB=PC ,则P 在 的中垂线上,P 还在∠ 的平分线上.2.△ABC 中,AB=AC=14,腰AB 的中垂线交AC 于D ,△BCD 周长为4cm,则BC= .3.△ABC 中,AB=AC ,∠A=120°,AB 中垂线交BC 于E ,则BCBE = . 4.正△ABC 内一点O 到三边距离相等,且OA=OB=OC.则∠BOC= .5.△ ABC 的边AC 、BC 的中垂线交于AB 上一点O ,且OC=BC ,则∠A= .6.若PA=PB ,DA=DB ,则PD 是AB 的 .四、解答(8分×2=16分)1.△ABC 中,∠C=90°,AB 的中垂线交AB 于D ,AC 于E.且∠EBC=40°,求∠A 及∠BED2.已知O 为等边三角形三边中线交点,求证BO 与CO 的中垂线必三等分BC.【素质优化训练】1.AD 为△ABC 的角平分线,DE ∥AC,交AB 于E.过E 作AD 的垂线交BC 延长线于F(图3.14-8),求证21(∠BAC+∠AFC )=90°-∠B.图3.14-82.如图,△ABC 中,AB=AC ,AE ∥BC,D 为直线AE 上任一点.求证DB+DC >2AB.【同步达纲练习】一、× × × √ × √二、D B C A C B三、1.BC,BAC 2.10 3.1∶3 4.120° 5.30° 6.中垂线四、1. ∠C=180°, ∠EBC=40°∴∠BEC=50°又AE=BE∴∠A=25° ∠DEB=65°2.提示:设CB 中垂线交BC 于D ,OC 中垂线交BC 于E ,连OD ,OE. ∴OD=BD OE=EC. 再证∠BOC=120° ∠BOD=COE=30°∴∠DOE=60° ∠ODE=60°∴OD=OE=DE 得BD=DE=EC.【素质优化训练】1. AD 为角平分线,DE ∥AC∴∠EAD=∠EDA EF 为中垂线∴∠ADF=∠ADF=∠B+∠BAD∴∠CAF=∠B ∠BAC+∠CAF+∠AFC+∠B=180° ∴21(∠BAC+∠AFC)=90°-∠B.2.延长BA 至F ,使BA=AF ,连FD ,AD ∥BC,AB=AC ∠FAD=∠ABC=∠ACB=∠DAC.AF=AC △FAD ≌△CAD FD=DC ,FD+DB >FB∴DB+DC >2AB.。
2020年春北师大版1.3线段的垂直平分线第一课时同步练习(八下)
2020年春北师大版1.3线段的垂直平分线第一课时同步练习(八下)基础巩固部分:1.如图,四边形ABCD中,AC垂直平分BD,垂足为E ,下列结论不一定成立的是( )A.AB=AD B.AC平分∠BCDC.AB=BD D.△BEC≌△DEC2.如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线DE分别交AB,BC于点D,E,则∠BAE=( )A.80°B.60°C.50°D.40°3.如图所示,A,B是直线l外两点,在l上求作一点P,使PA+PB最小,其作法是()A.连接BA并延长与l的交点为PB.连接AB,并作线段A月的垂直平分线与l的交点为PC.过点B作l的垂线,垂线与l的交点为PD.过点A作l的垂线段AO,O是垂足,延长AO到A′,使A′O=AO,再连接A′B,则A′B与L的交点为P4.如图,已知在△ABC中,DE是BC的垂直平分线,垂足为E,交AC于点D,若AB=6,AC=9,则△ABD的周长是5.如图,D为BC边上一点,且BC=BD+AD,则AD DC,点D在的垂直平分线上。
6.如图,在△ABC中,已知AB的垂直平分线交AC于点E,△ABC和△BEC的周长分别为24 cm和14 cm,求AB的长.能力提升部分:1.如图,在△ABC中,AD垂直平分BC,AC=EC,点B,D,C,E 在同一条直线上,则AB+DB与DE之间的数量关系是()A. AB+DB>DEB. AB+DB<DEC. AB+DB=DED. 无法判断2.已知在△ABC中,AB=AC,AB的垂直平分线交线段AC于D,若△ABC和△DBC的周长分别是60 cm和38 cm,则△ABC的腰长和底边BC的长分别是()A.24 cm和12 cm B.16 cm和22 cmC.20 cm和16 cm D.22 cm和16 cm3.如图,在△ABC中,AB=AC,∠BAC=36°,DE是线段AC的垂直平分线.若BE=a,AE=b,则用含a,b的代数式表示△ABC的周长为4、如图,一张直角三角形的纸片,象图中那样折叠,使A与B重合,∠B=30°,AC=3,则折痕DE等于.5.如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,则∠A等于.8.如图所示,在△ABC中,∠B=15°,∠C=90°,AB的垂直平分线交BC于点M,交AB于点N,BM=12 cm,求AC的长.9.如图所示,在△ABC中,∠BAC=110°,PM,QN分别垂直平分AB,AC,求∠PAQ的度数.。
北师版八年级数学----中垂线练习题
北师大版数学八年级下册1.3线段的垂直平分线课时练习一、选择题1.如图,△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,那么△BDC 的周长是〔〕A. 8B.9C. 10D.11答案:C解析:解:∵ED是AB的垂直平分线,∴AD=BD,∵△BDC的周长=DB+BC+CD,∴△BDC的周长=AD+BC+CD=AC+BC=6+4=10.应选C.分析:由ED是AB的垂直平分线,可得AD=BD,又由△BDC的周长=DB+BC+CD,即可得△BDC的周长=AD+BC+CD=AC+BC.2.如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.假设∠A=60°,∠ABD=24°,那么∠ACF的度数为〔〕A. 48°B. 36°C. 30°D. 24°答案:A解析:解:∵BD平分∠ABC,∴∠DBC=∠ABD=24°,∵∠A=60°,∴∠ACB=180°-60°-24°×2=72°,∵BC的中垂线交BC于点E,∴BF=CF,∴∠FCB=24°,∴∠ACF=72°-24°=48°,应选:A.分析:根据角平分线的性质可得∠DBC=∠ABD=24°,然后再计算出∠ACB的度数,再根据线段垂直平分线的性质可得BF=CF,进而可得∠FCB=24°,然后可算出∠ACF的度数. 3.如图,在等腰△ABC中,一腰AB的垂直平分线交另一腰AC于点G,假设AB=10,△GBC的周长为17,那么底BC的长为〔〕A. 10B. 9C. 7D. 5答案:C解析:解:如图,∵在等腰△ABC中,一腰AB的垂直平分线交另一腰AC于点G,∴AG=BG,∵AB=10,△GBC的周长为17,∴CG+BG+BC=CG+AG+BC=AC+BC=17,AC=AB=10,∴BC=7.应选C.分析:首先根据题意在等腰△ABC中,一腰AB的垂直平分线交另一腰AC于点G,根据线段垂直平分线的性质,可得AG=BG,继而可得△GBC的周长=AC+BC=17,那么可求得答案.4.如图,AB=AC,∠A=40°,AB的垂直平分线DE交AC于点E,垂足为D,那么∠EBC 的度数是〔〕A. 30°B. 40°C. 70°D. 80°答案:A解析:解:∵AB的垂直平分线DE交AC于点E,∴AE=BE,∴∠ABE=∠A=40°,∵AB=AC,∴∠ABC=∠C=70°,∴∠EBC=∠ABC-∠ABE=30°.应选A.分析:由AB的垂直平分线DE交AC于点E,可得AE=BE,继而求得∠ABE=∠A=40°,然后由AB=AC,求得∠ABC的度数,继而求得答案.5.如图,在△ABC中,AB的垂直平分线分别交AB,AC于D,E两点,且AC=10,BC=4,那么△BCE的周长为〔〕A. 6B. 14C. 18D. 24答案:B解析:解:∵AC=10,BC=4,∴AC+BC=10+4=14,∵DE是线段AB的垂直平分线,∴AE=BE,∴△BCE的周长=〔BE+CE〕+BC=AC+BC=14.应选B.分析:先根据AC=10,BC=4,可得出AC+BC的长,再根据DE是线段AB的垂直平分线可得到AE=BE,进而可得出答案.6.如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,那么△BCM的周长为〔〕A. 18B. 16C. 17D. 无法确定答案:C解析:解:在Rt△ABC中,∠C=90°,AC=12,AB=13,由勾股定理得,BC=5,∵MN是AB的垂直平分线,∴MB=MA,∴△BCM的周长=BC+CM+MB=BC+CM+MA=BC+CA=17,应选:C分析:根据勾股定理求出BC的长,根据线段垂直平分线的性质得到MB=MA,根据三角形的周长的计算方法代入计算即可.7.如果三角形三条边的中垂线的交点在三角形的外部,那么,这个三角形是〔〕A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 等边三角形答案:C解析:解:如图,O是边AB和边AC的垂直平分线的交点,那么AO=OB,AO=OC,所以∠OAB=∠OBA,∠OAC=∠OCA,∵∠BAC=∠OAB+∠OAC=∠OBA+∠OCA,∴∠BAC>∠ABC+∠ACB,∵∠BAC+∠ABC+∠ACB=180°,∴∠BAC>90°,即△ABC是钝角三角形,应选C分析:先根据题意画出图形,再根据线段垂直平分线性质、等腰三角形的性质、三角形的角和定理求出∠BAC>90°即可.8. MN是线段AB的垂直平分线,C,D是MN上任意两点,那么∠CAD和∠CBD之间的大小关系是〔〕A.∠CAD<∠CBD B.∠CAD=∠CBD C.∠CAD>∠CBD D.无法确定答案:B解析:解:∵MN是线段AB的垂直平分线,C,D是MN上任意两点,∴AC=BC,AD=BD,∴∠DAB=∠CBA,∠DAB=∠DBA,如图1,∠CAD=∠CAB+∠DAB,∠CBD=∠CBA+∠DBA,∴∠CAD=∠CBD;如图2,∠CAD=∠CAB-∠DAB,∠CBD=∠CBA-∠DBA,∴∠CAD=∠CBD.应选B.分析:首先根据题意画出图形,然后由MN是线段AB的垂直平分线,C,D是MN上任意两点,根据线段垂直平分线的性质可得:AC=BC,AD=BD,那么可证得∠DAB=∠CBA,∠DAB=∠DBA,继而求得答案.9. △ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60 cm 和38 cm,那么△ABC的腰和底边长分别为〔〕A.24 cm和12 cmB.16 cm和22 cmC.20 cm和16 cmD.22 cm和16 cm答案:D解析:解:如图,连接BD,∵D在线段AB的垂直平分线上,∴BD=AD,∴BD+DC+BC=AC+BC=38 cm,且AB+AC+BC=60 cm,∴AB=60 cm-38 cm =22 cm,∴AC=22 cm,∴BC=38 cm-AC=38 cm-22 cm =16 cm,即等腰三角形的腰为22 cm,底为16 cm,应选D.分析:连接BD,根据线段垂直平分线的性质可得到BD=AD,可知两三角形周长差为AB,结合条件可求得腰长,再由周长可求得BC,可得出答案.10.如图,地面上有三个洞口A、B、C,老鼠可以从任意一个洞口跑出,猫为能同时最省力地顾及到三个洞口〔到A、B、C三个点的距离相等〕,尽快抓到老鼠,应该蹲守在〔〕A.△ABC三边垂直平分线的交点B.△ABC三条角平分线的交点C.△ABC三条高所在直线的交点D.△ABC三条中线的交点答案:A解析:解:∵三角形三边垂直平分线的交点到三个顶点的距离相等,∴猫应该蹲守在△ABC三边垂直平分线的交点处.应选A分析:根据题意,知猫应该到三个洞口的距离相等,那么此点就是三角形三边垂直平分线的交点.11. 三角形有一点到三角形三顶点的距离相等,那么这点一定是三角形的〔〕A.三条中线的交点B.三边垂直平分线的交点C.三条高的交点D.三条角平分线的交点答案:B解析:解:三角形有一点到三角形三顶点的距离相等,那么这点一定是三角形的三边垂直平分线的交点,应选:B.分析:根据线段垂直平分线的性质:线段垂直平分线上任意一点,到线段两端点的距离相等可得答案.12. △ABC中,AB=AC,AB的垂直平分线与直线AC相交所成锐角为40°,那么此等腰三角形的顶角为〔〕A.50°B.60°C.150°D.50°或130°答案:D解析:解:〔1〕当AB的中垂线MN与AC相交时易得∠A=90°-40°=50°,〔2〕当AB的中垂线MN与CA的延长线相交时,易得∠DAB=90°-40°=50°,∴∠A=130°,应选D.分析:此题根据△ABC中∠A为锐角与钝角分为两种情况解答.13. 如图,在Rt△ABC中,∠C=90°,直线DE是斜边AB的垂直平分线交AC于D.假设AC=8,BC=6,那么△DBC的周长为〔〕A.12B.14C.16D.无法计算答案:B解析:解:∵DE是AB的垂直平分线,∴DA=DB,∴△DBC的周长为CB+CD+DB=CB+CD+DA=BC+CA=6+8=14,应选:B分析:根据线段的垂直平分线上的点到线段的两个端点的距离相等得到DA=DB,根据三角形周长公式求出周长.14. 如图,在△ABC中,AB=A,AC=B,BC边上的垂直平分线DE交BC、BA分别于点D、E,那么△AEC的周长等于〔〕A.A+B B.A-B C.2A+B D.A+2B答案:A解析:解:∵ED垂直且平分BC,∴BE=CE.∵AB=A,AC=B,∴AB=AE+BE=AE+CE=A.∴△AEC的周长为:AE+EC+AC=A+B.应选A分析:要求三角形的周长,知道AC=B,只要求得AE+EC即可,由DE是BC的垂直平分线,结合线段的垂直平分线的性质,知EC=BE,这样三角形周长的一局部AE+EC=AE+BE=AB,代入数值,答案可得.15. 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,那么超市应建在〔〕A.在AC,BC两边高线的交点处B.在AC,BC两边中线的交点处C.在AC,BC两边垂直平分线的交点处D.在∠A,∠B两角平分线的交点处答案:C解析:解:根据线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等.那么超市应建在AC,BC两边垂直平分线的交点处.应选C.分析:要求到三小区的距离相等,首先思考到A小区、B小区距离相等,根据线段垂直平分线定理的逆定理知满足条件的点在线段AB的垂直平分线上,同理到B小区、C小区的距离相等的点在线段BC的垂直平分线上,于是到三个小区的距离相等的点应是其交点,答案可得.二、填空题16.△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于E,交BC于F.假设FC=3 cm,那么BF=_________.答案:6 cm解析:解:连接AF.∵AB=AC,∠BAC=120°,∴∠B=∠C=30°;∵AC的垂直平分线EF交AC于点E,交BC于点F,∴CF=AF,∠FAC=30°,∴∠BAF=90°,∴BF=2AF〔30°直角边等于斜边的一半〕,∴BF=2CF=6 cm.故答案是:6 cm分析:利用辅助线,连接AF,求出CF=AF,∠BAF=90°,再根据AB=AC,∠BAC= 120°可求出∠B的度数,由直角三角形的性质即可求出BF=2AF=2CF=6 cm.17. 如图,ED为△ABC的AC边的垂直平分线,且AB=5,△BCE的周长为8,那么BC=________.答案:3解析:解:∵ED为AC上的垂直平分线,∴AE=EC,∵AB=AE+EB=5,△BCE的周长=AE+BE+BC=AB+BC=8,∴BC=8-5=3.故答案为:3分析:根据ED为AC上的垂直平分线,得出AE=CE,再根据AB=5,△BCE的周长为AB+BC=8,即可求得BC.18.如图,在△ABC中,AB=AC=10,DE垂直平分AB,垂足为E,DE交AC于D,假设△BDC的周长为16,那么BC=__________ .答案:6解析:解:∵DE垂直平分AB,∴AD=BD,∴AD+CD=BD+CD,即AC=BD+CD,∵AC=10,△BDC的周长为16,∴BC=16-AC=16-10=6.故答案为:6分析:先根据DE垂直平分AB可知,AD=BD,即AC=BD+CD,再由AC=10,△BDC的周长为16即可求出答案.19. 如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,∠ADE=40°,那么∠DBC=答案:15解析:解:∵DE垂直平分AB,∴AD=BD,∠AED=90°,∴∠A=∠ABD,∵∠ADE=40°,∴∠A=90°-40°=50°,∴∠ABD=∠A=50°,∵AB=AC,∴∠ABC=∠C=65°,∴∠DBC=∠ABC-∠ABD=65°-50°=15°,故答案为:15分析:根据线段垂直平分线求出AD=BD,推出∠A=∠ABD=50°,根据三角形角和定理和等腰三角形性质求出∠ABC,即可得出答案.20.点P在线段AB的垂直平分线上,PA=7,那么PB= _________.答案:7解析:解:∵点P在线段AB的垂直平分线上,PA=7,∴PB=PA=7,故答案为:7分析:根据线段垂直平分线的性质得出PA=PB,代入即可求出答案.三、解答题21. 某公园有海盗船、摩天轮、碰碰车三个娱乐工程,现要在公园建一个售票中心,使三个娱乐工程所处位置到售票中心的距离相等,请在图中确定售票中心的位置.答案:解:如图,①连接AB,AC,②分别作线段AB,AC的垂直平分线,两垂直平分线相较于点P,那么P即为售票中心解析:由三个娱乐工程所处位置到售票中心的距离相等,可得售票中心是海盗船、摩天轮、碰碰车三个娱乐场组成三角形的三边的垂直平分线的交点.22.如图,在△ABC中,∠C=90°,DE垂直平分AB,分别交AB,BC于D,E.假设∠CAE=∠B+30°,求∠AEB的度数答案:140°解析:解:∵DE垂直平分AB,∴AE=BE,∴∠B=∠EAB.∵∠C=90°,∠CAE=∠B+30°,∴∠B+30°+∠B+∠B=90°,∴∠B=20°,∴∠AEB=180°-20°-20°=140°.分析:根据线段垂直平分线求出AE=BE,推出∠B=∠EAB,根据和三角形角和定理得出∠B+30°+∠B+∠B=90°,求出∠B,即可得出答案.23.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.〔1〕求证:△ABD是等腰三角形;〔2〕假设∠A=40°,求∠DBC的度数;〔3〕假设AE=6,△CBD的周长为20,求△ABC的周长答案:〔1〕证明:∵AB的垂直平分线MN交AC于点D,∴DB=DA,∴△ABD是等腰三角形.〔2〕30°〔3〕32解析:解:〔1〕证明:∵AB的垂直平分线MN交AC于点D,∴DB=DA,∴△ABD是等腰三角形;〔2〕∵△ABD是等腰三角形,∠A=40°,∴∠ABD=∠A=40°,∠ABC=∠C=〔180°-40°〕÷2=70°.∴∠BDC=∠ABC-∠ABD=70°-40°=30°.〔3〕∵AB的垂直平分线MN交AC于点D,AE=6,∴AB=2AD=12.∵△CBD的周长为20,∴AC+BC=20,∴△ABC的周长=AB+AC+BC=12+20=32.分析:〔1〕根据线段的垂直平分线到线段两端点的距离相等即可得证;〔2〕首先利用三角形角和求得∠ABC的度数,然后减去∠ABD的度数即可得到答案;〔3〕将△ABC的周长转化为AB+AC+BC的长即可求得.24.如以下图,在△ABC中,DE是边AB的垂直平分线,交AB于E,交AC于D,连接BD.〔1〕假设∠ABC=∠C,∠A=50°,求∠DBC的度数.〔2〕假设AB=AC,且△BCD的周长为18 cm,△ABC的周长为30 cm,求BE的长.答案:〔1〕15°;〔2〕6 cm解析:解:〔1〕∵∠A=50°,∴∠ABC=∠C=65°.又∵DE垂直平分AB,∴∠A=∠ABD=50°,∴∠DBC=∠ABC-∠ABD=15°.〔2〕∵DE是AB的垂直平分线,∴AD=BD,AE=BE,∴△BCD的周长=BC+CD+BD=BC+CD+AD=BC+AC=18 cm.∵△ABC的周长=30 cm,∴AB=30-18=12 cm,∴BE=AE=6 cm.分析:〔1〕∠A=50°,易求∠ABC的度数.又因为DE垂直平分AB根据线段垂直平分线的性质易求出∠DBC的度数.〔2〕同样利用线段垂直平分线的性质:垂直平分线上任意一点,和线段两端点的距离相等可解.25.:如图,在△ABC中,MN是边AB的中垂线,∠MAC=50°,∠C=3∠B,求∠B的度数=26°答案:B解析:解:∵MN是边AB的中垂线,∴AM=BM,∴∠BAM=∠B.设∠B=x,那么∠BAM=x,∵∠C=3∠B,∴∠C=3x,在△ABC中,由三角形角和定理,得x+x+3x+50°=180°,∴x=26°,即∠B=26°分析:根据线段垂直平分线性质得出AM=BM,推出∠BAM=∠B,设∠B=x,那么∠BAM=x,∠C=3x,在△ABC中,由三角形角和定理得出方程x+x+3x+50°=180°,求出即可。
北师版八年级下册数学 第1章 1.3.1目标二 线段垂直平分线的判定 习题课件1
思维发散练
(1)求证:AG垂直平分BC. 证明:∵GB=GC,AB=AC, ∴点G、点A在BC的垂直平分线上. 又∵两点确定一条直线,∴AG垂直平分BC.
(2)点D在AG上,求证:DB=DC. 证明:∵AG垂直平分BC,点D在AG上, ∴DB=DC.
思维发散练
7 如图,在四边形ABCD中,AD∥BC,E为CD的中点, 连接AE并延长交BC的延长线于点F.
认知基础练
4 已知C,D是线段AB外的两点,AC=BC,AD=BD,
点P在直线CD上.若AP=5,则BP的长为( B )
A.2.5
B.5
C.10
D.25
认知基础练
5 如图,C是△ABE的边BE上一点,点F在AE上,点D是
BC的中点,且AB=AC=CE,对于下列结论:
①AD⊥BC;②CF⊥AE;
③∠1=∠2;④AB+BD=DE.
北师版 八年级下
第一章
三角形的证明
1.3. 线段的垂直平分线 1目 标 二 线 段 垂 直 平 分 线 的 判 定
习题链接
温馨提示:点击 进入讲评
1A 2B 3 ①②③ 4B
5B 6 7
答案呈现
认知基础练
1 如图,AC=AD,BC=BD,则有( A ) A.AB垂直平分CD B.CD垂直平分AB C.AB与CD互相垂直平分 D.以上都不正确
认知基础练
2 如图,点D在△ABC的边BC上,且BC=BD+AD,则 点D在线段( B )的垂直平分线上. A.AB B.AC C.BC D.不确定
认知基础练
3 有下列说法:①若直线PE是线段AB的垂直平分线, 则EA=EB,PA=PB;②若PA=PB,EA=EB,则直 线PE垂直平分线段AB;③若PA=PB,则P必是线段 AB的垂直平分线上的点;④若EA=EB,则过点E的 直线垂直平分线段AB.其中正确的是____①__②__③_____(填 序号).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.3线段的垂直平分线
一、选择题
1.已知MN是线段AB的垂直平分线,C,D是MN上任意两点,则∠CAD和∠CBD之间的大小关系是()
A.∠CAD<∠CBD
B.∠CAD=∠CBD
C.∠CAD>∠CBD
D.无法判断
2.如图1-75所示,在△ABC中,AD垂直平分BC,AC=EC,点B,D,C,E在同一条直线上,则AB+DB与DE 之间的数量关系是()
A. AB+DB>DE
B. AB+DB<DE
C. AB+DB=DE
D. 无法判断
3.已知在△ABC中,AB=AC,AB的垂直平分线交线段AC于D,若△ABC和△DBC的周长分别是60 cm 和38 cm,则△ABC的腰长和底边BC的长分别是()
A.24 cm和12 cm B.16 cm和22 cm
C.20 cm和16 cm D.22 cm和16 cm
4.如图1-76所示,A,B是直线l外两点,在l上求作一点P,使PA+PB最小,其作法是()
A.连接BA并延长与l的交点为P
B.连接AB,并作线段A月的垂直平分线与l的交点为P
C.过点B作l的垂线,垂线与l的交点为P
D.过点A作l的垂线段AO,O是垂足,延长AO到A′,使A′O=AO,再连接 A′B,则A′B与L的交点为P
5.若一个三角形两边的垂直平分线的交点在第三边上,则这个三角形是()
A.锐角三角形 B.钝角三角形 C.直角三角形 D.不能确定
三、解答题
8.如图l-77所示,在△ABC中,∠BAC=110°,PM,QN分别垂直平分AB,AC,求∠PAQ的度数.
9.如图1-78所示,在△ABC中,∠A=90°,AC=8 cm,AB=6 cm,BC边的垂直平分线DE交BC于E,交AC 于D,求△ABD的周长.
10.如图l-79所示,已知AB=AC=20 cm,DE垂直平分AB,垂足为E,DE交AC 于点D,若△DBC的周长为35 cm,求BC的长.
11.如图1-80所示,△ABC中,AB,AC的垂直平分线分别交BC于点D,E,已知
△ADE的周长为12 cm,求BC的长.
12.如图1-81所示,A,B是公路l(l为东西走向)两旁的两个村庄,A村到公路l的距离AC=1 km,B村到公路l的距离BD=2 km,B村在A村的南偏东45°方向上.
(1)求A,B两村之间的距离;
(2)为方便村民出行,计划在公路边新建一个公共汽车站P,要求该站到两村的距离相等,请用尺规在图中作出点P的位置.(保留清晰的作图痕迹,并简要写明作法)
13.如图1-82所示,∠BAC=∠ABD,AC=BD,点O是AD,BC的交点,点E是AB的中点.试判断OE和AB的位置关系,并给出证明.。
