数学实验六
06实验六 空间图形的画法

图6-4
绘制二元函数图形也可用简捷绘制的ezsurf指令,它的使 用格式为: ezsurf(f(x,y),[a,b,u,v]) 即可绘制函数在区域[a,b]×[u,v]上的图形。当省略区域 时,默认区间是[-2 ,2 ]×[- 2 , 2 ]。例如输入: ezsurf('x*exp(-x^2-y^2)') 则输出如图6-5所示。
图6-12
【例7】可以证明:函数z=xy的图形是双曲抛物面。在区 域-2≤x≤2,-2≤y≤2上作出它的图形。
输入: x=-2:0.1:2; y=-2:0.1:2; [xx,yy]=meshgrid(x,y); zz=xx.*yy; surf(xx,yy,zz) 输出如图6-13所示。
图6-13
例如,画出曲面 z x y 的图形。输入: x=-2:0.1:2; y=-2:0.1:2; [x,y]=meshgrid(x,y); z=x.^2+y.^2; surf(x,y,z) z x 2 y 2,见图6-2。 得到曲面
2 2
图6-2
执行下面的程序: x=-2:0.015:2; y=-2:0.015:2; [x,y]=meshgrid(x,y); z=x.^2+y.^2; i=find(x.^2+y.^2>4); z(i)=NaN; surf(x,y,z) 同样得到曲面(见图6-3)。 由于自变量的取值范围不同,图形也不同。不过,后者比 较好地反映了旋转曲面的特点,因此是常用的方法。
图6-3
又如,参数方程: x 2sin cos , y 2sin sin , z 2cos 是以原 点为中心、2为半径的球面,其中 0 , 0 2 因此只要输入: t=0:0.1:pi; r=0:0.1:2*pi; [r,t]=meshgrid(r,t); x=2*sin(t).*cos(r); y=2*sin(t).*sin(r); z=2*cos(t); surf(x,y,z) 2 2 2 2 便作出了方程为 x y z 2 的球面(见图6-4)。
实验六 古典密码与破译

定义在 Z26上的方阵 A 模 26 可逆的充要条件是:
det(A) 不能被 2 和 13 整除
模 26 可逆
Z26 中具有模 26 倒数的整数及其模 26 倒数表2
a a-1 1 1 3 5 7 9 11 15 17 19 21 23 25 9 21 15 3 19 7 23 11 5 17 25
N O P Q R S T U V W X Y Z 14 15 16 17 18 19 20 21 22 23 24 25 0
Hill2 解密举例
① 将密文字母分组,通过查表列出每组字母对应的向量 ② 求出加密矩阵 A 的 模 26 逆矩阵
1 8 B 0 9
③ 用 B 左乘每组密文字母组成的向量,然后再反查字母
Hill2 加密举例
反查字母表值得每个向量对应的字母组为:
16 , 12
1 15 , , 12 20
20 20
PL
AL
OT
TT
HDSDSXX
Hill2 加密
K L M
PLALOTTT
A B C D E F G H I J
③ 令 = B mod(m) ,由 的分量反查字母表值表,
得到相应的明文字母
Hill2 解密举例
甲方收到乙方(己方)的一个密文信息,内容为: WKVACPEAOCIXGWIZUROQWAB ALOHDKCEAFCLWWCVLEMIMCC 按照甲方与乙方的约定,他们之间采用 Hill2密码,密钥 1 2 为 A ,字母表值见下表,问这段密文的原文 0 3 是什么? A 1 B 2 C 3 D 4 E 5 F 6 G 7 H 8 I 9 J K L M 10 11 12 13
数学实验完整
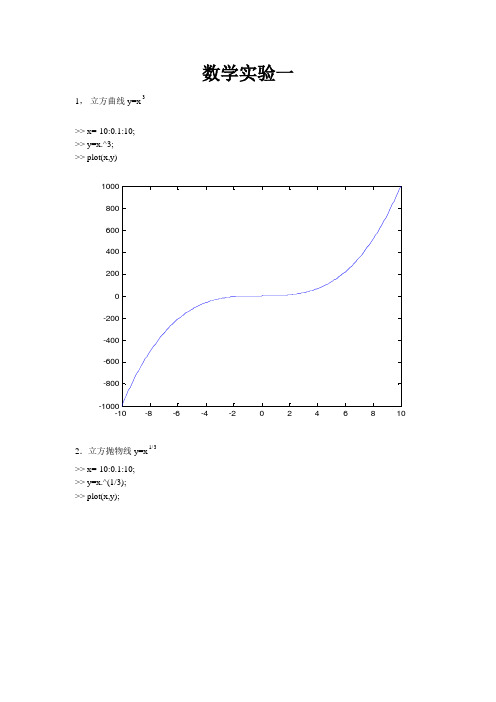
数学实验一1, 立方曲线y=x 3>> x=-10:0.1:10; >> y=x.^3; >> plot(x,y)-10-8-6-4-2246810-1000-800-600-400-200020040060080010002.立方抛物线y=x 1/3>> x=-10:0.1:10; >> y=x.^(1/3); >> plot(x,y);-10-8-6-4-2024681000.511.522.53,高斯曲线y=2x e以参数方程表示的曲线;>> x=-10:0.1:10; >> y=exp(-x.^2); >> plot(x,y);>>-10-8-6-4-224681000.10.20.30.40.50.60.70.80.91以参数方程表示的曲线: 4,奈尔抛物线 x=t 3y=t 2(y=x 2/3)>> x=-10:0.1:10; >> y=x.^(2/3); >> plot(x,y);-10-8-6-4-20246810-3-2-10123455,半立方抛物线 x=t 2y=t 3(y 2=x 3)>> x=-10:0.1:10; >> y=x.^(3/2); >> plot(x,y);-10-8-6-4-20246810-5051015202530356,笛卡尔曲线 x=3at 2) , y=3at 2/(1+t 2) (x 3+y 3-3axy=0)>> t=-10:0.1:10; >> a=8;>> x=3*a*t./(1+t.^2);y=3*a*t.^2./(1+t.^2); >> plot(x,y);-15-10-505101505101520257,蔓叶线 x=at 2/(1+t 2),y=at 3/(1+t 2) (y 2=x 3/(a-x)) t=-10:0.1:10; >> a=2;>> x=a*t.^2./(1+t.^2);y=a*t.^3./(1+t.^2); >> plot(x,y);00.20.40.60.81 1.2 1.4 1.6 1.82-20-15-10-5051015208,摆线 x=a(t-sint), y=b(1-cost) >> a=10; >> b=15; >> t=-10:0.1:10;>> x=a*(t-sin(t));y=a*(1-cos(t)); >> plot(x,y);-150-100-5050100150024681012141618209,内摆线(星形线) x=acos 3t, y=asin 3t (x 2/3+y2/3=a2/3)>> t=-10:0.1:10; >> a=5;>> x=a*(cos(t)).^3; y=a*(sin(t)).^3; >> plot(x,y);-5-4-3-2-101234510,圆的渐伸线(渐开线)x=a(cost+tsint) , y=a(sint- tcost )t=-10:0.1:10;>> a=5;>> x=a.*(cos(t)+t.*sin(t));y=a.*(sin(t)-t.*cos(t));>> plot(x,y);-40-30-20-1010203040-50-40-30-20-100102030405011,空间螺线 x=acost , y=bsint , z=ct 。
小学数学 六年级上 北师大数学实验班(六上)测试(一)

北师大数学实验班(六上)测试(一)学号:_______ 班级:_________ 姓名:_________ 成绩:_________一、直接写出得数。
(每题1分,共8分)3.14×3= 15×3.14= 8×3.14= 52×3.14=20×3.14= π×22= 72×π= 162=二、填空。
(每题2分,共26分)1、在同一个圆里,所有的直径都(),所有的半径都(),半径的长度是直径的()。
2、一个圆的半径是5厘米,它的直径是(),周长是(),面积是()。
3、用圆规画一个周长为31.4厘米的圆,两脚尖张开的距离是()厘米。
4、一个圆的半径扩大2倍,它的直径扩大()倍,周长扩大()倍,面积扩大()倍。
5、一座石英挂钟,它的分钟长8厘米,1小时分针尖端走过()厘米。
6、圆是轴对称图形,任何一条()都是圆的对称轴。
圆有()条对称轴。
三、判断。
(每题2分,共8分)1、同一个圆的直径都相等。
()2、半圆的周长等于整个圆周长的一半。
()3、π是一个无限不循环小数。
()4、半径是2厘米的圆,它的周长与面积相等。
()四、选择。
(每题2分,共6分)1、用12米长的绳子围成三种图形,其中面积最小的是()。
A、圆B、长方形C、正方形2、把一根长10米的铜丝,在一个圆盘上绕了3圈,还多0.58米,这个圆盘的半径是( )。
A 、0.5米B 、1米C 、1.5米3、大圆周长是小圆周长的4倍,小圆直径是大圆直径的( )。
A 、4倍B 、41 C 、81 D 、8倍 五、求下面各圆的周长和面积。
(每题6分,共12分)d=4.2分米 C=28.26米六、解决问题。
(每题10分,共40分)1、学校操场的跑道如下图所示,跑道两边是两个半圆,沿跑道跑一周的长度是多少米?2、育苗小学有一个圆形景点,它的直径是10米,景点中央有一个直径是5米的圆形喷水池,环绕水池的部分种植花草,种花草部分的面积是多少平方米?3、在一个周长是80厘米的正方形木板上,锯下一个最大的圆,这个圆的面积是多少平方厘米?4、计算下图阴影部分的面积。
数学实验六插值问题
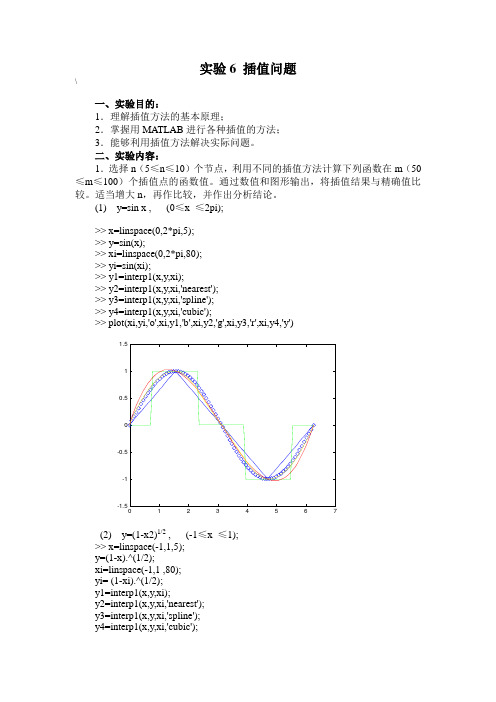
实验6 插值问题\一、实验目的:1.理解插值方法的基本原理;2.掌握用MATLAB进行各种插值的方法;3.能够利用插值方法解决实际问题。
二、实验内容:1.选择n(5≤n≤10)个节点,利用不同的插值方法计算下列函数在m(50≤m≤100)个插值点的函数值。
通过数值和图形输出,将插值结果与精确值比较。
适当增大n,再作比较,并作出分析结论。
(1) y=sin x , (0≤x ≤2pi);>> x=linspace(0,2*pi,5);>> y=sin(x);>> xi=linspace(0,2*pi,80);>> yi=sin(xi);>> y1=interp1(x,y,xi);>> y2=interp1(x,y,xi,'nearest');>> y3=interp1(x,y,xi,'spline');>> y4=interp1(x,y,xi,'cubic');>> plot(xi,yi,'o',xi,y1,'b',xi,y2,'g',xi,y3,'r',xi,y4,'y')(2) y=(1-x2)1/2 , (-1≤x ≤1);>> x=linspace(-1,1,5);y=(1-x).^(1/2);xi=linspace(-1,1 ,80);yi= (1-xi).^(1/2);y1=interp1(x,y,xi);y2=interp1(x,y,xi,'nearest');y3=interp1(x,y,xi,'spline');y4=interp1(x,y,xi,'cubic');>> plot(xi,yi,'o',xi,y1,'b',xi,y2,'g',xi,y3,'r',xi,y4,'y')(3) y=cos10x , (-2≤x ≤2);x=linspace(-2,2,5);y=cos(10*x);xi=linspace(-2,2,80);yi= cos(10*xi);y1=interp1(x,y,xi);y2=interp1(x,y,xi,'nearest');y3=interp1(x,y,xi,'spline');y4=interp1(x,y,xi,'cubic');plot(xi,yi,'o',xi,y1,'b',xi,y2,'g',xi,y3,'r',xi,y4,'y')(4)y=exp(-x2) , (-2≤x ≤2)x=linspace(-2,2,5);y=exp(-(x.^2));xi=linspace(-2,2,80);yi= exp(-(xi.^2));y1=interp1(x,y,xi);y2=interp1(x,y,xi,'nearest');y3=interp1(x,y,xi,'spline');y4=interp1(x,y,xi,'cubic');plot(xi,yi,'o',xi,y1,'b',xi,y2,'g',xi,y3,'r',xi,y4,'y')2.为了计算瑞士的国土面积,以由西向东方向为x轴,由南向北方向为y 轴,最西边界点到最东边界点在x轴上对应的区间为[0, 151],将此区间适当划分为若干段,在每个分点的y方向上测出南边界点y1和北边界点y2的坐标数据(精确值为41288km2)。
清华大学数学实验报告6

实验六非线性方程求解实验目的1. 掌握用matlab软件求解非线性方程和方程组的基本用法, 并对结果做初步分析.2. 练习用非线性方程和方程组建立实际问题的模型并进行求解.实验内容题目3(1)小张夫妇以按揭方式贷款买了1 套价值20 万元的房子,首付了5 万元,每月还款1000 元,15 年还清。
问贷款利率是多少?(2)某人欲贷款50 万元购房,他咨询了两家银行,第一家银行开出的条件是每月还4500 元,15 年还清;第二家银行开出的条件是每年还450000 元,20 年还清。
从利率方面看,哪家银行较优惠(简单地假设年利率=月利率×12)?建立模型:设房价为b,首付款为b0,银行按照月利率(复利)来计算,月利率为r,月付款(月末支付)为a,共需要支付的月数为n。
根据经济学中资金的时间价值概念,可以得到:房价在n个月之后的实际价值为:b(1+r)n按揭购房期间交的所有款项在第n个月末的实际价值为:b0(1+r)n+a(1+r)n−1+(1+r)n−2+⋯+1=b0(1+r)n+a×(1+r)n−1由于在第n个月末还清了贷款,因此上述两个时间价值相等,则得到下面的关系式,即为解答此问题的方程:b(1+r)n=b0(1+r)n+a×(1+r)n−1即:(b−b0)(1+r)n−a×(1+r)n−1=0(1)代入已知条件:b=200000,b0=50000,a=1000,n=180,利用MATLAB解此非线性方程,经过简单的估测之后,给定初始值为r0=0.001,得到结果为:r=0.0020812,即贷款月利率为0.20812%。
(2)I.第一家银行相应的已知条件为:b=500000,b0=0,a=4500,n=180,利用MATLAB计算,经过简单的估测之后,给定初始值为r0=0.005,得到结果为:r=0.0058508,即这家银行的贷款月利率为0.58508%。
人教版数学六年级下册实验报告
第()组
蹬一圈,自行车走()
实验报告(一)
第()组
蹬一圈,自行车走()
实验报告(一)
第()组
蹬一圈,自行车走()
实验报告(一)
第()组
蹬一圈,自行车走()
实验报告(一)
第()组
蹬一圈,自行车走(车走()
实验报告(一)
第()组
蹬一圈,自行车走()
实验报告
第()组
实验课题:蹬一圈,自行车能走多远?
1、车轮的直径是30CM。
2、前齿轮油()个齿,后齿轮有()个齿。
3、前齿轮的齿数×前齿轮转的圈数=后齿轮的齿数×()
根据以上规律得出:
4、前齿轮转一圈,后齿轮转()圈,后车轮转()圈。
5、结论:
蹬一圈自行车走的路程()×
6、蹬一圈自行车走()CM。
实验报告(二)
第()组
实验课题:蹬一圈,自行车能走多远?
1、车轮的直径是30CM。
2、前齿轮油()个齿,后齿轮有()个齿。
3、前齿轮的齿数×前齿轮转的圈数=后齿轮的齿数×()
根据以上规律得出:
4、前齿轮转一圈,后齿轮转()圈,后车轮转()圈。
5、结论:
蹬一圈自行车走的路程()×
6、蹬一圈自行车走()CM。
实验小学六年级数学(1)
安丘市实验小学六年级数学第一单元测试题班级:姓名:等级:书写:一、填空。
1、如果下降5米,记作-5米,那么上升4米记作()米;如果+2千克表示增加2千克,那么-3千克表示()。
2、二月份,妈妈在银行存入5000元,存折上应记作()元。
三月一日妈妈又取出1000元,存折上应记作()元。
3、+8.7读作(),-25读作()。
4、海平面的海拔高度记作0m,海拔高度为+450米,表示(),海拔高度为-102米,表示()。
5、如果把平均成绩记为0分,+9分表示比平均成绩(),-18分表示(),比平均成绩少2分,记作()。
6、数轴上所有的负数都在0的()边,所有正数都在0的()边。
7、在数轴上,从表示0的点出发,向右移动3个单位长度到A 点,A点表示的数是();从表示0的点出发向左移动6个单位长度到B点,B点表示的数是()。
8、比较大小。
-10○0.1 -0.3○0.02 -25○-52-99○3-7○-5 1.5○520○-2.5 -3○3二、判断对错。
1、零上12℃(+12℃)和零下12℃(-12℃)是两种相反意义的量。
()2、0是正数。
()3、数轴上左边的数比右边的数小。
()4、死海低于海平面400米,记作+400米。
()5、在8.2、-4、0、6、-27中,负数有3个。
()6、数轴是一条直线。
()7、在我们学的数中,既没有最大的数也没有最小的数。
()8、因为8大于6,所以-8大于-6。
()9、在0和-1之间没有负数。
()10、带有“-”的数一定是负数。
()三、选择正确答案的序号填在括号里。
1、低于正常水位0.16米记为-0.16,高于正常水位0.02米记作()。
A、+0.02B、-0.02C、+0.18D、-0.142、以明明家为起点,向东走为正,向西走为负。
如果明明从家走了+30米,又走了-30米,这时明明离家的距离是()米。
A、30B、-30C、60D、03、数轴上,-12在-18的()边。
A、左B、右C、北D、无法确定4、规定10吨记为0吨,11吨记为+1吨,则下列说法错误的是()。
实验小学六年级上册数学期末测试卷及答案
六年级数学期末测试卷同学们,一学期结束了,你一定有许多收获,快来挑战吧,只要认真审题,仔细答卷,就能取得好成绩哦!一、填空 (第9题2分,其余每空1分,共25分) 1、%40 3915.172 ⨯=⨯=⨯=÷)()()()( 2、一张半圆形纸片的半径为1分米,它的周长为( )分米,要剪一个这样的半圆形,至少需要一张面积为( )平方分米的长方形纸片。
3、六年级(3)班有男生24人,女生30人,女生人数是男生人数的( )%,女生人数比男生人数多( )%,男生人数比女生人数少( )%。
4、出勤率、出粉率、发芽率、合格率中,不可能达到100%的是( )。
5、盐占盐水的113,那么盐与水的质量比是( )。
6、工程队修一段路,4天修了全长的52,这时还有30米没修,这条路全长( )米。
7、合唱队有男生25人,女生20人。
男生人数是女生的( )倍,女生人数与男生人数的最简单的整数比是( ),女生人数占总人数的)()( 。
8、比80米多25%是( ),( )的51等于24的32。
9、丽丽面向北站立,向右转400后所面对的方向是( )偏( )( )0;丁丁面向西站立,向左转400后所面对的方向是( )。
10、如果要画一个周长是12.56厘米的圆,,圆规两脚之间的距离应该是( )厘米,这个圆的面积是( )平方厘米。
11、用109千克小麦可以磨出43千克面粉,每千克小麦可以磨面粉( )千克,要磨1千克面粉需要小麦( )千克。
12、小敏把一个数除以32错算为乘以32,得出结果6。
那么正确的计算结果应是( )。
13、)( =+++++641321161814121。
二、判断 (对的在括号里面画“√”,错的在括号里画“X")(共5分) 1、两根同样长的铁管,第一根用去了53米,第二根用去53,第二根用去的多。
( ) 2、假分数的倒数一定比这个假分数小。
( )3、小明和小军进行投篮练习,小明的命中率是65%,小军的命中率是70%,小军投中的次数多一些。
东明县刘楼镇实验学校六年级数学实践性作业
3.在设计、测量、整理等实践活动中感受数学与生活的密切联系,进一步提高
学习兴趣,发展自我反思能力。
设计方案
想一想,绘制家到学校的路线图前,要先做哪些方面的准备?我家到学校的 路线图中,需要收集哪些数据?如何收集这些数据?
绘制路线:
语言描述路线:
东明县刘楼镇实验学校六年级数学实践作业
活动内容 绘制家到学校的路线图 班级
姓名
1.通过“绘制家到学校的路线图”的实践操作活动,进一步理解并综合运用
图形位置、测量、数据收集等知识,积累“从头到尾思考问题的经验
活动目的
2.经历设计方案、动手实践、及时反思的活动过程,发展统筹规划和按方案操 作等综合实践能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验六1415100076陈田实验项目名称:优化实验时间:2016-5-27、2016-6—3实验地点:理学楼525实验目得:1、掌握Matlab优化工具箱得基本用法,利用优化工具包解线性规划与非线性规划得问题;对不同算法作初步分析、比较;2、练习实际问题得非线性最小二乘拟合.3、初步了解实际问题得线性规划与非线性规划得模型建立。
实验内容:1、教材205页习题2;function f=exam0702fun(x)f=exp(x(1))*(4*x(1)、^2+2*x(2)、^2+4*x(1)*x(2)+2*x(2)+1);endM文件:formatshortex0=[—1,1];’—--case1:bfgs-——'opt1=optimset('larges’,’off',’maxfunevals',1000);[x1,v1,exit1,out1]=fminunc('exam0702fun’,x0,opt1) pause'—-—case2:dfp--—'fopt=optimset(opt1,'hessupdate',’dfp');[x2,v2,exit2,out2]=fminunc('exam0702fun',x0,fopt)pause’——-case3:steep---'fopt=optimset(opt1,'hessupdate’,’steepdesc’);[x3,v3,exit3,out3]=fminunc('exam0702fun’,x0,fopt)pause'+++result ofsolutions +++’solutions=[x1;x2;x3];funvalues=[v1;v2;v3];iterations=[out1、funcCount;out2、funcCount;out3、fun cCount];[solutions,funvalues,iterations]运行结果:>〉c62ans=-—-case1:bfgs—--Local minimumfound、Optimizationpletedbecause the size of the gradient is less thanthe default valueof the optimality tolerance、〈stopp ingcriteria details>x1=5、0000e-01-1、0000e+00v1= 3、6609e—15exit1 = 1out1 = iterations:8funcCount:66stepsize: 6、3361e-07lssteplength: 1firstorderopt: 1、2284e-07algorithm:'quasi-newton'message:'Local minimum found、…'ans =-——case2:dfp—--Localminimum found、Optimization pleted because the sizeofthe gradient is less thanthe defaultvalue of the optimalitytolerance、<sto pping criteria details>x2= 5、0000e-01 -1、0000e+00v2 = 1、2447e—14exit2= 1out2 = iterations: 8funcCount: 51stepsize:3、7463e-06lssteplength: 1firstorderopt:5、8963e—07algorithm:'quasi—newton'message: 'Local minimumfound、…’ans=---case3:steep—--Local minimum possible、fminunc stoppedbecause the size of the current stepisless thanthe defaultvalue of thestep sizetolerance、〈st opping criteria details>x3= 5、0000e-01-1、0000e+00v3 = 9、0530e—12exit3 = 2out3= iterations:49funcCount: 306stepsize:1、1892e-06lssteplength: 1、0003e-01firstorderopt: 8、4759e-06algorithm: 'quasi—newton'message: ’Local minimumpossible、…'ans=+++result ofsolutions +++ans=5、0000e-01-1、0000e+003、6609e-156、6000e+015、0000e—01 -1、0000e+00 1、2447e—145、1000e+015、0000e-01-1、0000e+009、0530e—12 3、0600e+022、教材205页习题4,要求:实现非线性最小二乘拟合即可,对“用GN与LM两种方法求解、对y作一扰动后观察迭代收敛变慢得情况”不做;function y=F(x,t,c)y=x(1)+x(2)*exp(—x(4)*t)+x(3)*exp(-x(5)*t)-c;endM文件:x0=[、5 1、5 -1 、01、02];t=zeros(1,33);fori=1:33t(i)=10*(i-1);endc1=[、844、908 、932 、936 、925 、908 、881、850、818、784 、751 、718、685 、658 、628 、603 、580 、558 、538 、522、506 、490 、478 、467 、457 、448 、438 、431、424 、420、414、411 、406];c2=rand(1,33)/10—0、05;'--—case1:LM-—-’opt1=optimset('LargeScale','off','Maxfunevals',1000);[x11,norm11,res11]=lsqnonlin(’F’,x0,[],[],opt1,t,c1)'---case2:GM---'opt2=optimset(opt1,'Algorithm','Levenberg—Marquardt’);[x12,norm12,res12]=lsqnonlin(’F’,x0,[],[],opt2,t,c1)’—--case3:LM2--—’opt3=optimset(opt1,’Disp','iter’);[x21,norm21,res21]=lsqnonlin('F',x0,[],[],opt3,t,c2)'---case4:GM2—-—'opt4=optimset(opt2,'Disp’,’iter');[x22,norm22,res22]=lsqnonlin('F’,x0,[],[],opt4,t,c2)运行结果:〉> c64ans =——-case1:LM---x11=3、7541e—01 1、9358e+00 -1、4647e+00 1、2868e—02 2、2123e—02norm11=5、4649e-05ans =—-—case2:GM---x12 =3、7541e-011、9358e+00 —1、4647e+001、2868e-022、2123e-02norm12 =5、4649e-05ans =--—case3:LM2--—x21=—5、8167e+01 3、6217e-01 5、8127e+01 1、0049e-01 -3、6513e—06norm21=1、3721e-01ans=-——case4:GM2---x22 =-3、9056e+016、0942e+01-2、1883e+011、2573e-043、6102e-04norm22 =3、0733e-023、教材238页习题1;M文件:c=[1 -2 -1];A1=[-1 12;1 1 -1;1 2 0;0 1 1];A2=[0 1 —1];b1=[24 4 4];b2=[1];v1=[00 0];[x,f,exitflag,output,lag]=linprog(c,A1,b1,A2,b2,v1)lag、ineqlin运行结果:〉>c81Optimizationterminated、x =7、9996e-011、6000e+005、9999e-01f=-3、0000e+00exitflag =1output=iterations: 6algorithm:'interior-point—legacy'cgiterations:0message: ’Optimizationterminated、'constrviolation:2、6423e—14firstorderopt:2、4779e—13lag=ineqlin: [4x1double]eqlin:1、0000e+00upper:[3x1double]lower:[3x1double]>>lag、ineqlinans=1、0000e+001、1569e-141、7455e-131、8636e-14由运行结果可知所求最大值为—3、0000e+00,起作用约束为第一个约束4、教材239页习题5。
M文件:c1=[-20 -30];A=[1 2;5 4];b=[20 70];v1=[00];[x1,f1,exitflag1,output1,lag1]=linprog(c1,A,b,[],[],v1)y1=lag1、ineqlin运行结果:〉> c85Optimizationterminated、x1 =1、0000e+015、0000e+00f1=-3、5000e+02exitflag1 =1output1 =iterations: 5algorithm:’interior-point—legacy'cgiterations:0message:’Optimization terminated、'constrviolation:0firstorderopt:6、4731e—11lag1=ineqlin: [2x1 double]eqlin: [0x1 double]upper:[2x1double]lower: [2x1 double]y1=1、1667e+011、6667e+00由运行结果可知以甲乙分别20、30元出售时安排甲乙分别生产10、5件可使收入最大,当A、B增加1公斤时收入分别增加11、667、1、6667,考虑成本后由11、667-6=5、667,1、6667-2=-1、6667<0可知每进1公斤买A原料可增加利润5、667元,买B原料则会减少利润-1、667元,故应全部买进A原料。
