吉林省东北师范大学附属中学2019_2020学年高二数学下学期疫情延期开学考试(4月)试题理

合集下载

2019-2020学年吉林东北师范大学附属中学高一下学期期末数学试卷(1)

又∵直线过点
与线段有交点，
∴直线的倾斜角的取值范围为
，
故答案为
．
15 、【答案】【解析】 ∵所求直线方程与直线
∴设方程为
，
∵直线过点
，
∴
，
∴
，
∴所求直线方程为
，
故答案为：
．
垂直，
16 、【答案】 ;
【解析】由题意用这四个三角形作为一个三棱锥的四个面，构成如图所示的四面体
中
平面
，
，
，
，
，
，其
，
，
．
对称圆的方程．
21、在四棱锥，
中，底面
是边长为的菱形，
，、分别为、的中点．
，
平面
(1) 求证： (2) 求二面角
平面
．的大小．
第6页，共22页
学而思网校
22、已知点
，
，，分别为线段，上的动点，且满足
．
(1) 若
，求直线的方程．
(2) 证明：
的外接圆恒过定点（异于原点）．
且与直线
垂直，则直线的方程为
．
16、如图，正方形
的边长为，点，分别在边，上，且
．将此
正方形沿，，切割得到四个三角形，现用这四个三角形作为一个三棱锥的四个面，
则该三棱锥的内切球的体积为
，外接球的表面积为
．
三、解答题（本大题共 6 小题，共 56 分）
17、已知命题：关于的不等式的定义域为．如果
，
解得交点坐标
，
又∵直线过点，
显然斜率存在，
∴设直线为
，

2019-2020学年吉林省东北师范大学附属中学高二下学期疫情延期开学考试(4月)英语试题 Word+听力

切磋砥砺足千日紫电龙光助鹰扬东北师大附中2018 级高二年级下学期阶段验收（英语）学科试题注意：本试卷共 120 分，考试时间 90 分钟。

第I 卷选择题部分（满分72 分）第一部分听力（共两节，满分20 分）第一节（共5 小题；每小题1 分，满分5 分）听下面 5 段对话。

每段对话后有一个小题，从题中所给的 A、B、C 三个选项中选出最佳选项。

听完每段对话后，你都有10 秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1.What is Lucy doing?A.Watching TV.B. Doing her shopping.C. Attending a concert.2.Where is the woman’s phone?A.On the table.B. On the sofa.C. On the bed.3.Why is the man talking to the woman?A.To invite her to a party.B.To make a travel plan.C.To ask about her holiday.4.What is the probable relationship between the speakers?A.Interviewer and interviewee.B.Salesperson and customer.C.Boss and employee.5.In which season did the woman get to Prague?A.In summer.B. In autumn.C. In winter.第二节（共15 小题；每小题1 分，满分15 分）听下面 5 段对话或独白。

毎段对话或独白后有几个小题，从题中所给的 A、B、C 三个选项中选出最佳选项。

听每段对话或独白前，你将有时间阅读各个小题，每小题 5 秒钟；听完后，各小题将给出 5 秒钟的作答时间。

吉林省东北师范大学附属中学2019-2020学年高二下学期疫情延期开学考试(4月)语文试题 Word版含答案

切磋砥砺足千日紫电龙光助鹰扬东北师大附中2018级高二年级下学期阶段验收（语文）学科试题注意：本试卷共120分，考试时间90分钟。

一、论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成1～3题。

在当今时代，文学发展面临诸多不利或有利条件。

就不利条件来说，在世界范围内，文学在社会生活中的重要性已大大降低。

不管我们在感情上是否愿意接受，文学的日趋边缘化都是一个不争的事实。

造成这一状况的原因极为复杂。

随着科技的进步和社会的发展，随着社会分工的细密化和资讯的日益发达，原先属于文学的天然权利正在逐步丧失。

从文学的教育功能来看，社会教化的责任主要由小学、中学以及高等院校来承担；从文学描述、反映社会生活的功能来看，现代媒体早已取代文学，成为无远弗届、无孔不入的信息终端；而从娱乐功能方面来说，文学也已经有了一个更为强大的对手，那就是当今社会形形色色的娱乐和文化工业体系。

举例来说，在20世纪五六十年代，读小说还是日常生活中首屈一指的文化娱乐和消遣方式，而在今天，我们的业余时间大多为看电视、旅游、玩电子游戏、上互联网等娱乐方式所占据。

虽然文学不像过去那么重要，但我们无需为此感到担忧和悲观。

因为在人类发展的历史长河中，文学从来都是一项既非重要亦非不重要的事业。

孔子说“行有余力，则以学文”，表达的也是这个意思。

我们之所以会对文学在往昔的辉煌念念不忘，完全是因为文学黄金时代的出现。

这里所说的“黄金时代”，指的是从18世纪中期到20世纪中期差不多两百年的文学发展时期。

在这个时间段中，由于现代小说的兴起，文学的声望和影响力都达到了前所未有的顶峰。

然而，这个黄金时代在文学整个漫长的发展过程中，只不过是一个特例。

也许会有人问，这个黄金时代怎么会突然出现，又很快消失了呢？要回答这个问题并不容易。

按照伊格尔顿在《英国文学的起源》中的说法，文学之所以会忽然变得重要，首先是源于西方宗教的衰落，其次是因为资本主义的发展造成了人的异化和情感分裂。

吉林省东北师范大学附属中学2020-2021学年高一下学期期末考试数学试题 Word版含答案

东北师大附中2020——2021学年下学期期末考试高一年级数学科试卷命题人：高一数学学科组本试卷共3页，22小题，满分120分．考试用时120分钟．注意事项：1．答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在条形码粘贴区．2．选择题必须使用2B 铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔记清楚． 3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效．4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑．5．保持卡面清洁，不要折叠、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀．一、单项选择题：本题共8小题，每小题4分，共32分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．1．已知附属z 满足)2i z =，则z =（）A ．122i + B iC ．122i - D i2．树人中学为了庆祝中国共产党建党100周年举办党史知识竞赛，在十二进六的半决赛中，12名参赛同学成绩各不相同，小明同学已经知道了自己的成绩，为了判断自己是否能进入决赛，他还需要知道12名同学成绩的（） A ．平均数B ．中位数C ．众数D ．方差3．在ABC △中，角A ，B ，C 所对的边分别是a ，b ，c ，若3a =，c =6B π=，则b =（）A ．B ．C D4．向量a ，b ，c 在正方形网格中的位置如图所示，若向量c a b λ=+，则实数λ=（）A ．2-B ．1-C ．1D ．25．设平面α与平面β相交于直线m ，直线a 在平面α内，直线b 在平面β内，且b m ⊥，则“αβ⊥”是“a b ⊥”的（） A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件6．暑假期间，甲同学外出旅游的概率是23，乙同学外出旅游的概率是34，假定甲乙两人的行动互相之间没有影响，则暑假期间甲、乙两位同学恰有一人外出旅游的概率是（）A ．16B ．14C ．512D ．127．在长方体1111ABCD A B C D -中，1AB BC ==，1AA =则异面直线1AD 与1DB 所成角的余弦值为（）A ．15B C D 8．设点G 为ABC △的重心，过G 作一直线MN 分别交边AB ，AC 于点M ，N ，若AM xAB =，AN y AC =，则4x y +的最小值是（）A ．2B ．3C ．103D ．92二、多项选择题：本题共4小题，每小题4分，共16分．在每小题给出的选项中，有多项符合题目要求，全部选对的得4分，部分选对的得2分，有选错的得0分． 9．下列命题是真命题的是（）A ．两两相交且不过同一点的三条直线必在同一平面内B ．过空间中任意三点有且只有一个平面C ．若空间两条直线不相交，则这两条直线平行D ．若直线l ⊂平面α，直线m ⊥平面α，则m l ⊥10．抛掷两枚质地均匀的骰子（标记为Ⅰ号和Ⅱ号），观察两枚骰子分别可能出现的基本结果：记A =“Ⅰ号骰子出现的点数为1”；B =“Ⅱ号骰子出现的点数为2”；C =“两个点数之和为8”；D =“两个点数之和为7”，则（） A ．A 与B 相互独立B ．A 与D 相互独立C ．B 与C 相互独立D ．C 与D 相互独立11．在ABC △中，角A ，B ，C 所对的边分别为a ，b ，c ，且::4:5:6a b c =，则下列结论正确的是（） A ．sin :sin :sin 4:5:6A B C = B ．ABC △是钝角三角形C ．ABC △的最大内角是最小内角的2倍D ．若6c =，则ABC △ 12．如图，四棱锥P ABCD -的底部为矩形，PD ⊥平面ABCD ，1AD =，2PD AB ==，点E 是PB 的中点，过A ，D ，E 三点的平面α与平面PBC 的交线为l ，则（）A ．//l 平面PADB ．//AE 平面PCDC ．直线PA 与lD ．平面α截四棱锥P ABCD -所得的上，下两部分几何体的体积之比为35三、填空题：本题共4小题，每题4分，共16分．13．如图，M 是四面体OABC 的棱BC 的中点，点N 在线段OM 上，点P 在线段AN 上，且12MN ON =，34AP AN =，用向量OA ，OB ，OC 表示OP ，则OP =_______．14．某车间12名工人一天生产某产品（单位：kg ）的数量分别是13，13.5，13.6，13.8，14，14.6，14.8，15，15.2，15.4，15.7，15.8，则所给数据的第75百分位数是_______．15．已知动点P 在棱长为1的正方体1111ABCD A B C D -的表面上运动，且(0PA r r =<<，记点P 的轨迹长度为()f r ，则()1f f+=______．16．在锐角ABC △中，角A ，B ，C 所对边分别为a ，b ，c ，若a =3A π=,则223b c bc ++的取值范围是______．17．（本题满分8分）已知()1,0a =，()2,1b =．（1）当k 为何值时，ka b -与2a b +垂直？（2）若23AB a b =+，BC a mb =+，且A ，B ，C 三点共线，求m 的值．18．（本题满分8分）2021年起，部分省实行“3+1+2”高考新模式，为让学生适应新高考赋分模式，某校在一次模拟考试中，使用赋分制对选考化学的学生的化学成绩进行赋分，赋分的方案如下：先按照学生的原始分数从高到低排位，按比例划分A 、B 、C 、D 、E 共五个等级，然后在相应的区间内，利用转换公式进行赋分．等级排名占比与赋分区间如下表：现从全年级选考化学的学生中随机抽取100名学生的原始成绩（未赋分）进行分析，其频率分布表为：（1）求表中a 的值；（2）用样本估计总体的方法，估计该校本次化学成绩原始不少于多少分才能达到赋分后的C 等级以上（含C 等级）？（结果保留整数）（3）若采用样本量比例分配的分层随机抽样，从原始成绩在[)40,50与[)50,60内学生中抽取5人，查看他们的答题情况来分析知识点上缺漏，再从中选取2人进行调查分析，求这2人中恰好有1人原始成绩在[)40,50内的概率．19．（本题满分10分）在四棱锥P ABCD -中，底面ABCD 是边长为2的菱形，60BAD ∠=︒，若PA PD ==cos 10PAB ∠=．（1）证明：PAD ABCD ⊥平面平面；（2）求二面角B PD A --的正切值．20（本题满分10分）树人中学为了了解A ，B 两个校区高一年级学生期中考试的物理成绩（百分制），从A ，B 两个校区各随机抽取了100名学生的物理成绩，将收集到的数据按照[)0,20，[)20,40，[)40,60，[)60,80，[]80,100分组，绘制成成绩频率分布直方图如图：（1）从A 校区全体高一学生中随机抽取一名，估计这名学生的成绩不低于60分的概率；（2）如果把频率视为概率，从A 校区全体高一学生中随机选取一名，从B 校区全体高一学生中随机选取两名，求这三名学生至少有一名学生的成绩不低于80分的概率；（3）根据频率分布直方图，用样本估计总体的方法，试比较A ，B 两个校区的物理成绩，写出两条统计结论，并说明理由．21（本题满分10分）如图，正三棱柱111ABC A B C -的底面边长为2AB 的截面与上底面交于PQ ，且点P 是棱11A C 的中点，点Q 在棱11B C 上．（1）试在棱AC 上找一点D ，使得//QD 平面11ABB A ，并加以证明；（2）求四棱锥C ABQP -的体积．22．（本题满分10分）在ABC △中，角A ，B ，C 所对的边分别为a ，b ，c ，且111tan tan tan B C A+=．（1）求cos A 的最小值；（2）记ABC △的面积为S ，点P 是ABC △内一点，且PAB PBC PCA θ∠=∠=∠= ,证明：①2224tan SA b c a =+-；②tan 2tan A θ=．东北师大附中2020——2021学年下学期期末考试高一数学参考答案及评分标准选择题 1．A 2．B 3．C 4．D 5．A 6．C 7．C 8．B9．AD10．AB11．ACD12．ACD填空题 13．111444OA OB OC ++ 14．15.3 15．3π 16．(]11,15 解答题17．解（1）()()()1,02,12,1ka b k k -=-=--，()()()21,022,15,2a b +=+=．因为ka b -与2a b +垂直，所以()()52120k -+-⨯=，即51020k --=，得125k =．（2）()()()2321,032,18,3AB a b =+=+=，()()()1,02,121,BC a mb m m m =+=+=+．因为A ，B ，C 三点共线，所以//AB BC ，所以()83210m m -+=，即230m -=，所以32m =． 18．解（1）∵0.100.150.150.250.051a +++++=，∴0.30a =．（2）由已知等级达到C 级及以上所占排名等级占比为15%35%35%85%++= 设原始分数不少于x 分可达到赋分后的C 级及以上，易知5060x << 所以，0.150.10501053.330.250.10x -=+⨯≈-所以估计该校本次化学成绩原始分不少于54分才能达到赋分后的C 等级以上（含C 等级）（3）设A =“抽取2人中恰好有1人原始成绩在[)50,60内”由题设可知，原始得分在[)40,50和(]50,60内频率分别为0.10和0.15，则抽取的5人中，得分在[)40,50内的有2人，得分在[)50,60内的有3人．记得分在[)40,50内2位同学为a ，b ，得分在[)50,60的三位同学位B ，C ，D ．则从5人中任取2人，样本空间为()()()()()()()()()(){}=,,,,,,,,,,,,,,,,,,,a b a B a C a D b B b C b D B C B D C D Ω，共包含10个样本点()()()()()(){},,,,,,,,,,,M a B a C a D b B b C b D =，共包含6个样本点．所以，()63105P M == 故这2个人中恰好有1人原始成绩在[)40,50内的概率35．19．（1）证明：取AD 中点O ，连结PO ，BO ，BD ，在PAD △中，PA PD ==2AD =，则PO AD ⊥，2PO ===．在菱形ABCD 中，60BAD ∠=︒，2AB AD ==，∴2AB AD BD ===，∴BO AD ⊥，且BO ===PAB △中，cos PAB ∠=，∴2222cos 54227PB PA AB PA AB PAB =+-⋅⋅∠=+-=．在POB △中，222347OB PO PB +=+==，∴PO BO ⊥，且AD BO O ⋂= ∴PO ⊥平面ABCD ．又PO ⊂平面PAD ∴平面PAD ⊥平面ABCD ．（2）由（1）知平面PAD ⊥平面ABCD ，且平面PAD ⋂平面ABCD AD =，且BO AD ⊥， ∴BO ⊥平面ABCD ，作OE PD ⊥于E ，由三垂线定理，得BE PD ⊥． ∴BEO ∠就是二面角B PD A --的平面角，在Rt POD △中，OE PD ⊥，有PD OE PO OD ⋅=⋅21OE =⨯，∴OE =在Rt BOE △中，tan OB BEO OE ∠===∴二面角B PD A --．20．解：（1）从A 校区抽取的100名学生中随机选取一名，这名学生的成绩不低于60分的频率为()0.0240.010200.68+⨯=，利用频率估计概率可得这名学生的成绩不低于60分的概率为0.68；（2）由概率分布图可得A 校区随机选取一名学生，物理成绩不低于80分的概率约为0.010200.20⨯=，B 校区随机选取一名学生，物理成绩不低于80分的概率约为0.005200.10⨯=，则这三名学生物理成绩都低于80分的概率约为0.800.900.900.648⨯⨯=，这三名学生中至少有一名学生成绩都不低于80分的概率为10.6480.352-=．（3）①从众数看，A ，B 两个校区的众数都是70，所以A ，B 两个校区的众数相等． ②从中位数看，A 校区物理成绩的中位数高于B 校区物理成绩的中位数A 校区的中位数是0.500.32602067.50.800.32-+⨯=-B 校区的中位数是0.500.48602061.00.900.48-+⨯=- 因为67.561.0>，所以，A 校区物理成绩的中位数高于B 校区物理成绩的中位数．③从平均数看，A 校区物理成绩的平均数高于B 校区物理成绩的平均数A 校区成绩平均数为1100.00120300.00320500.01220700.02420900.0102065.6μ=⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯=， B 校区成绩平均数为，2100.00120300.00420500.01920700.02120900.0052060.0μ=⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯=，12u u >，所以，A 校区物理成绩的平均数高于B 校区物理成绩的平均数．④从方差看，B 校区物理成绩比A 校区物理成绩更集中．A 校区成绩方差为：()()()2222=1065.60.023065.60.065065.60.24AS -⨯+-⨯+-⨯+ ()()227065.60.489065.60.20324.64-⨯+-⨯=B 校区成绩方差为：()()()()()22222210600.0230600.0850600.3870600.4290600.10292B S =-⨯+-⨯+-⨯+-⨯+-⨯=因为22A B S S >，所以B 校区物理成绩比A 校区物理成绩更集中． 21．（1）证法1：（1）点D 为棱AC 的中点，证明如下：取AB 的中点M ，连接DM ，1B M ．∵11//AB A B ，AB ⊂平面ABQP ，11A B ⊄平面ABQP ，∴11//A B 平面ABQP ，∵11A B ⊂平面111A B C ，平面ABQP ⋂平面111A B C PQ =，∴11//PQ A B ．又P 是棱11A C 的中点，∴Q 是棱11B C 的中点，∴112QB BC ∥， ∵D ，M 分别为棱AC ，AB 的中点，∴12DM BC ∥，∴1QB DM ∥， ∴四边形1DMB Q 是平行四边形，∴1//QD B M ，∵1B M ⊂平面11ABB A ，OD ⊄平面11ABB A ，∴//QD 平面11ABB A ．证法2：D 为AC 的中点时，//QD 平面11ABB A ．证明如下：∵//AB 平面111A B C ，AB ⊂平面ABQP ，平面ABQP ⋂平面111A B C PQ =， ∴//PQ AB ，PQ ⊄平面11ABB A ，AB ⊂平面11ABB A ，所以//PQ 平面11ABB A ，又∵D 为AC 的中点，P 为11A C 的中点，∴1PDAA 是平行四边形，∴1//PD AA ，又∵PD ⊄平面11ABB A ，1AA ⊂平面11ABB A ，∴//PD 面11ABB A ，又∵PD 与PQ 在平面PDQ 内相交，∴面//PDQ 面11ABB A ，又∵QD ⊂面PDQ ，∴//DQ 平面11ABB A ．（2）解法一：连接BP ，四棱锥C ABQP -可视为三棱锥C BPQ -和C ABP -组合而成，三棱锥C ABP-可视为P ABC -，底面积24ABC S a ==△2，设1C BAP V V -=，体积为111322V ==．三棱锥C BPQ -与C ABP -等高，体积比为底面积之比，设2C BPQ V V -=，则21:::1:2BPQ BAP V V S S PQ AB ===△△，故211124V V ==，因此，1234C ABPQ V V V -=+=，即为所求．解法二：分别取AB 和11A B 的中点M ，N ，连接MN ，CM ，连接1C N 交PQ 于点G ，连接MG ，CG ． ∵ABC △和111A B C △是正三角形，且M ，N 分别是AB 和11A B 的中点， ∴CM AB ⊥，且1CM C N ∥，则C ，M ，N ，1C 四点共面． ∵1CC ⊥平面ABC ，AB ⊂平面ABC ，∴1CC AB ⊥，又CM ⊂平面1CMNC ，1CC ⊂平面1CMNC ，1CM CC C ⋂=，∴AB ⊥平面1CMNC ， ∵AB ⊂平面ABQP ，∴平面ABQP ⊥平面1CMNC ．在矩形1CMNC 中，1MN CC ==，1CN CM AB ===∴11C G NG CC MN ===，∴145C GC NGM ∠=∠=︒，且1CG ==， ∴90CGM ∠=︒，即CG MG ⊥．又平面ABQP ⊥平面1CMNC ，平面ABQP ⋂平面1CMNC MG =，CG ⊂平面1CMNC ，∴CG ⊥平面ABQP ．在等腰梯形ABQP 中，11112PQ A B ==，2AB =，BQ AP ===，∴等腰梯形ABQP 的高h ==∴四棱锥C ABQP -的体积()111332ABQP V CG S CG PQ AB h =⋅=⨯+⨯梯形()11312324=+=．22．解：（1）因为111tan tan tan B C A +=，所以cos cos cos sin sin sin B C AB C A+=，所以2cos sin sin cos sin cos sin sin sin sin sin B C B C AA ABC B C+==，由正弦定理可得2cos a A bc =，而由余弦定理得2222cos 2b c a a A bc bc+-==，所以2223a b c =+．因为22222223cos 233b c b c b c A bc bc ++-+==≥，当且仅当b c =时，等号成立，所以cos A 的最小值为23．（2）证明：设PA x =，PB y =，PC z =，PAB △，PBC △，PCA △的面积分别为1S ，2S ，3S ， ①因为222cos 2b c a A bc +-=，所以2222cos bc A b c a =+-，而1sin 2S bc A =，所以222sin 2sin 4tan cos 2cos A bc A S A A bc A b c a ===+-． ②由（1）中可得2223a b c =+，所以222242tan S S A b c a a==+-，在PAB △，PBC △，PCA △中，同理可得：312222222222444tan S S S c x y a y z b z x θ===+-+-+-，所以()22214tan S c x y θ=+-，()22224tan S a y z θ=+-，()22234tan S b z x θ=+-，所以()()222212344tan 4tan S S S S a b c a θθ=++=++=，即2tan S a θ=，所以tan 2tan A θ=．。

高考化学化水溶液中的离子平衡的综合热点考点难点含答案解析

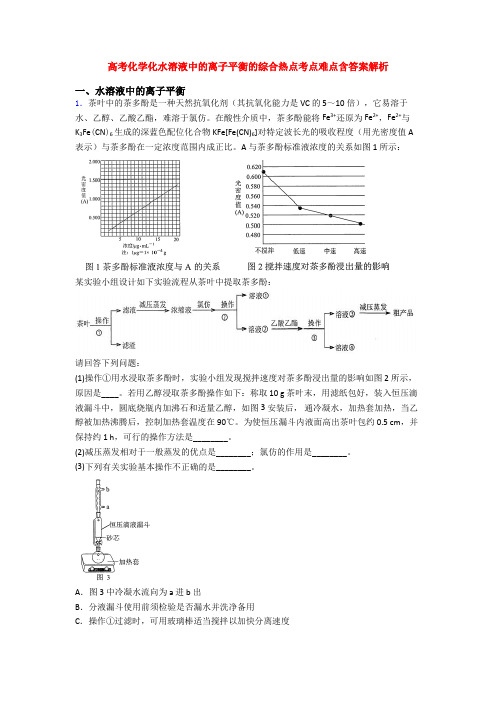
高考化学化水溶液中的离子平衡的综合热点考点难点含答案解析一、水溶液中的离子平衡1．茶叶中的茶多酚是一种天然抗氧化剂（其抗氧化能力是 VC 的 5～10 倍），它易溶于水、乙醇、乙酸乙酯，难溶于氯仿。

在酸性介质中，茶多酚能将 Fe3+还原为 Fe2+，Fe2+与K3Fe(CN)6生成的深蓝色配位化合物 KFe[Fe(CN)6]对特定波长光的吸收程度（用光密度值 A 表示）与茶多酚在一定浓度范围内成正比。

A 与茶多酚标准液浓度的关系如图 1 所示：某实验小组设计如下实验流程从茶叶中提取茶多酚：请回答下列问题：(1)操作①用水浸取茶多酚时，实验小组发现搅拌速度对茶多酚浸出量的影响如图 2 所示，原因是____。

若用乙醇浸取茶多酚操作如下：称取 10 g 茶叶末，用滤纸包好，装入恒压滴液漏斗中，圆底烧瓶内加沸石和适量乙醇，如图 3 安装后，通冷凝水，加热套加热，当乙醇被加热沸腾后，控制加热套温度在 90℃。

为使恒压漏斗内液面高出茶叶包约 0.5 cm，并保持约 1 h，可行的操作方法是________。

(2)减压蒸发相对于一般蒸发的优点是________；氯仿的作用是________。

(3)下列有关实验基本操作不正确的是________。

A．图 3 中冷凝水流向为 a 进 b 出B．分液漏斗使用前须检验是否漏水并洗净备用C．操作①过滤时，可用玻璃棒适当搅拌以加快分离速度D．萃取过程中，经振摇并放气后，将分液漏斗置于铁圈上立即分液(4)称取 1.25 g 粗产品，用蒸馏水溶解并定容至 1000 mL，移取该溶液 1.00 mL，加过量 Fe3+和 K3Fe(CN)6酸性溶液，用蒸馏水定容至 100 mL 后，测得溶液光密度值 A=0.800，则产品的纯度是_____ （以质量分数表示）。

【来源】吉林省东北师范大学附属中学2019-2020学年高二下学期疫情延期开学考试（4月)化学试题【答案】茶多酚易被氧气氧化，搅拌速度越快，茶多酚氧化速度越快，浸出率越低关闭活塞，当漏斗内液面高出茶叶包约0.5cm时，调节活塞使乙醇冷凝速度与漏斗放液速度一致降低蒸发温度防止产物氧化或分解萃取（或除杂） CD 96%【解析】【分析】茶叶用水浸泡时，茶多酚、氨基酸、茶碱等溶解在水中，过滤后，去除滤渣，得到的滤液减压蒸发，可降低蒸发温度，防止氧化反应的发生；往浓缩液中加入氯仿、分液，可得含氯仿的有机溶液①，水溶液②中含有茶多酚，用乙酸乙酯萃取、分液，可得茶多酚的乙酸乙酯溶液，然后减压蒸发，即可获得茶多酚粗产品。

吉林省长春市东北师范大学附属中学2021-2022学年高二上学期期末数学试题

10．某工厂加工一种零件，有两种不同的工艺选择，用这两种工艺加工一个零件所需时间 t
（单位：h）均近似服从正态分布，用工艺 1 加工一个零件所用时间 X ~ N
1
,
2 1
；用工艺
2 加工一个零件所用时间Y ~ N
2
,
2 2
，X，Y 的概率分布密度曲线如图，则（
）
试卷第 2页，共 5页
A．
1
13．某 n 重伯努利试验中，事件 A 发生的概率为 p，事件 A 发生的次数记为 X， E X 2 ，
D X 8 ，则 p ______．
5 14．如图，用四种不同的颜色分别给 A，B，C，D 四个区域涂色，相邻区域必须涂不同颜
试卷第 3页，共 5页
色，若允许同一种颜色多次使用，则不同的涂色方法的种数为______（用数字作答）
）
A．24 种
B．6 种
C．4 种
D．12 种
3．在空间直角坐标系中，a
2 x 4, x2 , 4
，b
1,
4,1
，若
a
∥
b
，则
x
的值为（
）
A．3
B．6
C．5
D．4
4．若 C160 C1x0 ，则 x 的值为（
）
A．4
B．6
C．4 或 6
5．已知随机变量 X 的分布列如表所示，则 P X 2 （
时， PQ 24 ． 7
(1)求椭圆 C 的标准方程；
(2)是否存在定直线 l2 : x t ，使得直线 AP 、 AQ 分别与 l2 相交于 M 、 N 两点，且点 B 总在
以线段 MN 为直径的圆上，若存在，求出所有满足条件的直线 l2 的方程；若不存在，请说明理由．

吉林省长春市东北师范大学附属中学2022-2023学年高二下学期期末数学试题(教师版)

2022-2023学年东北师大附中（高二）年级（数学）科试卷下学期期末考试第I 卷（选择题）一、单项选择题：本大题共8小题，每小题4分，共32分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知某质点运动的位移y （单位；cm ）与时间t （单位；s ）之间的关系为()()ln 21y t t =+，则该质点在2s =t 时的瞬时速度为（）A.15B.25C.2D.4【答案】B 【解析】【分析】对()()ln 21y t t =+求导得()221y t t '=+，从而可求质点在2s =t 时的瞬时速度()2y '.【详解】因为()()ln 21y t t =+，所以()221y t t '=+，所以该质点在2s =t 时的瞬时速度为()2222125y '==⨯+.故选：B.2.某中学课外活动小组为了研究经济走势，根据该市1999-2021年的GDP （国内生产总值）数据绘制出下面的散点图：该小组选择了如下2个模型来拟合GDP 值y 随年份x 的变化情况，模型一：(0,0)y kx b k x =+>>；模型二：e (0,0)x y k b k x =+>>，下列说法正确的是（）A.变量y 与x 负相关B.根据散点图的特征，模型一能更好地拟合GDP 值随年份的变化情况C.若选择模型二，e x y k b =+的图象一定经过点()x yD.当13x =时，通过模型计算得GDP 值为70，实际GDP 的值为71，则残差为1【答案】D 【解析】【分析】对于AB ，由散点图的变化趋势分析判断，对于C ，由线性回归方程的性判断，对于D ，结合残差的定义判断.【详解】对于A ，由散点图可知y 随年份x 的增大而增大，所以变量y 与x 正相关，所以A 错误，对于B ，由散点图可知变量y 与x 的变化趋向于一条曲线，所以模型二能更好地拟合GDP 值随年份的变化情况，所以B 错误，对于C ，若选择模型二：e (0,0)x y k b k x =+>>，令e x t =，则y kt b =+的图象经过点(),t y ，所以C 错误，对于D ，当13x =时，通过模型计算得GDP 值为70，实际GDP 的值为71，则残差为71701-=，所以D 正确，故选：D 3.函数21()ln 2f x x x =-的减区间为（）A.(1,1)-B.(,1)-∞ C.(0,1)D.(0,)+∞【答案】C 【解析】【分析】对函数求导，然后通分，进而令导函数小于0，最后求得单调递减区间.【详解】函数()21ln 2f x x x =-的定义域为()0,∞+，求导得()211x f x x x x ='-=-，令()210x f x x-'=<，0x >，01x ∴<<，因此函数()21ln 2f x x x =-的减区间为()0,1.故选：C.4.已知随机变量X 的分布列为X 012P131313设23Y X =+，则()D Y 等于（）A.83B.53C.43D.173【答案】A 【解析】【分析】根据分布列求出()E X ，()D X ，再根据条件得()()4D Y D x =，计算答案即可.【详解】由X 的分布列得()1110121333E X =⨯+⨯+⨯=，()()()()22211120111213333D X =-⨯+-⨯+-⨯=，因为23Y X =+，则()()843D Y D X ==.故选：A.5.某教育局为振兴乡村教育，将5名教师安排到3所乡村学校支教，若每名教师仅去一所学校，每所学校至少安排1名教师，则不同的安排情况有（）A.300种B.210种C.180种D.150种【答案】D 【解析】【分析】根据部分均匀分组分配求解即可.【详解】由于每所学校至少安排1名教师，则不同的安排情况有2233535322C C C A 150A ⎛⎫+= ⎪⎝⎭种.故选：D .6.已知数列{}n a ，{}n b ，其中11a =，且n a ，1n a +是方程220nn x b x -+=的实数根，则10b 等于（）A.24B.32C.48D.64【答案】D 【解析】【分析】根据题意，得到1n n n a a b ++=，12nn n a a +=，求得22a =，推出112n n a a +-=，进而可求出10a ，11a ，从而可求出结果.【详解】因为n a ，1n a +是方程220nn x b x -+=的实数根，所以1n n n a a b ++=，12nn n a a +=，又11a =，所以22a =；当2n ≥时，112n n n a a --=，所以11112n n n n n na a a a a a ++--==，因此4102232a a =⋅=，5111232a a =⋅=所以101011323264b a a =+=+=.故选：D.【点睛】本题主要考查由数列的递推关系求数列中的项，属于常考题型.7.已知函数e ()xf x ax x =-，,()0x ∈+∞，当210x x >>时，不等式()()1221f x f x x x <恒成立，则实数a 的取值范围为（）A.(,e]-∞B.(,e)-∞ C.e ,2⎛⎫-∞ ⎪⎝⎭D.e ,2⎛⎤-∞ ⎥⎝⎦【答案】D 【解析】【分析】根据不等式，构造函数并明确其单调性，进而可得导数的不等式，利用参数分离整理不等式，构造函数，利用导数求其最值，可得答案.【详解】当210x x >>时，不等式()()1221f x f x x x <恒成立，则()()1122f x x f x x <，即函数()()2e xg x xf x ax ==-在()0,∞+上单调递增，则()e 20xg x ax '=-≥，整理可得2x e a x ≤，令()e x m x x =，则()()21e xx m x x -'=.当()0,1x ∈时，()0m x '<，()m x 单调递减，当()1,x ∈+∞时，()0m x '>，()m x 单调递增，()()min 21e a m x m ∴≤==，e2a ∴≤.故选：D.8.设甲袋中有3个红球和4个白球，乙袋中有1个红球和2个白球，现从甲袋中任取1球放入乙袋，再从乙袋中任取2球，记事件A =“从甲袋中任取1球是红球”，事件B =“从乙袋中任取2球全是白球”，则下列说法正确的是（）A.9()14=P B B.6()7P AB =C.()15P A B =D.事件A 与事件B 相互独立【答案】C 【解析】【分析】由古典概型概率计算公式，以及条件概率公式分项求解判断即可.【详解】现从甲袋中任取1球放入乙袋，再从乙袋中任取2球可知，从甲袋中任取1球对乙袋中任取2球有影响，事件A 与事件B 不是相互独立关系，故D 错误；从甲袋中任取1球是红球的概率为：()37P A =，从甲袋中任取1球是白球的概率为：47，所以乙袋中任取2球全是白球的概率为：()1212324312127474C C C C 125+C C C C 14714==+=P B ，故A 错误；()12321274C C 1C C 14==P AB ，故B 错误；()()()11411455P AB P A B P B ==⨯=，故C 正确；故选：C二、多项选择题：本大题共4小题，每小题4分，共16分.在每小题给出的四个选项中，有多项符合题目要求。

吉林省东北师范大学附属中学2024-2025学年高二上学期第一次月考数学试卷

吉林省东北师范大学附属中学2024-2025学年高二上学期第一次月考数学试卷一、单选题1．若随机试验的样本空间为{}Ω0,1,2=，则下列说法不正确的是（） A ．事件{}1,2P =是随机事件 B ．事件{}0,1,2Q =是必然事件 C ．事件{}1,2M =--是不可能事件D ．事件{}1,0-是随机事件2．已知点()1,0A ，(B -，则直线AB 的倾斜角为（） A ．5π6B ．2π3 C ．π3D ．π63．投壶是从先秦延续至清末的汉民族传统礼仪和宴饮游戏，在春秋战国时期较为盛行.如图为一幅唐朝的投壶图，甲、乙、丙是唐朝的三位投壶游戏参与者，假设甲、乙、丙每次投壶时，投中的概率均为0.6且投壶结果互不影响.若甲、乙、丙各投壶1次，则这3人中至少有2人投中的概率为（）A ．0.648B ．0.432C ．0.36D ．0.3124．设,A B 是一个随机试验中的两个事件，且()()()131,,+252P A P B P A B ===，则()P A B =（） A ．13B ．15C ．25D ．1105．若()2,2,1A ，()0,0,1B ，()2,0,0C ，则点A 到直线BC 的距离为（）A B C D 6．某乒乓球队在长春训练基地进行封闭式集训，甲、乙两位队员进行对抗赛，每局依次轮．．．流．发球，连续赢2个球者获胜，通过分析甲、乙过去对抗赛的数据知，甲发球甲赢的概率为23，乙发球甲赢的概率为14，不同球的结果互不影响，已知某局甲先发球．则该局打4个球甲赢的概率为（） A ．13B ．16C ．112D ．5247．据史书记载，古代的算筹是由一根根同样长短和粗细的小棍制成，如图所示，据《孙子算经》记载，算筹记数法则是：凡算之法，先识其位，一纵十横，百立千僵，千十相望，万百相当．即在算筹计数法中，表示多位数时，个位用纵式，十位用横式，百位用纵式，千位用横式，以此类推．例如⊥‖表示62，＝T 表示26，现有6根算筹，据此表示方式任意表示两位数（算筹不剩余且个位不为0），则这个两位数不小于50的概率为（）A ．13B ．12C ．23D ．358．正三棱柱111ABC A B C -中，12,AB AA O =为BC 的中点，M 为棱11B C 上的动点，N 为棱AM 上的动点，且MN MOMO MA=，则线段MN 长度的取值范围为（）A ．⎣B ．⎣⎦C ．⎣⎦D ．二、多选题9．下列命题中正确的是（）A ．若表示两个空间向量的有向线段的终点不同，则这两个向量可能相等；B ．在所有棱长都相等的直平行六面体1111ABCD A BCD -中，BD ⊥平面11ACC A ；C ．对于空间三个非零向量,,a b c r r r，一定有()()a b c a b c ⋅⋅=⋅⋅r r r r r r 成立；D ．在棱长为2的正方体1111ABCD A B C D -中，点,M N 分别是棱11A D ，AB 的中点，则异面直线MD 与NC 所成角的余弦值为25． 10．连续抛掷一枚质地均匀的骰子两次，用数字x 表示第一次抛掷骰子的点数，数字y 表示第二次抛掷骰子的点数，用(),x y 表示一次试验的结果．记事件A =“7x y +=”，事件B=“3x ≤”，事件C =“()21N xy k k *=-∈”，则（）A ．()14P C =B ．A 与B 相互独立C ．A 与C 为对立事件D ．B 与C 相互独立11．在棱长为1的正方体1111ABCD A B C D -中，P 为棱1BB 上一点，且12B P PB =，Q 为正方形11BB C C 内一动点（含边界），则下列说法中正确的是（）A ．若1D Q ∥平面1A PD ，则动点QB ．存在点Q ，使得1D Q ⊥平面1A PDC ．三棱锥1Q A PD -的最大体积为518D ．若1D Q =，且1D Q 与平面1A PD 所成的角为θ，则sin θ三、填空题12．已知()3,2,1a =-r ，()2,1,2b =r，当()()2ka b a b +⊥-r r r r 时，实数k 的值为．13．柜子里有3双不同的鞋子，分别用121212,,,,,a a b b c c 表示6只鞋，从中有放回地．．．．取出2只，记事件M =“取出的鞋是一只左脚一只右脚的，但不是一双鞋”，则事件M 的概率是． 14．已知正四面体ABCD 的棱切球1T （正四面体的中心与球心重合，六条棱与球面相切）的半径为1，则该正四面体的内切球2T 的半径为；若动点,M N 分别在1T 与2T 的球面上运动，且满足MN xAB yAC z AD =++u u u u r u u u r u u u r u u u r，则2x y z ++的最大值为．四、解答题15．如图，在三棱柱111ABC A B C -中，,M N 分别是111,A B B C 上的点，且1112,2A M MB B N NC ==u u u u r u u u r u u u u r u u u u r ．设1,,AB a AC b AA c ===u u u r r u u u r r u u u r r ．(1)试用,,a b c r r r 表示向量MN u u u u r；(2)若11190,60,1BAC BAA CAA AB AC AA ∠=∠=∠====o o ，求异面直线MN 与AC 的夹角的余弦值．16．如图，在正四棱柱1111ABCD A B C D -中，122AA AB ==，,E F 分别为1BB ，1CC 的中点．(1)证明：1A F ∥平面CDE ； (2)求三棱锥1A CDE -的体积； (3)求直线1A E 与平面CDE 所成的角．17．2023年10月31日，东北师大附中以“邂逅数学之美，闪耀科技之光”为主题的第17届科技节在自由、青华两校区开幕.在科技节中数学教研室组织开展了“送书券”活动．该活动由三个游戏组成，每个游戏各玩一次且结果互不影响．连胜两个游戏可以获得一张书券，连胜三个游戏可以获得两张书券．游戏规则如下表：(1)分别求出游戏一，游戏二的获胜概率；(2)甲同学先玩了游戏一，当m 为何值时，接下来先玩游戏三比先玩游戏二获得书券的概率更大．18．球面三角学是研究球面三角形的边、角关系的一门学科．如图，球O 的半径为R ，A 、B 、C 为球面上的三点，设a O 表示以O 为圆心，且过B 、C 的圆，劣弧BC 的长度记为a ，同理，圆b O ，c O 的劣弧AC 、AB 的长度分别记为b ，c ，曲面ABC （阴影部分）叫做球面三角形．如果二面角,,C OA B A OB C B OC A ------的大小分别为,,αβγ，那么球面三角形的面积为()2++πABC S R αβγ=-V 球面．(1)若平面OAB 、平面OAC 、平面OBC 两两垂直，求球面三角形ABC 的面积；(2)若平面三角形ABC 为直角三角形，AC BC ⊥，设1AO C θ∠=，2BOC θ∠=，3AOB θ∠=． ①求证：123cos cos cos 1θθθ+-=；②延长AO 与球O 交于点D ，若直线DA ，DC 与平面ABC 所成的角分别为ππ,43，,(0,1]BE BD λλ=∈u u u r u u u r，S 为AC 的中点，T 为BC 的中点．设平面OBC 与平面EST 的夹角为θ，求cos θ的最大值及此时平面AEC 截球O 的面积．。

东北师大附中2019-2020学年高三年级下学期开学验收考试理科数学答案

=
11
1
e10
10
1，即 x0
=1 10
1
，则 e10
1 1−1.1ln1.1
2000 ， 1791
故有 1095 10 e 2000 .从而使得问题巧妙获证．
1000
1791
（二）选考题：共 10 分.请考生在 22,23 题中任选一题作答.如果多做,则按所做的第一题计分.
19（1）．解
试题分析：(1)先将参数方程转化为普通方程，再将普通方程转化为极坐标方程(2)利用极坐标计算出线段长
− x
x −1 −1+1
4
或
x
−1 x 1 +1− x +1
4
，或
x
+
1
x +
1 x −1
4
，
−2
x
−1或
−x
x
1或1
x
2
，
x
−2,
2
.
（2）证明：
f
(−a) +
f
1 a
=
−a + m
+
−a −
1 m
+
1 a
+m
+
1 a
−1 m
，
−a + m −a − 1
m
+ +
1 a 1 a
+m −1
故 S = 1 AB d = 1
2
2
1+ k 2 x1 − x2
m 1+ k2
=1 2
( x1 + )x2 2 − 4x1x2 m =
2 − m2 m

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

吉林省东北师范大学附属中学2019-2020学年高二数学下学期疫情延
期开学考试（4月）试题理
注意：本试卷共120 分，考试时间90分钟。

第Ⅰ卷（共60分）
一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1.某物体沿水平方向运动，其前进距离s （米）与时间t （秒）的关系为2
()52s t t t =+，则该
物体在运行前2秒的平均速度为（米/秒）
A. 18
B. 13
C.9
D. 132
2. 已知()ln f x x x =,若0()0f x '=,则0x = A.
1
e
B. 1
C.e
D.2e 3.函数()(1)x
f x x e =+的单调递增区间是
A. (,2)-∞
B. (0,2)
C.(2,0)-
D. (2,)-+∞ 4. 函数()ln(1)f x x x =-+的最小值为
A.-1
B. 0
C.1
D. 2
5.已知函数()f x 的定义域为(,)a b ，且导函数'
()f x 在(,)a b 内的图像如下图所示，则函数
()f x 在区间(,)a b 内的极大值点的个数为
A.3
B. 2
C.1
D. 0
6.已知函数()f x 的图像是折线ABC ，其中(0,4),(1,0),(5,4)A B C 则0
(3)(3)
2lim
x f x f x
∆→+∆-=∆
A.
1
2
B. 1
C.2
D. 4 7.若函数2
()ln f x x x bx =+-在[1,)+∞是增函数，则b 的最大值是 A.3 B. 22 C.2 D. 26
8. 已知3
21()(1)3
f x x f x x '=
-⋅+，则(1)f '的值为 A.-1 B. 0 C. 23 D. 3
2
9.若0,0,a b >>且函数3
2
()222f x x ax bx =--+在1x =处取极值，则2a b 的最大值是 A.
27
8
B. 4
C.9
D. 不存在 10.已知函数()f x 的定义域为R ，且(2)6f =，对任意x R ∈，()2f x '>，则()22f x x >+的解集为
A. (,2)-∞-
B. (2,)+∞
C.(2,2)-
D. (,)-∞+∞ 11. 若()f x 是定义在R 上的偶函数，且(2)0f =,当0x >时，()()0f x f x '+>恒成立，则不等式()0f x >的解集是
A. (,2)-∞-
B. (2,)+∞
C.(2,2)-
D. (,2)(2,)-∞-+∞U 12. 已知 ()(1)(2)(3)......()(2,)f x x x x x n n n N *
=++++≥∈，其导函数是()f x '，若
(1)
(0)
n f a f '-=
，则50a = A.
150! B. 150
C.50
D. 50! 第II 卷（共60分）
二、填空题：本题共4小题，每小题5分，共20分． 13. 函数3
21()313
f x x x x =
--+的极大值为a ，极小值为b ，则a b += ； 14. 函数cos sin ,(02)y x x x x π=-<<的单调减区间为； 15. 过点(1,1)做曲线3
y x =的切线，则切线方程是；
16. 若关于x 的方程2
()x
x
e mx e x -=恰有一个实根，则实数m 的取值范围是 . 三、解答题：本题共4小题，每小题10分，共40分．解答应写出文字说明、证明过程或演算步骤.
17.已知函数()2sin cos f x x x x =--. （I ）求曲线()y f x =在0x =处的切线方程；
（II ）当[],x ∈-ππ时，求函数()f x 的值域. 18.已知函数32
211()(32),(,)32
f x x x a a x b a b R =
---+-∈ （I ）若函数()f x 在区间(1,)+∞上是单调函数，求a 的取值范围；（II ）若函数()f x 在区间(1,1)-上不是单调函数，求a 的取值范围.
19.已知函数2
()(1)4x
f x x e ax ax a =+--+. （I ）当1a =时，求()f x 的极大值；
（II ）若函数()f x 的极小值大于零，求a 的取值范围.
20. 已知函数()ln (0)x a
f x e
x a a -=-+>.
（I ）当0a =时，证明()f x 有极小值点0x ，且01(,1)2
x ∈；（II ）证明()2f x ≥.
参考答案：
一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一
项是符合题目要求的．
二、填空题：本题共4小题，每小题5分，共20分．
13.;
14.;
15.;
16.
三、解答题：本题共4小题，每小题10分，共40分．解答应写出文字说明、证明过程或演
算步骤.
17.解：（I）由，得
，所以曲线
在
处的切线方程为
………………………………5分
（II）因为，所以函数
在
为增函数，
故有,即函数
的值域为.…………………………10分
18.解：（I）………………………………1分要使题意成立，必须且只需在区间
上成立.即
，即只需
，解得.………………5分
（II）解方程得
，………………………………6分
依题意即是方程在区间
有根.
故有，解得
………………………………10分
19.解：（I）函数的定义域为
，当
时，
，……………1分
函数在
和上单调递增，在上单调递减. ………………………2分
所以函数………………………3分
（II）函数的定义域为
，
.
1）当时，函数
在
上单调递减，在
上单调递增，
所以函数，所以
不合题意. ………………………5分
当时，令
解得
2）当时，即
时，函数
在
和上单调递增，
在上单调递减.
，解得
，结合
，有
，解得.………………………………7分
3）当时，函数
在
上单调递增，没有极值. ………………8分
4）当时，即
时，函数
在
和
上单调递增，
在上单调递减.
,解得结合，所以
.………………………………9分
综上所述，的取值范围是
.………………………………10分
20解：（I）函数的定义域为
，
………………………………1分
所以在
为增函数，且
，
于是存在使
，且
在递减，在递增.
所以是函数
的极小值点，且
.…….……4分
（II）因为在
为增函数.
当时，
.
所以在
有唯一零点
当时，
在
有唯一零点
.
当时，
.
所以在
有唯一零点. ………………………………7分故当，函数
在有唯一零点.因为为增函数.
所以在
递减，在
递减. ………………………………8分
所以，………………………………9分由
故，故
成立. ………………………………10分（II）学生找零点的方式不一定一样，可酌情给分.
因为在
为增函数.
比如：当时，
.所以
在有唯一零点，且
.
于是在
递减，在
递减.
且，由
故，而
，故
.。