克拉夫《结构动力学》习题答案汇总

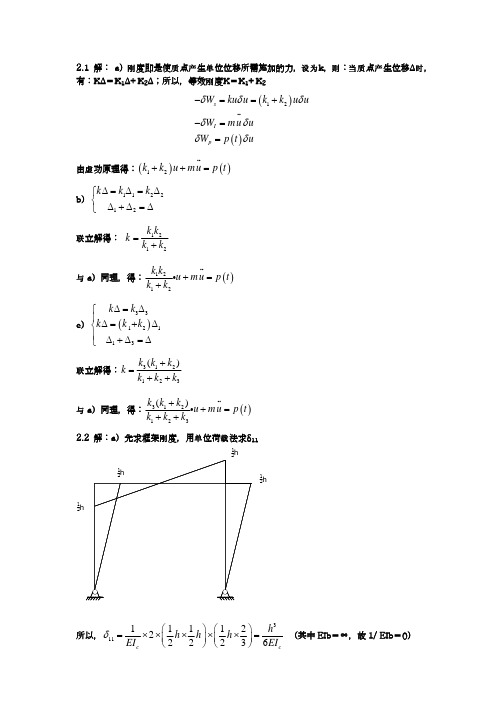
第二章 自由振动分析2-1（a ） 由例22T π=22()W K T gπ= 因此 max ()()D t kT νν= 其中 k=0、1、2……T D =0.64sec 如果ξ 很小，T D =T∴ 222200()49.9/0.64sec 386/sec kipsk kips in in π==⇒ 50/k kips in = （b ）211lnln n n v v v v δ+≡=δξ=→=1.2ln 0.3330.86δ==0.0529ξ==0.33320.05302δπξξπ=→==⇒ 5.3%ξ= (a ’)D ω=2T πω=T T =249.950/1k kips in ξ==- (c)2c m ξω=W m g=2T πω=4c T gπωξ=T T =241W c Tg πξξ=- 2240.05292000.64sec386/sec 10.0529kipsc in π=-0.539sec/c kips in =⋅ T=T D0.538sec/c kips in =⋅ ⇒0.54sec/c kips in =⋅2-22k mω=→4.47ω== (1/sec ) (0)(0)()sin (0)cos tD D Dv v t et v t ξωξωνωωω-⎡⎤⎛⎫+⎢⎥ ⎪=+⎢⎥ ⎪⎝⎭⎣⎦∴ (0)(0)()sin (0)(0)(0))cos t D D D v v t e t v v v t ξωξωνξωωξωξωωω-⎛⎫⎡⎤+⎧⎫⎡⎤ ⎪⎢⎥=-++-⎨⎬⎢⎥ ⎪⎢⎥⎣⎦⎩⎭⎣⎦⎝⎭()22(0)(0)()(0)cos sin D t D D Dv v t e v t t ξωξωξωωνωωω-⎛⎫⎡⎤++ ⎪⎣⎦=- ⎪ ⎪⎝⎭D ω=→()(0)cos (0)(0)sin t D D D t e v t v v t ξωωνωξωωω-⎛⎫⎡⎤=-+ ⎪⎢⎥⎣⎦⎝⎭()(0)cos tD D t ev t t ξωνωω-⎛⎫⎪= ⎪⎝⎭0.055922(2)(4.47)c cc m ξω=== (a) c=0→0ξ=→D ωω=∴ 5.6(1)sin 4.470.7cos 4.47 1.384.47v t in ==+=- (1) 5.6cos 4.47 4.47(0.7)sin 4.47 1.69/sec v t in ==-=⇒(1) 1.4v in =-,(1) 1.7/sec v in = (b)c=2.8→0.0559(2.8)0.157ξ==4.41D ω== (1/sec ) (0.157)(4.41)5.60.7(0.157)(4.47)(1)sin 4.410.7cos 4.414.41t e ν-⎡+⎤⎛⎫==+⎪⎢⎥⎝⎭⎣⎦(1)0.764t in ν==-(0.157)(4.41)(1) 5.6cos 4.41 4.41t e ν-⎛⎫== ⎪⎝⎭(1) 1.10/sec t in ν==⇒(1)0.76v in =-,(1) 1.1/sec v in =第三章 谐振荷载反应3-1根据公式有 ()()21sin sin 1R t w t wt ββ⎡⎤=-⎢⎥-⎣⎦0.8wwβ== ()()2.778sin 0.8sin1.25R t wt wt=-将t ω以80°为增量计算)(t R 并绘制曲线如下：80° 160° 240° 320° 400° 480° 560° 640° 720° 800° 00.547 1.71 -0.481 -3.214 0.357 4.33 -0.19 -4.9244.9241.25w w =tω)(t R3-2解：由题意得：22m kips s in =⋅ ， 20k kips in = ， (0)(0)0v v == ，w w =3.162w rad ===8wt π=（a ）0c =()()1sin cos 2R t wt wt wt =-将8wt π=代入上式得：()412.566R t π=-=- （b ）0.5c k s =⋅0.50.0395222 3.162c c c c mw ξ====⨯⨯()()(){}1exp 1cos exp sin 2R t wt wt wt wt ξξξξ=--+-⎡⎤⎡⎤⎣⎦⎣⎦将8wt π=代入上式得：()7.967R t =- （c ） 2.0c k s =⋅2.00.1582223.162c c c c mw ξ====⨯⨯()()(){}1exp 1cos exp sin 2R t wt wt wt wt ξξξξ=--+-⎡⎤⎡⎤⎣⎦⎣⎦将8wt π=代入上式得：() 3.105R t =-3-3解：（a ）：依据共振条件可知：10.983sec w w rad =====由2L T V w π==得：10.9833662.96022wL V ft s ππ⨯===（b ）：()()()122max2221212tgo v v ξββξβ⎡⎤+⎢⎥=⎢⎥-+⎣⎦1w w β==0.4ξ= 1.2go v in =代入公式可得：max 1.921tv in =（c ）：2L T V w π=='45min 66V h ft s ==226611.51336V w rad s ec L ππ⨯'===11.5131.04810.983w w β'===0.4ξ=代入数据得 ：()()()122max22212=1.85512tgov v in ξββξβ⎡⎤+⎢⎥=⎢⎥-+⎣⎦3-4解：按照实际情况，当设计一个隔振系统时，将使其在高于临界频率比β=在这种情况下，隔振体系可能有小的阻尼。

对于小阻尼 ： ()211TR β=-又因为： max 0.0050.03t go v TR v == 联立求的： 27β=2220125.6w f rad ππ==⨯=又因为：w ww β===联立得：222125.68004.6703867w W k kips in g β⨯===⨯3-5解：按照实际情况，当设计一个隔振系统时，将使其在高于临界频率比β=在这种情况下，隔振体系可能有小的阻尼。

对于小阻尼 ： ()211TR β=-又因为： max 50700t go v TR v == 联立求的： 215β=221275.36w f rad ππ==⨯=又因为：w w w β===联立得：22275.3665006.37638615w W k kips g β⨯===⨯3-6(a)由图3-17有，max s f k =ρ，则in lbf inlbff k s /260015.0390max===ρ(b)由方程3-66有22ρπξk E Deq =，由图3-17有221ρk E S=， 因为ωξm c 2=，所以，又因为，故 0713.0)29(4264=⋅⋅⋅==in lbf inlbf E E S D eq ππξωξm c eq eq 2=222ρωπξm E Deq =)/(78.36)15.0(/102622in s rad lbf in s rad inlbf E c Deq ⋅⋅=⋅⋅==πρωπ (c)由方程3-78有ξβζ2=，3-7(a)公式同题3.6(b)(b)公式同题3.6(c)(c)通过题3.6与题3.7的比较可知，ζ与ω无关，故滞变阻尼机理更合理。

3-8（原版英文书中为求D E 的值）由方程3-66有22ρπξk E eq D ⋅=，当k 与ρ不变时，若)(ωξξeq eq ≠，则)(ωD D E E ≠, 由题3.7可知%2.141426.00713.022==⨯==ξζ0713.0)29(4264=⋅⋅⋅==in lbf inlbf E E S D eq ππξ)/(39.18)15.0(/202622in s rad lbf in s rad inlbf E c Deq ⋅⋅=⋅⋅==πρωπ%2.141426.00713.022==⨯==ξζ)(ωD D E E =第五章 对冲击荷载的反应5-1解：(a)25.36 rad/sec ω=== 120.15T =0.248 sec0.6050.50.248t T πω===> *21/t πωωω=+120.94 rad/sec 0.15t ππω===20.94===0.82625.36ωβω ()*2=0.136 sec 20.94125.36/20.94t π=+(b)[]**0max 2215001(sin sin )sin(20.940.136)0.8489 in 110001(0.826)p v t t k ωβωβ=-=⨯=--,max max 10000.8489848.9 1S f kv b ==⨯=又10max 0.605 0.85 t pv D in T k=∴==5-2解： 设无阻尼(a)011()(/) 0< (1)mv kv p t p t t t t +==<cos sin c p v A t B t v Et F ωω=+=+带入（1）得：0011() 0 t pk Et F p F E t kt ⎛⎫+=== ⎪⎝⎭01p p tv k t =01=cos sin c p p tv v v A t B t k t ωω+=++0011(0)0 -p p v B B kt k t ωω=+== 0111v()(sin t) p t t k t t ωω=- 1 t t ≥当2011111121()sin sin()1sin cos()2p t v t t t t t t kt t ωωωω⎡⎤⎛⎫=-+--⎢⎥ ⎪⎝⎭⎣⎦（b ）1 :t t <<当0()2001112()1cos sin 2p p t v t t kt kt ωω=-= sin0 0,1,222ttn n ωωπ∴=→==±±max max 10121322sin()/3333v R t p k t ππ==--= max 23R →=解：(a)110 242T t t t ππωω<<=== 0cos (1)mv kv p t ω+=cos sin cos sin c p v A t B t v Et t Ft t ωωωω=+=+带入（1）得：000 22p pE F m k ωω=== 0cos sin sin 2c p p v v v A t B t t t kωωωω=+=++[]0(0)0(0)sin(0)(0)cos(0)020v A p v B kB ωωω===++== 0sin 2p v t t kωω=0011 ()sin 2224p p t t v t k kπππωωωω⎛⎫⎛⎫>== ⎪ ⎪⎝⎭⎝⎭ ()001()sin sin 22222p p v t k k πππωωωωωωωω⎡⎤⎛⎫⎛⎫⎛⎫=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦ 01v()sin cos 224p t t t k πωω⎛⎫=+ ⎪⎝⎭(b) max 1max 00 sin /2v tt t R t p k ωω<<== 1max 11 sin cos =024t t R t t t t t πωω>=+-≥解： (a)110.15t T = ,查表得：D=0.5 0,max max 00.3954015.8 S kp f v k D p D k k====⨯= (b)10max 010101112()()0.150.3532222t p v p t dt p t p t T m k k Tωπω====⨯⨯=⎰ ,max max 0.353207.06 S f v k k ==⨯=5-5解：1max 001()()t tv p t dt p t dt m ω==⎰⎰1012340()(424)53t tp t dt p p p p p ∆=++++=⎰max v =S,max max =0.3954015.8 k f v k =⨯= max ,max 15015.82370 S M d f k ft =⨯=⨯=⋅第六章6-1Solution:2ωπ==0.10.06366/0.2521F in lb m τωζπ∆===⨯⨯ 0.1sec τ∆= 2/k lb in π= (5)(2)(4)=⨯ (11)(9)(10)=- (7)(2)(3)=⨯ (12)(11)()F v t =⨯= (9)(6)(3)=⨯ (13)(12)()s K f t =⨯= (10)(8)(4)=⨯0.10.03183/0.2522F in lb m τωζπ∆===⨯⨯0.1sec τ∆=2/k lb in π=(5)(2)(4)=⨯ (7)(2)(3)=⨯ (11)(7)3-104=⨯⨯（） (12)(11)()F v t =⨯=(13)(12)()s K f t =⨯=0.10.02122/0.2523F in lb m τωζπ∆===⨯⨯0.1sec τ∆=2/k lb in π=(6)(2)(4)5=⨯⨯（） (9)(2)(3)5=⨯⨯（） (12)(8)3-114=⨯⨯（） (13)(12)()F v t =⨯=(14)(13)()s K f t =⨯=6-2Solution:30/rad s ω=20.209T s πω==0.0050.000277/3302F ft kips m τωζ∆===⨯⨯(5)(2)(4)=⨯ (14)(13)()F v t =⨯= (9)(2)(3)=⨯ (15)(14)()s K f t =⨯=(13)(8)3-124=⨯⨯（）6-3Solution:=5%=0.05ξ22700/K kips ft =exp()0.9925Mult t ξω=-∆= 0.0050.000277/3302F ft kips m τωζ∆===⨯⨯(5)(2)(4)=⨯ (9)(2)(3)=⨯ (13)(8)3-124=⨯⨯（） (14)(13)()F v t =⨯=(15)(14)()s K f t =⨯=6-4Solution:6.325/rad s ω= 0.4=0.158220.2 6.325c m ξω==⨯⨯ exp(2)exp(-20.158 6.3250.12)0.787t ξω-∆=⨯⨯⨯= 4exp()4exp(-0.158 6.3250.12) 3.548t ξω-∆=⨯⨯⨯⨯=-20.123.16210/0.2 6.3253F ft kips m τωζ∆===⨯⨯⨯(5)(2)(4)=⨯ (8)(6)(5)=⨯ (10)(2)(3)=⨯ (12)(11)(10)=⨯(14)(9)(3)-134=⨯⨯（）（） (15)(14)()F v t =⨯=第七章7-1由题意可知：h=0.12s等效刚度：K ̃(t)=K(t)+3c ℎ+6mℎ2=101.33 kips in ⁄ΔP ̃n=ΔP+[6mℎ2v̇(t)+3v̈(t )m ]+C[3v̇(t)+ℎ2v̈(t)] =ΔP+11.2v̇(t)+0.624v̈(t )Δv̇(t)=3ℎΔv(t)-3v̇(t)-ℎ2v̈(t)=25Δv-3v̇(t)-0.06v̈(t ) 加速度：v̈(t)=1m [P(t)-C v̇(t)-kv(t)] =10.2[P(t)-0.4v̇(t)-8v(t)] Δv̇=ΔP̃(t)k̃(t)又v(0)=v̇(0)=v̈(0)=0v(t)=v(t-Δt)+ Δv(t-Δt) v̇(t)=v̇(t −Δt)+ Δv̇(t −Δt)则由以上公式并结合题意可得下表:7-2由题意知：当|v|>1 in 时 K=0 其他公式同7-1 则有： K ̃(t)=K(t)+3c ℎ+6m ℎ2=K(t)+93.33 ΔP̃n=ΔP+[6m ℎ2v̇(t)+3v̈(t )m ]+C[3v̇(t)+ℎ2v̈(t)]=ΔP+11.2v̇(t)+0.624v̈(t )Δv̇(t)=3ℎΔv(t)-3v̇(t)-ℎ2v̈(t)=25Δv-3v̇(t)-0.06v̈(t ) 加速度：v̈(t)=1m [P(t)-C v̇(t)-kv(t)] =10.2[P(t)-0.4v̇(t)-8v(t)] Δv̇=ΔP̃(t)k̃(t) v(0)=v̇(0)=v̈(0)=0v(t)=v(t-Δt)+ Δv(t-Δt) v̇(t)=v̇(t −Δt)+ Δv̇(t −Δt)综上可得下表：7-3K=dfs dv=d12[23v−13(2v3)3]dv=8-329v 2 则K̃(t)=101.33-329v 2 其余方程如7-1有 h=0.12sΔP ̃n=ΔP+[6mℎ2v̇(t)+3v̈(t )m ]+C[3v̇(t)+ℎ2v̈(t)] =ΔP+11.2v̇(t)+0.624v̈(t )Δv̇(t)=3ℎΔv(t)-3v̇(t)-ℎ2v̈(t)=25Δv-3v̇(t)-0.06v̈(t )加速度：v̈(t)=1m [P(t)-C v̇(t)-kv(t)] =10.2[P(t)-0.4v̇(t)-8v(t)]Δv̇=ΔP̃(t)k̃(t) v(0)=v̇(0)=v̈(0)=0v(t)=v(t-Δt)+ Δv(t-Δt) v̇(t)=v̇(t −Δt)+ Δv̇(t −Δt)第八章广义单自由度体系8-1解：2 1.720T L==带入数据得：T=1.776 sec*4*334()21.771sec32m mLTEIkLππ⎫=-⎪⎪==⎬⎪=⋅⎪⎭3=2,rm rt I trgTππ==把带入得：8-2 解：[]2*2=(x)(x)(L)Lm m dx mψψ+⎰From例题 E8-3b可得：[][]422**30*2()()=0.228; ''()=320.228LLEIm m x x dx mL k EI x dx L W m mL I gπψψ==∴=+⎰⎰3*22222492*340010 1b0.2281101sec /20017430 1sec /32.22 /sec16510 1 62780 1/32(200 )m b ft ft b ft ft b ftk b ftft π⨯=⋅⨯+=⋅⨯⋅==（ ）22 3.311 sec 3.31sec T T ====*4*3334()2232r W m rtL g g T E k tr L ππππ⎫=-+⎪⎪=⎬⎪=⋅⋅⎪⎭8-3解：8-4 解：0202() ()8S I mL f kz t M I z t Lα=-=-=-0M=∑()() ()22S f S L LM f kz t ==-01()4I M mLz t =-()2F LM F =8-5解：[]1201()2()()(1)()s s f k y t f k y t z t f c z t =-=-+=-- 0AM=∑[][]1212()1()()2(2)()()(2)1()()2()()0 1 2s s P f s f s M p t LM f L ky t L M f L k y t z t L p t L ky t L k y t z t L ===-==-+--+=因此：（）B0M =∑ [][]20220()()()()22()()()22()12/211()()()()0 2226s D f s f D I L LM f k y t z t L LM f cz t L z t M I m L L k y t z t L cz t m z t L α==-+=-=-=-=-⋅-+--⋅=因此：（） ****12551,,,()()622m m c c k k p t p t ====-由式（），（）可得： 8-6解：42*200333(x)22140LLx x m m dx m dx mL L L ψ⎛⎫⎛⎫==-= ⎪ ⎪⎝⎭⎝⎭⎰⎰()2*''Lk EI dx ψ=⎰3221()(3)2x x x L L ψ=-223'()(2)2x x x L Lψ=-2213''()(66)(1)2x xx L L L Lψ=-=- *343300993(1)(1)(1)3LL EIL x x EIx EI k d L L L LL L ⎡⎤=---=--=⎢⎥⎣⎦⎰ *3()()8Lp t p x dx pL ψ==⎰8-7解：****33 G EIk k k k L=-= (a)[]222*003'()22LLGd L x k N x dx N dx dx x L ψ⎧⎫⎡⎤⎪⎪⎛⎫⎛⎫==-⎢⎥⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎪⎪⎣⎦⎩⎭⎰⎰22*23036325LG x x Nk N dx L L L ⎧⎫=-=⎨⎬⎩⎭⎰***2325G EI k k k N L L ⎛⎫∴=-=- ⎪⎝⎭(a)[]2*2342001'()N(1-)()()()4L L G L q L L L k N x dx dx x Lxx x ψ⎡⎤==-+⎢⎥⎣⎦⎰⎰*2345209N 513N()2()()()=L 448L L G L L L L k dx xx x x ⎡⎤=-+-⎢⎥⎣⎦⎰ ***2318G EI k k k N L L ⎛⎫∴=-=-⎪⎝⎭8-8解：（a ）2222222222222222=sinsincos sin sin sin sin cos sin sin cos cos xyaax y x y x a a a x a a a ax y x y ya a a y a a a ax y x y a a a y xππψψπππψππππψψπππψππππψψπππψ∂∂==-=-∂∂∂∂==-=-∂∂∂∂==∂∂∂∂[]222*20(,)(,)sin 4aA xarm r x y x y dA r dx a πψ⎡⎤===⎢⎥⎣⎦⎰⎰22222*22222222242222222()2(1)()()=()A A A k D dAx y x y x y dA dA x y a a a ψψψψψνψψπππψψ⎡⎤∂∂∂∂∂=+--⋅-⎢⎥∂∂∂∂∂∂⎣⎦∂∂+-=∂∂⎰⎰⎰其中： (b)22224422222242()=()()4A A AdA dA dA x y a a a aψψππππψψψ∂∂⋅--==∂∂⎰⎰⎰222200=cos cos 0a a A x y dA dxdy x y a a a ψπππ∂=∂∂⎰⎰⎰ 222200=cos cos 0a a A x y dA dxdy x y a a aψπππ∂=∂∂⎰⎰⎰444*2222(1)(1)42D k D D a a aπππνν=--=+*22(,)(,)sinsin4sinsinaaAaaxyp p x y x y dA p dxdyaaxya pp dx dy aaππψπππ====⎰⎰⎰⎰⎰8-9解：22241()-333A x r r r πππ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭()45195x x r x L L ⎛⎫=+-=- ⎪⎝⎭ 4514265A()9=3333x x x L L ππ⎡⎤⎡⎤=---⎢⎥⎢⎥⎣⎦⎣⎦4265265150200 1b/ft 333x x r A L L ρππ⎡⎤⎛⎫==⨯-=- ⎪⎢⎥⎣⎦⎝⎭2*202652001cos 32L Lx x m r dx dx L L πψπ⎛⎫⎛⎫==-- ⎪⎪⎝⎭⎝⎭⎰⎰12265()1cos 1.80823426()51cos 13.66732L x y y L y y L ππ⎛⎫⎛⎫==--= ⎪⎪⎝⎭⎝⎭⎛⎫⎛⎫==--= ⎪⎪⎝⎭⎝⎭()*0122004228.3 kips 3x m y y y π∆⎛⎫=++= ⎪⎝⎭[]2*0()''()L k EI x x dx ψ=⎰ 02853x r L=-228533x x I L π⎛⎫=- ⎪⎝⎭ 2''(x)cos 22x L L ππψ⎛⎫= ⎪⎝⎭*03.44()L k z x dx =⎰322()85cos 32x x z x L L π⎛⎫=- ⎪⎝⎭0(0)650.96z z == 1()19.012Lz z == 2()0z z L ==*83.4 kip/ft k =8-10解：02(,)()sin ()34v x t x z t L L x x x ψωψ=⎡⎤⎛⎫∴=-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦[]222max 0030124()''()2L EI v z EI x x dx z Lψ==⎰ 222L/22222max010101/2/2117T 2(34)34222235L L L L z m dx m z mL m x x ωω⎧⎫⎡⎤⎡⎤⎛⎫⎪⎪⎛⎫⎛⎫⎛⎫=-+-=+⎢⎥ ⎪⎢⎥⎨⎬ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎢⎥⎪⎪⎣⎦⎝⎭⎣⎦⎩⎭⎰由以上两式可得：23148EI =1L 2mL m ω∴⎛⎫+ ⎪⎝⎭(a)(b)8-1133()3()12PL x x x EIL L ν⎡⎤=-⎢⎥⎣⎦0(,)()sin x t x Z t νψω= ∴3()3()x xx L Lψ=-22max 001()()2LnZ EI x x dx νψ⎡⎤=⎣⎦⎰2223max00123()2Ld x x Z EI dx dx L L ν⎧⎫⎡⎤=-⎨⎬⎢⎥⎣⎦⎩⎭⎰ 22232max000663036112363Lx EI Z EI dx Z EI L Z L L L ν===⎰()*[]222max001()()2LT Z m x x dx ωψ=⎰ 22'200()[()]()i Li i i m m x x dx m I ψψψ*=++∑∑⎰22_2233max010123()3(1)12L x x T Z m dx m L L ω⎧⎫⎪⎪⎡⎤⎡⎤=-+-⎨⎬⎣⎦⎢⎥⎣⎦⎪⎪⎩⎭⎰ 22246max010129()6()()42Lx x x T Z m dx m L L L ω-⎧⎫⎡⎤=-++⎨⎬⎢⎥⎣⎦⎩⎭⎰ 22max0116123()()4257T Z m L L L m ω-⎧⎫⎡⎤=-++⎨⎬⎢⎥⎣⎦⎩⎭ 22max0116824255T Z m L m ω-⎧⎫=+⎨⎬⎩⎭**⎛⎫⎪⎝⎭由()*和**⎛⎫⎪⎝⎭：233112466834243535EI EI L m L m L m L m ω--==⎡⎤⎛⎫++ ⎪⎢⎥⎣⎦⎝⎭∴2T =(a) 22T ==2T =(b)如果1903m L -≡, 2T =14T m m L m α-=+ 2T m m L -=∴22T ==22π=∴229335α+=1735α=⇒1748.6%35α==8-1221232sec /m m m m kips in ====⋅12311400/23k k k k kips in ====(0)(0)(0)0()sin i i t Z t νψω=(0)11ψ=,(0)22/3ψ=,(0)31/3ψ=,(0)01Z = (a)002322(0)2(0)(0)2(0)max11141(1)2299i i i T Z m Z m ωψω=⎡⎤⎡⎤⎡⎤==++⎣⎦⎣⎦⎣⎦∑ 02(0)2(0)max 11429T Z m ω⎡⎤=⎣⎦ ()* 002322(0)(0)(0)(0)max111123()22999i i i v Z k Z k ψ=⎡⎤⎡⎤⎡⎤=∆=++⎣⎦⎣⎦⎣⎦∑ 02(0)(0)max1629vZ k ⎡⎤=⎣⎦ **⎛⎫ ⎪⎝⎭由()*和**⎛⎫ ⎪⎝⎭：200R k m ω=20020.679sec R T π== ⇒2000.679sec R T =(0)20(0)2(0)0i i i i i p m v z m ωωψ==21m v kω∆=22532m v kω∆= 2323m v k ω∆=(1)(1)34(0)(0)(1)4(0)00max001112314(1)2235315i i i i v Z Z m Z Z m ωψψω--===++∑ (1)4(0)40max0167245v Z Z m ωω-= ***⎛⎫ ⎪ ⎪ ⎪⎝⎭由()*和***⎛⎫ ⎪⎪ ⎪⎝⎭：(0)2001(1)070286767R Z k m Z ω-==20020.687sec R T π== ⇒2000.687sec R T = （c ）0022(1)32(1)6(1)6(1)max111916(1)2225225i ii TZ m Z m ωψω-=⎡⎤⎡⎤⎡⎤==++⎢⎥⎣⎦⎣⎦⎣⎦∑ 02(1)6(1)max13222225T Z m ω⎡⎤=⎣⎦****⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭由***⎛⎫ ⎪ ⎪ ⎪⎝⎭和****⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭：(0)2011(1)033567322161R Z k m Z ω-==21120.689sec R T π== ⇒2110.689sec R T =8-132123111sec /23m m m m kips in ====⋅123800/k k k k kips in ====（a ）02(0)2(0)max141(1)2()3()299T Z m m m ω⎡⎤⎡⎤=++⎢⎥⎣⎦⎣⎦ 02(0)2(0)max 12029T Z m ω⎡⎤=⎣⎦ ()* 0022(0)(0)(0)max111111()299923vZ k Z k ⎡⎤⎡⎤=++=⎣⎦⎣⎦ **⎛⎫⎪⎝⎭由()*和**⎛⎫ ⎪⎝⎭：200320R k m ω=20040.574sec R T π== ⇒2000.574sec R T =21m v kω∆= (1)22(1)011203m v Z k ωωψ-== 22532m v kω∆= 22173mv k ω=2323m v k ω∆= → 23103m v kω=(1)11ψ=,(1)21720ψ=,(1)312ψ=,(1)0203m Z k -=（b ）00(1)(1)4(0)max121711(1)2()()3()()232032vZ Z m m m ω-⎡⎤=+⎢⎥⎣⎦ 00(1)(1)4(0)max 179230v Z Z m ω-= ***⎛⎫⎪ ⎪ ⎪⎝⎭由()*和***⎛⎫ ⎪ ⎪ ⎪⎝⎭：(0)2001(1)020012001020237237793R Z k m m Z kω-===20020.624sec R T == ⇒2000.624sec R T = （c ）02(1)(1)6max128912324004T Z m m m ω-⎡⎤⎡⎤=++⎢⎥⎢⎥⎣⎦⎣⎦ 02(1)(1)6max16392200T Z m ω-⎡⎤=⎢⎥⎣⎦ ****⎛⎫⎪⎪ ⎪ ⎪⎝⎭由***⎛⎫ ⎪ ⎪ ⎪⎝⎭和****⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭：(0)2011(1)079(20)179(20)203(639)3(639)3R Z m Z k ω-== 21179639R kmω=21120.632sec R T == ⇒2000.632sec R T =第十章 结构特性矩阵的计算10-1由公式(10-21)有dxx x x EI k j i Loij )()()(''''ψψ⎰=， 所以 dxx x x EI k L o )()()(''3''223ψψ⎰=其中322)(2)(3)(L x Lx x -=ψ ,23)1()(L x x x -=ψ ,故32''2126)(L x L x -=ψ，L L x x 46)(2''3-=ψ,20200238)23(2)21(6)1(L EIdx L x L L x L L x EI k L-=--+=⎰10-2由公式(10-28)有dxx x x m m j i Loij )()()(ψψ⎰=， 所以 dxx x x m m L o )()()(3223ψψ⎰=其中322)(2)(3)(L x Lxx -=ψ，23)1()(L xx x -=ψ，故22322321)1(]23[)1(L mdx L x x L x L x L x m m Lo =--+=⎰）（）（10-3由公式(10-34b)有 dxx x t f t p i Li )()()()(0ψχ⎰=， 所以dxx x t f t p L )()()()(202ψχ⎰=其中，tp L xt f x t x p ωχsin )2()()(),(+==，L x x +=2)(χ ,t p t f ωsin )(=，322)(2)(3)(L xLxx -=ψ，故tL p dx L x L x L x t p t p Lωωsin 2027]23[)2(sin )(23202=-+=⎰）（）（10-4由公式(10-42)有dxx x x N k j i LoGij )()()(''ψψ⎰=， 所以dxx x x N k L o G )()()('3'223ψψ⎰=，其中，322)(2)(3)(L x L x x -=ψ，23)1()(L x x x -=ψ，则322'66)(2L x L x x -=ψ，)1(2)1()(2'3L x L x Lxx ---=ψ，故202327)]1(2)1)[(1(6)2(N dx L x L x L x L x L x L L x N k L o G -=-----=⎰10-5由公式(10-22)有⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧43212234321233233336633662v v v v L L L L L LL L L L L L L EI f f f f s s s s ，故 3026)2/(226233311L EI L EI L EI k =+=L L EIk 32321-= L L EI L L EIk 623)2/(223331-=-=L L EIk 32312-=LL EI L L EI L L EI k 6222)2/3(2)2/3()3(23232322=+=23233222)2/3()2/3()3(2L L EI L L EI k ==L L EI L L EIk 623)2/(223313-=-=23232322)2/3()2/3()3(2L L EI L L EI k ==2323233362)2/(2)2/(22)2/3(2)2/3()3(2L L EI L L EI L L EI k =+=故刚度矩阵[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=2222362626363302L L L L L L L L L EI K 10-6根据质量矩阵系数式（10-29）有⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧432122224321432213341322221315654132254156420v v v vL L L L L L L L L L L L L m f f f f I I I I故当11=v时： 4.147842023215642028.015642011L m L m LmL m m =++=L Lm m 2242021-=L L m L Lmm 4.442022242028.031-=-= 当12=v时：L Lm m 2242012-=22222314202344202324420L L m L L mL L m m =⎪⎭⎫ ⎝⎛+=2232481420233420232L L m L L m m -=⎪⎭⎫ ⎝⎛-= 当13=v时：L L m L Lmm 4.442022242028.013-=-= 2223481420233420232L L m L L m m -=⎪⎭⎫ ⎝⎛-= 222334.274202344202322442028.0L L m L L m L L m m =⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=故质量矩阵[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=22225484058840562044088440295688400L L L L LL L LL m M10-7根据式（10-32）有：4,3,2,1,)(),()(0==⎰i dxx t x p t p i Li ψ其中)(x iψ根据式（10-16）选取如下：321)(2)(31)(L x Lx x +-=ψ，322)(22)(3)(L xL x x =ψ23)1()(L x x x -=ψ，)1()(24-=L xL x x ψ)(81])2/(2)2/(31)[(23])21(2)21(31)[()2(),()2()()(322/0322/1011t L p dx L x L x t p t L p dx L x t x p L x t p t P L L LLζζζψψ=+--+-==-==⎰⎰)(16123)4/13/22/1(23)()(81])2/3()2/3(22/3[23)()(81)2/31()()121(4)()]([),()]2()[()(222/3032222/302/332/3042t L p L L t p t L p dx L x L x L x Lt p t L p dx L x x t p L t L p dx x t x p Lx t p t P L L L L L ζζζζζζζψψ=+-+-=+-+-=-+-=--=--=⎰⎰⎰)(325)3141(2)(43)3141(23)(23)12/(2/)(23)12/3(2/3)()]([),()]([),()(22/022/3022/42/02/2/342/302/33t L p L t L p L t L p dx L x L x t p dx L xL x t p dx x t x p dx x t x pt P L L L L L L L L ζζζζζψψ-=---=---=-+--=⎰⎰⎰⎰故{}⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-=L L t PL t P 524)(321)(ζ 10-8(a)[][][][][]⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=θθθθk k k k L L L L L L L L L EI K t t tt 2222312858151051020根据公式（10-47）有[][][][][]t t tt t k k k k k θθθθ1--= 故：[]331222233311655510128815]510[20L EIL L L EI L L L L L EI L L L EIL EI k t -=⎥⎦⎤⎢⎣⎡--⎥⎥⎦⎤⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡-----=-(b)单自由度无阻尼方程为;0)()(=+t kv t v m 0)(11655)(303=-t v L EIt vL m即0)(11611)(63=-t v LEIt vL m第十一章11-1解：mmmk2k3kv 1=1v 2=1v 3=1k 11=kk 21=-kk 31=0k 12=-k k 22=3k k 32=-2kk 13=0k 23=-2k k 33=5k-3k此框架的质量与刚度矩阵为：()2112/1ks in ⎡⎤⎢⎥=⨯⎢⎥⎢⎥⎣⎦m ()()40040001104001200800/400/13208002000025k in k in --⎡⎤⎡⎤⎢⎥⎢⎥=--=--⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦k（a ）由公式（11-6）得：[][]()2110400/1320025Bk m k in B Bω---=---=-- (2200B ω=) ()()()()()1355410B B B B B -------=3291860B B B -+-=解得：B 1= 0.4158 B 2 =2.293 B 3=6.29则：ω1=9.119rad/s ω1=9.119rad/s ω1=9.119rad/s （b ）B 1= 0.415812310.415810130.4158200250.4158v v v --⎡⎤⎡⎤⎢⎥⎢⎥---=⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦则10.5840.253⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦1Φ B 2 =2.2931231 2.2931013 2.29320025 2.293v v v --⎡⎤⎡⎤⎢⎥⎢⎥---=⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦则11.2930.955⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦2Φ B 3=6.291231 6.291013 6.2920025 6.29v v v --⎡⎤⎡⎤⎢⎥⎢⎥---=⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦则15.298.20⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦3Φ （c ）1231110.584 1.293 5.290.2530.9558.20⎡⎤⎢⎥==--⎢⎥⎢⎥-⎣⎦ΦΦΦΦ210.5840.2532001111 1.2930.9550200.584 1.293 5.29/1 5.298.200020.2530.9558.20ks in ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=----⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦T Φm Φ210.5840.25311121 1.2930.9550.584 1.293 5.29/1 5.298.200.2530.9558.20ks in ⎡⎤⎡⎤⎢⎥⎢⎥=----⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦1.4050.0030.01520.003 3.5840.0090.0150.00996.224⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦21.4050020 3.5840/0096.224ks in ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦故可知Φ对mass 满足直交条件。