高考数学 常见题型 导数的综合运用课件
合集下载
高中数学理科专题讲解高考大题专项(一)《导数的综合应用》教学课件

--
题型二 讨论函数的单调性例2(2019湖北八校联考一,21)已知函数f(x)=x3+ x2-4ax+1(a∈R).(1)略;(2)若函数h(x)=a(a-1)ln x-x3+3x+f(x),讨论函数h(x)的单调性.
--
--
解题心得在判断函数f(x)的单调性时,若f'(x)中含有参数不容易判断其正负时,需要对参数进行分类讨论,分类的标准:(1)按导函数是否有零点分大类;(2)在大类中按导函数零点的大小分小类;(3)在小类中按零点是否在定义域中分类.
当-1<x<0时,g'(x)<0;当x>0时,g'(x)>0.故当x>-1时,g(x)≥g(0)=0,且仅当x=0时,g(x)=0,从而f'(x)≥0,且仅当x=0时,f'(x)=0.所以f(x)在(-1,+∞)单调递增.又f(0)=0,故当-1<x<0时,f(x)<0;当x>0时,f(x)>0.
--
--
题型二 求函数的极值、最值例2(2019四川成都七中一模,21)已知函数f(x)=xsin x+2cos x+ax+2,其中a为常数.(1)略;(2)求函数f(x)在[0,π]上的最小值.
--
解: (2)对∀x∈[0,π],f'(x)=xcos x-sin x+a,令g(x)=xcos x-sin x+a,g'(x)=-xsin x≤0,所以f'(x)在区间[0,π]上单调递减.当a≤0时,f'(x)≤f'(0)=a≤0,∴f(x)在区间[0,π]上单调递减,故fmin(x)=f(π)=aπ.当a≥π时,f'(x)≥f'(π)=a-π≥0,∴f(x)在区间[0,π]上单调递增,故fmin(x)=f(0)=4.当0<a<π时,因为f'(0)=a>0,f'(π)=a-π<0,且f'(x)在区间[0,π]上单调递减,结合零点存在定理可知,存在唯一x0∈(0,π),使得f'(x0)=0,且f(x)在[0,x0]上单调递增,在[x0,π]上单调递减.故f(x)的最小值等于f(0)=4和f(π)=aπ中较小的一个值.
题型二 讨论函数的单调性例2(2019湖北八校联考一,21)已知函数f(x)=x3+ x2-4ax+1(a∈R).(1)略;(2)若函数h(x)=a(a-1)ln x-x3+3x+f(x),讨论函数h(x)的单调性.
--
--
解题心得在判断函数f(x)的单调性时,若f'(x)中含有参数不容易判断其正负时,需要对参数进行分类讨论,分类的标准:(1)按导函数是否有零点分大类;(2)在大类中按导函数零点的大小分小类;(3)在小类中按零点是否在定义域中分类.
当-1<x<0时,g'(x)<0;当x>0时,g'(x)>0.故当x>-1时,g(x)≥g(0)=0,且仅当x=0时,g(x)=0,从而f'(x)≥0,且仅当x=0时,f'(x)=0.所以f(x)在(-1,+∞)单调递增.又f(0)=0,故当-1<x<0时,f(x)<0;当x>0时,f(x)>0.
--
--
题型二 求函数的极值、最值例2(2019四川成都七中一模,21)已知函数f(x)=xsin x+2cos x+ax+2,其中a为常数.(1)略;(2)求函数f(x)在[0,π]上的最小值.
--
解: (2)对∀x∈[0,π],f'(x)=xcos x-sin x+a,令g(x)=xcos x-sin x+a,g'(x)=-xsin x≤0,所以f'(x)在区间[0,π]上单调递减.当a≤0时,f'(x)≤f'(0)=a≤0,∴f(x)在区间[0,π]上单调递减,故fmin(x)=f(π)=aπ.当a≥π时,f'(x)≥f'(π)=a-π≥0,∴f(x)在区间[0,π]上单调递增,故fmin(x)=f(0)=4.当0<a<π时,因为f'(0)=a>0,f'(π)=a-π<0,且f'(x)在区间[0,π]上单调递减,结合零点存在定理可知,存在唯一x0∈(0,π),使得f'(x0)=0,且f(x)在[0,x0]上单调递增,在[x0,π]上单调递减.故f(x)的最小值等于f(0)=4和f(π)=aπ中较小的一个值.
高考数学复习考点知识讲解课件15 导数的概念及运算

=
y′u·u′x
,即 y 对 x 的导数等于 y 对 u 的导数与 u 对 x 的导数的乘积.
— 7—
(新教材) 高三总复习•数学
— 返回 —
常用结论 1.f′(x0)代表函数 f(x)在 x=x0 处的导数值;[f(x0)]′是函数值 f(x0)的导数,则[f(x0)]′ =0. 2.在点处的切线,该点一定是切点,切线有且仅有一条;过点处的切线,该点不一 定是切点,切线至少有一条. 3.函数 y=f(x)的导数 f′(x)反映了函数 f(x)的瞬时变化趋势,其正负号反映了变化的 方向,其大小|f′(x)|反映了变化的快慢,|f′(x)|越大,曲线在这点处的切线越“陡”.
— 22 —
(新教材) 高三总复习•数学
— 返回 —
(1)求曲线在点 P(x0,y0)处的切线,则表明 P 点是切点,只需求出函数在 P 处的导数, 然后利用点斜式写出切线方程,若在该点 P 处的导数不存在,则切线垂直于 x 轴,切线方 程为 x=x0.
(2)求曲线的切线方程要分清“在点处”与“过点处”的切线方程的不同.过点处的 切点坐标不知道,要设出切点坐标,根据斜率相等建立方程(组)求解,求出切点坐标是解 题的关键.
— 13 —
(新教材) 高三总复习•数学
— 返回 —
6.(2022·江苏常州期末)已知定义域都是 R 的两个不同的函数 f(x),g(x)满足 f′(x)=
g(x),且 g′(x)=f(x).写出一个符合条件的函数 f(x)的解析式,则 f(x)= ______ex_+__e_-_x_(答__案__不__唯__一__)_________.
(-3Δt-6)=-6.
— 10 —
(新教材) 高三总复习•数学
高考数学一轮复习-《导数及应用》第3课时-导数的应用(二)—极值与最值课件
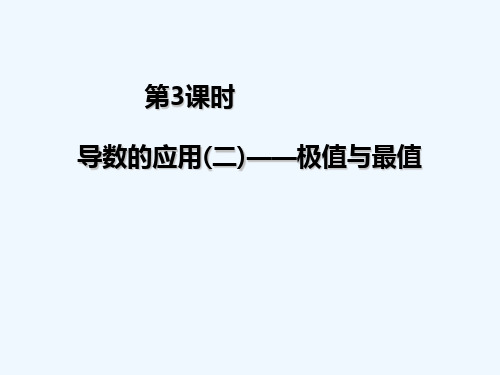
x>2
f′(x)>0
x<2
,解得c=6
授人以渔
题型一 利用导数研究函数极值
例1
已
知函数
f(x)=
ax3-
3x2+
3 1-a(a∈
R且
a≠
0),
求函数f(x)的极大值与极小值.
2 【解析】 由题设知a≠0,f′(x)=3ax2-6x=3ax(x-a).
2 令f′(x)=0得x=0或x=a.
• 当a>0时,随x的变化,f′(x)与f(x)的变化情况如下:
(2)若函数f(x)=x3-3x+a有3 个不同的零点,则实数a
的取值范围是(
)
A. (- 2,2)
B. [- 2,2]
C. (- ∞,- 1)
ቤተ መጻሕፍቲ ባይዱ
D.(1,+∞)
【解析】 f′(x)=3x2-3,令f′(x)=0,∴x=±1.三
次 函数 f(x)= 0有 3个根
⇔f(x)极大值>0且f(x)极小值<0 ∴x=-1为极大值点, x=1为极小值点.
2
43
f(x)极小值=f(a)=-a2-a+1.
• 探究1 掌握可导函数极值的步骤: • (1)确定函数的定义域. • (2)求方程f′(x)=0的根. • (3)用方程f′(x)=0的根和不可导点的x的值顺次将函数的定义域分成若干
个小开区间,并形成表格. • (4)由f′(x)=0的根左右的符号以及f′(x)在不可导点左右的符号来判断f′(x)
• 解析 y′=ex+m,则ex+m=0必有根,∴m=-ex<0.
• 4.已知f(x)=2x3-6x2+m(m为常数)在[-2,2]上有最大值3,那么此函 数在[-2,2]上的最小值是( )
2024年高考数学一轮复习(新高考版)《利用导数研究函数的零点》课件

即x-y-3=0.
(2)若函数f(x)在(0,16]上有两个零点,求a的取值范围.
①当 a≤0 时,f′(x)=ax- 1x<0, 则f(x)在(0,+∞)上单调递减,不符合题意; ②当 a>0 时,由 f(x)=aln x-2 x=0 可得2a=lnxx, 令 g(x)=lnxx,其中 x>0,则直线 y=2a与曲线 y=g(x)的图象在(0,16] 内有两个交点,
即 g(x)在π2,π上单调递减,又 gπ2=1>0,g(π)=-π<0, 则存在 m∈π2,π,使得 g(m)=0, 且当 x∈π2,m时,g(x)>g(m)=0, 即 f′(x)>0,则 f(x)在π2,m上单调递增, 当x∈(m,π]时,有g(x)<g(m)=0,即f′(x)<0, 则f(x)在(m,π]上单调递减,
由图可知,当 ln 2≤2a<2e,
即 e<a≤ln22时, 直线 y=2a与曲线 y=g(x)的图象在(0,16]内有 两个交点,
即f(x)在(0,16]上有两个零点, 因此,实数 a 的取值范围是e,ln22.
题型三 构造函数法研究函数的零点
例3 (12分)(2022·新高考全国Ⅰ)已知函数 f(x)=ex-ax和g(x)=ax-ln x有相同的最小值. (1)求a; [切入点:求f(x),g(x)的最小值] (2)证明:存在直线y=b,其与两条曲线y= f(x)和y=g(x)共有三个不同的交点,并且从 左到右的三个交点的横坐标成等差数列.
又 f π2=π2-1>0,f(π)=-1<0, 所以f(x)在(m,π]上有且只有一个零点, 综上,函数y=f(x)在[0,π]上有2个零点.
思维升华
2025年高考数学一轮复习课件第三章一元函数的导数及其应用-专题突破7导数的综合应用

并且从左到右的三个交点的横坐标成等差数列.
【拆解】
分类
第一问
第二问
参考赋分
6分
6分
难易
中上
难
返回至目录
续表
①总体看,题目为指数型函数与对数型函数的最值及图象交点问题,实际考
查利用导数研究函数零点问题.
②第一问是根据函数单调性求最值问题,根据最小值相等可求.注意分类讨
审题
要点
论.
③第二问是构造新函数利用零点个数解决问题.根据(1)可得当 > 1时,
所以函数 在 0,1 上单调递增,在 1, +∞ 上单调递减, 的最大值为 1 = 1.
所以 ≤ 1,即实数的取值范围是(−∞, 1].
返回至目录
考点三 利用导数研究函数零点
例3 已知函数 = − e + ,讨论函数 零点的个数.
解:′ = 1 − e .
返回至目录
第一问
在基础性的层次上考查
数学运算学科素养,和
.
2
e −1
恒成立.
− 1 + 1 > 0 ,所以′ = e ⋅ > 0,所以 在 0, +∞ 上单调
递增.
所以 > 0 = 0,所以ℎ′ > 0,所以ℎ 在 0, +∞ 上单调递增.
由洛必达法则,知 lim+ ℎ =
→0
e −1
lim
→0+
e − = 的解的个数、 − ln = 的解的个数均为2,构建新函数
= − ,利用导数可得该函数只有一个零点且可得 , 的
大小关系,根据存在直线 = 与曲线 = , = 有三个不同的交点
【拆解】
分类
第一问
第二问
参考赋分
6分
6分
难易
中上
难
返回至目录
续表
①总体看,题目为指数型函数与对数型函数的最值及图象交点问题,实际考
查利用导数研究函数零点问题.
②第一问是根据函数单调性求最值问题,根据最小值相等可求.注意分类讨
审题
要点
论.
③第二问是构造新函数利用零点个数解决问题.根据(1)可得当 > 1时,
所以函数 在 0,1 上单调递增,在 1, +∞ 上单调递减, 的最大值为 1 = 1.
所以 ≤ 1,即实数的取值范围是(−∞, 1].
返回至目录
考点三 利用导数研究函数零点
例3 已知函数 = − e + ,讨论函数 零点的个数.
解:′ = 1 − e .
返回至目录
第一问
在基础性的层次上考查
数学运算学科素养,和
.
2
e −1
恒成立.
− 1 + 1 > 0 ,所以′ = e ⋅ > 0,所以 在 0, +∞ 上单调
递增.
所以 > 0 = 0,所以ℎ′ > 0,所以ℎ 在 0, +∞ 上单调递增.
由洛必达法则,知 lim+ ℎ =
→0
e −1
lim
→0+
e − = 的解的个数、 − ln = 的解的个数均为2,构建新函数
= − ,利用导数可得该函数只有一个零点且可得 , 的
大小关系,根据存在直线 = 与曲线 = , = 有三个不同的交点
高考数学一轮复习导数在函数中的应用-教学课件

聚焦中考——语文 第五讲
表达方式与记叙的顺序
• (2013·荆门)阅读下文,完成习题。 • ①那天下午6点多,该上公交车的人早已上了车,唯独有个小女孩,在车
门边来回徘徊。眼看着司机就要开车了,我在想,这小女孩肯定是没钱 上车。 ②“小姑娘,上车吧,我帮你交车票钱。”当看到我为她刷完卡后,她 随即上了车,说了声“谢谢阿姨”,一时脸蛋儿全红了。近距离一看, 才发现,小女孩左侧脸上有颗小痣。几天前的一幕不由浮现眼前—— ③送走远方的朋友,我从火车站迎着风雨赶到就近的公交车站台,已是 下午5点多。这时正是下班高峰期,来了几辆公交车,我总也挤不上去。 雨还在急速地下着,人还在不断地涌来。当又一辆10路公交驶来后,我 和许多人一起先往前门挤,但挤不上去。等司机发话后,才从后门好不 容易挤上车。车内人头攒动,人满为患。这人贴人的,身体若要移动一 下都难。正感叹着,我突然感觉好像有一件事还没做。是什么事呢?哦, 对了,没买车票。本想挤到前面去交车钱,可大伙儿都好像没事人一样 在原地一动不动,根本挤不过去。见此情形,司机也没说什么,这样, 我也就心安理得地和大家一样坐了一次免费的公交车。
本题在当年的高考中,出错最多的就是将第(1)题 的 a=4 用到第(2)题中,从而避免讨论,当然这是错误的.
【互动探究】 1.(2011 届广东台州中学联考)设 f′(x)是函数 f(x)的导函数,
将 y=f(x)和 y=f′(x)的图象画在同一直角坐标系中,不可能正确 的是( D )
考点2 导数与函数的极值和最大(小)值
高考数学一轮复习导数在函数中的应用-教学课件
第2讲 导数在函数中的应用
考纲要求
考纲研读
1.了解函数单调性和导数的关系;能利用 1.用导数可求函数的单 导数研究函数的单调性,会求函数的单调 调区间或以单调区间为 区间(对多项式函数一般不超过三次). 载体求参数的范围.
高考数学-导数-专题复习课件

)
v0t
,求1物gt体2 在时刻
2
时的瞬t0时速度.
解析:
s(t)
v0
1 2
g
2t
v0
gt
∴物体在 t时0 刻瞬时速度为 s(t0 ) v0 gt0. 题型四 导数的几何意义及几何上的应用
【例4】(12分)已知曲线 y 1 x3 4 .
33
(1)求曲线在点P(2,4)处的切线方程; (2)求过点P(2,4)的曲线的切线方程.
x0
x0
x0
典例分析
题型一 利用导数求函数的单调区间
【例1】已知f(x)= e-xax-1,求f(x)的单调增区间.
分析 通过解f′(x)≥0,求单调递增区间.
解 ∵f(x)= -aexx -1,∴f′(x)= -a. ex 令f′(x)≥0,得 ≥ae. x 当a≤0时,有f′(x)>0在R上恒成立; 当a>0时,有x≥ln a. 综上,当a≤0时,f(x)的单调增区间为(-∞,+∞); 当a>0时,f(x)的单调增区间为[ln a,+∞).
分析 (1)在点P处的切线以点P为切点.关键是求出切线斜率k=f′(2). (2)过点P的切线,点P不一定是切点,需要设出切点坐标.
解(1)∵y′= ,…x2……………………………2′ ∴在点P(2,4)处的切线的斜率 k y |x..23′ 4. ∴曲线在点P(2,4)处的切线方程为y-4=4(x-2), 即4x-y-4=0……………………………………….4′ (2)设曲线 y 1 x过3 点4 .P(2,4)的切线相切于点
33
则切线的斜率 k y |xx0……x02…. …………..6′
∴切线方程为
y
(1 3
浙江省2020版高考数学专题3导数及其应用3.2导数的应用课件

3.当求出的函数单调区间(如单调增区间)有多个时,不能把这些区间取 并集. 4.f '(x)>0(或f '(x)<0)是f(x)在某一区间上为增函数(或减函数)的充分不必 要条件.
5.f '(x)≥0(或f '(x)≤0)是f(x)在某一区间上为增函数(或减函数)的必要不 充分条件. 考向突破 考向一 单调性的判断 例1 (2018浙江温州二模(3月),8)已知函数f(x)与f '(x)的图象如图所示,
1 1 1 3 (i)若1≤x≤2,则ln x≥0, f(x)=aln x+x- ≤x- ≤2- = . x x 2 2
当a=0,x=2时取等号. (10分)
(ii)若 ≤x<1,则ln x<0, f(x)=aln x+x- ≤- ln x+x- .
1 2 1 3 1 5 所以当 ≤x<1时,g(x)≤g = ln 2 . (13分) 2 2 2 2 5 3 5 3 3 3 因为 ln 2- < - =1< ,所以f(x)≤ . 2 2 2 2 2 2 3 综上, f(x)max= . 2 3 于是bmin= . (15分) 2
答案 C
考点二
考向基础
导数与极值、最值
1.设函数f(x)在点x0附近有定义,如果对x0附近的所有的点,都有f(x)< f(x0),则f(x0)是函数f(x)的一个极大值,记作y极大值=f(x0);如果对x0附近的所 有的点,都有f(x)>f(x0),则f(x0)是函数f(x)的一个极小值,记作y极小值=f(x0).极 大值与极小值统称为极值. 2.当函数f(x)在x=x0处连续时,判断f(x0)是极大(小)值的方法: (1)如果x<x0时有f '(x)>0,x>x0时有f '(x)<0,则f(x0)是① 极大值 ; (2)如果x<x0时有f '(x)<0,x>x0时有f '(x)>0,则f(x0)是② 极小值 . 3.函数的最大值与最小值 设函数f(x)在[a,b]上连续,在(a,b)内可导,先求f(x)在(a,b)内的极值;将f(x)
5.f '(x)≥0(或f '(x)≤0)是f(x)在某一区间上为增函数(或减函数)的必要不 充分条件. 考向突破 考向一 单调性的判断 例1 (2018浙江温州二模(3月),8)已知函数f(x)与f '(x)的图象如图所示,
1 1 1 3 (i)若1≤x≤2,则ln x≥0, f(x)=aln x+x- ≤x- ≤2- = . x x 2 2
当a=0,x=2时取等号. (10分)
(ii)若 ≤x<1,则ln x<0, f(x)=aln x+x- ≤- ln x+x- .
1 2 1 3 1 5 所以当 ≤x<1时,g(x)≤g = ln 2 . (13分) 2 2 2 2 5 3 5 3 3 3 因为 ln 2- < - =1< ,所以f(x)≤ . 2 2 2 2 2 2 3 综上, f(x)max= . 2 3 于是bmin= . (15分) 2
答案 C
考点二
考向基础
导数与极值、最值
1.设函数f(x)在点x0附近有定义,如果对x0附近的所有的点,都有f(x)< f(x0),则f(x0)是函数f(x)的一个极大值,记作y极大值=f(x0);如果对x0附近的所 有的点,都有f(x)>f(x0),则f(x0)是函数f(x)的一个极小值,记作y极小值=f(x0).极 大值与极小值统称为极值. 2.当函数f(x)在x=x0处连续时,判断f(x0)是极大(小)值的方法: (1)如果x<x0时有f '(x)>0,x>x0时有f '(x)<0,则f(x0)是① 极大值 ; (2)如果x<x0时有f '(x)<0,x>x0时有f '(x)>0,则f(x0)是② 极小值 . 3.函数的最大值与最小值 设函数f(x)在[a,b]上连续,在(a,b)内可导,先求f(x)在(a,b)内的极值;将f(x)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 点评:给定解析式求函数的图象是近几年高考重点,并且 难度在增大,多数需要利用导数研究单调性知其变化趋势, 利用导数求极值(最值)研究零点.
•
对点训练 (2015·杭州质检)设函数f(x)=x2sinx,则
函数f(x)的图象可能为( )
• 【解析】 因为f(-x)=(-x)2sin(-x)=-x2sinx=-f(x), 所以f(x)是奇函数.又因为f′(x)=2xsinx+x2cosx,所以f′(0) =0,排除A;且当x∈[0,π]时,函数值为正实数,排除B; 当x∈(π,2π)时,函数值为负实数,排除D,故选C.
(1)求 a,b; (2)证明:f(x)>1. 【解析】 (1)函数 f(x)的定义域为(0,+∞), f′(x)=aexlnx+axex-xb2ex-1+bxex-1. 由题意可得 f(1)=2,f′(1)=e.故 a=1,b=2.
(2)证明:由(1)知,f(x)=exlnx+2xex-1=exx(xlnx+2e), 从而 f(x)>1 等价于 xlnx>xe-x-2e. 设函数 g(x)=xlnx,则 g′(x)=1+lnx. 所以当 x∈0,1e时,g′(x)<0; 当 x∈1e,+∞时,g′(x)>0.
(2)由题设 g(x)=f′(x)-3x=1x-xm2-3x(x>0), 令 g(x)=0,得 m=-13x3+x(x>0). 设 φ(x)=-13x3+x(x≥0), 则 φ′(x)=-x2+1=-(x-1)(x+1). 当 x∈(0,1)时,φ′(x)>0,φ(x)在(0,1)上单调递增; 当 x∈(1,+∞)时,φ′(x)<0,φ(x)在(1,+∞)上单调递 减.
• 故f(x)的单调递减区间是(-∞,ln2),单调递增区间是(ln2,+∞).
• f(x)在x=ln2处取得极小值,极小值为f(ln2)=eln2-2ln2+2a=2(1-ln2 +a).
• (2)设g(x)=ex-x2+2ax-1,x∈R.于是g′(x)=ex-2x+ 2a,x∈R.
• 由(1)知当a>ln2-1时,g′(x)最小值为g′(ln2)=2(1-ln2+ a)>0.于是对任意x∈R,都有g′(x)>0,
g(x)在(0,+∞)上是增函数,可利用2x+2a,x∈R,得f′(x)=ex-2,x∈R.令 f′(x)=0,得x=ln2.
• 于是当x变化时,f′(x),f(x)的变化情况如下表:
x
(-∞,ln2)
ln2
(ln2,+∞)
f′(x)
-
0
+
f(x)
2(1-ln2+a)
题型二 导数与不等式
• 例2 (2015·沧州七校联考)设a为实数,函数f(x)=ex-2x+2a,x∈R. • (1)求f(x)的单调区间与极值; • (2)求证:当a>ln2-1且x>0时,ex>x2-2ax+1. • 【思路】 (1)令f′(x)=0,求极值点,然后讨论在各个区间上的单调
性. • (2)构造函数g(x)=ex-x2+2ax-1(x∈R),注意到g(0)=0,只需证明
【解析】 (1)由题设,当 m=e 时,f(x)=lnx+ex, 则 f′(x)=x-x2 e. ∴当 x∈(0,e)时,f′(x)<0,f(x)在(0,e)上单调递减; 当 x∈(e,+∞)时,f′(x)>0,f(x)在(e,+∞)上单调递 增. ∴当 x=e 时,f(x)取得极小值 f(e)=lne+ee=2. ∴f(x)的极小值为 2.
• 所以g(x)在R内单调递增. • 于是当a>ln2-1时,对任意x∈(0,+∞),都有
g(x)>g(0). • 又g(0)=0,从而对任意x∈(0,+∞),g(x)>0. • 即ex-x2+2ax-1>0,故ex>x2-2ax+1.
• 点评:利用导数工具,证明不等式的关键在于要构造好函 数的形式,转化为研究函数的最值或值域问题,有时需用 到放缩技巧.
题型三 导数与方程
例 3 (2014·陕西文)设函数 f(x)=lnx+mx ,m∈R. (1)当 m=e(e 为自然对数的底数)时,求 f(x)的极小值; (2)讨论函数 g(x)=f′(x)-3x零点的个数; (3)若对任意 b>a>0,fbb--faa<1 恒成立,求实数 m 的取 值范围.
• 求证不等式f(x)≥g(x),一种常见思路是用图像法来说明函 数f(x)的图像在函数g(x)图像的上方,但通常不易说明.于 是通常构造函数F(x)=f(x)-g(x),通过导数研究函数F(x) 的性质,进而证明欲证不等式.
对点训练 (2014·新 课 标 全 国 Ⅰ 理 ) 设 函 数 f(x) = aexlnx+be··exx,曲线 y=f(x)在点(1,f(1))处的切线方程为 y=e(x -1)+2.
导数的综合运用
题型一 导数与函数图象
例 1 (2015·潍坊模拟)已知 f(x)=14x2+sin(π2+x),f′(x) 为 f(x)的导函数,则 y=f′(x)的图象大致是( )
【解析】 因为 f(x)=14x2+cosx,所以 f′(x)=12x-sinx, f′(x)为奇函数,排除 B,D,令 g(x)=12x-sinx,则 g′(x) =12-cosx,当 0<x<π3时,g′(x)<0,f′(x)单调递减,当π3<x<53π 时,g′(x)>0,f′(x)单调递增,当53π<x<2π 时,g′(x)<0,f′(x) 单调递减,故选 A.
故 g(x)在0,1e上单调递减,在1e,+∞上单调递增, 从而 g(x)在(0,+∞)上的最小值为 g1e=-1e.
设函数 h(x)=xe-x-2e=exx-2e,则 h′(x)=e-x(1-x). 所以当 x∈(0,1)时,h′(x)>0;当 x∈(1,+∞)时,h′(x)<0. 故 h(x)在(0,1)上单调递增,在(1,+∞)上单调递减.从而 h(x) 在(0,+∞)上的最大值为 h(1)=-1e. 综上,当 x>0 时,g(x)>h(x),即 f(x)>1.
