七年级平行线性质练习题
初中七年级的平行线的判定与性质练习试题带含答案

读书破万卷下笔如有神平行线的判断与性质练习一、选择题1.以下命题中,不正确的选项是____[]A.两条直线被第三条直线所截,假好像位角相等,那么这两条直线平行B.两条直线被第三条直线所截,假好像旁内角互补,那么这两条直线平行C.两条直线被第三条直线所截,那么这两条直线平行D.若是两条直线都和第三条直线平行,那么这两条直线也互相平行2.如图,可以获取DE∥BC的条件是______[]( 2 题)( 3 题)( 5 题)A .∠=∠BAC B.∠+∠=180° C .∠+∠=180° D .∠=∠BADACB ABC BAE ACB BAD ACB 3.如图,直线a、 b 被直线 c 所截,现给出以下四个条件:(1)∠ 1=∠ 2, (2) ∠ 3=∠ 6, (3) ∠4+∠ 7=180°, (4) ∠ 5+∠ 8=180°,其中能判断a∥b 的条件是_________[ ]A. (1)(3) B . (2)(4) C . (1)(3)(4)D . (1)(2)(3)(4) 4.一辆汽车在笔直的公路上行驶,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是 ________[ ]A.第一次向右拐40°,第二次向左拐40° B .第一次向右拐50°,第二次向左拐130°C.第一次向右拐50°,第二次向右拐130° D .第一次向左拐50°,第二次向左拐130°5.如图,若是∠ 1=∠ 2,那么下面结论正确的选项是_________. [ ]A.∥B.∥ C .∠ 3=∠ 4D .∠ =∠C AD BC AB CD A6.如图, a∥ b, a、 b 被 c 所截,获取∠1=∠2 的依照是()A.两直线平行,同位角相等B.两直线平行,内错角相等C.同位角相等,两直线平行D.内错角相等,两直线平行(6题) (8 题) (9 题)7.同一平面内有四条直线a、 b、 c、 d,若 a∥ b, a⊥c, b⊥ d,则直线 c、 d 的地址关系为()A.互相垂直B.互相平行C.订交D.无法确定8.如图, AB∥ CD,那么()A.∠ 1=∠ 4 B.∠ 1=∠ 3C.∠ 2=∠ 3D.∠ 1=∠59.如图,在平行四边形ABCD中,以下各式不用然正确的选项是()A.∠ 1+∠ 2=180°B.∠ 2+∠ 3=180°C.∠ 3+∠ 4=180°D.∠ 2+∠ 4=180°10.如图, AD∥ BC,∠ B=30°, DB均分∠ ADE,则∠ DEC的度数为()A. 30°B.60°C.90°D.120°(10 题)(11题)二、填空题11.如图,由以下条件可判断哪两条直线平行,并说明依照.(1) ∠ 1=∠ 2,________________________ . (2) ∠A=∠ 3, ________________________ . (3) ∠ABC+ ∠ C=180°,________________________.12.若是两条直线被第三条直线所截,一组同旁内角的度数之比为3∶ 2,差为 36°,那么这两条直线的地址关系是________.13.同垂直于一条直线的两条直线________.14.如图,直线EF分别交AB、CD于G、H.∠ 1=60°,∠ 2=120°,那么直线AB与CD的关系是 ________,原由是: ____________________________________________ .( 14 题)(15题)15.如图, AB∥ EF, BC∥DE,则∠ E+∠ B 的度数为 ________.三、解答题16.已知:如图,∠ 1=∠ 2,且BD均分∠ABC.求证:AB∥CD.17.已知:如图,AD 是一条直线,∠1=65°,∠ 2=115°.求证: BE∥ CF.18.已知:如图,∠1=∠2,∠ 3=100°,∠B=80°.求证:EF∥C D.19.已知:如图,FA⊥ AC, EB⊥ AC,垂足分别为A、 B,且∠ BED+∠ D=180°.求证: AF∥ C D.20. 如图,已知∠ AMB=∠ EBF,∠ BCN=∠ BDE,求证:∠ CAF=∠ AFD.21. 如图,一条公路修到湖畔时,需拐弯绕湖而过,若是第一次拐的角A120°,第二次拐的角 B是是 150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯从前的道路平行,问∠ C是多少度?说明你的原由.23.( 1)如图,若 AB∥ DE,∠ B=135°,∠ D=145°,你能求出∠C 的度数吗?(2)在 AB∥DE的条件下,你能得出∠B、∠ C、∠ D 之间的数量关系吗?并说明原由.24.如图,在折线 ABCDEFG中,已知∠ 1=∠ 2=∠ 3=∠ 4=?∠ 5,?延长 AB、GF交于点 M.试试究∠ AMG与∠ 3 的关系,并说明原由.25.(开放题)已知如图,四边形 ABCD中, AB∥ CD,BC∥ AD,那么∠ A 与∠ C,∠ B 与∠ D 的大小关系如何?请说明你的原由.答案: CBDAB ABDDB7. (1)AD∥ BC 内错角相等,两直线平行(2)AD ∥BC 同位角相等,两直线平行(3) AB∥ DC 同旁内角互补,两直线平行8.平行9.平行10.平行∵∠ EHD =180°-∠ 2=180°- 120° =60 °,∠ 1=60°,∴∠ 1=∠ EHD ,∴ AB∥ CD (同位角相等,两直线平行). 8.证明:∵∠AMB=∠ DMN,又∠ENF=∠ AMB,∴∠ DMN=∠ ENF,∴BD∥CE.∴∠ BDE+∠ DEC=180°.又∠ BDE=∠ BCN,∴∠ BCN+∠ CED=180°,∴BC∥DE,∴∠ CAF=∠ AFD.点拨:本题重点是观察两直线平行的判断与性质.21.解:∠ C=150°.原由:如答图,过点 B 作 BE∥AD,则∠ ABE=∠ A=120°(两直线平行,内错角相等).∴∠ CBE=∠ ABC-∠ ABE=150° -120 ° =30°.∵BE∥ AD, CF∥ AD,∴BE∥ CF(平行于同一条直线的两直线平行).∴∠ C+∠ CBE=180°(两直线平行,同旁内角互补).∴∠ C=180°- ∠ CBE=180° -30 °=150°.22.解:( 1)如答图5-3-2 ,过点 C 作 CF∥AB,则∠ 1=180° - ∠B=180° -135 ° =45°(两直线平行,同旁内角互补).∵C F∥ AB, DE∥ AB,∴CF∥ DE(平行于同一条直线的两直线平行).∴∠ 2=∠ 180° - ∠ D=180° -145 ° =35°(两直线平行,同旁内角互补).∴∠ BCD=∠ 1+∠ 2=45° +35° =80°.(2)∠ B+∠ C+∠ D=360°.原由:如答图5-3-2 过点 C 作 CF∥ AB,得∠ B+∠1=180°(两直线平行,?同旁内角互补).∵C F∥ AB, DE∥ AB,∴CF∥ DE(平行于同一条直线的两直线平行).∴∠ D+∠ 2=180°(两直线平行,同旁内角互补).∴∠ B+∠ 1+∠ 2+∠ D=360°.即∠ B+∠ BCD+∠ D=360°.点拨:辅助线CF是联系 AB 与 DE的纽带.23.( 1) B(2)C24.解:∠ AMG=∠ 3.原由:∵∠ 1=∠ 2,∴AB∥ CD(内错角相等,两直线平行).∵∠ 3=∠ 4,∴CD∥ EF(内错角相等,两直线平行).∴AB∥ EF(平行于同一条直线的两直线平行).∴∠ AMG=∠ 5(两直线平行,同位角相等).又∠ 5=∠ 3,∴∠ AMG=∠ 3.点拨:因为∠ 3=∠ 5,所以欲证∠ AMG=∠3,只要证AM∥ EF即可.25.解:∠ A=∠ C,∠ B=∠ D.原由:∵ AD∥ BC,AB∥ CD,∴∠ A+∠ B=180°(两直线平行,同旁内角互补).∠C+∠ B=180°.∴∠ A=∠ C.同理∠ B=∠ D.。
平行线的判定与性质 专项强化练习 2022-2023学年人教版七年级数学下册

人教版七年级数学下册《平行线的判定与性质》专项强化练习一、选择题1.如图,AB∥CD,EF∥GH,且∠1=50°,下列结论错误的是( )A.∠2=130°B.∠3=50°C.∠4=130°D.∠5=50°2.如图,在下列条件中,不能判定直线a与b平行的是( )A.∠1=∠2B.∠2=∠3C.∠3=∠5D.∠3+∠4=180°3.如图,直线a,b被直线c所截,下列条件能判断a∥b的是( )A.∠1=∠2B.∠1=∠4C.∠3+∠4=180°D.∠2=30°,∠4=35°4.如图,BD∥EF,AE与BD交于点C,∠B=30°,∠A=75°,则∠E的度数为( )A.135° B.125° C.115° D.105°5.一条公路两次转弯后又回到到原来的方向(即AB∥CD,如图),如果第一次转弯时的∠B=140°,那么∠C应是( )A.40°B.140°C.100°D.180°6.如图,直线a∥b,直线c与直线a,b分别交于点D,E,射线DF⊥直线c,则图中与∠1互余的角有( )A.4个B.3个C.2个D.1个7.如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F;三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为()A.0B.1C.2D.38.如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数为()A.50°B.45°C.40°D.30°9.如图,直线a∥b,将一块含30°角(∠BAC=30°)的直角三角尺按图中方式放置,其中A和C两点分别落在直线a和b上.若∠1=20°,则∠2的度数为( )A.20° B.30° C.40° D.50°10.如图,直线AE∥CD,∠EBF=135°,∠BFD=60°,则∠D等于( )A.75°B.45°C.30°D.15°11.如图,l1∥l2,则下列式子成立的是( )A.∠α+∠β+∠γ=180°B.∠α+∠β-∠γ=180°C.∠β+∠γ-∠α=180°D.∠α-∠β+∠γ=180°12.如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°. 则下列结论:①∠BOE=12(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的个数有()A.1个B.2个C.3个D.4个二、填空题13.如图,请你添加一个条件,使得AD∥BC,你添加的条件是__________.14.如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=________.15.如图,a∥b,∠1=110°,∠3=40°,则∠2=.16.如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5;则一定能判定AB∥CD的条件有_____(填写所有正确的序号).17.已知一副三角板如图1摆放,其中两条斜边互相平行,则图2中∠1=________.18.如图,已知AB∥EF,∠C=90°,则α、β与γ的关系是.三、解答题19.如图,已知∠A=∠ADE,∠C=∠E.(1)若∠EDC=3∠C,求∠C的度数;(2)求证:BE∥CD.20.如图,已知∠1+∠2=180°,∠DEF=∠A,试判断∠ACB与∠DEB的大小关系,并证明.21.如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2,∠3=80°.(1)试证明∠2=∠DCB;(2)试证明DG∥BC;(3)求∠BCA的度数.22.如图,已知AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.(1)求证:AB∥CD;(2)求∠C的度数.23.如图,已知∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.24.如图,已知直线l1∥l2,直线l3和直线l1,l2交于点C和D,直线l3上有一点P.(1)如图1,若P点在C,D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化,并说明理由;(2)若点P在C,D两点的外侧运动时(P点与点C,D不重合,如图2和3),试直接写出∠PAC,∠APB,∠PBD之间的关系,不必写理由.25.(1)读读做做:平行线是平面几何中最基本、也是非常重要的图形.在解决某些平面几何问题时,若能依据问题的需要,添加恰当的平行线,往往能使证明顺畅、简洁.请根据上述思想解决教材中的问题:如图①,AB∥CD,则∠B+∠D ∠E(用“>”、“=”或“<”填空);(2)倒过来想:写出(1)中命题的逆命题,判断逆命题的真假并说明理由.(3)灵活应用如图②,已知AB∥CD,在∠ACD的平分线上取两个点M、N,使得∠AMN=∠ANM.求证:∠CAM=∠BAN.答案1.C2.C.3.B.4.D.5.B6.A.7.D8.C9.C10.D11.B12.C13.答案为:本题答案不唯一,如∠1=∠B.14.答案为:63°30′15.答案为:70°.16.答案为:①③④17.答案为:15°.18.答案为:α+β﹣γ=90°.19.证明:(1)∵∠A=∠ADE,∴AC∥DE.∴∠EDC+∠C=180°.又∵∠EDC=3∠C,∴4∠C=180°.即∠C=45°.(2)证明:∵AC∥DE,∴∠E=∠ABE.又∵∠C=∠E,∴∠C=∠ABE.∴BE∥CD.20.解:∠ACB与∠DEB相等,理由如下:证明:∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义),∴∠2=∠DFE(同角的补角相等),∴AB∥EF(内错角相等两直线平行),∴∠BDE=∠DEF(两直线平行,内错角相等),∵∠DEF=∠A(已知),∴∠BDE=∠A(等量代换),∴DE∥AC(同位角相等两直线平行),∴∠ACB=∠DEB(两直线平行,同位角相等).21.(1)证明:∵CD⊥AB于D,FE⊥AB,∴CD∥EF,∴∠2=∠DCB(2)证明:∵∠2=∠DCB,∠1=∠2,∴DG∥BC(3)解:∵DG∥BC,∠3=80°,∴∠BCA=∠3=80°22.解:(1)证明:∵AE⊥BC,FG⊥BC,∴AE∥GF.∴∠2=∠A.∵∠1=∠2,∴∠1=∠A.∴AB∥CD.(2)∵AB∥CD,∴∠D+∠CBD+∠3=180°.∵∠D=∠3+60°,∠CBD=70°,∴∠3=25°.∵AB∥CD,∴∠C=∠3=25°.23.证明:∵∠ABC+∠ECB=180°,∴AB∥DE,∴∠ABC=∠BCD,∵∠P=∠Q,∴PB∥CQ,∴∠PBC=∠BCQ,∵∠1=∠ABC﹣∠PBC,∠2=∠BCD﹣∠BCQ,∴∠1=∠2.24.解:(1)当P点在C,D之间运动时,∠APB=∠PAC+∠PBD. 理由:过点P作PE∥l1,∵l1∥l2,∴PE∥l2∥l1.∴∠PAC=∠APE,∠PBD=∠BPE.∴∠APB=∠APE+∠BPE=∠PAC+∠PBD.(2)当点P在C,D两点的外侧运动时,在l2下方时,则∠PAC=∠PBD+∠APB;在l1上方时,则∠PBD=∠PAC+∠APB.25.(1)解:过E作EF∥AB,如图①所示:则EF∥AB∥CD,∴∠B=∠BEF,∠D=∠DEF,∴∠B+∠D=∠BEF+∠DEF,即∠B+∠D=∠BED;故答案为:=;(2)解:逆命题为:若∠B+∠D=∠BED,则AB∥CD;该逆命题为真命题;理由如下:过E作EF∥AB,如图①所示:则∠B=∠BEF,∵∠B+∠D=∠BED,∠BEF+∠DEF=∠BED,∴∠D=∠BED﹣∠B,∠DEF=∠BED﹣∠BEF,∴∠D=∠DEF,∴EF∥CD,∵EF∥AB,∴AB∥CD;(3)证明:过点N作NG∥AB,交AM于点G,如图②所示:则NG∥AB∥CD,∴∠BAN=∠ANG,∠GNC=∠NCD,∵∠AMN是△ACM的一个外角,∴∠AMN=∠ACM+∠CAM,又∵∠AMN=∠ANM,∠ANM=∠ANG+∠GNC,∴∠ACM+∠CAM=∠ANG+∠GNC,∴∠ACM+∠CAM=∠BAN+∠NCD,∵CN平分∠ACD,∴∠ACM=∠NCD,∴∠CAM=∠BAN.。
(完整word版)七年级平行线的判定与性质练习题带答案
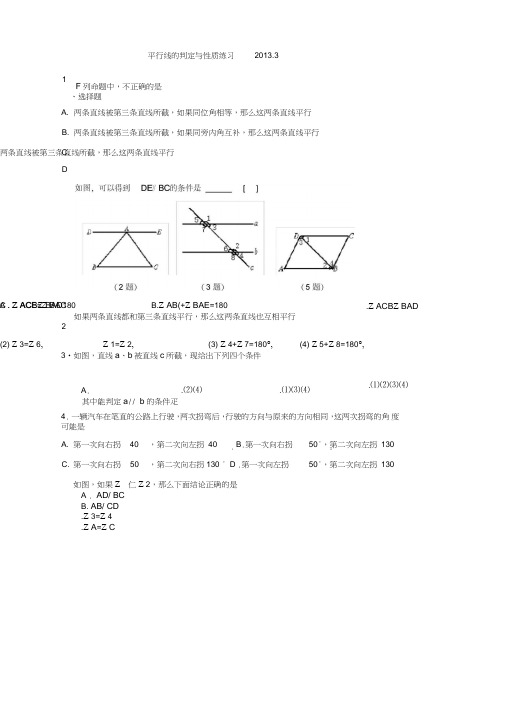
、选择题两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行如果两条直线都和第三条直线平行,那么这两条直线也互相平行3•如图,直线a 、b 被直线c 所截,现给出下列四个条件其中能判定a // b 的条件疋4. 一辆汽车在笔直的公路上行驶,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角 度可能是A . AD/ BC B. AB/ CD .Z 3=Z 4 .Z A =Z C平行线的判定与性质练习 2013.3A. 第一次向右拐 40 ,第二次向左拐 40B .第一次向右拐 50°,第二次向左拐 130C. 第一次向右拐 50 ,第二次向右拐130 ° D .第一次向左拐 50°,第二次向左拐 130如图,如果Z 仁Z 2,那么下面结论正确的是1. F 列命题中,不正确的是 A. C.两条直线被第三条直线所截,那么这两条直线平行 B. D.A . Z ACE =Z BAC B.Z AB(+Z BAE =180 C ACB Z BAD 180 .Z ACB Z BADZ 1=Z 2, (2) Z 3=Z 6, (3) Z 4+Z 7=180°, (4) Z 5+Z 8=180°,A .(1)(3) .⑵⑷ .⑴⑶⑷.⑴⑵⑶⑷2.OOA .两直线平行,同位角相等B .两直线平行,内错角相等C .同位角相等,两直线平行 A .互相垂直 8.如图,AB// CD 那么二、填空题11.如图,由下列条件可判定哪两条直线平行,并说明根据.7 C =180°,6.如图,a IIb , a 、 b 被c 所截, 得到/仁/2的依据是(A.Z 仁/4 B .Z 2=7 3 D . Z 1 = / 59.如图,在平行四边形ABCD 中,下列各式不一定正确的是(C. 7 10 .如图, 1 + 7 2=180° 3+7 4=180°AD// BC, 7 B=30°.7 2+7 3=180° .7 2+7 4=180°,DB 平分7 ADE 则7 DEC 的度数为((1) 7 1 = 7 2,.(2) 7 A =7 3, .(3) 7 AB (+D .内错角相等,两直线平行D .无法确定B .互相平行.相交C 7.同c 、d 的位置关系为((10 题)A. 30° B . 60°直线的位置关系是13 .同垂直于一条直线的两条直线12 .如果两条直线被第三条直线所截,一组同旁内角的度数之比为3 : 2,差为 36°,那么这两条14.如图,直线EF分别交ABCD于GH Z仁60°,/ 2=120°,那么直线AB与CD的关系是____________理由是:________________________________________________ .15 .如图,AB// EF, BC// DE 则Z E+Z B 的度数为(14 题)(15 题)求证:EF// CD.B,且Z BED Z D =180三、解答题BE // CF .OA、20.如图,已知/ AMB=/ EBF / BCN 2 BDE 求证:/ CAF=/ AFD23. (1)如图,若 AB// DE / B=135°,Z D=145°,你能求出/ C 的度数吗?(2)在AB// DE 的条件下,你能得出/ B 、/ C 、/ D 之间的数量关系吗?并说明理由.24. 如图,在折线 ABCDEF 叩,已知/ 1 = / 2=/ 3=/ 4=?/ 5, ?延长AB GF 交于点 M.试探索/ AMG与/ 3的关系,并说明理由.25.(开放题)已知如图,四边形 ABCD 中, AB// CD BC// AD,那么/ A 与/ C,/B 与/ D 的大小关系如何?请说明你的理由.21.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角 A 是120。
2022-2023学年人教版七年级数学下册《5-3平行线的性质》同步练习题(附答案)

2022-2023学年人教版七年级数学下册《5.3平行线的性质》同步练习题(附答案)一.选择题1.如图,AB∥EC,则下列结论正确的是()A.∠A=∠ECD B.∠A=∠ACE C.∠B=∠ACE D.∠B=∠ACB 2.如图,已知AB∥EF,DE∥BC,则与∠1相等的角有()A.1个B.2个C.3个D.4个3.已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为()A.20°B.30°C.45°D.50°4.如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为()A.40°B.50°C.60°D.70°5.如图,直线a∥b,直线c与a、b相交,∠1=55°,则∠2=()6.如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于()A.112°B.110°C.108°D.106°7.如图,直线a,b,a∥b,点C在直线b上,∠DCB=90°,若∠1=70°,则∠2的度数为()A.20°B.25°C.30°D.40°8.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐弯处的∠A是66°,第二次拐弯处的角是∠B,第三次拐弯处的∠C是153°,这时道路恰好和第一次拐弯之前的道路平行,则∠B是()A.87°B.93°C.39°D.109°9.一艘轮船从A港出发,沿着北偏东63°的方向航行,行驶至B处时发现前方有暗礁,所以转向北偏西27°方向航行,到达C后需要把航向恢复到出发时的航向,此时轮船航行的航向向顺时针方向转过的度数为()10.一把直尺与一块直角三角板按如图方式摆放,若∠1=47°,则∠2=()A.40°B.43°C.45°D.47°二.填空题(共6小题)11.如图,已知AB∥CD,CE平分∠ACD,交AB于点B,∠ABE=150°,则∠A为.12.如图,AB∥DE,FC⊥CD于点C,∠ABC=107°,∠CDE=130°,点G在BC的延长线上,则∠FCG的度数是.13.如图,直线a∥b,直线c与直线a,b分别交于点A,B.若∠1=45°,则∠2=.14.如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°),按如图所示放置,若∠1=55°,则∠2的度数为.15.如图,已知l1∥l2,直线l与l1、l2相交于C、D两点,把一块含30°角的三角尺按如图位置摆放.若∠1=130°,则∠2=.16.如图1是我们常用的折叠式小刀,图2中刀柄外形是一个矩形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图2所示的∠1与∠2,则∠1与∠2的度数和是度.三.解答题(共6小题)17.如图:已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.18.如图,MN∥BC,BD⊥DC,∠1=∠2=60°.(1)AB与DE平行吗?请说明理由;(2)若DC是∠NDE的平分线.①试说明∠ABC=∠C;②试说明BD是∠ABC的平分线.19.如图所示,已知AB∥CD,分别探讨下面四个图形中,∠APC,∠P AB与∠PCD的关系.20.如图所示,直线a∥b,AC丄AB,AC交直线b于点C,∠1=60°,求∠2的度数.21.如图,∠BAP+∠APD=180°,∠1=∠2,求证:∠E=∠F.22.如图,已知AB∥ED,∠C=90°,∠ABC=∠DEF,∠D=130°,∠F=100°,求∠E的大小.参考答案一.选择题1.解:∵AB∥EC,∴∠A=∠ACE,∠B=∠ECD.故选:B.2.解:如图所示,与∠1相等的角有∠B、∠DEF、∠EFC共3个,故选:C.3.解:∵直线m∥n,∴∠2=∠ABC+∠1=30°+20°=50°,故选:D.4.解:∵CD∥AB,∠ACD=40°,∴∠A=∠ACD=40°,∵在△ABC中,∠ACB=90°,∴∠B=90°﹣∠A=50°.故选:B.5.解:∵a∥b,∴∠1=∠3,∵∠1=55°,∴∠3=55°,又∵∠2=∠3,∴∠2=55°,故选:A.6.解:∵∠AGE=32°,∴∠DGE=148°,由折叠可得,∠DGH=∠DGE=74°,∵AD∥BC,∴∠GHC=180°﹣∠DGH=106°,故选:D.7.解:∵∠1=70°,∠1与∠3是对顶角,∴∠3=∠1=70°.∵a∥b,点C在直线b上,∠DCB=90°,∴∠2+∠DCB+∠3=180°,∴∠2=180°﹣∠3﹣∠DCB=180°﹣70°﹣90°=20°.故选:A.8.解:如图:过B作直线b平行于拐弯之前的道路a,由平行线的传递性得a∥b∥c,∵a∥b,∴∠A=∠1=66°,∵b∥c,∴∠2=180°﹣∠C=180°﹣153°=27°,∴∠ABC=∠1+∠2=66°+27°=93°.故选:B.9.解:根据题意,得AE∥BF,AM∥CN;∠A=63°,∠FBC=27°.∵AE∥BF,∴∠1=∠A=63°.∵AM∥CN,∴∠DCN=∠DBM=∠1+∠FBC=63°+27°=90°.故选:C.10.解:方法1:如图,∵∠1=47°,∠4=45°,∴∠3=∠1+∠4=92°,∵矩形对边平行,∴∠5=∠3=92°,∵∠6=45°,∴∠2=180°﹣45°﹣92°=43°.方法2:如图,作矩形两边的平行线,∵矩形对边平行,∴∠3=∠1=47°,∵∠3+∠4=90°,∴∠4=90°﹣47°=43°∴∠2=∠4=43°.故选:B.二.填空题11.解:∠ABC=180°﹣∠ABE=180°﹣150°=30.∵AB∥CD,∴∠BCD=∠ABC=30°.∵CE平分∠ACD,∴∠ACD=2∠BCD=60°.∴∠A=180°﹣∠ACD=180°﹣60°=120°.故答案为:120°.12.解:过点C作CH∥AB∴∠GCH=∠ABC=107°∴∠HCD+∠CDE=180°∴∠HCD=180°﹣130°=50°∴∠GCD=∠GCH﹣∠HCD=107°﹣50°=57°∴∠FCG=90°﹣57°=33°.故答案为33°.13.解:∵直线a∥b,∠1=45°,∴∠3=45°,∴∠2=180°﹣45°=135°.故答案为:135°.14.解:∵∠1=55°,∠A=60°,∴∠3=∠4=65°,∵a∥b,∴∠4+∠2=180°,∴∠2=115°.故答案为:115°.15.解:∵∠1=130°,∴∠3=50°,又∵l1∥l2,∴∠BDC=50°,又∵∠ADB=30°,∴∠2=20°,故答案为:20°.16.解:如图2,AB∥CD,∠AEC=90°,作EF∥AB,则EF∥CD,所以∠1=∠AEF,∠2=∠CEF,所以∠1+∠2=∠AEF+∠CEF=∠AEC=90°.故答案为90.三.解答题17.解:∵AB∥CF,∠ABC=70°,∴∠BCF=∠ABC=70°,又∵DE∥CF,∠CDE=130°,∴∠DCF+∠CDE=180°,∴∠DCF=50°,∴∠BCD=∠BCF﹣∠DCF=70°﹣50°=20°.18.解:(1)AB∥DE,理由如下:∵MN∥BC,(已知)∴∠ABC=∠1=60°.(两直线平行,内错角相等)又∵∠1=∠2,(已知)∴∠ABC=∠2.(等量代换)∴AB∥DE.(同位角相等,两直线平行);(2)①∵MN∥BC,∴∠NDE+∠2=180°,∴∠NDE=180°﹣∠2=180°﹣60°=120°.∵DC是∠NDE的平分线,∴∠EDC=∠NDC=∠NDE=60°.∵MN∥BC,∴∠C=∠NDC=60°.∴∠ABC=∠C.②∠ADC=180°﹣∠NDC=180°﹣60°=120°,∵BD⊥DC,∴∠BDC=90°.∴∠ADB=∠ADC﹣∠BDC=120°﹣90°=30°.∵MN∥BC,∴∠DBC=∠ADB=30°.∴∠ABD=∠DBC=∠ABC.∴BD是∠ABC的平分线.19.解:图1:∠APC=∠P AB+∠PCD.理由:过点P作PE∥AB,∵AB∥CD,∴AB∥PE∥CD(平行线的传递性),∴∠1=∠A,∠2=∠C,∴∠APC=∠1+∠2=∠P AB+∠PCD,即∠APC=∠P AB+∠PCD;图2:∠APC+∠P AB+∠PCD=360°.理由:过点P作PE∥AB.∵AB∥CD,∴AB∥PE∥CD(平行线的传递性),∴∠A+∠1=180°,∠2+∠C=180°,∴∠A+∠1+∠2+∠C=360°,∴∠APC+∠P AB+∠PCD=360°;图3:∠APC=∠PCD﹣∠P AB.理由:延长DC交AP于点E.∵AB∥CD,∴∠1=∠P AB(两直线平行,同位角相等);又∵∠PCD=∠1+∠APC,∴∠APC=∠PCD﹣∠P AB;图4:∴∠P AB=∠APC+∠PCD.理由:∵AB∥CD,∴∠1=∠P AB(两直线平行,内错角相等);又∵∠1=∠APC+∠PCD,∴∠P AB=∠APC+∠PCD.20.解:∵AC丄AB,∴∠BAC=90°,∵∠1=60°,∴∠B=180°﹣∠1﹣∠BAC=30°,∵a∥b,∴∠2=∠B=30°.21.证明:∵∠BAP+∠APD=180°(已知),∴AB∥CD(同旁内角互补,两直线平行).∴∠BAP=∠APC(两直线平行,内错角相等).又∵∠1=∠2(已知),∴∠FP A=∠EAP,∴AE∥PF(内错角相等,两直线平行).∴∠E=∠F(两直线平行,内错角相等).22.解:延长DC、AB交于G,∵ED∥AB,∠D=130°,∴∠G=50°,又∵∠BCD=90°,∠BCD=∠G+∠CBG,∴∠CBG=40°,∴∠ABC=140°,∴∠E=∠ABC=140°.。
七年级下册数学第五章第3节《平行线的性质》提高训练题 (25)(含答案解析)

【解析】
由平行线的性质可得∠A=∠3,由∠1=∠2可得AC∥DE,进而可得∠3=∠E,进一步即可得出结论.
解:∵AD∥BE(已知),
∴∠A=∠3(两直线平行,同位角相等),
又∵∠1=∠2(已知),
∴AC∥DE(内错角相等,两直线平行),
∴∠3=∠E(两直线平行,内错角相等),
∴∠A=∠E(等量代换).
七年级下册数学第五章第3节《平行线的性质》提高训练题 (25)
一、单选题
1.如图,将三角板的直角顶点放在直尺的一边上,若∠1=25°,则∠2的度数为()
A.55°B.60°C.65°D.75°
2.如图,已知CB∥DF,则下列结论成立的是()
A.∠1=∠2B.∠2=∠3C.∠1=∠3D.∠1+∠2=180º
2.B
【解析】
根据两条直线平行,同位角相等,即可判断.
解:∵CB∥DF,
∴∠2=∠3(两条直线平行,同位角相等).
故选:B.
本题考查了平行线的性质,解决本题的关键是掌握平行线的性质.
3.C
【解析】
根据两条直线平行,同位角相等得∠1的同位角是40°,再根据平角的定义和垂直定义即可求得∠2.
解:∵a∥b,
26.如图 ∥ , ____________
27.如图,若a//b,则图中x的度数是______________度.
28.一副直角三角尺按如图1所示方式叠放,现将含45°角的三角尺ADE固定不动,将含30°角的三角尺ABC绕顶点A顺时针转动,当两块三角尺至少有一组边互相平行,则∠BAD(0°<∠BAD<90°)所有符合条件的度数为_____.
∵FG⊥AB,CD⊥AB(已知).
∴∠GFB=90°,∠CDB=90°(垂直的定义).
七年级下数学《平行线的判定与性质》练习题 (26)

七年级下数学《平行线的判定与性质》练习题
1.“因为a∥b,b∥c,所以a∥c”,这个推理的依据是()
A.过直线外一点,有且只有一条直线与已知直线垂直
B.垂线段最短
C.平行于同一直线的两条直线平行
D.过一点有且只有一条直线与已知直线平行
【分析】根据平行公理的推论得出即可.
【解答】解:∵a∥b,b∥c,
∴a∥c(平行于同一直线的两直线平行),
由a∥b,b∥c推出a∥c不是根据过直线外一点,有且只有一条直线与已知直线垂直;
也不是根据垂相等最短,更不是根据过直线外一点有且只有一条直线与已知直线平行,而是根据平行于同一直线的两直线平行,
故选:C.
1。
七年级下册数学平行线的性质随堂练习题

七年级下册数学平行线的性质随堂练习题一、单选题1. 如图,已知a∥b,小华把三角板的直角顶点放在直线b上.若∠1=40∘,则∠2的度数为( ).A. 100∘B. 110∘C. 120∘D. 130∘2. 如图,已知直线a,b被直线c所截,且a∥b,若∠α=40∘,则∠β的度数为( )A. 140∘B. 50∘C. 60∘D. 40∘3. 在下列各图中,可以由题目条件得出∠1=∠2的图形个数为( )A. 1B. 2C. 3D. 44. 如图,∠ACD是△ABC的外角,CE∥AB.若∠ACB=75∘,∠ECD=50∘,则∠A的度数为( )A. 50∘B. 55∘C. 70∘D. 75∘5. 如图,已知直线a∥b,∠1=50∘,则∠2的度数为( )A. 140∘B. 130∘C. 50∘D. 40∘6. 如图,△ABC中,∠A=60∘,∠B=40∘,DE∥BC,则∠AED的度数是( )A. 50∘B. 60∘C. 70∘D. 80∘7. 如图,DA⊥AB,CD⊥DA,∠B=56∘,则∠C的度数是( )A. 154∘B. 144∘C. 134∘D. 124∘二、填空题8. 如图,AC∥BD,BC平分∠ABD,若∠EAF=130∘,则∠ACB=____.9. 如图,AB∥CD,AD平分∠BAE,∠D=25∘,则∠AEC的度数为____.10. 如图,a∥b,c与a,b都相交,∠1=50∘,则∠2=____.七年级下册数学平行线的性质随堂练习题答案和解析1. 【答案】D【解析】∵∠1+∠3=90∘,∠1=40∘∴∠3=90∘−40∘=50∘,∵a∥b,∴∠2+∠3=180∘,∴∠2=180∘−50∘=130∘.故答案是:130∘.2. 【答案】D【解析】首先根据对顶角相等可得∠1的度数,再根据平行线的性质可得∠β的度数.解:∵∠α=40∘,∴∠1=∠α=40∘,∵a∥b,∴∠β=∠1=40∘.故选:D.3. 【答案】C【解析】根据等腰三角形的性质对第一个图形进行判断,根据对顶角相等对第2个图进行判断;根据平行线的性质和对顶角相等对第3个图进行判断;根据三角形外角性质对第4个图进行判断.解:在第一个图中,∵AB=AC,∴∠1=∠2;在第二个图中,∠1=∠2;在第三个图中,∵a∥b,∴∠2=∠3,而∠1=∠3,∴∠1=∠2;在第四个图中,∠1>∠2.故选:C.4. 【答案】B【解析】先根据平角求出∠ACE,再根据平行线的性质得出∠A=∠ACE,代入求出即可.解:∵∠ACB=75∘,∠ECD=50∘,∴∠ACE=180∘−∠ACB−∠ECD=55∘,∵AB∥CE,∴∠A=∠ACE=55∘,故选:B.5. 【答案】B【解析】本题考查了平行线的性质以及邻补角,牢记"两直线平行,同位角相等"是解题的关键.由直线a∥b,利用"两直线平行,同位角相等"可求出∠3的度数,再结合∠2和∠3互补,即可求出∠2的度数.解:∵直线a∥b,∴∠3=∠1=50∘.又∵∠2+∠3=180∘,∴∠2=130∘.故选:B.6. 【答案】D【解析】利用三角形内角和定理求出∠C,再根据平行线的性质求出∠AED即可.解:∵∠C=180∘−∠A−∠B,∠A=60∘,∠B=40∘,∴∠C=80∘,∵DE∥BC,∴∠AED=∠C=80∘,故选:D.7. 【答案】D【解析】本题考查了平行线的判定和性质,熟练掌握平行线的判定和性质定理是解题的关键.根据平行线的判定和性质定理即可得到结论.解:∵DA⊥AB,CD⊥DA,∴∠A=∠D=90∘,∴∠A+∠D=180∘,∴AB∥CD,∴∠B+∠C=180∘,∵∠B=56∘,∴∠C=180∘−∠B=124∘,故选:D.8. 【答案】25∘【解析】根据邻补角的定义可求∠FAC,利用平行线的性质结合角平分线的定义,得出∠CBD=1∠ABD=25∘,进而得出答案.2解:∵∠EAF=130∘,∴∠FAC=50∘,∵AC∥BD,∴∠ABD=50∘,∵BC平分∠ABD,∠ABD=25∘,∴∠CBD=12∴∠ACB=25∘.故答案为:25∘.9. 【答案】50∘【解析】根据AB∥CD,AD平分∠BAE,∠D=25∘和平行线的性质、角平分线的性质,可以求得∠AEC的度数.解:∵AB∥CD,AD平分∠BAE,∠D=25∘,∴∠BAD=∠D,∠BAD=∠EAD,∴∠D=∠EAD=25∘,∵∠AEC=∠D+∠EAD,∴∠AEC=50∘,故答案为:50∘.10. 【答案】130∘【解析】∵a∥b,∠1=50∘,∴∠1=∠3=50∘,∴∠2=180∘−∠3=130∘.故答案为:130∘.。
北师大版七年级数学下册《平行线性质与判定的综合》基础训练(含答案)

《平行线性质与判定的综合》基础训练知识点1 综合运用平行线的性质与判定进行计算或说理1.如图,已知a∥b,∠1=58°,则∠2的大小是()A.122°B.85°C.58°D.32°2.如图,直线EB∥FD,直线c分别交EB、FD于点A、C,∠BAC的平分线交直线FD于点G,若∠2=50°,则∠1的度数是()A.50°B.60°C.80°D.100°3.如图,一块含有30°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是()A.14°B.15°C.16°D.17°4.如图,直线,,,a b c d ,已知,c a c b ⊥⊥,直线,,b c d 交于一点.若150︒∠=,则2∠等于( )A.60︒B.50︒C.40︒D.30︒5.如图,直线,a b 被直线,c d 所截.若12,3125︒∠=∠∠=,则4∠的度数是()A.65︒B.60︒C.55︒D.75︒6.如图,若180A ABC ︒∠+∠=,则下列结论正确的是( )A.12∠=∠B.23∠=∠C.13∠=∠D.24∠=∠7.如图,12,60A ︒∠=∠∠=,则ADC ∠=____________.8.如图,//,180BC DE E B ︒∠+∠=,则AB 和EF 的位置关系为____________.9.如图所示,//,,AB DC ABC ADC BF ∠=∠和DE 分别平分ABC ∠和ADC ∠.试说明://ED BF .解:因为BF 和DE 分别平分ABC ∠和ADC ∠(已知),所以EDC ∠=____________,ADC FBA ∠∠=_________ABC ∠(角平分线的定义). 又因为ADC ABC ∠=∠(已知),所以∠___________FBA =∠(等量代换). 因为//AB DC (已知),所以AED EDC ∠=∠(______________).所以∠______=∠_______(等量代换).所以//ED BF (______________).10.如图,已知180,B BCD B D ︒∠+∠=∠=∠.请你观察图形,写出E ∠和DFE ∠满足什么数量关系?并说明理由.知识点2 利用平行线的性质与判定解决实际问題11.如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120,为使管道对接,另一侧铺设的角度大小应为()A.120︒B.100︒C.80︒D.60︒12.如图,在,A B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42,,A B 两地同时开工,B地所挖水渠走向应为南偏东_________.13.一条建设中的高速公路要穿过一山体开挖一条隧道,甲、乙两工程队分别从山体两侧的,A B两点同时开工,现甲队从A点测得道路的走向是北偏东55,为了不浪费人力、物力,问乙队在B点处应该按β∠等于多少度开挖,才能够保证隧道准确接通?14.如图,B处在A处的南偏西45°方向,C处在B处的北偏东80°方向.(1)求∠ABC的度数;(2)要使CD∥AB,D处应在C处的什么方向?15.如图,已知CD⊥AB,GF⊥AB,∠B=∠ADE,试说明∠1=∠2.16.如图,已知AB∥CD,∠1=∠2,∠3=∠4,求证:(1)∠4=∠DAC;(2)AD∥BE.参考答案1、B 2.C 3.D4.答案:C解析:∵a ∥b,∴∠1=∠2,∵∠1=58°,∴∠2=58°,故选C.5.答案:C解析:∵EB ∥FD,∴∠BAG=∠2=50°,∵AG 平分∠BAC,∴∠GAC=∠BAG=50°,∴∠1=180°-∠BAG-∠GAC=80°,故选C.6.答案:C解析:根据题意可知∠2+∠3=60°,因为∠2=44°,所以∠3=16°,再根据直尺的对边平行,可知∠1=∠3=16°.7.120 8.平行 9.12 12EDC 两直线平行,内错角相等 FBA AED 同位角相等,两直线平行10.解:E DFE ∠=∠.理由如下:因为180,B BCD B D ︒∠+∠=∠=∠,所以180D BCD ︒∠+∠=.所以//AD BE .所以E DFE ∠=∠.11.D 12.4213.解:因为指北方向平行,且,A B 两点走向形成一条直线,即//CA DB ,所以a ∠和β∠就构成了一对同旁内角.所以180a β︒∠+∠=,即18055125β︒︒︒∠=-=.因此,乙队在B 点处应该按125β︒∠=开挖.14.答案:见解析解析:(1)如图,由题意,得∠FAB=45°.因为AF ∥BE,所以∠FAB=∠ABE=45°,因为∠EBC=80°,所以∠ABC=35°.(2)D处在C处的南偏西45°方向.理由如下:如图,因为CG∥BE,所以∠GCB=∠EBC=80°.因为∠GCD=45°,所以∠BCD=35°,所以∠ABC=∠BCD=35°,所以CD∥AB.15.答案:见解析解析:证明:∵∠B=∠ADE(已知),∴DE∥BC(同位角相等,两直线平行),∴∠1=∠DCB(两直线平行,内错角相等).∵CD⊥AB,GF⊥AB,∴∠BDC=90°,∠BFG=90°, ∴CD∥FG(同位角相等,两直线平行),∴∠2=∠DCB(两直线平行,同位角相等).∴∠1=∠2(等量代换).16.答案:见解析解析:证明:(1)∵AB∥CD,∴∠4=∠BAF.∵∠1=∠2,∴∠BAF=∠1+∠CAF=∠2+∠CAF=∠DAC,∴∠4=∠DAC.(2)∵∠4=∠DAC,∠3=∠4,∴∠3=∠DAC,∴AD∥BE.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行线的性质练习题1.如图,直线AB∥CD,EF平分∠AEG,∠DFH=13°,∠H=21°,求∠EFG的度数.2.完成下面的证明:如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD,求证:∠EGF=90°.证明:∵AB∥GH(已知),∴∠1=∠3(),又∵CD∥GH(已知),∴(两直线平行,内错角相等)∵AB∥CD(已知),∴∠BEF+=180°(两直线平行,同旁内角互补)∵EG平分∠BEF(已知),(角平分线定义),∴∠1=12又∵FG平分∠EFD(已知),∠EFD(),∴∠2=12(+∠EFD)∴∠1+∠2=12∴∠l+∠2=90°,∴∠3+∠4=90°(等量代换),即∠EGF=90°.3.如图,AB//DG, AD∥EF,(1)试说明:∠1+∠2=180°;(2)若DG是∠ADC的平分线,∠2=140°,求∠B的度数.4.如图,AB∥DC,AD∥BC,E为AB延长线上一点,连结DE与BC相交于点F,若∠BFE=∠E.试说明DE平分∠ADC.5.完成下面证明:如图,B是射线AD上一点,∠DAE=∠CAE,∠DAC=∠C=∠CBE (1)求证:∠DBE=∠CBE证明:∵∠C=∠CBE(已知)∴BE∥AC________∴∠DBE=∠DAC________∵∠DAC=∠C(已知)∴∠DBE=∠CBE________(2)请模仿(1)的证明过程,尝试说明∠E=∠BAE.6.已知AB∥DE,∠ABC=800,∠CDE=1400.请你探索出一种(只须一种)添加辅助线求出∠BCD度数的方法,并求出∠BCD的度数.7.已知:如图,AC∥DE,DC∥EF,CD平分∠BCA.试说明:EF平分∠BED.8.如图,在四边形ABCD中,∠BAD的角平分线与边BC交于点E,∠ADC的角平分线交直线AE于点O.(1)若点O在四边形ABCD的内部,①如图,若AD//BC,∠B=40°,∠C=70°,则∠DOE=_______°;②如图,试探索∠B、∠C、∠DOE之间的数量关系,并将你的探索过程写下来.(2)如图,若点O是四边形ABCD的外部,请你直接写出∠B、∠C、∠DOE之间的数量关系.9.如图,已知AB//CD,分别探究下列三个图形中∠APC和∠PAB,∠PCD的关系.结论:(1)__________________________(2)__________________________(3)__________________________10.已知射线AB∥射线CD,点E、F分别在射线AB、CD上.(1)如图①,点P在线段EF上,若∠A=25°,∠APC=70°,求∠C的度数;(2)如图②,若点P在射线FE上运动(不包括线段EF),猜想∠APC、∠A、∠C之间有怎样的数量关系?说明理由;(3)如图③,若点P在射线EF上运动(不包括线段EF),请直接写出∠A、∠APC、∠C之间的数量关系,不必说明理由.11.阅读第(1)题解答过程填理由,并解答第(2)题(1)已知:如图1 AB∥CD,P 为AB、CD 之间一点,求∠B+∠C+∠BPC 的大小.解:过点P 作PM∥AB∵AB∥CD(已知)∴PM∥CD _________∴∠B+∠1=180°________________∴∠C+∠2=180°______________∵∠BPC=∠1+∠2∴∠B+∠C+∠BPC=360°(2)我们生活中经常接触小刀,小刀刀柄外形是一个直角梯形(挖去一个小半圈)如图2,刀片上、下是平行的,转动刀片时会形成∠1 和∠2,那么∠1+∠2 的大小是否会随刀片的转动面改变?说明理由.12.小红和小明在研究一个数学问题:已知AB∥CD,AB和CD都不经过点E,探索∠E与∠A,∠C的数量关系.(一)发现:在如图1中,小红和小明都发现:∠AEC=∠A+∠C;小红是这样证明的:如图7过点E作EQ∥AB.∴∠AEQ=∠A()∵EQ∥AB,AB∥CD.∴EQ∥CD()∴∠CEQ=∠C∴∠AEQ+∠CEQ=∠A+∠C 即∠AEC=∠A+∠C.小明是这样证明的:如图7过点E作EQ∥AB∥CD.∴∠AEQ=∠A,∠CEQ=∠C∴∠AEQ+∠CEQ=∠A+∠C即∠AEC=∠A+∠C请在上面证明过程的横线上,填写依据:两人的证明过程中,完全正确的是.(二)尝试:(1)在如图2中,若∠A=110°,∠C=130°,则∠E的度数为;(2)在如图3中,若∠A=20°,∠C=50°,则∠E的度数为.(三)探索:装置如图4中,探索∠E与∠A,∠C的数量关系,并说明理由.(四)猜想:(1)如图5,∠B、∠D、∠E、∠F、∠G之间有什么关系?(直接写出结论)(2)如图6,你可以得到什么结论?(直接写出结论)13.在综合与实践课上,同学们以“一个含30∘的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线a,b且a//b和直角三角形ABC,∠BCA=900,∠BAC=30∘,∠ABC=60∘.操作发现:(1)在如图1中,∠1=46∘,求∠2的度数;(2)如图2,创新小组的同学把直线a向上平移,并把∠2的位置改变,发现∠2−∠1= 120∘,说明理由;实践探究:(3)缜密小组在创新小组发现结论的基础上,将如图中的图形继续变化得到如图,AC 平分∠BAM,此时发现∠1与∠2又存在新的数量关系,请直接写出∠1与∠2的数量关系.14.实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b 反射出的光线n与光线m平行,且∠1=38°,则∠2=°,∠3=°.(2)在(1)中,若∠1=55°,则∠3=°;若∠1=40°,则∠3=°.(3)由(1)、(2),请你猜想:当两平面镜a、b的夹角∠3=°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.你能说明理由吗?参考答案1.(1)76°,90°;(2)90°,90°(3)90°.【解析】【分析】(1)根据平面镜反射光线的规律,可得∠1=∠5,∠7=∠6,根据平角的定义可得∠4=104°,根据m∥n,所以∠2=76°,∠5=38°,根据三角形内角和为180°,即可求出答案;(2)结合题(1)可得∠3的度数都是90°;(3)证明m∥n,由∠3=90°,证得∠2与∠4互补即可.【详解】(1)由平面镜反射光线的规律可得:∠1=∠5,∠7=∠6.又∵∠1=38°,∴∠5=38°,∴∠4=180°﹣∠1﹣∠5=104°.∵m∥n,∴∠2=180°﹣∠4=76°,∴∠6=(180°﹣76°)÷2=52°,∴∠3=180°﹣∠6﹣∠5=90°;(2)同(1)可得当∠1=55°和∠1=40°时,∠3的度数都是90°;(3)∵∠3=90°,∴∠6+∠5=90°,又由题意知∠1=∠5,∠7=∠6,∴∠2+∠4=180°﹣(∠7+∠6)+180°﹣(∠1+∠5)=360°﹣2∠5﹣2∠6=360°﹣2(∠5+∠6)=180°.由同旁内角互补,两直线平行,可知:m∥n.故答案为:76°,90°,90°,90°90°.【点睛】本题考查了平行线的判定与性质,本题是数学知识与物理知识的有机结合,充分体现了各学科之间的渗透性.2.73°【解析】【分析】先根据三角形外角性质以及平行线的性质,求出∠AEG的度数,然后根据角平分线的定义求出∠AEF的度数,然后根据两直线平行内错角相等,即可求出∠EFG的度数.【详解】∵∠DFH=13°,∠H=21°,∴∠EGF=13°+21°=34°,∵AB∥CD,∴∠AEG+∠FGE=180°,∴∠AEG=146°,∵EF平分∠AEG,∠AEG=73°,∴∠AEF=12∵AB∥CD,∴∠EFG=∠AEF=73°.【点睛】此题考查了平行线的性质,解题的关键是:熟记两直线平行同位角相等;两直线平行内错角相等;两直线平行同旁内角互补.3.两直线平行,内错角相等;∠2=∠4;∠EFD;∠BEF;角平分线定义;∠BEF【解析】【分析】依据平行线的性质和判定定理以及角平分线的定义,结合解答过程进行填空即可.【详解】∵AB∥GH(已知),∴∠1=∠3(两直线平行,内错角相等),又∵CD∥GH(已知),∴∠2=∠4(两直线平行,内错角相等)∵AB∥CD(已知),∴∠BEF+∠EFD=180°(两直线平行,同旁内角互补)∵EG平分∠BEF(已知)∠BEF(角平分线定义),∴∠1=12又∵FG平分∠EFD(已知),∴∠2=1∠EFD(角平分线定义),2∴∠1+∠2=1(∠BEF+∠EFD)2∴∠1+∠2=90°,∴∠3+∠4=90°(等量代换),即∠EGF=90°.故答案为:两直线平行,内错角相等;∠2=∠4;∠EFD;∠BEF;角平分线定义;∠BEF.【点睛】考查的是平行线的性质和判定,熟练掌握平行线的性质和判定定理是解题的关键.4.(1)180°;(2)40°.【解析】【分析】(1)由AB//DG可得∠1=∠BAD,由AD//EF可得∠BAD+∠2=180°,然后由等量代换可证∠1+∠2=180°;(2)由∠1+∠2=180°, ∠2=140°,可求出∠1=40°,由DG平分∠ADC,可求∠CDG=∠1=40°,然后根据平行线的性质可求∠B的值.【详解】(1)∵AB//DG,∴∠1=∠BAD.∵AD//EF,∴∠BAD+∠2=180°,∴∠1+∠2=180°;(2) ∵∠1+∠2=180°, ∠2=140°,∴∠1=40°,∵DG平分∠ADC,∴∠CDG=∠1=40°,∵AB//DG,∴∠B=∠CDG =40°.【点睛】本题主要考查了平行线的性质与判定的综合应用,熟练掌握平行线的性质与判定方法是解答本题的关键.解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.5.见解析.【解析】【分析】根据平行线的性质得到∠CDE=∠E,∠ADE=∠BFE,等量代换即可得到结论.【详解】解:∵AB∥DC,∴∠CDE=∠E,∵AD∥BC,∴∠ADE=∠BFE,∵∠BFE=∠E,∴∠CDE =∠ADE.∴DE平分∠ADC.【点睛】此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.6.(1)内错角相等,两直线平行;两直线平行,同位角相等;等量代换;(2)详见解析. 【解析】【分析】(1)先根据平行线的判定定理得出BE∥AC,故可得出∠DBE=∠DAC,再由∠DAC=∠C 即可得出结论;(2)根据∠C=∠CBE得出BE∥AC,故∠CAE=∠E,再由∠DAE=∠CAE即可得出结论.【详解】(1)内错角相等,两直线平行;两直线平行,同位角相等;等量代换(2)证明:∵∠C=∠CBE(已知),∴BE∥AC(内错角相等,两直线平行),∴∠CAE=∠E(两直线平行,内错角相等).∵∠DAE=∠CAE(已知),∴∠DAE=∠E(等量代换)【点睛】本题考查平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.7.∠BCD=40°【解析】【分析】过点C作FG∥AB,根据平行线的传递性得到FG∥DE,根据平行线的性质得到∠B=∠BCF,∠CDE+∠DCF=180°,根据已知条件等量代换得到∠BCF=80°,由等式性质得到∠DCF=40°,于是得到结论.【详解】解:过C作CF∥DE∵CF∥DE(作图)AB∥DE(已知)∴AB∥DE∥CF(平行于同一条直线的两条直线平行)∴∠BCF=∠B=80°(两直线平行,内错角相等)∠DCF+∠D=180°(两直线平行,同旁内角互补)又∵∠D=140°(已知)∴∠DCF=40°(等量代换)又∵∠BCD=∠BCF-∠DCF(角的和差定义)∴∠BCD=80°-40°(等量代换)即∠BCD=40°【点睛】本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,8.(1)①125°;②∠DOE=180°−12∠B−12∠C;(2)∠DOE=12∠B+12∠C.【解析】【分析】(1)①根据平行线的性质和角平分线的定义可求∠BAE,∠CDO,再根据三角形外角的性质可求∠AEC,再根据四边形内角和等于360°可求∠DOE的度数;②根据三角形外角的性质和角平分线的定义可得∠DOE和∠BAD、∠ADC的关系,再根据四边形内角和等于360°可求∠B、∠C、∠DOE之间的数量关系;(2)根据四边形和三角形的内角和得到∠BAD+∠ADC=360°-∠B-∠C,∠EAD+∠ADO=180°-∠DOE,根据角平分线的定义得到∠BAD=2∠EAD,∠ADC=2∠ADO,于是得到结论.【详解】解:(1)①)①∵AD∥BC,∠B=40°,∠C=70°,∴∠BAD=140°,∠ADC=110°,∵AE、DO分别平分∠BAD、∠CDA,∴∠BAE=70°,∠ODC=55°,∴∠AEC=110°,∴∠DOE=360°-110°-70°-55°=125°;故答案为:125;②∵AE平分∠BAD∴∠DAE=12∠BAD∵DO平分∠ADC∵∠ADO=12 ADC∴∠DAE+∠ADO=12∠BAD+12ADC=12(∠BAD+∠ADC)∵∠B+∠C+∠BAD+∠ADC=360°∴∠BAD+∠ADC=360°−∠B−∠C∴∠DAE+∠ADO=12(360°−∠B−∠C)=180°−12∠B−12∠C∴∠AOD=180°−(∠DAE+∠ADO)=12∠B+12∠C∴∠DOE=180°−∠AOD=180°−12∠B−12∠C.(2)∠DOE=12∠B+12∠C.【点睛】本题考查多边形内角与外角,平行线的性质,角平分线的定义,关键是熟练掌握四边形内角和等于360°的知识点.9.见解析【解析】【分析】要证明EF平分∠BED,即证∠4=∠5,由平行线的性质,∠4=∠3=∠1,∠5=∠2,只需证明∠1=∠2,而这是已知条件,故问题得证.【详解】证明:∵AC∥DE(已知),∴∠BCA=∠BED(两直线平行,同位角相等),即∠1+∠2=∠4+∠5,∵AC∥DE,∴∠1=∠3(两直线平行,内错角相等);∵DC∥EF(已知),∴∠3=∠4(两直线平行,内错角相等);∴∠1=∠4(等量代换),∴∠2=∠5(等式性质);∵CD平分∠BCA(已知),∴∠1=∠2(角平分线的定义),∴∠4=∠5(等量代换),∴EF平分∠BED(角平分线的定义).【点睛】本题考查了角平分线的定义及平行线的性质.10.(1)∠1+∠2=∠3,证明见解析;(2)∠1+∠3=∠2或∠2+∠3=∠1,证明见解析.【解析】【分析】(1)过点P作l1的平行线,依据平行线的性质可得∠1=∠CPQ,∠2=∠DPQ,根据∠CPQ+∠DPQ=∠3,即可得到∠1+∠2=∠3;(2)当点P在下侧时,过点P作l1的平行线PQ,依据平行线的性质可得∠1-∠2=∠3;当点P在上侧时,同理可得:∠2-∠1=∠3.【详解】解:(1)∠1+∠2=∠3;理由:如图,过点P作l1的平行线,∵l1∥l2,∴l1∥l2∥PQ,∴∠1=∠CPQ,∠2=∠DPQ,∵∠CPQ+∠DPQ=∠3,∴∠1+∠2=∠3;(2)∠1-∠2=∠3或∠2-∠1=∠3;理由:当点P在下侧时,过点P作l1的平行线PQ,∵l1∥l2,∴l1∥l2∥PQ,∴∠2=∠4,∠1=∠3+∠4,(两直线平行,内错角相等)∴∠1-∠2=∠3;当点P在上侧时,同理可得:∠2-∠1=∠3.【点睛】本题考查平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.11.(1)∠A+∠P+∠C=360°;(2)∠APC=∠A+∠C;(3)∠C=∠A+∠P【解析】【分析】(1)过点P作PE∥AB,则AB∥PE∥CD,再根据两直线平行同旁内角互补即可解答;(2)过点P作PF∥AB,则AB∥CD∥PF,再根据两直线内错角相等即可解答;(3)根据AB∥CD,可得出∠PEB=∠PCD,再根据三角形外角的性质进行解答;【详解】解:(1)过点P作PE∥AB,则AB∥PE∥CD,∴∠1+∠PAB=180°,∠2+∠PCD=180°,∴∠APC+∠PAB+∠PCD=360°.故填:∠A+∠APC+∠C=360°;(2)过点P作直线PF∥AB,∵AB∥CD,∴AB∥PF∥CD,∴∠PAB=∠1,∠PCD=∠2,∴∠APC=∠PAB+∠PCD.故填:∠APC=∠A+∠C;(3)∵AB∥CD,∴∠1=∠C,∵∠1=∠A+∠P,∴∠C=∠A+∠P.故填:∠C=∠A+∠P.【点睛】本题考查的是平行线的性质及三角形外角的性质,能根据题意作出辅助线,再利用平行线的性质进行解答是解答此题的关键.12.(1)∠C=45°;(2)∠APC=∠C-∠A,理由详见解析;(3)∠APC=∠A-∠C.【解析】【分析】(1)过P作PQ∥CD,根据平行线的性质得∠2=∠C,由AB∥CD得到AB∥PQ,则∠APC=∠1+∠2=∠A+∠C,把∠A=25°,∠APC=70°代入计算可得到∠C的度数;(2)证明方法与(1)一样,可得到∠APC=∠C-∠A;(3)证明方法与(1)一样,可得到∠APC=∠A-∠C.【详解】(1)解:过点P作PQ∥AB(如图),∵AB∥CD(已知),∴PQ∥CD,(平行于同一条直线的两直线互相平行).∴∠C=∠2,(两直线平行,内错角相等)∵PQ∥AB,∴∠A=∠1,(两直线平行,内错角相等),∴∠APC=∠1+∠2=∠A+∠C∵∠A=25°,∠APC=70°,∴∠C=∠APC-∠A=70°-25°=45°.(2)∠APC=∠C-∠A,理由如下:过点P作PQ∥AB(如图),∵AB∥CD(已知),∴PQ∥CD,(平行于同一条直线的两直线互相平行)∴∠C=∠CPQ,(两直线平行,内错角相等)∵PQ∥AB,∴∠A=∠APQ,(两直线平行,内错角相等),∵∠APC=∠CPQ-∠APQ,∴∠APC=∠C-∠A.(3)∠APC=∠A-∠C.【点睛】本题考查了平行线的性质:两直线平行,内错角相等,熟练掌握相关知识是解题的关键.13.(1)见解析;(2)∠1+∠2=90°不会变,理由见解析.【解析】【分析】(1)利用平行线的性质,根据两直线平行,同旁内角互补,即可求得答案;(2)首先过点E作EF∥AB,根据两直线平行,内错角相等,即可求得答案.【详解】(1)过点P 作PM∥AB∵AB∥CD(已知)∴PM∥CD(两条直线都与第三条直线平行,那么这两条直线也互相平行)∴∠B+∠1=180°(两直线平行,同旁内角互补),∴∠C+∠2=180°(两直线平行,同旁内角互补),∵∠BPC=∠1+∠2,∴∠B+∠C+∠BPC=360°.(2)∠1+∠2=90°不会变.理由:如图,过点E 作EF∥AB,∵AB∥CD,∴AB∥EF∥CD,∴∠3=∠1,∠4=∠2∵∠AEC=90°,即∠3+∠4=90°,∴∠1+∠2=90°.【点睛】本题考查了平行线的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.14.(一)(两直线平行,内错角相等)(平行于同一条直线的两直线平行),小明的证法;(二)120°,30°;(三)见解析;(四) (1)∠E+∠G=∠B+∠F+∠D;(2)见解析.【解析】【分析】(一)小红、小明的做法,都是做了平行线,利用平行线的性质;(二)的(1)、(四)都可仿照(一),通过添加平行线把分散的角集中起来.【详解】(一)(两直线平行,内错角相等),(平行于同一条直线的两直线平行);完全正确的是:小明的证法;(二)尝试:(1)(1)过点E作EF∥AB,∵AB∥CD,∴EF∥CD.∵EF∥AB,∴∠A+∠AEF=180°,∵∠A=110°,∴∠AEF=70°.∵EF∥CD,∴∠C+∠CEF=180°,∵∠C=130°,∴∠CEF=50°.∴∠AEC=∠AEF+∠CEF=70°+50°=120°.(2)如图,∵AB∥CD,∴∠EOB=∠C=50°,∵∠EOB=∠A+∠E,∵∠E=∠EOB-∠A=50°-20°=30°.答案:120°,30°.(三)∠E=∠EAB−∠C.理由:延长EA,交CD于点F.∵AB∥CD,∴∠EFD=∠EAB.∵∠EFD=∠C+∠E,∴∠EAB=∠C+∠E,∴∠E=∠EAB−∠C.(四)(1)可通过过点E、F、G分别做AB的平行线,得到结论:∠E+∠G=∠B+∠F+∠D.(2)同上道理一样,可得到结论:∠E1+∠E2+…+∠E n=∠F1+∠F2+…∠F n+∠B+∠D.【点睛】本题考查了平行线的性质与判定、三角形的外角与内角关系及角的和差.添加平行线把分散的角集中起来,是解决问题的关键.15.操作发现:(1)∠2=44∘;(2)见解析;实践探究:(3)∠1=∠2.【解析】【分析】(1)如图1,根据平角定义先求出∠3的度数,再根据两直线平行,同位角相等即可得;(2)如图2,过点B作BD//a,则有∠2+∠ABD=180°,根据已知条件可得∠ABD =60°-∠1,继而可得∠2+60°-∠1=180°,即可求得结论;(3)∠1=∠2,如图3,过点C作CD//a,由已知可得∠CAM=∠BAC=30°,∠BAM=2∠BAC=60°,根据平行线的性质可得∠BCD=∠2,继而可求得∠1=∠BAM=60°,再根据∠BCD=∠BCA-∠DCA求得∠BCD=60°,即可求得∠1=∠2.【详解】(1)如图1,∵∠BCA=90°,∠1=46°,∴∠3=180°-∠BCA-∠1=44°,∵a//b,∴∠2=∠3=44°;(2)理由如下:如图2,过点B作BD//a,∴∠2+∠ABD=180°,∵a//b,∴b//BD,∴∠1=∠DBC,∴∠ABD=∠ABC-∠DBC=60°-∠1,∴∠2+60°-∠1=180°,∴∠2-∠1=120°;(3)∠1=∠2,理由如下:如图3,过点C作CD//a,∵AC平分∠BAM,∴∠CAM=∠BAC=30°,∠BAM=2∠BAC=2×30°=60°,∵CD//a,∴∠BCD=∠2,∵a//b,∴∠1=∠BAM=60°,b//CD,∴∠DCA=∠CAM=30°,∵∠BCD=∠BCA-∠DCA,∴∠BCD=90°-30°=60°,∴∠2=60°,∴∠1=∠2.【点睛】本题考查了平行线的判定与性质,三角板的知识,正确添加辅助线,熟练掌握平行线的判定与性质是解题的关键.。
