三角函数3
(完整版)三角函数三角函数公式表

(完整版)三角函数公式表1. 正弦函数 (sin):定义:正弦函数是直角三角形中对边与斜边的比值。
公式:sin(θ) = 对边 / 斜边范围:1 ≤ sin(θ) ≤ 1特殊值:sin(0°) = 0, sin(30°) = 1/2, sin(45°) = √2/2, sin(60°) = √3/2, sin(90°) = 12. 余弦函数 (cos):定义:余弦函数是直角三角形中邻边与斜边的比值。
公式:cos(θ) = 邻边 / 斜边范围:1 ≤ cos(θ) ≤ 1特殊值:cos(0°) = 1, cos(30°) = √3/2, cos(45°) = √2/2, cos(60°) = 1/2, cos(90°) = 03. 正切函数 (tan):定义:正切函数是直角三角形中对边与邻边的比值。
公式:tan(θ) = 对边 / 邻边范围:tan(θ) 可以取任意实数值特殊值:tan(0°) = 0, tan(30°) = 1/√3, tan(45°) = 1, tan(60°)= √3, tan(90°) 不存在(无穷大)4. 余切函数 (cot):定义:余切函数是直角三角形中邻边与对边的比值。
公式:cot(θ) = 邻边 / 对边范围:cot(θ) 可以取任意实数值特殊值:cot(0°) 不存在(无穷大), cot(30°) = √3, cot(45°) = 1, cot(60°) = 1/√3, cot(90°) = 05. 正割函数 (sec):定义:正割函数是直角三角形中斜边与邻边的比值。
公式:sec(θ)= 1 / cos(θ)范围:sec(θ) 可以取任意实数值特殊值:sec(0°) = 1, sec(30°) = 2, sec(45°) = √2, sec(60°) = 2/√3, sec(90°) 不存在(无穷大)6. 余割函数 (csc):定义:余割函数是直角三角形中斜边与对边的比值。
总第04课时——3 三角函数的计算

tan27.35°= 0.517 244 127;
数学
北师版九年级下册
课件目录
首
页
末
页
(3)按键顺序: sin
3 9 D′M′ S 5 7 D′M′ S 6
D′M′ S = ,显示结果:sin 39°57′6″=0.642 141 164.
【点悟】 利用计算器求锐角的三角函数值,不同的计算器的 操作步骤有所不同.
0.620 0 ;cos78°43′16″=___________ 0.195 6 ;tan57°26′= __________ 1.565 7 . ___________
2.用计算器求锐角α(精确到1°):
14° ; (1)若sinα =0.247 6,则α ≈________
65° ; (2)若cosα =0.417 4,则α ≈________ 11° . (3)若tanα =0.189 0,则α ≈________
数学
北师版九年级下册
课件目录
首
页
末
页
度分秒形式:如果锐角α的度数为度、分、秒形式,如α=
53°23′18″,求它的三角函数值时,可仿下面的按键 方法进行:
按键顺序: tan 5 3 D′ M′ S = 2 3 D′ M ′ S 1 8
D′ M′ S
显示结果: tan53° 23′18″= 1.345 928 498.
数学
北师版九年级下册
课件目录
首
页
末
页
数学
北师版九年级下册
课件目录
首
页
末
页
同一水平面上,求该铁塔的高AE(参考数据:sin36°52′≈0.60, tan36°52′≈0.75).
专题四 三角函数(3)

专题四 三角函数(3)一、 选择题:1.下列各区间,使函数y=sin(x+π)的单调递增的区间是 ( ) A .[π2,π] B . [0,π4] C .[-π,0] D . [π4,π2]2.下列函数中,周期为π2的偶函数是 ( )A .y=sin4xB . y=cos 22x -sin 22xC . y=tan2xD . y=cos2x 3.下列命题中正确的是 ( )A .若α、β是第一象限角,且α>β,且sin α>sin βB .函数y=sinxcotx 的单调递增区间是(2k π-π2,2k π+π2),k ∈ZC .函数y=1-cos2xsin2x的最小正周期是2πD .函数y=sinxcos2φ-cosxsin2φ的图象关于y 轴对称,则φ=k π2+π4,k ∈Z4.下列函数中,既为偶函数又在(0,π)上单调递增的是( )(2003年上海理13) A .y=tan|x |.B .y=cos(-x ).C .).2sin(π-=x y D .|2cot |x y =.5.函数y= 12sin(2x+θ)的图象关于y 轴对称的充要条件是 ( )A .θ=2k π+π2B .θ=k π+π2C .θ=2k π+πD .θ=k π+π(k ∈Z)6.y=tan(12x -π3)在一个周期内的图象是 ( )7.当0≤x ≤π2时,函数f(x)= sinx+1cosx+1的 ( )A .最大值为2,最小值为12B .最大值为2,最小值为0C .最大值为2,最小值不存在D .最大值不存在,最小值为08.已知关于x 的方程cos 2x -sinx+a=0,若0<x <π2时方程有解,则a 的取值范围是( )A .[-1,1]B .(-1,1)C .[-1,0]D .(-∞,-54) 9.函数f(x)=log 13(sin2x+cos2x)的单调递减区间是 ( )-A .(k π-π4,k π+π8)(k ∈Z)B .(k π-π8,k π+π8)(k ∈Z)C .(k π+π8,k π+3π8)(k ∈Z)D .(k π+π8,k π+ 5π8)(k ∈Z)10.在△ABC 中,若2cosBsinA=sinC ,则△ABC 的形状一定是 ( )A .等腰直角三角形B .直角三角形C .等腰三角形D .等边三角形 11.函数=∈=-)(]23,2[,sin )(1x fx x x f 的反函数ππ( )(2003年全国理9) A .]1,1[,arcsin -∈-x x B .]1,1[,arcsin -∈--x x π C .]1,1[,arcsin -∈+-x x π D .]1,1[,arcsin -∈-x x π12.关于函数221()sin ()32xf x x =-+,有下面四个结论:(2003年上海春16) (1)f(x)是奇函数;(2)当x>2003时,1()2f x >恒成立;(3)f(x)的最大值是32;(4)f(x)的最小值是12-。
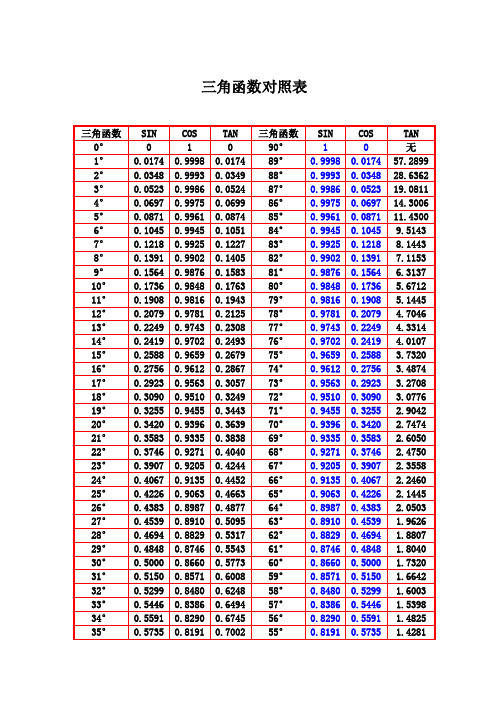
三角函数对照表
商的关系
sin tan sec
cos
csc
cos cot csc
sin
sec
平方关系
2
2
sin cos 1
2
2
1 tan sec
2
2
1 cot csc
诱导公式
sin() sin
cos( ) cos tan() tan
cot() cot
sin( ) cos 2
cos( ) sin 2
0.9998 0.9993 0.9986 0.9975 0.9961 0.9945 0.9925 0.9902 0.9876 0.9848 0.9816 0.9781 0.9743 0.9702 0.9659 0.9612 0.9563 0.9510 0.9455 0.9396 0.9335 0.9271 0.9205 0.9135 0.9063 0.8987 0.8910 0.8829 0.8746 0.8660 0.8571 0.8480 0.8386 0.8290 0.8191
36° 37° 38° 39° 40° 41° 42° 43° 44° 45°
0.5877 0.6018 0.6156 0.6293 0.6427 0.6560 0.6691 0.6819 0.6946 0.7071
0.8090 0.7986 0.7880 0.7771 0.7660 0.7547 0.7431 0.7313 0.7193 0.7071
TAN 0
0.0174 0.0349 0.0524 0.0699 0.0874 0.1051 0.1227 0.1405 0.1583 0.1763 0.1943 0.2125 0.2308 0.2493 0.2679 0.2867 0.3057 0.3249 0.3443 0.3639 0.3838 0.4040 0.4244 0.4452 0.4663 0.4877 0.5095 0.5317 0.5543 0.5773 0.6008 0.6248 0.6494 0.6745 0.7002
锐角三角函数(3)

tanA=
∠A的对边 ∠A的邻边
=
a
b
B
锐角A的邻边与对边的比叫做∠A的 余 切,记作 cotA,即
斜边c
cotA=
∠A的邻边
∠A的对边
=
b
A
∠A的邻边b
∠A的对边a
C
正切函数的取值范围
余切函数的取值范围
tanA>0
cotA>0
例1.请计算30º、45º、60º的正切和余切值分别是多少? 特殊角的正切、余切函数值 tan30º = cot30º =
3 3
tan45º =1
tan60º = cot60º =
3
3 3
3
cot45º =1
例2.在Rt△ABC中,∠C=90°,求 (1)tanA,cotA (2)tanA· cotA;(3)tanA· tanB
你有什 么发现?
例3.在Rt△ABC中,∠C=90º ,a=5,b=12,求tanB和cotB.
例7.如图,在等腰Rt△ABC中,∠C=90º ,AC=6,D是 AC上一点,tan∠DBA= 1 ,求AD的长。 A 5
DCE来自,求B例8.已知直线y=3x-6与x轴所成的角为 四个三角函数值。
的
2 2 例9.等腰梯形的腰长为6cm,底角的余弦值为 3
,上
底长为
2
,求梯形的面积。
达标演练
课堂小结
7.同一锐角的正余切之积有什么关系?
问题导入
当直角三角形的一个锐角的大小确定时, 其对边与邻边比值也是惟一确定的吗?为 B 什么? 其邻边与对边的比值呢?
A
斜边c
∠A的对边a
∠A的邻边b
C
探究新知
三角函数知识点归纳(3)[1]
![三角函数知识点归纳(3)[1]](https://img.taocdn.com/s3/m/e28251dfb52acfc788ebc920.png)
三角函数知识点归纳(3)(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(三角函数知识点归纳(3)(word 版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为三角函数知识点归纳(3)(word版可编辑修改)的全部内容。
三角函数一、任意角、弧度制及任意角的三角函数1.任意角(1)角的概念的推广①按旋转方向不同分为正角、负角、零角.⎧⎪⎨⎪⎩正角:按逆时针方向旋转形成的角任意角负角:按顺时针方向旋转形成的角零角:不作任何旋转形成的角②按终边位置不同分为象限角和轴线角.角α的顶点与原点重合,角的始边与x 轴的非负半轴重合,终边落在第几象限,则称α为第几象限角.第一象限角的集合为{}36036090,k k k αα⋅<<⋅+∈Z 第二象限角的集合为{}36090360180,k k k α⋅+<⋅+∈Z 第三象限角的集合为{}360180360270,k k k αα⋅+<<⋅+∈Z 第四象限角的集合为{}360270360360,k k k αα⋅+<<⋅+∈Z 终边在x 轴上的角的集合为{}180,k k αα=⋅∈Z 终边在y 轴上的角的集合为{}18090,k k αα=⋅+∈Z 终边在坐标轴上的角的集合为{}90,k k αα=⋅∈Z(2)终边与角α相同的角可写成α+k ·360°(k ∈Z ).终边与角α相同的角的集合为{}360,k k ββα=⋅+∈Z(3)弧度制①1弧度的角:把长度等于半径长的弧所对的圆心角叫做1弧度的角. ②弧度与角度的换算:360°=2π弧度;180°=π弧度.③半径为r 的圆的圆心角α所对弧的长为l ,则角α的弧度数的绝对值是lrα=④若扇形的圆心角为()αα为弧度制,半径为r ,弧长为l ,周长为C ,面积为S ,则l r α=,2C r l =+,21122S lr r α==.2.任意角的三角函数定义设α是一个任意角,角α的终边上任意一点P (x ,y ),它与原点的距离为(r r =,那么角α的正弦、余弦、正切分别是:sin α=错误!,cos α=错误!,tan α=错误!.(三角函数值在各象限的符号规律概括为:一全正、二正弦、三正切、四余弦)3.特殊角的三角函数值二、同角三角函数的基本关系与诱导公式A 。
3特殊锐角的三角函数
2 2 2 2
-1
= 1
= 1 -1
= 0
2、求满足下列条件的锐角α .
1 ① sinα = 2
3 ② cosα = 2
解:α =30° ③ 2sinα = 3 解:sinα =
3 2
解:α =30° ④ 3 tan(80°-α )-1=0 解: 3tan (80-α )= 1
α =60°
3 tan (80-α )= 3 80°-α =30°
第一轮
课本
P80
练习:1、2
第二轮
课本
P82
练习:3
你对本节课所学的内容存在疑问吗?欢迎提出来,共同讨论!
锐角α 三角函数
30°
1 2
3 2 3 3
45°
60°
sinα cosα tanα
2 2 2 2
1
3 2
1 2
3
1、求下列各式的值. ① sin260°+cos260°
1 3 2 ) + ( )2 2 2 3 1 = + 4 4
cos 45 ② sin 45 -tan 45
解:原式= (
解:原式=
α =50°
3、(1)如图,在Rt△ABC中,∠C=90°,AB= 6 , BC= 3 ,求∠A的度数.
(2)如图,已知圆锥的高AO是它的地面半径OB 的 3 倍,求α . B
6 3
A
(1)
C
(2)
1 2
BC 3 解:(1)∵sinA= AB = 6 = ∴∠A=45° AO (2)∵tanα = = 3 OB ∴∠α =60°
1、尽最大的努力,做最好的自己。
2、不叫一日闲过,坚持就有收获。
30°
三角3--三角函数的图像和性质
三角函数的图象与性质(1)近几年高考降低了对三角变换的考查要求,而加强了对三角函数的图象与性质的考查,因为函数的性质是研究函数的一个重要内容,是学习高等数学和应用技术学科的基础,又是解决生产实际问题的工具,因此三角函数的性质是本章复习的重点。
在复习时要充分运用数形结合的思想,把图象与性质结合起来,即利用图象的直观性得出函数的性质,或由单位圆上线段表示的三角函数值来获得函数的性质,同时也要能利用函数的性质来描绘函数的图象,这样既有利于掌握函数的图象与性质,又能熟练地运用数形结合的思想方法。
一、基本知识回顾1. 正弦函数、余弦函数、正切函数的图像2. 三角函数的单调区间:x y sin =的递增区间是 )(Z k ∈,递减区间是 )(Z k ∈;x y cos =的递增区间是 )(Z k ∈,递减区间是 )(Z k ∈,x y tan =的递增区间是 )(Z k ∈,3. 对称轴与对称中心:sin y x =的对称轴为 ,对称中心为 ; cos y x =的对称轴为 ,对称中心为 ;x y tan =的对称中心是4. 函数B x A y ++=)sin(ϕω),(其中00>>ωA最大值是 ,最小值是 ,周期是 ,频率是 ,相位是 ,初相是 ;其图象的对称轴是直线 ,凡是该图象与直线 的交点都是该图象的对称中心。
5. 由y =sin x 的图象变换出y =sin (ωx +ϕ)的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换。
利用图象的变换作图象时,提倡先平移后伸缩,但先伸缩后平移也经常出现无论哪种变形,请切记每一个变换总是对字母x 而言,即图象变换要看“变量”起多大变化,而不是“角变化”多少。
途径一:先平移变换再周期变换(伸缩变换)先将y =sin x 的图象向左(ϕ>0)或向右(ϕ<0)平移|ϕ|个单位,再将图象上各点的横坐标变为原来的ω1倍(ω>0),便得y =sin (ωx +ϕ)的图象。
三角函数公式(最全)
正弦定理变形可得:
五、其他公式
2、余弦定理
对于如图所示的边长为a、b、c而相应角为α、β、γ的△ABC, 有:
3、降幂公式
sin²α=[1-cos(2α)]/2 cos²α=[1+cos(2α)]/2 tan²α=[1-cos(2α)]/[1+cos(2α)]
4、三角和
sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+ cosα·cosβ·sinγ-sinα·sinβ·sinγ
ln(1+x)=x-x2/2+x3/3-…+(-1)k-1xk/k, x∈(-1,1)
sin x = x-x3/3!+x5/5!-…+(-1)k-1x2k-1/(2k-1)!+…, x∈R
cos x = 1-x2/2!+x4/4!-…+(-1)kx2k/(2k)!+…, x∈R
arcsin x = x + x3/(2*3) + (1*3)x5/(2*4*5) + (1*3*5)x7/(2* 4*6*7)…+(2k+1)!!*x2k+1/(2k!!*(2k+1))+…, x∈(-1,1)(!!表 示双阶乘)
1
一、定义公式
三角函数公式
锐角三角函数 任意角三角函数
正弦(sin) 余弦(cos) 正切(tan或tg) 余切(cot或ctg) 正割(sec) 余割(csc) 正弦(sin) 余弦(cos) 正切(tan或tg) 余切(cot或ctg) 正割(sec) 余割(csc)
1、倒数关系
二、函数关系
3三角函数的值域与最值
三角函数的值域与最值【知识回顾】1. 辅助角公式的应用:y=()sin cos a x b x x θ+=+(其中θ角所在的象限由a, b 的符号确定,θ角的值由tan baθ=确定)在求最值、化简时起着重要作用。
2. 化二次或高次函数,如y=x x 2cos 2sin - 【基础练习】1.函数x x y cos 3sin +=在区间[0,]2π上的最小值为 .2.函数)(2cos 21cos )(R x x x x f ∈-=的最大值等于 ______.3.函数tan()2y x π=-(44x ππ-≤≤且0)x ≠的值域是___________________.4.当20π<<x 时,函数x xx x f 2sin sin 82cos 1)(2++=的最小值为 _____ .5.已知k <-4,则函数y =cos2x +k(cosx -1)的最小值是 _____ .6.若2αβπ+=,则cos 6sin y βα=-的最大值与最小值之和为________. 【范例解析】例1.(1)已知1sin sin 3x y +=,求2sin cos y x -的最大值与最小值.(2)求函数sin cos sin cos y x x x x =⋅++的最大值.例2.求函数2cos (0)sin xy x xπ-=<<的最小值.例3. 已知函数f(x)=Asin(ωx +ϕ),x∈R (其中A>0,ω>0,0<ϕ<π2)的周期为π,且图象上一个最低点为M(2π3,-2). (1)求f(x)的解析式;(2)当x∈[0,π12]时,求f(x)的最值.例4.扇形AOB 的半径为1,中心角为60︒,PQRS 是扇形的内接矩形,问P 在怎样的位置时,矩形PQRS 的面积最大,并求出最大值. ,ABORS PQ【反馈演练】1.函数))(6cos()3sin(2R x x x y ∈+--=ππ的最小值等于___________.2.已知函数()3s i n f x x =,3()sin()2g x x π=-,直线m x =和它们分别交于M ,N ,则=m a x MN _________.3.当04x π<<时,函数22cos ()cos sin sin xf x x x x =-的最小值是_____________.4.函数sin cos 2xy x =+的最大值为_______,最小值为________.5.函数cos tan y x x =⋅的值域为 .6.已知函数11()(sin cos )|sin cos |22f x x x x x =+--,则()f x 的值域是 .7.已知函数()2sin (0)f x x ωω=>在区间,34ππ⎡⎤-⎢⎥⎣⎦上的最小值是2-,则ω的最小值等于_________.8.(1)已知(0,)θπ∈,函数y =的最大值是_______. (2)已知(0,)x π∈,函数2sin sin y x x=+的最小值是____________. 9.在△OAB 中,O 为坐标原点,]2,0(),1,(sin ),cos ,1(πθθθ∈B A ,则当△OAB 的面积达最大值时,=θ_____________ . 10.已知函数()2cos (sin cos )1f x x x x x =-+∈R ,. (1)求函数()f x 的最小正周期;(2)求函数()f x 在区间π3π84⎡⎤⎢⎥⎣⎦,上的最小值和最大值.11.若函数)4sin(sin )2sin(22cos 1)(2ππ+++-+=x a x x x x f 的最大值为32+,试确定常数a 的值.12.已知函数2()2sin sin 2f x x x =+.(1)若[0,2]x π∈.求使()f x 为正值的x 的集合;(2)若关于x 的方程2[()]()0f x f x a ++=在[0,]4π内有实根,求实数a 的取值范围.专题十二: 三角函数的值域与最值【知识回顾】3. 辅助角公式的应用:y=()sin cos a x b x x θ+=+(其中θ角所在的象限由a, b 的符号确定,θ角的值由tan baθ=确定)在求最值、化简时起着重要作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 三角函数 姓名: 班级: 1.(2014•广西)已知角α的终边经过点(﹣4,3),则cosα=( ) A. B. C. ﹣ D. ﹣ 2.(2014•河南)若tanα>0,则( ) A. sinα>0 B. cosα>0 C. sin2α>0 D. cos2α>0 3.(2014•广西)设a=sin33°,b=cos55°,c=tan35°,则( ) A. a>b>c B. b>c>a C. c>b>a D. c>a>b 4.(2014•辽宁)将函数y=3sin(2x+)的图象向右平移个单位长度,所得图象对应的函数( ) A. 在区间7,1212上单调递减 B. 在区间7,1212上单调递增 C. 在区间,63上单调递减 D. 在区间,63上单调递增 5.(2014•福建)将函数y=sinx的图象向左平移个单位,得到函数y=f(x)的函数图象,则下列说法正确的是( ) A. y=f(x)是奇函数 B. y=f(x)的周期为π C. y=f(x)的图象关于直线x=对称 D. y=f(x)的图象关于点(﹣,0)对称 6.(2014•四川)为了得到函数y=sin(2x+1)的图象,只需把y=sin2x的图象上所有的点( ) A. 向左平行移动个单位长度 B. 向右平行移动个单位长度 C. 向左平行移动1个单位长度 D. 向右平行一定1个单位长度 7.(2014•浙江)为了得到函数y=sin3x+cos3x的图象,可以将函数y=cos3x的图象( ) A. 向右平移个单位 B. 向左平移个单位 C. 向右平移个单位 D. 向左平移个单位 8.(2014•四川)为了得到函数y=sin(x+1)的图象,只需把函数y=sinx的图象上所有的点( ) A. 向左平行移动1个单位长度 B. 向右平行移动1个单位长度 C. 向左平行移动π个单位长度 D. 向右平行移动π个单位长度 9.(2014•陕西)函数f(x)=cos(2x+)的最小正周期是( ) A. B. π C. 2π D. 4π
10.(2013•广东)已知,那么cosα=( ) A. B. C. D.
11.(2013•上海)既是偶函数又在区间(0,π)上单调递减的函数是( ) A. y=sinx B. y=cosx C. y=sin2x D. y=cos2x
12.(2013•山东)函数y=sin(2x+φ)的图象沿x轴向左平移个单位后,得到一个偶函数的图象,则φ的一个可能的值为( ) A. B. C. 0 D.
13.(2013•四川)函数f(x)=2sin(ωx+φ)(ω>0,﹣<φ<)的部分图象如图所示,则ω,φ的值分别是( )
A. B. C. D. 14.(2013•浙江)函数f(x)=sinxcosx+cos2x的最小正周期和振幅分别是( ) A. π,1 B. π,2 C. 2π,1 D. 2π,2
15.(2012•北京模拟)函数y=cos4x﹣sin4x的最小正周期是( ) A. B. π C. 2π D. 4π
16.(2012•福建)函数f(x)=sin(x﹣)的图象的一条对称轴是( ) A. x= B. x= C. x=﹣ D. x=﹣
17.(2012•广东模拟)函数y=sin(2x+)的图象的一条对称轴的方程是( ) 2
A. x=﹣ B. x=﹣ C. x= D. x= 18.(2012•安徽)要得到函数y=cos(2x+1)的图象,只要将函数y=cos2x的图象( ) A. 向左平移1个单位 B. 向右平移1个单位 C. 向左平移个单位 D. 向右平移个单位 19.(2012•德阳二模)要得到函数的图象,只需将函数y=sin2x的图象( ) A. 向左平行移动 B. 向右平行移动 C. 向左平行移动 D. 向右平行移动 20.(2011•惠州模拟)y=(sinx﹣cosx)2﹣1是( ) A. 最小正周期为2π的偶函数 B. 最小正周期为2π的奇函数 C. 最小正周期为π的偶函数 D. 最小正周期为π的奇函数 21.(2010•重庆)已知函数y=sin(ωx+φ)(ω>0,|φ|<)的部分图象如图所示,则( ) A. ω=1,φ= B. ω=1,φ=﹣ C. ω=2,φ= D. ω=2,φ=﹣ 22.(2009•广东)函数y=2cos2(x﹣)﹣1是( ) A. 最小正周期为π的奇函数 B. 最小正周期为π的偶函数 C. 最小正周期为的奇函数 D. 最小正周期为的偶函数 23.(2009•石景山区一模)函数y=sin2x•cos2x的最小正周期是( ) A. 2π B. 4π C. D. 24.(2008•四川)已知,则=( ) A. 2 B. ﹣2 C. 3 D. ﹣3 25.(2008•浙江)若,则tanα=( ) A. B. 2 C. D. ﹣2 26.(2008•四川)已知,则=( ) A. 2 B. ﹣2 C. 3 D. ﹣3 27.(2008•陕西)sin330°等于( ) A. B. C. D.
28.(2008•天津)设,,,则( ) A. a<b<c B. a<c<b C. b<c<a D. b<a<c 29.(2008•安徽)函数y=sin(2x+)图象的对称轴方程可能是( ) A. x=﹣ B. x=﹣ C. x= D. x=
30.(2008•湖南)函数的单调递增区间是( ) A. B.
C. D. 31.(2008•海南)已知函数y=2sin(ωx+φ)(ω>0))在区间[0,2π]的图象如图:那么ω=( ) A. 1 B. 2 C. 12 D. 13
32.(2007•湖北)tan690°的值为( ) A. ﹣ B. C. {ax} D. 33.(2007•江苏)下列函数中,周期为的是( ) A. B. y=sin2x C. D. y=cos4x
34.(2007•山东)函数的最小正周期和最大值分别为( ) A. π,1 B. C. 2π,1 D. 35.(2007•浙江)若函数f(x)=2sin(ωx+φ),x∈R(其中ω>0,)的最小正周期是π,且
,则( ) 3
A. B. C. D. 36.(2007•北京)函数f(x)=sin2x﹣cos2x的最小正周期是( ) A. B. π C. 2π D. 4π 37.(2007•江西)函数y=5tan(2x+1)的最小正周期为( ) A. B. C. π D. 2π 38. (2007•海南)函数在区间的简图是( ) A. B. C. D. 39.(2006•四川)下列函数中,图象的一部分如图所示的是( ) A. B. C. D. 40.(2006•浙江)函数的值域是( ) A. 13,22 B. 31,22 C. 2121,2222 D. 2121,2222 41.(2005•黑龙江)函数f(x)=|sinx+cosx|的最小正周期是( ) A. B. C. π D. 2π 42.(2005•天津)函数y=Asin(ωx+φ)(ω>0,|φ|<,x∈R)的部分图象如图所示,则函数表达式为( )
A. y=﹣4sin() B. y=4sin() C. y=﹣4sin() D. y=4sin()
43.(2004•陕西)函数的最小正周期是( ) A. B. π C. 2π D. 4π
44.(2014•重庆)将函数f(x)=sin(ωx+φ)(ω>0,﹣≤φ<)图象上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移个单位长度得到y=sinx的图象,则f()= . 45.(2014•广西)函数y=cos2x+2sinx的最大值为 .
46.(2013•江西)函数y=最小正周期T为 .
47.(2013•江苏)函数y=3sin(2x+)的最小正周期为 . 48.(2014•上海)函数y=1﹣2cos2(2x)的最小正周期是 . 49.(2014•山东)函数y=sin2x+cos2x的最小正周期为 . 50.(2013•上海)若cosxcosy+sinxsiny=,则cos(2x﹣2y)= 解三角形 1.(2014•江西)在△ABC中,内角A,B,C所对的边分别是a,b,c,若c2=(a﹣b)2+6,C=,则△ABC的面积是( ) A. B. C. D. 3 4
2.(2014•江西)在△ABC中,内角A,B,C所对的边分别是a,b,c,若3a=2b,则的值为( ) A. ﹣ B. C. 1 D. 3.(2013•陕西)设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为( ) A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不确定 4.(2013•北京)在△ABC中,a=3,b=5,sinA=,则sinB=( ) A. B. C. D. 1 5.(2013•山东)△ABC的内角A、B、C的对边分别是a、b、c,若B=2A,a=1,b=,则c=( ) A. B. 2 C. D. 1 6.(2013•天津)在△ABC中,,则sin∠BAC=( ) A. B. C. D. 7.(2012•上海)在△ABC中,若sin2A+sin2B<sin2C,则△ABC的形状是( ) A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不能确定 8.(2011•辽宁)△ABC的三个内角A、B、C所对的边分别为a,b,c,asinAsinB+bcos2A=a,则=( ) A. 2 B. 2 C. D. 9.(2012•广东)在△ABC中,若∠A=60°,∠B=45°,,则AC=( ) A. B. C. D. 10.(2013•湖南)在锐角△ABC中,角A,B所对的边长分别为a,b.若2asinB=b,则角A等于( ) A. B. C. D. 11.(2013•辽宁)在△ABC,内角A,B,C所对的边长分别为a,b,c.asinBcosC+csinBcosA=b,且a>b,则∠B=( ) A. B. C. D. 12.(2013•安徽)设△ABC的内角A,B,C所对边的长分别为a,b,c,若b+c=2a,3sinA=5sinB,则角C=( ) A. B. C. D. 13.(2014•福建)在△ABC中,A=60°,AC=4,BC=2,则△ABC的面积等于 . 14.(2014•河南)已知a,b,c分别为△ABC三个内角A,B,C的对边,a=2,且(2+b)(sinA﹣sinB)=(c﹣b)sinC,则△ABC面积的最大值为 .
