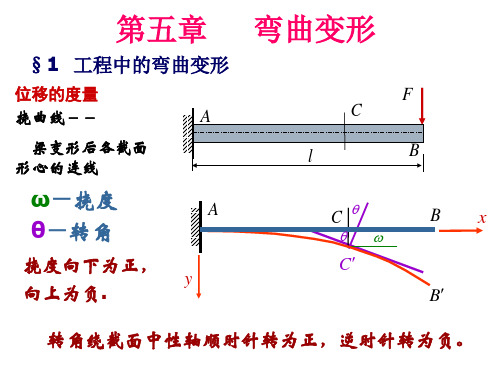
第四讲:弯曲变形+简单超静定问题
合集下载
材料力学-简单的超静定问题

2021/6/16
4
2021/6/16
5
2021/6/16
6
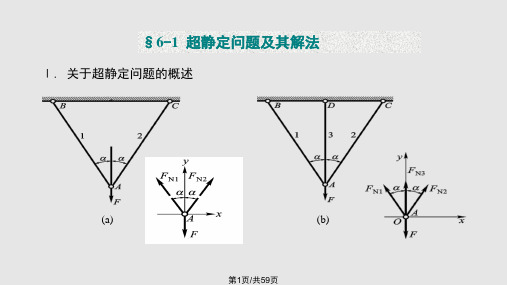
§6-2 拉压超静定问题
拉压变形时的胡克定律 l FN l EA
综合考虑变形的协调条件、虎克定律和静力 学平衡条件求解拉压超静定问题。
2021/6/16
7
例 已知1、2杆抗拉刚度为E1A1, 3杆抗拉刚度为E3A3, F的大小已知,求各杆内力。
13
2
l
A
A*
l3
FN 3l E3 A3
9
4、联解方程
FN1
2 cos
F
E 3 A3
E 1 A1 c o s 2
FN 3
1
2
F E 1 A1
cos3
E 3 A3
2021/6/16
10
装配应力的计算:超静定结构中由于加工误 差, 装配产生的应力。
平衡方程:
FN1 FN2
F N 3(F N 1F N 2)cos
超静定问题:若未知力的个数多于独立的平
衡方程的个数,仅用静力平衡方程便无法确定
全部未知力,这类问题为超静定问题。相应结
构称为超静定结构。
2021/6/16
2
超静定次数:未知力个数与独立平衡方程数之 差,也等于多余约束数。
多余约束:在结构上加上的一个或几个约束, 对于维持平衡来说是不必要的约束称多余约束。 对应的约束力称多余约束反力。
由于超静定结构能有效降低结构的内力及变 形,在工程上应用非常广泛。
2021/6/16
3
基本静定系:解除多余约束代之于未知力后的 结构。
●超静定问题的解法:综合考虑变形的几何相 容条件、物理关系和静力学平衡条件。
材料力学第5章弯曲变形ppt课件
qL
4.22kNm
4.22kNm
M
max
32 M
max
76.4MPa
WZ
d 3
例题
20kN m
A
4m
FA
20kN m
A
MA
4m
试求图示梁的支反力
40kN
B
D
2m
2m
B
B1 FB
FB 40kN
B
D
B2
2m
2m
在小变形条件下,B点轴向力较小可忽略不
计,所以为一次超静定.
C
B1 B2
FBBBMF12AA2383qFEqELBqqLI84LI2LLZZ32F35BFF4FEFB83PBPLIEL7Z3L12IZ.218352.k75N5kFkN2PNmEL2IZ2
x
边界条件
A
L2
B
L2
C
y
连续条件
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
全梁仅一个挠曲线方程
C
q
EA
共有两个积分常数 边界条件
L1
A
x
B
EI Z
L
y
例题 5.5
用积分法求图示各梁挠曲线方程时,试问在列各梁 的挠曲线近似微分方程时应分几段;将分别出现几个 积分常数,并写出其确定积分常数的边界条件
q
a
B C LBC
B
2a
FN
B
q2a4
8EIZ
FN 2a3
3EIZ
C
FN
a
D
6-简单超静定问题

4、补充方程
FN 1l FN 3l cos EA cos EA FN 1 FN 3 cos 2
5、求解方程组得
FN 1 FN 2
F cos 2 1 2 cos 3
FN 3
F 1 2 cos 3
目 录
二、装配应力
构件的加工误差是难以避免的。对静定结构,加工误 差只是引起结构几何形状的微小变化,而不会在构件内引 起应力。但对静不定结构,加工误差就要在构件内引起应 力。这种由于装配而引起的应力称为装配应力。 装配应力是结构构件在载荷作用之前已具有的应力, 因而是一种初应力。
超静定结构中才有温度应力。
目 录
解题思路: 平衡方程:RA = RB 变形几何关系: 物理关系:
(t 时)
lT lF
lT l t
RB L
RB l lF EA
EA Lt
补充方程:
联立求解: RA RB EAt
EAt t Et A
目 录
一静定问题及超静定问题三基本静定系或相当系统是一个静定结构该结构上作用有荷载和多余约束力61超静定问题及其解法61超静定问题及其解法二多余约束及多余约束力在静定结构的基础上增加的约束
第六章
简单的超静定问题
§6–1 概述
§6–2 §6–3 §6–4 拉压超静定问题 扭转超静定问题 简单超静定梁
目的与要求:
M
max
WZ
32 M
d
max 3
76.4MPa
目 录
例题
结构如图示,设梁AB和CD的弯曲刚度EIz相同. 拉杆BC的拉压刚度EA为已知,求拉杆BC的轴力.
a
C
将杆CB移除,则AB,CD均为静定结构, 杆CB的未知轴力FN作用在AB,CD梁上。为1 D 次超静定。
FN 1l FN 3l cos EA cos EA FN 1 FN 3 cos 2
5、求解方程组得
FN 1 FN 2
F cos 2 1 2 cos 3
FN 3
F 1 2 cos 3
目 录
二、装配应力
构件的加工误差是难以避免的。对静定结构,加工误 差只是引起结构几何形状的微小变化,而不会在构件内引 起应力。但对静不定结构,加工误差就要在构件内引起应 力。这种由于装配而引起的应力称为装配应力。 装配应力是结构构件在载荷作用之前已具有的应力, 因而是一种初应力。
超静定结构中才有温度应力。
目 录
解题思路: 平衡方程:RA = RB 变形几何关系: 物理关系:
(t 时)
lT lF
lT l t
RB L
RB l lF EA
EA Lt
补充方程:
联立求解: RA RB EAt
EAt t Et A
目 录
一静定问题及超静定问题三基本静定系或相当系统是一个静定结构该结构上作用有荷载和多余约束力61超静定问题及其解法61超静定问题及其解法二多余约束及多余约束力在静定结构的基础上增加的约束
第六章
简单的超静定问题
§6–1 概述
§6–2 §6–3 §6–4 拉压超静定问题 扭转超静定问题 简单超静定梁
目的与要求:
M
max
WZ
32 M
d
max 3
76.4MPa
目 录
例题
结构如图示,设梁AB和CD的弯曲刚度EIz相同. 拉杆BC的拉压刚度EA为已知,求拉杆BC的轴力.
a
C
将杆CB移除,则AB,CD均为静定结构, 杆CB的未知轴力FN作用在AB,CD梁上。为1 D 次超静定。
第四章 平面弯曲解析

14
4.2.2 剪力方程和弯矩方程 剪力图和弯矩图
(1)剪力方程和弯矩方程
剪力和弯矩沿着梁轴线分布的数学表达 式:
Q=Q(x) M=M(x)
(2)剪力方程和弯矩图
以x为横坐标,剪力Q为纵坐标→Q-x图。 以x为横坐标,弯矩M为纵坐标→M-x图。
15
[例4-1] 试作出如图所示简支梁的剪力图和弯矩图。
第4章 平面弯曲
平面弯曲计算 简单超静定梁的求解 压杆的稳定性简介
1
第
4.1 平面弯曲的概念和实例
4
4.2 平面弯曲的内力分析
章
4.3 平面弯曲的正应力计算
4.4 平面弯曲的变形计算
平
面 4.5 简单超静定梁的求解
弯 曲 4.6 压杆稳定性简介
目录
2
4.1 平面弯曲的概念和实例
(1)实例:
桥式起重机
A
y 2 dA
2 h
y2
bdy
b13
2
y
3
2
h
2
bh3 12
bh3
WZ
IZ ym ax
12
h
2
bh2
6
28
(2)圆形截面
D
Iz
y2dA
A
3 sin 2 dd
2
2
3d sin 2 d
D 4
0
0
64
(3)圆环形截面
Wz
Iz ymax
D4 64 D3
D 2 32
内径为d 外径为
2) 纵线(a-a,b-b)弯曲成曲线, 且梁的一侧伸长,另一侧缩 短。
纯弯曲梁的变形特点 图4-10 纯弯曲梁的变形特点
超静定问题PPT课件
FN1 cos FN2 cos FN3 F 0
FN1
FN 3
EA cos2
E3 A3
FN3 1 2
F EA
cos2
E3 A3
FN1
FN 2
1 2cos
F
E
E3 A3
A cos2
第13页/共59页
B 1
1
Δl3
D
3
C 2
A
3 F2
A
Δl1A' NhomakorabeaFA A C
F
B FB
14
b
a
l
第六章 简单的超静定问题
例题2 求图a所示等直杆AB上,下端的约束力, 并求C截面的位移。杆的拉压刚度为EA。
解: 1. 列平衡方程 有两个未知约束力FA , FB(见图a),但只有一个独 立的平衡方程
FA+FB-F=0 为一次超静定问题。
第14页/共59页
2. 取固定端B为“多余”约束。相应 的相当系统如图b,它应满足相容条件 ΔBF+ΔBB=0,参见图c,d。
MA 0
F a F 2a 0
A
B
P
FN1 a
A
FN2 a
FN3 B
P
第17页/共59页
变形协调方程:
ΔL 1
L1 L3 2(L2 L3 ) (2)
物理方程:
l1
FN 1l EA
l2
FN 2l EA
l3
FN 3l EA
(3)
联解(1)(2)(3)式得:
F 5P 6
F
2
1 3
P
F
3
1 6
D
由位移相容条
简单的超静定问题 超静定问题及其解法

( wB ) FBy
C C F F
8FBy a 3 3EI
(b) (b)
B B
所以
3 14 Fa 3 8FBy a 0 3EI 3EI
MA
MA MA
A A
B B (c) (c) B B B (d) (d) FBy FBy
FA y
A A A
C C
7 FBy F 4
4)由整体平衡条件求其他约束反力
第六章 简单的超静定问题
§6-1 超静定问题及其解法
§6-2 拉压超静定问题
§6-3 扭转超静定问题 §6-4 简单超静定梁
§6-1 超静定问题及其解法
超静定问题与超静定结构:未知力个数多于独立 的平衡方程数。 超静定次数:未知力个数与独立平衡方程数之差。 变形几何相容方程:有多余约束的存在,杆件(或 结构)的变形受到多于静定结构的附加限制。根据 变形的几何相容条件,建立附加的方程。
7-6
目录
采用超静定结构
MA MA FA y FA y
A A 2a 2a (a) (a) A A
B B a a
F F
C C
例 求梁的支反力,梁的抗弯 刚度为EI。 解:
1)判定超静定次数
(b) (b)
B B F F FBy FBy B B B
C C
2)解除多余约束,建立相当系统 3)进行变形比较,列出变形协调 条件
FN1 FN 2 33.3kN
FN 2 2 33.3MPa A2
FN 1 1 66.7MPa A1
例:设温度变化为t,1、2杆的膨胀系数为1, 3杆
的膨胀系数为3,由温差引起的变形为l= •t •l,
求各杆温度应力。
简单超静定问题
05
案例分析
案例一:简支梁的超静定问题
总结词
简支梁的超静定问题通常涉及到梁的弯曲变形和剪切变形,需要利用材料力学和弹性力学的基本原理进行分析。
详细描述
简支梁的超静定问题是指具有简支边界条件的梁在受到外力作用时发生的弯曲变形和剪切变形。这类问题需要考 虑梁的弯曲刚度和剪切刚度,通过建立力和位移的关系来求解。在分析过程中,需要利用材料力学和弹性力学的 基本原理,如弯曲理论、剪切理论等,来推导梁的位移和内力分布。
机械系统的超静定问题
机械系统的超静定问题主要涉及到复杂机械装置和设备,如多自由度机构、柔性 机构和机器人等。这些机构的运动学和动力学特性需要采用超静定分析方法来准 确描述。
超静定问题在机械设计中具有重要意义,通过对机械系统的超静定分析,可以更 好地了解机构的运动性能、动态响应和稳定性等,有助于优化设计并提高机械设 备的性能和可靠性。
超静定问题在桥梁设计中具有重要意义,因为它们能够提供 更精确的结构内力和变形分析,有助于优化设计并提高结构 的安全性和稳定性。
建筑物的超静定问题
建筑物的超静定问题主要涉及到高层建筑、大跨度结构和 复杂结构体系等。这些结构的几何非线性和材料非线性使 得传统的静力分析方法无法得到准确的结果。
超静定问题在建筑设计中同样重要,通过对建筑物的超静 定分析,可以更好地了解结构的动力响应、地震作用和风 荷载等,从而优化设计方案,提高建筑物的安全性和稳定 性。
02
03
解析法
通过建立系统的平衡方程 和多余约束力的方程,求 解未知数的方法。
试算法
通过尝试不同的解法,逐 步逼近最优解的方法。
迭代法
通过不断迭代修正解的方 法,直到满足精度要求为 止。
03
简单的超静定问题
•补充方程:为求出超静定结构的全部未知力,除了利用平衡 方程以外,还必须寻找补充方程,且使补充方程的数目等于 多余未知力的数目。 •根据变形几何相容条件,建立变形几何相容方程,结合物理 关系(胡克定律),则可得出需要的补充方程。 •补充方程的获得,体现了超静定问题的求解技巧。本章节我 们将以轴向拉压、扭转、弯曲的超静定问题进行说明。
例 一平行杆系,三杆的横截面面积、长度和弹性模量均
分别相同,用A、l、E 表示。设AC为一刚性横梁,试求在
荷载F 作用下各杆的轴力
解: (1)受力分析--平衡方程
1
23
FN1
FN2
FN3
A
B
C
l
a
a
a 2
DC
D
F
A BF
Y 0 , F N 1 F N 2 F N 3 F 0
M D 0 , 1 . 5 F N 1 0 . 5 F N 2 0 . 5 F N 3 0
l1l3coas
(3)胡克定理
l1
FN1l EA
l3
FN3l c o E3A3
sa
(4)得出补充方程
FN1
FN3
EAco2sa
E3A3
联立平衡方程、补充方程,求解得
F 3)建立物理方程(如胡克定律,热膨胀规律等)。 F F 超静定结构的未知力的N 数1目多于独N 立2的平衡方程的数目;
2coasEEAcA osa 杆单例的凭两变 静端形力固包学定括平的两衡圆部方截分程面:不杆即能A由解B温出,度全在变部截化未面所知C引力处起的受的问一变题扭形,转,称力以为偶及超矩与静温定M度问e 作内题用力。如相3图应。的3弹2性变形。
(3) 胡刚克定度理(物的理关比系)值有关
简单的超静定问题
M A Me M B 0
Me MB
A
C
B
2、变形协调方程
B 0
即
BM BM 0
e B
Me
MB
A
C
B
3、补充方程
BM
e
M e a GI p
BM
BM Bl GI p NhomakorabeaM e a M Bl 0 GI p GI p
M ea MB l
4、联立解得
3、物理方程
FN 1l l1 EA FN 3 l l 3 EA FN 2 l l 2 EA
得
FN 1 FN 2 FN 3
F 12 F 3
C′
补充方程 FN 1 FN 3 2FN 2
7F 12
例题3:如图所示结构,杆①、②的刚度为EA,梁BD 为刚体,载荷F=50kN,许用应力[s]160MPa。试确 定各杆的横截面积。 解: 1、确定各杆内力 取横梁为研究对象 平衡方程
FB aEAT
由平衡方程得 FA FB aEAT
例题5:如图所示结构,三杆的刚度均为EA,杆③的长 度比设计长度l短了d。试求装配后各杆的轴力。
A
D
① ③ a a C′ C l2 ②
B
解:对称结构,内力对称 变形协调方程
l1 d l 3 cos a
l
d
l3 l1
lt a1 T l1 a 2 T l 2
A
l1
C
l2
B
约束力产生的变形
l FB FB l1 F l B2 E1 A1 E2 A2
lt
FB
变形协调方程
工程力学:11第十一章 简单的超静定问题
第十一章
简单的超静定问题
超静定问题及其解法
❖ 静定问题:其约束力或构件内力可通过静力平衡方 程求解的问题
❖ 超静定问题:仅凭静力学平衡方程不能求解的问题 ❖ “多余约束”:在超静定问题中多于维持平衡所需
的约束,如支座、杆件等 ❖ 超静定次数:未知力超过平衡方程的数目(个数) ❖ 变形几何相容方程:根据多余约束处的几何相容条
件建立的构件变形关系。
超静定梁 基本静定系
静定梁 约束反力比平衡方程数多1
C点的变形状况: wC=0
❖ 超静定问题的解法
1、选定多余约束,解除多余约束,根据约束状况代 以约束反力,得到基本静定系。
2、建立平衡方程
3、由几何相容条件,建立补充方程。
(a) 确定被解除约束点的实际位移(角位移、线位 移);
(b) 根据基本静定系计算各反力在该点的位移代数 和并让其等于实际位移值,得到该点的位移方程;
© 将物理方程带入该点的位移方程,从而得到有 约束反力表示的补充方程;
4、联立上述方程,从而解得该点约束反力。
11-1 拉压超静定问题
❖ 拉压超静定问题实例
已知l1=l2=l, E1=E2=E, A1=A2=A, l3 ,E3,A3 求P作用下结构各杆件的轴力
F
FN 3
1
2
EA E3 A3 cos3
11-2 装配应力、温度应力
一、装配应力 二、温度应力
11-3 扭转超静定问题
11-4 简单超静定 梁
未知反力的数目多于平衡方程的 数目,仅由静力平衡方程不能求 解的梁,称为超静定梁
例:已知q、l,求A、B支座反力。
解除B 处约束, 代之以约束反力
RB
存在变形协调条件
简单的超静定问题
超静定问题及其解法
❖ 静定问题:其约束力或构件内力可通过静力平衡方 程求解的问题
❖ 超静定问题:仅凭静力学平衡方程不能求解的问题 ❖ “多余约束”:在超静定问题中多于维持平衡所需
的约束,如支座、杆件等 ❖ 超静定次数:未知力超过平衡方程的数目(个数) ❖ 变形几何相容方程:根据多余约束处的几何相容条
件建立的构件变形关系。
超静定梁 基本静定系
静定梁 约束反力比平衡方程数多1
C点的变形状况: wC=0
❖ 超静定问题的解法
1、选定多余约束,解除多余约束,根据约束状况代 以约束反力,得到基本静定系。
2、建立平衡方程
3、由几何相容条件,建立补充方程。
(a) 确定被解除约束点的实际位移(角位移、线位 移);
(b) 根据基本静定系计算各反力在该点的位移代数 和并让其等于实际位移值,得到该点的位移方程;
© 将物理方程带入该点的位移方程,从而得到有 约束反力表示的补充方程;
4、联立上述方程,从而解得该点约束反力。
11-1 拉压超静定问题
❖ 拉压超静定问题实例
已知l1=l2=l, E1=E2=E, A1=A2=A, l3 ,E3,A3 求P作用下结构各杆件的轴力
F
FN 3
1
2
EA E3 A3 cos3
11-2 装配应力、温度应力
一、装配应力 二、温度应力
11-3 扭转超静定问题
11-4 简单超静定 梁
未知反力的数目多于平衡方程的 数目,仅由静力平衡方程不能求 解的梁,称为超静定梁
例:已知q、l,求A、B支座反力。
解除B 处约束, 代之以约束反力
RB
存在变形协调条件
