作业(二)答案:单自由度机械系统动力学等效转动惯量等效力矩
机械设计课后习题第7章作业

第7章作业7—1等效转动惯量和等效力矩各自的等效条件是什么?7—2在什么情况下机械才会作周期性速度波动?速度波动有何危害?如何调节?答: 当作用在机械上的驱动力(力矩)周期性变化时,机械的速度会周期性波动。
机械的速度波动不仅影响机械的工作质量,而且会影响机械的效率和寿命。
调节周期性速度波动的方法是在机械中安装一个具有很大转动惯量的飞轮。
7—3飞轮为什么可以调速?能否利用飞轮来调节非周期性速度波动,为什么?答: 飞轮可以凋速的原因是飞轮具有很大的转动惯量,因而要使其转速发生变化.就需要较大的能量,当机械出现盈功时,飞轮轴的角速度只作微小上升,即可将多余的能量吸收储存起来;而当机械出现亏功时,机械运转速度减慢.飞轮又可将其储存的能量释放,以弥补能最的不足,而其角速度只作小幅度的下降。
非周期性速度波动的原因是作用在机械上的驱动力(力矩)和阻力(力矩)的变化是非周期性的。
当长时问内驱动力(力矩)和阻力(力矩)做功不相等,机械就会越转越快或越转越慢.而安装飞轮并不能改变驱动力(力矩)或阻力(力矩)的大小也就不能改变驱动功与阻力功不相等的状况,起不到调速的作用,所以不能利用飞轮来调节非周期陛速度波动。
7—4为什么说在锻压设备等中安装飞轮可以起到节能的作用?解: 因为安装飞轮后,飞轮起到一个能量储存器的作用,它可以用动能的形式把能量储存或释放出来。
对于锻压机械来说,在一个工作周期中,工作时间很短.而峰值载荷很大。
安装飞轮后.可以利用飞轮在机械非工作时间所储存能量来帮助克服其尖峰载荷,从而可以选用较小功率的原动机来拖动,达到节能的目的,因此可以说安装飞轮能起到节能的作用。
7—5由式J F =△W max /(ωm 2 [δ]),你能总结出哪些重要结论(希望能作较全面的分析)? 答:①当△W max 与ωm 一定时,若[δ]下降,则J F 增加。
所以,过分追求机械运转速度的均匀性,将会使飞轮过于笨重。
②由于J F 不可能为无穷大,若△W max ≠0,则[δ]不可能为零,即安装飞轮后机械的速度仍有波动,只是幅度有所减小而已。
第3章 单自由度系统
来描述。将A、B、C三点的M、 值代入可得到一个线性方程组:
解方程组可得到系数
式中
用B、C两点构造一条直线,则M为 的一次函数,可参看例题3.2.1
例题3.2.1某用于起吊重物的电动葫芦的电动机,型号为 额定功率
,同步转速 ,额定转速 求该电动机在额定转速附近的机械特性。
生产阻力:完成有用功时,作用于机械上的阻力,此力作负功。
重力:它随重心向上运动或向下运动而作负功或正功,在一个循环内作功为零。在许多情
况下(尤其是高速机械中)重力可以忽略不计,但对不少重型机械要计及重力。
摩擦力:由运动副表面摩擦产生的有害阻力,作负功。在许多情况下可忽略不计,但对一
些效率较低的机构则应计入摩擦力的影响。
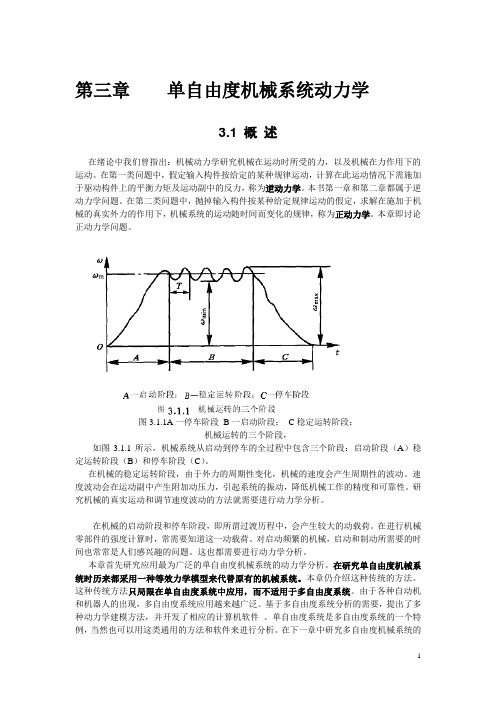
图3.2三相交流异步电动机机械特性
图3.2.1所示为三相异步电动机的机械特性。其中AC段运转是稳定的,当外载荷加大而导致机械减速时,输出力矩将增加,并与外载荷达到新的平衡。而在AD段运转是不稳定的,当外载荷增加导致转速下降时,输出力矩也下降,更无法与外载荷平衡,造成转速进一步下降,直至停车。因此三相异步电动机应在AC段工作。
图3.3.2曲柄滑块机构
例题3.3.2在图3.3.2所示之曲柄滑块机构中,已知:曲柄长 ,连杆长 ,点B到连杆质心 的距离 ,连杆质量 ,滑块质量 ,曲柄对其转动中心的转动惯量 ,连杆对其质心 的转动惯量 。用数值方法计算以曲柄为等效构件时的等效转动惯量 及其导数 随转角的变化规律。
解 用平面连杆机构分析的解析方法可以列出机构各杆的角速度、角加速度的表达式和各杆质心的速度、加速度的表达式。然后利用式(3.3.1)计算等效转动惯量。
式中
机械原理_试题及答案

模拟试题八(机械原理A)一、判断题(10分)[对者画√,错者画×]1、对心曲柄滑块机构都具有急回特性。
()2、渐开线直齿圆柱齿轮的分度圆与节圆相等。
()3、当两直齿圆柱齿轮的安装中心距大于标准中心距时,为保证无侧隙啮合,应采用正传动。
()4、凸轮机构中当从动件的速度有有限量突变时,存在柔性冲击。
()5、用飞轮调节周期性速度波动时,可将机械的速度波动调为零。
()6、动平衡的转子一定满足静平衡条件。
()7、斜齿圆柱齿轮的法面压力角大于端面压力角。
()8、加工负变位齿轮时,齿条刀具的分度线应向远离轮坯的方向移动。
( )9、在铰链四杆机构中,固定最短杆的邻边可得曲柄摇杆机构。
()10、平底直动从动件盘状凸轮机构的压力角为常数。
()二、填空题(10分)1、机构具有确定运动的条件为________________________。
2、平面八杆机构共有_________瞬心。
3、渐开线齿廓上最大压力角在________圆上。
4、当行程速比系数K=1.5时,机构的极位夹角θ=__________。
5、举出两种可实现间歇运动的机构。
________________________。
6、偏置滚子(尖顶)直动从动件盘状凸轮机构的压力角表达式tgα=______。
7、渐开线齿轮的齿廓形状与哪些参数有关?_____________。
8、机械中安装飞轮的目的是_____________。
9、直齿圆锥齿轮的当量齿数Zv=__________。
10、在连杆机构中处于死点位置的γ=__________;α=__________。
三、简答题(10分)1、为了实现定传动比传动,对齿轮轮廓曲线有什么要求?2、计算机构自由度时有哪些注意事项?3、计算混合轮系传动比有哪些步骤?4、铰链四杆机构中存在双曲柄的条件是什么?5、机构等效动力学模型中的四个等效量有哪些?分别是根据何种原理求得?四、计算如图8.1发动机配气机构的自由度。
(8分)图8.1图8.2五、在图示8.2的回归轮系中,已知:Z1=20,Z2=48,m1= m2=2mm,Z3=18,Z4=36,m3= m4=2.5mm该两对齿轮均为标准渐开线直齿圆柱齿轮,且安装中心距相等。
第一章单自由度机械系统动力学建模解析

静力分析(static) 动态静力分析(kinetio-static) 动力分析(dynamic) 弹性动力分析(elastodynamic)
1 静力分析
对低速机械,运动中产生的惯性可以忽略不计,对机 械的运动过程中的各个位置,可以用静力学方法求出 为平衡载荷而需在驱动构件上施加的驱动力或力矩, 以及各运动副中的约束反力,可用此进行原动机功率 的计算、构件和运动副承载能力的计算。
v32
(M1
1
v3
F3 )v3
me
n i 1
mi
vsi v
2
等 J效si质 量vi
2 me
Fe
n i 1
Fi
程,其维数等于机构的自由度数目; 另一类是含运动副约束反力的代数与微分混合型
方程,其维数大于机构的自由度数目。
机构动力学分析的发展与现状
建立复杂机构动力学模型的常用力学方法有: * 牛顿-欧拉(Newton-Euler)法 * 拉格朗日(Lagrange)法 * 虚功原理法 * 凯恩(Kane)法 * 旋量法和R-W法等。
机械系统动力学
绪论
机械系统动力学是应用力学的基本理论解决 机械系统中动力学问题的一门学科,其核心 问题是建立机械系统的运动状态与其内部参 数、外部条件之间的关系,找到解决问题的 途径
三体机械臂
可伸展卫星太阳能电池板
汽车
五轴并联机床
机械动力学研究内容 :
机械原理由三部分组成:
机械结构学、机构运动学和机械动力学
4 弹性动力分析
随着机械系统向高速轻质化发展,构件的柔度加大,惯 性力急剧加大,构件的弹性变形可能给机械的运动输出 带来误差。机械系统柔度 系统的固有频率 ,机械 运转速度 激振频率 可能会发生共振,破坏运动精度 ,影响疲劳强度,引发噪声。
#《机械动力学》期末复习题和答案

期末复习题一、判断题(每小题2分,共30题,共60分)1、机构平衡问题在本质上是一种以动态静力分析为基础的动力学综合,或动力学设计。
()2、平衡是在运动设计完成之前的一种动力学设计。
()3、平衡分析着眼于全部消除或部分消除引起震动的激振力。
()4、优化平衡就是采用优化的方法获得一个绝对最佳解。
()5、在动力分析中主要涉及的力是驱动力和生产阻力。
()6、通路定理是用来判断能否实现摆动力完全平衡的理论。
()7、惯性力的计算是建立在主动构件作理想运动的假定的基础上的。
()8、当取直线运动的构件作为等效构件时,作用于系统上的全部外力折算到该构件上得到等效力。
()9、无论如何,等效力和机械驱动构件的真实速度无关。
()10、等效质量和等效转动惯量和机械驱动构件的真实速度无关。
()11、摆动力的平衡一定会导致机械结构的复杂化。
()12、综合平衡不仅考虑机构在机座上的平衡,同时也考虑运动副动压力的平衡和输入转矩的平衡。
()13、作用于等效构件上的等效力(或等效力矩)所作的功等于作用于系统上的外力所作的功。
()14、机器人操作机是一个多自由度的闭环的空间机构。
()15、速度越快,系统的固有频率越大。
()16、两点动代换后的系统和原有系统在静力学上是完全等效的。
()17、质量代换是将构件的质量用若干集中质量来代换,使这些代换质量和原有质量在运动学上等效。
()18、平衡的实质就是采用构件质量再分配等手段完全地或部分地消除惯性载荷。
()19、对于不存在多余约束和多个自由度的机构,动态静力分析是一个静定问题。
()20、弹性动力分析考虑构件的弹性变形。
()21、优化综合平衡是一个多目标的优化问题,是一种部分平衡。
()22、摆动力的完全平衡常常会导致机械结构的简单化。
()23、机构摆动力矩完全平衡的条件为机构的质量矩为常数。
()24、机构摆动力完全平衡的条件为机构的质量矩为常数。
()25、机构摆动力完全平衡的条件是:机构运动时,其总质心作变速直线运动。
机械原理练习册

班级学号姓名
8、如图所示已知曲柄的长度L、转角 卜、等角速度3及中心距-要求确定导杆的转角 肌、角 速度33和角加速度3,以及滑块在导杆上的位置S、滑动速度VB2B3及加速度aE233o(用复数矢量法, 推导出方程式即可)
第四章平面机构的力分析
一、是非、填空与选择题
1、 按照力对运动的影响,可将力分为和_
2、 在机械运动中总是有摩擦力存在,因此,机械的效率总是。
3、 具有自锁性的机构其正行程运动,反行程运动。
4、 下列式子中不是机械效率表达式的是一 _
AMWVdB、Pf/FdC、Fo/FD、M/M
5、 三角螺纹的摩擦力矩⑴方牙螺纹的摩擦力矩,因此,它多用于(2)。
(1)A、小于B、等于C、大于
(2)A、传递动力B、紧固联接
7、下图所示的正切机构中,已知h=500mm3i=10rad/s(为常数),构件3的重量Q=10N重心在其轴线上,生产阻力R=100N其余构件的重力和惯性力均略去不计。试求当 『=60°时,需 加在构件1上的平衡力矩M。
第五章 机械的效率和自锁
一、选择与填空题
1在机械运转过程中,考虑摩擦的转动副,总反力作用线总于摩擦圆。
2、有一楔形滑块沿倾斜V形导路滑动,见图,已知,=35°,0=60°,摩擦系数f=0.13,载 荷Q=1000N试求滑块等速上升和下降时的P和P、效率n和n'及反行程自锁条件。
5、已知机构各构件的长度LacLbc,原动件1以等角速度31逆时针转动,用矢量方程图解法求图 示位置构件2、构件3的角速度32、33和角加速度2、3(列出相关的速度和加速度矢量方程
式;作出速度图和加速度图)。
机械原理作业册
班级学号姓名
6、下图所示的摇杆机构中,如果Lab=0.03mLac=0.1m, bd=0.05mLd=0.04m曲柄1以等角速度
单自由度机械系统动力学
•位移和转角叫广义坐标, •速度和角速度叫广义速度。
vk
,
j
; vk v
, j v
称为传动速比。
12
Confucius said: “A gentleman neither worries nor fears.”
v
13
Confucius said: “A gentleman neither worries nor fears.”
for(i=0;i<37;i++)
{
phi1=i*h;
//Euler(double phi1);
Runge_Kutta(phi1);
printf("%3.0f %8.3f\n",phi1*180/pi,omega10);
omega10=omega1;
}
}
66
欧拉法:
void Euler(double phi1) {
❖ 研究方法: 等效力学模型
2
2.2 驱动力和工作阻力
2.2.1 系统受力 主要受力有:驱动力、惯性力、工作阻力、介质阻
力、重力和摩擦阻力等。 ❖驱动力:原动机产生的力,做正功。
驱动力的变化规律为:1)常数;2)是位移的函 数;3)是速度的函数。 ❖工作阻力:工作构件的阻力,做负功。
工作阻力的变化规律为:1)常数;2)是位移的 函数;3)是速度的函数;4)是时间的函数。
#define pi 3.1416
#define h 10*pi/180
30
double l1,l2,ls2,e,J01,J2,m2,m3;
double phi1,Je,dJe,omega1,Vc;
int i;
机械原理的选择和判断题带答案
A.不需再考虑平衡问题B.进行平衡试验C.重新进行计算D.确定平衡精度后再做试验
3.刚性转子动平衡的力学原理
正确答案:B
A.平面汇交力系平衡B.空间力系平衡C.振动梁理论D.动能定理
4.当需要比较两个转子的平衡效果时,适宜采用
正确答案:B
A.许用质径积法B.许用偏心距C.质量代换法D.力系平衡
对错
14.转子的平衡精度越高越好
正确答案:错
对错
15.转子的许用不平衡量与转子的速度无关。
正确答案:错
对错
16.只要经过平衡计算后的转子就可以达到平衡精度的要求。
正确答案:错
对错
17.对于任何动不平衡的转子,不论其不平衡质量分布在几个平面内,只要在两个平衡基面内分别加上或除 去一个适当的平衡质量,即可达到完全平衡。
正确答案:C
A.等速运动规律B.等加速等减速运动规律C.摆线运动规律D.简谐运动规律
5.对心直动尖顶推杆盘形凸轮机构的推程压力角超过许用值时,可采用措施来解决。
正确答案:错
对错
18.任何机构都是由机架加原动件, 再加若干自由度为零的杆组组成的。 所以说杆组是自由度为零的运动链 ()
正确答案:对
对错
19.只有自由度为1的机构才具有确定的运动。()
正确答案:错
对错
20.具有一个自由度的运动副称为Ⅰ级副。()
正确答案:错
对错
第
选择题(每小题10分,共70分)
1.某机构中有6个构件,则该机构的全部瞬心数目为()。
正确答案:A
A.至少应有2个B.最多有2个C.只有2个D.不受限制
11.机构作确定运动的基本条件是其自由度必须大于零。()
智慧树知道网课《机械原理(青岛理工大学)》章节测试满分答案.
第一章测试1【多选题】(10分)各种机构都是用来传递与变换()和()的可动的装置。
A.力B.运动C.质量D.转动惯量2【多选题】(10分)机器是用来变换与传递()、()和()的执行机械运动装置。
A.质量B.物料C.能量D.信息3【单选题】(10分)对于不同的机器,就其组成来说,都是由各种()组合而成。
A.装置B.机构C.部件D.零件4【多选题】(10分)现代机械朝着()方向发展。
A.高精度B.低能耗C.重载D.高速5【判断题】(10分)对机构进行运动分析,是了解现有机械运动性能的必要手段。
A.对B.错6【判断题】(10分)机械是机器和机构的总成。
A.错B.对第二章测试1【单选题】(10分)一种相同的机构()组成不同的机器。
A.可以B.不一定C.不能2【单选题】(10分)从制造角度出发,任何机器都是由许多()组合而成。
A.构件B.零件C.机构3【单选题】(10分)机构具有确定运动的条件是()。
A.原动件数目等于自由度数目B.原动件数目大于等于自由度数目C.原动件数目小于等于自由度数目4【单选题】(10分)在平面机构中,每个自由构件具有()个自由度。
A.4B.3C.1D.25【单选题】(10分)把最后不能再拆的最简单的自由度为()的构件组称为基本杆组。
A.B.3C.1D.26【多选题】(10分)常见平面运动副中的低副有以下哪几个?()A.移动副B.转动副C.球销副D.球面副7【多选题】(10分)机构运动简图一般采用以下哪些模型或符号绘制而成?()A.运动副符号B.一般构件表示方法C.常用机构运动简图符号8【判断题】(10分)平面机构中若引入一个低副将带入2个约束。
A.错B.对9【判断题】(10分)平面机构中若引入一个高副将带入2个约束。
A.对B.错10【判断题】(10分)机构的组成原理是任何机构都可以看作是由若干基本杆组依次连接于原动件上而成的。
A.对B.错第三章测试1【单选题】(10分)速度影像和加速度影像只适用于()。
自由度机械系统动力学
1. 解析法
d
t t0 Je 0 Me()
(3.4.6)
若
Me()ab
则
再求出其 反函数
t
t0
Je b
ln ab ab0
f (t)
(3.4.7)
若
d
tt0Je 0abc2
演讲完毕,感谢观 看
(3.4.8)
一、等效力和等效力矩 二、等效质量和等效转动惯量
等效力学模型
等效原则: 等效构件具有的动能=各构件动能之和
M e
n j 1
m
j
vSj v
2
J
j
j
v
2
J e
n j 1
m
j
vSj
2
J
j
j
2
(3.3.3)
等效质量和等效转动惯量与传动比有关, 而与机械驱动构件的真实速度无关
2W()
Je()
(3.4.3)
若
是以表达式
给出,且为可积函数时,
(3.4.3)可得到解析解。
但是
常常是以线
图或表格形式给出,则只
能用数值积分法来求解。
常用的数值积分法有梯形
法和辛普生法。
运动方程式的求解方法
一、等效力矩是位置的函数时运动方程的求解
二、等效转动惯量是常数、等效力矩是角速度的函数时运动方程
单自由度机械系统可以采用等效力学模型来进行研究,即系统的动力学问题转化为一个等效构件的动力学问题来研究,可以 使问题得到简化。
当取作定轴转动的构件作为等效构件时,作用于系统上 的全部外力折算到该构件上得到等效力矩,系统的全部 质量和转动惯量折算到该构件上得到等效转动惯量。
当取作直线运动的构件作为等效构件时,作用于系统上 的全部外力折算到该构件上得到等效力,系统的全部质 量和转动惯量折算到该构件上得到等效质量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作业(二)单自由度机械系统动力学等效转动惯量等效力矩 1 .如题图1所示的六杆机构中,已知滑块5的质量为
m 5=20kg ,
1AB =1 ED =100mm , 1BC =1 CD =1 EF =200mm ,扪=©2= ©3=90°,作用在 滑
块5上的力P = 500N .当取曲柄AB 为等效构件时,求机构在图 示位置的等效转动惯量和力P 的等效力矩.
答案:解此题的思路是:①运动分析求出机构处在该位置时,质心点 的速度及各构件的角速度.
②根据等效转动惯量,等效力矩的公式求出. 做出机构的位置图,用图解法进行运动分析.
V C =V B = 31 XI AB
3 2=0
V D =V C = 31 X| AB 且 3 3 =V C /I CD = 31 V F =V D = 31 XI AB (方向水平向右)
34=0
n
J e [m^)2
由等效转动惯量的公式:
i1
1
n
V i
i M e
[ F i cos D M i(—^]
i 1 1
1
2 J sD ]
1
J e =m 5(V F / 3 1)2
=20kg X ( 31 X A B /3 1 )2 = 0
2kgm 2
由等效力矩的定义:
图1
M e =500 X31 X|AB X COS180°/® 1 = —50Nm (因为V F的方向
与P方向相反,所以a= 180°)
2.题图2所示的轮系中,已知各轮齿数:z i=Z2' =20 , Z2=Z3=40 ,
J I=J2' =0 . 01kg m2,J2=J3=0 . 04kg m2.作用在轴O 3 上的阻力矩M 3 = 40N m .当取齿轮1为等效构件时,求机构的等效转动惯量
和阻力矩M 3的等效力
矩.
答案:该轮系为定轴轮系.
i12= 31/ 32 = (-1) 1Z2/Z 1 1 32 ' = 32= —0 . 5 X31 32 = — 3 1 /2= —0. 5 X31
i2 ' 3= 32 ' / 33 = (-1) 1Z3/Z 2'二亠 3 3=0 . 25 X31 根据等效转动惯量公式
n
J e [m i(VSL)2J si(」)2]
i 1 1 1
J e= J 1 x( 3 1/ 3 1)2+ J2 X( 3 2/ 3 1)2+ J2 'X(32 ' / 31)2+ J3 X( 3 3/ 31)2
=J1 + J2 /4 + J2 ' /4 + J3 / 16
=0 . 01 +0 . 04/4+0 . 01 /4+0 . 04/16 =0. 025 kg m 2
n
V
M e
[F i COS —) M i (T]
根据等效力矩的公式:
i1
1
1
M e =M 3 Xw 3/ 31=40 X 0. 25 31/ 31=10N m
3.在题图3所示减速器中,已知各轮的齿数:Z 1=Z 3=25 ,Z 2=Z 4=50 , J 1=J 3=0 . 04kg m 2, J 2=J 4=0 . 16kg m 2,(忽略各
33= 3 2= 3 1/2
i 34= 33/ 34=Z 4/Z 3
轴的转动惯量), 作用在轴皿上的阻力矩 M 3=100N m .试求选取轴 I 为等效构件时, 该机构的等效转动惯量
J 和M 3的等效阻力矩M r
.
答案:i 12= 3
1
/ 3 2=Z 2/Z 1 3 2 = 3 1/2
各轮的转动惯量
34 =31/4
等效转动惯量:
J=J 1(3 1/ 31)2+J2(32/ 31)2+J3(3 3/ 31)2+j4(34/ 3 1)2
=0 . 042+0 . 16 x(1/2)2+0 . 04 x(1/2)2+0 . 16 x(1/4)2
=0 . 04+0 . 04+0 . 01+0 . 01
=0 . 1 kg m2
等效阻力矩:
M r=M 3 X34/ 3 1 = 100/4=25(N m)
4.题图4所示为一简易机床的主传动系统,由一级带传动和两级齿轮传动组成.已知直流电动机的转速n o= 1500r/mi n ,小带轮直径d=100mm,转动惯量J d=0 . 1kg m2,大带轮直径D = 200mm , 转动惯量J D=0 . 3kg m2.各齿轮的齿数和转动惯量分别为:z1=32 ,
J1=0 . 1kg m2, Z2=56 , J2=0 . 2kg m2, Z2' =32 , J2' =0 . 4kg m2, Z3=56 , J3=0 . 25kg m2.
要求在切断电源后2秒,利用装在轴上的制动器将整个传动系统制动住.求所需的制动力矩M1.
图4
答案:电机的转速n o = 1500r/min
其角速度3 0 = 2 nX I500/60=50 n (rad⑸
三根轴的转速分别为:
3i=d x®o/D=25 n (rad⑸
3 2=z i X®I/Z2=32 X25 兀/56=1429 n (rad/s)
33=Z2' X^/Z3=32 X1429 兀/56=816 n (rad/s)
轴的等效转动惯量:
J v=J d X( 30/ 31)2+J D X(3l/ 31)2+J l X( 31/ GJ 1)2+J 2 X( 3 2/ 31)2+ J 2' X (32/ 3 1)2+ J 3 X( 33/ 31)2
••J V=0 .1 X(5o 兀/25 兀)2+0 .3 X12+O .1 X12+(0 . 2+0 . 1) X(14 . 29 兀/25 n2+0 . 25 X(8. 16 兀/25 %)2
=0 . 4+0 . 4+0 . 098+0 . 027
=0 . 925 (kg m2)
轴制动前的初始角速度3 1 =25n,制动阶段做减速运动,即可求出制动时的角加速度
• •3= 3 0 —s t 即0 = 25 n—2 e
I E=12 . 5 n
则在2秒内制动,其制动力矩M为:
M=J V X =0 . 925 X12 . 5=36 . 31 (kg m)
5 .在题图5所示定轴轮系中,已知各轮齿数为:Z1=Z2' =20 , Z2=Z3=40 ;各轮对其轮心的转动惯量分别为JJ' =0 . 01kg m2,
J2=J3=O . 04kg m2;作用在轮1上的驱动力矩M d=60N m,作用在轮3上的阻力矩M r=120N m .设该轮系原来静止,试求在M d和
M r作用下,运转到t=15s时,轮1的角速度 a和角加速度a l .
图5
答案:i12= 31/ 32=(-1) 1X Z2/Z1 32二一3 l/2
i13= 31/ 3 3 = (-1) 2X Z2 X Z3/Z 1 X Z2' 3 3=20 X20 X31/40 X40= 3
1/4
轮1的等效力矩M为:
M= M d X31/ 31+M r X33/ 31 =60 X1 —120/4=30 N m
轮1的等效转动惯量J为:
J =J 1 ( 3 1/ 3 1 )2+(J 2' +J2)( 3 2/ 3 1)2+J 3(3 3/ 3 1)2=0 . 01 X 1+(0 . 01+0 . 04)/4+0 . 04/16=0 . 025 (kg m2)
,.1M=J X£•••角加速度£=M/J = 1200 (rad/s 2) 初始角速度30 = 0 「•31= 3 0+ £X
i A31=1200 X1 . 5=1800(rad/s)。
