全国高考理科数学试题分类汇编平面向量

合集下载

高考数学试题分类汇编——平面向量

高考数学试题分类汇编平面向量一．选择题：1.（全国一5）在ABC △中，AB c =，AC b =．若点D 满足2BD DC =，则AD =（ A ）A ．2133b c +B ．5233c b -C ．2133b c -D ．1233b c + 2.（安徽卷2）若(2,4)AB =，(1,3)AC =, 则BC =（ B ）A ．（1，1）B ．（－1，－1）C ．（3，7）D ．（-3,-7）3.（安徽卷5）在三角形ABC 中，5,3,7AB AC BC ===,则BAC ∠的大小为（ A ）A ．23πB ．56πC ．34πD ．3π 4.（北京卷4）已知ABC △中，2a =3b =60B =，那么角A 等于（ C ）A ．135B ．90C ．45D ．305.（福建卷8)在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，若a 2+c 2-b 3ac ,则角B 的值为A A.6π B.3π C.6π或56π D.3π或23π 6.（广东卷3）已知平面向量(1,2)a =，(2,)b m =-，且a //b ，则23a b +＝（ B ）A 、(5,10)--B 、(4,8)--C 、(3,6)--D 、(2,4)--7.（海南卷5）已知平面向量a =（1，－3），b =（4，－2），a b λ+与a 垂直，则λ是（ A ）A. －1B. 1C. －2D. 28.（海南卷9）平面向量a ，b 共线的充要条件是（ D ）A. a ，b 方向相同B. a ，b 两向量中至少有一个为零向量 C. R λ∃∈， b a λ= D. 存在不全为零的实数1λ，2λ，120a b λλ+=9.（湖北卷设1）)2,1(-=a ,)4,3(-=b ,则=•+c b a )2( CA.(15,12)-B.0C.3-D.11-10.（湖南卷7）在ABC ∆中，AB=3，AC=2，BC=10，则AB AC ⋅= ( D )A ．23-B ．32-C ．32D ．23 11.（辽宁卷5）已知四边形ABCD 的三个顶点(02)A ，，(12)B --，，(31)C ，，且2BC AD =，则顶点D 的坐标为（ A ）A ．722⎛⎫ ⎪⎝⎭，B ．122⎛⎫- ⎪⎝⎭，C ．(32)，D ．(13)，12.（山东卷8）已知a b c ，，为ABC △的三个内角A B C ，，的对边，向量31)(cos sin )A A =-=，，，m n ．若⊥m n ，且cos cos sin a B b A c C +=，则角A B ，的大小分别为（ C ）A ．ππ63，B ．2ππ36，C ．ππ36，D ．ππ33， 13.（四川卷3）设平面向量()()3,5,2,1a b ==-，则2a b -=( A )（Ａ）()7,3 （Ｂ）()7,7 （Ｃ）()1,7 （Ｄ）()1,314.（四川卷7）ABC ∆的三内角,,A B C 的对边边长分别为,,a b c ，若5,22a b A B ==，则cos B =( B ) 5 5 5 515.（重庆卷4)若点P 分有向线段AB 所成的比为-13，则点B 分有向线段PA 所成的比是A (A)-32 (B)-12 (C) 12(D)3 二．填空题：1.（全国二13）设向量(12)(23)==，，，a b ，若向量λ+a b 与向量(47)=--，c 共线，则=λ ．22.（北京卷11）已知向量a 与b 的夹角为120，且4==a b ，那么b a •的值为．8-3.（湖北卷12）在△ABC 中，a ，b ，c 分别是角A ，B ，C 所对的边，已知3,3,30,a b c ===︒则A ＝ . 6π 4.（湖南卷11）已知向量)3,1(=a ，)0,2(-=b ，则b a +=_____________________.25.（江苏卷5）a ，b 的夹角为120︒，1a =，3b = 则5a b -= ．76.（江苏卷13）若2BC ，则ABC S ∆的最大值．227.（江西卷16）如图，正六边形ABCDEF 中，有下列四个命题：A ．2AC AF BC +=B ．22AD AB AF =+C ．AC AD AD AB ⋅=⋅D ．()()AD AF EF AD AF EF ⋅=⋅ 其中真命题的代号是（写出所有真命题的代号）．A 、B 、D8.（陕西卷15）关于平面向量，，a b c ．有下列三个命题： ①若c a b a ⋅=⋅，则=b c ．②若(1)(26)k ==-，，，a b ，∥a b ，则3k =-． ③非零向量a 和b 满足||||||==-a b a b ，则a 与+a b 的夹角为60．其中真命题的序号为 ② ．（写出所有真命题的序号）A B D E CF9.（上海卷5）若向量a ，b 满足12a b ==，且a 与b 的夹角为3π，则a b += ．710.（天津卷14）已知平面向量(24)=，a ，(12)=-，b ，若()=-c a a b b ，则=c ．211.（浙江卷14）在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，若()C a A c b cos cos 3=-，则=A cos 312.（浙江卷16）已知a 是平面内的单位向量，若向量b 满足()0b a b -=，则||b 的取值范围是。

2021年高考数学分项汇编专题5 平面向量(含解析)理

2021年高考数学分项汇编专题5 平面向量（含解析）理一．基础题组1. 【xx全国卷Ⅰ，理6】设a、b、c是单位向量，且a·b=0，则（a-c）·（b-c）的最小值为（）A.-2B.C.-1D.【答案】：D2. 【xx全国1，理3】在中，，．若点满足，则（）A．B．C．D．【答案】A.3. 【xx课标Ⅰ，理15】已知为圆上的三点，若，则与的夹角为_______．【答案】．4. 【xx全国，理13】已知向量a，b夹角为45°，且|a|＝1，|2a－b|＝，则|b|＝__________．【答案】：5. 【xx高考新课标1，理7】设为所在平面内一点，则（）（A） (B)（C） (D)【答案】A【考点定位】平面向量的线性运算二．能力题组1. 【xx全国，理9】设平面向量a1，a2，a3的和a1+a2+a3=0.如果平面各量b1，b2，b3满足│b i│=2│a i│，且a i的顺时针旋转后与b i同向，其中i-1，2，3，则（）（A）-b1+b2+b3=0 （B）b1-b2+b3=0（C）b1+b2-b3=0 （D）b1+b2+b3=0【答案】D2. 【xx课标全国Ⅰ，理13】已知两个单位向量a，b的夹角为60°，c＝t a＋(1－t)b.若b·c＝0，则t ＝__________.【答案】：2三．拔高题组1. 【2011全国，理12】设向量a，b，c满足|a|＝|b|＝1，，〈a－c，b－c〉＝60°，则|c|的最大值等于( )A．2 B． C． D．1【答案】：A20493 500D 倍 gT25851 64FB 擻24874 612A 愪35674 8B5A 譚35228 899C 覜 31294 7A3E 稾n33973 84B5 蒵36567 8ED7 軗&。

高考数学真题汇编---平面向量(有解析)

高考数学真题汇编---平面向量学校：___________姓名：___________班级：___________考号：___________一．选择题（共10小题）1．（2017•新课标Ⅱ）设非零向量，满足|+|=|﹣|则（）A．⊥B．||=||C．∥D．||＞||2．（2017•新课标Ⅲ）在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上．若=λ+μ，则λ+μ的最大值为（）A．3 B．2C．D．23．（2017•新课标Ⅱ）已知△ABC是边长为2的等边三角形，P为平面ABC内一点，则•（+）的最小值是（）A．﹣2 B．﹣C．﹣D．﹣14．（2017•浙江）如图，已知平面四边形ABCD，AB⊥BC，AB=BC=AD=2，CD=3，AC与BD交于点O，记I1=•，I2=•，I3=•，则（）A．I1＜I2＜I3B．I1＜I3＜I2C．I3＜I1＜I2D．I2＜I1＜I35．（2016•新课标Ⅲ）已知向量=（，），=（，），则∠ABC=（）A．30°B．45°C．60°D．120°6．（2016•新课标Ⅱ）已知向量=（1，m），=（3，﹣2），且（+）⊥，则m=（）A．﹣8 B．﹣6 C ．6 D．87．（2016•天津）已知△ABC是边长为1的等边三角形，点D、E分别是边AB、BC的中点，连接DE并延长到点F，使得DE=2EF，则•的值为（）A．﹣B．C．D．8．（2016•山东）已知非零向量，满足4||=3||，cos＜，＞=．若⊥（t+），则实数t的值为（）A．4 B．﹣4 C．D．﹣9．（2016•四川）在平面内，定点A，B，C，D满足==，•=•=•=﹣2，动点P，M满足=1，=，则||2的最大值是（）A．B．C．D．10．（2016•四川）已知正三角形ABC的边长为2，平面ABC内的动点P，M 满足||=1，=，则||2的最大值是（）A．B．C．D．二．填空题（共20小题）11．（2017•山东）已知向量=（2，6），=（﹣1，λ），若，则λ=．12．（2017•新课标Ⅲ）已知向量=（﹣2，3），=（3，m），且，则m=．13．（2017•新课标Ⅰ）已知向量=（﹣1，2），=（m，1），若向量+与垂直，则m=．14．（2017•新课标Ⅰ）已知向量，的夹角为60°，||=2，||=1，则|+2|=．15．（2017•山东）已知，是互相垂直的单位向量，若﹣与+λ的夹角为60°，则实数λ的值是．16．（2017•江苏）在平面直角坐标系xOy中，A（﹣12，0），B（0，6），点P在圆O：x2+y2=50上．若≤20，则点P的横坐标的取值范围是．17．（2017•北京）已知点P在圆x2+y2=1上，点A的坐标为（﹣2，0），O为原点，则•的最大值为．18．（2017•江苏）如图，在同一个平面内，向量，，的模分别为1，1，，与的夹角为α，且tanα=7，与的夹角为45°．若=m+n（m，n∈R），则m+n=．19．（2017•天津）在△ABC中，∠A=60°，AB=3，AC=2．若=2，=λ﹣（λ∈R），且=﹣4，则λ的值为．20．（2016•新课标Ⅱ）已知向量=（m，4），=（3，﹣2），且∥，则m=．21．（2016•上海）在平面直角坐标系中，已知A（1，0），B（0，﹣1），P是曲线y=上一个动点，则•的取值范围是．22．（2016•新课标Ⅰ）设向量=（m，1），=（1，2），且|+|2=||2+||2，则m=．23．（2016•山东）已知向量=（1，﹣1），=（6，﹣4），若⊥（t+），则实数t的值为．24．（2016•新课标Ⅰ）设向量=（x，x+1），=（1，2），且⊥，则x=．25．（2016•浙江）已知平面向量，，||=1，||=2，=1，若为平面单位向量，则||+||的最大值是．26．（2016•上海）如图，已知点O（0，0），A（1，0），B（0，﹣1），P是曲线y=上一个动点，则•的取值范围是．27．（2016•江苏）如图，在△ABC中，D是BC的中点，E，F是AD上的两个三等分点，•=4，•=﹣1，则•的值是．28．（2016•北京）已知向量=（1，），=（，1），则与夹角的大小为．29．（2016•上海）如图，在平面直角坐标系xOy中，O为正八边形A1A2…A8的中心，A1（1，0）任取不同的两点A i，A j，点P满足++=，则点P落在第一象限的概率是．30．（2016•浙江）已知向量，，||=1，||=2，若对任意单位向量，均有|•|+|•|≤，则•的最大值是．三．解答题（共1小题）31．（2017•山东）在△ABC中，角A，B，C的对边分别为a，b，c，已知b=3，= =3，求A和a．﹣6，S△ABC高考数学真题汇编---平面向量参考答案与试题解析一．选择题（共10小题）1．【分析】由已知得，从而=0，由此得到．【解答】解：∵非零向量，满足|+|=|﹣|，∴，解得=0，∴．故选：A．2．【分析】如图：以A为原点，以AB，AD所在的直线为x，y轴建立如图所示的坐标系，先求出圆的标准方程，再设点P的坐标为（cosθ+1，sinθ+2），根据=λ+μ，求出λ，μ，根据三角函数的性质即可求出最值．【解答】解：如图：以A为原点，以AB，AD所在的直线为x，y轴建立如图所示的坐标系，则A（0，0），B（1，0），D（0，2），C（1，2），∵动点P在以点C为圆心且与BD相切的圆上，设圆的半径为r，∵BC=2，CD=1，∴BD==∴BC•CD=BD•r，∴r=，∴圆的方程为（x﹣1）2+（y﹣2）2=，设点P的坐标为（cosθ+1，sinθ+2），∵=λ+μ，∴（cosθ+1，sinθ+2）=λ（1，0）+μ（0，2）=（λ，2μ），∴cosθ+1=λ，sinθ+2=2μ，∴λ+μ=cosθ+sinθ+2=sin（θ+φ）+2，其中tanφ=2，∵﹣1≤sin（θ+φ）≤1，∴1≤λ+μ≤3，故λ+μ的最大值为3，故选：A．3．【分析】根据条件建立坐标系，求出点的坐标，利用坐标法结合向量数量积的公式进行计算即可．【解答】解：建立如图所示的坐标系，以BC中点为坐标原点，则A（0，），B（﹣1，0），C（1，0），设P（x，y），则=（﹣x，﹣y），=（﹣1﹣x，﹣y），=（1﹣x，﹣y），则•（+）=2x2﹣2y+2y2=2[x2+（y﹣）2﹣]∴当x=0，y=时，取得最小值2×（﹣）=﹣，故选：B．4．【分析】根据向量数量积的定义结合图象边角关系进行判断即可．【解答】解：∵AB⊥BC，AB=BC=AD=2，CD=3，∴AC=2，∴∠AOB=∠COD＞90°，由图象知OA＜OC，OB＜OD，∴0＞•＞•，•＞0，即I3＜I1＜I2，故选：C．5．【分析】根据向量的坐标便可求出，及的值，从而根据向量夹角余弦公式即可求出cos∠ABC的值，根据∠ABC的范围便可得出∠ABC 的值．【解答】解：，；∴；又0°≤∠ABC≤180°；∴∠ABC=30°．故选：A．【分析】求出向量+的坐标，根据向量垂直的充要条件，构造关于m的方程，解得答案．【解答】解：∵向量=（1，m），=（3，﹣2），∴+=（4，m﹣2），又∵（+）⊥，∴12﹣2（m﹣2）=0，解得：m=8，故选：D．7．【分析】由题意画出图形，把、都用表示，然后代入数量积公式得答案．【解答】解：如图，∵D、E分别是边AB、BC的中点，且DE=2EF，∴•========．故选：C．【分析】若⊥（t+），则•（t+）=0，进而可得实数t的值．【解答】解：∵4||=3||，cos＜，＞=，⊥（t+），∴•（t+）=t•+2=t||•||•+||2=（）||2=0，解得：t=﹣4，故选：B．9．【分析】由==，可得D为△ABC的外心，又•=•=•，可得可得D为△ABC的垂心，则D为△ABC的中心，即△ABC为正三角形．运用向量的数量积定义可得△ABC的边长，以A为坐标原点，AD所在直线为x轴建立直角坐标系xOy，求得B，C的坐标，再设P（cosθ，sinθ），（0≤θ＜2π），由中点坐标公式可得M的坐标，运用两点的距离公式可得BM的长，运用三角函数的恒等变换公式，结合正弦函数的值域，即可得到最大值．【解答】解：由==，可得D为△ABC的外心，又•=•=•，可得•（﹣）=0，•（﹣）=0，即•=•=0，即有⊥，⊥，可得D为△ABC的垂心，则D为△ABC的中心，即△ABC为正三角形．由•=﹣2，即有||•||cos120°=﹣2，解得||=2，△ABC的边长为4cos30°=2，以A为坐标原点，AD所在直线为x轴建立直角坐标系xOy，可得B（3，﹣），C（3，），D（2，0），由=1，可设P（cosθ，sinθ），（0≤θ＜2π），由=，可得M为PC的中点，即有M（，），则||2=（3﹣）2+（+）2=+==，当sin（θ﹣）=1，即θ=时，取得最大值，且为．故选：B．10．【分析】如图所示，建立直角坐标系．B（0，0），C．A．点P的轨迹方程为：=1，令x=+cosθ，y=3+sinθ，θ∈[0，2π）．又=，可得M，代入||2=+3sin，即可得出．【解答】解：如图所示，建立直角坐标系．B（0，0），C．A．∵M满足||=1，∴点P的轨迹方程为：=1，令x=+cosθ，y=3+sinθ，θ∈[0，2π）．又=，则M，∴||2=+=+3sin≤．∴||2的最大值是．也可以以点A为坐标原点建立坐标系．解法二：取AC中点N，MN=，从而M轨迹为以N为圆心，为半径的圆，B，N，M三点共线时，BM为最大值．所以BM最大值为3+=．故选：B．二．填空题（共20小题）11．【分析】利用向量共线定理即可得出．【解答】解：∵，∴﹣6﹣2λ=0，解得λ=﹣3．故答案为：﹣3．12．【分析】利用平面向量数量积坐标运算法则和向量垂直的性质求解．【解答】解：∵向量=（﹣2，3），=（3，m），且，∴=﹣6+3m=0，解得m=2．故答案为：2．13．【分析】利用平面向量坐标运算法则先求出，再由向量+与垂直，利用向量垂直的条件能求出m的值．【解答】解：∵向量=（﹣1，2），=（m，1），∴=（﹣1+m，3），∵向量+与垂直，∴（）•=（﹣1+m）×（﹣1）+3×2=0，解得m=7．故答案为：7．14．【分析】根据平面向量的数量积求出模长即可．【解答】解：【解法一】向量，的夹角为60°，且||=2，||=1，∴=+4•+4=22+4×2×1×cos60°+4×12=12，∴|+2|=2．【解法二】根据题意画出图形，如图所示；结合图形=+=+2；在△OAC中，由余弦定理得||==2，即|+2|=2．故答案为：2．15．【分析】根据平面向量的数量积运算与单位向量的定义，列出方程解方程即可求出λ的值．【解答】解：【方法一】由题意，设=（1，0），=（0，1），则﹣=（，﹣1），+λ=（1，λ）；又夹角为60°，∴（﹣）•（+λ）=﹣λ=2××cos60°，即﹣λ=，解得λ=．【方法二】，是互相垂直的单位向量，∴||=||=1，且•=0；又﹣与+λ的夹角为60°，∴（﹣）•（+λ）=|﹣|×|+λ|×cos60°，即+（﹣1）•﹣λ=××，化简得﹣λ=××，即﹣λ=，解得λ=．故答案为：．16．【分析】根据题意，设P（x0，y0），由数量积的坐标计算公式化简变形可得2x0+y0+5≤0，分析可得其表示表示直线2x+y+5≤0以及直线下方的区域，联立直线与圆的方程可得交点的横坐标，结合图形分析可得答案．【解答】解：根据题意，设P（x0，y0），则有x02+y02=50，=（﹣12﹣x0，﹣y0）•（﹣x0，6﹣y0）=（12+x0）x0﹣y0（6﹣y0）=12x0+6y+x02+y02≤20，化为：12x0﹣6y0+30≤0，即2x0﹣y0+5≤0，表示直线2x﹣y+5=0以及直线上方的区域，联立，解可得x0=﹣5或x0=1，结合图形分析可得：点P的横坐标x0的取值范围是[﹣5，1]，故答案为：[﹣5，1]．17．【分析】设P（cosα，sinα）．可得=（2，0），=（cosα+2，sinα）．利用数量积运算性质、三角函数的单调性与值域即可得出．【解答】解：设P（cosα，sinα）.=（2，0），=（cosα+2，sinα）．则•=2（cosα+2）≤6，当且仅当cosα=1时取等号．故答案为：6．18．【分析】如图所示，建立直角坐标系．A（1，0）．由与的夹角为α，且tanα=7．可得cosα=，sinα=．C．可得cos（α+45°）=．sin（α+45°）=．B．利用=m+n（m，n∈R），即可得出．【解答】解：如图所示，建立直角坐标系．A（1，0）．由与的夹角为α，且tanα=7．∴cosα=，sinα=．∴C．cos（α+45°）=（cosα﹣sinα）=．sin（α+45°）=（sinα+cosα）=．∴B．∵=m+n（m，n∈R），∴=m﹣n，=0+n，解得n=，m=．则m+n=3．故答案为：3．19．【分析】根据题意画出图形，结合图形，利用、表示出，再根据平面向量的数量积列出方程求出λ的值．【解答】解：如图所示，△ABC中，∠A=60°，AB=3，AC=2，=2，∴=+=+=+（﹣）=+，又=λ﹣（λ∈R），∴=（+）•（λ﹣）=（λ﹣）•﹣+λ=（λ﹣）×3×2×cos60°﹣×32+λ×22=﹣4，∴λ=1，解得λ=．故答案为：．20．【分析】直接利用向量共线的充要条件列出方程求解即可．【解答】解：向量=（m，4），=（3，﹣2），且∥，可得12=﹣2m，解得m=﹣6．故答案为：﹣6．21．【分析】设P（cosα，sinα），α∈[0，π]，则=（1，1），=（cosα，sinα+1），由此能求出•的取值范围．【解答】解：∵在平面直角坐标系中，A（1，0），B（0，﹣1），P是曲线y=上一个动点，∴设P（cosα，sinα），α∈[0，π]，∴=（1，1），=（cosα，sinα+1），=cosα+sinα+1=，∴•的取值范围是[0，1+]．故答案为：[0，1+]．22．【分析】利用已知条件，通过数量积判断两个向量垂直，然后列出方程求解即可．【解答】解：|+|2=||2+||2，可得•=0．向量=（m，1），=（1，2），可得m+2=0，解得m=﹣2．故答案为：﹣2．23．【分析】根据向量的坐标运算和向量的数量积计算即可．【解答】解：∵向量=（1，﹣1），=（6，﹣4），∴t+=（t+6，﹣t﹣4），∵⊥（t+），∴•（t+）=t+6+t+4=0，解得t=﹣5，故答案为：﹣5．24．【分析】根据向量垂直的充要条件便可得出，进行向量数量积的坐标运算即可得出关于x的方程，解方程便可得出x的值．【解答】解：∵；∴；即x+2（x+1）=0；∴．故答案为：．25．【分析】由题意可知，||+||为在上的投影的绝对值与在上投影的绝对值的和，由此可知，当与共线时，||+||取得最大值，即．【解答】解：||+||=，其几何意义为在上的投影的绝对值与在上投影的绝对值的和，当与共线时，取得最大值．∴=．故答案为：．26．【分析】设出=（x，y），得到•=x+，令x=cosθ，根据三角函数的性质得到•=sinθ+cosθ=sin（θ+），从而求出•的范围即可．【解答】解：设=（x，y），则=（x，），由A（1，0），B（0，﹣1），得：=（1，1），∴•=x+，令x=cosθ，θ∈[0，π]，则•=sinθ+cosθ=sin（θ+），θ∈[0，π]，故•的范围是[﹣，1，]，故答案为：[﹣1，]．27．【分析】由已知可得=+，=﹣+，=+3，=﹣+3，=+2，=﹣+2，结合已知求出2=，2=，可得答案．【解答】解：∵D是BC的中点，E，F是AD上的两个三等分点，∴=+，=﹣+，=+3，=﹣+3，∴•=2﹣2=﹣1，•=92﹣2=4，∴2=，2=，又∵=+2，=﹣+2，∴•=42﹣2=，故答案为：28．【分析】根据已知中向量的坐标，代入向量夹角公式，可得答案．【解答】解：∵向量=（1，），=（，1），∴与夹角θ满足：cosθ===，又∵θ∈[0，π]，∴θ=，故答案为：．29．【分析】利用组合数公式求出从正八边形A1A2…A8的八个顶点中任取两个的事件总数，满足++=，且点P落在第一象限，则需向量+的终点落在第三象限，列出事件数，再利用古典概型概率计算公式求得答案．【解答】解：从正八边形A1A2…A8的八个顶点中任取两个，基本事件总数为．满足++=，且点P落在第一象限，对应的A i，A j，为：（A4，A7），（A5，A8），（A5，A6），（A6，A7），（A5，A7）共5种取法．∴点P落在第一象限的概率是，故答案为：．30．【分析】根据向量三角形不等式的关系以及向量数量积的应用进行计算即可得到结论．【解答】解：由绝对值不等式得≥|•|+|•|≥|•+•|=|（+）•|，于是对任意的单位向量，均有|（+）•|≤，∵|（+）|2=||2+||2+2•=5+2•，∴|（+）|=，因此|（+）•|的最大值≤，则•≤，下面证明：•可以取得，（1）若|•|+|•|=|•+•|，则显然满足条件．（2）若|•|+|•|=|•﹣•|，此时|﹣|2=||2+||2﹣2•=5﹣1=4，此时|﹣|=2于是|•|+|•|=|•﹣•|≤2，符合题意，综上•的最大值是，法2：由于任意单位向量，可设=，则|•|+|•|=||+||≥||+|=||=|+|，∵|•|+|•|≤，∴|+|≤，即（+）2≤6，即||2+||2+2•≤6，∵||=1，||=2，∴•≤，即•的最大值是．法三：设=，=，=，则=+，=﹣，|•|+|•|=||+||=||≤||，由题设当且仅当与同向时，等号成立，此时（+）2取得最大值6，第21页（共22页）由于|+|2+|﹣|）2=2（||2+||2）=10，于是（﹣）2取得最小值4，则•=，•的最大值是．故答案为：．三．解答题（共1小题）31．【分析】根据向量的数量积和三角形的面积公式可得tanA=﹣1，求出A和c的值，再根据余弦定理即可求出a．【解答】解：由=﹣6可得bccosA=﹣6，①，由三角形的面积公式可得S△ABC=bcsinA=3，②∴tanA=﹣1，∵0＜A＜180°，∴A=135°，∴c==2，由余弦定理可得a2=b2+c2﹣2bccosA=9+8+12=29∴a=第22页（共22页）。

高考数学(理)试题分类汇编专题平面向量

1.【2015高考新课标1，理7】设D 为ABC ∆所在平面内一点3BC CD =，则（）（A ）1433AD AB AC =-+ (B)1433AD AB AC =- （C ）4133AD AB AC =+ (D)4133AD AB AC =- 【答案】A【解析】由题知11()33AD AC CD AC BC AC AC AB =+=+=+-==1433AB AC -+，故选A. 【考点定位】平面向量的线性运算【名师指点】本题以三角形为载体考查了平面向量的加法、减法及实数与向量的积的法则与运算性质，是基础题，解答本题的关键是结合图形会利用向量加法将向量AD 表示为AC CD +，再用已知条件和向量减法将CD 用,AB AC 表示出来.2.【2015高考山东，理4】已知菱形ABCD 的边长为a ，60ABC ∠=,则BD CD ⋅=（）（A ）232a -（B ）234a -（C ）234a （D ）232a 【答案】D【解析】因为()BD CD BD BA BA BC BA ⋅=⋅=+⋅()22223cos602BA BC BA a a a +⋅=+=故选D.【考点定位】平面向量的线性运算与数量积.【名师指点】本题考查了平面向量的基础知识，重点考查学生对平面向量的线性运算和数量积的理解与掌握，属基础题，要注意结合图形的性质，灵活运用向量的运算解决问题. 3.【2015高考陕西，理7】对任意向量,a b ，下列关系式中不恒成立的是（） A ．||||||a b a b ⋅≤ B ．||||||||a b a b -≤-C ．22()||a b a b +=+ D ．22()()a b a b a b +-=-【答案】B【解析】因为cos ,a b a b a b a b ⋅=≤，所以选项A 正确；当a 与b 方向相反时，a b a b -≤-不成立，所以选项B 错误；向量的平方等于向量的模的平方，所以选项C 正确；()()22a ba b ab +-=-，所以选项D 正确．故选B ．【考点定位】1、向量的模；2、向量的数量积．【名师点晴】本题主要考查的是向量的模和向量的数量积，属于容易题．解题时一定要抓住重要字眼“不”，否则很容易出现错误．解本题需要掌握的知识点是向量的模和向量的数量积，即cos ,a b a b a b ⋅=，22a a =4.【2015高考四川，理7】设四边形ABCD 为平行四边形，6AB =，4AD =.若点M ，N 满足3BM MC =，2DN NC =，则AM NM ⋅=（）（A ）20 （B ）15 （C ）9 （D ）6 【答案】C 【解析】311,443AM AB AD NM CM CN AD AB =+=-=-+，所以 221111(43)(43)(169)(1636916)94124848AM NM AB AD AB AD AB AD =+-=-=⨯-⨯=，选C.【考点定位】平面向量.【名师指点】涉及图形的向量运算问题，一般应选两个向量作为基底，选基底的原则是这两个向量有尽量多的已知元素.本题中，由于6AB =，4AD =故可选,AB AD 作为基底.5.【2015高考重庆，理6】若非零向量a ，b 满足|a |=3|b |，且（a -b ）⊥（3a +2b ），则a 与b 的夹角为（） A 、4π B 、2πC 、34πD 、π【答案】A【考点定位】向量的夹角.【名师指点】本题考查两向量的夹角，涉及到向量的模，向量的垂直，向量的数量积等知识，体现了数学问题的综合性，考查学生运算求解能力，综合运用能力.6.【2015高考安徽，理8】C ∆AB 是边长为2的等边三角形，已知向量a ，b 满足2a AB =，C 2a b A =+，则下列结论正确的是（）（A ）1b = （B ）a b ⊥ （C ）1a b ⋅= （D ）()4C a b +⊥B 【答案】D【解析】如图，由题意，(2)2BC AC AB a b a b =-=+-=，则||2b =，故A 错误；|2|2||2a a ==，所以||1a =，又22(2)4||222cos 602AB AC a a b a ab ⋅=⋅+=+=⨯=，所以1a b ⋅=-，故,B C 错误；设,B C 中点为D ，则2AB AC AD +=，且A D B C ⊥，而22(2)4A D a a b a b =++=+，所以()4C a b +⊥B ，故选D.【考点定位】1.平面向量的线性运算；2.平面向量的数量积.【名师指点】平面向量问题中，向量的线性运算和数量积是高频考点.当出现线性运算问题时，注意两个向量的差OA OB BA -=，这是一个易错点，两个向量的和2OA OB OD +=（D 点是AB 的中点）.另外，要选好基底向量，如本题就要灵活使用向量,AB AC ，当涉及到向量数量积时，要记熟向量数量积的公式、坐标公式、几何意义等.7.【2015高考福建，理9】已知1,,AB AC AB AC t t⊥== ，若P 点是ABC ∆ 所在平面内一点，且4AB AC AP ABAC=+，则PB PC ⋅ 的最大值等于（）A ．13B ．15C ．19D ．21 【答案】A【解析】以A 为坐标原点，建立平面直角坐标系，如图所示，则1(,0)B t，(0,)C t ，1AP =（，0)+4(0,1)=(1,4)，即1P （，4)，所以11PB t-=（，-4)，1PC -=（，t-4)，因此PB PC ⋅11416t t =--+117(4)t t =-+，因为144t t +≥=，所以PB PC ⋅ 的最大值等于13，当14t t=，即12t =时取等号．【考点】1、平面向量数量积；2、基本不等式．【名师指点】本题考查平面向量线性运算和数量积运算，通过构建直角坐标系，使得向量运算完全代数化，实现了数形的紧密结合，同时将数量积的最大值问题转化为函数的最大值问题，本题容易出错的地方是对AB AB的理解不到位，从而导致解题失败．8.【2015高考北京，理13】在ABC △中，点M ，N 满足2AM MC =，BN NC =．若MN x AB y AC =+，则x =；y =．【答案】11,26-【考点定位】本题考点为平面向量有关知识与计算，利用向量相等解题.【名师指点】本题考查平面向量的有关知识及及向量运算，利用向量相等条件求值，本题属于基础题.利用坐标运算要建立适当的之间坐标系，准确写出相关点的坐标、向量的坐标，利用向量相等，列方程组，解出未知数的值.9.【2015高考湖北，理11】已知向量OA AB ⊥，||3OA =，则OA OB ∙=.【答案】9【解析】因为OA AB ⊥，||3OA =，所以OA OB ∙=93||||)(222===∙+=+∙. 【考点定位】平面向量的加法法则，向量垂直，向量的模与数量积.【名师指点】平面向量是新教材新增内容，而且由于向量的双重“身份”是研究一些数学问题的工具.这类问题难度不大，以考查基础知识为主.10.【2015高考天津，理14】在等腰梯形ABCD 中,已知//,2,1,60AB DC AB BC ABC ==∠= ,动点E 和F 分别在线段BC 和DC 上,且,1,,9BE BC DF DC λλ== 则AE AF ⋅的最小值为. 【答案】2918【解析】因为1,9DF DC λ=12DC AB =，119199918CF DF DC DC DC DC AB λλλλλ--=-=-==，AE AB BE AB BC λ=+=+，19191818AF AB BC CF AB BC AB AB BC λλλλ-+=++=++=+，()221919191181818AE AF AB BC AB BC AB BC AB BC λλλλλλλλλ+++⎛⎫⎛⎫⋅=+⋅+=+++⋅⋅ ⎪ ⎪⎝⎭⎝⎭19199421cos1201818λλλλ++=⨯++⨯⨯⨯︒2117172992181818λλ=++≥= 当且仅当2192λλ=即23λ=时AE AF ⋅的最小值为2918. BA【考点定位】向量的几何运算、向量的数量积与基本不等式.【名师指点】本题主要考查向量的几何运算、向量的数量积与基本不等式.运用向量的几何运算求,AE AF ，体现了数形结合的基本思想，再运用向量数量积的定义计算AE AF ⋅，体现了数学定义的运用，再利用基本不等式求最小值，体现了数学知识的综合应用能力.是思维能力与计算能力的综合体现.11.【2015高考浙江，理15】已知12,e e 是空间单位向量，1212e e ⋅=，若空间向量b 满足1252,2b e b e ⋅=⋅=，且对于任意,x y R ∈，12010200()()1(,)b xe ye b x e y e x y R -+≥-+=∈，则0x =，0y =，b =．【答案】1，2，22.【考点定位】1.平面向量的模长；2.函数的最值【名师指点】本题主要考查了以平面向量模长为背景下的函数最值的求解，属于较难题，分析题意可得问题等价于12()b xe ye -+当且仅当0x x =，0y y =时取到最小值1，这是解决此题的关键突破口，也是最小值的本质，两边平方后转化为一个关于x ，y 的二元二次函数的最值求解，此类函数最值的求解对考生来说相对陌生，此时需将其视为关于某个字母的二次函数或利用配方的方法求解，关于二元二次函数求最值的问题，在14年杭州二模的试题出现过类似的问题，在复习时应予以关注.12.【2015高考新课标2，理13】设向量a ，b 不平行，向量a b λ+与2a b +平行，则实数λ=_________．【答案】12【解析】因为向量a b λ+与2a b +平行，所以2a b k a b λ+=+（），则12,k k λ=⎧⎨=⎩，所以12λ=．【考点定位】向量共线．【名师指点】本题考查向量共线，明确平面向量共线定理，利用待定系数法得参数的关系是解题关键，属于基础题．13.【2015江苏高考，14】设向量a k (cos ,sin cos )(0,1,2,,12)666k k k k πππ=+=，则11k =∑(a k a k+1)的值为【答案】【解析】a k a k+1(1)(1)(1)(cos,sin cos )(cos ,sin cos )666666k k k k k k ππππππ+++=+⋅+ (1)(1)(1)coscos (sin cos )(sin cos )666666k k k k k k ππππππ+++=++⋅+(1)(1)(1)(1)(1)(cos cos sin sin )(sin cos cos sin )cos cos 6666666666k k k k k k k k k k ππππππππππ+++++=++++22(1)21cos sincos cos sin cos sin666666266k k k k k k k ππππππππππ+++=++++-21sin cos )sin 6343k k k ππππ+=+++-21(21)sin cos626k k πππ++=++ 因为21(21)sin cos 626k k πππ++，的周期皆为6，一个周期的和皆为零，因此110k =∑(a k a k+1)12==【考点定位】向量数量积，三角函数性质【名师点晴】向量数量积在本题中仅是一个表示，实质是三角函数化简求和，首先根据角之间的差别与联系，对通项进行重新搭配，对不可搭配的项再一次展开，重新配角搭配，这样将通项化为一次式，利用三角函数周期性进行求和.作为压轴题，主要考查学生基础题型的识别与综合应用.14.【2015江苏高考，6】已知向量a =)1,2(，b=)2,1(-, 若m a +n b =)8,9(-(R n m ∈,), 则n m -的值为______. 【答案】3-【解析】由题意得：29,282,5, 3.m n m n m n m n +=-=-⇒==-=- 【考点定位】向量相等【名师点晴】明确两向量相等的充要条件，它们的对应坐标相等.其实质为平面向量基本定理应用. 向量共线的充要条件的坐标表示：若1122()()a x y b x y ==，，，，则a b ∥⇔12210x y x y =-.向量垂直的充要条件的坐标表示：若1122()()a x y b x y ==，，，，则a b ⊥⇔1212+0x x y y =.15.【2015高考湖南，理8】已知点A ，B ，C 在圆221x y +=上运动，且AB BC ⊥，若点P 的坐标为(2,0)，则PA PB PC ++的最大值为（） A.6 B.7 C.8 D.9 【答案】B. 【解析】【考点定位】1.圆的性质；2.平面向量的坐标运算及其几何意义.【名师指点】本题主要考查向量的坐标运算，向量的几何意义以及点到圆上点的距离的最值问题，属于中档题，结合转化思想和数形结合思想求解最值，关键是把向量的模的最值问题转化为点与圆上点的距离的最值问题，即圆221x y +=上的动点到点)0,6(距离的最大值.。

数学理高考试题分类汇编：专题05平面向量

，向量 a sin 2 ，cos ，b cos ，1 ，若 a // b ，则 2
------ 珍贵文档 ! 值得收藏！ ------
------ 精品文档 ! 值得拥有！ ------
6. 【 2014 高考安徽卷理第 10 题】在平面直角坐标系 xOy 中，已知向量 a, b, a b 1,a b 0, 点 Q 满足
R ），则
||
.
------ 珍贵文档 ! 值得收藏！ ------
------ 精品文档 ! 值得拥有！ ------
8. 【 2014 高考湖北卷理第 11 题】设向量 a (3,3) ， b (1, 1)，若 a b a b ，则实数
. 【答案】 3
10. 【 2014 江西高考理第 15 题】已知单位向量 e1 与 e2 的夹角为，且 cos
1 ，向量 a 3e1 2e2 与
3
b 3e1 e2 的夹角为，则 cos =
.
11. 【 2014 辽宁高考理第 5 题】设 a, b, c 是非零向量，已知命题 P：若 a b 0 ， b c 0 ，则 a c 0 ；
命题 q：若 a / /b,b / /c ，则 a / /c ，则下列命题中真命题是（
2
夹角为 _______．
【考点定位】 1、平面向量基本定理； 2、圆的性质．
13. 【 2014 全国 2 高考理第 3 题】设向量 a,b 满足 |a+b|= 10 ， |a-b|= 6 ，则 a b = ( )
A. 1
B. 2
C. 3
D. 5
14. 【 2014 高考安徽卷理第 15 题】已知两个不相等的非零向量 a,b, 两组向量 x1, x2 , x3, x4, x5 和 y1, y2, y3, y4 , y5 均由 2 个 a 和 3 个 b 排列而成 .记 S x1 y1 x2 y2 x3 y3 x4 y4 x5 y5 ，Smin 表示 S

2013---2017近五年全国1卷高考理科数学分类汇编---平面向量

2013---2017近五年全国1卷高考理科数学分类汇编---平面向量
1.已知向量a，b的夹角为60°，|a|=2，|b|=1，则|a+2b|=23.
2.设向量a=(m,1)，b=(1,2)，且|a+b|2=|a|2+|b|2，则m=-2.
3.设D为ABC所在平面内一点,BC=3CD，则AD=-
AB+AC。

4.已知A,B,C是圆O上的三点，若AO=AB+AC，则AB 与AC的夹角为。

5.已知两个单位向量a，b的夹角为60°，c=ta+(1-t)b，若b•c=0，则t=1/2.
解析：
1.根据向量加法公式，
|a+2b|=√[(2+2cos60°)²+(2sin60°)²]=23.
2.根据向量的数量积及坐标运算，|a+b|²=(m+1)²+(1+2)²，|a|²=m²+1，|b|²=5，代入得到m=-2.
3.根据向量的加法和减法，
AD=AC+CD=AC+BC=AC+(AC-AB)=-AB+AC。

4.根据向量的减法和模长的定义，
AO²=AB²+BO²=AB²+AC²+2AB·ACcos∠BAC，代入得到cos∠BAC=(AB²+AC²-AO²)/(2AB·AC)，再利用余弦定理求出∠BAC。

5.根据向量的线性运算和数量积的定义，b•c=t(b•a)+(1-t)(b•b)=tcos60°+(1-t)=1/2-t/2，令其为0解得t=1/2.。

最新高考数学理试题分类汇编：平面向量资料

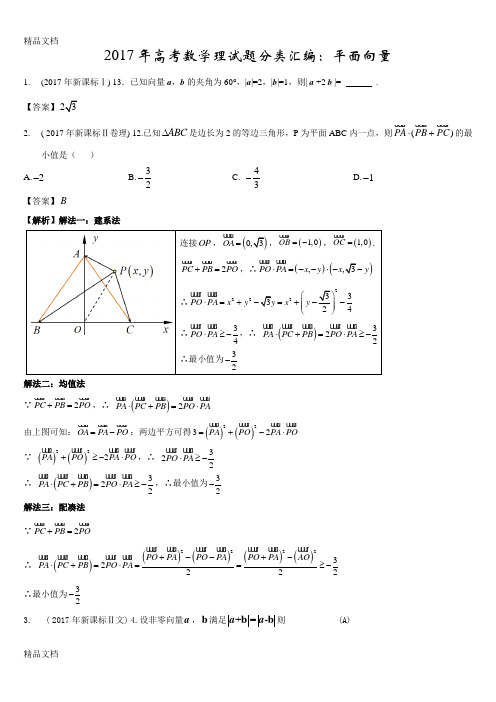
2017年高考数学理试题分类汇编：平面向量1. (2017年新课标Ⅰ) 13．已知向量a ，b 的夹角为60°，|a |=2，|b |=1，则| a +2 b |= . 【答案】232. ( 2017年新课标Ⅱ卷理) 12.已知ABC ∆是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC ⋅+u u u r u u u r u u u r的最小值是（）A.2-B.32-C. 43- D.1- 【答案】B【解析】解法一：建系法连接OP ，()0,3OA =u u u r，()1,0OB =-u u u r ，()1,0OC =u u u r .2PC PB PO +=u u u r u u u r u u u r ，∴()(),,3PO PA x y x y ⋅=--⋅--u u u r u u u r∴222233324PO PA x y y x y ⎛⎫⋅=+-=+-- ⎪ ⎪⎝⎭u u u r u u u r ∴34PO PA ⋅≥-u u u r u u u r ，∴ ()322PA PC PB PO PA ⋅+=⋅≥-u u u r u u u r u u u r u u u r u u u r∴最小值为32-解法二：均值法∵2PC PB PO +=u u u r u u u r u u u r ，∴ ()2PA PC PB PO PA ⋅+=⋅u u u r u u u r u u u r u u u r u u u r由上图可知：OA PA PO =-u u u r u u u r u u u r ；两边平方可得()()2232PA POPA PO =+-⋅u u u r u u u ru u u r u u u r∵ ()()222PA POPA PO +≥-⋅u u u r u u u ru u u r u u u r ，∴ 322PO PA ⋅≥-u u u r u u u r∴ ()322PA PC PB PO PA ⋅+=⋅≥-u u u r u u u r u u u r u u u r u u u r ，∴最小值为32-解法三：配凑法 ∵2PC PB PO +=u u u r u u u r u u u r∴ ()()()()()222232222PO PA PO PAPO PA AOPA PC PB PO PA +--+-⋅+=⋅==≥-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r∴最小值为32-3. ( 2017年新课标Ⅱ文)4.设非零向量a ，b 满足+=-b b a a 则 (A)A a ⊥b B. =b a C. a ∥b D. >b a4. (2017年北京卷理) （6）设m ,n 为非零向量，则“存在负数λ，使得λ=m n ”是“0<⋅m n ”的（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件【答案】A【解析】若0λ∃<，使m n λ=r r，即两向量反向，夹角是0180，那么0cos1800m n m n m n ⋅==-<r r r rr r，反过来，若0m n ⋅<r r，那么两向量的夹角为(0090,180⎤⎦ ，学科网并不一定反向，即不一定存在负数λ，使得λ=m n ，所以是充分不必要条件，故选A.5. (2017年新课标Ⅰ文)已知向量a =（–1，2），b =（m ，1）.若向量a +b 与a 垂直，则m =______7_______.6. (2017年江苏卷) 12．如图，在同一个平面内，向量OA u u u r ，OB u u u r ，OC u u u r 的模分别为1，1，2，OA u u u r 与OC u u u r的夹角为α，且tan α=7，OB u u u r 与OC u u u r 的夹角为45°．若OC mOA nOB =+u u u r u u u r u u u r(,)m n ∈R ，则m n += ▲ ．【解析】:n m OB n OA m OB OC OB OC OB o+-=+=⋅⋅=⋅53)(45cos 2153=+-∴n m 5153=-n m 同理，3=+∴n m7. (2017年浙江卷)如图，已知平面四边形ABCD ，AB ⊥BC ，AB ＝BC ＝AD ＝2，CD ＝3，AC 与BD 交于点O ，记1·I OA OB u u u r u u u r＝，2·I OB OC u u u r u u u r ＝，3·I OC OD u u u r u u u r＝，则A ．I １<I ２<I ３B ．I １<I ３<I ２C ． I ３<I １<I ２D ．I ２<I １<I ３【答案】C8. (2017年浙江卷)已知向量a ，b 满足1,2,==a b 则++-a b a b 的最小值是________，最大值是_______. 【答案】4，25【解析】设向量,a b r r 的夹角为θ，由余弦定理有：2212212cos 54cos a b θθ-=+-⨯⨯⨯=-r r，()2212212cos 54cos a b πθθ+=+-⨯⨯⨯-=+r r，则：54cos 54cos a b a b θθ++-=++-r r r r，令54cos 54cos y x x =++-，则[]221022516cos 16,20y θ=+-∈，据此可得：()()maxmin2025,164a b a ba b a b++-==++-==r r r rr r r r，即a b a b ++-r r r r的最小值是4，最大值是25.9. (2017年新课标Ⅲ卷理)在矩形ABCD 中，AB=1，AD=2，动点P 在以点C 为圆心且与BD 相切的圆上．若AP u u u r=λAB u u u r +μAD u u u r，则λ+μ的最大值为A ．3B ．22C ．5D ．2【答案】A【解析】如图，建立平面直角坐标系设()()()()0,1,0,0,2,1,,A B D P x y 5()22425x y -+=()()(),1,0,1,2,0AP x y AB AD =-=-=u u u r u u u r u u u r ，若满足AP AB AD λμ=+u u u r u u u r u u u r即21x y μλ=⎧⎨-=-⎩ ，,12x y μλ==- ，所以12x y λμ+=-+，设12x z y =-+ ，即102xy z -+-=，点(),P x y 在圆()22425x y -+=上，所以圆心到直线的距离d r ≤，即221514z -≤+ ，解得13z ≤≤，所以z 的最大值是3，即λμ+的最大值是3，故选A.10. (2017年江苏卷)已知向量(cos ,sin ),(3,3),[0,π].x x x ==-∈a b （1）若a ∥b ，求x 的值；（2）记()f x =⋅a b ，求()f x 的最大值和最小值以及对应的x 的值．16. 【解析】（1）∵a ∥b ，∴3sin 3cos x x =-，又cos 0x ≠，∴3tan 3x =-，∵，∴5π6x =. （2）()π3cos 3sin 23sin()3f x x x x =-=--.∵，∴ππ2π[,]333x -∈-，∴3πsin()123x -≤-≤，∴()233f x -≤≤，当ππ33x -=-，即0x =时，取得最大值，为3；当ππ32x -=，即5π6x =时，取得最小值，为3-11.12. ( 2017年全国Ⅲ卷文)已知向量)3,2(-=→a ，),3(m b =→，且→→⊥b a ，则m = 。

高考数学真题专题分类汇编专题七平面向量(学生版)

专题七平面向量与解三角形真题卷题号考点考向2023新课标1卷3 向量的数量积向量数量积的坐标运算17 解三角形正、余弦定理解三角形2023新课标2卷13 向量的数量积利用向量数量积求模长17 解三角形解三角形的综合应用2022新高考1卷3 平面向量的线性运算向量的加减及数乘运算18 解三角形正弦定理变形、三角恒等变形2022新高考2卷4 向量的数量积向量数量积的坐标运算18 解三角形正余弦定理解三角形2021新高考1卷10 向量的坐标运算求向量的模、向量数量积的坐标运算19 解三角形正、余弦定理解三角形2021新高考2卷15 向量的数量积向量数量积的运算18 解三角形正弦定理解三角形、余弦定理判断三角形的形状2020新高考1卷7 向量的数量积求向量数量积的取值范围17 解三角形正、余弦定理解三角形2020新高考2卷3 向量的线性运算向量的加、减法运算17 解三角形正、余弦定理解三角形【2023年真题】1.（2023·新课标I 卷第3题）已知向量(1,1)a = ，(1,1).b=− 若()()a b a b λµ+⊥+，则( ) A. 1λµ+=B.1λµ+=− C. 1λµ= D. 1λµ=−2. （2023·新课标II 卷第13题）已知向量a ，b 满足||a b − |||2|a b a b +=− ，则||b = __________ 3. （2023·新课标I 卷第17题）已知在ABC 中，3A B C +=，2sin()sin .A C B −=(1)求sin A ；(2)设5AB =，求AB 边上的高.4. （2023·新课标II 卷第17题）记ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知ABC 面积为D 为BC 的中点，且 1.AD =(1)若3ADC π∠=，求tan B ；(2)若228b c +=，求b ，.c【2022年真题】5.（2022·新高考I 卷第3题）在ABC 中，点D 在边AB 上，2.BD DA =记CA m =，CD n =，则CB =( )A. 32m n −B. 23m n −+C. 32m n +D. 23m n +6.（2022·新高考II 卷第4题）已知向量(3,4)a =，(1,0)b =，c a tb =+，若,,a c b c <>=<>，则实数t =( ) A. 6−B. 5−C. 5D. 67.（2022·新高考I 卷第18题）记ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知cos sin 2.1sin 1cos 2A BA B=++(1)若23C π=，求;B (2)求222a b c +的最小值.8.（2022·新高考II 卷第18题）记ABC 的三个内角分别为A ，B ，C ，其对边分别为a ，b ，c ，分别以a ，b ，c 为边长的三个正三角形的面积依次为1S ，2S ，3S ，且123S S S −+，1sin .3B =(1)求ABC 的面积;(2)若sin sin A C =.b【2021年真题】9.（2021·新高考I 卷第10题）（多选）已知O 为坐标原点，点1(cos ,sin )P αα，2(cos ,sin)P ββ−，3(cos (),sin ())P αβαβ++，(1,0)A ，则( )A. 12||||OP OP =B. 12||||AP AP =C. 312OA OP OP OP ⋅=⋅D. 123OA OP OP OP ⋅=⋅10.（2021·新高考I 卷第19题）记ABC 的内角A ，B ，C 的对边分别为a ，b ，.c 已知2b ac =，点D 在边AC 上，sin sin .BD ABC a C ∠=(1)证明：.BD b =(2)若2AD DC =，求cos .ABC ∠11.（2021·新高考II 卷第15题）已知向量0a b c ++= ，1,2a b c === ，a b b c c a ⋅+⋅+⋅=__________.12.（2021·新高考II 卷第18题）在ABC 中，角,,A B C 所对的边长分别为,,,1, 2.a b c b a c a =+=+(1)若2sin 3sin C A =，求ABC 的面积；(2)是否存在正整数a ，使得ABC 为钝角三角形？若存在，求出a 的值；若不存在，说明理由．【2020年真题】13.（2020·新高考I 卷第7题）已知P 是边长为2的正六边形ABCDEF 内的一点，则AP AB ⋅的取值范围是 ( ) A. (2,6)−B. (6,2)−C. (2,4)−D. (4,6)−14.（2020·新高考II 卷第3题）在ABC 中，D 是AB 边上的中点，则CB =( ) A. 2CD CA +B. 2CD CA −C. 2CD CA −D. 2CD CA +15.（2020·新高考I 卷第17题、II 卷第17题）)在①ac =，②sin 3c A =，③c =这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求c 的值;若问题中的三角形不存在，说明理由.问题：是否存在ABC ，它的内角A ，B ，C 的对边分别为a ，b ，c ，且sin A B =，6C π=，__________?注：如果选择多个条件分别解答，按第一个解答计分.【答案解析】1.（2023·新课标I 卷第3题）解：22()()()()2(1)0a b a b a a b b λµλµλµλµ+⋅+=++⋅+=+= ，所以1;λµ=−故选.D 2. （2023·新课标II 卷第13题）解：将原式平方：化简可得：即23b =，故||b =3. （2023·新课标I 卷第17题）解：(1)3A B C +=，3C C π∴−=，解得.4C π=2sin()sin A C B ∴−=可化为2sin()sin()44A A πππ−=−−，即32sin()sin()44A A ππ−=−，A A A A =，整理得sin 3cos A A =，将1cos sin 3A A =代入22sin cos 1A A +=，得210sin 19A =，29sin 10A ∴=，sin A =(2)由(1)知sin A =，1cos sin 3A A==4C π=，又sin sin AC AB B C=，sin sin AB BACC ∴== AB ∴边上的高sin 6.h AC A === 4. （2023·新课标II 卷第17题）解：(1)ABC S =，D 为BC 的中点，ADC S ∴11sin 122AD CD ADC CD ⋅⋅∠=××=，解得2CD =，则 2.BD =过点A 作AE CD ⊥于点E ，则在ADE中，AE =12DE =，∴在Rt AEB 中，52BE BD DE =+=，tan AEB BE==(2) 在ABC 中，1()2AD AB AC =+，222222111||()(||||2)(2cos )444AD AB AC AB AC AB AC c b bc A ∴=+=++⋅=++ ，11(82cos )4bc A ∴=+，即cos 2bc A =−，又1sin 2ABC S bc A ==，sin bc A ∴，sin tan cos bc A Abc A ∴==23A π∴=，sin A =， 4.bc =再将4b c=代入228b c +=，即可解得 2.b c ==【2022年真题】5.（2022·新高考I 卷第3题）解：2133CD CA CB =+ ，3223.CB CD CA m n =−=−+6.（2022·新高考II 卷第4题）解：由已知有(3,4)c t =+ ，cos a < ，cos ,c b c >=<> ，，故9316351t t c c +++=⋅⋅ ，解得 5.t =7.（2022·新高考I 卷第18题）解：cos sin 2(1)1sin 1cos 2A B A B =++ ，22222cos sin 2sin cos 2212cos 1cos sin 2sin cos 2222A AB B A A A A B −∴=+−++且cos 0B ≠， cos sin 1tansin 222tan cos cos sin 1tan 222A A AB B A A A B −−∴=∴=++，tan()tan 42A B π∴−=，又A ，(0,)B π∈，(,)4244A πππ−∈−，.42AB π∴−=又23C π=，3A B π∴+=，.6B π∴=(2)由正弦定理sin sin sin a b cA B C==，得2222222221cos 2()1cos 242sin sin ()sin sin 4222sin sin ()1cos 2()42422AA A A a b AB A A cC A A ππππ−−−+−+++===+−−+−21cos 21sin 2sin sin 11sin 1sin A A A A A A−+−−+=++，(0,)(0,)2(0,)42A A AB ππππ∈⇒∈ −=∈ ，令1sin (1,2)t A =+∈，则22(1)(1)1425t t y t t t −−−+==−+，(1,2)t ∈，425y t t=−+在t ∈时递减，在2)t ∈时递增，因此t =时，min5.y =− 8.（2022·新高考II 卷第18题）解：(1) 边长为a2，222123)S S S a b c ∴−+=−+=cos 1ac B =，由1sin 3B =得：cos B =1cos ac B ∴==，故111sin 223ABC S ac B ===(2)由正弦定理得：229.sin sin sin sin sin 4b a c ac B A C A C ===，故31sin .22b B = 9.（2021·新高考I 卷第10题）（多选）解：根据题意，依次分析选项：对于A 、12||||1OP OP ==，A 正确；对于B、1||AP ==，，B 不正确；对于C 、3cos ()OA OP αβ⋅=+， 12cos cos sin sin cos ()OP OP αβαβαβ⋅=−=+ ，C 正确；对于D 、1cos OA OP α⋅=，23cos cos()sin sin ()cos (2)OP OP βαββαβαβ⋅=+−+=+ ，D 不正确；故选.AC10.（2021·新高考I 卷第19题）证明：(1)BDsin sin ABC a C ∠=，sin sin a CBD ABC∴=∠，由正弦定理可知sin sin b a ABC A =∠，得sin sin b AABC a ∠=，2sin sin sin sin a C a C acBD b A b A b a∴===，又2b ac = ，.BD b ∴=解：(2)2AD DC = ，∴可知3bDC =，则23b AD =，在ABD 中，222222213()39cos 24233b b bc c ADB b b b +−−∠==⋅，在BCD 中，22222210()39cos 2233bb b a a CDB b b b +−−∠==⋅， ADB CDB π∠=−∠ ，cos cos ADB CDB ∴∠=−∠，即2222221310994233b bc a b b −−=−，整理得22261130a b c −+=，又2b ac =，则2261130a ac c −+=，即()()2330a c a c −−=，可得32c a =或3ca =，当32c a =时，b =，在ABC 中，由余弦定理可得，当3c a =时，b =，此时b c a <−，不合实际，则舍去，故：7cos .12ABC ∠=11.（2021·新高考II 卷第15题）解：由已知可得()()()22222920a b ca b c a b b c c a a b b c c a ++=+++⋅+⋅+⋅=+⋅+⋅+⋅=，因此，9.2a b b c c a ⋅+⋅+⋅=−故答案为：9.2−12.（2021·新高考II 卷第18题）解：(1)因为2sin 3sin C A =，根据正弦定理可知()2223c a a =+=，则4a =，故5b =，6c =，2221cos 028a b c C ab +−==>，所以C 为锐角，则sin C ，因此，11sin 4522ABC S ab C ==××=(2)显然c b a >>，若ABC 为钝角三角形，则C 为钝角，由余弦定理可得，又0a >，则2230a a −−<，即(1)(3)0a a +−<，解得13a −<<，则03a <<，由三角形三边关系可得12a a a ++>+，可得1a >，a Z ∈ ，故 2.a =13.（2020·新高考I 卷第7题）解：由投影定义知，当点P 与点F 重合时，AP AB ⋅取最小值当点P 与点C 重合时，AP AB ⋅取最大值故AP AB ⋅的取值范围是(2,6).− 故选.A14.（2020·新高考II 卷第3题）解：在ABC 中，D 是AB 边上的中点，则CB CD DB CD AD =+=+ ()CD AC CD =++ 2.CD CA −故选：.C 15.（2020·新高考I 卷第17题、II 卷第17题）解：sin A B =，由正弦定理得a = ，6C π=，由余弦定理得：222cos 2a b c C ab +−==，c = ；假设三角形存在，若选①，有ac =，则有ac =，则1, 1.a b c ==故存在满足题意的三角形， 1.c =若选②，有sin 3c A =，则有2221cos 22b c a A bc +−===−，则sin A =，故c =，6,a b ==故存在满足题意的三角形，c =若选③，有c =，由题意有,a a ，则有b c =，这和c =矛盾，故不存在满足题意的三角形.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2013年全国高考理科数学试题分类汇编：平面向量
一、选择题
1 ．（2013年高考上海卷（理））
在边长为1的正六边形ABCDEF中,记以A为起点,其余顶点为

终点的向量分别为12345,,,,aaaaa;以D为起点,其余顶点为终点的向量分别为

12345
,,,,ddddd
.若,mM分别为()()ijkrstaaaddd的最小值、最大值,其中

{,,}{1,2,3,4,5}ijk,{,,}{1,2,3,4,5}rst,则,mM
满足（）

A．0,0mMB．0,0mMC．0,0mMD．0,0mM
【答案】
D．
2 ．（2013年普通高等学校招生统一考试辽宁数学（理）试题（WORD版））
已知点


1,3,4,1,ABAB则与向量同方向的单位向量为
（）

A．3455，-B．4355，-C．3455，D．4355，
【答案】
A
3 ．（2013年普通高等学校招生统一考试浙江数学（理）试题（纯WORD版））
设0,PABC是边

AB上一定点,满足ABBP410,且对于边AB上任一点P
,恒有

CPBPPCPB00••
.则（）

A．090ABCB．090BACC．ACABD．BCAC
【答案】
D [来.源：全,品…中&高*考+网]
4 ．（2013年普通高等学校招生统一考试福建数学（理）试题（纯WORD版））
在四边形ABCD

中,(1,2)AC,(4,2)BD,则四边形的面积为（）[来.源：全,品…中&高*考+
网]
A．5B．25C．5D．10
【答案】
C
5 ．（2013年普通高等学校招生统一考试安徽数学（理）试题（纯WORD版））
在平面直角坐标

系中,O是坐标原点,两定点,AB满足2,OAOBOAOB则点集

|,1,,POPOAOBR
所表示的区域的面积是（）

A．22B．23C．42D．43
【答案】
D
6 ．（2013年普通高等学校招生统一考试重庆数学（理）试题（含答案））
在平面
上,12ABAB,121OBOB,12APABAB.若12OP,则OA的取值范围
是（）[来.源：全,品…中&高*考+网]

A．50,2B．57,22C．5,22D．7,22
【答案】
D
7 ．（2013年高考湖南卷（理））
已知,ab是单位向量,0ab.若向量c满足

1,cabc则的取值范围是
（）

A．2-1,2+1，B．2-1,2+2，
C．1,2+1，D．1,2+2，
【答案】
A
8 ．（2013年普通高等学校招生统一考试大纲版数学（理）WORD版含答案（已校对））
已知向量


1,1,2,2mn
,若mnmn,则=（）

A．4B．3C．2D．-1
【答案】
B

9 ．（2013年高考湖北卷（理））
已知点1,1A.1,2B.2,1C.3,4D,则向量
AB

在CD方向上的投影为（）
A．322B．3152C．322D．3152
【答案】
A
二、填空题
10．（2013年普通高等学校招生统一考试新课标Ⅱ卷数学（理）
已知正方形ABCD的边长为

2,E
为CD的中点,则AEBD_______.

【答案】
2
11．2013年上海市春季高考数学试卷
已知向量(1 )ak，,(9 6)bk，.若//ab,则实数
k
__________

【答案】
3
4


12
．（2013年普通高等学校招生统一考试山东数学（理）试题（含答案））
已知向量AB与
AC
的夹角为120°,且3AB,2AC,若APABAC,且APBC,
则实数的值为__________.
【答案】
7
12

13．（2013年高考新课标1（理））
已知两个单位向量a,b的夹角为60°,c=ta+(1-t)b,若b·c=0,
则t=_____.
【答案】
t
=2.

14．（2013年高考北京卷（理））
向量a,b,c在正方形网格中的位置如图所示.若c=λa+
μb

(λ,μ∈R),则=_________.

【答案】
4
15．（2013年普通高等学校招生统一考试浙江数学（理）试题（纯WORD版））
设21,ee为单位向

量,非零向量Ryxeyexb,,21,若21,ee的夹角为6,则||||bx的最大值等于
________.
【答案】
2
16．（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD版含附加题））

设ED，分别是ABC的边BCAB，上的点,ABAD21,BCBE32,若

ACABDE21
(21，为实数),则21的值为__________.

【答案】
1
2

17．（2013年高考四川卷（理））
在平行四边形ABCD中,对角线AC与BD交于点
O,ABADAO,则
_________.

【答案】
2
18．（2013年高考江西卷（理））
设1e,2e为单位向量.且1e,2e的夹角为3,若

123aee,1
2be
,则向量a在b方向上的射影为 ___________

【答案】
5
2

b
c
a
19．（2013年普通高等学校招生统一考试天津数学（理）试题（含答案））
在平行四边形
ABCD
中, AD = 1, 60BAD, E为CD的中点. 若·1ADBE, 则AB的长为______.
【答案】
1
2