合陈初级中学八年级数学阶段检测试卷(不等式分式)
不等式练习题初二含答案

不等式练习题初二含答案1. 解下列不等式:a) 2x + 5 ≥ 9b) 3 - x < 10c) 4(x - 2) > 8d) 2(x + 3) ≤ 10解析:a) 2x + 5 ≥ 9首先,我们需要将不等式转化为x的形式。
移项得到2x ≥ 4,接着将系数2除到右侧得到x ≥ 2,即解为x大于等于2。
b) 3 - x < 10将式子转化为x的形式,得到-x < 7。
由于x的系数为-1,需要将不等号取反,即x > -7,解为x大于-7。
c) 4(x - 2) > 8进行分配律,得到4x - 8 > 8。
将常数项8移到右侧,得到4x > 16。
除以系数4以求解,得到x > 4,解为x大于4。
d) 2(x + 3) ≤ 10将分配律应用于左侧,得到2x + 6 ≤ 10。
将常数项6移到右侧,得到2x ≤ 4。
除以系数2以求解,得到x ≤ 2,解为x小于等于2。
2. 根据不等式绘制数轴,并确定不等式的解集。
a) x > -3b) -2 ≤ x < 5c) x ≥ -1d) x < 2 or x ≥ 7解析:a) x > -3在数轴上标记-3,并在-3的右侧表示不等式。
解集为开区间(-3, +∞),即-3之后的所有实数。
b) -2 ≤ x < 5在数轴上标记-2和5,并在两个标记之间表示不等式。
解集为闭区间[-2, 5),即从-2开始到5结束,包括-2但不包括5的所有实数。
c) x ≥ -1在数轴上标记-1,并在-1的右侧表示不等式。
解集为闭区间[-1, +∞),即-1之后的所有实数。
d) x < 2 or x ≥ 7在数轴上标记2和7,并在这两个标记之外的区域表示不等式。
解集为两个开区间(-∞, 2)和[7, +∞),即小于2或大于等于7的所有实数。
3. 根据给定的不等式,找到解集。
a) x + 3 > 6 and 2x - 4 < 8解析:首先,我们将两个不等式分析并解出x的范围,然后找到它们的交集。
八年级下期中(三角形相似、分式、分式方程、不等式(组)
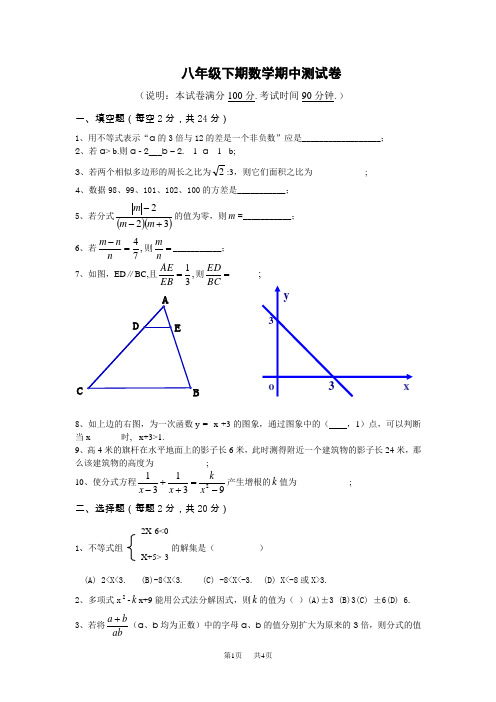
八年级下期数学期中测试卷(说明:本试卷满分100分.考试时间90分钟.)一、填空题(每空2分,共24分)1、用不等式表示“a 的3倍与12的差是一个非负数”应是__________________;2、若a > b.则a - 2___b – 2. 1- a __1 - b;3、若两个相似多边形的周长之比为2:3,则它们面积之比为____________;4、数据98、99、101、102、100的方差是___________;5、若分式()()322+--m m m 的值为零,则m =___________;6、若,74=-n n m 则=nm___________; 7、如图,ED ∥BC,且,31=EB AE 则_____;=BCEDC8、如上边的右图,为一次函数y = -x +3的图象,通过图象中的( ,1)点,可以判断当x_______时, - x+3>1.9、高4米的旗杆在水平地面上的影子长6米,此时测得附近一个建筑物的影子长24米,那么该建筑物的高度为____________; 10、使分式方程931312-=++-x k x x 产生增根的k 值为____________; 二、选择题(每题2分,共20分)1、不等式组 的解集是( )(A) 2<X<3. (B)-8<X<3. (C) -8<X<-3. (D) X<-8或X>3.2、多项式x 2-k x+9能用公式法分解因式,则k 的值为( )(A)±3 (B)3(C) ±6(D) 6.3、若将abba +(a 、b 均为正数)中的字母a 、b 的值分别扩大为原来的3倍,则分式的值 2X-6<0X+5>-3(A)扩大为原来的3倍 ; (B)缩小为原来的91 ; (C)不变; (D) 缩小为原来的31. 4使分式1122+-x x 有意义的x 的取值为( )(A)x≠±1 (B)x≠1(C) x≠-1 (D) x 为任意实数 .5、已知关于x 的不等式2x-a >-3的解集如图所示,则a 的值等于( )(A)-1 ; (B)0; (C)1; (D) 2.6、某校有500人学生参加外语口语考试,考试成绩在70分—85分之间的有120人,则这个分数段的频率是( )(A)0.2 ; (B)0.12; (C)0.24; (D)0.25.7、把一个矩形剪去一个正方形,若所剩矩形与原矩形相似,这个矩形称为黄金矩形,则黄金矩形的长与宽之比为( ) (A)()15-:2 ; (B)3:2; (C)()15+:2; (D)()53-:2.8、下列语句正确的是( )(A) 相似图形一定是位似图形,位似图形一定是相似图形 ; (B) 位似图形一定是相似图形,而且位似比等于相似比; (C) 利用位似变换只能放大图形,不能缩小图形; (D) 利用位似变换只能缩小图形,不能扩大图形. 9、等边三角形的边长扩大了2倍,则面积扩大了( )(A)4倍 ; (B)3倍; (C)9倍; (D)8倍.10、如果(m+1)x > m+1的解集为x < 1,则m 的取值范围是( ). (A)m<0 ; (B) m<-1; (C)m>-1; (D)m 是任意实数.三、作图题:(6分)已知:四边形ABC D .求作:四边形A 1B 1C 1D 1.使得四边形A 1B 1C 1D 1与四边形ABC D 位似比为1:2.至少采用两种不同的方法. BB四、分解因式:(4+8=12分)1、根据分解因式的结果连线:22 a ( 5+4a)(5 - 4a)2、把下列各式分解因式:(1)m(x - y)- n(y - x); (2)3224-x . 五、解答题(共38分)(一) 解不等式组并在数轴上表示其解集;(6分(二)计算:(2×5=10分) (1)xx -+-32962; (2) .1222b a b a a -÷--(三)、解分式方程(6分):32121---=-xxx ;(四)、列分式方程解应用题(6分):我校八年级学生军训时,有一个急行军训练课程,预计行60千米的行程可在下午5点钟到达集训地,由于同学们士气高昂,实际速度比原计划速度快51,结果4点钟到达集训地,求实际行走的速度。
八年级第二学期第一次段考数学试卷

八年级第二学期中段考数学测试题一、选择题:(每小题 3分共30分)1、若分式242--x x 的值为零,则x 的值是( )A.2或-2B.2C.-2D.42、实验表明,人体内某种细胞的形状可近似地看作球,它的直径约为0.00000156m ,则这个数用科学记数法表示是( )(A )50.15610-⨯ (B )50.15610⨯ (C )61.5610-⨯ (D )61.5610⨯ 3、点(0,-2)在( ).A.x 轴上B.y 轴上C.第三象限内D.第四象限内4、如果矩形的面积为6cm 2,那么它的长y cm 与宽x cm 之间的函数关系用图象表示大致( )5、如果反比例函数xky =的图像经过点(-3,-4),那么函数的图像应在( ) A 、 第一、三象限 B 、 第一、二象限 C 、 第二、四象限 D 、 第三、四象限6、王大爷饭后出去散步,从家中走 20 分钟到一个离家 900 米的公园,与朋友聊天10分钟后,然后用15分钟返回家里。
A B C D7、甲、乙两人各自安装10台仪器,甲比乙每小时多安装2台,结果甲比乙少用1小时完成安装任务。
如果设乙每小时安装x 台,根据题意得 ( ) A 、121012=-+x x;B 、11010=-;C 、110210=--xx ;D 、121010=-+x x8、如图,△ABC ≌△BAD ,A 与B ,C 与D 是对应点,若AB=4cm ,BD=4.5cm ,AD=1.5cm ,则BC 的长为( )A. 4cmB.4.5cmC.1.5cmD. 不能确定9. 如图,AD 平分∠BAC ,AB=AC ,连接BD ,CD ,并延长相交AC ,AB 于点F ,E ,则此图形中有几对全等三角形( ) A 3对 B 4对 C 5对 D 6对10、如图,∠1=∠2,∠C=∠D 。
AC ,BD 交于点E ,结论中不正确的是( ) A. △DAB ≌△CBA B. △DEA 与△CEB 不全等 C. CE=DE D. ∠DAE=∠CBE 二、填空题:(每小题3分共15分) 11、当 x_______时,分式x 2x -3有意义。
八年级数学不等式分式检测题

八年级数学不等式、分式检测题1、 选择题(每小题2分,共20分)。
1.不等式的解集在数轴上表示正确的是()A.B.C.D.2.不等式组的解集是( )A.B.C.D.3、下列式子:、、、、、+,分式的个数有()A、 3个 B 、4个 C、 5个 D、 2个4.关于x的不等式2x-a≤-1的解集如图9-3所示,则a的取值是().A.0 B.-3 C.-2 D.-11-1-2图9-35、能使分式的值为零的所有x的值是()A x=0B x=1C x=0 或x=1D x=0或 x=±16.如果|x-2|=x-2,那么x的取值范围是( ).A.x≤2 B.x≥2 C.x<2 D.x>2 7.若方程3m(x+1)+1=m(3-x)-5x的解是负数,则m的取值范围是( ).A.m>-1.25 B.m<-1.25 C.m>1.25D.m<1.258、下列各式中正确的是( )A. B. C. D.9.如果的值为0,则代数式+x的值为()A、0B、 2C、 -2D、 ±210.某商店销售一种小电器,元月的营业额为5000元.为了扩大销量,在2月将每件小电器按原价的八折销售,销售量比元月增加了20件,营业额比元月增加了600元,设元月每件小电器的售价为x元,则可列方程为()A、-=20B、—=20C、= -20D、-=20二、填空(每小题2分,共20分)。
11.若分式有意义,则x的取值范围是 。
12.若一次函数=2-6,当_____时,是非正数.13.当时,与的大小关系是_______________.14.若点P(1-m,m)在第二象限,则(m-1)x>1- m的解集为_______________.15.已知x=3是方程—2=x—1的解,那么不等式(2—) x<的解集是.16.若分式方程=1有增根,则m的值为 。
17.若不等式组的解集是x>3,则m的取值范围是.18.已知关于x的不等式组的整数解共有5个,则a的取值范围是.19.从小明家到学校的路程是2400米,如果小明早上7点离家,要在7点30分到40分之间到达学校,设步行速度为米/分,则可列不等式组为__________________,小明步行的速度范围是_________.20.某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则至多可打.三、解答题 21.(10分)解不等式及不等式组,并把它的解集表示在数轴上:(1)(2)22.(10分)计算与化简:(1)(-)÷(-)·() (2)23.(10分)解分式方程:(1)(2)24.(8分)解不等式组并写出该不等式组的整数解.26.(12分)2009年我市某县筹备20周年县庆,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个种造型需甲种花卉80盆,乙种花卉40盆,搭配一个种造型需甲种花卉50盆,乙种花卉90盆.(1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.(2)若搭配一个种造型的成本是800元,搭配一个种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?25、(10分)在“情系汶川”捐款活动中,小明对甲、乙两班捐款情况进行了统计:甲班捐款人数比乙班捐款人数多3人,甲班共捐款2400元,乙班共捐款1800元,乙班平均每人捐款的钱数是甲班平均每人捐款钱数的倍,求甲、乙两班各有多少人捐款?(假如甲乙两班每位同学都捐款)选做题:27.(10分)先阅读下面的材料,然后回答问题:方程x+=2+的解为x=2, x=;方程x+=3+的解为x=3, x=;方程x+=4+的解为x1=4,x=; ……(1)观察上述方程的解,猜想关于x的方程x+=5+的解是 ;(2)根据上面的规律,猜想关于x的方程x+=的解是 ;(3)由(2)可知,在解方程:y+=时,可变形转化为x+=的形式求值,按要求写出你的变形求解过程。
初二数学《不等式分式》提高练习题

初二数学《不等式、分式》提高练习题1、四个小朋友玩跷跷板,他们的体重分别为P、Q、R、S,如图所示,则他们的体重大小关系是( )A.B. C. D.2、若,则的大小关系为()A. B.C. D.不能确定3、若,则下列式子:①;②;③;④中,正确的有()A.1个 B.2个 C.3个 D.4个4、不等式2x-7<5-2x的正整数解有()A.1个B.2个 C.3个 D.4个5、小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为69千克,坐在跷跷板的一端,体重只有妈妈一半的小宝和妈妈同坐在跷跷板的另一端。
这时爸爸的一端仍然着地.后来小宅借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果爸爸被跷起离地.小宝体重可能是()A.19.9于克 B.22千克 C.23千克 D.23.3千克6、若式子有意义,则X应满足()A. X≠-2 且X≠1B. X≠2且X≠-2C. X=± 2且X≠1D. X=± 27、韩日“世界杯”期间,重庆球迷一行56人从旅馆乘出租车到球场为中国队加油,现有A、B两个出租车队,A队比B队少3辆车,若全部安排乘A队的车,每辆坐5人,车不够,每辆坐6人,有的车未满;若全部安排B队的车,每辆车4人,车不够,每辆坐5人,•有的车未满,则A队有出租车()A.11辆 B.10辆 C.9辆 D.8辆8、使代数式有意义的自变量的取值范围是______________.9、已知的值.10、已知:求代数式的值。
11每户每月用水量不超过10吨(含10吨)超过10吨的部分水费单价 1.30元/吨 2.00元/吨(1(2)若小华家四月份付水费17元,问他家四月份用水多少吨?(3)已知某住宅小区100户居民五月份交水费共1682元,且该月每户用水量均不超过15吨(含15吨),求该月用水量不超过10吨的居民最多可能有多少户?12、县公路局为了对某段公路进行绿化,计划购买A、B两种树共900棵,A、B两种树的相关信息如下表:项目单价(元/棵) 成活率品种A 80 92%B 100 98%设购买A种树x棵,购树所需的总费用为y元.(1)求y与x之间的函数关系式;(2)若购树的总费用不超过82000元,则购A种树不少于多少棵?(3)若希望这批树的成活率不低于94%,且使购树的总费用最低,应选购A、B两种树各多少棵?此时最低费用为多少?13、某公司有型产品40件,型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:型利润型利润甲店200 170乙店160 150(1)设分配给甲店型产品件,这家公司卖出这100件产品的总利润为(元),求关于的函数关系式,并求出的取值范围;(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;(3)为了促销,公司决定仅对甲店型产品让利销售,每件让利元,但让利后型产品的每件利润仍高于甲店型产品的每件利润.甲店的型产品以及乙店的型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?14、求不等式的整数解。
人教版初中八年级数学《不等式》章节测试题与答案

人教版初中八年级数学《不等式》章节测试题一、单选题1、若a <b ,则下列各式中不成立的是( )A 、a+2<b+2B 、﹣3a <﹣3bC 、2﹣a >2﹣bD 、3a <3b 2、设“○”、“□”、“△”分别表示三种不同的物体,用天平比较它们质量的大小,两次情况如图所示,那么每个“○”、“□”、“△”这样的物体,按质量从小到大的顺序排列为( )A 、○□△B 、○△□C 、□○△D 、△□○3、贵阳市今年5月份的最高气温为27△,最低气温为18△,已知某一天的气温为t△,则下面表示气温之间的不等关系正确的是( )A 、18<t <27B 、18≤t <27C 、18<t≤27D 、18≤t≤274、如果不等式(a ﹣2)x >a ﹣2的解集是x <1,那么a 必须满足( ) A 、a <0 B 、a >1 C 、a >2 D 、a <25、若﹣<﹣,则a 一定满足是( )A 、a >0B 、a <0C 、a≥0D 、a≤06、若a 、b 是有理数,则下列说法正确的是( )A 、若a 2>b 2 ,则a >bB 、若a >b ,则a 2>b 2C 、若|a|>b ,则a 2>b 2D 、若|a|≠|b|,则a 2≠b 27、当1≤x≤2时,ax+2>0,则a 的取值范围是( )A 、a >﹣1B 、a >﹣2C 、a >0D 、a >﹣1且a≠0 8、(2016•大庆)当0<x <1时,x 2、x 、的大小顺序是( ) A 、x 2 B 、<x <x 2 C 、<x D 、x <x 2<二、填空题9、用不等式表示下列关系:x 的3倍与8的和比y 的2倍小: ___. 10、如果2x ﹣5<2y ﹣5,那么﹣x ﹣y (填“<、>、或=”) 11、下列判断中,正确的序号为_ ___ .△若﹣a >b >0,则ab <0; △若ab >0,则a >0,b >0;△若a >b ,c≠0,则ac >bc ;△若a >b ,c≠0,则ac 2>bc 2;△若a >b , c≠0,则﹣a ﹣c <﹣b ﹣c . 12、已知数a 、b 的对应点在数轴上的位置如图所示,则a ﹣3 __ _____b ﹣313、若关于x 的不等式(1﹣a )x >2可化为x >,则a 的取值范围是 。
分式不等式初二练习题
分式不等式初二练习题分式不等式初中练习题题目一:解下列分式不等式,并将解集表示在数轴上:1. $\frac{2}{x} < 3$2. $\frac{3}{x-1} > 5$解答与解集:1. 首先,移项得到:$\frac{2}{x} - 3 < 0$接着,找到不等式的临界点,即使分母等于零的点:$x = 0$然后,根据临界点将数轴分割成三个区间:$(-\infty, 0), (0, +\infty)$对于每个区间,选取一个测试点进行代入,可以选择$x = -1$和$x = 1$当$x = -1$时,$\frac{2}{-1} - 3 = -2 - 3 = -5$,小于零当$x = 1$时,$\frac{2}{1} - 3 = 2 - 3 = -1$,小于零因此,对于区间$(-\infty, 0)$和$(0, +\infty)$,不等式成立。
将解集表示在数轴上,用开区间表示为:$x \in (-\infty, 0) \cup (0, +\infty)$2. 首先,移项得到:$\frac{3}{x-1} - 5 > 0$接着,找到不等式的临界点,即使分母等于零的点:$x = 1$然后,根据临界点将数轴分割成三个区间:$(-\infty, 1), (1, +\infty)$对于每个区间,选取一个测试点进行代入,可以选择$x = 0$和$x = 2$当$x = 0$时,$\frac{3}{0-1} - 5 = 3 + 5 = 8$,大于零当$x = 2$时,$\frac{3}{2-1} - 5 = 3 - 5 = -2$,小于零因此,对于区间$(-\infty, 1)$,不等式不成立;对于区间$(1,+\infty)$,不等式成立。
将解集表示在数轴上,用开区间表示为:$x \in (1, +\infty)$题目二:通过求解下列分式不等式来确定常数$k$的取值范围,并将解集表示在数轴上:1. $\frac{x}{x+2} \geq k$2. $\frac{x-1}{x-3} < k$解答与解集:1. 首先,进行化简:$\frac{x}{x+2} \geq k$接着,将不等式转换为等价形式:$\frac{x}{x+2} - k \geq 0$然后,找到不等式的临界点,即使分母等于零的点:$x + 2 = 0\Rightarrow x = -2$然后,根据临界点将数轴分割成三个区间:$(-\infty, -2), (-2,+\infty)$对于每个区间,选取一个测试点进行代入,可以选择$x = -3$和$x = 0$当$x = -3$时,$\frac{-3}{-3+2} - k = -3 + k$,大于等于零当$x = 0$时,$\frac{0}{0+2} - k = -k$,小于等于零根据测试点的结果,可以得出以下结论:- 当$k = 0$时,不等式成立;- 当$k > 0$时,不等式不成立;- 当$k < 0$时,不等式成立。
八年级下学期 阶段测试(不等式 分式 反比例函数)
苏科版八年级数学阶段检测试卷(不等式 分式 反比例函数)(总分:150分 时间:120分钟)(每题3分,共30分)请注意:考生必须将所选答案的字母写到相应的题号内!.a>0 B .a<0 C .a ≠0 D .a 为任意数 232yx中,x,y 的值都变为原来的一半,则分式的值 ( ) A .不变 B .扩大2倍 C .缩小2倍 D .以上都不对(1)yx y x y x -=--122;(2)c a b a a c a b --=--;(3)1-=--b a ab ;(4)y x y x y x y x +-=--+- )A 、1个B 、2 个C 、 3 个D 、 4 个 1=x-1与反比例函数y2=x2 A (2,1),B (-1,-2),则使y1>y2的x的取值范围是( ) x>2 B. x>2 或-1<x<0 C. -1<x<2 D. x>2 或x<-1 xx x x 35352-=-从左至右变形成立的条件是( )A 、x <0B 、x >0C 、x ≠0D 、x ≠0且x ≠3⎩⎨⎧>-<+nx x x 731的解集是4>x ,则n 的取值范围是A .4≥nB .4≤nC .4=nD .4<n .若关于x的方程x a cb x d-=-有解,则必须满足条件 、c ≠d B 、c ≠-d C 、bc ≠-ad D 、a ≠b 280页,要在两周借期内读完,当他读了一半时,发现平时每天要多读21页才能在借期内读完.他读了前一半时,平均每天读多少页?如果设读前一半时,平均每天读x 页,则下列方程中,正确的是 ( )A 、1421140140=-+x x B 、1421280280=++x x C 、1211010=++x x D 、1421140140=++x x9.在函数1y x =的图象上有三个点的坐标分别为(1,1y )、(12,2y )、(3-,3y ),函数值y 1、y 2、y 3的大小关系是( )A .y 1<y 2<y 3B .y 3<y 2<y 1C .y 2<y 1<y 3D .y 3<y 1<y 210.(2008济南)如图:等腰直角三角形ABC 位于第一象限,AB=AC=2,直角顶点A 在直线y =x 上,其中A 点的横坐标为1,且两条直角边AB 、AC 分别平行于x 轴、y 轴,若双曲线ky x=(k ≠0)与ABC ∆有交点,则k 的取值范围是( ) A .12k << B .13k ≤≤ C .14k ≤≤ D .14k <≤二、填空(每题3分,共24分) 11.已知a=x+2,b=x-1,且a>3>b ,则x 的取值范围是12.不等式a ≤x ≤3只有5个整数解,则a 的范围是13.不等式组533(2),13822x x x x ->-⎧⎪⎨≤-⎪⎩的非负整数解是______________。
数学八年级上下册不等式试卷
1、若a > b,则下列不等式中一定成立的是:A. a - 2 < b - 2B. 2a < 2bC. -a > -bD. a + c > b + c解析:根据不等式的性质,当两边同时加上或减去同一个数时,不等号的方向不变。
因此,对于选项D,a + c > b + c,由于a > b,所以加上相同的数c后,不等号方向仍然保持,故D选项正确。
(答案:D)2、若x < 5,则下列不等式中错误的是:A. x + 3 < 8B. x - 2 < 3C. 2x < 10D. x/2 > 2.5解析:对于选项D,若x < 5,则x除以2应小于2.5,而非大于2.5。
因此,D选项是错误的。
(答案:D)3、若-3 < x < 2,则下列哪个区间是x + 5的取值范围?A. -8 < x + 5 < -3B. -3 < x + 5 < 2C. 2 < x + 5 < 7D. -8 < x + 5 < 7解析:根据不等式的性质,当两边同时加上或减去同一个数时,不等号的方向不变。
因此,对于-3 < x < 2,两边同时加5,得到2 < x + 5 < 7。
(答案:C)4、若a > b,c < 0,则下列不等式中一定成立的是:A. ac > bcB. a/c > b/cC. a - c > b - cD. a + c > b + c解析:对于选项C,由于a > b,且-c > 0(因为c < 0),所以两边同时加上-c,不等号方向不变,得到a - c > b - c。
(答案:C)5、若x > y > 0,则下列不等式中不一定成立的是:A. x2 > y2B. √x > √yC. 1/x < 1/yD. x3 < y3解析:对于选项D,由于x > y > 0,且三次方函数在整个实数范围内是单调递增的,所以x3 > y3,而非x3 < y3。
八年级不等式试题及答案
八年级不等式试题及答案1. 若不等式 \( ax + b > 0 \) 的解集为 \( x < -\frac{b}{a} \),求 \( a \) 和 \( b \) 的符号。
答案:\( a < 0 \) 且 \( b > 0 \)。
2. 解不等式 \( 3x - 7 < 0 \)。
答案:\( x < \frac{7}{3} \)。
3. 若 \( x \) 是不等式 \( 2x - 5 < 0 \) 的解,求 \( x \) 的取值范围。
答案:\( x < \frac{5}{2} \)。
4. 已知 \( x \) 和 \( y \) 满足 \( x + y > 0 \) 且 \( x - y < 0 \),求 \( x \) 和 \( y \) 的关系。
答案:\( x < y \)。
5. 解不等式组 \( \begin{cases} x - 2 > 0 \\ 3x + 4 \leq 8\end{cases} \)。
答案:\( 2 < x \leq \frac{4}{3} \)。
6. 已知 \( a \) 和 \( b \) 是两个正整数,且 \( a + b > 10 \),求 \( a \) 和 \( b \) 的最小值。
答案:\( a = 1 \),\( b = 10 \)。
7. 若不等式 \( 2x + 3 > 5x - 7 \) 的解集为 \( x < 5 \),求\( x \) 的取值范围。
答案:\( x < 5 \)。
8. 已知 \( x \) 是不等式 \( 3x - 2 \geq 4 \) 的解,求 \( x \) 的取值范围。
答案:\( x \geq 2 \)。
9. 解不等式 \( \frac{x - 1}{2} \leq 3 \)。
答案:\( x \leq 7 \)。
10. 若 \( x \) 和 \( y \) 满足 \( 2x - 3y < 0 \) 且 \( x + y > 0 \),求 \( x \) 和 \( y \) 的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3x+1>0 的解集是
-0.5x+1>0 7.如果不等式组⎩⎨⎧>-<+n x x x 7
31的解集是4>x ,则n 的取值范围是
A .4≥n
B .4≤n
C .4=n
D .4<n
8.如果把分式
2xy
x y
+中的x 和y 都扩大3倍,那么分式的值 A 、扩大3倍 B 、缩小3倍
C 、缩小6倍
D 、不变
9.若有m 人a 天完成某项工程,则(m+n )个同样工作效率的人完成这项工程
需要的天数是
A 、a+m
B 、n m ma +
C 、n m a +
D 、ma
n
m +
10.观察下列图像,可以得出不等式组
A.x <3
1 B.-3
1<x <0 C.0<x <2 D.-3
1
<x <2 11.已知a ,b 为实数,且ab=1,设M=
11+++b b a a ,N=1
1
11++
+b a ,则M ,N 的大小关系是
A 、M>N
B 、M=N
C 、M<N
D 、不确定
12.关于x 的不等式组010x a x ->⎧⎨->⎩
,
只有3个整数解,则a 的取值范围是
A. -3≤a ≤-2
B. -3≤a <-2
C. -3<a ≤-2
D. -3<a <-2
二、填空(每题3分,共24分)
13.不等式38x -<的负整数解是 。
14.
())0(,10 53≠=a axy xy a =b
a ab
2
205__________。
15.已知点M
(1 - a ,a + 2)在第二象限,则a 的取值范围是_______.
16.不等式组533(2),13
822
x x x x ->-⎧⎪
⎨≤-⎪⎩的非负整数解是______________。
17.
1111
.....(1)(1)(2)(2)(3)(2007)(2008)
x x x x x x x x ++++
+++++++= . 18.已知1
1
y x y +=
-,用含x 的代数式表示y 为______________。
19.已知a 2
-3a+1=0,则a a 1+
=_______________,22
1a
a +=____________
20.已知x 为整数,且分式1
3-x
的值为整数,则x 可取的值为____________。
三、解答题
(1)约分(4’×2)
21.2
3
2636yz
z xy - 22.22444a a a -+-
(2)通分(4’×2) 23.b a a 251,21 24.4
1293,94222+--m m m
(3)分式计算(5’×3)
25.
a b a b b a +-- 26. 24111a a
a a
++
--
27.
11
2
---a a a
28. 解不等式x -
3x-24 ≥2(1+x)
3
-1,将解集在数轴上表示出来,且写出它的正整数解。
(6)
. (5’×2) 33213(1)8x x x x -⎧+≥⎪⎨⎪--<-⎩ 30.⎪⎩⎪
⎨⎧<+>-3)4(2
10
12x x
x 、y 的方程组⎩⎨⎧=-=+m
y x y x 21
2.
)求这个方程组的解;
)当m 取何值时,这个方程组的解中,x 大于1,y 不小于-1. (3+4’)
四、灵活运用
32. 一个三角形的 三边长分别是xcm 、(1)x cm +、(2)x cm +,它的周长不超过
39cm 。
求x 的取值范围。
(6’)
33.把一堆苹果分给几个孩子,如果每人分3个,那么多8个。
如果前面每人分5个,
那么最后一人得到的苹果不足3个,问有几个孩子?有多少个苹果?(6)
五、实际应用
“一34.今年5月12日,四川汶川发生了里氏8.0级大地震,给当地人民造成了巨大的损失.
方有难,八方支援”,我市锦华中学全体师生积极捐款,其中九年级的3个班学生的捐款金额如下表:
吴老师统计时不小心把墨水滴到了其中两个班级的捐款金额上,但他知道下面三条信息:信息一:这三个班的捐款总金额是7700元;
信息二:(2)班的捐款金额比(3)班的捐款金额多300元;
信息三:(1)班学生平均每人捐款的金额大于
..51元.
..48元,小于
请根据以上信息,帮助吴老师解决下列问题:
(1)求出(2)班与(3)班的捐款金额各是多少元;(5’)
(2)求出(1)班的学生人数.(5’)。
