第二章-结构的几何构造分析(龙驭球第三版)
结构力学龙驭球第三版课后习题答案精编版

结构力学
1
2
3
三链杆交于一点,瞬变
3
习题解答
P.37 2-2(b)
结构力学
4
习题解答
结构力学
几何不变,无多余约束
5
习题解答
P.37 2-3(c)
结构力学
有一个多余 约束
1
2 3
几何不变,有一个多余约束
6
习题解答
P.37 2-4(d)
O(I、III) O(II、III)
I
结构力学
II
1
2
O(I、II)
3.1 梁的内力
P.107 3-1 (b) (c) (e) P.108 3-2
结构力学
21
习题解答
P.107 3-1 (b) 用分段叠加法作梁的M 图
结构力学
ql2 8
q
A l
ql2 8
B
ql2 8
ql2
8
ql2
8
22
习题解答
结构力学
FP l F4P l
4 A
FP FP
C
A
l
C
l
2l
2l
2
2
FP l F4P l B4
B
C
A
C
B
A FP l
FBP l
F4P l
F4P l
4
4
FP l
F2P l
M2图
23
习题解答
P.107 3-1 (e) 用分段叠加法作梁的M 图
结构力学
22kkNN..mm
33kkNN//mm
AA 44mm
BB 22mm
66
((44))
22
龙驭球《结构力学Ⅰ》(配套题库【课后习题】(结构的几何构造分析)

第1章绪论本章无课后习题。
第2章结构的几何构造分析2-1 试分析图2-1所示体系的几何构造。
图2-1解:(1)如图2-2所示,ABC和DEF为两个二元体,可以撤除,剩下的杆CD通过不共点的三链杆与基础相连,形成几何不变体,二元体不影响原结构的几何不变性,故体系为几何不变体系,且无多余约束。
图2-2(2)如图2-3所示,刚片AB通过不共点三链杆1、2、3与基础相连,形成几何不变体。
将刚片AB和基础视为基础,刚片CD通过链杆BC、DE及链杆4与基础相连,但是这三链杆交于同一点,即链杆4与刚片CD的交点,故体系为有一个多余约束的瞬变体系。
注:瞬变体系必定有多余约束。
图2-3(3)如图2-4所示,ABC和DCE为二元体,将其撤除,视刚片HI与地基固结为一个基础,刚片EG、FH通过不共线的三个铰G、F、H与基础相连,形成几何不变体,二元体不影响原结构的几何不变性,所以该体系为几何不变体系,且无多余约束。
图2-42-2 试分析图2-5所示体系的几何构造。
图2-5解:(1)如图2-6(a)所示,将刚片1和2、刚片3和4、刚片5和6、刚片7和8、刚片9和10、刚片11和12视为二元体,将其依次撤除,只剩下大地基础,故体系为几何不变体系,且无多余约束。
(2)如图2-6(b)所示,杆2、4、10通过不共线的三个铰相连,构成一个刚片a,同理可构成刚片b、c、d,刚片a、b与杆1通过不共线的三个铰相连构成一个几何不变体,且无多余约束,并与刚片c、d通过不共线的三个铰相连构成几何不变体,再与基础通过不共点的三个链杆14、15、16相连构成几何不变体,故体系为几何不变体系,且无多余约束。
(3)如图2-6(c)所示,下部由基本三角形Ⅰ、Ⅱ和Ⅲ组成,为几何不变体系,可视为一个大的刚片,上部依次拆除二元体1和2、3和4、5和6,刚片7和8与下部大的刚片通过共线的三铰相连,形成瞬变体,故体系为有一个多余约束的瞬变体系。
图2-62-3 试分析图2-7所示体系的几何构造。
龙驭球《结构力学Ⅰ》(第3版上册)名校考研真题【圣才出品】
圣才电子书 十万种考研考证电子书、题库视频学习平台
的铰 E 和链杆 FC 相连形成几何不变体系,DGH 即为一个多余约束。 2.如图 2-6(a)所示体系的几何组成为________体系。[南京理工大学 2011 研]
图 2-6 【答案】无多余约束的几何不变 【解析】由于体系与基础呈简支状态,因此,可去除基础只分析上部体系的几何组成特 性。简化后的体系如图 2-6(b)所示,选择刚片Ⅰ、Ⅱ、Ⅲ,三刚片通过不在同一直线上 的三铰两两相连,满足三刚片规则,所以,原体系为无多余约束的几何不变体系。
图 2-3
2.图 2-4(a)所示体系的几何组成是( )。[武汉大学 2012 研、郑州大学 2010 研、华南理工大学 2007 研、河海大学 2007 研]
A.无多余约束的几何不变体系 B.几何可变体系 C.有多余约束的几何不变体系
2 / 45
圣才电子书
D.瞬变十万种考研考证电子书、题库视频学习平台
图 2-9 (2)几何构成分析 本题上部体系与基础呈简支状态,故去除基础只分析上部体系。首先选 ACDB 作为刚 片Ⅰ,然后顺杆件 CE 和 DF 找到杆件 EF 作为刚片Ⅱ,再由杆件 EG 和 FH 找到杆件 GH 作 为刚片Ⅲ,最后由杆件 GA 和 HB 回到刚片Ⅰ,如图 2-9(c)所示,由三个瞬铰的位置可 以判断其满足三刚片规则,所以,原体系为无多余约束的几何不变体系。 4.对图 2-10(a)平面体系进行几何组成分析,给出必要分析过程和说明。[宁波大学 2013 研、大连理工大学 2005 研]
二、选择题 1.图 2-2 所示平面体系的几何组成是( )。[浙江大学 2010 研] A.几何不变,无多余约束 B.几何不变,有多余约束 C.几何常变
结构力学《第二章几何组成分析》龙奴球

第二章 结构的几何构造分析
瞬变体系(
×)
体系是由三个刚片用三个共线的铰 ABC相连,故为瞬变体系。( )
×
第二章 结构的几何构造分析
几种常用的分析途径
1、去掉二元体,将体系简单化,然 后再分析。
D A
C
B
依次去掉二元体A、B、C、D后, 剩下大地。故该体系为无多余约 束的几何不变体系。
第二章 结构的几何构造分析 2、如上部体系与基础用满足要求三个约束相联可去掉 基础,只分析上部。
第二章 结构的几何构造分析
用一链杆将一刚片与地面相联 两刚片用一链杆相联
1、2、3、4是链杆, 折线型链杆、曲线型 链杆可用直线型链杆 代替。
3 6 4
Ⅰ
1 5
5、6不是链杆。
第二章 结构的几何构造分析
单铰:联结两个刚片的铰称为单铰
一个单铰相当于几个约束呢? 在平面内两个刚片自由 度等于6 加入一个单铰后自由度 等于4,减少了2个自由 度
A
C B
规则4 三刚片以不在一条直线 上的三铰 两两相连,组成无多余 约束的几何不变体系。
如约束不满足限制条件,将出现下列几种形式的瞬变体系
三铰共线瞬变体系
第二章 结构的几何构造分析
关于无穷远瞬铰的情况
1 C II
I A
2
B
III
图示体系,一个瞬铰C在无穷远处,铰A、 B连线与形成瞬铰的链杆1、2不平行,故三个 铰不在同一直线上,该体系几何不变且无多 余约束。
(3) 各∞点都在同一直线上,此直线称为∞线。
(4) 各有限远点都不在∞线上。
第二章 结构的几何构造分析
§2-2 几何不变体系的组成规则
基本规律:三角形规律
龙驭球结构力学答案==-2022年学习资料

P1093-3b-速画M图-2-B-9u2-B02-9a2-9u3-8-79a2-A-39
P1093-3d-速画M图-qh2-C-B-++-A-D-40
P109-3-3-速画M图-9l2-A-B-加-w图-41
P1103-3-G-速画M图-MM-E-A-B-42
P1103-4a判断M图的正误,并改正错误-B-C-F-A-D-atd-z-43
P.112-3-8a作三铰刚架的内力图-2kN/m-2.08-思-月-2.5-o-7.5-5m-FN图-5
P112-3-8d作三铰刚架的内力图-3.13q-12.5q-9.37q-2.81q-M图-7.5q-58
P.112-3-8d作三铰刚架的内力图-5q-2.5q-⊕-0.91q-FQ图-59
P392-9-a-15
O、-OI、-OⅡ、-几何不变,无多余约束-16
OI、-O1、-OI、W-三铰共线,瞬变-17
OL、-7-III-OⅡ、-OⅫ、-几何不变,无多余约束-18
P39-2-10b-A-B-铰A、B的连线与1、2-两链杆平行,体系瞬变-19
P392-12-S=3m-3g+2h+b-=3×1-3×4+2×0+3-=3×8-3×2+2×9+3-=2-=-3-几何不变,12个多余约束-几何不变,3个多余约束-20
1083-2-判断内力图正确与否,将错误改正-d-M图-Fo图-33
P1083-2-判断内力图正确与否,将错误改正-M图-FQ图-e-Fp-Fo图-依-34
P1083-2-判断内力图正确与否,将错误改正-M图-FQ图-Fp2-依-35
P1083-2-判断内力图正确与否,将错误改正-M图-FQ图-Fp2-Fo图-依-36
结构力学(龙球奴)考试重点

形状是可以改变的。
一般结构必须是几何不变体系
2. 自由度 自由度个数=体系运动时可以独立改变的坐标数
平面内一点有两种独立运动方式, 即一点在平面内有两个自由度。
一个刚片在平面内有三种独立运动方式, 即一个刚片在平面内有三个自由度。
瞬变体系(三链杆交于同一点)
规律4(如图(b) ) 两个刚片用三根链杆相连,且三链杆不交于同一点,
则组成几何不变的整体,且没有多余约束。
单链杆:连接两点的链杆 相当于一个约束
复链杆:连接n个点的链杆 相当于2n-3个单链杆
自由度算法1(体系由刚片加约束组成)
m—体系中刚片的个数
g—单刚结个数
h—单铰结个数 b—单链杆根数
体系计算自由度:W=3m-(3g+2h+b)
自由度算法2(体系由结点加链杆组成)
j—体系中结点的个数 b—单链杆根数 体系计算自由度: W=2j-b
关于计算自由度数W
W的数值 W>0 W=0
W<0
几何构造特性 对象的自由度数大于约束数 体系为几何可变,不能用作结构 对象的自由度数等于约束数 如体系为几何不变,则无多余约束,为静定结构 如体系为几何可变,则有多余约束
第1章 绪论
结构的概念和结构力学的研究内容 结构计算简图的简化要点 杆件结构的分类 荷载的分类
第2章 结构的几何构造分析
几何构造分析的概念 平面几何不变体系的组成规律 平面杆件体系的计算自由度
几何构造分析的几个概念
1. 几何不变体系和几何可变体系 几何不变体系—在不考虑材料应变的条件下,体系的位置
(2)当结点无荷载作用时, 结点单杆的内力必为零
《结构力学》_龙驭球_第2章_结构的几何构造分析(2)
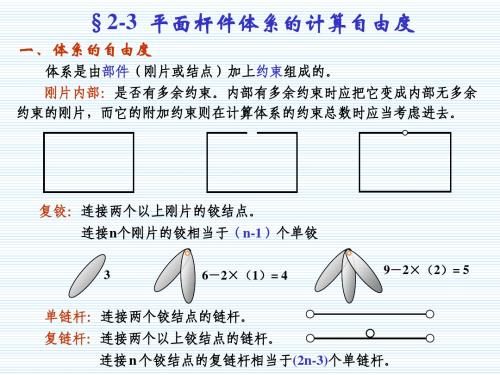
3) 9 9 0
I A II
m3 g 0 h3 b3
例2-3.4:求图示体系的计算自由度。 解:
m 2 g 1 h 1 b 5 W 3 2 (3 1 2 1 5) 6 10 4
单链杆:连接两个铰结点的链杆。 复链杆:连接两个以上铰结点的链杆。
连接 n 个铰结点的复链杆相当于(2n-3)个单链杆。
二、平面体系的计算自由度 W
1、平面刚片体系公式 —— 将体系中刚片为被约束对象,铰、刚结和链杆 为约束。则计算自由度公式为:
W 3m (3g 2h b)
m — 刚片数; g — 简单刚结数(固定支座);
4
D
5
7
E 10
例2-3-4 求图示体系的计算自由度。
A
1 2 3
B
4 I
C 5 6
D
7 8
E 9
10
解: 用混合公式计算。
m 1
j 5 g 2 b 10
W (3 1 2 5) (3 2 10) 13 16 3
W 3m (3g 2h b) b =3 m =4 h =4
W = 3×4-(2×4)-3=1
W 2 j b
j=8 b =12+ 4
W 2 j b
j=4 b = 4+ 3 W =2×4-4-3=1
W=2×8-12-4=0
练习2-3.1:试求图示体系的计算自由度。 A I II 1 B 解: W 3m (3g 2h b)
§2-3 平面杆件体系的计算自由度
一、体系的自由度
体系是由部件(刚片或结点)加上约束组成的。 刚片内部:是否有多余约束。内部有多余约束时应把它变成内部无多余 约束的刚片,而它的附加约束则在计算体系的约束总数时应当考虑进去。
结构力学第三版课后习题答案精选全文

20kN/m
M图
4.5kN
8.98
4
4.5
6 11
4.5 FQ图
M图 (kN.m)
FQ图(kN)
37
3.3 静定平面刚架
必作题: P.109 3-3 (b) (d) (f) (j) P.110 3-4 (a — i) P.111 3-7 (a) P.112 3-8 (a) (d)
选作题: P.109 3-3 (a) (e) (g) (l) P.112 3-8 (c) P.112 3-9 (a) P.113 3-11
2
P.37 2-1(b)
1
2
3
三链杆交于一点,瞬变
3
P.37 2-2(b)
4几何不变,无多余约束5P.37 2-3(c)
有一个多余 约束
1
2 3
几何不变,有一个多余约束
6
P.37 2-4(d)
O(I、III) O(II、III) I
II
1
2
O(I、II)
III
铰O(I、II)、 O(II、III)的连线与1、2两链 杆不平行,体系几何不变,无多余约束
2.5m 5m 5m 2.5m
FN图
60
3.4 静定平面桁架
必作题:
P.113 P.114 P.115
选作题:
P.116 P.117
3-13 (b) (d) (f) 3-14 (a) (b) (c) 3-17 (a) (d)
3-18 (a) 3-20
P.116 3-18 (b)
61
P.113 3-13 (b) 分析桁架类型,指出零杆
FP
联合桁架,10根零杆。
62
P.113 3-13 (d) 分析桁架类型,指出零杆
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章结构的几何构造分析
本章内容:§2-1 几何构造分析的几个概念
§2-2 平面几何不变体系的组成规律
§2-3 平面杆件体系的计算自由度
§2-4 在求解器中输入平面结构体系(略)
§2-5 用求解器进行几何构造分析(略)
§2-6 小结
主要内容:
第三讲
§2-1 几何构造分析的几个概念
1. 几何不变体系和几何可变体系
一般结构必须是几何不变体系
几何不变体系—在不考虑材料应变的条件下,体系的位置和形状是不能改变的。
几何可变体系—在不考虑材料应变的条件下,体系的位置和形状是可以改变的。
2. 自由度
平面内一点有两种独立运动方式,即一点在平面内有两个自由度。
一个刚片在平面内有三种独立运动方式,即一个刚片在平面内有三个自由度。
自由度个数=体系运动时可以独立改变的坐标数
3. 约束
一个支杆相当于一个约束,如图(a);一个铰相当于两个约束,如图(b);一个刚性结合相当于三个约束,如图(c)
4. 多余约束
如果在一个体系中增加一个约束,而体系的自由度并不减少,此约束称为多余约束。
有一根链杆是多余约束
5. 瞬变体系
特点:从微小运动的角度看,这是一个可变体系;经微小位移后又成为几何不变体系;在任一瞬变体系中必然存在多余约束。
可变体系
瞬变体系:可产生微小位移
常变体系:可发生大位移
6. 瞬铰
O为两根链杆轴线的交点,刚片I可发生以O为中心的微小转动,O点称为瞬时转动中心。
两根链杆所起的约束作用相当于在链杆交点处的一个铰所起的约束作用,这个铰称为瞬铰。
7. 无穷远处的瞬铰
两根平行的链杆把刚片I与基础相连接,则两根链杆的交点在无穷远处。
两根链杆所起的约束作用相当于无穷远处的瞬铰所起的作用。
无穷远处的含义
(1)每一个方向有一个∞点;
(2)不同方向有不同的∞点;
(3)各∞点都在同一直线上,此直线称为∞线;
(4)各有限点都不在线∞上。
§2-2 平面几何不变体系的组成规律
1. 三个点之间的连接方式
规律1 不共线的三个点用三个链杆两两相连,则所组成的铰接三角形体系是一个几何不变的整体,且没有多余约束。
2. 一个点与一个刚片之间的连接方式
规律2 一个刚片与一个点用两根链杆相连,且三个铰不在一直线上,则组成几何不变的整体,且没有多余约束。
3. 两个刚片之间的连接方式
规律3 两个刚片用一个铰和一根链杆相连,且三个铰不在一直线上,则组成几何不变的整体,且没有多余约束。
4. 三个刚片之间的连接方式
规律4 三个刚片用三个铰两两相连,且三个铰不在一直线上,则组成几何不变的整体,且没有多余约束。
如图(a)。
两根链杆的约束作用相当于一个瞬铰的约束作用,如图(b)。
瞬变体系(三链杆交于同一点)
规律5(如图(b) )
两个刚片用三根链杆相连,且三链杆不交于同一点,则组成几何不变的整体,且没有多余约束。
四种基本组成规律三种基本装配格式
(1)固定一个结点的装配格式:用不共线的两根链杆将结点固定在基本刚片上,称为简单装配格式。
如图:
(2)固定一个刚片的装配格式:用不共线的铰和一根链杆,或用不共点的三根链杆将一个刚片II固定在基本刚片I上,称为联合装配格式。
如图:
(3)固定两个刚片的装配格式:用不共线的三个铰将两个刚片Ⅱ、Ⅲ固定在基本刚片I上,称为复合装配格式。
如图:
装配过程有两种:
(1)从基础出发进行装配:取基础作为基本刚片,将周围某个部件按基本装配格式固定在基本刚片上,形成一个扩大的基本刚片,直至形成整个体系。
如图:
(2)从内部刚片出发进行装配:在体系内部选取一个或几个刚片作为基本刚片,将周围的部件按基本装配格式进行装配,形成一个或几个扩大的基本刚片。
将扩大的基本刚片与地基装配起来形成整个体系。
如图:
例2-1 试分析图示体系的几何构造。
解(1)分析图(a)中的体系
三角形ADE—刚片I,三角形AFG—刚片Ⅱ,基础—刚片Ⅲ,A、B、C、三个铰不共线,则体系为无多余约束的几何不变体系。
(2)分析图(b)中的体系
折线杆AC—链杆2,折线杆BD—链杆3,T形刚片由链杆1、2、3与基础相连。
如三链杆共点,则体系是瞬变的。
否则,体系为无多余约束的几何不变体系。
例2-2 试分析图示体系的几何构造。
解(1)分析图(a)中的体系
以刚片ⅠⅡⅢ为对象,由于三个瞬铰不共线,因此体系内部为几何不变,且无多余约束。
作为一个整体,体系对地面有三个自由度。
(2)分析图(b)中的体系
同样方法进行分析,由于三个瞬铰共线,因此体系内部也是瞬变的。
例2-3 试用无穷远瞬铰的概念,分析图示各三铰拱的几何不变性。
刚片ⅠⅡ与基础Ⅲ用三个铰OⅠ,Ⅱ、OⅡ,Ⅲ、OⅠ,Ⅲ两两相连,其中OⅠ,Ⅱ为无穷远瞬铰。
如果另外两铰的连线与链杆1、2平行,则三铰共线,体系是瞬变的。
否则,体系为几何不变,且无多余约束。
刚片ⅠⅡ与基础Ⅲ用三个铰两两相连,其中OⅠ,Ⅱ和OⅡ,Ⅲ是两个不同方向的无穷远瞬铰,它们对应∞线上的两个不同的点。
铰OⅠ,Ⅲ对应有限点。
因有限点不在∞线上,则三铰不共线,体系为几何不变,且无多余约束。
刚片ⅠⅡ与基础Ⅲ之间的三个铰都在无穷远瞬点。
由于各∞点都在同一直线上,因此体系是瞬变的。
总结
(1)体系一般是由多个构造单元逐步形成的。
(2)要注意约束的等效替换。
(3)体系的装配方式可以不同。
§2-3 平面杆件体系的计算自由度
S—体系自由度的个数
n—体系多余约束的个数
W—计算自由度
体系是由部件加约束组成:
a—各部件的自由度数的总和
c—全部约束中的非多余约束数
d—全部约束的总数
S=a-c W=a-d S-W=n
S≥0 n≥0
S≥W n≥-W
W 是自由度数S 的下限,(–W)是多余约束数n的下限
(a)内部没有多余约束的刚片
(b)内部有一个多余约束的刚片
(c)内部有两个多余约束的刚片
(d)内部有三个多余约束的刚片
图(a)两个刚片ⅠⅡ间的结合为单结合。
图(b)三个刚片间的结合相当于两个单结合,n个刚片间的结合相当于(n-1)个单结合。
单链杆:连接两点的链杆相当于一个约束
复链杆:连接n个点的链杆相当于2n-3个单链杆
自由度算法一(体系由刚片加约束组成)
m—体系中刚片的个数
g—单刚结个数
h—单铰结个数
b—单链杆根数
刚片自由度个数总和:3m
体系约束总数:3g+2h+b
体系计算自由度:
W=3m-(3g+2h+b)
自由度算法二(体系由结点加链杆组成)
j—体系中结点的个数
b—单链杆根数
结点自由度个数总和:2j
体系约束总数: b
体系计算自由度:W=2j-b
若W>0,则S >0,体系是几何可变的
若W=0,则S=n,如无多余约束则为几何不变,如有多余约束则
为几何可变
若W<0,则n>0,体系有多余约束
例2-4 试计算图示体系的W。
方法一:
m=7,h=9,b=3,g=0
W=3m-2h-b=3×7-2×9-3=0
方法二:
j=7,b=14
W=2j-b=2×7-14=0
例2-5 试计算图示体系的W。
将图(a)中全部支座去掉,在G处切开,如图(b) m=1,h=0,b=4,g=3
W=3m-(3g+2h+b)=3×1-(3×3+2×0+4)=-10
体系几何不变,S=0 n=S-W=0-(-10)=10 具有10个多余约束的几何不变体系
例2-6 试计算图示体系的W。
两个体系j=6,b=9,W=2j-b=2×6-9=3 图(a)是一个内部几何不变且无多余约束的体系
S-3=0 n=0
图(b)是一个内部瞬变且有多余约束的体系
S-3= n>0
§2-6 小结
1 几何构造分析的两个主要问题
对杆件体系进行几何构造分析
判断体系是否可变,确定S
判断体系中有无多余约束,确定n
对杆件结构进行几何构造分析
结构应是几何不变体系,S=0
结构分为静定(n=0)和超静定(n>0)。
