中考复习专题之构造辅助圆
部编数学九年级上册专题24定点定长构造辅助圆(解析版)含答案
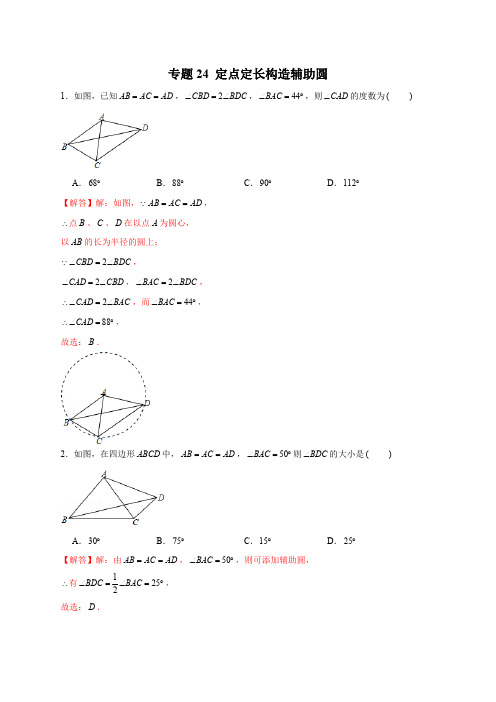
专题24 定点定长构造辅助圆1.如图,已知AB AC AD==,2CBD BDCÐ=Ð,44BACÐ=°,则CADÐ的度数为( )A.68°B.88°C.90°D.112°【解答】解:如图,AB AC AD==Q,\点B、C、D在以点A为圆心,以AB的长为半径的圆上;2CBD BDCÐ=ÐQ,2CAD CBDÐ=Ð,2BAC BDCÐ=Ð,2CAD BAC\Ð=Ð,而44BACÐ=°,88CAD\Ð=°,故选:B.2.如图,在四边形ABCD中,AB AC AD==,50BACÐ=°则BDCÐ的大小是( )A.30°B.75°C.15°D.25°【解答】解:由AB AC AD==,50BACÐ=°,则可添加辅助圆,\有1252BDC BACÐ=Ð=°,故选:D.3.如图,在矩形ABCD 中,已知3AB =,4BC =,点P 是BC 边上一动点(点P 不与B ,C 重合),连接AP ,作点B 关于直线AP 的对称点M ,则线段MC 的最小值为( )A .2B .52C .3D 【解答】解:连接AM ,Q 点B 和M 关于AP 对称,3AB AM \==,M \在以A 圆心,3为半径的圆上,\当A ,M ,C 三点共线时,CM 最短,5AC ==Q ,3AM AB ==,532CM \=-=,故选:A .4.如图,正方形ABCD 中,E 为AB 中点,FE AB ^,2AF AE =,FC 交BD 于O ,则DOC Ð的度数为( )A .60°B .67.5°C .75°D .54°【解答】解:如图,连接DF 、BF .FE AB ^Q ,AE EB =,FA FB \=,2AF AE =Q ,AF AB FB \==,AFB \D 是等边三角形,AF AD AB ==Q ,\点A 是DBF D 的外接圆的圆心,1302FDB FAB \Ð=Ð=°,Q 四边形ABCD 是正方形,AD BC \=,90DAB ABC Ð=Ð=°,45ADB DBC Ð=Ð=°,FAD FBC \Ð=Ð,FAD FBC \D @D ,15ADF FCB \Ð=Ð=°,60DOC OBC OCB \Ð=Ð+Ð=°.解法二:连接BF .易知15FCB Ð=°,451560DOC OBC FCB Ð=Ð+Ð=°+°=°故选:A .5.如图,已知等边ABC D 的边长为8,以AB 为直径的圆交BC 于点F .以C 为圆心,CF 长为半径作图,D 是C e 上一动点,E 为BD 的中点,当AE 最大时,BD 的长为( )A .B .C .2D .12【解答】解:点D 在C e 上运动时,点E 在以F 为圆心的圆上运动,要使AE 最大,则AE 过F ,连接CD ,ABC D Q 是等边三角形,AB 是直径,EF BC \^,F \是BC 的中点,E Q 为BD 的中点,EF \为BCD D 的中位线,//CD EF \,CD BC \^,8BC =,4CD =,故BD ===,故选:B .二.填空题(共6小题)6.如图,点A ,B 的坐标分别为(4,0)A ,(0,4)B ,C 为坐标平面内一点,2BC =,点M 为线段AC的中点,连接OM ,OM 的最大值为 1+ .【解答】解:C Q 为坐标平面内一点,2BC =,\点C 的运动轨迹是在半径为2的B e 上,如图,取4OD OA ==,连接OD ,Q 点M 为线段AC 的中点,OM \是ACD D 的中位线,12OM CD \=,OM \最大值时,CD 取最大值,此时D 、B 、C 三点共线,此时在Rt OBD D 中,BD ==,2CD \=+,OM \的最大值是1+.故答案为:1+.7.如图,四边形ABCD 中,AB AC AD ==,且3CAD BAC Ð=Ð,若42DBC Ð=°,则CAD Ð= 84° ,BDC Ð= .【解答】解:AB AC AD ==Q ,\点B ,C ,D 在以A 为圆心的圆上,42DBC Ð=°Q ,284CAD DBC \Ð=Ð=°,3CAD BAC Ð=ÐQ ,1283BAC CAD \Ð=Ð=°,12BDC BAC Ð=ÐQ ,128142BDC \Ð=´°=°.故答案为:84°,14°.8.如图所示,AB AC AD ==,18DBC Ð=°,则CAD Ð= 36° .【解答】解:AB AC AD ==Q ,B \、C 、D 三点在以点A 为圆心,以AB 为半径的圆上.18DBC Ð=°Q ,236CAD DBC \Ð=Ð=°.故答案为:36°.9.如图,四边形ABCD 中,AE 、AF 分别是BC ,CD 的中垂线,80EAF Ð=°,30CBD Ð=°,则ABC Ð= 40° ,ADC Ð= .【解答】解:连接AC,AEQ、AF分别是BC、CD的中垂线,\==,AB AC ADB\、C、D在以A为圆心,AB为半径的圆上,Q,Ð=°CBD30\Ð=Ð=°,DAC DBC260=,Q,CF DFAF CD^DAF\Ð=°,30\Ð=°,ADC60又803050Q,EACÐ=°-°=°\Ð=Ð=°-°=°.905040ABC ACE故答案为:40°,60°.10.如图,AB AC ADÐ是BDCÐ的k倍,那么DBCÐ的 k 倍.Ð是CAB==,如果DAC【解答】解:AB AC AD==Q,\点B、C、D在以A为圆心的圆上,12BDC CAB \Ð=Ð,12DBC DAC Ð=Ð,DAC k CAB Ð=ÐQ ,222k k DBC CAB BDC k BDC \Ð=Ð=´Ð=Ð,故答案为:k11.如图,矩形ABCD 中,4AB =,8BC =,P 是直线AB 上的一个动点,2AE =,APE D 沿PE翻折形成FPE D ,连接PF 、EF ,则FC 的最小值是 2 ,点F 到线段BC 的最短距离是 .【解答】解:连接CE ,作EG BC ^于G ,2AE EF ==Q ,\点F 在以E 为圆心,AE 为半径的圆上运动,在Rt CDE D 中,由勾股定理得,CE ===,FC \的最小值为22CE -=,90DAB ABC BGE Ð=Ð=Ð=°Q ,\四边形ABGE 是矩形,4EG AB \==,\点F 到线段BC 的最短距离是2,故答案为:2-,2.三.解答题(共9小题)12.如图,在ABC D 中,AB AC =,过点B 作BD BC ^,BD BC =,连接AD 交BC 于点F .E 是CD 的中点,连接AE 交BC 于G .(1)若AB BD =,求ADC Ð的度数;(2)若4BC BF =,且4AB =,求四边形ABDC 的面积.【解答】解:(1)如图1中,AB AC =Q ,BD BC =,AB BD =,AB BC AC \==,ABC \D 是等边三角形,60ABC \Ð=°,BA BC BD ==Q ,A \、C 、D 三点在B e 上,1302ADC ABC \Ð=Ð=°.(2)如图2中,连接BE .90DBC Ð=°Q ,DE EC =,BE EC DE \==,AB AC =Q ,AE \垂直平分BC ,BG CG \=,设BG CG a ==,则2BC BD a ==,14BF BC =Q ,BF FG \=,//BD AG Q ,BFD GFA \D D ∽,\1BF BD FG AG==,2BD AG a \==,在Rt ABG D 中,222AB AG BG =+Q ,22164a a \=+,2165a \=,21111642222422225ABCD S BC AG BC BD a a a a a \=××+××=´´+´´==四边形.13.如图,AB AC AD ==,2CBD BDC Ð=Ð,40BAC Ð=°,求CAD Ð的度数.【解答】解:AB AC AD ==Q ,B \,C ,D 在以A 为圆心,AB 为半径的圆上,2CAD CBD \Ð=Ð,2BAC BDC Ð=Ð,2CBD BDC Ð=ÐQ ,40BAC Ð=°,280CAD BAC \Ð=Ð=°.14.圆的定义:在同一平面内,到定点的距离等于定长的所有点所组成的图形.(1)已知:如图1,OA OB OC ==,请利用圆规画出过A 、B .C 三点的圆.若70AOB Ð=°,则ACB Ð= 35° .如图,Rt ABC D 中,90ABC Ð=°,30BCA Ð=°,2AB =.(2)已知,如图2.点P 为AC 边的中点,将AC 沿BA 方向平移2个单位长度,点A 、P 、C 的对应点分别为点D 、E 、F ,求四边形BDFC 的面积和BEA Ð的大小.(3)如图3,将AC 边沿BC 方向平移a 个单位至DF ,是否存在这样的a ,使得直线DF 上有一点Q ,满足45BQA Ð=°且此时四边形BADF 的面积最大?若存在,求出四边形BADF 面积的最大值及平移距离a ,若不存在,说明理由.【解答】(1)以O 为圆心,OA 为半径作辅助圆,如图,,70AOB Ð=°Q ,35ACB \Ð=°,故答案为35°.(2)连接PB ,PE ,如图,,Rt ABC D 中,90ABC Ð=°,30BCA Ð=°,2AB =.4AC \=,60BAC Ð=°,BC =.P Q 为Rt ABC D 斜边AC 中点,122BP AC \==,线段AC 平移到DF 之后,2AB AD PE ===,2BP AE ==,\四边形ABPE 为菱形,60BAC Ð=°Q ,30BEA \Ð=°,//CF BD Q ,且90ABC Ð=°,\四边形BDFC 为直角梯形,11()622S BD CF BC \=+´=´´=,(3)如图所示,当AC 边沿BC 方向平移2个单位至DF 时,满足45BQA Ð=°且此时四边形BADF 的面积最大,此时直角梯形ABFD 的最大面积为,11()22)2422S BF AQ AB =´+´=´+´=+15.在Rt ABC D 中,90ABC Ð=°,BE AC ^,EG 、EF 分别平分AEB Ð和CEB Ð,求证:BG BF =.【解答】解:连接GF ,取GF 中点O ,连接BO ,EO ,BE AC ^Q ,90AEB BEC \Ð=Ð=°,EG Q 、EF 分别平分AEB Ð和CEB Ð,45GEB FEB \Ð=Ð=°,90GEF \Ð=°,在Rt GBFD中,BO,EO分别是斜边的中线,D和Rt GEF==,BO GO FO\==,EO GO FO\===,BO EO GO FO\、B、F、E四点在以O为圆心,BO为半径的圆上,G\Ð=Ð=°,45BGF BEF\D是等腰直角三角形,GBF\=.GB FB16.如图,在ABCÐ=°,连接BDCBD=,DE垂直平分AC,且30D中,AB AC=;(1)求证:AB ADD是等腰三角形,求ABC(2)设AD交BC于点P,若ABPÐ的度数.【解答】解:(1)证明:作BDCD的外接圆,延长DE交圆于点F,连接CF、AF,如图所示,则有30Ð=Ð=°.DBC DFCDEQ垂直平分AC,\=,AF FC\Ð=Ð=°,30AFE CFE\Ð=°,60AFCAFC\D是等边三角形,\=.AF AC=Q,AB AC\==,AF AC AB\点A为所作圆的圆心,AB AD\=.=,(2)①若PA PB则ABC BAPÐ=Ð.Q,AB AC=\Ð=Ð.ABC ACBQ,260Ð=Ð=°DAC DBC\Ð=Ð+Ð=°+Ð,APB PAC ACB ACB60\Ð=°+Ð.APB ABC60Q,Ð+Ð+Ð=°ABC BAP APB180\Ð+°=°,ABC360180解得:40Ð=°ABC=,②若BA BP同理可得:20ABCÐ=°.=,③AB AP此时P与C重合,则D与E重合,不符合题意,故舍去.综上所述:当ABPD是等腰三角形时,ABCÐ的度数为40°或20°.17.【阅读】辅助线是几何解题中沟通条件与结论的桥梁.在众多类型的辅助线中,辅助圆作为一条曲线型辅助线,显得独特而隐蔽.性质:如图①,若90Ð=Ð=°,则点D在经过A,B,C三点的圆上.ACB ADB【问题解决】运用上述材料中的信息解决以下问题:(1)如图②,已知DA DB DC==.求证:2ADB ACBÐ=Ð.(2)如图③,点A,B位于直线l两侧.用尺规在直线l上作出点C,使得90Ð=°.(要求:ACB要有画图痕迹,不用写画法)(3)如图④,在四边形ABCD中,90^,点F在CA的延长线上,连接DF,CADÐ=°,CB DBÐ=Ð.ADF ABD求证:DF是ACDD外接圆的切线.【解答】解:(1)如图②,由DA DB DC==,可知点A,B,C在以D为圆心,DA为半径的圆上.所以,2Ð=Ð.ADB ACB(2)如图③,点1C ,2C 就是所要求作的点.(3)如图④,取CD 的中点O 为圆心,CD 为直径作圆O ,则O e 是ACD D 的外接圆;由90DAC DBC Ð=Ð=°,可得点B 在ACD D 的外接圆上.ACD ABD \Ð=Ð.ADF ABD Ð=ÐQ ,ACD ADF \Ð=Ð.90ACD ADC Ð+Ð=°Q ,90ADF ADC \Ð+Ð=°.90CDF \Ð=°.即CD DF ^.DF \是ACD D 外接圆的切线.18.在Rt ABC D 中,90A Ð=°,4AC AB ==,D ,E 分别是边AB ,AC 的中点,若等腰Rt ADE D 绕点A 逆时针旋转,得到等腰Rt △11AD E ,设旋转角为(0180)a a <°…,记直线1BD 与1CE 的交点为P .(1)如图1,当90a =°时,线段1BD 的长等于 线段1CE 的长等于 ;(直接填写结果)(2)如图2,当135a =°时,求证:11BD CE =,且11BD CE ^;(3)求点P 到AB 所在直线的距离的最大值.(直接写出结果)【解答】(1)解:90A Ð=°Q ,4AC AB ==,D ,E 分别是边AB ,AC 的中点,2AE AD \==,Q 等腰Rt ADE D 绕点A 逆时针旋转,得到等腰Rt △11AD E ,设旋转角为(0180)a a <°…,\当90a =°时,12AE =,190E AE Ð=°,1BD \==1E C ==故答案为:,;(2)证明:当135a =°时,如图2,Rt Q △11AD E 是由Rt ADE D 绕点A 逆时针旋转135°得到,11AD AE \=,11135D AB E AC Ð=Ð=°,在△1D AB 和△1E AC 中Q 1111AD AE D AB E AC AB AC =ìïÐ=Ðíï=î,\△1D AB @△1()E AC SAS ,11BD CE \=,且11D BA E CA Ð=Ð,记直线1BD 与AC 交于点F ,BFA CFP \Ð=Ð,90CPF FAB \Ð=Ð=°,11BD CE \^;(3)解:如图3,作PG AB^,交AB 所在直线于点G ,1D Q ,1E 在以A 为圆心,AD 为半径的圆上,当1BD 所在直线与A e 相切时,直线1BD 与1CE 的交点P 到直线AB 的距离最大,此时四边形11AD PE 是正方形,12PD =,则1BD ==故30ABP Ð=°,则2PB =+,故点P 到AB 所在直线的距离的最大值为:1PG =.19.如图,在Rt ABC D 中,90C Ð=°,6AC =,8BC =,点F 在边AC 上,并且2CF =,点E 为BC 边上的动点,将FCE D 沿直线EF 翻折,点C 落在点P 处,求点P 到边AB 距离的最小值.【解答】解:如图,延长FP 交AB 于M ,2FP CF ==Q ,\点P 在以F 为圆心,CF 为半径的圆上运动,当FP AB ^时,点P 到AB 的距离最小,A A Ð=ÐQ ,90AMF C Ð=Ð=°,AMF ACB \D D ∽,\AF FM AB BC=,2CF =Q ,6AC =,8BC =,4AF \=,10AB ==,\4108FM =,3.2FM \=,2PF CF ==Q ,1.2PM \=,\点P 到边AB 距离的最小值为1.2.20.如图,ABC D 中,4AC BC ==,90ACB Ð=°,过点C 任作一条直线CD ,将线段BC 沿直线CD 翻折得线段CE ,直线AE 交直线CD 于点F .(1)小智同学通过思考推得当点E 在AB 上方时,AEB Ð的角度是不变的,请按小智的思路帮助小智完成以下推理过程:AC BC EC ==Q ,A \、B 、E 三点在以C 为圆心以AC 为半径的圆上.AEB \Ð=ACB = °.(2)若2BE =,求CF 的长.(3)线段AE 最大值为 ;若取BC 的中点M ,则线段MF 的最小值为 .【解答】解:(1)AC BC EC ==Q ,A \、B 、E 三点在以C 为圆心以AC 为半径的圆上,1452AEB ACB \Ð=Ð=°,故答案为:12,45;(2)由折叠可知,CD 垂直平分BE ,BE CD \^,设CD 、BE 交于点G ,则112GE BG BE ===,90FGE \Ð=°,45AEB Ð=°Q ,1FG GE \==,在Rt CEG D 中,由勾股定理得,CG ==1CF CG FG \=-=-;(3)A Q ,B ,E ,三点在以C 为圆心,以AC 为半径的圆上,\当AE 经过圆心C 时,线段AE 的最大值为28AC =,在Rt ABC D 中,4AC BC ==,90ACB Ð=°,AB \==122BM CM BC ===,45ABC BAC Ð=Ð=°,连接BF ,取AB 的中点O ,连接OF ,如图,CD Q 垂直平分BE ,45AEB Ð=°,BF EF \=,45EBF AEB \Ð=Ð=°,90EFB \Ð=°,90AFB \Ð=°,12OF AB OA OB \====,\点F 在以点O 为圆心,AB 为直径的圆上,90ACB Ð=°Q ,\点C 在O e 上,\当OF 经过点M 时,MF 最短,此时OF BC ^,tan 212OM BM ABC \=×Ð=´=,2MF OF OM \=-=-,即线段MF 的最小值为2,故答案为:8;2.。
2025年数学中考总复习第一部分整体知识梳理第六章圆微专题构造辅助圆

D,E,O三点
三点共线时,线段
DE
有最值,其
的一动点,
共线时,线段
最大值为d+r
=
2r,最小值为d求DE的最
DE有最值,
r=0(点D,E重合)
值(其中
其最大值为
OD=d,半 若点D 在☉O内(d<r),当D,E,O
d+r,最小值
径为r)
三点共线时,线段 DE 有最值,
为|d-r|
其最大值为d+r,最小值为r一d
为8-4=4.
图1
-5-
微专题
构造辅助圆
(2)如图2,过点C作CH⊥AB于点H,延长HC交☉C于
点D,此时△ABD的面积最大,易得AB=10,CH=4.8,
∴DH=8.8,∴S△ABD=1/2×10×8.8=44.(3)如图3,由
题意可得当BD为☉C的切线且D为切点时,∠CBD的度
数最大,此时sin ∠CBD=CD/BC=1/2,∴∠CBD的度数
2
即A'C最大,当点C在A'B的延长线上时,A'C最大,此时
A'C=A'B+BC=2 2+1,∴OM= 2 +
2+
1
,∴OM的最大值是
2
1
.
2
答案图1
-9-
微专题
构造辅助圆
解法2:连接AB,取AB的中点D,连接DM.由A(2,0),B(0,
1
1
2),得D(1,1),∵D,M分别为AB,AC的中点,∴DM= BC= ,
定值),则点A,B,C在以点O为圆心,d
为半径的圆上
-2-
微专题
“构造辅助圆”在初中数学解题中的灵活运用

2023年9月下半月㊀解题研究㊀㊀㊀㊀构造辅助圆 在初中数学解题中的灵活运用◉吉林师范大学数学与计算机学院㊀王㊀雪㊀㊀摘要:在数学解题过程中,常规的解题思路并不能应对一些比较复杂的几何问题,这时候就需要转换思路,有时利用 圆 ,就可以有效解答一类问题.借助 辅助圆 将几何问题中分散的条件集中,有助于发现题目中的隐含条件,从而起到化繁为简的作用.本文中通过实例分析,帮助学生明确辅助圆的应用环境,以及针对不同题型如何构造辅助圆.关键词:辅助圆;初中数学;几何问题㊀㊀构造辅助圆 是指在原有的几何图形上,构建一个辅助圆,利用圆的特性来完成题目的解答.通过辅助圆的构造,能够将几何题目中较为繁杂的已知条件进行集中处理,同时能够发现几何图形中的隐藏条件,利用对这部分条件的分析,快速解决问题.本文中结合实例,帮助学生明确辅助圆的应用环境,以及针对不同题型如何构造辅助圆.1构造辅助圆 解决数学问题的应用现状目前初中生在解题的过程中,较少应用辅助圆,且应用效果不理想.在几何题的解答过程中,辅助线的应用是比较常见的,但是有部分题目通过辅助线来解答依旧存在难度,甚至需要多条辅助线才能完成,如果学生用这种方法应对选择题和填空题,就会浪费大量的时间.而应用辅助圆则可以为相关问题披上圆的外衣,这样就可以依据圆的性质进行解题,从根本上起到化繁为简的作用[1].2构造辅助圆 解决数学问题的实际案例2.1辅助圆在求线段长度的几何问题中的应用在解决求线段长度的几何问题中,通常是利用相同端点的线段构造辅助圆,以端点作为圆心,选取相等的线段作为半径或直径,完成辅助圆的构建后再利用圆的基本性质求解线段长度[2].例1㊀在四边形D C B E 中,点A 在B E 上,A E ʊC D ,A B =A C =A D =A E =5c m ,且B C =19c m ,求对角线B D 的长度.解析:由A E ʊC D ,得øB D C =øD B E .图1由A B =A C =A D =A E ,将点D ,C ,B ,E 视为圆上的点构建辅助圆,如图1.于是弦D E 与弦B C 的长度相等.又由B C =19c m ,得B C =D E =19c m .因为E B 为辅助圆的直径,所以øE D B =90ʎ.所以在R tәE D B 中,根据勾股定理可知,B D =E B 2-E D 2.又A B =5c m ,E B 为圆A 的直径,则E B =10c m .所以B D =102-(19)2=9(c m ).2.2辅助圆在求度数的几何问题中的应用在解决求度数的几何问题中,通常可以将公共点作为顶点,作三角形的外接圆.在构建辅助圆的过程中要将三角形与辅助圆建立明确的关系.图2例2㊀如图2所示,әA B C为等腰三角形,且A B =A C ,直线A P 为әA B C 外侧直线,点B 与点D 关于A P 轴对称.求证:ø1=ø2.证明:ȵ点B ,D 关于直线A P 对称,ʑ直线A P 为线段B D 的垂直平分线.ʑәA D B 为等腰三角形.图3ʑA D =A B =A C .故可以A C 为半径,点A 为圆心,构建如图3所示的辅助圆.ȵP 为B D 中点,且A P 为过点E 的直线,ʑәD E B 为等腰三角形.ʑD E =B E .ʑøE D B =øE B D .ʑø2=2øE D B .又ø1=2øC D B (同弧所对的圆心角是圆周角的2倍),ʑø1=ø2.2.3辅助圆在求图形面积问题中的应用在数学中考题中,涉及面积的题型也很多,当题目条件较多且分散的几何图形很难运用面积公式时,可以尝试构建辅助圆,利用圆的基本性质以及圆的面37Copyright ©博看网. All Rights Reserved.解题研究2023年9月下半月㊀㊀㊀积公式进行计算[3].例3㊀如图4,әA B C 为等边三角形,且A B =A D ,AH ʅC D 于点H ,且P C ʅBC ,C P 与AH 交于点P ,求证:S әA B C =34A PB D .图4㊀㊀㊀图5解析:依题意可知A B =A C =B C =A D ,构建以点A 为圆心,A B 为半径的圆,得到如图5所示的辅助圆.ȵәA B C 为等边三角形,ʑøB A C =øA C B =øA B C =60ʎ.ʑøB D C =12øB A C =30ʎ.又øB C P =90ʎ,øB C A =60ʎ,ʑøP C A =øC D B =30ʎ.ȵøC B D =12øC A D =øP A C ,ʑәB C D ʐәA P C .ʑB C ʒA P =B D ʒA C .又B C =A C ,ʑB C 2=A P ˑB D .ʑS әA B C =34A PB D .2.4辅助圆在求线段比或面积比问题中的应用图形中的某两条线段成比例或图形面积成比例这类题型是中考的难点和重点.利用辅助圆则可以结合圆的性质,通过圆中的线与角的关系进行求解.构建辅助圆时,要将有关线段置于辅助圆的关键位置,例如,可作为直径㊁半径或弧所对的弦.这样容易发现线段之间的关系,从而更加简便地进行解答[4].例4㊀在R t әA B C 中,A C =B C ,øA C B =90ʎ,P是C B 延长线上的一点,B P ʒB C =k ,已知0ɤk ɤ1,过点B 作A B 的垂线,过点P 作A P 的垂线,使两条垂线相交于点Q ,且A P =P Q ,连接A Q ,求әA B C 与әA P Q 的面积比.分析:根据已知条件分析,әA P Q 的面积较难求解,所以可以根据әA P Q 来构建辅助圆.解析:以A Q 为直径,A Q 的中点O 为圆心,构建如图6所示的辅助圆.ȵA P =P Q ,且øA P Q =90ʎ,ʑәA P Q 为等腰直角三角形.设B C =A C =m .图6ȵB P ʒB C =k ,ʑB P =k m ,P C =(k +1)m .ʑP A =m 2+[(k +1)m ]2=m k 2+2k +2.ʑS әA B C ʒS әA P Q=12A C 212P A 2=12m 212(k 2+2k +2)m 2=1ʒ(k 2+2k +2).2.5辅助圆在求线段极值问题中的应用辅助圆在求线段极值问题中有着广泛的应用,特别是在数学竞赛中经常遇到.例5㊀在边长为4的正方形A B C D 中,P 为对角线B D 上的一个动点,且与点B ,D 不重合,连接A P ,过B 作A P 的垂线,垂足为H ,连接DH ,求线段DH 的最小值.图7分析:由于无论点P 如何运动,A B 的长度都不会改变,因此可以A B 为直径,A B 的中点E 为圆心构建辅助圆,通过圆确定点H 的运动轨迹.解析:取A B 中点E ,连接D E ,构建如图7所示的几何图形,可得D E =(12A B )2+A D 2=42+22=25.当点H 与点M 重合时,线段DH 的长度最短,此时DH =DM =D E -M E =25-2.综上所述, 构造辅助圆 在初中数学解题中的广泛应用,不仅包含大量的几何问题,而且部分代数问题中也可使用.构建辅助圆时,要结合题目的具体情况,根据四点共圆的条件确定辅助圆.通过辅助圆在不同类型几何问题中的应用,明确构建辅助圆在初中数学解题中的可行性与实用性,通过辅助圆的灵活应用,提升学生的实际解题能力.参考文献:[1]刘怀权. 构造辅助圆 在初中数学解题中的应用[J ].数理天地(初中版),2022(12):21G22.[2]蒋天林.从江苏高考试题谈辅助圆在解题中的运用[J ].中学生数理化(高考使用),2020(5):11G12.[3]黄磊. 圆 来如此简单 辅助圆 构造的解题探究[J ].数理化解题研究,2021(14):10G11.[4]徐勤.辅助圆在中考数学试题中的应用[J ].科学大众:科学中考,2022(4):13G15.Z47Copyright ©博看网. All Rights Reserved.。
中考复习讲义三种构造辅助圆解题的模型

中考热点:三种构造辅助圆解题的模型一、问题导读“圆”是一个完美的图形,在初中数学中具有丰富内容,其中大部分是及角度相关性质,如在圆周角中能轻易找到,等角和直角并及圆心角联系也比较紧密,通过在图形中构造辅助圆往往能获得意想不到的效果,如果题目中出现了以下条件:三点及三点以上到同一点距离相等,作辅助圆;同一侧有相等的角,或者需要构造出相等的角时,作辅助圆;若一个四边形的一组对角互补,则它的四个顶点共圆.在这些情况下,借助圆去解决一些问题都是非常好的一个选择,下面举例说明这三种构造辅助圆解题的模型应用。
二、典例精析类型1 根据共端点等线段模型,根据圆的定义构造圆1.如图,已知==,且∠=k∠,则∠是∠的()A.2倍 B.k倍 C.2k D.1【分析】由==,得到A,B,C在以O为圆心的同一个圆上,则∠=2∠,∠=2∠,而∠=k∠,即可得到∠=k∠.【解答】∵==,∴A,B,C在以O为圆心的同一个圆上,如图,∴∠=2∠,∠=2∠,而∠=k∠,即2∠=k2∠,∴∠=k∠.故选:B.2.如图,在△中,∠C=90°,=6,=8,点F在边上,并且=2,点E为边上的动点,将△沿直线翻折,点C落在点P处,则点P到边距离的最小值是()A.1.5 B.1.2 C.2.4 D.以上都不对【分析】先依据勾股定理求得的长,然后依据翻折的性质可知=,故此点P在以F为圆心,以2为半径的圆上,依据垂线段最短可知当⊥时,点P到的距离最短,然后依据题意画出图形,最后,利用相似三角形的性质求解即可.【解答】如图所示:当∥.在△中,∵∠C=90°,=6,=8,∴由勾股定理可求得=10,由翻折的性质可知:==2,∠=∠C=90°.∵∥,∴∠=90°.由垂线段最短可知此时有最小值.又∵为定值,∴有最小值.又∵∠A=∠A,∠=∠,∴△∽△.∴,即4/108,解得:=3.2.∴=﹣=3.2﹣2=1.2.故选:B.3.如图2所示,在凸四边形中,∠80°,则∠的度数为度【解析】∵==,得到A,C,D在以B为圆心的同一个圆上,∴∠1/2∠, ∠1/2∠,∵∠∠ +∠ =80°,∴∠∠1/2∠1/2∠1/2(∠∠)= 1/2×80°=40°,∴∠=180°﹣(∠∠)=180°﹣40°=140°.故答案为:140.4. 如图,在四边形中,==,若∠=25°,∠=75°,则∠=度,∠=度.【解析】法一:∵==,∴点B,C,D在以A为圆心的圆上,∵∠=25°,∴∠=1/2∠=12.5°,∵∠=75°,∴∠=1/2∠=37.5°.故答案为:12.5,37.5.法二:∵==,∴∠=∠,∠=∠,∠=∠,∵∠=25°,∠=75°,∴∠=(180°﹣25°)÷2=77.5°,∠=∠∠=100°,∠=∠=(180°﹣75°)÷2=52.5°,∴∠=(180°﹣100°)÷2=40°,∴∠=∠﹣∠=52.5°﹣40°=12.5°,∠=∠∠=52.5°+77.5°=130°,∴∠=180°﹣∠﹣∠=180°﹣130°﹣12.5°=37.5°.∴∠=12.5°,∠=37.5°.类型2 直角模型,依据直径所对的圆周角是直角,构造三角形的外接圆解题5. 如图所示,矩形及矩形全等,点在一条直线上,∠的顶点P在线段上移动,使得∠为直角的点P的个数是个.【分析】∵∠的顶点P在线段上移动,且∠为直角,∴点P也在以为直径的⊙O的圆上运动;∴以为直径作⊙O,⊙O及的交点即为所求.【解答】∵点在一条直线上,∠的顶点P在线段上移动,∠为直角,∴点P在以为直径的⊙O的圆上运动,∴点P就是⊙O及的交点,由图示知,及⊙O有2个交点.故答案为:2.【点评】本题主要考查了圆周角定理:直径所对的圆周角是直角.解答该题时,采用了“数形结合”的数学思想.6. 已知:如图,直尺的宽度为2,A、B两点在直尺的一条边上,=6,C、D两点在直尺的另一条边上.若∠=∠=90°,则C、D两点之间的距离为.【分析】由∠=∠=90°,根据90°的圆周角所对的弦是直径,可得A,B,C,D在以为直径的圆上,C,D即是此圆及直尺的交点,设E为中点,可得是半径为3,然后作⊥交于F,根据垂径定理可得:=2,然后由勾股定理求得的长,继而求得答案.【解答】设E为中点,∵∠=∠=90°,∴A,B,C,D在以为直径的圆上,连接,,则==1/2=3,作⊥交于F,∴=2,∵∥,∴=2,在△和△中,=√5,∴=2√5.故答案为:2√5.【点评】此题考查了圆周角定理,垂径定理以及勾股定理等知识.此题拿度适中,解题的关键是由∠=∠=90°,根据90°的圆周角所对的弦是直径,得到A,B,C,D在以为直径的圆上.7. 已知△中,=5,=12,∠=90°,P是边上的动点(及点A、B不重合),Q是边上的动点(及点B、C不重合)(1)如图,当∥,且Q为的中点时,求线段的长;(2)当及不平行时,△可能为直角三角形吗?若有可能,请求出线段的长的取值范围;若不可能,请说明理由.【分析】(1)根据平行线等分线段定理得到点P是斜边的中点,再直角三角形斜边上的中线等于斜边的一半,要求线段的长,只需根据勾股定理求得的长.(2)若及不平行,则要使△成为直角三角形.只需保证∠=90°.根据直径所对的圆周角是直角,则分析以为直径的圆和斜边的公共点的情况:一是半圆和相切;二是半圆和相交.首先求得相切时的值,即可进一步求得相交时的范围.【解答】(1)在△中∠=90°,=5,=12,∴=13;∵Q是的中点,∴=;又∵∥,∴=,即P是的中点,∴△中,=13/2.(2)当及不平行时,只有∠为直角,△才可能是直角三角形.以为直径作半圆D,①当半圆D及相切时,设切点为M,连接,则⊥,且==5,∴=﹣=13﹣5=8;设=x,则=x,=12﹣x;在△中,=,即(12﹣x)=8,解之得x=10/3,∴=2x=20/3;即当=20/3且点P运动到切点M位置时,△为直角三角形.②当20/3<<12时,半圆D及直线有两个交点,当点P运动到这两个交点的位置时,△为直角三角形③当0<<20/3时,半圆D及直线相离,即点P在边上运动时,均在半圆D外,∠<90°,此时△不可能为直角三角形.∴当20/3≤<12时,△可能为直角三角形.8.已知平面直角坐标系中两定点A(-1,0)(4,0),抛物线2过点,顶点为C,点P()为抛物线上一点,其中n<0.(1)求抛物线的解析式和顶点C的坐标;(2)当∠为钝角时,求m的取值范围.【分析】(1)利用待定系数法求出解析式,再利用x=0得出y的值即可得出C点坐标.(2)因为为直径,所以当抛物线上的点P在⊙C的内部时,满足∠为钝角,进而得出m 的取值范围;]解:(1) (1)∵抛物线y=﹣2(a≠0)过点A,B,∴2=0, 1642=0,解得:1/2, 3/2,∴抛物线的解析式为:y=1/2x﹣3/2x﹣2,当x=0时,y=﹣2,∴C(0,﹣2);(2)∵A(-1,0)(4,0),抛物线及y轴的交点D的坐标为(02),如图,抛物线的对称轴及x轴的交点为M(3/2,0),∵1+2=5(4+1) =254+2=16+4=20,则,由勾股定理的逆定理,知△是直角三角形,∠90°,以M为圆心,以为半径作圆,则☉M经过点D,则☉M内抛物线上的所有的点都可以是P点,且使∠为钝角,根据抛物线及圆的对称性,☉M及抛物线的另一个交点坐标为(32),则满足条件的m的取值范围为1<m<0或3<m<4.类型3 四点共圆模型(1)若一个四边形的一组对角互补,则它的四个顶点共圆;(2)动点对定线段所张的角为定值.9. 如图2,在平面直角坐标系中,点A的坐标为(0,m),点B的坐标为(0,n),其中m>n>0.点P为x轴正半轴上的一个动点,当∠达到最大时,直接写出此时点P的坐标.【解析】当以为弦的圆及x轴正半轴相切时,对应的∠最大,根据垂径定理和勾股定理即可求解.当以为弦的圆及x轴正半轴相切时,作⊥y轴,连接、.∵A的坐标为(0,m),点B的坐标为(0,n),10. 在平面直角坐标系中,已知点A(4,0)、B(﹣6,0),点C是y轴上的一个动点,当∠=45°时,点C的坐标为.【分析】如解答图所示,构造含有90°圆心角的⊙P,则⊙P及y轴的交点即为所求的点C.注意点C有两个.【解答】设线段的中点为E,∵点A(4,0)、B(﹣6,0),∴=10,E(﹣1,0).(1)如答图1所示,过点E在第二象限作⊥,且=1/2=5,则易知△为等腰直角三角形,∠=90°,==5√2;以点P为圆心,(或)长为半径作⊙P,及y轴的正半轴交于点C,∵∠为⊙P的圆周角,∴∠=1/2∠=45°,即则点C即为所求.过点P作⊥y轴于点F,则==5,=1,在△中,=1,=5√2,由勾股定理得:=7,∴==5+7=12,∴点C坐标为(0,12);(2)如答图2所示,在第3象限可以参照(1)作同样操作,同理求得y轴负半轴上的点C坐标为(0,﹣12).综上所述,点C坐标为(0,12)或(0,﹣12).故答案为:(0,12)或(0,﹣12).【点评】本题难度较大.由45°的圆周角联想到90°的圆心角是解题的突破口,也是本题的难点所在.11. 已知△是等腰直角三角形,==2,D是边上一中点,将△绕C逆时针向旋α得到△,其点E是点A的对应点,点F是点D的对应点.及交于点M;当α从90°变化到180°时,点M运动的路径长为.【分析】先证明A、D、M、C四点共圆,得到∠=∠=45°,即可推出点M在以为直径的⊙O上,运动路径是弧,利用弧长公式即可解决问题.【解答】∵=,=,∴∠=∠,∠=∠∵∠=∠,∴∠=∠,∵2∠∠=180°,2∠∠=180°,∴∠=∠,∴A、D、M、C四点共圆,∴∠=∠=45°,∴∠=180°﹣∠=135°.(补充:不用四点共圆的方法:由△∽△,推出△∽△,推出∠=∠,即可证明∠=∠∠=∠∠=∠=45°)∵O是中点,连接、.∵=,=,∴⊥,∴∠=90°,∵A、D、M、C四点共圆,∴当α从90°变化到180°时,点M在以为直径的⊙O上,运动路径是弧,【点评】本题考查几何变换综合题、等腰直角三角形的性质、平行线的判定和性质、弧长公式、四点共圆等知识,解题的关键是发现A、D、M、C四点共圆,最后一个问题的关键,正确探究出点M的运动路径,记住弧长公式,属于中考压轴题.三、总结提升圆是我们初中阶段学习的唯一一个曲线图形,除了它本身的基本性质和计算常被考察到以外,还可以用作辅助线。
2023年中考数学专项复习课件:辅助圆在解题中的应用

模型分析
(2)当∠C=90°时,点C在⊙O上运动(如图②,不与点A,B重合).其中 AB为⊙O的直径;(3)当∠C>90°时,点C在如图③所示的 上运动( 不与点A,B重合).其中 ∠AOB+∠ACBA=B 180°
1 2
模型应用
12. 如图,在矩形 ABCD中,AB=4,BC=6,E是矩形内部的一个动点 ,且AE⊥BE,则线段CE的最小值为2__1_0__2___.
r-d
0
d-r
连接OD并延长交
连接OD交⊙O于
此时点E的位置
点E与点D重合
⊙O于点E
点E
模型应用 1. 如图,在平面直角坐标系中,⊙M的半径为2,圆心M的坐标为(3,4) ,P是⊙M上的任意一点,PA⊥PB,且PA,PB分别与x轴交于点A,B. 若点A,B关于原点O对称,则AB的最小值为_6_______.
对的劣弧BD上运动,连接OA,OP,则AP≤OA+OP,
∴当O,A,P三点共线时,AP取得最大值,最大值即为OA+OP的值.
过点O作OQ⊥AB于点Q,
∵∠DPB=120°,∴∠BAD=60°,
∵AD=BD=6,∴∠OAQ=30°,AQ= 1 AB=3,
2
∴OA=2 3 ,∴OA+OP=4 3,
∴AP的最大值为4 3 .
15 4
过点C作CP的垂线,与PB的延长线交于点Q,则CQ的最大值为______.
第8题图
第9题图
10. 如图,在四边形ABCD中,BD=4,∠BAD=∠BCD=90°,则四边
形ABCD面积的最大值为___8_____.
11. 如图,等腰直角△ABC的斜边AB下方有一动点D,∠ADB=90°,
CE
第1题图
2025年中考数学总复习第一部分考点精讲第六章圆微专题(十三)构造辅助圆

2025版
数学
甘肃专版
如图,在四边形ABCD中,AB=AC=AD,∠BDC=14°,则
∠BAC=
28° .
【方法指导】定点是点A,定长是AB,找出圆心和半径,作图即可.
2025版
数学
甘肃专版
类型二:定弦定角构造辅助圆
解题方法模型构造
遇到动点C和定线段AB所构成的∠ACB为定角时,通常把∠ACB转化为圆
∴△ABE≌△BCF(SAS),∴∠BAE=∠CBF,
∵∠CBF+∠ABF=90°,∴∠BAE+∠ABF=90°,
∴∠APB=90°,∴点P在以AB为直径的圆上,
设AB的中点为G,当C,P,G在同一直线上时,CP有最小值,
∵CG= 2 + 2=2 5,PG=AG=BG=2,∴CP=2 5-2.
【方法指导】定长为BC,∠BAC=∠BDC,四点共圆.
.
2025版
数学
甘肃专版
1.如图,在矩形ABCD中,AB=4,AD=6,点E是AB边的中点,F是线
段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则
B′D的最小值是 2 -2
.
【方法指导】定点是点E,定长是AE,找出圆心和半径,作图即可.
作A′G⊥CD,EH⊥CD,垂足分别为G,H,
∵四边形ABCD是矩形,AB=3,
1
3
EA′=EA= AB= ,∠BAD=∠ADC=90°,
2
2
AD=BC=4,CD=AB=3,
∴四边形AEHD是矩形,EH=AD=4,
2025版
数学
1
3
∵S△CA′D= CD∙A′G= A′G,
2
2
∴当A′G最小时,S△CA′D最小,
中考数学复习专题解读——《辅助圆》问题(共19张PPT)
3.如图,四边形ABCD中,AB=AC=AD,若 ∠CAD=76°,则∠CBD= 度。
4.如图,在△ABC中,∠C为钝角,点E,H分别 是边AB上的点,点K和M分别是边AC和BC上的 点,且AH=AC,EB=BC,AE=AK,BH=BM。
判定3:共底边的两个三角形顶角相等,且 在底边的同侧,则四个顶点共圆。
判定4:对于凸四边形ABCD,若对角互补 或一个外角等于其邻补角的内对角,则A、 B、C、D四点共圆。
判定5:对于凸四边形ABCD其对角线AC、 BD交于点P,若PA·PC=PB·PD,则A、B、C、 D四点共圆。(相交弦定理的逆定理)
例1.已知:四边形ABCD中, ∠ ABC=∠ ADC=90°, E、F分别是AC、BD的中点.求证:EF⊥BD.
例1.已知:四边形ABCD中, ∠ ABC=∠ ADC=90°, E、 F分别是AC、BD的中点.求证:EF⊥BD.
本题考察知识点比较隐蔽,没有添 加辅助线对于学生来讲是一个难点 ,变式性比较强,图形可变,条件 也可以变,施展的平台可以借助于 四点共圆来实现更多的变式。
(1)求证:E、H、M、K四点共圆; (2)若KE=EH,CE=3,求线段KM的长。
F分别是AC、BD的中点. 求证:∠ABD=∠ACD
练习反馈
1. 锐角△ABC的三条高AD、BE、CF交于H, 在A、B、C、D、E、F、H七个点中。能组 成四点共圆的组数是( )
A. 4组 B. 5组 C. 6组 D. 7组
2如图,A,B,C,D是圆上四点,AD,BC 的延长线交于点P,弧AB、弧CD分别为 100°、40°,则∠P的度数为( )
解析:证明:连接BE、DE ∠ ∠ ABC=∠ ADC=90°,
中考数学备考课件:辅助圆问题 (共19张PPT)
BM C
∴△ABM≌△BCN(SAS)
∴ BAM CBN
∵ ABP CBN 90o ∴ ABP BAM 90o ∴ APB 90o ∴点 P 在以 AB 为直径的圆上
运动,设圆心为 O,连接 OC 交⊙O 于 P,此时 PC 最小 ∵ AB 4 ∴ OP OB 2
A
D
O
N
P B MC
解:∵ AB AC AD 2
E
∴点 B,C,D 在以点 A 为圆心, 半径为 2 的圆上延长 BA 交 D ⊙A 于 E,连接 DE
∵AB∥CD ∴ EBD BDC
A
B
C
∵ DE DE , BC BC ∴ EAD 2EBD ,
BAC 2BDC
∴ EAD BAC
E
A
B
∴ ED BC 1
小值为 BC sin B 3 3
∴DE 长的最小值为
3 2
PC
3 2
3
3
9 2
.
类型二 定点 定长模型 方法与技巧 常见图形中共顶点的多条线段相等,可考虑利用到 定点的距离等于定长推导共圆,再利用圆有关性质 解决问题.
3.如图,在四边形 ABCD 中, AB AC AD 2 , BC 1,AB∥CD.求 BD 的长.
由勾股定理,得 OC OB2 BC2 2 5
∴ PC OC OP 2 5 2
∴PC 长的最小值为 2 5 2 .
2.如图,在 Rt△ ABC 中, ACB 90o , AB 5,
cos
B
4 5
,⊙A
与边
BC
交于点
C,过
A
作
DE∥BC,
交⊙A 于点 D,E,点 F 在 DC 上,连接 EF,过 A 作
2024年中考数学二轮复习题型突破课件—构造辅助圆解题
典例9图答案
强化练习
1. 如图,正方形ABCD的边长为2,点E在边BC上,沿AE将正方形进行折
叠,使点B落在正方形ABCD内部的点P处,则CP长的最小值是( C )
A. 2
B. 2-
C. 2-2
D. 2+2
第1题
1
2
3
4
5
6
7
8
9
10
11
12
2. 如图,在Rt△ABC中,∠ACB=90°,BC=3,AB=5,D是边BC上一
圆心,圆心角为360°-2α的劣弧上运动(点O,C在AB的异侧).
典例7 如图,∠ABC=∠EAD=90°,D是线段AB上的动点且AC⊥ED于
点G,AB=AE=4,则BG长的最小值为( C )
A. 2
B. 2-1
C. 2-2
D.
典例7图
典例8 如图,O是等边三角形ABC内一点,连接OA,OB,OC,且
8
9
10
11
12
5. (2023·亳州谯城一模)如图,在矩形ABCD中,AB=4,BC=6,P是
矩形ABCD内的一点,连接PA,PC,PD.若PA⊥PD,则PC长的最小值
为( C )
A. 2-4
B. 2-3
C. 2
D. 4
第5题
1
2
4
5
6
7
8
9
10
11
12
6. (2023·合肥瑶海一模)如图,在△ABC中,∠B=45°,AC=2,以
1
2
3
4
5
6
7
8
9
.
10
11
中考总复习专题六辅助圆
例题解析
300 1.如图,已知:AB=AC=AD,∠BAC=60o,则∠BDC=_______.
思路点拨:
A
600
本题用一般的方法较难解决, 注意到已知条件AB=AC=AD ,可以点A为圆心,AB长为半 D 径作圆,则点C、D都在此圆 上,从而运用圆周角定理求解 .
练习
B
Q
20 ②当 CQ 12时,圆O与直线AB 3 有两个交点,当点 P运动到这两个交
M(P)
20 3
12
O
点时,CP Q为直角三角形 .
C
5
A
20 ③当0 CQ 时,圆O与直线AB 3 相离,点P在圆O外,CPQ小于90, CPQ不可能为直角三角形 .
20 综上所述,当 CQ 12时, CPQ 可能为直角三角形 . 3
可以点E为圆心,AO长为直径 作圆,如果圆E与直线x=b有交
O
C x=b
x
点,则存在四边形DEFB为矩
形.反之,则不存在.
例题解析
(3)设直线x=b与x轴交于点C,问四边形DEFB能不能是矩形? 若能,求出t的值;若不能,说明理由.
解:能。以点E为圆心,AO长为直
y
径作圆,则半径为EO=4.
F B (b,t) D
(2)S=2b
O
C x=b
x
例题解析
(3)设直线x=b与x轴交于点C,问四边形DEFB能不能是矩形? 若能,求出t的值;若不能,说明理由. 思路点拨:
y
因为四边形DEFB是平行四边 形,所以四边形DEFB要成为
F B (b,t) D
(0,8) A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6/8/2017
可构造圆的条件2
• 什么条件让你想到可以构造圆,可以构造 圆的依据是什么? 直角 • 条件2: • 依据: 90°的圆周角所对的弦是直径. 直角 •小结2:当遇有 时 , 通常以 斜边为直径 ,构造辅助圆.
6/8/2017
探究3.在平面直角坐标系中,已知点A(4,0)、 B(﹣6,0),点C是y轴上的一个动点,当 ∠BCA=45°时,点C的坐标为 .
பைடு நூலகம்
变式2:如果把“∠BCA=45°”改成“∠ BCA=θ ° 还能做吗?
6/8/2017
可构造圆的条件3
• 什么条件让你想到可以构造圆,可以构造 圆的依据是什么? 动点对定线段所张的角为定值 • 条件3: • 依据:不在同一直线上的三点确定一个圆 或:同弧所对的圆周角相等且等于 这条弧所对的圆心角的一半 •小结3: 当遇有 动点对定线段所张的角为定值时, 通常 把张角转化为圆周角 构造辅助圆.
定张角
定线段
6/8/2017
探究3.在平面直角坐标系中,已知点A(4,0)、 B(﹣6,0),点C是y轴上的一个动点,当 ∠BCA=45°时,点C的坐标为 .
变式1:如果把∠BCA=45°改成∠BCA=30°, 还会做吗?
6/8/2017
探究3.在平面直角坐标系中,已知点A(4,0)、 B(﹣6,0),点C是y轴上的一个动点,当 ∠BCA=45°时,点C的坐标为 .
A D F B E C G
一题多解
证法1 AE=EF 证法2
A M B E
图 18
证法3
D F
A D F B E C G
D F C G
A
B
E
图 19
C N
A
G
H
图 20
A
D F
D Q F C G
证法5
B P E C
证法4
G
B
E
图 22
图 21
3.(2014年山东淄博市中考数学)如图,点A与 点B的坐标分别是(1,0),(5,0),点P是 该直角坐标系内的一个动点。 (1)使∠APB=30°的点P有 个; (2)若点P在y轴上且∠APB=30°, 求满足条件的点P的坐标;
6/8/2017
可构造圆的条件1
• 什么条件让你想到可以构造圆,可以构造 圆的依据是什么? • 条件1: 同一个端点出发的几条等长线段 • 依据: 圆的定义 •小结1: 当遇有 同一个端点出发的等长线段 时, 等线段长 为半径, 通常以 这个端点 为圆心, 构造辅助圆.
6/8/2017
探究2.如图,矩形ABCG的与矩形CDEF全等, 并且AB=1,BC=3,点B、C、D在同一条直 线上,∠APE 的顶点P在线段BD上移动,使 ∠APE 为直角的点P的个数是 ( ) A.0 B.1 C.2 D.3
(3)当点P在y轴上移动时,∠APB是否
有最大值?若有,求点P的坐标,并说明
此时∠APB最大的理由;若没有,也请说
明理由. 6/8/2017
6/8/2017
6/8/2017
四.课堂小结
条件1
构造圆的条件:
条件2
•o
O
定张角 条件 3 …… 定线段 条件…
图中无圆,心中有圆
• 今天研究的这三类问题,从表面上看似乎 与圆无关,但如果我们能深入挖掘题目中 的隐含条件,善于联想所学定理,巧妙地 构造符合题意特征的辅助圆,再利用圆的 有关性质来解决问题,往往能起到化隐为 显、化难为易的解题效果!
中考专题复习之
构造辅助圆
6/8/2017
一.复习旧知
圆的“集合”定义是什么?
圆是所有到定点 的距离等于定长 的点的集合
• o
A
圆周角定理?
D
同弧所对的圆周角相等,
且等于这条弧所对圆心 角的一半
O
B
C
C
直径所对的圆周角是直角,
A
O
B
90°的圆周角所对的弦 是直径
二.探索新知
探究1.如图所示,在四边形ABCD中, AB=AC=AD,∠BAC=20°∠CAD=80°,则 ∠BDC=______度,∠DBC=______度
6/8/2017
6/8/2017
三.巩固练习
1.(2011湖北鄂州中考)如下图OA=OB=OC且 ∠ACB=30°,则∠AOB的大小是( ) A.40° B.50° C.60° D.70°
D C
30°
A
6/8/2017
B
2. (2012青海中考) 如图,四边形A BCD是正方形,点E是边BC的中点, ∠AEF=90,EF交正方形外角的平分线C F于 F。求证:AE=EF。(人教版八年 级下册第69页)
