概率公钥系统
加密|n|+k bit明文的高效公钥概率加密体制

Jn ay 2 0 a u r 0 8
Vo . 4 NO 1 13 .
第3 卷 第 1 4 期
加 密 I +kbt 文 的 高效 公 钥概 率 加 密 体 制 I i 明
姜 正 涛
( 京 航 空 航 天 大 学 计 算 机 学 院 , 京 10 8 ) 北 北 0 0 3
刘建 伟
p o e a a ee s a t o ti c e sn h e t fc p e tx s h fiin y a d t e sz fp a n e t fa r p r p r m tr nd wih u n r a i g t e lngh o i h re t ,t e efc e c n h ie o l i tx so p o a iitc p l — e n r p in s he e p o o e y Palira d Pon c v lwe e i p o e r b b lsi ub i k y e c y to c m r p s d b i e n i the a r m r v d. T m p o e c l he i r v d e c y to c e a n r p I n r p i n s h me c n e c y t I+k bi me s g swi i h re c e c . S c rt n f ce c n l sso n t s a e t h g e f i n y h i eui ade y i in y a ay i f t e i p o e n r p in s h me we e a s r v d d, a d t e s c rt ft e i r v d s h me i q v ln o h m r v d e c y to c e r lo p o i e n h e u i o h mp o e c e s e uiae tt y t a ft e o ii a n r p i n s he e,t e h g rr sd o i r b e a d q a r tcr sdu st r b e mo u h to h rgn le c y to c m h ihe e i u st p o l m n u d a i e i o iy p o lm d — y l o n. Co mpa e o h rgn lPalirPo n c e a e c y to c m e. t e i r v d e c y to s h me ha r d t t e o ii a i e — i th v l n r p in s he l h mp o e n r p in c e s f au e fh g e f ce c e tr so ih re i in y,l we r fi a e a a g rsz fp a n e t. o rta f d t nd l r e ie o l i tx s c
【国家自然科学基金】_rsa公钥密码体制_基金支持热词逐年推荐_【万方软件创新助手】_20140802
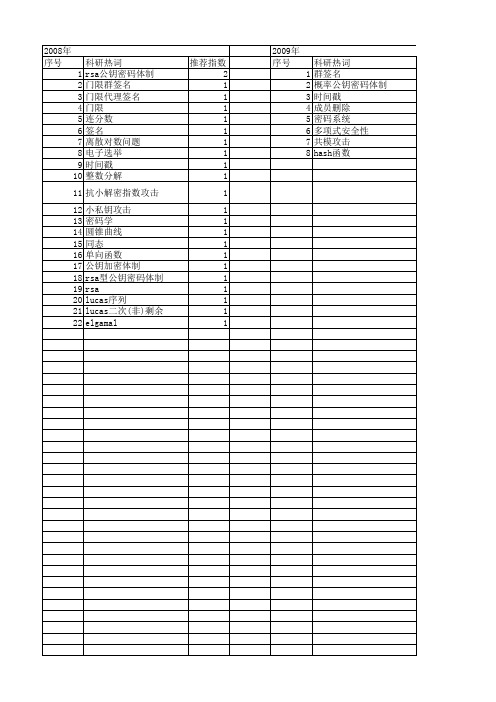
推荐指数 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年 序号 1 2 3 4 5 6 7 8 9 10 11
2014年 科研热词 推荐指数 陑性同余方程 1 离散私钥比特泄漏 1 格构造方法 1 格攻击 1 格基规约 1 格基约化算法 1 格 1 小根 1 公钥密码 1 rsa算法 1 learning with errors(lwe) 1
2012年 序号 1 2 3 4 5 6 7
科研热词 蒙哥马利算法 无线传感器网络 剩余类环 公钥密码 中国剩余定理 一元多项式 rsa
推荐指数 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
科研热词 盲签名 模幂运算 数字签名 公钥密码体制 量子计算 电子投票 欧几里得及其扩展定理 平方-乘算法 存取结构 多秘密共享 固定基窗口方法 哈希技术 哈希 后量子密码算法 同态加密 可验证性 双变量单向函数 匿名性 公开可验证性 云计算 smm算法 rsa密码体制 rsa公钥密码 rsa niederreiter算法 mceliece算法 matlab仿真 lwe
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
科研热词 rsa公钥密码体制 门限群签名 门限代理签名 门限 连分数 签名 离散对数问题 电子选举 时间戳 整数分解 抗小解密指数攻击 小私钥攻击 密码学 圆锥曲线 同态 单向函数 公钥加密体制 rsa型公钥密码体制 rsa lucas序列 lucas二次(非)剩余 elgamal
公钥密码体制研究与应用

公钥密码体制研究与应用公钥密码体制是一种基于数学难题的密码体制,它区别于传统的对称密钥密码体制,通过使用两个不同的密钥:公钥和私钥,以加密解密信息。
公钥是公开的,任何人都可以使用它来加密信息。
而私钥只有接收者拥有,可以用于解密已加密的信息。
本文将介绍公钥密码体制的基本原理、安全性、应用场景以及未来发展趋势。
一、公钥密码体制的基本原理公钥密码体制是以数学难题作为加解密算法中的核心难点。
这些数学难题在计算上非常困难且可逆性极小,因此可以满足高强度的安全要求。
在使用公钥密码体制时,发送者与接收者都要生成自己的一组密钥对:一个公共键和一个私有键。
发送方可以使用接收方已经发布过的公共键来对信息进行加密,并将其发送给接收方。
接收方收到加密后的信息后使用自己所持有相应配对好的私有键进行解密。
最重要的是,无论是谁都不能从加密后的数据推算出私有键或共有键,并且该机制还能够保证安全数据传输。
二、公钥密码体制的安全性公钥密码体制在密码学中是一种非常安全的方式,它比对称密钥密码体制更为安全。
这是因为对于对称密钥密码体制来说,加密和解密都是使用同一把秘钥,如果这把秘钥被盗取或者被破解了,那么所有传输的数据都会受到影响。
而对于公钥密码体制来说,则不存在这个问题。
与此同时,公钥密码体制还具有其他的优点。
例如,在使用公共网络传输信息时,使用公钥加密技术可以防止中间人攻击、窃听和篡改信息。
在实际应用中,公钥密码体制也具有一定的不足之处。
由于它消耗计算资源大、速度较慢等缺点,使得其在实际应用中不能完全替代对称密钥加密技术。
三、公钥密码体系的应用场景网络安全随着现代社会的发展,网络已成为人们进行通信、交流和商业活动的重要手段。
而网络传输中数据容易受到黑客攻击和窃取等威胁。
在保证数据传输安全性方面,公钥加密技术已被广泛应用,例如HTTPS、SSL等安全协议均采用了公钥加密技术,从而有效地保障了网络安全和数据传输的保密性。
数字签名数字签名是一种保证数据完整性和不可抵赖性的技术。
密钥密码体系和公钥密码体系

密钥密码体系和公钥密码体系
密钥密码体系和公钥密码体系是两种常见的加密算法体系,它们在密钥管理和加密解密过程中的原理和方式有所不同。
密钥密码体系:
密钥密码体系是使用相同的密钥对明文进行加密和解密的算法体系。
在密钥密码体系中,发送方和接收方必须互相知道并共享相同的密钥,才能进行加密解密通信。
常见的对称加密算法,如DES、AES等,属于密钥密码体系。
密钥密码体系的优点
是加密解密速度快,但缺点是密钥管理比较困难,需要事先安全地共享密钥,并确保密钥的安全性。
公钥密码体系:
公钥密码体系是使用不同的密钥对明文进行加密和解密的算法体系。
在公钥密码体系中,发送方和接收方使用不同的密钥,一个是公钥,一个是私钥。
公钥可以公开给任何人,用于加密明文,而私钥只有接收方知道,用于解密密文。
常见的公钥加密算法,如RSA、ElGamal等,属于公钥密码体系。
公钥密码体系的优点是密钥管理相对容易,只需要保证私钥的安全性,但缺点是加密解密速度相对较慢。
综上所述,密钥密码体系和公钥密码体系是两种不同的加密算法体系,各有优缺点,可以根据具体的安全需求和场景选择使用。
04计算机安全- 公钥密码体系

公钥密码体制的要求:
1. 2. 3. 4. 5. 6. 产生一对密钥是计算可行的 已知公钥和明文,产生密文是计算可行的 接收方利用私钥来解密密文是计算可行的 对于攻击者,利用公钥来推断私钥是计算不可行的 已知公钥和密文,恢复明文是计算不可行的 (可选)加密和解密的顺序可交换 可选)
公钥密码的安全性依赖于从已知的公钥, 加密算法和密文中无法求出明文或秘钥。 Diffie和Hellman提出了一种陷门单向函 数概念,为建立公钥密码体制找到了一 种途径。
= 2(2 1)5(5 1)(3 1) = 80
p , q为 素 数 , ( pq ) = ?
( pq) = ( p) (q) = ( p 1)(q 1)
一.
1.
RSA密码体制的描述
密钥生成算法:每个用户执行以下操作
随机生成两个不同大素数p,q; ② 计算n=pq,φ(n)=(p-1)(q-1); ③ 随机选取整数e,1<e<φ(n),满足(e,φ(n))=1; ④ 利用扩展欧基里德算法求出满足ed=1 mod(φ(n))的 整数d; ⑤ 公开(n,e),保密(p,q,φ(n),d)。其中e就是加密密钥, (n,e) (p,q,φ(n),d) e 而d就是解密密钥,n称为模数。
平方和乘算法的复杂度:执行次数至少要k次模乘,最多 需要2k次模乘
素数分布
(素数定理)设π (x)为不大于x的素数个数,则 lnx π lim (x) =1 x →∞ x
π (x) ≈
x lnx
512
2512 长度小于512位的数中素数的个数π (2 ) ≈ ln2512 2256 2255 长度为256位的数中素数的个数π (2 )-π (2 ) ≈ ≈ 3.25 ×1074, 256 255 ln2 ln2 可计算出在所有的256位的数中有0.56%的数是素数
公钥密码系统

❖本章我们将讨论解密密钥与加密密钥不同 的情况。非对称密码系统的解密密钥与加 密密钥是不同的,一个称为公开密钥,另 一个称为私人密钥(或秘密密钥),因此 这种密码体系也称为公钥密码体系。公钥 密码除可用于加密外,还可用于数字签名。 《 中 华 人 民 共 和 国 电 子 签 名 法 》 已 于 2005 年4月1日实行。
k1
k2
28
Company Logo
中间人攻击
❖ Alice用密钥k1给Bob发送消息;Carol截获消 息后用k1解密就可读取消息;然后将获得的明文 消息用k2加密(加密前可能会对消息作某些修改) 后发送给Bob。
❖ 对Bob发送给Alice的消息,Carol同样可以读 取和修改。造成中间人攻击的原因是DiffieHellman密钥交换不认证对方。利用数字签名 可以挫败中间人攻击。
(2) Bob发送公开值给Alice,Carol截获它然后把 自己的公开值(a’和p’)发送给Alice。
(3) Alice和Carol计算出二人之间的共享密钥k1。 (4) Bob和Carol计算出另外一对共享密钥k2。
27
Company Logo
中间人攻击
a,p
a',p'
Alice
Carol
Bob
Bob
X
产生随机数y
计算X=ax mod p
计算Y=ay mod p
计算k=Yx mod p
Y
计算k'=Xy mod p
26
Company Logo
中间人攻击
❖ Diffie-Hellman密钥交换容易遭受中间人攻击:
(1) Alice发送公开值(a和p)给Bob,攻击者Carol 截获这些值并把自己产生的公开值发送给Bob。
第7讲 公钥密码体制
二、RSA密码体制
参数选择:
独立地选取两大素数p1和p2(各512bit的数), 计算 n=p1×p2 其欧拉函数值(n)=(p1-1)(p2-1) 随机选一整数e, 1e<(n),((n), e)=1(因而在模(n)下e有逆元) d=e-1 mod (n) 公钥为n,e; 私钥为d (p1, p2不再需要,可以销毁)
* MIPS-年指以每秒执行1,000,000条指令的计算机运行一年
二、RSA密码体制
安全性:分解模数n
技术进展使分解算法和计算能力在不断提高,计算所需的硬件费用在不断下降 RSA-129: 110位十进制数字早已能分解。 Rivest等最初悬赏$100的RSA-129,已经 由包括五大洲43个国家600多人参加,用1600台机子同时产生820条指令数据, 通过Internet网,耗时8个月,于1994年4月2日
但数学上至今还未证明分解模就是攻击RSA的最佳方法,
也未证明分解大整数就是NP问题, 可能有尚未发现的多项式时间分解算法。 人们完全可以设想有另外的途径破译RSA, 如求出解密指数d或找到(p1-1)(p2-1)等。 但这些途径都不比分解n来得容易。 甚至Alexi等[1988]曾揭示,从RSA加密的密文恢复某些比特的困难性也和 恢复整组明文一样困难。 这一视在困难性问题是个NP问题,但还没人证明它为NPC问题。
因为(e1, e2,)=1,所以由Euclidean算法有r e1+s e2=1
计算 (y1-1)-r y2s = x mod n (假设r是负数)
二、RSA密码体制
安全性:低加密指数攻击
小的e可加快加密和验证签字速度,且所需的存储密钥空间小
但若加密钥e选择得太小,则容易受到攻击 网中三用户的加密钥e均选3,分别模n1, n2, n3 (互素,否则可求出公因子,而降低安全性)
Blum-Goldwasser概率密码体制的一种改进方案
使数据膨胀率 降低到 l / ; +k 文章“ 于二次剩余理论的新概 率密码 的研究” 提 出了B m 基 中, G概率密码的一种改进方案, 使
得数据膨胀率 降低 到 l (-) +k1 m;对此 进行 改进,使得数据膨胀 率降低为 l ( 2/ / +k ) - m. 关键宇:确 定密码体制;概率 密码;数据膨胀率;二次剩余
2 概率密码基础 知识
定理1 ( 中国剩 余 定理)
假定 m - . ,m 为两两互素的正整数, 又假定 a, l …口 为整数. 么同余方程组 三a m d f ( ≤ 那  ̄ o m) 1 (
有模 M =m × ×m 的唯一解, 1… 此解由下式给 出: : 口 y m dM 其中 M o =M / 且 = .m d f f , m, f 『 o m ,1 . .
中图 分 类 号 : N9 81 T 1. 文 献 标 识 码 :A
d i 1 . 60i n10 —4 3 0 2 30 o: 0 9 9 .s.0 32 8 . 1 . . 3 s 2 0 8
1 绪论
密码学的目的是使得两个人在不安全信道中通信, 其他人不能识别通信内容, 密码学包括密码编码学和密码 分析学, 密码体制分为对称密码体制和非对称密码体制¨ J非对称密码体制大多数都是确定性 的密码体制, . 确 定性密码体制是指给定明文, 任何时间加密得到的密文都是相同的, 这样就会存在一个缺点, 如果 用该密码体 制多次加密 明文得到密文, 攻击者就可以从密文之间发现规律, 从而获得破解明文或者获得明文部分信息. 针 对 确 定性 密 码体 制 的这一 缺 陷,God se和 Mi l 于 二 次剩余 理 论设 计 了一 种 非确 定 性密 码 , 率 lwasr ci a基 即概 密码. 在计算假设下, 不可能在多项式时间内通过检查密文的手段得到有关明文 的任何信息 . 但是具有非常 高 的数据扩展,因为每个明文比特被加密成一个长度为ln比特的密文. b 为了避免分解 应该取 0 4 , 为12 比特长 的整数, 而此时密文长度是明文长度的10倍. 00 Bu 与G l as 给 出了一个更有效的概率公钥密码体制, l m o w se d r 使数据膨胀率降低到1 k ,此方案是基于二 + / m 次剩余问题, 明文与一个等长的伪随机序列异或得到密文. 将
什么是公钥密码体制
什么是公钥密码体制
公钥密码体制也称非对称密码体制或者双钥密码体制,是基于数学函数(如单向陷门函数)而不是基于置换和代换的工具。
公钥密码算法的最大特点是采用两个相关密钥将加密和解密能力分开,其中一个是公开的,称为公钥,用于加密;其中一个是为用户专用的,是保密的,称为私钥,用于解密。
公钥密码体制是为了解决对称密码体制中最难解决的2个问题而提出的:
1.密钥分配问题:在对称密码中,接受方和发送方使用相同密钥。
一般情况下该密钥
通过加密信道进行传输。
但是加密信道可能会被攻击者攻击。
2.数字签名问题:如果使用对称加密来进行数字签名,那么在对密钥进行管理和分发
时带来被攻击者攻击的问题。
在公钥密码体制中存在2个密钥:公钥,私钥。
公钥和加密算法是公开的,公钥用于加密数据;私钥是保密的,用于解密。
以上内容仅供参考,如需获取更多详细信息,建议查阅公钥密码体制相关的资料或咨询数学领域专业人士。
量子 共享密钥 密钥池
量子共享密钥密钥池
量子共享密钥和密钥池是量子通信和量子密码学中的概念。
量子共享密钥是一种使用量子态的性质来保证密钥的安全传输的方法。
传统的加密方式中,使用公钥加密和私钥解密的方式来进行通信,但是这种方式容易受到中间人攻击。
采用量子共享密钥,可以通过利用量子态的特殊性质,即量子态的测量会改变其状态,来确保密钥的安全传输。
量子共享密钥的基本原理是,发送方(Alice)和接收方(Bob)使用一种被称为量子密钥分发(quantum key distribution,QKD)的协议,通过发送一系列的量子比特(通常是光子)
来共享密钥。
由于量子态的观测特性,任何对量子比特的截取或窃听都会导致量子态的破坏,从而被Alice和Bob察觉到。
因此,只有通过安全的信道传输的量子密钥才能分享。
密钥池是一种存储和管理密钥的系统。
在现实世界的通信中,需要大量的密钥来确保通信的安全性,密钥池就是用来管理这些密钥的。
密钥池可以是一个物理设备或者一个虚拟的软件系统,用来存储和生成密钥,并提供给通信的参与者使用。
在量子通信中,密钥池可以用来存储和生成量子共享密钥。
一般情况下,密钥池会包含一系列的预先分享的密钥,这些密钥可以通过QKD协议来实现。
当通信的参与者需要共享密钥时,他们可以从密钥池中获取密钥,并进行加密和解密操作。
总之,量子共享密钥和密钥池都是为了保证量子通信的安全性
而设计的。
量子共享密钥通过利用量子态的观测特性来确保密钥的安全传输,而密钥池则是用来存储和生成密钥,并提供给通信的参与者使用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ci
t
ri2 mod n ri2 mod n
mi 0 mi 1
C (C1, C2 ,Cv )
m是的密文
显然当 mi = 0时是模二次剩余,而当 mi= 1时 C i 是模n非
二次剩余
解密算法
接收者用自己的私钥p,对每位密文计算 C i
ei
Ci p
, mi
,
容易察觉相同明文传送两次
虽然可以通过在明文后面附上随机生成指定长度的字符串挫败 上述攻击,但是要付出时空代价。
我们说公钥密码系统在语义上是安全的 (Semantically Secure)是指在多项式时间内从密文不 会泄露关于明文的任何信息,即对手有多项式界定的计 算资源,他不能从密文悟出明文的任何信息。
4
1
t 1
mod
(
p
1)
,a2
q 1t1 4
mod (q
1)
⑵计算
b1
x a1 t 1
mod
p
,b2
x a2 t 1
mod
q
⑶使用自己的私钥p,q,a,b,计算 x0 b2ap b1bq mod n
⑷
对 i 1, 2,, t 做 xi
的最后一位
输出长度为t的伪随机序列 (z1 , z2 ,, zt )
Blum-Goldwasser概率公钥密码系统
密钥生成
n选=p择.两q 个,不用同扩的展大的随E机uc素lid数epan和算q法,计p 算qa,3b使moadp4+b,q计=1算。
公布公钥n,保密私钥p,q,a,b
加密算法
首m 先 得m1到m对2 方真mt实,公其钥中n。m令i长k度为lhg,n1, ≤hi≤ t。lg k , 明文
0 1
ei 1 ei 1
明文为 m (m1, m2 ,, mv )
,1 i v
Goldwasser-Micali 概率公钥密码系统的缺点是消息
加密后扩展 ln n 倍。所以该密码系统适用于对单bit 加密,
否则运算量大、速度慢。
3.4.2 Blum-Goldwa的两个大素数p和q作为私钥,计算n=p.q
选择一个模n非二次剩余正整数t且 t 1 。具体步骤为:
⑴在Z
* p
n
中有一半是模p非二次剩余,选取
a
Z
* p
使之满足
a p
1
⑵同样选取
b Zq*
使之满足
b q
1
t a mod p
⑶解同余方程 t b mod q , 0 t n 1 。显然
t n
a p
b q
1
公布公钥n和t,p和q是私钥。
加密算法
首先得到对方的公钥 (t, n) 。
对明文,mi {0,1} 1 i v 。对明文的每一位 mi随机选择 ri计算
xt1 mod
p
,即x( p1) / 42 t 1
xt1 mod p
依次递推下去
b1
x a1 t 1
mod
p
x0
mod
p
x 下面给出在第3)步中计算 x0 的推理过程。从加密过程知
是
t
模n二次剩余,由Euler准则知
x ( p1) / 2 t
1mod
p
而 p 3mod4
Blum-Goldwasser概率公钥密码在消息扩展和运算速度上都可 以跟RSA相比美,它是目前最有效的概率加密方案。为此我们先 介绍Blum-Goldwasser概率公钥密码中需要的一种BBS伪随机 位生成器(Blum-Blum-Shub Pseudo-Random Bit
Generator )
Blum-Blum-Shub PRBG
取
r
Z
* n
,令 x0 r 2 mod n
对 i 1, 2, , t 做 xi xi21 mod n 且 Ci mi xi 的最后h位
计算 xt1 xt2 mod n
将 C (C1, C2 ,,Ct , xt1 ) 传送给对方
解密算法
⑴计算
a1
p
首先生成两个大素数 p q 3 mod 4 ,令 n p q ,n称为Blum数 选取随机整数 w, 1 w n 1 ,使 gcd(w, n) 1。W称为种子,计算
x0 w2 mod n 。
对
i 1, 2,, t
,计算 xi
x2 i 1
mod n
,zi
xi
x2 i 1
mod
n
且 mi Ci xi 的最后h位
x 下面给出在第3)步中计算 x0 的推理过程。从加密过程知 t 是
模n二次剩余,由Euler准则知
x ( p1) / 2 t
1mod
p
而
p 3mod4 ,
x ( p1) / 4 t 1
xt mod
p ,同理
x ( p1) / 4 t
,
x ( p1) / 4 t 1
xt mod
p,同理 xt( p1) / 4
xt1 mod
p
,即x( p1) / 42 t 1
xt1 mod p
依次递推下去
b1
x a1 t 1
mod
p
二次剩余公钥加密是一种概率加密(Probabilistic Encryption)技术,使敌手在多项式时间内不能从密 文得到关于明文的任何信息。因此,假设二次剩余问题 是难解问题,那么二次剩余公钥密码系统是在语义上安 全的。
3.4.1 Goldwasser-Micali 概率公钥密码系统
公私钥对的生成
3.4 概率公钥系统
• 为了针对一个被动敌手从密文恢复出相应的明文,我们要求解 密算法对几乎所有明文都难以解出明文。这是最起码的要求。 如何能达到更强一些的安全性呢?我们回想RSA, Rabin, 背包 等公钥加密算法它们都是确定的加密算法,即相同的密钥和相
同的明文总是加密成相同的密文。对确定的加密算法可能有如 下缺点:
对有的消息空间概率分布算法不都是安全的。例如消息0或1加 密后不变,所以很容易查出来;
有时容易从密文得到明文的部分信息。如明文m的RSA密文
C me mod n 从密文的直接得到明文的Jacobi值 从而得到明文的一位信息。
m n
me n
C n
