角平分线背景下线段倒数和定值问题(修订版)
【中考数学必备专题】几何辅助线大揭秘 之角平分线问题(含答案)
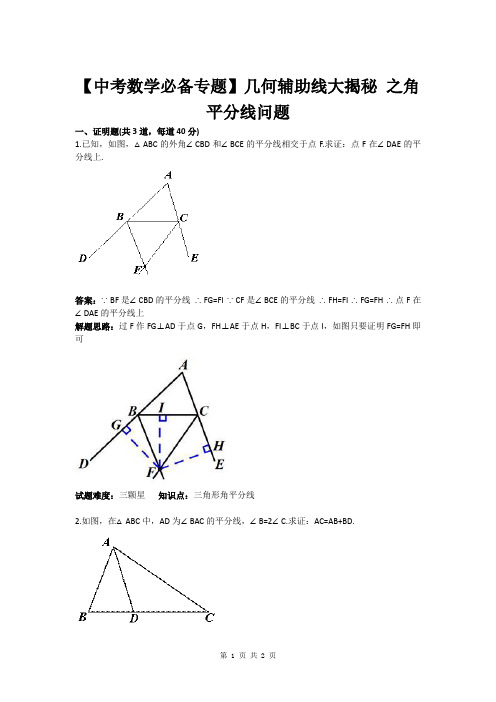
【中考数学必备专题】几何辅助线大揭秘之角
平分线问题
一、证明题(共3道,每道40分)
1.已知,如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F.求证:点F在∠DAE的平分线上.
答案:∵BF是∠CBD的平分线∴FG=FI ∵CF是∠BCE的平分线∴FH=FI ∴FG=FH ∴点F在∠DAE的平分线上
解题思路:过F作FG⊥AD于点G,FH⊥AE于点H,FI⊥BC于点I,如图只要证明FG=FH即可
试题难度:三颗星知识点:三角形角平分线
2.如图,在△ABC中,AD为∠BAC的平分线,∠B=2∠C.求证:AC=AB+BD.
答案:∵AD是∠BAC的平分线∴∠BAD=∠EAD 在△ABD和△AED中AB=AE ∠BAD=∠EAD AD=AD ∴△ABD≌△AED(SAS)∴BD=ED,∠B=∠AED ∵∠AED=∠B=2∠C ∴∠CDE=∠AED ﹣∠C=∠C ∴DE=CE ∴BD=CE ∵AC=AE+CE ∴AC=AB+BD
解题思路:在AC上截取AE=AB,连接DE,如图只要证明BD=CE即可
试题难度:三颗星知识点:三角形角平分线
3.已知:如图,在△ABC中,BE平分∠ABC,AD⊥BE,垂足为点D.求证:∠BAD=∠DAE+∠C.
答案:∵BE平分∠ABC,AD⊥BE ∴△ABF为等腰三角形(三线合一)∴∠BAD=∠BFD ∵∠BFD 为△ACF的外角∴∠BFD=∠DAE+∠C ∴∠BAD=∠DAE+∠C
解题思路:延长AD与BC交于点F,如图只要证明∠BFD=∠BAD即可
试题难度:三颗星知识点:三角形角平分线。
北师大版八年级数学下册教材配套教学课件 1.4.1角平分线(第1课时)(课件)

第一章 三角形的证明
●1.4 角平分线
第1课时 角平分线
一、情景导入
如图,要在S区建一个贸易市场,使它到铁路和公路距离相等,离公
路与铁路交叉处500米,这个集贸市场应建在何处?(比例尺为1︰20000)
O
解:作夹角的角平分线OC, 截取OD=2.5cm ,D即为所求.
D S
C
二、探索新知
定理
内容
条件
结论
图示
性质 角平分线上的点到 定理 角两边的距离相等.
OP 平分∠AOB,
PD⊥OA,PE⊥OB
PD = PE
判定 定理
在一个角的内部,到 角两边距离相等的点 在角的平分线
O
PD⊥OA,PE⊥OB,
PD=PE.
OP 平分∠AOB
A D
C P
EB
三、典例精练
知识点一:角平分线的性质 例1 :如图,在△ABC中,∠BAC=60°,点D在BC上,AD=10,
角的内部到角的两边的距离相等的点在角的平分线上.
应用所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边的距离相等.
几何语言:
O
∵ PD⊥OA,PE⊥OB,PD=PE.
∴点P 在∠AOB的平分线上.
A
D C
P
E
B
应用:常用来证明点在直线上(或直线经过某一点)
角平分线性质与判定定理
角平分线的性质: 角的平分线上的点到角的两边的距离相等.
逆
命
O
题
AD CPE NhomakorabeaB
角的内部到角的两边距离相等的点在角的平分线上. 思考:这个 结论正确吗?
北师大版八年级数学下册 第一章 1.4 角平分线 第1课时 角平分线的性质定理及逆定理 【名校教案 集体备课】

1.4 角平分线第1课时角平分线的性质定理及逆定理【教学目标】【知识与技能】会证明角平分线的性质定理及其逆定理【过程与方法】经历探索、猜测、证明的过程,进一步提高学生的推理证明意识和能力.体验解决问题的方法,发展实践能力和创新意识.【情感态度】经历探索、猜想、证明使学生掌握研究解决问题的方法.【教学重点】1.复习角平分线的相关知识,探究归纳角平分线的性质和判定定理;2.正确地表述角平分线性质定理的逆命题及其证明.【教学难点】能够正确地表述角平分线性质定理的逆命题及其证明.【教学过程】一、情境导入问题:在S区有一个集贸市场P,它建在公路与铁路所成角的平分线上,要从P点建两条路,一条到公路,一条到铁路.问题1:怎样修建道路最短?问题2:往哪条路走更近呢?二、合作探究探究点一:角平分线的性质定理【类型一】 应用角平分线的性质定理证明线段相等如图,在△ABC 中,∠C =90°,AD 是∠BAC 的平分线,DE ⊥AB 于E ,F 在AC 上,BD =DF .求证:(1)CF =EB ;(2)AB =AF +2EB .解析:(1)根据角平分线的性质,可得点D 到AB 的距离等于点D 到AC 的距离,即CD =DE .再根据Rt △CDF ≌Rt △EBD ,得CF =EB ;(2)利用角平分线的性质证明△ADC 和△ADE 全等得到AC =AE ,然后通过线段之间的相互转化进行证明.证明:(1)∵AD 是∠BAC 的平分线,DE ⊥AB ,DC ⊥AC ,∴DE =DC .在Rt △DCF 和Rt △DEB 中,∵⎩⎪⎨⎪⎧BD =DF ,DC =DE ,∴Rt △CDF ≌Rt △EBD (HL).∴CF =EB ; (2)∵AD 是∠BAC 的平分线,DE ⊥AB ,DC ⊥AC ,∴CD =DE .在△ADC 与△ADE 中,∵⎩⎪⎨⎪⎧CD =DE ,AD =AD ,∴△ADC ≌△ADE (HL),∴AC =AE ,∴AB =AE +BE =AC +EB =AF +CF +EB =AF +2EB .方法总结:角平分线的性质是判定线段相等的一个重要依据,在应用时一定要注意是两条“垂线段”相等.【类型二】 角平分线的性质定理与三角形面积的综合运用如图,AD 是△ABC 的角平分线,DE ⊥AB ,垂足为E ,S △ABC =7,DE =2,AB =4,则AC 的长是( )A .6B .5C .4D .3解析:过点D 作DF ⊥AC 于F ,∵AD 是△ABC 的角平分线,DE ⊥AB ,∴DF =DE =2,∴S △ABC =12×4×2+12×AC ×2=7,解得AC =3.故选D. 方法总结:利用角平分线的性质作辅助线构造三角形的高,再利用三角形面积公式求出线段的长度是常用的方法.【类型三】 角平分线的性质定理与全等三角形的综合运用如图所示,D 是△ABC 外角∠ACG 的平分线上的一点.DE ⊥AC ,DF ⊥CG ,垂足分别为E ,F .求证:CE =CF .解析:由角平分线上的性质可得DE =DF ,再利用“HL ”证明Rt △CDE 和Rt △CDF 全等,根据全等三角形对应边相等证明即可.证明:∵CD 是∠ACG 的平分线,DE ⊥AC ,DF ⊥CG ,∴DE =DF .在Rt △CDE 和Rt △CDF 中,∵⎩⎪⎨⎪⎧CD =CD ,DE =DF ,∴Rt △CDE ≌Rt △CDF (HL),∴CE =CF . 方法总结:全等三角形的判定离不开边,而角平分线的性质是判定线段相等的主要依据,可作为判定三角形全等的条件.探究点二:角平分线的判定定理【类型一】 角平分线的判定如图,BE =CF ,DE ⊥AB 的延长线于点E ,DF ⊥AC 于点F ,且DB =DC ,求证:AD 是∠BAC 的平分线.解析:先判定Rt △BDE 和Rt △CDF 全等,得出DE =DF ,再由角平分线的判定可知AD 是∠BAC 的平分线.证明:∵DE ⊥AB 的延长线于点E ,DF ⊥AC 于点F ,∴∠BED =∠CFD ,∴△BDE 与△CDF 是直角三角形.在Rt △BDE 和Rt △CDF 中,∵⎩⎪⎨⎪⎧BE =CF ,BD =CD ,∴Rt △BDE ≌Rt △CDF (HL),∴DE =DF .∵DE ⊥AB ,DF ⊥AC ,∴AD 是∠BAC 的平分线.方法总结:证明一条射线是角平分线的方法有两种:一是利用三角形全等证明两角相等;二是角的内部到角两边距离相等的点在角平分线上.【类型二】 角平分线的性质和判定的综合如图所示,△ABC 中,AB =AC ,AD 是∠BAC 的平分线,DE ⊥AB ,DF ⊥AC ,垂足分别是E 、F .下面给出四个结论,①AD 平分∠EDF ;②AE =AF ;③AD 上的点到B 、C 两点的距离相等;④到AE 、AF 距离相等的点,到DE 、DF 的距离也相等.其中正确的结论有( )A .1个B .2个C .3个D .4个解析:由AD 平分∠BAC ,DE ⊥AB ,DF ⊥AC 可得DE =DF ,由此易得△ADE ≌△ADF ,故∠ADE =∠ADF ,即①AD 平分∠EDF 正确;②AE =AF 正确;中垂线上的点到两端点的距离相等,故③正确;∵④到AE 、AF 距离相等的点,在∠BAC 的角平分线AD 上,到DE 、DF 的距离相等的点在∠EDF 的平分线DA 上,两者同一条直线上,所以到DE 、DF 的距离也相等正确,故④正确;①②③④都正确.故选D.方法总结:运用角平分线的性质或判定时,可以省去证明三角形全等的过程,可以直接得到线段或角相等.【类型三】 添加辅助线解决角平分线的问题如图,△ABC 的∠ABC 和∠ACB 的外角平分线交于点D .求证:AD 是∠BAC 的平分线.解析:分别过点D 作DE 、DF 、DG 垂直于AB 、BC 、AC ,垂足分别为E 、F 、G ,然后利用角平分线上的点到角两边的距离相等可知DE =DG ,再利用到角两边距离相等的点在角平分线上来证明.证明:分别过D 作DE 、DF 、DG 垂直于AB 、BC 、AC ,垂足分别为E 、F 、G .∵BD 平分∠CBE ,DE ⊥BE ,DF ⊥BC ,∴DE =DF .同理DG =DF ,∴DE =DG ,∴点D 在∠BAC 的平分线上,∴AD 是∠BAC 的平分线.方法总结:在遇到角平分线的问题时,往往过角平分线上的一点作角两边的垂线段,利用角平分线的判定或性质解决问题.【类型四】 线段垂直平分线与角平分线的综合运用如图,在四边形ADBC 中,AB 与CD 互相垂直平分,垂足为点O .(1)找出图中相等的线段;(2)OE ,OF 分别是点O 到∠CAD 两边的垂线段,试说明它们的大小有什么关系.解析:(1)由垂直平分线的性质可得出相等的线段;(2)由条件可证明△AOC ≌△AOD ,可得AO 平分∠DAC ,根据角平分线的性质可得OE =OF .解:(1)∵AB 、CD 互相垂直平分,∴OC =OD ,AO =OB ,且AC =BC =AD =BD ;(2)OE =OF ,理由如下:在△AOC 和△AOD 中,∵⎩⎪⎨⎪⎧AC =AD ,OC =OD ,AO =AO ,∴△AOC ≌△AOD (SSS),∴∠CAO =∠DAO .又∵OE ⊥AC ,OF ⊥AD ,∴OE =OF .方法总结:本题是线段垂直平分线的性质和角平分线的性质的综合,掌握它们的适用条件和表示方法是解题的关键.三、当堂检测1.如图,已知:∠C=90°,DE 是AB 的垂直平分线,D 为垂足,交BC 于E ,AB=2AC. 求证:CE=DE.证明:连接AE,由于∠C=90°,AB=2AC,∴∠B=30°,∠CAB=60°.∵DE是AB的垂直平分线,∴AE=BE,∴∠EAB=∠B=30°,∴∠CAE=60°-30°=30°,即AE是∠CAB的角平分线,∴CE=DE.2.如图,已知:E是∠AOB的平分线上的一点,且EC⊥OA,ED⊥OB,垂足分别是C、D. 求证:OE垂直平分CD.证明:∵OE是∠AOB的平分线,∴CE=DE,∴Rt△OCE≌Rt△ODE,∴OC=OD,∴O与E都在CD的垂直平分线上,∴OE垂直平分CD.3.如图,已知:在△ABC中,∠BAC的平分线交BC于D,且DE⊥AB,DF⊥AC,垂足分别是E、F. 求证:AD是EF的垂直平分线.证明:∵AD是∠BAC的平分线,且DE⊥AB,DF⊥AC,∴DE=DF,∴Rt△ADE≌Rt△ADF,∴AE=AF,∴A与D都在EF的垂直平分线上,∴AD就是EF的垂直平分线.四、板书设计1.角平分线的性质定理角平分线上的点到这个角的两边的距离相等.2.角平分线的判定定理在一个角的内部,到角的两边距离相等的点在这个角的平分线上.五、教学反思本节课由于采用了动手操作以及讨论交流等教学方法,从而有效地增强了学生对角以及角平分线的性质的感性认识,提高了学生对新知识的理解与感悟,因而本节课的教学效果较好,学生对所学的新知识掌握较好,达到了教学的目的.不足之处是少数学生在性质的运用上还存在问题,需要在今后的教学与作业中进一步的加强巩固和训练.这节课证明了角平分线的性质定理和判定定理,在有角的平分线(或证明是角的平分线)时,过角平分线上的点向两边作垂线段,利用角平分线的判定或性质则使问题迅速得到解决.学生掌握较好.。
八年级数学角平分线的性质定理及其逆定理

M
F
D P
O
E
N
挑战自我
如图,在△ABC中,已知AC=BC,∠C=900,AD
是△ABC的角平分线,DE⊥AB,垂足为E.
(1)如果CD=4cm,AC的长 (2)求证:AB=AC+CD.
A
E C B
D
独立作业
2
2.已知:如图,△ABC的外角∠CBD和∠BCE的 角平分线相交于点F. 求证:点F在∠DAE的平分线上. A
E B D C
例:已知:如图,∠C= ∠C′=90° ,AC=AC ′ . 求证(1) ∠ABC= ∠ABC ′ ;(2)BC=BC ′ .(要 求不用三角形全等的判定)
A
C C′
B
三.尺规作图 角平分线的作法
用尺规作角的平分线. 已知:∠AOB,如图. 求作:射线OC,使∠AOC=∠BOC 作法:
思 考 分 析
二.角平分线性质定理的逆定理
逆定理: 到一个角的两边距离相等的 点,在这个角的平分线上.
用符号语言表示为: ∵PD⊥OA,PE⊥OB,垂足 分别是D,E,且PD=PE ∴点P在∠AOB的平分线上
A D O E P C
B
温馨提示:这个结论又是经常用来证明点在直线 上(或直线经过某一点)的根据之一.
如图:若想在两条公路围成的A区域内建一个化 工厂,为了减少环境污染,要求化工厂到桥头的 距离是500米,同时为了交通方便,要求化工厂 到两条公路的距离相等,假如你是工程师,你 能在图上找到化工厂的位置吗?
焦寺
(比例尺为1:50000)
A区域
桥头
旁堤刘
24.8角平分线的性质定 理及其逆定理
定理:角平分线上的点到角的两边的距离相等
1.4.2角平分线-2020-2021学年北师大版八年级数学下册课件

E
(1)AMD 90
(2) ME MC, MB MC
MC MB M为BC的中点.
(3) DE CD, AE AB
AD AE DE CD AB.
达标检测
5.如图①,在△ABC中,∠ABC、∠ACB的平分线交于O点,
过O点作DE//BC,求证:DE=BD+CE ; 如图②,过A点作DE//BC,其它条件不变,探索DE,AB,AC 之间有什么关系?并证明你的结论.
第一章 三角形的证明
1.4.2 角平分线
学习目标
1.理解证明角的平分线的性质定理和判定定理相关 的结论,掌握角平分线的性质定理和判定定理的 灵活运用.
2.进一步发展推理证明意识和能力,培养转化数学 语言的能力,提高综合运用数学知识和方法解决 问题的能力.
3.在探究的过程中培养独立思考的习惯,学会合作 探讨交流,感受数学的作用.
例3.如图,在△ABC中.AC=BC,∠C=90°, AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)已知CD=4 cm,求AC的长; (2)求证:AB=AC+CD.
(1)解:AD是ABC的角平分线,DC AC, DE AB.
DE CD 4cm.
AC BCB BAC 45
BDE 90 45 45 BE DE BD 2DE2 4 2cm
解:SABC SABD SBCD
1 AB DE 1 BC DE
2
2
192 162
2215来自标检测4.如图,∠B=∠C=90°,AM平分∠DAB,DM平分∠ADC,
(1)求∠AMD的度数
(2)求证:M是BC的中点.
(3)猜想CD、AD、AB的数量关系,并说明理由。
解:作ME AD于点E.AMD 90
初中数学三角形中的倒角模型-高分线模型、双(三)垂直模型及参考答案
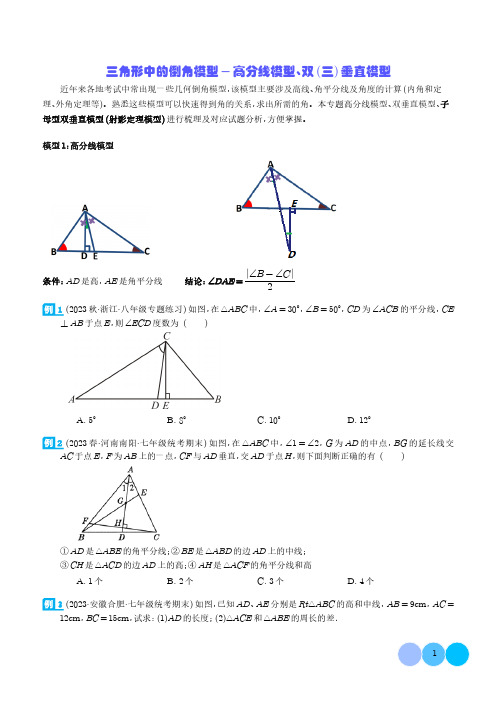
三角形中的倒角模型-高分线模型、双(三)垂直模型近年来各地考试中常出现一些几何倒角模型,该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。
熟悉这些模型可以快速得到角的关系,求出所需的角。
本专题高分线模型、双垂直模型、子母型双垂直模型(射影定理模型)进行梳理及对应试题分析,方便掌握。
模型1:高分线模型条件:AD是高,AE是角平分线结论:∠DAE=∠B-∠C21(2023秋·浙江·八年级专题练习)如图,在△ABC中,∠A=30°,∠B=50°,CD为∠ACB的平分线,CE ⊥AB于点E,则∠ECD度数为()A.5°B.8°C.10°D.12°2(2023春·河南南阳·七年级统考期末)如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的有()①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH是△ACD的边AD上的高;④AH是△ACF的角平分线和高A.1个B.2个C.3个D.4个3(2023·安徽合肥·七年级统考期末)如图,已知AD、AE分别是Rt△ABC的高和中线,AB=9cm,AC= 12cm,BC=15cm,试求:(1)AD的长度;(2)△ACE和△ABE的周长的差.模型2:双垂直模型结论:①∠A=∠C;②∠B=∠AFD=∠CFE;③AB⋅CD=AE⋅BC。
4(2023·陕西咸阳·统考一模)如图,在△ABC中,CD,BE分别是AB,AC边上的高,并且CD,BE交于点P,若∠A=50°,则∠BPC的度数为()A.130°B.120°C.110°D.100°5(2022秋·安徽宿州·八年级校考期中)如图,在△ABC中,CD和BE分别是AB,AC边上的高,若CD= 12,BE=16,则ACAB的值为( ).A.35B.34C.43D.586(2023春·河南周口·七年级统考期末)如图,在△ABC中,AB=8,BC=10,CF⊥AB于点F,AD⊥BC于点D,AD与CF交于点E,∠B=46°.(1)求∠AEC的度数.(2)若AD=6,求CF的长.模型3:子母型双垂直模型(射影定理模型)结论:①∠B=∠CAD;②∠C=∠BAD;③AB⋅AC=AD⋅BC。
八年级数学下册 1.4 角平分线 第2课时 试题资料库素材 (新版)北师大版
角平分线第2课时例1. 在ABC ∆中,90=∠C ,AD 平分BAC ∠,AB DE ⊥于E ,F 在AC 上,DF BD =。
求证:EB CF =。
证明:∵AD 平分∠BAC ,∠C =90,DE ⊥AB∴DC =DE (角平分线上一点到角的两边的距离相等) 在Rt ∆CDF 和Rt ∆EDB 中,⎩⎨⎧==DB DF DE DC∴Rt ∆CDF ≅Rt ∆EDB (HL )∴CF =EB (全等三角形的对应边相等)角平分线的集合解释到一个角两边距离相等的点,在这个角的平分线上。
因此,角的平分线的集合解释是:角平分线是到角两边距离相等的所有点的组成的集合。
符号语言:的平分线)是的平分线上(或写成:在点又AOB OP AOB P OBPE OA PD PEPD ∠∠∴⊥⊥=,例2. 如图,已知在∆ABC 中,BD =DC ,∠1=∠2,求证:AD 平分∠BAC 。
证明:过点D 作DE ⊥AB 于E ,DF ⊥AC 于F. 在∆BED 和∆CFB 中,⎪⎩⎪⎨⎧==∠=∠∠=∠CD BD CFD BED 9021 ∴∆BED ≅∆CFD (AAS )∴DE =DB∴AD 平分∠BAC利用角平分线的性质证明两条线段相等例3. 如图已知AB =AC ,BD =CD ,DE ⊥AB 交AB 于E ,DF ⊥AC 交AC 于F 。
求证:DE =DF 。
证明:连结AD ,在∆ABD 和∆ACD 中⎪⎩⎪⎨⎧===AD AD CD BD AC AB∴∆ABD ≅∆ACD (SSS )∴∠BAD =∠CAD ,即AD 平分∠BAC 。
又∵DE ⊥AB ,DF ⊥AC∴DE =DF (角平分线上的点到角两边距离相等)利用全等三角形的性质证明线段及角的相等关系例4. 如图,在∆AFD 和∆BEC 中,点A 、E 、F 、C 在同一直线上,有下面四个论断:(1)AD =CB ;(2)AE =CF ;(3)∠B =∠D ;(4)AD//BC 。
北师大版数学八年级下册1.4《角平分线》ppt课件1 (共22张PPT)
2、 已知:如图2,PB、PC分别是△ABC的外 角平分线, 相交于点P.
求证:P在∠A的平分线上
A
B E P 图2 H
C
G
证明:作PE⊥AB,交AB延长线于E。PH⊥BC 于H,PG⊥AC,交AC的延长线于点G ∵BP是角平分线 ∴PE=PH A ∵PC是角平分线 ∴PH=PG ∴PE=PG B H C P A ∴ 在∠ 的平分线上
E
G
P
图2
3、如图,某个居民小区C附近有三条两两相交的道路 MN、OA、OB,拟在MN上建造一个大型超市,使得 它到OA、OB的距离相等,请确定该超市的位置P。
A M
P
小区C
N O B
4、在平面直角坐标系xOy中,边长为a(a为大于0的常数)的 正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半 轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的 正半轴都不包含原点O),顶点C、D都在第一象限. 求证:无论点A在x轴正半轴上、点B在y轴正半轴上怎样运 动,点P都在∠AOB的平分线上;
布置作业
1.从教材习题中选取 2.完成练习册本课时的习题
人类要在竞争中生存,便 要奋斗。——孙中山
′
已知:如图, 点P为∠AOB内一点, PD⊥OA, PE⊥OB, 垂足分别为 O D,E,且PD=PE. 求证:点P在∠AOB的平分线上. 分析:要证明点P在∠AOB的平分线上, 可以先作出过点P的射线OC,然后证明 ∠AOC=∠BOC.
D
P
C
E
B
证明:∵PD⊥OA,PE⊥OB,
∴∠PDO =∠PEO = 90°.
已知:OC是∠AOB的平分线,点P在 OC上,PD ⊥OA ,PE ⊥OB.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题1、如图,OQ 平分∠AOB ,点P 为OQ 上一点,过点P 作一直线分别交OA 、OB 于点M 、N ,若OP =a ,∠AOB =α,则ON
OM 11+
是否为定值?【解析】
方法一、相似法
过点P 作PE ∥OA
△NPE ∽△NMO ,∴OM PE ON NE =,即OM PE ON OE -ON =,即1=+OM
PE ON OE 易证△OPE 为等腰三角形,∴OE =PE ∴OE ON OM 111=+/PE 1,2
2αcos OP OE =∴
OP 2a cos ON OM 211=+.方法二、面积法
过点P 分别向OA 、OB 作垂线,垂足分别为E 、
F
ONP OMP MON S S S △△△+=,即ONsinαOM αsin OP ON αsin OP OM ⋅=⋅⋅+⋅⋅2
121212121化简得αsin OP sinαON OM OM ON 21⋅=⋅+,由于sinα=2sin α21αcos 21⋅.化简完即为OP 2
a cos ON OM 211=
+by 万开同老师
【思考】
①条件有哪些隐晦的表达方式?
例如:角平分线可以如何隐藏?如何设置好背景,避开结果中三角函数值的出现?②结论可以作哪些延伸问法?例如:ON OM 11+化简后为ON
OM ON OM ⋅+,既然为定值,若再添加“OM +ON 为定值”,则可提问△OMN 的面积问题.
例如:由于结果涉及到α2
1的三角函数值,所以一般条件会设置好角度,比如120°、90°、60°,那么结果将只与线段OP 相关.所以若∠AOB 不变,当OP 发生变化时,必然有ON
OM 11+的最值问题.【习题】
1、(2105·河池)如图,菱形ABCD 的边长为1,直线l 过点C ,交AB 的延长线于M ,交AD 的延长线于N ,则AN
AM 11+是否为定值?
2、(2015·无锡)如图,C 为∠AOB 的边OA 上一点,OC =6,N 为边OB 上异于点O 的一动点,P 是线段CN 上一点,过点P 分别作PQ ∥OA 交OB 于点Q ,PM ∥OB 交OA 于点M .当点N 在边OB 上运动时,四边形OMPQ 始终保持为菱形.问:1OM -1ON
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
3、在直角坐标系xOy 中,已知反比例函数y =
x k (x >0)图象经过点(4,3),点D 为反比例函数y =x
k (x >0)上的任意一点,以D 为圆心的圆始终与y 轴相切于点A .如图,当⊙D 与x 轴相切于点E 时,过点D 作直线l ,分别交x 轴的正半轴于点M ,交y 轴的正半轴于点N ,则ON
OM 11+是否为定值?若是,请证明:若不是,请说明理由.
4、(2018·锡山区期末)如图,已知二次函数c bx x -y ++=23
1的图像与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点C (0,3),且抛物线的对称轴为直线x =3.
(1)直接写出b 的值及点A 的坐标;
(2)∠BAC 的平分线交y 轴于点D ,过点D 的直线l 与射线AC ,AB 分别交于点M ,N .当直线l 绕点D 旋转时,AN AM 11+是否为定值,若是,求出这个值,若不是,说明理由.
5、(2015·慈溪市一模)在平面直角坐标系中△ABC 的边AB 在x 轴上,且OA >OB ,以AB 为直径的⊙P 过点C ,若C 的坐标为(0,2),AB =5,经过A 、B 、C 三点的抛物线为c bx ax y ++=2.
(1)求点A 、B 的坐标及抛物线的解析式.
(2)若∠ACB 的平分线所在的直线l 交x 轴于点D ,交圆于点E .
①求证:PE ⊥x 轴;
②试求直线l 对应的一次函数的解析式.
(3)过点D 任作一直线l 分别交射线CA ,CB (点C 除外)于点M ,N ,则
CN CM 11+的值是否为定值?若是,求出定值;若不是,请说明理由.。
