材料力学(第八讲)
合集下载
《材料力学》第八章课后习题参考答案
解题方法与技巧归纳
受力分析
在解题前首先要对物体进行受力分析， 明确各力的大小和方向，以便后续进 行应力和应变的计算。
图形结合
对于一些复杂的力学问题，可以画出 相应的示意图或变形图，帮助理解和 分析问题。
公式应用
熟练掌握材料力学的相关公式，能够 准确应用公式进行计算和分析。
检查结果
在解题完成后，要对结果进行检查和 验证，确保答案的正确性和合理性。
压杆稳定
探讨细长压杆在压缩载荷作用下的稳定性问题。
解题方法与技巧
准确理解题意
仔细审题，明确题目要求和考查的知识点。
选择合适的公式
根据题目类型和所给条件，选用相应的公式 进行计算。
注意单位换算
在计算过程中，要注意各物理量的单位换算， 确保计算结果的准确性。
检查答案合理性
得出答案后，要检查其是否符合实际情况和 物理规律，避免出现错误。
相关题型拓展与延伸
组合变形问题
超静定问题
涉及多种基本变形的组合，如弯曲与扭转 的组合、拉伸与压缩的组合等，需要综合 运用所学知识进行分析和计算。
超静定结构是指未知力数目多于静力平衡 方程数目的结构，需要通过变形协调条件 或力法、位移法等方法进行求解。
稳定性问题
疲劳强度问题
研究细长压杆在压力作用下的稳定性问题 ，需要考虑压杆的临界力和失稳形式等因 素。
研究材料在交变应力作用下的疲劳破坏行为 ，需要了解疲劳极限、疲劳寿命等概念和计 算方法。
THANKS FOR WATCHING
感谢您的观看
重点知识点回顾
材料的力学性质
包括弹性、塑性、强度、硬度等基本概念和 性质。
杆件的拉伸与压缩
涉及杆件在拉伸和压缩状态下的应力、应变及 变形分析。
材料力学第八章应力状态分析
2
四、最大剪应力
max
※解题注意事项：
1 3
2
⒈ 上述公式中各项均为代数量，应用公式解题时，首先
应写清已知条件。
⑴x、y 以拉为正，以压为负； ⑵x 沿单元体顺时针转为正，逆时针转为负； ⑶ 为斜截面的外法线与x 轴正向间夹角，逆时针转为 正，顺时针转为负。
⒉ 求得主应力ˊ、〞与0排序，确定1、2、3的值。 ⒊ 0为主应力ˊ所在截面的外法线与x 轴正向间夹角， 逆时针转为正，顺时针转为负。
x 1
圆上D1点代表x 截面； D2点代表y 截面；
E点代表方位为 角的斜截面； A1、 A2 点代表两个主平面。
1、单元体各斜截面与圆上各点相对应（点面相对应） 结论 2、圆上各点横、纵坐标与各斜截面的正、剪应力对应。
3、转向相同，夹角两倍关系
x
A1
2
D1
y x y
y x x
y 0,
x 40MPa,
' 80 0 80 0 2 ( ) 40 2 40 56.57 " 2 2
1 16.57 MPa, 2 0, 3 96.57 MPa 1 max [(16.57 (96.57)] 56.57 MPa 2
x cos2 y sin 2 x sin 2
1 cos 2 1 cos 2 x y x sin 2 2 2 x y x y cos 2 x sin 2 2 2
同理，由
F
F
z zy
yx xy
yz zy
zx xz
A
A
四、最大剪应力
max
※解题注意事项：
1 3
2
⒈ 上述公式中各项均为代数量，应用公式解题时，首先
应写清已知条件。
⑴x、y 以拉为正，以压为负； ⑵x 沿单元体顺时针转为正，逆时针转为负； ⑶ 为斜截面的外法线与x 轴正向间夹角，逆时针转为 正，顺时针转为负。
⒉ 求得主应力ˊ、〞与0排序，确定1、2、3的值。 ⒊ 0为主应力ˊ所在截面的外法线与x 轴正向间夹角， 逆时针转为正，顺时针转为负。
x 1
圆上D1点代表x 截面； D2点代表y 截面；
E点代表方位为 角的斜截面； A1、 A2 点代表两个主平面。
1、单元体各斜截面与圆上各点相对应（点面相对应） 结论 2、圆上各点横、纵坐标与各斜截面的正、剪应力对应。
3、转向相同，夹角两倍关系
x
A1
2
D1
y x y
y x x
y 0,
x 40MPa,
' 80 0 80 0 2 ( ) 40 2 40 56.57 " 2 2
1 16.57 MPa, 2 0, 3 96.57 MPa 1 max [(16.57 (96.57)] 56.57 MPa 2
x cos2 y sin 2 x sin 2
1 cos 2 1 cos 2 x y x sin 2 2 2 x y x y cos 2 x sin 2 2 2
同理，由
F
F
z zy
yx xy
yz zy
zx xz
A
A
材料力学 第八章：应力状态分析
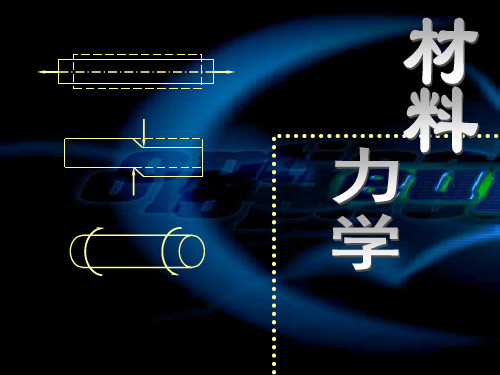
2 )2
材料力学
整理可得：
(
x
2
y
)2
2
(
x
2
y
)2
x2
(3)
(3)式为以 、为变量的圆方程。
圆心坐标
(
x
y
,0)
横坐标为平均应力
2
半径
(
x
2
y
)2
2 x
为最大剪应力
材料力学
x x
y
x y
2
(
x
2
y
)2
2 x
材料力学
方法一：
27.5
x
2
y
x
y
2
cos(2 27.5) x
sin(2 27.5)
70 70 cos55 50sin 55 22
96MPa
96MPa
27.5
70MPa
62.5 50MPa 26MPa
117.5
x
上的应力对应-坐标系中的Dy点。Dy
点的横坐标
OF
、纵坐标
y
FDy
y
;连接
Dx、Dy与轴的交点C为圆心 , CDx 或
CDy 为半径画一圆，这个圆是该单元
体所对应的应力圆。
材料力学
n
y
x
y
x
x
y
F o
Dy
(y,y)
Dx(x,x) CK
材料力学
证明：
DxCK DyCF (对顶角) Dy FC DxKC (直角)
北京交通大学材料力学八组合变形PPT课件
第八章 组合变形
§8-1 组合变形的叠加原理 §8-2 拉伸或压缩与弯曲的组合 §8-3 偏心压缩和截面核心 §8-4 扭转与弯曲的组合
§8-1 组合变形的叠加原理
一、组合变形的概念
构件在荷载作用下发生两种或两种以上的基本变形,则构件的变形称为组合变形.
拉伸（压缩）与弯曲的组合；偏心压缩；扭转与弯曲的组合
A
最大切应力及方位
d d
2[
x
y cos 2
2
xy sin 2 ]
0
tan 21
x 2 xy
y
11 90
max min
(
x
2
y
)2
2 xy
1 2
max
min
直接将1 和1 +90代入公式计算出最大最小切应力
• 最大切应力(第三强度)理论： r3 1 3
• 畸变能密度(第四强度)理论：
r4
1 2
1
2 2
2
3 2
1
3 2
三向拉伸状态,无论是塑性还是脆性都发生脆性破坏,选用第一或第二强度理论; 三向压缩状态时,无论是塑性还是脆性都发生塑性破坏,选用第三或第四强度理论.
2.偏心拉伸（压缩）组合变形——单向偏心拉伸（压缩）时，分解为轴向拉伸（压缩）和 一个平面弯曲，双向偏心拉伸（压缩）时，分解为轴向拉伸（压缩）和两个形心主惯性平 面内的平面弯曲。 3. 弯曲和扭转组合变形——分解为平面弯曲和扭转；
组合变形的强度计算：
1.危险点为单向应力状态：拉（压）弯、偏心拉伸（压缩）组合变 形的强度计算时只需求出危险点的最大正应力并与材料的许用正应 力比较即可
蔡中兵《材料力学》8组合变形及连接部分的计算
叠加之后是两个互相垂直方向的平面弯曲的组合。
盐城工学院力学课程组
材料力学
mechanics of materials
F2 a m
z F1 C(y,z)
O
z
my
y
x
m z
O Mz
My m y
求应力：m-m截面上第一象限某点C(y，z)
(1) F2单独作用下 (2) F1单独作用下
M z F2 ( x a)
O1
A(yF,zF)
y
x
FF
z
e
y
Fe
盐城工学院力学课程组
材料力学
mechanics of materials
F 使杆发生拉伸变形
My 使杆发生xOz平面内的弯 曲变形（y 为中性轴）
Mz 使杆发生 xOy 平面内的弯 曲变形（z 为中性轴）
x
F
z
My O1 Mz
y
盐城工学院力学课程组
材料力学
mechanics of materials
M y F1 x,
M z F2 ( x a)
盐城工学院力学课程组
材料力学
mechanics of materials
F2 m
a
z F1 C(y,z)
O
z
my
y
x
m z
O Mz
My m y
在F2 单独作用下，梁在竖直平面内发生平面弯曲， z轴为中性轴。
在F1 单独作用下，梁在水平平面内发生平面弯曲， y轴为中性轴。
具有双对称截 面的梁，它在任何 一个纵向对称面内 弯曲时均为平面弯 曲。
故具有双对称截面的梁在两个纵向对称面内同时承受横向 外力作用时，在线弹性且小变形情况下，可以分别按平面弯曲 计算每一弯曲情况下横截面上的应力和位移，然后叠加。
《材料力学》第八章组合变形
解 (1)外力分析，确定变形类型—拉弯组合；
（2）内力分析，确定危险截面—整个轴；
M=600(kN·cm) FN=15(kN)
(3)应力计算，确定危险点—ａ、b点；
P产生拉伸正应力： t
FN AFNd 2源自4FNd 24
M拉产弯生组弯合曲：的正应力：wmax
M Wy
M
d3
32
32M
d3
P M= a Pe
补例8.1 已知： P=2kN,L求=：1mσm,Iazx=628×104mm4,Iy=64×1040mm2740 2844
解:1.分解P力。 Py Pcos φ Pz Psin φ 2．画弯矩图，确定危险截面--固定端截面。 3．画应力分布图，确定危险点—A、 B点
σ” σ’
A
x
y
Pyl
M
z
践中，在计算中，往往忽略轴力的影响。
4.大家考虑扭转、斜弯曲与拉（压）的组合怎么处理？
例8.5 图8.14a是某滚齿机传动轴AB的示意图。轴的直径为35 mm，材料为45钢， [σ]=85 MPa。轴是由P=2.2kW的电动机通过
带轮C带动的，转速为n=966r／min。带轮的直径为D=132 mm，
Mz Py l - x Pcosφ l - x Mcosφ My Pz l - x Psinφ l - x Msinφ
式中的总弯矩为：M Pl- x
3.计算两个平面弯曲的正应力。在x截面上任取一点A(z 、y)，
与弯矩Mz、My对应的正应力分别为σ’和σ”，故
- Mz y , - M yz
第八章 组合变形
基本要求: 掌握弯曲与拉伸（或压缩）的组合、扭转与弯曲的组合 的强度计算。
重点： 弯曲与拉伸（或压缩）的组合，扭转与弯曲的组合。
（2）内力分析，确定危险截面—整个轴；
M=600(kN·cm) FN=15(kN)
(3)应力计算，确定危险点—ａ、b点；
P产生拉伸正应力： t
FN AFNd 2源自4FNd 24
M拉产弯生组弯合曲：的正应力：wmax
M Wy
M
d3
32
32M
d3
P M= a Pe
补例8.1 已知： P=2kN,L求=：1mσm,Iazx=628×104mm4,Iy=64×1040mm2740 2844
解:1.分解P力。 Py Pcos φ Pz Psin φ 2．画弯矩图，确定危险截面--固定端截面。 3．画应力分布图，确定危险点—A、 B点
σ” σ’
A
x
y
Pyl
M
z
践中，在计算中，往往忽略轴力的影响。
4.大家考虑扭转、斜弯曲与拉（压）的组合怎么处理？
例8.5 图8.14a是某滚齿机传动轴AB的示意图。轴的直径为35 mm，材料为45钢， [σ]=85 MPa。轴是由P=2.2kW的电动机通过
带轮C带动的，转速为n=966r／min。带轮的直径为D=132 mm，
Mz Py l - x Pcosφ l - x Mcosφ My Pz l - x Psinφ l - x Msinφ
式中的总弯矩为：M Pl- x
3.计算两个平面弯曲的正应力。在x截面上任取一点A(z 、y)，
与弯矩Mz、My对应的正应力分别为σ’和σ”，故
- Mz y , - M yz
第八章 组合变形
基本要求: 掌握弯曲与拉伸（或压缩）的组合、扭转与弯曲的组合 的强度计算。
重点： 弯曲与拉伸（或压缩）的组合，扭转与弯曲的组合。
材料力学课件第八章 组合变形-3-4
(
3
2
1 )2
2
2 3 2
3
M2
2
W02W0.75T3d22WM3 ,2,
W pWT1pd63
圆截面杆弯扭组合变形时的相当应力：
[ ] r3
M2 T2 W
[ ] r4
M 2 0.75T 2 W
d3
W 32
8.3 弯拉（压）组合
弯曲与拉伸（压缩）组合变形：当杆上的外力除横向力外，
还受有轴向拉（压）力时，所发生的组合变形。
q
F
F
y
x
一、计算方法：
1.分别计算轴向力引起的正应力和横力弯曲引起的正应力； 2.按叠加原理求正应力的代数和。
二、注意事项：
1.如果材料许用拉应力和许用压应力不同，且横截面部分区 域受拉，部分区域受压，应分别计算出最大拉应力和最大压应 力，并分别按拉伸、压缩进行强度计算。
=+
10
t,max
=+
c,max
c
F A
t,max
=+
t,max
Fl W
c,max
c,max
Fl W
t,max
Fl W
F A
[ t ]
c,max
Fl W
F A
[ c ]
偏心拉伸或压缩：
F
MZ=Fb
F
My=Fa
FN F A cd
My Wy
Fa dc2
6
Mz Wz
Fb cd 2
6
8.4弯曲与扭转的组合变形 F
Fl Fa
F Fa
A截面为危险截面：
M Fl T Fa
k1
M
W
材料力学第8章-能量法
能量法/超静定问题 力法
能量法/超静定问题 力法
A
B
F
C
A
B
F
X1
A
B
F
X1
例 如图超静定梁, EI为常数,试求B点的约束反力。
解: (1) 判断超静定次数:
一次超静定!
(2) 解除多余约束,构造静定基:
B. 解除B点的可动铰支座,补充横向集中反力
A. 解除A点固定端的转动约束变为固定铰支座, 补充反力偶作用
单位力偶作用下的弯矩图
力F作用下的弯矩图
能量法/超静定问题 力法
Fa/2-Fa2/[4(a+b)]
Fa2/[4(a+b)]
1
1
1
Fa/2
根据力法正则方程：
M10
MF
根据图形互乘法：
所以有：
则：
弯矩图如图所示
能量法/超静定问题 力法
A，B两点有无相对水平位移？如何计算？
F
X1
X1
F/2
F/2
能量法/超静定问题 力法
qa2/2
qa2/2
a
a
1
a
1
解：为两次超静定问题。解除A点的约束， 并作用水平和铅垂的单位集中力。
在静定基上分别作均布力和两个单位集中 力的弯矩图如下图所示。
令水平力为‘第一’个未知反力，铅垂力为第二个。
能量法/超静定问题 力法
根据图形互乘法有：
1
代入力法正则方程：
2
有：
3
能量法/超静定问题 力法
F/2
F/2
结构由三次超静定转化为一次超静定问题。
能量法/超静定问题 力法
1
1
1
能量法/超静定问题 力法
A
B
F
C
A
B
F
X1
A
B
F
X1
例 如图超静定梁, EI为常数,试求B点的约束反力。
解: (1) 判断超静定次数:
一次超静定!
(2) 解除多余约束,构造静定基:
B. 解除B点的可动铰支座,补充横向集中反力
A. 解除A点固定端的转动约束变为固定铰支座, 补充反力偶作用
单位力偶作用下的弯矩图
力F作用下的弯矩图
能量法/超静定问题 力法
Fa/2-Fa2/[4(a+b)]
Fa2/[4(a+b)]
1
1
1
Fa/2
根据力法正则方程：
M10
MF
根据图形互乘法：
所以有：
则：
弯矩图如图所示
能量法/超静定问题 力法
A，B两点有无相对水平位移？如何计算？
F
X1
X1
F/2
F/2
能量法/超静定问题 力法
qa2/2
qa2/2
a
a
1
a
1
解：为两次超静定问题。解除A点的约束， 并作用水平和铅垂的单位集中力。
在静定基上分别作均布力和两个单位集中 力的弯矩图如下图所示。
令水平力为‘第一’个未知反力，铅垂力为第二个。
能量法/超静定问题 力法
根据图形互乘法有：
1
代入力法正则方程：
2
有：
3
能量法/超静定问题 力法
F/2
F/2
结构由三次超静定转化为一次超静定问题。
能量法/超静定问题 力法
1
1
1