数学建模习题--第五章
数学建模之软件篇Mathematica使用介绍

第一章 数学软件Mathematica简介
6.%在Mathematica中代表什么含义
几乎所有的计算都可能用到前面已经计算好的结果,这时 Mathematica提供了一种简单的调用方式:
第一章 数学软件Mathematica简介
7.如何计算结果的近似值
在实际应用中,我们通常需要的是一个精确度很高的数值结果, 而不是一个绝对准确但表示非常复杂的结果,比如Sin[2/3]或者一个 一元四次方程的解。但如果参与运算的量都是精确的,则Mathematica 按精确值的方式输出。我们常用N函数把结果转换为数值结果。
表称为List,是由大括号“{ }”括起来的若干元素,元素间用逗号分 隔。其直接形式为:表名={元素1,元素2,…}。所以Mathematica中的表 其实就是我们通常所用的集合。它可以用来表示集合、矩阵、数组、向 量、数列等一些我们在计算机中常用的结构。 (1)参数表 在后面的学习中,我们经常会在Mathematica的内部函数的参数中看见 大括号,这就是参数表。下面我们列出常用参数表的含义:
取值范围可以是:Intergers,Rationals,Real,Complexes(即整数,有 理数,实数,复数)。
例:
第二章 初等数学篇
7.Mathematica中常用的多项式操作函数
在Mathematica中,你可以对多项式(包括一元和多元多项式)直接 进行加、减、乘、除、乘方等运算,此外系统还提供了丰富的函数以满足 用户对多项式操作的需要。 下面给出多项式的常用操作函数:
第二章 初等数学篇
3.Mathematica中的表指什么
(5)表的运算
第二章 初等数学篇
4.如何求解一元n次方程
解一元多项式方程主要的函数是Solve,该函数的目标是尽量找出方程 的精确解。Mathematica总可以解出四阶及以下的多项式方程,对于三次或 四次方程,结果可能相当复杂。在解四次以上的多项式方程时, Mathematica碰到数学理论上的障碍(即一般的四次以上的多项式方程不能 根式求解)而可能给不出精确解,但总可以给出数值解,并且对某些高次 方程Solve是可以给出精确结果的.
微积分的应用雨中行走 药物浓度 水流问题 最速降线

•前表面淋雨量
C2
(v cos
v
u
I )wh(L
/
u)
v cos u I是前面的降雨强度。
v
•总淋雨量(基本模型)
C
C1
C2
wdL [sin
u
h d
(v cos
v
u)]
因为考虑了降雨的方向,淋湿的部位只有顶部和前
面。分两部分计算淋雨量。
取参数v 4m / s, I 2cm / h
第五章 微积分的应用
本章通过用学习过的高等数学知识解决一些简单的问题, 以增加同学们学习数学的兴趣和应用数学的能力。同时,也 通过对其中一些问题的不断深入讨论来体会数学建模没有最 好、只有更好的精神。
1. 雨中行走问题 2. 体内药物浓度的变化 3. 水的流出问题 4. 最速降线问题
1. 雨中行走问题
16
2. 体内药物浓度的变化
医生给病人开处方时必须注明两点:服药的剂量 和服药的时间间隔。超剂量的药物会对患者产生不 良的后果,甚至死亡;剂量不足,则不能达到治疗 的效果。已知患者服药后,随时间推移,药物在体 内被逐渐吸收,发生化学反应,也就是体内药物的 浓度逐渐降低。药物浓度降低的速率与体内当时药 物的浓度成正比。当服药量为A、服药时间间隔为T 时,试分析体内药物的浓度随时间的变化规律。
2)在同样时间内,水从小孔流出的体积为 BS
--- S是从小孔流出的水时在时间段 内流t 经的距离
由质量守恒得
Ah BS
两端同除以 ,t 并令 t取极0 限得
25
可得一阶方程: dh B ds
dt
A dt
由于 ds v, 代入上式得 dt
计算机仿真-数学建模

§2 对偶理论与灵敏度分析
• 2.1 原始问题和对偶问题
1.对偶问题 考虑下列一对线性规划模型:
max cT x s.t. Ax b, x 0 (P) min bT y 和 s.t. AT y c, y 0 (D)
称(P)为原始问题,(D)为它的对偶问题。 不太严谨地说,对偶问题可被看作是原始问题的“行列转置”:原始
1.1 线性规划的实例与定义
例1 某机床厂生产甲、乙两种机床,每台销售后的利润 分别为4000元与3000元。生产甲机床需用 机器加工, 加工时间分别为每台2小时和1小时;生产乙机床需用 三 种机器加工,加工时间为每台各一小时。若每天可用于 加工的机器时数分别为 机器10小时、 机器8小时和 机器 7小时,问该厂应生产甲、乙机床各几台,才能使总利润 最大?
为线性函数,故被称x为1,线x2性规0 划问题。
1.2线性规划的Matlab标准形式
• 线性规划的目标函数可以是求最大值,也可以是求最
小值,约束条件的不等号可以是小于号也可以是大于
号。为了避免这种形式多样性带来的不便,Matlab中
规定线性规划的标准形式为
min cT x such that Ax b
问题中的第 列系数与其对偶问题中的第 行的系数相同;原始目标函数的 各个系数行与其对偶问题右侧的各常数列相同;原始问题右侧的各常数 列与其对偶目标函数的各个系数行相同;在这一对问题中,不等式方向 和优化方向相反。
对偶问题的基本性质
14、 可对行称解性是:最对优偶解问时题的的性对质偶:是设原问是题原。问题的可行解, 2是、对弱偶对问偶题性的:可若行解是,原当问题时的,可是行最解优,解是。对偶问题的可 行5、解对。偶则定存理在:。若原问题有最优解,那么对偶问题也有最 3优、解无;界且性目:标若函原数问值题相(同对。偶问题)为无界解,则其对偶 问6、题互(补原松问弛题性):无若可分行别解是。原问题和对偶问题的最优解。
数学建模测试题-线性规划部分
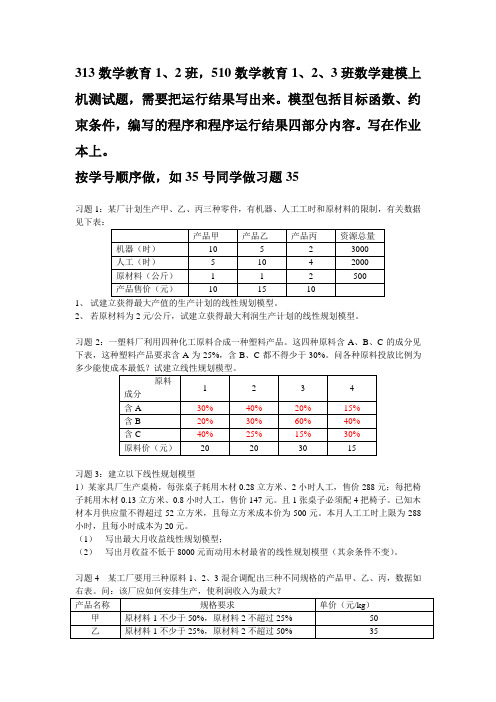
313数学教育1、2班,510数学教育1、2、3班数学建模上机测试题,需要把运行结果写出来。
模型包括目标函数、约束条件,编写的程序和程序运行结果四部分内容。
写在作业本上。
按学号顺序做,如35号同学做习题35习题1:某厂计划生产甲、乙、丙三种零件,有机器、人工工时和原材料的限制,有关数据1、2、若原材料为2元/公斤,试建立获得最大利润生产计划的线性规划模型。
习题2:一塑料厂利用四种化工原料合成一种塑料产品。
这四种原料含A、B、C的成分见下表,这种塑料产品要求含A为25%,含B、C都不得少于30%。
问各种原料投放比例为习题3:建立以下线性规划模型1)某家具厂生产桌椅,每张桌子耗用木材0.28立方米、2小时人工,售价288元;每把椅子耗用木材0.13立方米、0.8小时人工,售价147元。
且1张桌子必须配4把椅子。
已知木材本月供应量不得超过52立方米,且每立方米成本价为500元。
本月人工工时上限为288小时,且每小时成本为20元。
(1)写出最大月收益线性规划模型;(2)写出月收益不低于8000元而动用木材最省的线性规划模型(其余条件不变)。
习题4 某工厂要用三种原料1、2、3混合调配出三种不同规格的产品甲、乙、丙,数据如右表。
问:该厂应如何安排生产,使利润收入为最大?习题5、某部门现有资金200万元,今后五年内考虑给以下的项目投资。
已知:项目A :从第一年到第五年每年年初都可投资,当年末能收回本利110%;项目B :从第一年到第四年每年年初都可投资,次年末能收回本利125%,但规定每年最大投资额不超过30万元;项目C :需在第三年年初投资,第五年末能收回本利140%,但规定最大投资额不能超过80万元;项目D :需在第二年年初投资,第五年末能收回本利155%,但规定最大投资额不能超过100万元;问:a.应如何确定这些项目的每年投资额,使得第五年年末拥有资金的本利金额为最大? b.应如何确定这些项目的每年投资额,使得第五年年末拥有资金的本利在330万元的基础上使得其投资总的风险系数为最小?习题6 某公司计划在三年的计划期内,有四个建设项目可以投资:项目Ⅰ从第一年到第三年年初都可以投资。
高中数学 第五章 三角函数 5.5 三角恒等变换 5.5.2 简单的三角恒等变换精品练习(含解析)新

5.5.2 简单的三角恒等变换知识点三 三角恒等变换的应用7.函数y =cos 2ωx -sin 2ωx (ω>0)的最小正周期是π,则函数f (x )=2sin ⎝ ⎛⎭⎪⎫ωx +π4的一个单调递增区间是( )A.⎣⎢⎡⎦⎥⎤-π2,π2B.⎣⎢⎡⎦⎥⎤5π4,9π4C.⎣⎢⎡⎦⎥⎤-π4,3π4D.⎣⎢⎡⎦⎥⎤π4,5π48.在△ABC 中,求证:tan A 2tan B 2+tan B 2tan C 2+tan C 2tan A2=1.9.如图所示,要把半径为R 的半圆形木料截成长方形,应怎样截取,才能使△OAB 的周长最大?关键能力综合练 一、选择题1.设5π<θ<6π,cos θ2=a ,则sin θ4等于( )A.1+a 2 B.1-a2 C .-21+a2D .-21-a22.若2sin x =1+cos x ,则tan x2的值等于( )A.12B.12或不存在学科素养升级练1.(多选题)对于函数f (x )=sin x +3cos x ,给出下列选项其中不正确的是( )A .函数f (x )的图象关于点⎝ ⎛⎭⎪⎫π6,0对称B .存在α∈⎝⎛⎭⎪⎫0,π3,使f (α)=1C .存在α∈⎝ ⎛⎭⎪⎫0,π3,使函数f (x +α)的图象关于y 轴对称D .存在α∈⎝⎛⎭⎪⎫0,π3,使f (x +α)=f (x +3α)恒成立 2.已知A +B =2π3,那么cos 2A +cos 2B 的最大值是________,最小值是________.3.(学科素养—数学建模)如图所示,已知OPQ 是半径为1,圆心角为π3的扇形,四边形ABCD 是扇形的内接矩形,B ,C 两点在圆弧上,OE 是∠POQ 的平分线,E 在PQ 上,连接OC ,记∠COE =α,则角α为何值时矩形ABCD 的面积最大?并求最大面积.5.5.2 简单的三角恒等变换必备知识基础练1.解析:∵3π<θ<7π2,sin θ=-35,∴cos θ=-1-⎝ ⎛⎭⎪⎫-352=-45,∵3π<θ<7π2,∴3π2<θ2<7π4.则tan θ2=-1-cos θ1+cos θ=-1+451-45=-3. 答案:B2.解析:因为2π<θ<3π,所以π<θ2<3π2.又cos θ=m ,所以sin θ2=-1-cos θ2=-1-m2,故选A. 答案:A3.解析:y =1+cos ⎝ ⎛⎭⎪⎫2x -π62+1-cos ⎝ ⎛⎭⎪⎫2x +π62-1=12⎣⎢⎡⎦⎥⎤cos ⎝ ⎛⎭⎪⎫2x -π6-cos ⎝ ⎛⎭⎪⎫2x +π6=12sin 2x ,是奇函数.故选A.答案:A4.解析:f (x )=sin x -cos ⎝⎛⎭⎪⎫x +π6=sin x -32cos x +12sin x =32sin x -32cos x =3sin ⎝⎛⎭⎪⎫x -π6,所以函数f (x )的值域为[-3,3],故选B. 答案:B5.解析:∵f (x )=2⎝ ⎛⎭⎪⎫12sin x -32cos x =2sin ⎝ ⎛⎭⎪⎫x -π3.∴f (x )∈[-2,2]. 答案:[-2,2]6.解析:(1)2(cos x -sin x )=2×2⎝⎛⎭⎪⎫22cos x -22sin x=2⎝ ⎛⎭⎪⎫cos π4cos x -sin π4sin x =2cos ⎝ ⎛⎭⎪⎫π4+x .(2)315sin x +35cos x =65⎝⎛⎭⎪⎫32sin x +12cos x=65⎝ ⎛⎭⎪⎫sin π3sin x +cos π3cos x =65cos ⎝ ⎛⎭⎪⎫x -π3.7.解析:y =cos 2ωx -sin 2ωx =cos 2ωx (ω>0), 因为函数的最小正周期为π,故2π2ω=π,所以ω=1.则f (x )=2sin ⎝ ⎛⎭⎪⎫ωx +π4=2sin ⎝ ⎛⎭⎪⎫x +π4. 由2k π-π2≤x +π4≤2k π+π2,得2k π-3π4≤x ≤2k π+π4(k ∈Z ),当k =1时,函数的一个单调递增区间是⎣⎢⎡⎦⎥⎤5π4,9π4.答案:B8.证明:∵A ,B ,C 是△ABC 的三个内角, ∴A +B +C =π,从而有A +C 2=π2-B2.左边=tan B 2⎝ ⎛⎭⎪⎫tan A2+tan C 2+tan A 2tan C2=tan B 2tan ⎝ ⎛⎭⎪⎫A 2+C 2⎝ ⎛⎭⎪⎫1-tan A 2tan C 2+tan A 2tan C2=tan B 2tan ⎝ ⎛⎭⎪⎫π2-B 2⎝ ⎛⎭⎪⎫1-tan A 2tan C 2+tan A 2tan C2=1-tan A 2tan C 2+tan A 2tan C2=1=右边, ∴等式成立.9.解析:设∠AOB =α,则0<α<π2,△OAB 的周长为l ,则AB =R sin α,OB =R cos α, ∴l =OA +AB +OB =R +R sin α+R cos α =R (sin α+cos α)+R =2R sin ⎝ ⎛⎭⎪⎫α+π4+R . ∵0<α<π2,∴π4<α+π4<3π4.∴l 的最大值为2R +R =(2+1)R , 此时,α+π4=π2,即α=π4,即当α=π4时,△OAB 的周长最大.关键能力综合练1.解析:若5π<θ<6π,则5π4<θ4<3π2,则sin θ4=-1-cosθ22=-1-a2=-21-a2. 答案:D2.解析:由已知得sin x 1+cos x =12,tan x2=sinx2cosx2=2sin x 2cosx22cos 2x 2=sin x 1+cos x =12.当x =π+2k π,k ∈Z 时,tan x2不存在.答案:B3.解析:由题意可知,a =sin 24°,b =sin 26°,c =sin 25°,而当0°<x <90°,y =sin x 为增函数,∴a <c <b ,故选C.答案:C 4.解析:cos ⎝⎛⎭⎪⎫2π3+2α=2cos 2⎝ ⎛⎭⎪⎫π3+α-1.∵⎝ ⎛⎭⎪⎫π6-α+⎝ ⎛⎭⎪⎫π3+α=π2, ∴cos ⎝ ⎛⎭⎪⎫π3+α=sin ⎝ ⎛⎭⎪⎫π6-α=13.∴cos ⎝⎛⎭⎪⎫2π3+2α=2×⎝ ⎛⎭⎪⎫132-1=-79.故选A.答案:A5.解析:由cos α=-45,α是第三象限角,可得sin α=-1-cos 2α=-35.所以1+tan α21-tan α2=cos α2+sin α2cos α2-sin α2=1+sin αcos α=1-35-45=-12.答案:A6.解析:f (x )=2cos 2x +3sin 2x +a =1+cos 2x +3sin 2x +a =2sin ⎝⎛⎭⎪⎫2x +π6+a +1. 当x ∈⎣⎢⎡⎦⎥⎤0,π2时,2x +π6∈⎣⎢⎡⎦⎥⎤π6,7π6, ∴f (x )min =2·⎝ ⎛⎭⎪⎫-12+a +1=-4. ∴a =-4. 答案:C7.解析:1+sin 2=sin 21+cos 21+2sin 1cos 1 =sin 1+cos 12=|sin 1+cos 1|,因为1∈⎝⎛⎭⎪⎫0,π2,所以sin 1>0,cos 1>0,则1+sin 2=sin 1+cos 1. 答案:sin 1+cos 18.解析:由25sin 2θ+sin θ-24=0, 又θ是第二象限角,得sin θ=2425或sin θ=-1(舍去).故cos θ=-1-sin 2θ=-725,由cos2θ2=1+cos θ2得cos2θ2=925. 又θ2是第一、三象限角,所以cos θ2=±35.答案:±359.解析:y =sin 2x +sin x cos x +1=1-cos 2x 2+sin 2x 2+1=22sin ⎝⎛⎭⎪⎫2x -π4+32.最小正周期T =2π2=π.令-π2+2k π<2x -π4<π2+2k π,k ∈Z ,解得-π8+k π<x <3π8+k π,k ∈Z .所以f (x )的单调递增区间是⎝ ⎛⎭⎪⎫k π-π8,k π+3π8(k ∈Z ).答案:π ⎝ ⎛⎭⎪⎫k π-π8,k π+3π8,k ∈Z10.证明:左边=2sin 2x cos 2x 2cos 22x ·cos 2x 1+cos 2x ·cos x1+cos x =sin 2x 1+cos 2x ·cos x 1+cos x =2sin x cos x 2cos 2x ·cos x1+cos x =sin x 1+cos x =2sin x 2cosx22cos2x 2=tan x2=右边. 所以原等式成立.学科素养升级练1.解析:函数f (x )=sin x +3cos x =2sin ⎝⎛⎭⎪⎫x +π3,对于A :函数f (x )=2sin ⎝ ⎛⎭⎪⎫x +π3,当x =π6时,2sin ⎝ ⎛⎭⎪⎫π6+π3=2,不能得到函数f (x )的图象关于点⎝ ⎛⎭⎪⎫π6,0对称.∴A 不对.对于B :α∈⎝ ⎛⎭⎪⎫0,π3,可得α+π3∈⎝ ⎛⎭⎪⎫π3,2π3,f (α)∈(3,2],不存在f (α)=1.∴B 不对.对于C :函数f (x +α)的对称轴方程为:x +α+π3=π2+k π,可得x =k π+π6-α(k ∈Z ),当k =0,α=π6时,可得图象关于y 轴对称.∴C 对.对于D :f (x +α)=f (x +3α)说明2α是函数的周期,函数f (x )的周期为2π,故α=π,∴不存在α∈⎝⎛⎭⎪⎫0,π3,使f (x +α)=f (x +3α)恒成立,∴D 不对.故选A ,B ,D.答案:ABD2.解析:∵A +B =2π3,∴cos 2A +cos 2B =12(1+cos 2A +1+cos 2B )=1+12(cos 2A +cos 2B )=1+cos(A +B )cos(A -B )=1+cos 2π3·cos(A -B )=1-12cos(A -B ),∴当cos(A -B )=-1时, 原式取得最大值32;当cos(A -B )=1时,原式取得最小值12.答案:32123.word - 11 - / 11解析:如图所示, 设OE 交AD 于M ,交BC 于N ,显然矩形ABCD 关于OE 对称,而M ,N 分别为AD ,BC 的中点,在Rt△ONC 中,=sin α,ON =cos α,OM =DM tan π6=3DM =3=3sin α, 所以MN =ON -OM =cos α-3sin α,即AB =cos α-3sin α,而BC =2=2sin α,故S 矩形ABCD =AB ·BC =()cos α-3sin α·2sin α=2sin αcos α-23sin 2α=sin 2α-3(1-cos 2α)=sin 2α+3cos 2α-3=2⎝ ⎛⎭⎪⎫12sin 2α+32cos 2α- 3=2sin ⎝ ⎛⎭⎪⎫2α+π3- 3.因为0<α<π6,所以0<2α<π3,π3<2α+π3<2π3.故当2α+π3=π2,即α=π12时,S 矩形ABCD 取得最大值,此时S 矩形ABCD =2- 3.。
数学建模期末答案模型解释1~4

第六章军事模型§6.1 核武器竞赛问题:甲乙双方(两国),均将对方视为假想敌,在某种“国家安全”的定义下发展核武器,展开核军备竞赛。
问题:在这场核军备竞赛中,双方拥有的核武器会无限增长呢,还是存在某种平衡状态?一.模型假设1.分别以、表示甲乙双方拥有的核武器数目,这里视之为非负实数(即连续型变量),以、表示甲乙双方对对方施行一次致命性打击所需的核武器数目;2.甲乙双方的“国家安全”概念均采用保守定义:即在招到对方“倾泻性”核打击后,保证有足够的核武器被保存下来以给对方致命的还击;3.分别以、()表示甲乙双方,其一枚核弹头在遭受对方一枚核弹头袭击后有可能被保存下来的概率,这里假定不同核弹头在遭受对方一枚核弹头袭击后有可能被保存下来的机会是相对独立的。
二.模型建立定性分析模型:应当存在二函数、,分别表示当甲乙双方拥有的核武器数目为、时,对方在遵照模型假设中所给出的有关“国家安全”概念,乙方、甲方所应拥有最少的核武器数目。
即当甲方拥有的核武器数目为时,须有时,乙方才会确认自己是安全的。
显然,、均应当为单调增函数。
这里称为双方安全区,是核军备竞赛的稳定区域。
问:是否为空集?若为空集,即说明核军备竞赛是没有尽头的,其终究构成人类持久和平愿望的最大威胁。
所附四图仅仅是在双方安全曲线满足单调增函数的条件下给出的四种可能情形,有阴影存在的区域表示存在双方安全区。
但实际当中应当是哪一种呢?定量分析模型:在前述模型假设的基础上,不难得到:,即、分别为甲乙双方的安全曲线,而上面附图的后三幅给出的三种可能的典型情形,显然第四幅表示与两者至少有一个满足时方可出现。
在模型中涉及到的几个参数的取值,比如影响的主要因素可以考虑双方的国土、一枚核弹爆炸的破坏力,以及各自的防空能力。
三.模型分析通过定量分析模型得到的结果表明,核武器竞赛是不容乐观的,要么不存在稳定区域,要么稳定区域是一有界区域。
也即表明建立在本文“安全概念”基础上的核武器竞赛从根本上应当撇弃,因为即使在稳定区域非空,由于某一方(或双方)不克制的态度最终导致核武器竞赛的灾难性后果。
LPS诱导小胶质细胞活化的模型建立 (数学建模作业)
摘要
神经退行性疾病是影响人类健康的一类疾病的总称,包括阿尔茨海默病,帕金森病等。小胶质细胞在中枢神经系统的炎症进程中发挥重要作用。小胶质细胞的适度激活对神经元具有保护作用,然而过度激活的小胶质细胞释放大量的神经毒性因子,如一氧化氮(NO),而神经毒性因子会导致神经退行性疾病的发生。因此小胶质细胞的活化是多种神经退行性疾病的根本原因。
关键词:神经退行性疾病小胶质细胞NO优克那非N-乙酰半胱氨酸数学建模
ABSTRACT
Neurodegenerative diseases that affect human health, the general term for a class of diseases, including Alzheimer's disease, Parkinson's disease. Microglia in central nervous system play an important role in the inflammatory process. Moderate microglia activation has a protective effect on neurons, but excessive activation of microglia release large amounts of neurotoxic factors, such as nitric oxide (NO), the neural toxicity factor will lead to neurodegenerative diseases. Therefore, the activation of microglia is a variety of underlying causes of neurodegenerative diseases.
第五章 一元一次方程(知识归纳+题型突破)(解析版)
第五章一元一次方程(1)经历从具体问题中的数量相等关系,列出方程的过程,体会并认识到方程是刻画现实世界的一个有效的数学模型;(2)了解方程、一元一次方程以及方程的解等基本概念,了解方程的基本变形及在解方程中的作用;(3)会解一元一次方程,并经历和体会解方程中“转化”的过程和思想。
了解一元一次方程解法的一般步骤,并能正确、灵活应用;(4)会根据具体问题中的数量关系列出一元一次方程并求解,能根据问题的实际意义检验所得结果是否合理;(5)通过实践与探索,经历“问题情境——建立数学模型——解释、应用与拓展”的过程,体会数学建模思想,提高分析和解决实际问题的能力;(6)在学习和探索一元一次方程的解法和应用中,通过自主学习,提高学习能力,增强合作意识。
知识点1 一元一次方程1.概念:只含一个未知数(元)且未知数的次数都是1的方程;标准式:ax+b=0(x是未知数,a、b是已知数,且a≠0);2.方程的解:使方程等号左右两边相等的未知数的值知识点2 等式的性质等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等;如果a=b,那么a±c=b±c;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等;如果a=b,那次么ac=bc;如果a=b,c0,那么;知识点3含参一元一方程1、次数含参:主要考察一元一次方程定义2、常数项含参:求解一个常数项含参的一元一次方程,依然采用常规的五步法解题3、解已知或可求:将解代入参数方程,求出参数知识点4 解一元一次方程解一元一次方程的步骤:1.去分母两边同乘最简公分母2.去括号(1)先去小括号,再去 中括号,最后去大括号(2)乘法分配律应满足分配到每一项注意 :特别是去掉括号,符合变化3.移项(1)定义: 把含有未知数的项移到方程的一边,不含有未知数的项移到另一边;(2)注意: ①移项要变符号 ; ②一般把含有未知数的项移到左边 ,其余项移到右边 .4. 合并同类项(1)定义: 把方程中的同类项分别合并,化成“ ax = b ”的形式( a ≠ 0 );(2)注意:合并同类项时,把同类项的系数相加,字母不变.5. 系数化为 1(1)定义: 方程两边同除以未知数的系数 a ,得 a b x =; (2)注意:分子、分母不能颠倒知识点5:一元一次方程的应用【题型1 和、差、倍、分问题】【题型2 行程问题】距离=速度·时间【题型3 工程问题】工作量=工效×工时工程问题常用等量关系: 先做的+后做的=完成量【题型4 顺水逆水问题】顺流速度=静水速度+水流速度,逆流速度=静水速度-水流速度;顺水逆水问题常用等量关系: 顺水路程=逆水路程【题型5 商品利润问题】售价=定价 ;%100⨯-=成本成本销售价利润率利润问题常用等量关系:售价-进价=利润【题型6 分配问题】【题型7 配套问题】【题型8 数字与日历问题】【题型9 方案选择问题】【题型10 分段计费问题】【题型11 隧道或过桥问题】【题型12 几何图形问题】【题型1 方程及一元一次方程的定义】【典例1-1】下列各式中,是方程的是( )A.7x﹣4=3x B.4x﹣6C.4+3=7D.2x<5【答案】A【解答】解:A、7x﹣4=3x是方程;B、4x﹣6不是等式,不是方程;C、4+3=7没有未知数,不是方程;D、2x<5不是等式,不是方程;故选:A.【典例1-2】下列方程中是一元一次方程的是( )A.B.4x2=24C.x+y=80D.【答案】A【解答】解:A.方程﹣=1是一元一次方程,故本选项符合题意;B.方程4x2=24是一元二次方程,不是一元一次方程,故本选项不符合题意;C.方程x+y=80是二元一次方程,不是一元一次方程,故本选项不符合题意;D.方程+2=6是分式方程,不是一元一次方程,故本选项不符合题意.故选:A.【变式1-1】下列式子中,是一元一次方程的是( )A.x+1=0B.x2﹣x=0C.x+y=1D.﹣2=1【答案】A【解答】解:A、含有一个未知数且最高次数为1的等式,故符合题意;B、含未知数的项最高次数为2,故不符合题意;C、含有两个未知数,故不符合题意;D、该式子是分式方程,故不符合题意;故选:A.【变式1-1】在下列方程中,是一元一次方程的是( )A.2xy=4B.x2=1C.2x=0D.x+y=2【答案】C【解答】解:A.是二元二次方程,故本选项不符合题意;B.未知数的最高次数2次,不是一元一次方程,故本选项不合题意;C.是一元一次方程,故本选项符合题意;D.是二元一次方程,故本选项不合题意.故选:C.【题型2 利用一元一次方程的定义求值】【典例2】若(m﹣2)x|m|﹣1=5是关于x的一元一次方程,则m的值为( )A.﹣2B.﹣1C.1D.2【答案】A【解答】解:由题意可知:,解得:m=﹣2,故选:A.【变式2-1】若方程(a﹣2)x|a|﹣1=a+3是关于x的一元一次方程,则a的值是( )A.2B.﹣2C.±2D.±1【答案】B【解答】解:由题意得:|a|﹣1=1,且a﹣2≠0,解得a=﹣2.故选:B.【变式2-2】已知关于x的方程3﹣(m+1)x|m|=0是一元一次方程,则m的值为( )A.1B.﹣1C.1或﹣1D.以上结果均不正确【答案】A【解答】解:根据题意,得|m|=1且m+1≠0.解得m=1.故选:A.【题型3 方程的解】【典例3】已知x=3是关于x的方程ax+2x﹣3=0的解,则a的值为( )A.﹣1B.﹣2C.﹣3D.1【答案】A【解答】解:将x=3代入方程得:3a+2×3﹣3=0,解得:a=﹣1.故选:A.【变式3-1】已知x=﹣3是方程ax﹣6=a+10的解,则a= ﹣4 .【答案】见试题解答内容【解答】解:把x=﹣3代入方程ax﹣6=a+10,得:﹣3a﹣6=a+10,解方程得:a=﹣4.故填:﹣4.【变式3-2】如果x=﹣1是方程x+a=3的解,则a= 4 .【答案】见试题解答内容【解答】解:把x=1代入方程,得:﹣1+a=3,解得:a=4.故答案为:4.【变式3-3】若2是方程2a﹣3x=2的解,则a= 4 .【答案】见试题解答内容【解答】解:把x=2代入方程,得2a﹣6=2,解得a=4.故答案为:4.【题型4 利用等式的性质变形】【典例4】下列变形中,不正确的是( )A.若a﹣3=b﹣3,则a=b B.若ac=bc,则a=bC.若a=b,则a﹣3=b﹣3D.若,则a=b【答案】B【解答】解:A、若a﹣3=b﹣3,则a=b,故A不符合题意;B、若ac=bc(c≠0),则a=b,故B符合题意;C、若a=b,则a﹣3=b﹣3,故C不符合题意;D、若,则a=b,故D不符合题意;故选:B.【变式4-1】运用等式性质进行的变形,不一定成立的是( )A.如果a=b,那么ac=bcB.如果a=b,那么3﹣2a=3﹣2bC.如果a2=2a,那么a=2D.如果,那么4a=3b【答案】C【解答】解:A.符合性质2,该变形成立,故A不符合题意;B.符合性质1、性质2,该变形成立,故B不符合题意;C.不符合性质2,等式两边同时除以a,当a不为零时,该变形才成立,故C符合题意;D.符合性质2,该变形成立,故D不符合题意;故选:C.【变式4-2】下列运用等式性质正确的是( )A.如果a=b,那么a+c=b﹣cB.如果ac=bc,那么a=bC.如果=,那么a=bD.如果a2=ab,那么a=b【答案】C【解答】解:根据等式的基本性质1和等式的基本性质2可知:A,B,D都不符合题意,C符合题意,故选:C.【变式4-3】下列说法正确的是( )A.如果a=b,那么a+c=b﹣cB.如果a=b,那么ac=bcC.如果a=b,那么D.如果a=﹣b,那么a2+b2>0【答案】B【解答】解:A.如果a=b,那么a+c=b+c或a﹣c=b﹣c,故A不正确;B.如果a=b,那么ac=bc,故B正确;C.如果a=b,x2﹣1=0,那么不成立,故C不正确;D.如果a=﹣b=0,那么a2+b2>0不成立,故D不正确.故选:B.【题型5 方程的解中遮挡问题】【典例5】下面是一个被墨水污染过的方程:2x﹣=3x+,答案显示此方程的解是x=﹣1,被墨水遮盖的是一个常数,则这个常数是( )A.1B.﹣1C.﹣D.【答案】D【解答】解:∵x=﹣1是方程的解,∴2×(﹣1)﹣=3×(﹣1)+,﹣2﹣=﹣3+,解得=.故选:D.【变式5-1】下面是一个被墨水污染过的方程:2x﹣=x﹣,答案显示此方程的解是x=,被墨水遮盖的是一个常数,则这个常数是( )A.2B.﹣2C.D.﹣【答案】B【解答】解:设被墨水遮盖的常数是a,根据题意得:﹣=﹣a,解得:a=﹣2.故选:B.【变式5-2】下面是一个被墨水污染过的方程:2x=3x+■,答案显示此方程的解是x=1,被墨水遮盖的是一个常数,则这个常数是( )A.5B.﹣5C.D.【答案】C【解答】解:∵x=1是方程2x=3x+■的解,∴2=3+■,∴■=﹣,故选:C.【变式5-3】下面是一个被墨水污染过的方程:2x﹣=3x+★,答案显示此方程的解是x=﹣1,被墨水遮盖的是一个常数,则这个常数是( )A.1B.﹣1C.﹣D.【答案】D【解答】解:设被墨水遮盖的常数为t,将x=﹣1代入方程,得﹣2﹣=﹣3+t,解得t=.即这个常数是.故选:D.【题型6 解一元一次方程】【典例6】解方程:(1)3x+5=4x+1;(2).【答案】(1)x=4;(2)x=﹣.【解答】解:(1)原方程移项,合并同类项得:﹣x=﹣4,系数化为1得:x=4;(2)原方程去分母得:7x﹣2x+40=2x﹣16,移项,合并同类项得:3x=﹣56,系数化为1得:x=﹣.【变式6-1】解方程:(1)5x+3=﹣2x﹣11;(2).【答案】(1)x=2;(2)x=.【解答】解:(1)5x+3=﹣2x﹣11,移项,得5x+2x=﹣11﹣3,合并同类项,得7x=﹣14,系数化成1,得x=﹣2;(2),去分母,得2x+1=6﹣2(5x﹣2),去括号,得2x+1=6﹣10x+4,移项,得2x+10x=6+4﹣1,合并同类项,得12x=9,系数化成1,得x=.【变式6-2】解方程:(1)3(2x﹣7)=1﹣(x+8);(2).【答案】(1)x=2;(2)x=﹣.【解答】解:(1)3(2x﹣7)=1﹣(x+8),6x﹣21=1﹣x﹣86x+x=﹣7+21,7x=14,x=2;(2),3(3x+5)=2(2x﹣1),9x+15=4x﹣2,9x﹣4x=﹣2﹣15,5x=﹣17,x=﹣.【变式6-3】解下列方程:(1)3(x﹣1)+5(x﹣1)=16.(2).【答案】(1)x=3;(2)x=﹣1.【解答】解:(1)3(x﹣1)+5(x﹣1)=16,去括号,得3x﹣3+5x﹣5=16,移项,得3x+5x=16+3+5,合并同类项,得8x=24,系数化成1,得x=3;(2),去分母,得3(3x﹣1)﹣12=2(5x﹣7),去括号,得9x﹣3﹣12=10x﹣14,移项,得9x﹣10x=﹣14+3+12,合并同类项,得﹣x=1,系数化成1,得x=﹣1.【题型7 根据两个一元一次方程的解之间的关系求参数】【典例7】若2(a+3)的值与﹣5互为相反数,则a的值为( )A.B.C.D.5【答案】C【解答】解:∵2(a+3)的值与﹣5互为相反数,∴2(a+3)+(﹣5)=0,∴a=﹣,故选:C.【变式7-1】若多项式3x+5与5x﹣7的值相等,则x的值为( )A.6B.5C.4D.3【答案】A【解答】解:∵多项式3x+5与5x﹣7的值相等,∴3x+5=5x﹣7,移项,可得:3x﹣5x=﹣7﹣5,合并同类项,可得:﹣2x=﹣12,系数化为1,可得:x=6.故选:A.【变式7-2】当x= ﹣4 时,代数式2x﹣1的值与代数式3x+3的值相等.【答案】﹣4.【解答】解:2x﹣1=3x+3,3x﹣2x=﹣1﹣3,∴x=﹣4,∴当x=﹣4时,代数式2x﹣1的值与代数式3x+3的值相等.故答案为:﹣4.【变式7-3】若代数式3a+1的值与代数式3(a﹣1)的值互为相反数,则a= .【答案】.【解答】解:根据题意得:3a+1+3(a﹣1)=0,去括号得:3a+1+3a﹣3=0,移项得:3+3a=3﹣1,合并同类项得:6a=2,系数化为1得:.故答案为:.【题型8 错解一元一次方程的问题】【典例8】某同学解方程3x﹣1=□x+3时,把□处数字看错后解得x=﹣2,那么他把□处看成了( )A.4B.﹣4C.5D.﹣5【答案】C【解答】解:依题意,得3×(﹣2)﹣1=(﹣2)×□+3,即(﹣2)×□=﹣10,解得:□=5.故选:C.【变式8-1】某同学在解方程5x﹣1=■x+3时,把■处的数字看错了,解得x=﹣,则该同学把■看成了( )A.3B.﹣3C.﹣8D.8【答案】D【解答】解:设■处的数字为a,把x=﹣代入方程5x﹣1=ax+3中得:﹣﹣1=﹣a+3,a=3+1+,a=,a=8,故选:D.【变式8-2】同学小明在解关于x的方程5x﹣4=( )x时,把( )处的数看错,得错解x=﹣1,则小明把( )处看成了 9 .【答案】见试题解答内容【解答】解:设( )内的数为a,则错解得方程为5x﹣4=ax,根据题意,将x=﹣1代入得:﹣5﹣4=﹣a,解得:a=9,故答案为:9.【题型9 一元一次方程的解在新定义中运用】【典例9】新定义:如果两个一元一次方程的解互为相反数,就称这两个方程为“友好方程”,如:方程2x=6和3x+9=0为“友好方程”.(1)若关于x的方程3x+m=0与方程2x﹣6=4是“友好方程”,求m的值.(2)若某“友好方程”的两个解的差为6,其中一个解为n,求n的值.【答案】(1)15;(2)±3.【解答】解:(1)方程2x﹣6=4解为x=5,∵关于x的方程3x+m=0与方程2x﹣6=4是“友好方程”,∴关于x的方程3x+m=0的解为x=﹣5,∴3×(﹣5)+m=0,∴m=15;(2)∵某“友好方程”的一个解为n,∴“友好方程”的另一个解为﹣n,∴n﹣(﹣n)=6或﹣n﹣n=6,∴n=3或n=﹣3.∴n=±3.【变式9-1】定义一种新运算⊗:a⊗b=4a+b,试根据条件回答问题(1)计算:2⊗(﹣3)= 5 ;(2)若x⊗(﹣6)=3⊗x,请求出x的值;(3)这种新定义的运算是否满足交换律,若不满足请举一个反例,若满足,请说明理由.【答案】见试题解答内容【解答】解:(1)根据题意得:2⊗(﹣3)=8﹣3=5;故答案为:5;(2)由题意得4x﹣6=3×4+x,移项、合并得3x=18,解得x=6;(3)不满足交换律,反例如:2⊗1=9,1⊗2=6,显然2⊗1≠1⊗2.【变式9-2】对有理数a,b规定新运算※的意义是:a※b=a+2b,则方程3x※x=2﹣x的解是( )A.B.3C.﹣3D.【答案】A【解答】解:∵a※b=a+2b,且3x※x=2﹣x,∴3x+2x=2﹣x,移项,可得:3x+2x+x=2,合并同类项,可得:6x=2,系数化为1,可得:x=.故选:A.【变式9-3】新华商店店庆促销,有一种新型书包,原价每个x元,第一次降价打八折,第二次降价每个又减10元,经两次降价后售价为70元.则所列方程是( )A.70﹣0.8x=10B.0.08x﹣10=70C.0.8x﹣10=70D.x﹣0.8x﹣10=70【答案】C【解答】解:根据题意得:0.8x﹣10=70.故选:C.【变式9-4】新定义一种运算“☆”,规定a☆b=ab+a﹣b.若2☆x=x☆2,则x的值为 2 .【答案】见试题解答内容【解答】解:∵a☆b=ab+a﹣b,2☆x=x☆2,∴2x+2﹣x=2x+x﹣2,整理,可得:2x=4,解得x=2.故答案为:2.【变式9-5】新定义一种运算符号“△”,规定x△y=xy+x2﹣3y,已知2△m=6,则m的值为 ﹣2 .【答案】﹣2.【解答】解:由题意,得2m+4﹣3m=6,﹣m=2,解得m=﹣2.故答案为:﹣2.【题型10 和、差、倍、分问题】【典例10】某班举行了“庆祝建党90周年知识竞赛”活动,班长安排张小明购买奖品,如图两幅图是张小明买回奖品时与班长的对话情况:请根据图1、图2的信息,解答下列问题:(1)张小明买了两种笔记本各多少本?(说明:要求列一元一次方程解决问题)(2)请你解释为什么班长说不可能找回68元钱.【答案】见试题解答内容【解答】解:(1)设买x本5元的笔记本,则买(40﹣x)本8元的笔记本,依题意得,5x+8(40﹣x)=300﹣68+13,解得x=25,则40﹣x=15(本).答:张小明买了5元的笔记本25本,8元的笔记本15本;(2)设买x本5元的笔记本,则买(40﹣x)本8元的笔记本,根据题意,得5x+8(40﹣x)=300﹣68,解得x=,不是整数,故不能找回68元.【变式10-1】A种饮料比B种饮料单价少1元,小峰买了2瓶A种饮料和3瓶B种饮料,一共花了13元,如果设A种饮料单价为x元/瓶,那么下面所列方程正确的是( )A.2(x﹣1)+3x=13B.2(x+1)+3x=13C.2x+3(x+1)=13D.2x+3(x﹣1)=13【答案】C【解答】解:设A种饮料单价为x元/瓶,则B种饮料单价为(x+1)元,根据小峰买了2瓶A种饮料和3瓶B种饮料,一共花了13元,可得方程为:2x+3(x+1)=13.故选:C.【变式10-2】方方同学用50元钱去购买笔记本和彩色水笔共20件,已知每本笔记本4元,每支彩色水笔2元,设方方同学买了x本笔记本,则( )A.2x+4(20﹣x)=50B.2(20﹣x)+4x=50C.2x+4(50﹣x)=20D.2(50﹣x)+4x=20【答案】B【解答】解:∵方方同学购买笔记本和彩色水笔共20件,且购买了x本笔记本,∴购买了(20﹣x)支彩色水笔.根据题意得:2(20﹣x)+4x=50.故选:B.【变式10-3】青骄课堂2023年禁毒知识竞赛答题,共设20道选择题,要求每题必答,每答对一题得5分,答错一题扣1分,小新一共得了82分,他答对了 17 道题.【答案】17.【解答】解:设小新答对了x道题,则答错(20﹣x)道题,根据题意得:5x﹣(20﹣x)=82,解得:x=17,∴小新答对了17道题.故答案为:17.【题型11 行程问题】【典例11】甲、乙两列火车分别从A、B两城同时相向开出,当两车相遇后,又继续前进,甲车行了全程的时,乙车恰好行了全程的.这时两车相距364km.A、B两城相距多少千米?【答案】A、B两城相距780千米.【解答】解:设A、B两城相距x千米,根据题意得x+x﹣x=364,解得x=780,答:A、B两城相距780千米.【变式11-1】甲地到乙地的高铁开通后,运行时间由原来的3.5小时缩短至1小时,运行里程缩短了40千米.已知高铁的平均速度比普通列车的平均速度每小时快200千米,求高铁的平均速度.【答案】高铁的平均速度为296km/h.【解答】解:设高铁的平均速度为xkm/h,由题意得:x+40=3.5(x﹣200),解得:x=296,答:高铁的平均速度为296km/h.【变式11-2】甲乙两地相距900千米,一列快车从甲地出发匀速开往乙地,速度为120千米/时:快车开出30分钟时,一列慢车从乙地出发匀速开往甲地,速度为90千米时.设慢车行驶的时间为x小时,快车到达乙地后停止行驶,根据题意解答下列问题.(1)当快车与慢车相遇时,求慢车行驶的时间;(2)当两车之间的距离为315千米时,求快车所行的路程.【答案】(1)慢车行驶的时间为4小时;(2)当两车之间的距离为315千米时,快车所行的路程为360千米或720千米.【解答】解:(1)由题意得,120(x+0.5)+90x=900,解得:x=4,∴慢车行驶的时间为4小时;(2)①两车相遇前相距315千米,120(x+0.5)+90x=900﹣315,解得:x=2.5,此时快车行驶的路程:120×(2.5+0.5)=360(千米);②两车相遇后相距315千米,120(x+0.5)+90x=900+315,解得:x=5.5,此时快车行驶的路程:120×(5.5+0.5)=720(千米);③当快车到达乙地,快车行驶了7.5小时,慢车行驶了7小时,7×90=630>315,此种情况不存在;∴当两车之间的距离为315千米时,快车所行的路程为360千米或720千米.【变式11-3】两辆汽车同时从相距300千米的两地相对开出,2小时后相遇.已知两辆车的速度比是2:3,求较慢的一辆车每小时行驶多少千米?【答案】较慢的一辆车每小时行驶60千米.【解答】解:设较慢的一辆车每小时行驶x千米,∵两辆车的速度比是2:3,∴较快的一辆车每小时行驶x千米,根据题意得2(x+x)=300,解得x=60,答:较慢的一辆车每小时行驶60千米.【题型12 工程问题】【典例12】整理一批图书,由一个人做要40小时完成,现计划由一部分人先做4小时,然后增加2人与他们一起做8小时,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?【答案】应先安排2人工作.【解答】解:设应先安排x人工作,根据题意得:+=1化简可得:+=1,即:x+2(x+2)=10解可得:x=2答:应先安排2人工作.【变式12-1】学校举办一年一届的科技文化艺术节活动,需制作一块活动展板,请来甲和乙两名工人.已知甲单独完成需要4天,乙单独完成需要6天.(1)两个人一起做需要 2.4 天完成;(2)现由乙先做1天,再由两个人一起做,还需要多少天可以完成这项工作?【答案】(1)2.4;(2)2.【解答】解:(1)1÷(+)=1÷=2.4(天).答:两个人一起做,需要2.4天可以完成.故答案为2.4;(2)设乙先做1天,再两人一起做,还需x天完成这项工作,由题意可得:+=1,解得:x=2.答:还需2天可以完成这项工作.【变式12-2】某公司需要粉刷一些相同的房间,经调查3名师傅一天粉刷8个房间,还剩40m2刷不完;5名徒弟一天可以粉刷9个房间;每名师傅比徒弟一天多刷30m2的墙面.(1)求每个房间需要粉刷的面积;(2)该公司现有36个这样的房间需要粉刷,若只聘请1名师傅和2名徒弟一起粉刷,需要几天完成?【答案】(1)每个房间需要粉刷的面积为50m2;(2)需要6天完成.【解答】解:(1)设每个房间需要粉刷的面积为xm2,由题意得:﹣=30,解得:x=50,∴每个房间需要粉刷的面积为50m2,答:每个房间需要粉刷的面积为50m2;(2)每名徒弟一天粉刷的面积为:=90(m2),每名师傅一天粉刷的面积为:=120(m2),∴=6(天),答:需要6天完成.【题型13 顺水逆水问题】【典例13】两架飞机从同一机场同时出发反向而飞,甲飞机顺风飞行,乙飞机逆风飞行.已知两飞机在无风的速度都是500千米每小时,风速是a千米每小时.(1)甲、乙飞机飞行时的速度分别是多少?(2)3小时后两机的行程分别是多少?(3)求3小时后两机相距多远?(4)3小时后,甲飞机比乙飞机多航行多少千米?【答案】(1)甲飞机飞行时的速度为(500+a)千米/小时,乙飞机飞行时的速度为(500﹣a)千米/小时;(2)甲飞机3小时后飞行的路程为:3(500+a)=(1500+3a)千米,乙飞机3小时后飞行的路程为:3(500﹣a)=(1500﹣3a)千米;(3)3小时后两机相距为3000千米;(4)3小时后,甲飞机比乙飞机多航行6a千米.【解答】解:(1)∵甲飞机顺风飞行,乙飞机逆风飞行,∴甲飞机飞行时的速度为(500+a)千米/小时,乙飞机飞行时的速度为(500﹣a)千米/小时;(2)根据(1)中写出的甲、乙飞机飞行时的速度,则甲飞机3小时后飞行的路程为:3(500+a)=(1500+3a)千米,乙飞机3小时后飞行的路程为:3(500﹣a)=(1500﹣3a)千米;(3)∵两架飞机从同一机场同时出发反向而飞,∴3小时后两机相距为:1500+3a+1500﹣3a=3000(千米);(4)3小时后,甲飞机比乙飞机多航行的距离为:(1500+3a)﹣(1500﹣3a)=6a(千米).【变式13-1】一架飞机在A,B两城市之间飞行,风速为20km/h,顺风飞行需要8h,逆风飞行需要8.5h.求无风时飞机的飞行速度和A,B两城市之间的航程.【答案】无风时飞机的飞行速度为660km/h,A,B两城市之间的航程为5440km.【解答】解:设无风时飞机的飞行速度为xkm/h,由题意得:8(x+20)=8.5(x﹣20),解得:x=660,则8(x+20)=8×(660+20)=5440,答:无风时飞机的飞行速度为660km/h,A,B两城市之间的航程为5440km.【变式13-2】在风速为24km/h的条件下,一架飞机顺风从A机场飞到B机场要用2.8h,它逆风飞行同样的航线要用3h.求(1)无风时这架飞机在这一航线的平均航速;(2)两机场之间的航程是多少?【答案】见试题解答内容【解答】解:(1)设无风时飞机的航速是x千米/时,依题意得:2.8×(x+24)=3×(x﹣24),解得:x=696.答:无风时飞机的航速是696千米/时.(2)由(1)知,无风时飞机的航速是696千米/时,则3×(696﹣24)=2016(千米).答:两机场之间的航程是2016千米.【变式13-3】一架飞机在两城之间飞行,风速为24千米/时.顺风飞行需要2小时,逆风飞行需要3小时,求无风时飞机的速度.【答案】120千米/时.【解答】解:设无风时飞机的速度为x千米/时,根据题意得:(x+24)×2=(x﹣24)×3,解得:x=120.答:无风时飞机的速度为120千米/时.【变式13-4】一架飞机在两城之间飞行,风速为24千米/小时,顺风飞行需2小时,逆风飞行需要3小时.(1)求无风时飞机的飞行速度;(2)求两城之间的距离.【答案】见试题解答内容【解答】解:(1)设无风时飞机的飞行速度为x千米/小时,由题意得2(x+24)=3(x﹣24)解得:x=120答:无风时飞机的飞行速度是120千米/时;(2)2(x+24)=288千米答:两城之间的距离是288千米.【题型14 商品利润问题】【典例14】某商店购进甲、乙两种型号的节能灯共100只,购进100只节能灯的进货款恰好为2600元,达两种节能灯的进价、预售价如表:(利润=售价﹣进价)型号进价(元/只)预售价(元/只)甲型2025乙型3540(1)求该商店购进甲、乙两种型号的节能灯各多少只?(2)在实际销售过程中,商店按预售价将购进的全部甲型号节能灯和部分乙型号节能灯售出后,决定将剩下的乙型号节能灯打九折销售,两种节能灯全部售完后,共获得利润380元,求乙型号节能灯按预售价售出了多少只.【答案】(1)购进甲种型号的节能灯60只,购进乙种型号的节能灯40只;(2)乙型节能灯按预售价售出的数量是10只.【解答】解:(1)设该商店购进甲种型号的节能灯x只,则可以购进乙种型号的节能灯(100﹣x)只,由题意可得:20x+35(100﹣x)=2600,解得:x=60,100﹣60=40(只),答:该商店购进甲种型号的节能灯60只,购进乙种型号的节能灯40只;(2)设乙型节能灯按预售价售出的数量是y只,由题意得60×(25﹣20)+(40﹣35)y+(40﹣y)×(40×90%﹣35)=380,解得:y=10,答:乙型节能灯按预售价售出的数量是10只.【变式14-1】一件大衣按其进价提高50%后标价.由于季节原因,现以标价的七折售出,结果仍盈利18元.这件上衣的进价是多少元?(提示:利润=售价﹣进价)【答案】360.【解答】解:设这件上衣的进价为x元,由题意得,70%•(1+50%)x﹣x=18,解之得,x=360,答:这件上衣的进价是360元.【变式14-2】一台手机进价是2800元,按照标价3400元的九折出售;一块电子手表进价是600元,按照标价的八折出售,结果每台手机的利润比每块手表的利润多140元,问手表的标价是多少元?【答案】900.【解答】解:设每块手表的标价为x元,根据题意得:3400×90%﹣2800﹣(80%x﹣600)=140,0.8x=720,解得:x=900,答:每块手表的标价为900元.【变式14-3】我校七年级社会实践小组去某商场调查商品的销售情况,了解到该商场以每条80元的价格购进了某品牌裤子500条,并以每条120元的价格销售了400条,商场准备采取促销措施,将剩下的裤子降价销售.(1)前400条裤子的利润是多少元?(2)当每条裤子降价多少元时,销售完这批裤子正好达到盈利45%的预期目标?【答案】(1)16000元;(2)当每条裤子降价20元时,销售完这批裤子正好达到盈利45%的预期目标.【解答】解:(1)由题意可得,前400条裤子的利润是:(120﹣80)×400=40×400=16000(元),答:前400条裤子的利润是16000元;(2)设当每条裤子降价x元时,销售完这批裤子正好达到盈利45%的预期目标,由题意可得:(120﹣x﹣80)×(500﹣400)+16000=500×80×45%,解得x=20,答:当每条裤子降价20元时,销售完这批裤子正好达到盈利45%的预期目标.【题型15 分配问题】【典例15】《九章算术》中“盈不足术”有这样的问题:“今有共买羊,人出六,不足四十五;人出八,不足三.问人数、羊价各几何?”题意是:若干人共同出资买羊,每人出6元,则差45元;每人出8元,则差3元.求人数和羊价各是多少?设买羊人数为x人,则根据题意可列方程为( )A.6x+45=8x+3B.6x+45=8x﹣3C.6x﹣45=8x+3D.6x﹣45=8x﹣3【答案】A【解答】解:设买羊人数为x人,则根据题意可列方程为6x+45=8x+3.故选:A.【变式15-1】我国明代数学读本《算法统宗》中有一道题,其题意为:客人一起分银子,若每人7两,还剩4两;若每人9两,还差8两.问银子共有几两?设银子共有x两,则可列方程为( )A.7x+4=9x﹣8B.7x﹣4=9x+8C.D.【答案】D【解答】解:∵银子共有x两,每人7两,还剩4两,∴分银子的人共人;∵银子共有x两,每人9两,还差8两,∴分银子的人共人.又∵分银子的人数不变,∴可列方程组=.故选:D.【变式15-2】近年来,网购的蓬勃发展方便了人们的生活.某快递分派站现有包裹若干件需快递员派送,若每个快递员派送10件,还剩6件;若每个快递员派送12件,还差6件,设该分派站有x名快递员,则可列方程为( )A.10x﹣6=12x+6B.10x+6=12x﹣6C.D.【答案】B【解答】解:设该分派站有x名快递员,则可列方程为:10x+6=12x﹣6.故选:B.【变式15-3】某学校有x间男生宿舍和y个男生,若每间宿舍住8个人,则还多4个人无法安置;若每间宿舍安排10个人,则还多6张空床位,据此信息列出方程,下列4个方程中正确的是( )①8x﹣4=10x+6;②;③;④8x+4=10x﹣6.A.①③B.②④C.①②D.③④【答案】B【解答】解:按照男生人数不变列出方程8x+4=10x﹣6;按照男生宿舍间数不变列出方程=.∴正确的方程是②④.故选:B.【变式15-4】为了阻断新冠疫情传播,疫情居家期间,居民购买的蔬菜包由志愿者统一派送.若每位志愿者派送8个蔬菜包,则少5个;若每个志愿者派送6个,则剩下4个未送,设安排x个志愿者派送,则下面所列方程中正确的是( )A.8x﹣5=6x+4B.8x+5=6x+4C.8x+5=6x﹣4D.8x﹣5=6x﹣4【答案】A【解答】解:由题意可得:8x﹣5=6x+4,故选:A.【题型16 配套问题】【典例16】某车间为提高生产总量,在原有16名工人的基础上,新调入若干名工人,使得调整后车间的总人数是调入工人人数的3倍多4人.(1)求调入多少名工人;(2)在(1)的条件下,每名工人每天可以生产240个螺栓或400个螺母,1个螺栓需要2个螺母,为使每天生产的螺栓和螺母刚好配套,应该安排生产螺栓和螺母的工人各多少名?【答案】(1)调入6名工人;(2)10名工人生产螺栓,12名工人生产螺母,可使每天生产的螺栓和螺母刚好配套.【解答】解:(1)设调入x名工人,根据题意得:16+x=3x+4,解得x=6,∴调入6名工人;(2)由(1)知,调入6名工人后,车间有工人16+6=22(名),设y名工人生产螺栓,则(22﹣y)名工人生产螺母,∵每天生产的螺栓和螺母刚好配套,∴240y×2=400(22﹣y),解得y=10,∴22﹣y=22﹣10=12,答:10名工人生产螺栓,12名工人生产螺母,可使每天生产的螺栓和螺母刚好配套.【变式16-1】现用90立方米木料制作桌子和椅子,已知一张桌子配4张椅子,1立方米木料可做5张椅子或1张桌子,要使桌子和椅子刚好配套.设用x立方米的木料做桌子,则依题意可列方程为( )A.4x=5(90﹣x)B.5x=4(90﹣x)C.x=4(90﹣x)×5D.4x×5=90﹣x【答案】A【解答】解:设用x立方米的木料做桌子,则用(90﹣x)立方米的木料做椅子,依题意,得:4x=5(90﹣x).故选:A.【变式16-2】某车间有28名工人生产螺丝和螺母,每人每天生产1200个螺丝或1800个螺母,现有x个工人生产螺丝,恰好每天生产的螺母和螺丝按2:1配套.为求x,可列方程( )。
pm2.5的预测和治理(数学建模)
-1-
第一章 问题重述
大气为地球上生命的繁衍与人类的发展提供了理想的环境。它的状态和变 化,直接影响着人类的生产、生活和生存。为更好的治理环境,研究环境,规 定空气质量指数 AQI 作为空气质量监测指标,它的分项监测指标为 6 个基本监 测指标(二氧化硫 SO2、二氧化氮 NO2、可吸入颗粒物 PM10、细颗粒物 PM2.5、 臭氧 O3 和一氧化碳 CO 等 6 项) 。 问题一: 依据给定的数据或自行采集数据,利用或建立适当的数学模型,对 AQI 中 6 个基本监测指标的相关与独立性进行定量分析,尤其是对其中 PM2.5(含量) 与其它 5 项分指标及其对应污染物(含量)之间的相关性及其关系进行分析。 问题二: 1、描述该地区内 PM2.5 的时空分布及其规律,并结合环境保护部新修订的 《环境空气质量标准》分区进行污染评估。 2、建立能够刻画该地区 PM2.5 的发生和演变(扩散与衰减等)规律的数学 模型,并利用该地区的数据进行定量与定性分析。 3、假设该地区某监测点处的 PM2.5 的浓度突然增至数倍,且延续数小时, 建立针对这种突发情形的污染扩散预测与评估方法。并以该地区 PM2.5 监测数 据最高的一天为例,在全地区 PM2.5 浓度最高点处的浓度增至 2 倍,持续 2 小 时,利用你们的模型进行预测评估,给出重度污染和可能安全区域。 4、采用适当方法检验你们模型和方法的合理性,并根据已有研究成果探索 PM2.5 的成因、演变等一般性规律。 问题三: 1、该地区目前 PM2.5 的年平均浓度估计为 280(单位为μg/m³) ,要求未 来五年内逐年减少 PM2.5 的年平均浓度, 最终达到年终平均浓度统计指标 35 (单 位为μg/m³) ,请给出合理的治理计划,给出每年的全年年终平均治理指标。 2、为研究区设计有效的专项治理计划,使得既达到预定 PM2.5 减排计划, 同时使经费投入较为合理,给出投入总经费和逐年经费投入预算计划,并论述 该方案的合理性。
数学建模统计模型教学教案
数学建模统计模型教学教案教学内容反思:
在教学《数学建模》第五章——统计模型时,我深刻认识到统计学不仅是数学的一个分支,更是应用数学解决实际问题的有力工具。
统计模型的建立和应用是研究和解决社会、经济、科学等领域问题的有效手段。
因此,在本节课中,我致力于使学生掌握描述统计的基本方法,理解概率分布的概念,熟练运用假设检验、回归分析和方差分析等统计方法。
教学方法反思:
在教学过程中,我注重理论与实践相结合,通过生动的例子和实际问题引出统计模型的概念,让学生在解决问题的过程中体会统计学的价值。
同时,我鼓励学生积极参与课堂讨论,提问和回答问题,以增强学生的互动性和参与感。
我也注重时间管理,确保每个知识点都有足够的讲解和练习时间,使学生在有限的课堂时间内掌握更多的知识。
教学效果评估:
根据课后收到的学生反馈和作业完成情况来看,学生们对统计模型的理解和应用能力有了显著提高。
他们能够运用所学的知识对实际问题进行建模和分析,这说明本节课的教学目标是基本达到了。
但同时,我也注意到部分学生在概率分布的计算和假设检验的推导上还存在一定的困难,这需要在今后的教学中进行针对性的辅导和强化。
教学改进:
1. 对于难点内容,如概率分布的计算和假设检验的推导,需要放慢讲解速度,给予学生更多的时间理解和消化。
2. 通过增加案例分析和课后实践项目,让学生在实际操作中加强对统计模型的应用能力。
3. 鼓励学生提出问题,及时解答学生的疑惑,提高学生的学习效率。
4. 开展小组讨论和同伴学习,让学生在讨论中加深对统计模型的理解,并培养合作学习能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习 题 1、对于5.1节传染病的SIR模型证明; ①若/10s,则)(ti先增加,在/1s处达到最大 ,然后减少并趋于零;)(ts单
调减少至s。 ②若/10s,则)(ti单调减少并趋于零,)(ts单调减少至s。 2、对于传染病的SIR模型证明(20)~(22)式。 3、在5.2节经济增长模型中,为了适用于不同的对象可将产量函数)(tQ折算成现金,仍用)(tQ表示。考虑到物价上升因素我们记物价上升指数为)(tp(设1)0(p)。则产品的表面价值)(ty、实际价值)(tQ和物价指数)(tp之间满足)(ty)()(tPtQ。 ①导出)(ty、)(tQ、)(tp的相对增长率之间的关系,并作解释。 ②设雇佣工人数目为)(tL,每个工人工资为)(tW,企业的利润简化为从产品的收入)(ty中扣除工人的工资和固定的成本。利用5.2节的(5)式讨论,企业应雇佣多少工人能
使利润最大。 4、在5.4节的房室模型中证明方程(3)对应的齐次方程通解如(4)、(5)式所示,说明方程的两个特征根和一定是负实根。 5、模仿5.4节建立的二室模型建立一室模型(只有中心室),在快速静脉注射、恒速静脉滴注(持续时间为)和口服或肌肉注射3种给药方式下求解血药浓度,并画出浓度曲线图。 6、利用上题建立的一室模型,讨论按固定时间间隔T每次给予固定剂量D的多次重复给药方式。为了维持药品的疗效和保证机体的安全,要求血药浓度C控制在(21,CC)范围内。设中心室容积V为已知。 ① 在快速静脉注射的多次重复给药方式下,写出血药浓度表达式并作图,讨论怎样确定T和D使血药浓度的变化满足上述要求。 ② 在恒速静脉滴注和口服(或肌肉注射)的多次重复给药方式下,给出血药浓度变化的简图,并在这两种方式选择一种来讨论确定T和D的问题。 7、在5.5节香烟过滤嘴模型中, ① 设800M毫克,801l毫米,202l毫米,02.0b(1/秒),08.0(1/秒),50v毫米/秒,3.0a,求Q和21/QQ。 ②若有一支不带过滤嘴的香烟,参数同上。比较全部吸完和只吸到1l处的情况下,进入人体毒物量的区别。 8、在5.6节水电站调压塔模型中,设调压塔出口水流速度在稳定值0v附近有一阶跃变化,即
0,00,1)(1tt
tv
利用方程(8)讨论调压塔水位)(th在稳定值0h附近的变化过程)(1th。 9、在5.7节人口的预测和控制模型中,总和生育率)(t和生育模式),(trh是两种控制人口增长的手段。试说明我国目前的人口政策,如提倡一对夫妇只生一个孩子,晚婚晚育,及生第2胎的一些规定,怎样通过这两种控制手段加以实施。 10、在5.8节连续交通流模型中,考察在],[ttt内公路段],[xxx的流量),(txq和密度),(tx的变化,直接导出交通流方程(5)。 11、在5.8节红绿灯模型中,讨论初始密度是拥挤流即*0时密度函数),(tx的变化(类似于图5-23对于稀疏流*0的分析,画出分阶段的),(tx示意图,求出“追上车队”和“堵塞消失”的时刻,分析间断点的变化规律等)。 12、证明红绿灯模型中左右间断线)(txsl和)(txsr当t足够大后以相同速度向前移动。 13、讨论绿灯模型。设初始密度(0t)为 0,00,)0,(xx
xm
①画出0t时),(tx的示意图。 ②证明(0t)时位于)0(ddx处的车辆通过0x的时刻为mudt4。
③证明],0[T内通过0x的车辆数为Tumm4。 14、将5.10节得到的万有引力定律(18)式与熟知的形式(19)进行比较。查询太阳质量、地球运行轨道(椭圆)的长半轴、引力常数等数据,说明二者是一致的。 *15. 对于技术革新的推广,在下列几种情况下分别建立模型。 ① 推广工作通过已经采用新技术的人进行,推广速度与已采用新技术的人数成正比,推广是无限的。 ② 总人数有限,因而推广速度随着尚未采用新技术人数的减少而降低, ③ 在②的前提下还要考虑广告等媒介的传播作用]27,10[。 *16. 建立耐用消费品市场销售量的模型。如果知道了过去若干时期销售量的情况,如何确定模型的参数。 *17、 根据经验当一种新商品设入市场后,随着人们对它的拥有量的增加,其销售量)(ts
的下降速度与)(ts成正比。广告宣传可给销量添加一个增长速度,它与广告费)(ta成正比,但广告只能影响这种商品在市场上尚未饱和的部分(设饱和量为M)。建立销量)(ts的模型。若广告宣传只进行有限时间,且广告费为常数a,问)(ts如何变化]10[。 *18.人工肾是帮助人体从血液中带走废物的装置。它通过一层薄膜与需要带走废物的血管相通(见图5-26)。人工肾中通以某种液体,其流动方向与血液在血管中的流动方向相反,血液中的废物透过薄膜进入人工肾。
设血液和人工肾中液体的流速均为常数,废物进入人工肾的数量与它在这两种液体中的浓度差成正比。人工肾总长L。建立单位时间内人工肾带走废物数量的模型]10[。 *19. 在鱼塘中投放0n尾鱼苗,随着时间的增长,尾数将减少而每尾的重量将增加。
① 设尾数)(tn的相对减少率nn为常数;由于喂养引起的每尾鱼量的增加率与鱼表面积成正比,由于消耗引起的每尾鱼量的减少率与鱼重量成正比。分别建立尾数和每尾鱼重的微分方程,并求解。 ② 用控制网眼的办法不捕小鱼,到时刻T才开始捕捞,捕捞能力用尾数的相对减少量|/|nn表示,记作E,即单位时间捕获量是)(tEn。问如何选择T和E,使从T开始的捕
获量最大 ]10[。 *20. 侦察机搜索潜艇。设0t时艇在O点,飞机在A点,6OA海里(见图5-27)。此时艇潜入水中并沿着飞机不知道的某一方向以直线形式逃去,艇速20海里/时,飞机以速度40海里/时按照待定的航线搜索潜艇,当且仅当飞到艇的正上方时才可发现它。 ① 在极坐标系中设时刻t飞机在(,r),艇在(dr,)。证明飞机为了与艇在),(ddrr相遇,航线必是对数螺线300err,其中),(00r是满足0021APOP的
某一点0p的坐标,例如)0,2(0p。即飞机先由A点沿直线飞到0p点,再沿对数螺线飞行。画出航线示意图。说明飞机最多沿螺线飞一周(360)总可发现潜艇。 ②证明;为了使整条航线是一条光滑曲线,飞机应先飞到)2,32(1p点,再沿螺线飞行。 ③在所有可以发现潜艇的航线中哪一条航线最短,长度若干。光滑航线的长度又若干]28[。
*21. 建立铅球掷远模型。不考虑阻力,设铅球初速为v,出手高度为h,出手角度为
(与地面夹角),建立投掷距离与v、h、的关系式,并在v、h一定的条件下求最佳出手角度。 *22. 建立肿瘤生长模型。通过大量医疗实践发现肿瘤细胞的生长有以下现象:i)当肿瘤细胞数目超过1110时是临床可观察的;ii)在肿瘤生长初期几乎每经过一定时间肿瘤细胞就增加一倍;iii)在肿瘤生长后期由于各种生理条件限制肿瘤细胞数目趋向某个稳定值。
① 比较Logistic模型与Gompertz模型:Nnndtdnln,其中)(tn是细胞数,N是极值,是参数。 ②说明上述两个模型是Usher模型:Nnndtdn1的特例,解释参数的意义]19[。
*23. 建立一个模型说明要用三级火箭发射人造卫星的道理。
① 设卫星绕地球作匀速圆周运动,证明其速度为rgRv,R为地球半径,r为卫星与地心距离,g为地球表面重力加速度。v也就是火箭的末速。问要把卫星送上离地面600公里的轨道,火箭末速应为多少。 ② 设火箭飞行中速度为)(tv,质量为)(tm,初速为零,初始质量0m,火箭喷出的气体相对于火箭的速度为u,忽略重力和阻力对火箭的影响。用动量守恒原理证明
)(ln)(0tmmutv。由此你认为要提高火箭的末速应采取什么措施。
③ 火箭质量包括3部分;有效载荷(卫星)pm;燃料fm;结构(外壳、燃料仓等)sm。其中sm在fm+sm中的比例难以小于10%。证明当pm=0(火箭不带卫星),燃料用完时火箭达到的最大速度为1uinvm。已知目前的3u千米/秒,取=10%,求vLm。这个结果说明什么。 ④ 假设火箭燃料燃烧的同时,不断丢弃无用的结构部分,即结构质量与燃料质量以
和1的比例同时减少。用动量守恒原理证明)(ln)1()(0tmmutv。问燃料用完时火箭末速为多少。与前面的结果有何不同。 ⑤ ④是个理想化的模型,实际上只能用建造多级火箭的办法一段段地丢弃无用的结构。记im为第i级火箭质量(燃料和结构),im为结构质量(对各级是一样的)。有效载荷仍用pm表示。当第1级的燃料用完时丢弃第1级的结构,同时第2级点火,再设燃烧级的初始质量与其负载质量之比保持不变,比例系数为k。证明3级火箭的末速
11ln33kkuv。计算要使5.103v千米/秒,发射1吨重的卫星需要多重的火箭(u、
用以前的数据)。若用2级或4级火箭,结果如何。由此得出使用3级火箭发射卫星的道理]48[。
