高中数学总复习课件:双曲线(精选)
合集下载
高中数学一轮复习课件 第8章 椭圆双曲线双曲线
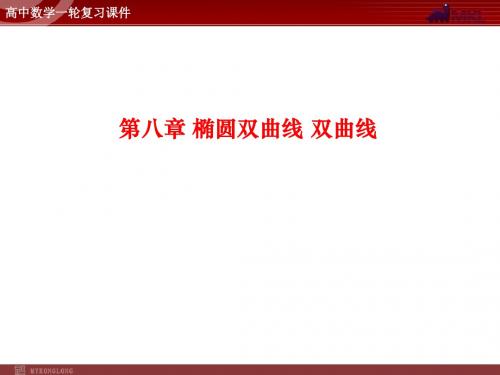
(a>0,b>0),其中c =a +b ,
2 2 2
焦点坐标为(0,±c). 确定一个双曲线的标准方程,必须要有一个定位条件(即确定焦点的 位置)和两个条件(即确定a,b的大小),主要有定义法、待定系数法,有
高中数学一轮复习课件
时还可根据条件用代入法.用待定系数法求双曲线方程的一般步骤
是: 第一,作判断:根据条件判断双曲线焦点在x轴上还是在y轴上,还是不 确定在哪个坐标轴上.
高中数学一轮复习课件
1.双曲线的定义 平面内到两个定点F1,F2的距离之差的绝对值等于常数2a (小于|F1F2 |)的点的轨迹叫作双曲线,这两个定点F1,F2叫作双曲线的焦点,两焦 点F1,F2间的距离叫做双曲线的焦距. (1)定义的数学表达式为:||PF1|-|PF2||=2a(2a<|F1F2|). (2)在双曲线的定义中,若2a=|F1F2|时,动点的轨迹是两条射线;当|F1F2|
y 要把双曲线方程写成 x =λ y 是 ± =0, - ,再根据已知条件确定λ的值,
2
x a
2
求出双曲线方程.若求得λ>0,则焦点在x轴上,若求得λ<0,则焦点在y 轴上.
b
a2
b2
5.双曲线相关问题,如中点弦、弦长、与直线的位置关系等,要牢牢
抓住方程组思想、消元法、根与系数之间的关系、弦长公式等方法.
关于x轴、y轴、原点对称 顶点(0,±a) (0,±c) 实轴长|A1A2|=2a,虚轴长|B1B2|=2b |F1F2|=2c
c ∈(1,+∞) e= a
c2=a2+b2
高中数学一轮复习课件
一般而言:
①双曲线有两条对称轴,它们分别是两焦点的连线及两焦点连线段 的中垂线. ②双曲线都有两个顶点,顶点是曲线与它本身的对称轴的交点. ③离心率反映双曲线开口的程度,当离心率越大,双曲线的开口越大.
第6节 第1课时 双曲线的定义、方程与性质--2025高中数学一轮复习课件基础版(新高考新教材)

= 50,
解得
= 100 2,
2
2
所以双曲线的方程是2 500 − 20 000=1.
题组三 连线高考
8.(2023·
北京,12)已知双曲线C的焦点为(-2,0)和(2,0),离心率为
2 ,则C的方
2
2
− =1
程为__________.
2
2
解析 令双曲线 C 的实半轴长、虚半轴长分别为 a,b,显然双曲线 C 的中心为
( C )
A.
3
2
B.
6
2
2 2
解析 双曲线 -x =1 的焦点在
3
2
2 3
所以离心率为 = =
.
3
3
2 3
C. 3
y 轴上,a= 3,b=1,c= 3 + 1=2,
6.(人教 A 版选择性必修第一册 3.2.1 节练习第 3
y2
=1
+1
解析
2 6
D. 3
2
题改编)已知方程 +2
−
(-∞,-2)∪(-1,+∞)
圆C2:(x-3)2+y2=1的圆心为C2(3,0),半径r2=1.
由于动圆E与圆C1,C2都外切,
设动圆E的半径为r,则|EC1|=r+3,|EC2|=r+1,
所以|EC1|-|EC2|=3-1=2<|C1C2|,
所以点E的轨迹是以C1,C2为焦点的双曲线的右支.
2
设双曲线的方程为 2
−
所以 E 的轨迹方程为
平面内与两个定点F1,F2的____________________等于非零常数(小于
双曲线-高中数学复习

个定点 F 1, F 2
|| MF 1|-| MF 2||=2 a
0<2 a <| F 1 F 2|
结论1
M 点的轨
迹为双曲
线
结论2
F 1, F 2
焦点;
| F 1 F 2|
为双曲线的
为双曲线
的焦距
提醒 (1)当2 a =| F 1 F 2|时, M 点的轨迹是两条射线;
(2)当2 a >| F 1 F 2|时, M 点不存在.
高中总复习·数学
2. 双曲线的标准方程和几何性质
标准方程
图形
高中总复习·数学
范围
性
质
对称性
顶点
渐近线
x ≥ a 或 x ≤- a , y
∈R
对称轴: 坐标轴
A 1(- a ,0),
A 2( a ,0)
y ≤- a 或 y ≥ a , x ∈R
;对称中心: 原点
A 1(0,- a ), A 2(0, a )
2|=4或16.
高中总复习·数学
1. 双曲线方程的常见设法
2
2
(1)与双曲线 2 - 2 =1( a >0, b >0)共渐近线的方程可设为
2
2
- 2 =λ(λ≠0);
2
(2)若渐近线的方程为 y =± x ( a >0, b >0),则可设双曲线
2
2
方程为 2 - 2 =λ(λ≠0).
高中总复习·数学
2. 双曲线中的常用结论
(1)双曲线的焦点到其渐近线的距离为 b ;
(2)若 P 是双曲线右支上一点, F 1, F 2分别为双曲线的左、右焦
|| MF 1|-| MF 2||=2 a
0<2 a <| F 1 F 2|
结论1
M 点的轨
迹为双曲
线
结论2
F 1, F 2
焦点;
| F 1 F 2|
为双曲线的
为双曲线
的焦距
提醒 (1)当2 a =| F 1 F 2|时, M 点的轨迹是两条射线;
(2)当2 a >| F 1 F 2|时, M 点不存在.
高中总复习·数学
2. 双曲线的标准方程和几何性质
标准方程
图形
高中总复习·数学
范围
性
质
对称性
顶点
渐近线
x ≥ a 或 x ≤- a , y
∈R
对称轴: 坐标轴
A 1(- a ,0),
A 2( a ,0)
y ≤- a 或 y ≥ a , x ∈R
;对称中心: 原点
A 1(0,- a ), A 2(0, a )
2|=4或16.
高中总复习·数学
1. 双曲线方程的常见设法
2
2
(1)与双曲线 2 - 2 =1( a >0, b >0)共渐近线的方程可设为
2
2
- 2 =λ(λ≠0);
2
(2)若渐近线的方程为 y =± x ( a >0, b >0),则可设双曲线
2
2
方程为 2 - 2 =λ(λ≠0).
高中总复习·数学
2. 双曲线中的常用结论
(1)双曲线的焦点到其渐近线的距离为 b ;
(2)若 P 是双曲线右支上一点, F 1, F 2分别为双曲线的左、右焦
高考数学复习考点知识专题讲解课件第49讲 双曲线

2 +2
(4)离心率e= =
=
1+
2
.
2
课前基础巩固
(5)等轴双曲线的渐近线互相垂直,离心率等于 2.等轴双曲线上任意一点到中心
的距离是它到两焦点距离的等比中项.
(6)共轭双曲线有共同的渐近线;它们的四个焦点共圆;它们的离心率的倒数的平
方和等于1.
(7)若P是双曲线上不同于实轴两端点的任意一点,F1,F2分别为双曲线的左、右
2. 双曲线的标准方程
2
2
Байду номын сангаас
2
2
(1)中心在坐标原点,焦点在x轴上的双曲线的标准方程为 2 - 2 =1(a>0,b>0);
(2)中心在坐标原点,焦点在y轴上的双曲线的标准方程为 2 - 2 =1(a>0,b>0).
课前基础巩固
3. 双曲线的性质
标准方程
图形
2 2
=1(a>0,b>0)
− +
课堂考点探究
变式题 (1)[2020·全国卷Ⅲ]
2 2
设双曲线C: 2 - 2 =1(a>0,b>0)的左、右焦点分别
为F1,F2,离心率为 5.P是C上一点,且F1P⊥F2P.若△PF1F2的面积为4,则a= (A
A.1
B.2
C.4
D.8
2
2
2
[解析]由条件可得||PF1|-|PF2||=2a,因为F1P⊥F2P,所以|PF1| +|PF2| =4c ,故
轨迹是两条射线.
课前基础巩固
高考数学复习考点知识讲解课件47 双曲线

解法二:当其中的一条渐近线方程y= 3 x中的x=2时,y=2 3 >3,又点(2,3)在第一
象限,所以双曲线的焦点在x轴上,设双曲线的标准方程是
x2 a2
-
y2 b2
=1(a>0,b>0),由题意
得aba42=-b932=,1,
解得ab= =1,3, 所以该双曲线的标准方程为x2-y32=1,故选C.
解法三:因为双曲线的渐近线方程为y=±
3 x,即
y 3
=±x,所以可设双曲线的方程
是x2-y32=λ(λ≠0),将点(2,3)代入,得λ=1,所以该双曲线的标准方程为x2-y32=1,故选
C.
— 22 —
(新教材) 高三总复习•数学
— 返回 —
3.经过点P(3,2 7),Q(-6 2,7)的双曲线的标准方程为______2_y5_2 -__7_x5_2 =__1___.
(2)与双曲线ax22-by22=1有相同渐近线时可设所求双曲线方程为ax22-by22=λ(λ≠0).
— 24 —
(新教材) 高三总复习•数学
— 返回 —
考点三 双曲线的简单几何性质——多维探究
角度1:双曲线的渐近线问题
【例2】
(1)(2022·杭州模拟)设F1,F2是双曲线C:
x2 a2
-
y2 b2
=1(a>0,b>0)的左、右焦
点,P是双曲线C右支上一点,若|PF1|+|PF2|=4a,且∠F1PF2=60°,则双曲线C的渐近
线方程是( C )
A. 3x±y=0 B.2x± 7y=0
C. 3x±2y=0 D.2x± 3y=0
(2)焦点在x轴上,焦距为10,且与双曲线y42-x2=1有相同渐近线的双曲线的标准方程
《高中数学双曲线》PPT课件
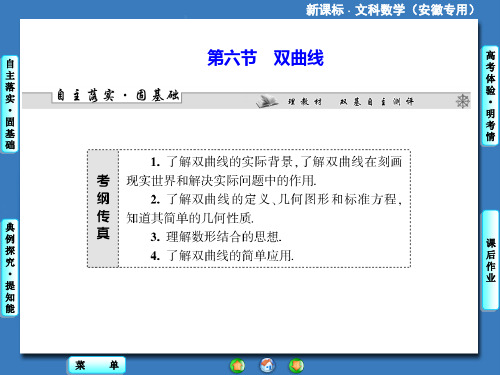
其两个焦点,点P为双曲线上一点,若PF1⊥PF2,则|PF1|+
体 验 ·
· 固
|PF2|的值为________.
明 考
基
情
础
【解析】 设P在双曲线的右支上,|PF1|=2+x,
|PF2|=x(x>0),因为PF1⊥PF2,
所以(x+2)2+x2=(2c)2=8,所以x= 3 -1,x+2=
典
例 探
· 明 考 情
础
性 质
顶点
顶点坐标:
顶点坐标:A1_(_0_ ,
A1_(_-____a_,___0__)_,A2_(_a_, ____0_)_ ___-___a__)_,A2_(_0__,___a__)
典
渐近线
____y=__±__ba_x____
___y_=__±_ab_x___
例 探 究
离心率 e=ac,e∈__(_1_,__+__∞_)__,其中c=__a_2_+__b_2__
明 考 情
图形
典
例
课
探
后
究
作
·
业
提
知
能
菜单
新课标 ·文科数学(安徽专用)
高
自 主
范围
_x_≥__a_或__x_≤__-__a___
_y_≤__-__a_或__y_≥__a_
考 体
落
验
实 · 固 基
对称性
对称轴:_坐___标__轴__ 对称中心:_原__点____
对称轴:_坐__标__轴__ 对称中心:_原__点__
典
例 焦点在x轴上,可知其焦点坐标是(±3,0).
课
探
后
究
作
·
高中数学课件-双曲线2

C 的离心率为( )
A. 5
B.2
C. 3
D. 2
解析 (1)不妨设一条渐近线的方程为 y=bax,则 F2 到 y=bax 的距离 d= a|b2+c| b2=b,
在 Rt△F2PO 中,|F2O|=c,所以|PO|=a,所以|PF1|= 6a,又|F1O|=c,所以在△F1PO 与 Rt△F2PO 中,根据余弦定理得 cos∠POF1=a2+c2-2a(c 6a)2=-cos∠POF2=
今日课前思
@《创新设计》
你能得到什么??
1
知识衍化体验
考点聚集突破
核心素养提升
@《创新设计》
角度2 求双曲线的离心率 【例 3-2】 (1)(2018·全国Ⅲ卷)设 F1,F2 是双曲线 C:ax22-by22=1(a>0,b>0)的左、右
焦点,O 是坐标原点.过 F2 作 C 的一条渐近线的垂线,垂足为 P.若|PF1|= 6|OP|,则
c2-a2,所以 c2>4(c2-a2),即 c2<43a2,所以 e=ac<233,又知 e>1,所以双曲线 C1 的
离3心率的取值范围为1,2
3 .
知识衍化体验
考点聚集突破
核心素养提升
@《创新设计》
4
知识衍化体验
考点聚集突破
核心素养提升
A.1,2
3
3
2 B.
3
3,+∞
(2)由双曲线方程可得其渐近线方程为
C.(1,2) D.(2,+∞) y=±bax,即 bx±ay=0,圆
C2:x2+y2-2ax+34a2
=0 可化为(x-a)2+y2=14a2,圆心 C2 的坐标为(a,0),半径 r=12a,由双曲线 C1 的一
