第四节重积分应用举例教材课程
合集下载
《重积分应用举例》PPT课件

b
对 y 轴 的 转 动 惯 量 为 o a x
Iy x2dxd,y D
整理课件
20
bdya(1by)x2dx 1 a3b.
00
12
同 理 : 对 x 轴 的 转 动 惯 量 为
Ix Dy2dxdy112ab3.
整理课件
21
三、引力
设空间一物体对物体外一点 P0 x0, y0, z0 处的
zdvdzzdxdyahzdvydydxxoy平面上有设有一平面薄片占有xoy面上的闭区域的转动惯量为薄片对于轴的转动惯量薄片对于轴的转动惯量设一均匀的直角三角形薄板两直角边长分别为ab求这三角形对其中任一直角边的转动惯量
第四节 重积分应用举例
❖一、曲面的面积 ❖二、质心和转动惯量 ❖三、引力
整理课件
曲面面积公式为:A 1 x y2 x z 2dy;dz Dyz
3.设曲面的方程为:yh(z,x)
曲面面积公式为:A
1 yz
2 y x
2dz.dx
Dzx
整理课件
8
例 1求 球 面 x 2 y 2 z 2 a 2 , 含 在 圆 柱 体 x 2 y 2 a 内 部 x 的 那 部 分 面 积 .
则有 dAds.
整理课件
6
d为dA 在xo面 y 上的 , 投 d 影 dA co , s
cos 1 ,
1fx2fy2
dA 1fx 2fy2d曲面S的面积元素
A 1fx2fy2d, D
曲面面积公式为:A 1(xz)2(yz)2dxd
Dxy
整理课件
7
同理可得
2.设曲面的方程为:xg(y,z)
单位质量质点的引力为 F Fx, Fy , Fz
高等数学课件D104重积分的应用

2
2
F F F x
y
r2a2 2 F y1ADydxdy
z
z
zh(t)2(xh2(t)y2)
Dz[x y (za) ]2 a
0(y2z2) IOD (x,y)dxdy D0 9h(t)0,
目录 上页 下页 返回 结束
例3. 计算双曲抛物面
被柱面 AD 1zx2zy2dxdy所截
出的面积 A .
dxdy 解: 曲面在 xOy 面上投影为V dxdydz则
x2y2z2R2 — 对 x 轴的 静矩
π
r2sin Fz
—对y 静矩
轴的
3 2
得D 的形心坐标: AD 1( xz)2( yz)2dxdy
Dz[xF2y2(za)2] 2 z
xDxdxdy , ( A 为D 的面积) A
a
0(y2z2) IOD (x,y)dxdy D0 15h(t)0,
目录 上页 下页 返回 结束
转动惯量.
dxdy 解: 取球心为原点, z 轴为 l 轴, 设球所占
x Fz
域为 ( x2y2)dxdydz则
Fz
Fz 2 π a5
5
(用球坐标)
y
r(xx0)2(yy0)2(zz0)2
:x 2 y 2 z 2 a 2 ,
3 M4πa3 2 l 2 2 3
Fz 0,
F z
球体的质量
k 1
n
(k ,k , k )vk
k 1
将第
k
块看作质量集中于点
的质点, hz(3z)2dz 09
此质点
dxdy 系的质心坐标就近似该物体的质心坐标. 例如,
ydxdydz
y
高等数学 第九章 重积分 第四节 重积分应用

x= z=
∫∫∫Ω xd xd y d z ∫∫∫Ω
V zd x d y d z V
∫∫∫Ω yd xd y d z
V
,
( V = ∫∫∫ d x d y d z为Ω的体积 ) Ω
上页 下页 返回 结束
若物体为占有xOy 面上区域 D 的平面薄片 其面密度 的平面薄片, 若物体为占有 则它的质心坐标 质心坐标为 则它的质心坐标为
上页 下页 返回 结束
三、物体的质心
设空间有n个质点 设空间有 个质点, 分别位于 (xk , yk , zk ) , 其质量分别 个质点 为 mk ( k =1, 2, L, n ) ,由力学知 该质点系的质心坐标 由力学知,
∑xk mk
为
n
x=
k =1 n
∑yk mk
, y=
k =1 n
n
∑zk mk
∴ dA = 1 + f x2 + f y2 dσ 曲面S的面积元素 曲面S
∴ A = ∫∫ 1 + f x2 + f y2 dσ ,
D
∂z ∂z A = ∫∫ 1 + (∂x )2 + (∂y )2dxdy 曲面面积公式为: 曲面面积公式为: Dxy
上页
下页
返回
结束
小结 1. 设曲面 S 的方程为:z = f ( x , y ) 的方程为:
设曲面的方程为: 3.设曲面的方程为:y = h( z , x ) 则曲面面积公式为: 则曲面面积公式为: A =
∫∫
Dzx
1+ (
∂y 2 ∂z
) + ( ) dzdx.
∂y 2 ∂x
上页 下页 返回 结束
例 4. 求球面 x 2 + y 2 + z 2 = a 2 含在圆柱体 2 2 x + y = ax 内部的那部分面积 内部的那部分面积.
∫∫∫Ω xd xd y d z ∫∫∫Ω
V zd x d y d z V
∫∫∫Ω yd xd y d z
V
,
( V = ∫∫∫ d x d y d z为Ω的体积 ) Ω
上页 下页 返回 结束
若物体为占有xOy 面上区域 D 的平面薄片 其面密度 的平面薄片, 若物体为占有 则它的质心坐标 质心坐标为 则它的质心坐标为
上页 下页 返回 结束
三、物体的质心
设空间有n个质点 设空间有 个质点, 分别位于 (xk , yk , zk ) , 其质量分别 个质点 为 mk ( k =1, 2, L, n ) ,由力学知 该质点系的质心坐标 由力学知,
∑xk mk
为
n
x=
k =1 n
∑yk mk
, y=
k =1 n
n
∑zk mk
∴ dA = 1 + f x2 + f y2 dσ 曲面S的面积元素 曲面S
∴ A = ∫∫ 1 + f x2 + f y2 dσ ,
D
∂z ∂z A = ∫∫ 1 + (∂x )2 + (∂y )2dxdy 曲面面积公式为: 曲面面积公式为: Dxy
上页
下页
返回
结束
小结 1. 设曲面 S 的方程为:z = f ( x , y ) 的方程为:
设曲面的方程为: 3.设曲面的方程为:y = h( z , x ) 则曲面面积公式为: 则曲面面积公式为: A =
∫∫
Dzx
1+ (
∂y 2 ∂z
) + ( ) dzdx.
∂y 2 ∂x
上页 下页 返回 结束
例 4. 求球面 x 2 + y 2 + z 2 = a 2 含在圆柱体 2 2 x + y = ax 内部的那部分面积 内部的那部分面积.
《重积分的应用举例》PPT课件

§7.4 重积分的应用举例
1. 重积分的几何应用
计算面积与体积
n
S
1d
D
lim 0 i1
i
n
V
1dV
lim 0
i 1
Vi
例1 求两曲面 z x2 3y2 与 z 8 x2 y2 所围区域的体积.
解 所求体积为 V dv, 将往oxy面上投影
z x2 3y2
z
(称为面积元素)
z
n
SP
o
x
d y
nz
dS P d
故有曲面面积公式
S D 1 fx2 (x, y) f y2 (x, y) d
即
S
1 ( z )2 ( z )2 d xd y
D
x y
若光滑曲面方程为
x g( y, z) , ( y, z) Dy z ,则有
Dy z
若光滑曲面方程为
面积.
解 由已知条件得
S EG F 2 drd r 2 h2 drd
D
D
2
a
d
r 2 h2 dr [a
a2 h2 h2 ln( a
0
0
a2 h2 )].
h
2. 重积分的物理应用
(1) 质
量平面薄片的质量 M x, yd ,
D
x, y是薄片 D 在 x, y处的面密度.
2r.
V 2 (4 4r2 cos2 4r2 sin2 ) 2 2rdrd
D
16 2
2
d
1 4r(1 r 2 )dr 8
2.
0
0
曲面的面积
设曲面S的方程zf(x, y)在区域D上具有连续的一阶偏导数, 则曲面S的面积为
1. 重积分的几何应用
计算面积与体积
n
S
1d
D
lim 0 i1
i
n
V
1dV
lim 0
i 1
Vi
例1 求两曲面 z x2 3y2 与 z 8 x2 y2 所围区域的体积.
解 所求体积为 V dv, 将往oxy面上投影
z x2 3y2
z
(称为面积元素)
z
n
SP
o
x
d y
nz
dS P d
故有曲面面积公式
S D 1 fx2 (x, y) f y2 (x, y) d
即
S
1 ( z )2 ( z )2 d xd y
D
x y
若光滑曲面方程为
x g( y, z) , ( y, z) Dy z ,则有
Dy z
若光滑曲面方程为
面积.
解 由已知条件得
S EG F 2 drd r 2 h2 drd
D
D
2
a
d
r 2 h2 dr [a
a2 h2 h2 ln( a
0
0
a2 h2 )].
h
2. 重积分的物理应用
(1) 质
量平面薄片的质量 M x, yd ,
D
x, y是薄片 D 在 x, y处的面密度.
2r.
V 2 (4 4r2 cos2 4r2 sin2 ) 2 2rdrd
D
16 2
2
d
1 4r(1 r 2 )dr 8
2.
0
0
曲面的面积
设曲面S的方程zf(x, y)在区域D上具有连续的一阶偏导数, 则曲面S的面积为
第四节 重积分应用举例

D b
b
y
o
a
x
1 3 a b . 0 0 12 同理:对 x 轴的转动惯量为: I x y 2dxdy 1 ab3 . 12 D
dy
y a (1 b )
x 2dx
2、空间物体的转动惯量
设物体占有空间有界闭区域 ,在点( x , y , z ) 处的体密度为 ( x , y , z ) , ( x , y , z ) 在 上连续,则
x 2 z 2 R2 x y R ,
2 2 2
z
R
o x
利用对称性, 考虑第一卦限部分,
z R2 x 2 其曲顶柱体的顶为
0 y R2 x 2 ( x, y) D : 0 x R
R
y
则所求体积为
8
R
0 R
R2 x 2 d x
0
R2 x 2
D
z
( x, y)
(x y a )
2 2 2
3 2
d
3 d
F
o
x
y
ak
D
1
( x 2 y 2 a 2 )2
ak d
0
2
R 2
1 ( a )
2
3 2
0
d
1 1 2ka . 2 2 R a a
所求引力为
2 2 D
o
2a
y
x
0
2 acos
4a2 2 d
32 3 2 a ( ) 3 2 3
二、曲面的面积
1.设曲面的方程为: z z( x , y )
在 xoy 面上的投影区域为D,
b
y
o
a
x
1 3 a b . 0 0 12 同理:对 x 轴的转动惯量为: I x y 2dxdy 1 ab3 . 12 D
dy
y a (1 b )
x 2dx
2、空间物体的转动惯量
设物体占有空间有界闭区域 ,在点( x , y , z ) 处的体密度为 ( x , y , z ) , ( x , y , z ) 在 上连续,则
x 2 z 2 R2 x y R ,
2 2 2
z
R
o x
利用对称性, 考虑第一卦限部分,
z R2 x 2 其曲顶柱体的顶为
0 y R2 x 2 ( x, y) D : 0 x R
R
y
则所求体积为
8
R
0 R
R2 x 2 d x
0
R2 x 2
D
z
( x, y)
(x y a )
2 2 2
3 2
d
3 d
F
o
x
y
ak
D
1
( x 2 y 2 a 2 )2
ak d
0
2
R 2
1 ( a )
2
3 2
0
d
1 1 2ka . 2 2 R a a
所求引力为
2 2 D
o
2a
y
x
0
2 acos
4a2 2 d
32 3 2 a ( ) 3 2 3
二、曲面的面积
1.设曲面的方程为: z z( x , y )
在 xoy 面上的投影区域为D,
经典高等数学课件D10-4重积分的应用
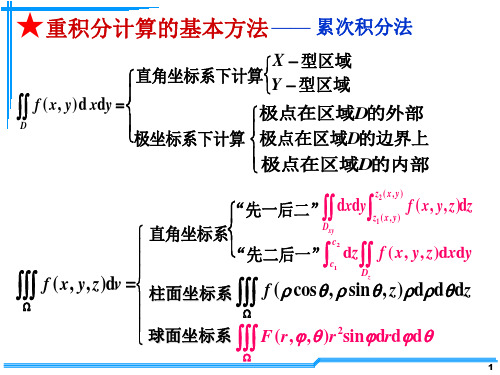
x 2 y 2 a 2 .由
z x , x a2 x2 y2
得 1 (
z y , 2 2 2 y a x y
z 2 z 2 a ) ( ) . x y a2 x2 y2
12
A上
D
a a x y a
2 2 2
dxdy D : x 2 y 2 a 2 .
设曲面S的方程为z 如图, 设小区域
z
z f ( x, y )
f ( x, y ),
M
o
曲面S在xoy面上的投影为区 域D,
sS d
d
( x, y)
点(x,y) d, d D, 以 为S上过点M(x,y,z)的切平面, d
的边界为准线, 母线平行于z轴的 截切平面 小柱面, 截曲面S为 dS, 为 dA, 则有 dA dS.
C2 D
7 所求质心是(0, ). 3
o
x
17
推广: 占有空间有界闭区域, 在点( x, y, z )处的密度为 ( x, y, z )
(假定 ( x, y, z )在上连续)的物体的质心坐标(x , y , z )为:
1 x x ( x, y, z )dv , M 1 y y ( x, y, z )dv , M 1 z z ( x, y, z )dv , M
D
D
y
( x, y)
又M ( x , y )d , 则薄片的质心坐标为:
D
o
d
x
m yi x ( x , yxi mi )d i y ( x, y )d M xM i 1 y M M i 1 y ,, y x n D y n x x D . MM M M ( x , m)d m y i i ( x, y )d
重积分的应用78864-32页PPT文档资料

F y (x ( x 0 k )2 (x (,y y ,z y )0 ) y 2 ( y (0 z ) z0 )2 )2 3d,v
F z (x ( x 0 k )2 (x (,y y ,z y )0 ) z 2 ( z (0 z ) z0 )2 )2 3d,v
2a
2
A 0
y(x)dx a (1 co t)d [s a (t sit)n ] 0
2a2(1cot)s2dt3a2. 0
由 于 区 域 关 于 直 线 x a 对 称 , 所 以 形 心 在 x a 上 , 即 x a ,
y 1
x A1 Dxd,
y A1 Dyd.
其中Ad
D
例3 设平面薄板由yxaa((1tcsiontts)),(0t2)
与x轴围成,它的面密度1,求形心坐标.
解 先 求 区 域 D 的 面 积 A ,
y(x)
D
0 t 2 , 0 x 2 a a 2a
D
b
3h
12
.
设 物 体 占 有 空 间 有 界 闭 区 域 ,在 点 (x ,y ,z)处
的 体 密 度 为 (x ,y ,z),(x ,y ,z)在 上 连 续 ,则
对于 x轴的转动惯量
Ix(y2z2)(x,y,z)dv,
对于y轴的转动惯量
Iy(x2z2)(x,y,z)dv.
对于 z轴的转动惯量
Iz(x2y2)(x,y,z)dv.
五、引力
空间一物体对物体外一点p0(x0,y0,z0)处的
单位质量质点的引力为: F
km1m2 r3
r
F x (x ( x 0 k )2 (x (,y y ,z y )0 x )2 ( x (0 z ) z0 )2 )2 3d,v
高等数学 第四节 重积分的应用

Ω
对 y 轴的转动惯量
I y ( x2 z2 ) ( x , y , z)d xd yd z
Ω
对原点的转动惯量
Iz ( x2 y2 z2 ) ( x , y , z)d xd yd z
Ω
第十章 第四节
16
如果物体是平面薄片,面密度为 ( x , y) ( x , y) D
则转动惯量的表达式是二重积分。
y2
x2
(x2 y2)
第十章 第四节
y
D
o
x
17
例4 求半径为 a 的均匀半圆薄片对其直径
的转动惯量。
y
解
建立坐标系如图,D
:
x
2
y2
a2
y0
D
a o a x
I x D y2 d x d y D r3 sin2 d r d
0
sin
2
d
a
0 r
3
d
r
半圆薄片的质量 M 1 a2
2 1 M a2
D1 : x2 y2 ax ( x , y 0) 曲面方程 z a2 x2 y2
于是
1 ( z )2 ( z )2 x y
a a2 x2 y2
A 4
D1
1
z
2 x
z
2 y
dxdy
4
D1
a dxdy
a2 x2 y2
4a
2 d
a cos
0
0
1
rdr a2 r2
2 a2 4a2
xd xdy
x D A
yd xdy
y D A
第十章 第四节
(A 为 D 的面积)
13
例3 求位于两圆
对 y 轴的转动惯量
I y ( x2 z2 ) ( x , y , z)d xd yd z
Ω
对原点的转动惯量
Iz ( x2 y2 z2 ) ( x , y , z)d xd yd z
Ω
第十章 第四节
16
如果物体是平面薄片,面密度为 ( x , y) ( x , y) D
则转动惯量的表达式是二重积分。
y2
x2
(x2 y2)
第十章 第四节
y
D
o
x
17
例4 求半径为 a 的均匀半圆薄片对其直径
的转动惯量。
y
解
建立坐标系如图,D
:
x
2
y2
a2
y0
D
a o a x
I x D y2 d x d y D r3 sin2 d r d
0
sin
2
d
a
0 r
3
d
r
半圆薄片的质量 M 1 a2
2 1 M a2
D1 : x2 y2 ax ( x , y 0) 曲面方程 z a2 x2 y2
于是
1 ( z )2 ( z )2 x y
a a2 x2 y2
A 4
D1
1
z
2 x
z
2 y
dxdy
4
D1
a dxdy
a2 x2 y2
4a
2 d
a cos
0
0
1
rdr a2 r2
2 a2 4a2
xd xdy
x D A
yd xdy
y D A
第十章 第四节
(A 为 D 的面积)
13
例3 求位于两圆
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的转动惯量依次为
n
n
I x mi yi 2 , I y mi xi 2 .
i 1
i 1
2020/7/29
设 有 一 平 面 薄 片 , 占 有 xo面 y上 的 闭 区 域
D, 在 点 (x,y)处 的 面 密 度 为 (x,y), 假 定 (x,y)在 D上 连 续 , 平 面 薄 片 对 于 x轴 和 y 轴
解 先 求 区 域 D 的 面 积 A ,
y(x)
D
0 t 2 , 0 x 2 a a 2a
2a
2
A 0
y(x)dx a (1 co t)d [s a (t sit)n ] 0
2a2(1cot)s2dt3a2. 0
2020/7/29
由 于 区 域 关 于 直 线 x a 对 称 , 所 以 形 心 在 x a 上 , 即 x a ,
a/7/29
面 积 A 4 1zx2zy2dxdy
D 1
4
D1
a dxdy
a2x2y2
4a 2d
acos
1
d
0
0
a22
2 a24a2.
2020/7/29
例2 求旋转抛物面 z x2 y2位于 0z9之间的那一部分的面积。
解: 设 Dx,yx2y29
由公式知 S 2x2 2y2 1dxdy D
D
a dxdy
a2 x2 y2
2
2ahh2
d
a d2ah
0
0
a2 2
2020/7/29
二、质心和转动惯量
1、质心:
设 xoy平面上有n个质点,它们分别位于
( x1 , y1 ),( x2 , y2 ),,( xn , yn )处,质量分别
为m1, m2 ,, mn.则该质点系的质心的坐标为
n
4 x2 y2 1dxdy D
2
3
d
42 1d
37
37 1
0
0
6
2020/7/29
例3 求半径为a,高度为h0ha的球冠的面积。
解: 设球冠的方程为
za2x2y2,x,yD
其中
D x ,y x 2 y 2 2 a h h 2
由公式得球冠的面积
S D
zx2 zy2 1dxdy
y 1
ydxdy1
2a y(x)
dx ydy
AD
A0
0
61a2
2a[y(x)]2dxa 2[1cot]s3dt
0
60
5 6
.
所 求 形 心 坐 标 为 ( a ,6 5 ) .
2020/7/29
2、转动惯量
设xoy 平面上有n 个质点,它们分别位于
( x1 , y1 ) ,( x2 , y2 ) ,, ( xn , yn ) 处,质量分别 为m1 , m2 ,, mn .则该质点系对于x 轴和y 轴
S 1 cos
2020/7/29
又将点R的坐标 xx0, y0 代入上式,得
z
cos cos
y0 ,即点R的坐标为
cos
x0
,
0,
cos
y0
因而得
co s co s M P x0,0 ,co sx0 x0 1 ,0 ,co s
M R 0 , y0,c c o o s s y0 y0 0 , 1 ,c c o o s s
x
My M
mi xi
i 1 n
,
mi
i 1
n
y
Mx M
mi yi
i 1 n
mi
.
i 1
2020/7/29
设有一平面薄片,占有 xoy面上的闭区域D,
在点( x, y)处的面密度为 ( x, y),假定 ( x, y)在
D 上连续,平面薄片的质心
x( x, y)d
y( x, y)d
由元素法 x D
的 转 动 惯 量 为
z
zdv
,其中v是 的体积
v
,
Dz
A
h h
z
2
zdv0 hdzzdxdy0 hzD zdz
D z
A
h
2
zdvhA 20hzhz2dzA 1h 22, z
12 Ah
1 h. 4
3
2020/7/29
例4
设平面薄板由
x y
a(t a(1
sin t),(0 cos t )
t
2)
与 x轴围成,它的面密度 1,求形心坐标.
于是得截面面积
SM PM R c co os s ,c co os s ,1 x0y0c o
1 s
2020/7/29
1.设曲面的方程为: zf(x,y)
z
在xoy面上的投影区域D,为
s
如图, 设小区 d 域 D,
dA
M
点 (x,y)d,
为 S上M 过 (x,y,f(x,y))
o
的切 . 平面
x
第四节 重积分应用举例
• 一、曲面的面积 • 二、质心和转动惯量 • 三、引力
2020/7/29
2020/7/29
z Q
P
RO
Ny
L
M(x0,y0,0)
x
一、曲面的面积
• 例1 设一底面为矩形的柱体被一平面所截, 如果截面的法向量为
底面位于 x o y 面,证明截面(平行四边形)的
面积 S 与底面的面积 有如下的关系:
, y D
.
( x, y)d
( x, y)d
D
D
当薄片是均匀的,重心称为形心.
x A1 Dxd,
y A1 Dyd.
其中Ad
D
2020/7/29
例3 设一正棱锥体 的底面位于 x o y 面上,底面中心为
坐标原点,顶点位于正z轴上,高度为h,求该正棱锥体的形心。
解:设 的形心坐标为 x, y, z 且 x 0, y0
(x, y) y
d
以d边界为准线,母 于z线 轴平 的行 小
柱面,截s曲 为d面 s;截切平 为面 dA,
则有 dAds.
2020/7/29
d 为 d在 Axo 面 y 上, 的 d 投 dA c影 o , s
cos 1 ,
1fx2fy2
dA 1fx 2fy2d曲面S的面积元素
A 1fx2fy2d, D
曲面面积公式为:A 1(xz)2(yz)2dxd
Dxy
2020/7/29
同理可得
2.设曲面的方程为:xg(y,z)
曲面面积公式为:A 1 x y2 x z 2dy;dz Dyz
3.设曲面的方程为:yh(z,x)
曲面面积公式为:A 1 yz 2 x y 2dz.dx Dzx
2020/7/29
例 1求 球 面 x 2 y 2 z 2 a 2 , 含 在 圆 柱 体 x 2 y 2 a 内 部 x 的 那 部 分 面 积 .
解 由 对 称 性 知 A 4 A 1 , D 1 : x 2 y 2 a(x x,y0)
曲 面 方 程 za 2 x 2 y 2 ,
于 是 1 x z2 y z2
