双向板按弹性方法计算实例
双向板的弹性计算法

双向板的弹性计算法双向板的弹性计算法双向板的受力特点前已述及。
双向板常用于工业建筑楼盖、公共建筑门厅部分以及横隔墙较多的民用房屋。
当民用房屋横隔墙间距较小时(如住宅),可将板直接支承于四周的砖墙上,以减少楼盖的结构高度。
1.双向板的计算双向板的内力计算有弹性计算法和塑性计算法两种,本书仅介绍双向板内力的弹性计算法。
弹性计算法是以弹性薄板理论为依据而进行计算的一种方法,由于这种方法内力分析比较复杂,为简化计算,通常是直接应用根据弹性薄板理论编制的弯矩系数表(附表)进行计算。
(1)单跨双向板的计算单跨双向板按其四边支承情况的不同,在楼盖中常会遇到如下六种情况:四边简支(图1a);一边固定三边简支(图1b);两对边固定、两对边简支(图1c);两邻边固定、两邻边简支(图1d);三边固定、一边简支(图7.1.38e);四边固定(图7.1.38f)。
(a)(b)(c)(d)(e)(f)图1 双向板的六种四边支承情况根据不同支承情况,可从附表中查出弯矩系数,即可求得弯矩:M=表中系数×ql2(1)式中M ——跨中或支座单位板宽内的弯矩;q ——均布荷载(kN /m2)l ——板的较小跨度(m)。
附表中给出了图1所示六种边界条件的单跨板在均布荷载作用下的挠度系数、支座弯矩系数以及泊松比μ =0时的跨中弯矩系数。
钢筋混凝土结构的泊松比μ=1/6,故对跨中弯矩应按下式计算:M x(μ )=M X +μM y(2)M y (μ)=M y+μM X (3)式中M X、M y——按附表查得的板跨中弯矩系数计算得到的跨中弯矩值。
【例1】某砖混结构卫生间的现浇板l1×l2=3600mm×6000mm,四周与圈梁整体现浇,现浇板厚h=90mm,墙体厚240 mm,板承受恒载设计值g=3.6KN/m,活载设计值q=2.8KN/m,采用C20砼,受力钢筋HPB235。
试确定该现浇板受力钢筋用量。
【解】长边与短边之比l2/l1=6000/3600=1.67<2,按双向板计算。
双向板设计与计算

式中
M max
1 (g 8
q)l
2 0
g 、q ——作用于梯段板上的沿水平投影方向的
恒载及活载设计值;
l0 ——梯段板的计算跨度。
简支斜板(梁)在竖向均布荷载作用下的最大剪力为:
Vmax
1 (g 2
q)ln
式中 ln ——净跨的水平投影长度。
但在配筋计算时,考虑到梯段板与平台梁整体连接,平 台梁对梯段板有一定的弹性约束作用,计算时最大弯矩可 取:
,
⑤跨内最大正弯矩
通过上述荷载的等效处理,等区格连续双向板在荷载g’ 、q’作用下,都可转化成 单区格板利用附表3-2计算出跨内弯矩值。最后按式(3-21)计算出两种荷载情 况的实际跨中弯矩,并进行叠加,即可作为所求的跨内最大正弯矩。
2.求支座弯矩
假定全板各区格满布活荷载时支座弯矩最大,内区格可按四边固定的单跨双向板计算 其支座弯矩,边区格,其边支座边界条件按实际情况考虑,内支座按固定边考虑, 计算其支座弯矩。
M
1 (g 10
q
)l
2 0
○6 由于梯段板为斜向搁置的受弯构件,还将产生轴向力, 但其影响很小,设计时可不考虑。
○7 梯段斜板和一般板计算一样,可不必进行斜截面抗剪承 载力验算。
2)构造要求
梯段斜板配筋可采用弯起式或分离式。采用弯起式配筋时,一半 钢筋伸入支座,一半靠近支座处弯起,支座截面负筋的用量一般可取 与跨中截面相同。受力钢筋的弯起点位置见图7.3.3。在垂直受力钢 筋方向仍应按构造配置分布钢筋φ6@250,并要求每一个踏步下至少 放置一根钢筋。
2)构造要求 斜边梁构造要求与一般简支受弯构件相同,斜边梁的 纵筋在平台梁中应有足够的锚固长度。
双向板按弹性方法计算实例[精华]
![双向板按弹性方法计算实例[精华]](https://img.taocdn.com/s3/m/0ce4411517fc700abb68a98271fe910ef12daea7.png)
双向板按弹性方法计算实例1.楼盖平面布置双向板肋形楼盖梁板结构布置如图1,钢筋混凝土板厚150h mm =,楼面面层为20mm 厚水泥砂浆抹面(320/kN m γ=),板底为15mm 厚石灰砂浆粉刷(317/kN m γ=)活载标准值25.4/k q kN m =,混凝土为35C 级,板中受力筋及分布筋采用HPB300级钢筋;梁中受力筋采用HRB335级钢筋;梁中箍筋和架立筋采用HPB300级钢筋。
柱距为6900mm ,板的弯矩折减系数为:B1为0.8;B2,B3均为1.0图1 楼盖平面布置2.板的荷载计算恒载 20mm 厚水泥砂浆抹面 200.020.4⨯= KN/2m150mm 钢筋混凝土板 200.15 3.75⨯= KN/2m15mm 石灰砂浆 170.0150.26⨯=KN/2m标准值 0.4 3.750.26=4.41k g =++ KN/2m活载 标准值 5.4k q = KN/2m可变荷载效应起控制作用, 1.2G γ= 1.3Q γ=设计值 1.2 4.41 5.292g =⨯=KN/2m ,设计值 1.3 5.47.02q =⨯= KN/2m荷载设计值 5.2927.0212.312p g q =+=+= KN/2m /2 5.2927.02/28.80p g q '=+=+= KN/2m/27.02/2 3.51p q ''±=== KN/2m3. 板的内力计算及配筋3.1中间区格板1B计算跨度: 6.9x l m = 6.9y l m = / 1.0x y l l =单位板宽弯矩(/KN m m ∙)跨中弯矩:荷载按棋盘布x M =系数(6)2x p l '+系数(1)2x p l '' =( 0.02058.800.0429 3.51⨯+⨯) 26.915.76⨯= y M =系数(6)2x p l '+系数(1)2xp l ''=( 0.02058.800.0429 3.51⨯+⨯) 26.915.76⨯=支座弯矩:荷载按满布a 支座a x M =系数(6)2x pl =20.051312.312 6.930.07-⨯⨯=-b 支座by M =系数(6)2x pl =20.051312.312 6.930.07-⨯⨯=-配筋计算:s γ=0.95,0130x h mm =,0120y h mm =。
弹性双向板计算(带公式)
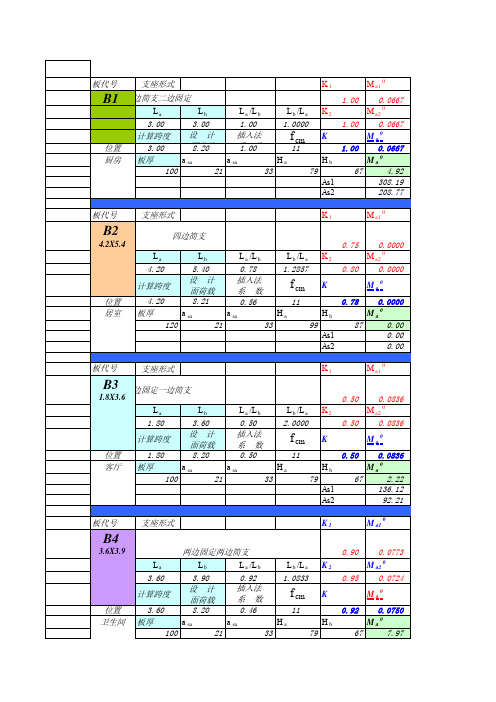
支座形式
K1
M a1 0
B1 二边简支二边固定
1.00 0.0667
La
Lb
L a /L b
L b /L a K 2
M a2 0
3.00
3.00
1.00
1.0000
1.00 0.0667
计算跨度
位置
3.00
设计 面8.荷20载
插入法 系1.00数
f cm K
Ma0
11
1.00 0.0667
厨房
D
S
As
12
150 753.982224
M b1 0
0.0667 M b2 0
0.0667 Mb0
0.0667 Mb0
4.92 369.28 250.16
Ma1
0.0234 Ma2
0.0234
Ma 0.0234
Ma 2.07
126.86 85.94
Mb1
0.0234 Mb2
0.0234
Mb 0.0234
Mb 2.07
150.51 101.96
M b1 0
Ma1
Mb1
0.0000 M b2 0
0.0000
0.0619 Ma2
0.0560
0.0318 Mb2
0.0334
Mb0
0.0000 Mb0
0.00 0.00 0.00
Ma
0.0586
Ma 9.44
475.73 322.27
Mb
0.0327
Mb 6.43
f cm
11
K2
M a2 0
0.50 0.1177
K
Ma0
0.50 0.1177
(整理)(一)双向板按弹性理论的计算方法.

(一)双向板按弹性理论的计算方法1.单跨双向板的弯矩计算为便于应用,单跨双向板按弹性理论计算,已编制成弯矩系数表,供设计者查用。
在教材的附表中,列出了均布荷载作用下,六种不同支承情况的双向板弯矩系数表。
板的弯矩可按下列公式计算:M = 弯矩系数×(g+p)l x2式中M 为跨中或支座单位板宽内的弯矩(kN·m/m);g、p为板上恒载及活载设计值(kN/m2);l x为板的跨度(m)。
显示更多隐藏2.多跨连续双向板的弯矩计算(1)跨中弯矩双向板跨中弯矩的最不利活载位置图多跨连续双向板也需要考虑活载的最不利位置。
当求某跨跨中最大弯矩时,应在该跨布置活载,并在其前后左右每隔一区格布置活载,形成如上图(a)所示棋盘格式布置。
图(b)为A-A剖面中第2、第4区格板跨中弯矩的最不利活载位置。
为了能利用单跨双向板的弯矩系数表,可将图(b)的活载分解为图(c)的对称荷载情况和图(d)的反对称荷载情况,将图(c)与(d)叠加即为与图(b)等效的活载分布。
在对称荷载作用下,板在中间支座处的转角很小,可近似地认为转角为零,中间支座均可视为固定支座。
因此,所有中间区格均可按四边固定的单跨双向板计算;如边支座为简支,则边区格按三边固定、一边简支的单跨双向板计算;角区格按两邻边固定、两邻边简支的单跨双向板计算。
在反对称荷载作用下,板在中间支座处转角方向一致,大小相等接近于简支板的转角,所有中间支座均可视为简支支座。
因此,每个区格均可按四边简支的单跨双向板计算。
将上述两种荷载作用下求得的弯矩叠加,即为在棋盘式活载不利位置下板的跨中最大弯矩。
(2)支座弯矩支座弯矩的活载不利位置,应在该支座两侧区格内布置活载,然后再隔跨布置,考虑到隔跨活载的影响很小,可假定板上所有区格均满布荷载(g+p)时得出的支座弯矩,即为支座的最大弯矩。
这样,所有中间支座均可视为固定支座,边支座则按实际情况考虑,因此可直接由单跨双向板的弯矩系数表查得弯矩系数,计算支座弯距。
双向板的弹性和塑性计算

双向板的弹性和塑性计算双向板是一种结构,在受到外力作用时,发生弹性变形和塑性变形。
弹性变形是指材料在外力作用下会发生形变,但在外力去除后能够恢复原状。
塑性变形是指材料在外力作用下会发生形变,并且即使在外力去除后也无法完全恢复原状。
下面将分别介绍双向板的弹性和塑性计算方法。
1.双向板的弹性计算弹性模量是材料的一种力学性质,表示单位面积内的应力与应变之间的关系。
材料的弹性模量一般通过材料试验来确定。
泊松比是材料的另一个力学性质,表示材料在一方向受到压缩时在另一方向的膨胀程度。
泊松比一般也通过材料试验来确定。
双向板的应力-应变关系可以用胡克定律来描述,即应力等于弹性模量乘以应变。
对于双向板,需要考虑两个方向的应变,因此应力等于弹性模量分别乘以两个方向的应变。
根据双向板的几何形状和外力,可以计算出两个方向上的应变。
将两个方向上的应变代入应力-应变关系,可以得到两个方向上的应力。
2.双向板的塑性计算双向板的塑性计算可以通过材料的流变模型来进行。
流变模型是一种描述材料变形行为的数学模型。
常见的流变模型有线性本构模型和非线性本构模型。
线性本构模型是一种简化的模型,假设材料的应力和应变之间存在线性关系。
在受到小应力作用时,线性本构模型可以比较准确地描述材料的变形行为。
通过材料试验或拟合实验数据,可以确定线性本构模型的参数,如线性弹性模量。
非线性本构模型是一种更加复杂的模型,适用于材料受到大应力作用时的变形行为。
常见的非线性本构模型有塑性模型和粘弹模型。
塑性模型是一种将材料的塑性变形考虑进去的模型,可以描述材料受到大应力作用时发生的不可逆形变。
通过材料试验或拟合实验数据,可以确定塑性模型的参数,如屈服应力和流动应力。
双向板的塑性计算需要将应力施加到材料上,并根据材料的流变模型计算出材料的应变和应力。
对于塑性模型,还需要判断材料是否发生塑性变形,以及计算塑性变形的程度。
根据材料的力学性质和几何形状,可以通过数值方法进行塑性计算,如有限元分析方法。
双向板按弹性理论的计算方法
双向板按弹性理论的计算方法双向板是一种常见的结构元件,其受力特点与单向板有所不同。
在计算双向板的设计参数时,可以采用弹性理论中的一些方法来进行计算。
双向板的受力分析主要涉及以下几个方面:弯矩、剪力和扭矩的计算、板的变形以及板的稳定性计算。
首先,我们来看双向板的弯矩计算。
在双向板上,由于受到两个方向的载荷作用,会同时产生正弯矩和负弯矩。
在计算弯矩时,可以采用叠加法。
假设双向板在x和y方向上的弯矩分别为Mx和My,那么总弯矩M为M=Mx+My。
其次,剪力的计算也是双向板设计时需要考虑的问题。
在计算剪力时,可以将双向板看作一个复杂的梁结构,采用横截面法来计算剪力。
与此同时,双向板还会产生扭矩。
扭矩的计算可以借助于剪力的计算结果,具体方法可以参考弹性理论中的扭矩公式。
双向板的变形分为平面变形和空间变形两种情况。
在计算平面变形时,可以采用等效弹性模量法。
通过考虑不同方向上的刚度系数和位移系数,将双向板的变形进行等效处理,从而简化计算过程。
而空间变形的计算则需要考虑额外的因素,例如板的高度、边界条件等。
最后,双向板的稳定性也是需要进行计算的重要参数。
在计算稳定性时,可以引入边界条件、支撑条件等因素,采用弹性理论中的稳定性计算方法进行分析。
总之,双向板按照弹性理论的计算方法主要包括弯矩、剪力和扭矩的计算、板的变形以及板的稳定性计算。
在实际工程中,双向板的设计与计算还需要综合考虑其他因素,例如材料的强度特性、施工工艺、荷载条件等。
因此,在进行双向板的设计与计算时,需要综合运用弹性理论以及其他相关知识,进行全面而准确的分析。
双向板的弹性计算法
双向板的弹性计算法双向板的弹性计算法双向板的受力特点前已述及。
双向板常用于工业建筑楼盖、公共建筑门厅部分以及横隔墙较多的民用房屋。
当民用房屋横隔墙间距较小时(如住宅),可将板直接支承于四周的砖墙上,以减少楼盖的结构高度。
1.双向板的计算双向板的内力计算有弹性计算法和塑性计算法两种,本书仅介绍双向板内力的弹性计算法。
弹性计算法是以弹性薄板理论为依据而进行计算的一种方法,由于这种方法内力分析比较复杂,为简化计算,通常是直接应用根据弹性薄板理论编制的弯矩系数表(附表)进行计算。
(1)单跨双向板的计算单跨双向板按其四边支承情况的不同,在楼盖中常会遇到如下六种情况:四边简支(图1a);一边固定三边简支(图1b);两对边固定、两对边简支(图1c);两邻边固定、两邻边简支(图1d);三边固定、一边简支(图7.1.38e);四边固定(图7.1.38f)。
(a)(b)(c)(d)(e)(f)图1 双向板的六种四边支承情况根据不同支承情况,可从附表中查出弯矩系数,即可求得弯矩:M=表中系数×ql2(1)式中M ——跨中或支座单位板宽内的弯矩;q ——均布荷载(kN /m2)l ——板的较小跨度(m)。
附表中给出了图1所示六种边界条件的单跨板在均布荷载作用下的挠度系数、支座弯矩系数以及泊松比μ =0时的跨中弯矩系数。
钢筋混凝土结构的泊松比μ=1/6,故对跨中弯矩应按下式计算:M x(μ )=M X +μM y(2)M y (μ)=M y+μM X (3)式中M X、M y——按附表查得的板跨中弯矩系数计算得到的跨中弯矩值。
【例1】某砖混结构卫生间的现浇板l1×l2=3600mm×6000mm,四周与圈梁整体现浇,现浇板厚h=90mm,墙体厚240 mm,板承受恒载设计值g=3.6KN/m,活载设计值q=2.8KN/m,采用C20砼,受力钢筋HPB235。
试确定该现浇板受力钢筋用量。
【解】长边与短边之比l2/l1=6000/3600=1.67<2,按双向板计算。
板计算
板计算(按弹性理论计算)板的L2/L1=5/3.3=1.52<2,所以按双向板计算。
板的厚度构造要求h>(1/30~1/40)×L1=1/30×3300=110mm,取h=120mm。
荷载荷载标准值20mm水泥砂浆面层0.02×20KN/m3=0.4KN/m3;120mm钢筋混凝土板0.12×25KN/m3=3KN/m3;G k=0.4+3=3.4KN/m3恒载设计值G=γk×G k=1.05×3.4=3.57KN/m3;活载设计值Q=γQ1×Q k=1.2×3=3.6KN/m3;合计,即每米板宽7.17KN/m3。
内力计算在求各区板格内正弯矩时,按恒载均布及活载棋盘式布置计算,取荷载G'=G+Q/2=5.37KN/m3;Q'=Q/2=1.8KN/m3;在G'作用下,各内支座均可视为固定,某些区隔板内最大正弯矩不在板的中心点处。
在Q'作用下,各区隔板四边均可视作简支,跨内最大正弯矩则在中心点处,计算时可近似取二者之和作为跨内做大正弯矩值。
在求中间支座最大负弯矩时,按恒荷载及活荷载均满布各区隔板计算,取荷载G+Q=7.171.8KN/m3;按照《建筑结构静力计算手册》进行内力计算,计算结果见下表:双向板弯矩计算区格 ALox/Loy 0.65跨内υ=0M x(0.075×5.37+0.075×1.8)×3.32=5.86KN·m/mM y(0.0271×5.37+0.0271×1.8)×3.32=2.12KN·m/m υ=0.2M x 5.86+0.2×2.12=6.28KN·m/mM y 2.12+0.2×5.86=3.29KN·m/m。
双向板按弹性理论计算过程
双向板按弹性理论计算过程弹性变形是双向板在受到外力作用时产生变形或者尺寸的变化,且能够恢复的变形为弹性变形。
塑性变形双向板在外力作用下产生不可恢复的永久变形。
弹性分析方法是最基本和最成熟的结构分析方法,也是其他分析方法的基础和特例。
它是一种假设和简化的方法,不考虑双向板离散性和非线性性质。
适用于普通结构。
塑性内力重分布的分析方法可用于超静定混凝土结构设计。
弹塑性分析方法以钢筋混凝土的实际力学性能为依据,考虑塑性变形内力重分布。
引入相应的本构关系后,可进行结构受力全过程分析,且可以较好地解决各种体型和受力复杂结构的分析问题。
1、双向板按按弹性计算,同时应对支座弯矩进行调幅。
当边界支承位移对双向板的内力及变形有较大影响时,在分析中宜考虑边界支承竖向变形及扭转的影响。
重力荷载作用下的框架、框架-剪力墙结构中的现浇梁以及双向板等,经弹性分析求得内力后,可对支座或节点弯矩进行适度调幅,并确定相应的跨中弯矩。
钢筋混凝土板的负弯矩调幅幅度不宜大于20%。
2、连续单向板宜按塑性计算,同时应满足正常使用极限状态的要求或采取有效的构造措施。
混凝土连续梁和连续单向板,可采用塑性内力重分布方法进行分析。
3、双向板也可按塑性极限分析方法,主要用于周边有梁或墙支承的双向板设计。
承受均布荷载的周边支承的双向矩形板,可采用塑性铰线法或条带法等塑性极限分析方法进行承载能力极限状态的分析与设计。
从理论上说,弹性方法与塑性方法都没问题,但在实际工程中不同的计算方法钢筋用量相差20%。
针对不同的工程和板不同情况采用不同的结构分析方法,然后应根据经验取塑性或弹性计算结果作为最终的计算配筋。
4、工业建筑采用弹性方法,民用建筑采用塑性方法。
5、直接承受动荷载或重复荷载作用的构件、裂缝控制等级为一级或二级的构件、采用无明显屈服台阶钢筋的构件以及要求安全储备较高的结构应采用弹性方法。
6、地下室顶板、屋面板等有防水要求且荷载较大,考虑裂缝和徐变对构件刚度的影响,建议采用弹性理论计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双向板按弹性方法计算实例
1.楼盖平面布置
双向板肋形楼盖梁板结构布置如图1,钢筋混凝土板厚150h mm =,楼面面层为20mm 厚水泥砂浆抹面(320/kN m γ=),板底为15mm 厚石灰砂浆粉刷(317/kN m γ=)活载标准值25.4/k q kN m =,混凝土为35C 级,板中受力筋及分布筋采用HPB300级钢筋;梁中受力筋采用HRB335级钢筋;梁中箍筋和架立筋采用HPB300级钢筋。
柱距为6900mm ,板的弯矩折减系数为:B1为0.8;B2,B3均为1.0
图1 楼盖平面布置
2.板的荷载计算
恒载 20mm 厚水泥砂浆抹面 200.020.4⨯= KN/2m
150mm 钢筋混凝土板 200.15 3.75⨯= KN/2m 15mm 石灰砂浆 170.0150.26⨯=KN/2m 标准值 0.4 3.750.26=4.41k g =++ KN/2m
活载 标准值 5.4k q = KN/2m
可变荷载效应起控制作用, 1.2G γ= 1.3Q γ= 设计值 1.2 4.41 5.292g =⨯=KN/2m , 设计值 1.3 5.47.02q =⨯= KN/2m
荷载设计值 5.2927.0212.312p g q =+=+= KN/2m
/2 5.2927.02/28.80p g q '=+=+= KN/2m
/27.02/2 3.51p q ''±=== KN/2m 3. 板的内力计算及配筋 3.1中间区格板
1
B
计算跨度: 6.9x l m = 6.9y l m = / 1.0x y l l = 单位板宽弯矩(/KN m m •)
跨中弯矩:荷载按棋盘布
x M =系数(6)2x p l '+系数(1)2x p l '' =( 0.02058.800.0429 3.51⨯+⨯) 26.915.76⨯= y M =系数(6)2x p l '+系数(1)2x p l ''=( 0.02058.800.0429 3.51⨯+⨯) 26.915.76⨯=
支座弯矩:荷载按满布
a 支座a x M =系数(6)2x pl =20.051312.312 6.930.07-⨯⨯=-
b 支座b
y M =系数(6)2x pl =20.051312.312 6.930.07-⨯⨯=-
配筋计算:s γ=0.95,0130x h mm =,0120y h mm =。
跨中正弯矩配筋选用HPB300
钢,
2270/y f N mm =,min 0.45/0.45 1.57/2700.262%t y f f ρ==⨯= 2,min min 0.002621000150393s A bh mm ρ==⨯⨯=
跨中截面:6
2,min 00.80.815.76103782700.95130
x sx s y s x M A mm A f h γ⨯⨯===<⨯⨯
6200.80.815.76104102700.95120
y sy y s y
M A mm f h γ⨯⨯=
==⨯⨯ 实配钢筋28/10@150,429mm φ(x,y 方向相同)
a 支座 6
200.80.830.0710*******.95130
a
a
x sx
y s x M A mm f h γ⨯⨯⨯===⨯⨯
实配钢筋212@150,754mm φ
3.2 边区格板
2
B
计算跨度: 6.9x l m =, 6.90.120.150.3 6.93y l m =--+=, /1x y l l = 单位板宽弯矩(/KN m m •)
跨中弯矩:荷载按棋盘布(/KN m m •)
x M =系数(5)2x p l '+系数(1)2x p l ''=2(0.02618.800.0429 3.51) 6.918.11⨯+⨯⨯= y M =系数(5)2x p l '+系数(1)2x p l ''=2(0.02198.800.0429 3.51) 6.916.34⨯+⨯⨯=
支座弯矩:荷载按满布
b 支座 b
y
M =系数(5)2x pl = 20.0512.312 6.929.31-⨯⨯=- c 支座 c x M =系数(5)2x pl =20.0612.312 6.935.17-⨯⨯=-
d 支座 d x M =系数(5)2x pl =20.0612.312 6.935.17-⨯⨯=- 配筋计算:
跨中截面 6
2018.11105432700.95130x sx y s x M A mm f h γ⨯===⨯⨯
62016.34105312700.95120
y sy y s y
M A mm f h γ⨯=
==⨯⨯ 实配钢筋210/12@150,639mm φ(x,y 方向相同) 支座截面
b 支座 支座弯矩取板2B 与板1B 计算中的较大值30.07/KN m m g
6
230.0710*******.95120
b sy
A mm ⨯==⨯⨯ 实配钢筋210@75,1047mm φ
c 支座 6
235.171010552700.95130
c sx
A mm ⨯==⨯⨯ 实配钢筋210/12@75,1277mm φ
d 支座配筋计算见3B 3.3角区格板
3
B
计算跨度: 6.90.120.150.3 6.93x l mm =--+=, 6.93y l mm =,/ 1.0x y l l = 单位板宽弯矩(/KN m m •)
跨中弯矩:荷载按棋盘布(/KN m m •)
x M =系数(4)2x p l '+系数(1)2x p l ''=2(0.02818.80.0429 3.51) 6.9319.11⨯+⨯⨯= y M =系数(4)2x p l '+系数(1)2x p l ''=2(0.02898.80.0429 3.51) 6.9319.45⨯+⨯⨯=
支座弯矩:荷载按满布
d 支座d x M =系数(4)2x pl =20.067712.312 6.9340.03-⨯⨯=- 配筋计算:
跨中截面 6
2019.11105732700.95130x sx y s x M A mm f h γ⨯===⨯⨯
6
2019.45106322700.95120
y sy y s y
M A mm f h γ⨯=
==⨯⨯ 实配钢筋210/12@150,639mm φ(x,y 方向相同)
d 支座 6
2040.0310********.95130
d d x sx
y s x M A mm f h γ⨯=
==⨯⨯ 实配钢筋210/12@75,1277mm φ。
