线性代数 南开大学 第一章
精算培养方案最新版
一、南开大学（经济学院风险管理与保险系）(一)本科生教育风险管理与保险学系设有全日制保险专业本科生、保险学专业硕士研究生（包括保险经营管理方向、国际保险方向、卫生经济与医疗保障方向）、精算学专业硕士研究生（精算学方向、风险管理方向）和保险学专业博士生（保险产业经济、国际保险、保险经济学方向）等多方向、多层次、多形式的人才培养体系。
南开大学保险专业所开设的主要专业课程有：政治经济学（资本主义、社会主义）、经济学原理、西方经济学（中级微观、中级宏观）、统计学、计量经济学、货币银行学、财政学、国际金融、国际经济学、会计学、保险学原理、财产保险、人身保险、海上保险、国际保险、再保险、责任和信用保险、社会保险、保险投资学、保险公司会计与财务管理、保险法学、保险理论与实务专题等；所开设的精算课程有：利息理论、寿险精算、非寿险精算、寿险精算实务、非寿险精算实务、应用统计、生命表构造、损失模型、随机过程、金融风险管理等。
风险管理与保险学系下设的保险和精算两个专业均为高中起点，本科4年学制，毕业颁发经济学学士学位。
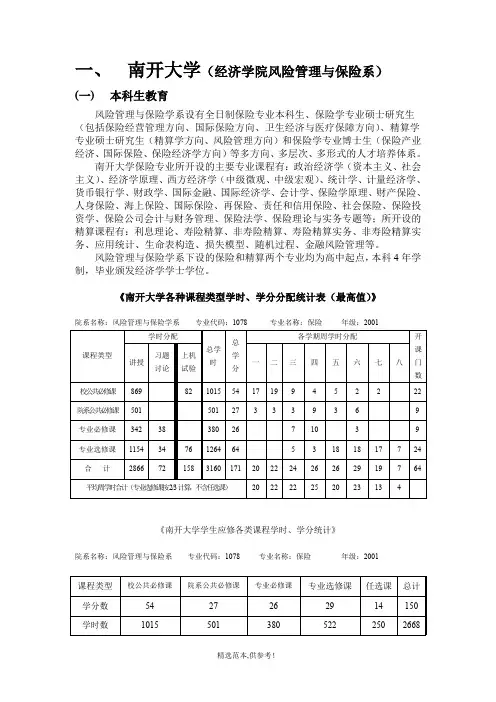
《南开大学各种课程类型学时、学分分配统计表（最高值）》院系名称：风险管理与保险学系专业代码：1078 专业名称：保险年级：2001《南开大学学生应修各类课程学时、学分统计》院系名称：风险管理与保险系专业代码：1078 专业名称：保险年级：2001《南开大学本科教学计划》课程类型：校公共必修课程院系名称：风险管理与保险系专业名称：保险年级：2001课程类型：院系公共必修课程院系名称：风险管理与保险系专业名称：保险年级：2001《南开大学本科教学计划》课程类型：专业必修课程院系名称：风险管理与保险系专业名称：保险年级：2001课程类型：专业选修课程院系名称：风险管理与保险系专业名称：保险年级：2001课程类型：辅修必修课程院系名称：风险管理与保险系专业名称：保险年级：2001《南开大学本科教学计划》课程类型：辅修选修课程院系名称：风险管理与保险系专业名称：保险年级：2001(二)研究生教育经济学院131·风险管理与保险学系（博士研究生）专业：保险学研究方向：1、保险产业经济2、国际保险3、保险经济学专业培养方案课程设置与学分分配表注：带“*”课程为本专业必选课。
2018在职研究生1月联考线性代数如何拿满分
2018在职研究生1月联考线性代数如何拿满分？在职研究生数学考试是很多在职人员得分不理想的一科，其中的线性代数失分比较多，在职人员怎么在考试中获得高分呢?下面小编就给大家简单介绍几点。
一、线性代数特点线性代数这门课相对计算技巧较少，贯穿始终的计算方法几乎只有初等变换这一种，但知识点却比另两门学科都要抽象的多。
首先，在职人员可以体会下向量组的线性相关、无关其实是和齐次线性方程组有无非零解一一对应的。
其次，矩阵的“秩”想说明的是方程组中本“质”方程或有效方程的个数，在职人员利用初等行变换化出的那些全零行，实际就是去掉那些“无效”方程组的过程;于是r(A)个有效方程只能限定r(A)个未知数，那么原有的n个未知数中就有n- r(A)个无法限定，所以称为自由未知量，进一步就可以得到方程组解中的一组极大无关组，也就是我们说的基础解系(利用最少的解向量去表示所有的解)。
在职人员还可以思考线性表示和非齐次线性方程组解之间的关系，这样线代这些抽象的概念就会变得简单了。
二、线性代数知识基本概念——三大工具：行列式、矩阵、向量组;基本计算——求解线性方程组;简单应用——利用方程组的解反过来研究矩阵的特征值、特征向量及对角化;还可以研究简单的非线性组合关系即二次型的基本概念和性质。
在职人员在学习过程中可以以矩阵为主线，具体展开复习。
如行列式可以看成方阵的一种运算;解方程组的过程其实也主要利用的是矩阵的初等行变换;二次型的研究也主要是对其对应的二次型矩阵的变换等等。
还可以利用矩阵可逆的充要条件去串联整个线性代数的前后章节，它们分别是：行列式不等于0;方阵是满秩的;矩阵的行或列向量组组性无关;对应齐次线性方程组只有零解;矩阵没有0特征值;正负惯性指数之和为n等;这样大家就可以更简洁明了的做到前后知识的融会贯通了。
三、重点题型在职人员对重点题型的研究是最为关键的。
数学考试三个卷种，对线性代数的要求基本一致，大小题加一起也都是五道且可考的题型相对固定。
精算师考试用书
准精算师考试有9门，得先通过，相应的考试科目及对应的参考书目如下：（一）科目名称：数学基础I中国精算师资格考试1、科目代码：01中国精算师资格考试2、考试时间：3小时中国精算师资格考试3、考试形式：标准化试题中国精算师资格考试4、考试内容：中国精算师资格考试5、参考书：①《高等数学讲义》（第二篇数学分析）樊映川编著高等教育出版社中国精算师资格考试②《线性代数》胡显佑四川人民出版社中国精算师资格考试③《运筹学》（修订版）1990年《运筹学》教材编写组清华大学出版社中国精算师资格考试除以上参考书外，也可参看其他同等水平的参考书。
中国精算师资格考试建议买同济高数第五或六版，考研的也行，差不多（二）科目名称：数学基础II中国精算师资格考试1、科目代码：02中国精算师资格考试2、考试时间：3小时中国精算师资格考试3、考试形式：标准化试题中国精算师资格考试4、考试内容：中国精算师资格考试（1）概率论（分数比例：50%）中国精算师资格考试（2）数理统计（分数比例：35%）（3）应用统计（分数比例：15%）中国精算师资格考试如果有统计学基础就牛B了，刚刚好5、参考书：①《概率论第一册》复旦大学编人民教育出版社1979年4月第1版中国精算师资格考试②《概率论第二册》（第一、二分册）复旦大学编人民教育出版社1979年8月第1版中国精算师资格考试③《概率论与数理统计》陈希孺编著中国科学技术大学出版社2000年3月第1版中国精算师资格考试④《应用线性回归》（美）S.Weisberg著王静龙、梁小筠等译中国统计出版社1998年3月第1版中国精算师资格考试（三）科目名称：复利数学中国精算师资格考试1、科目代码：03中国精算师资格考试2、考试时间：2小时中国精算师资格考试3、考试形式：标准化试题中国精算师资格考试4、考试内容：利息理论中国精算师资格考试5、参考书：《利息理论》（中国精算师资格考试用书）刘占国主编南开大学出版社2000年9月第1版中国精算师资格考试（四）科目名称：寿险精算数学中国精算师资格考试1、科目代码：04中国精算师资格考试2、考试时间：4小时中国精算师资格考试3、考试形式：标准化试题中国精算师资格考试4、考试内容：寿险精算数学中国精算师资格考试5、参考书：《寿险精算数学》（中国精算师资格考试用书）卢仿先、曾庆五编著，南开大学出版社，2000年6月第一版。
数学系数学专业研究生研究方向
华南理工大学的研究型全国重点大学，是国家“985”工程和“211”工程重点建设大学。
学校现有博士学位授权点73个、硕士学位授权点176个，有工程硕士（23个专业领域）、建筑学硕士、工商管理硕士（MBA、EMBA）、公共管理硕士（MPA）、风景园林硕士、法律硕士6个硕士专业学位授予权。
2010年拟招收攻读硕士学位研究生约3500人。
西安交通大学理学院相关专业专业课考研试卷西安交通大学所有院系相关专业课考研试卷-进入概率论与数理统计热门书籍《概率论与数理统计教程——高等学校教材》魏宗舒等价格 21.1《概率论与数理统计学习辅导与习题选解（浙大二、三版）》浙江大学盛骤、谢式千、潘承毅编价格 15《高等代数（第3版）——高等学校教材》北京大学数学系几何与代数教研室前代数小组编王萼芳、石生明修订价格 19.2《离散数学——理论·分析·题解》左孝凌、李为鑑、刘永才编价格 22《数学分析中的典型问题与方法》裴礼文价格 33.4《概率统计（第3版）》同济大学概率统计教研组编著价格 21《数学分析（第3版）（上册）（面向21世纪课程教材）》华东师范大学数学系编价格 20.9《概率论与数理统计（第2版）——普通高等教育“九五”国家级重点教材》茆诗松、周纪芗编著价格 36《数学分析（第2版）（上册）——面向21世纪课程教材》陈纪修、於崇华、金路价格 31.7《数学分析经典习题解析》孙涛价格 28.6《数学分析（第2版）（下册）——高等学校教材》复旦大学数学系陈传璋、金福临、朱学炎、欧阳光中编价格 15.7《概率论与数理统计习题与解答（普通高等教育“九五”国家级重点教材）》茆诗松周纪芗价格 30《高等代数解题方法与技巧》主编：李师正副主编：张玉芬、李桂荣、高玉玲价格 23.7《概率论与数理统计（第2版）》范大茵、陈永华价格 15《概率论与数理统计习题全解指南（浙大·二、三版）——大学数学学习辅导丛书》浙江大学盛骤、谢式千、潘承毅编价格 15《概率论基础（第2版）（高等学校教材）》复旦大学李贤平编价格 13.9《概率统计讲义（第3版）——高等学校教材》陈家鼎、刘婉如、汪仁官编著价格 18.2《概率论与数理统计》陈希孺编著价格 26概率论与数理统计2008 招生目录（本专业招生 6 人）研究方向01人工智能与专家系统学科名称:概率论和数理统计学科代码:所属学科:概率论和数理统计学科概括:概率论和树立统计专业点1986年获得硕士学位授予权。
南开大学化学学院14-15第一学期-课表
南开大学化学学院14-15第一学期-课表化学院本科生2014 —2015学年第一学期课程表2014级化学专业星期课目节次一二三四五上午1思想道德与法律基础二主楼B202姚静化学概论2-11、2班邱晓航二主楼B2023、4班李姝二主楼计算机基础中心机房化学1-3刘哲理4、5 班许昱玮体育4-1操场1高宝华等2B2043基础外语2-11、3班二主楼A309贺权宁2、4班二主楼A310秦妍5班二主楼A313 史逢阳计算机基础新阶105刘哲理基础外语2-11、3班二主楼A309贺权宁2、4班二主楼A310秦妍5班二主楼A313史逢阳一元函数积分主楼211于志玲一元函数微分主楼211于志玲化学概论2-11、2班邱晓航二主楼B2023、4班李姝二主楼B2044下午5 基础无机化学实验化学概论一元函数积分主楼基础无机化学实验英语自主学习二主61班任红霞2班马越3班田金磊综合实验楼C 区2楼2-15班叶世海二主楼B204211于志玲一元函数微分主楼211于志玲4班马建功5班王一菁综合楼C区2楼楼B402二主楼B4037 化学概论2-15班叶世海二主楼B204 8晚9 当代化上10 学前沿2-1 联合大楼汤平平化学院本科生2014—2015学年第一学期课程表2014级分子专业星期课目节次一二三四五上午1基础外语2-11班二主楼A309贺权宁2班二主楼A310秦妍一元函数积分主楼232由同顺一元函数微分主楼232由同顺基础外语2-11班二主楼A309贺权宁2班二主楼A310秦妍英语自主学习计算机基础新阶105王恺23 化学概论2-1程鹏陈朗星二主楼A104计算机基础中心机房王恺4下午5分析化学实验综合楼C区s三楼化学概论2-1程鹏陈朗星二主楼A104一元函数积分主楼232由同顺一元函数微分主楼232由同顺基础无机化学实验综合楼C区二楼1班王庆伦2班顾文体育4-1操场1高宝华等678晚上9有机化学2-1庞美丽二主楼B201思想道德与法律基础二主楼B302陈文旭当代化学前沿2-1联合大楼汤平平大学语文金鑫七教小礼堂111化学院本科生2014—2015学年第一学期课程表2014级化学生物学专业星期课目节次一二三四五上午1 普通生物学二主楼B302张金红基础外语2-1二主楼A107外聘教师英语自主学习23 基础外语2-1二主楼A107外聘教师普通生物学二主楼B302张金红一元函数积分主楼211于志玲一元函4数微分主楼211 于志玲下午5 化学概论2-1叶世海二主楼B204一元函数积分主楼211于志玲一元函数微分主楼211于志玲计算机基础李敏计算机基础中心机房李敏体育4-1操场1高宝华等67化学概论2-1叶世海二主楼B2048晚9 思想道当代化上10 德与法律基础二主楼B302陈文旭学前沿2-1联合大楼汤平平11化学院本科生2014—2015学年第一学期课程表2014级伯苓班星期课目节次一二三四五上午1 英语综合技能2-11班主楼514Armin计算机基础机房1外聘教师一元函数积分主楼327徐锬一元函数微分主楼327徐锬英语综合技能2-12班主楼516Armin 23无机化学2-1程鹏邱晓航二主楼A104计算机基础二主楼A404外聘教师语言文化及交流2-11班主楼516李蜜语言文化及交流2-12班主楼516李蜜4下午5 一元函数积分主楼327徐锬无机化学2-1程鹏邱晓航二主楼无机化学实验2-1邱晓航体育4-1操场1高宝华等6一元函数微分主楼327 徐锬A104 朱宝林综合楼C区二楼7 思修专题徐曼二主楼A201 8晚上9有机化学2-1王佰全二主楼A104当代化学前沿2-1联合大楼汤平平大学语文金鑫七教小礼堂1化学院本科生2014 —2015 学年第一学期课程表2013级化学专业星期一二三四五上午1 大学物理2-2有机化学实验2-14班大学物理2-2主楼23 中国近现代史纲要高分子科学导论D类课4下午5 有机化学2-21-3班有机化学实验2-11班李玉新2班胡大学基础物理实验实验楼有机化学2-21-3班678晚上9 12012级《外语听说》、《体育》是校必修课，允许学生选择任意教师听课，因此学校不再指定课程教师，相同类型课程只许选一个选课序号，不得重复选相同课程。
《风险理论》教学大纲.doc
《风险理论》教学大纲英文名称： Risk Theory课程编号： 91134059学分 / 总学时： 3/ 54（其中课堂： 36 学时；课内实验：18 学时）先修课程：高等数学、线性代数、概率统计等授课对象：应用统计学专业学生一、教学性质与目的：本课程是统计学专业（保险与精算方向）的专业课，是数学方法应用于金融保险所形成的一套理论体系，在金融保险领域发挥着越来越重要的作用。
通过本课程的学习，使学生掌握风险理论的基本概念、经典风险度量模型模，掌握构建模型常用的经验法和参数估计法，能够利用模拟技术方法来模拟模型，从而使学生初步掌握处理随机风险的基本思想方法，培养学生运用基本理论分析和解决问题的能力。
二、教学内容与要求：第一章风险理论基础（ 2 学时）【基本内容】第一节风险与风险理论概述第二节随机变量1.2.1随机变量的概率分布1.2.2随机变量的数字特征第三节条件期望1.3.1条件分布与条件期望1.3.2条件期望的性质1.3.3条件方差第四节矩母函数1.4.1矩母函数的概念1.4.2矩母函数的性质1.4.3多元矩母函数及其性质【基本要求】1.了解风险和风险理论的含义，的性质和条件方差；熟悉矩母函数的概念、矩母函数的性质、多元矩母函数及其性质。
【重点及难点】重点：条件期望和方差、常见分布的矩母函数难点：矩母函数【教学活动与教学方式】要求学生回顾概率论中关于条件分布的性质和常见的分布函数；本章主要以讲授和自学为主。
第二章个体保单的理赔额与理赔次数模型（ 6 学时）【基本内容】第一节理赔额的分布2.1.1保单限额2.1.2免赔额2.1.3保单限额+免赔额2.1.4相对免赔额2.1.5比例分担免赔第二节理赔次数的分布2.2.1 （ a， b， 0）分布族2.2.2 （ a， b， 1）分布族2.2.3理赔次数分布的混合模型2.2.4免赔额对理赔次数的影响【基本要求】1.理解损失与理赔额、免赔额、保单限额的概念；2.掌握常见的损失额分布以及不同赔偿方式下理赔额的分布；3.掌握单个保单理赔次数的分布以及(a ， b， 0) 分布类和 (a ， b， 1) 分布类。
矩阵的可对角化及其应用
附件：分类号O15商洛学院学士学位论文矩阵的可对角化及其应用作者单位数学与计算科学系指导老师刘晓民作者姓名陈毕专业﹑班级数学与应用数学专业07级1班提交时间二0一一年五月矩阵的可对角化及其应用陈毕（数学与计算科学系2007级1班）指导老师刘晓民摘要：矩阵可对角化问题是矩阵理论中的一个重要问题，可对角化矩阵作为一类特殊的矩阵，在理论上和应用上有着十分重要的意义。
本文对可对角化矩阵做出了全面的概括和分析，并利用高等代数和线性代数的有关理论给出了矩阵可对角化的若干条件，同时也讨论了化矩阵为对角形的求解方法，最后总结出可对角化矩阵在求方阵的高次幂﹑利用特征值求行列式的值﹑由特征值和特征向量反求矩阵﹑判断矩阵是否相似﹑向量空间﹑线性变换等方面的应用.关键词：对角化；特征值；特征向量；相似；线性变换Matrix diagonolization and its applicationChen Bi(Class 1,Grade 2007,The Depart of Math and Calculation Science)Advisor:Lecturer Liu Xiao MinAbstract: Matrix diagonolization problem is an important problem in matrix theory diagonolization matrix, as a kind of special matrix, in theory and application has the extremely vital significance. This paper has made diagonolization matrix analysis and generalization, and using higher algebra and linear algebra are given the relevant theory of matrix several conditions diagonolization, also discussed the matrix of the diagonal shape of solving method, and finally summarized; diagonolization matrix in high power, the policy of using eigenvalue beg determinant by characteristic value and value, feature vector reverse matrix, judgment matrix is similar, vector Spaces, the application of linear transformation, etc.Key words: The diagonalization; Eigenvalue; Feature vector; Similar; Linear transformation引言所谓矩阵可对角化指的是矩阵与对角阵相似，而说线性变换是可对角化的指的是这个线性变换在某一组基下是对角阵（或者说线性变换在一组基下的矩阵是可对角化的），同样可以把问题归到矩阵是否可对角化。
《应用多元分析》(第三版,前言、目录、参考文献)
前言多元统计分析是统计学中内容十分丰富、应用性极强的一个重要分支，它在自然科学、社会科学和经济学等各领域中得到了越来越广泛的应用，是一种非常重要和实用的多元数据处理方法。
本书此次又在第二版的基础上作了较大幅度的改写和扩充，使之更能适应当今统计教学的需要。
本教材主要是针对财经类院校的统计学和数理统计学专业的本科生而写的，也可作为其他各专业读者的多元统计分析教材或教学参考书。
整本书写得比较细致，便于自学，书中的绝大部分内容曾向上海财经大学统计学系的本科生和研究生分别讲授过十多届。
本教材有如下一些特点：(1)全书对数学基础知识的要求较低，只需读者掌握初步的微积分、线性代数和概率统计知识。
尽管如此，为便于非统计专业的读者也能顺利地阅读本书，书中前几个章节对矩阵代数及一元统计知识作了简单的回顾和介绍，其所述的预备知识内容对于本书的阅读基本上已足够了。
(2)本教材以简明和深入浅出的方式阐述了多元统计分析的基本概念、统计思想和数据处理方法，在充分考虑到适合财经院校学生使用的前提下进行了严谨的论述，有助于学生深刻地理解并掌握多元分析的基本思想方法。
(3)书中提供的许多例题和习题为读者展示了多元分析在社会科学和经济学等领域中的应用，每章的例题和习题安排侧重于对基本概念的理解和知识的实际应用，并不注重解题的数学技巧和难度。
为便于读者的学习（特别是自学），书后的附录一给出了习题参考答案及部分解答。
(4)本书与SAS软件紧密结合，在每一章后面都附有SAS的应用，这有利于将SAS软件更好地融入各章的内容中，使读者对多元分析的意义能够有贴切的体会，便于读者进入应用的领域。
全书共分十章。
第一章介绍了多元分析中常用的矩阵代数知识，这是全书的基础。
第二章至第四章介绍的基本上是一元统计推广到多元统计的内容，主要阐述了多元分布的基本概念和多元正态分布及其统计推断。
第五章至第十章是多元统计独有的内容，这部分内容具有很强的实用性，特别是介绍了各种降维技术，将原始的多个指标化为少数几个综合指标，便于对数据进行分析。