深大电磁学第三章及第四章作业题解答

合集下载

电磁场与电磁波：第三章作业答案

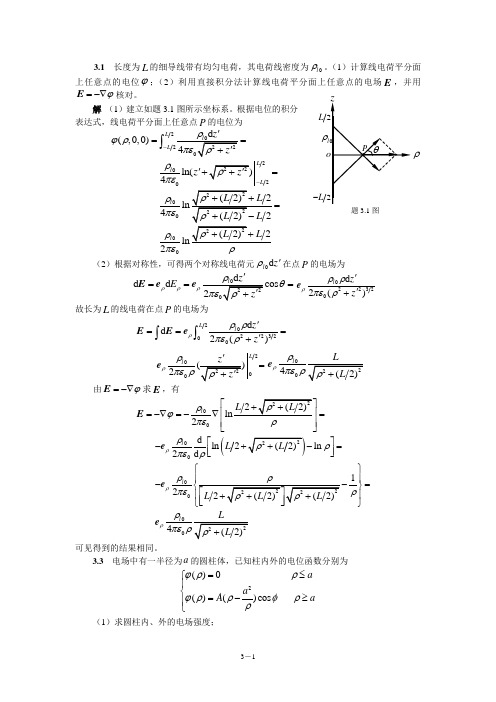
3.1 长度为L 的细导线带有均匀电荷，其电荷线密度为0l ρ。

（1）计算线电荷平分面上任意点的电位ϕ；（2）利用直接积分法计算线电荷平分面上任意点的电场E ，并用ϕ=-∇E 核对。

解（1）建立如题3.1图所示坐标系。

根据电位的积分表达式，线电荷平分面上任意点P 的电位为2(,0,0)L L ϕρ-==⎰2ln(4L l L z ρπε-'+=04l ρπε=02l ρπε （2）根据对称性，可得两个对称线电荷元z l 'd 0ρ在点P 的电场为d d E ρρρθ'===Ee e 022320d 2()l z z ρρρπερ''+e故长为L 的线电荷在点P 的电场为2022320d d 2()L l z z ρρρπερ'==='+⎰⎰E E e20002L l ρρπερ'=e ρe 由ϕ=-∇E 求E ，有002l ρϕπε⎡⎢=-∇=-∇=⎢⎥⎣⎦E(00d ln 2ln 2d l L ρρρπερ⎡⎤-+-=⎢⎥⎣⎦e0012l ρρπερ⎧⎫⎪--=⎬⎪⎭e ρe可见得到的结果相同。

3.3 电场中有一半径为a 的圆柱体，已知柱内外的电位函数分别为2()0()()cos a a A aϕρρϕρρφρρ=≤⎧⎪⎨=-≥⎪⎩（1）求圆柱内、外的电场强度；L L -ρρ题3.1图（2）这个圆柱是什么材料制成的？表面有电荷分布吗？试求之。

解（1）由ϕ=-∇E ，可得到a ρ<时， 0ϕ=-∇=Ea ρ>时， ϕ=-∇=E 22[()cos ][()cos ]a a A A ρφρφρφρρρφρ∂∂----=∂∂e e 2222(1)cos (1)sin a a A A ρφφφρρ-++-e e（2）该圆柱体为等位体，所以是由导体制成的，其表面有电荷分布，电荷面密度为0002cos S n a a A ρρρρεεεφ=====-e E e E3.4 已知0>y的空间中没有电荷，下列几个函数中哪些是可能的电位的解? （1）cosh y e x -；（2）x e y cos -；（3）cos sin e x x （4）z y x sin sin sin 。

电磁场与电磁波课后习题及答案四章习题解答

如题图所示为一长方形截面的导体槽，槽可视为无限长，其上有一块与槽相绝缘的盖板，槽的电位为零，上边盖板的电位为，求槽内的电位函数。

解根据题意，电位满足的边界条件为①②③根据条件①和②，电位的通解应取为题图由条件③，有两边同乘以，并从0到对积分，得到故得到槽内的电位分布两平行无限大导体平面，距离为，其间有一极薄的导体片由到。

上板和薄片保持电位，下板保持零电位，求板间电位的解。

设在薄片平面上，从到，电位线性变化，。

题图解应用叠加原理，设板间的电位为其中，为不存在薄片的平行无限大导体平面间（电压为）的电位，即；是两个电位为零的平行导体板间有导体薄片时的电位，其边界条件为：①②③根据条件①和②，可设的通解为由条件③有两边同乘以，并从0到对积分，得到故得到求在上题的解中，除开一项外，其他所有项对电场总储能的贡献。

并按定出边缘电容。

解在导体板（）上，相应于的电荷面密度则导体板上（沿方向单位长）相应的总电荷相应的电场储能为其边缘电容为如题图所示的导体槽，底面保持电位，其余两面电位为零，求槽内的电位的解。

解根据题意，电位满足的边界条件为①题图②③根据条件①和②，电位的通解应取为由条件③，有两边同乘以，并从0到对积分，得到故得到槽内的电位分布为一长、宽、高分别为、、的长方体表面保持零电位，体积内填充密度为的电荷。

求体积内的电位。

解在体积内，电位满足泊松方程（1）长方体表面上，电位满足边界条件。

由此设电位的通解为代入泊松方程（1），可得由此可得或（2）由式（2），可得故如题图所示的一对无限大接地平行导体板，板间有一与轴平行的线电荷，其位置为。

求板间的电位函数。

解由于在处有一与轴平行的线电荷，以为界将场空间分割为和两个区域，则这两个区域中的电位和都满足拉普拉斯方程。

而在的分界面上，可利用函数将线电荷表示成电荷面密度。

电位的边界条件为题图①②③由条件①和②，可设电位函数的通解为由条件③，有（1）（2）由式（1），可得（3）将式（2）两边同乘以，并从到对积分，有（4）由式（3）和（4）解得故如题图所示的矩形导体槽的电位为零，槽中有一与槽平行的线电荷。

电磁学(赵凯华,陈熙谋第三版)第三章习题解答

新概念物理教程・电磁学" 第三章电磁感应电磁场的相对论变换" 习题解答
" " ! ! ! " 如本题图所示，一很长的直导线有交变电流（ # $）% &# !"#!$，它旁边有一长方形线圈 ’ ( ) *，长为 +，宽为（ , !-），线圈和导线在同一平面内。求：（ $ ）穿过回路 ’()* 的磁通量 "；（ % ）回路 ’ ( ) * 中的感应电动势 !" # # # # # &# % 解：（$） ( % !"#! $， %!. %!. , # # &# + # # &# + , !"# $， " " "% $. !"#! $ % ! %# - %!. %! ## + ! $" , & &’! $" %! " （ % ） " " ! %! ! %# # $$ %! -
与无关从而由正则方程相应的正则动量守恒新概念物理教程电磁学第三章电磁感应电磁场的相对论变换习题解答如果在一个参考系中则在任意其它参照系中也有如果在一个参考系中和
新概念物理教程・电磁学! 第三章电磁感应电磁场的相对论变换! 习题解答
! ! ! ! " " 一横截面积为 # $ "# !"" 的空心螺绕环，每厘米长度上绕有 $# 匝，环外绕有 $ 匝的副线圆，副线圈与电流计串联，构成一个电阻为 % $ " " # 今使螺绕环中的电流每秒减少 "# #，求副线圈中的感应电动 ! 的闭合回路。势 ! 和感应电流。 $! $( ! ! 解： ! ! ! ! ! $ & # $ "# ’ ( #， ! % ! $!) $!) "# ’ # $* $* $!$ + & + ’ " (& + (# !) + $# + (# " + "# + (# !& + （!"# ） % $ ( " ’ + (# !’ % $ ( " ’ "% ； ! ( " ’ + (# !’ ! ! ! ! ! ! ($ $ # $ * " ’ + (# !& # $ # " *’ "#" % "" #

电磁场与电磁波课后习题及答案三章习题解答

三章习题解答3.1 真空中半径为a 的一个球面，球的两极点处分别设置点电荷q 和q -，试计算球赤道平面上电通密度的通量Φ(如题3.1图所示)。

解由点电荷q 和q -共同产生的电通密度为33[]4q R R π+-+-=-=R R D 22322232()(){}4[()][()]r z r z r z a r z a q r z a r z a π+-++-+-++e e e e 则球赤道平面上电通密度的通量d d zz SSS Φ====⎰⎰D S D e g g22322232()[]2d 4()()aq a ar r r a r a ππ--=++⎰22121)0.293()aqaq q r a =-=-+ 3.2 1911年卢瑟福在实验中使用的是半径为a r 的球体原子模型，其球体内均匀分布有总电荷量为Ze -的电子云，在球心有一正电荷Ze （Z 是原子序数，e 是质子电荷量），通过实验得到球体内的电通量密度表达式为02314ra Ze r r r π⎛⎫=- ⎪⎝⎭D e ，试证明之。

解位于球心的正电荷Ze 球体内产生的电通量密度为 124rZer π=D e 原子内电子云的电荷体密度为 333434a a Ze Zer r ρππ=-=- 电子云在原子内产生的电通量密度则为 32234344r ra r Ze rr r ρπππ==-D e e题3.1 图题3. 3图()a故原子内总的电通量密度为 122314ra Ze r r r π⎛⎫=+=- ⎪⎝⎭D D D e 3.3 电荷均匀分布于两圆柱面间的区域中，体密度为30C m ρ, 两圆柱面半径分别为a 和b ，轴线相距为c )(a b c -<，如题3.3图()a 所示。

求空间各部分的电场。

解由于两圆柱面间的电荷不是轴对称分布，不能直接用高斯定律求解。

但可把半径为a 的小圆柱面内看作同时具有体密度分别为0ρ±的两种电荷分布，这样在半径为b 的整个圆柱体内具有体密度为0ρ的均匀电荷分布，而在半径为a 的整个圆柱体内则具有体密度为0ρ-的均匀电荷分布，如题3.3图()b 所示。

电磁场与电磁波（第4版）第3章部分习题参考解答

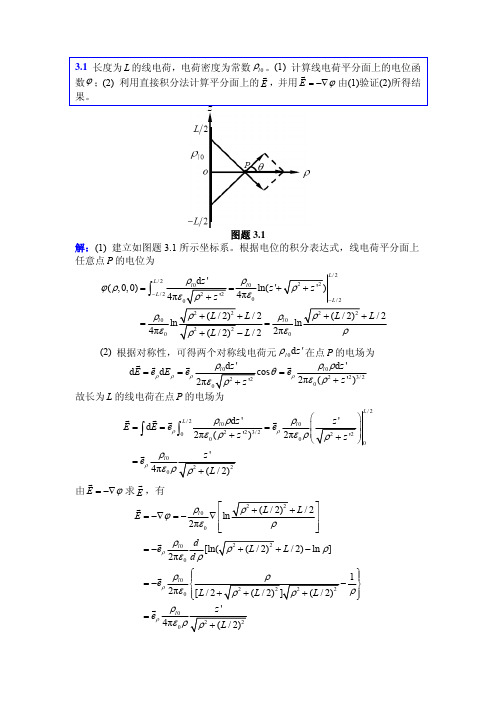
ρ ≥ a 时， E = −∇ϕ = −eρ
G
G ∂ ∂ρ
3.4 已知 y > 0 的空间中没有电荷，试判断下列函数中哪些是可能的电位解？ (1) e− y cosh x ；(2) e− y cos x ；(3) e− 2 sin x cos x ；(4) sin x sin y sin z 。解：在电荷体密度 ρ = 0 的空间，电位函数应满足拉普拉斯方程 ∇ 2ϕ = 0 。
∂2 − y ∂2 − y ∂2 − y (e cosh x) + 2 (e cosh x) + 2 (e cosh x) = 2e− y cosh x ≠ 0 (1) ∂x 2 ∂y ∂z −y 所以函数 e cosh x 不是 y > 0 空间中的电位解； ∂2 − y ∂2 − y ∂2 − y (e cos x) + 2 (e cos x) + 2 (e cos x) = −e− y cos x + e− y cos x = 0 (2) ∂x 2 ∂y ∂z −y 所以函数 e cos x 是 y > 0 空间中可能的电位解； ∂ − 2 ∂ ∂ (e sin x cos x) + 2 (e− 2 sin x cos x) + 2 (e − 2 sin x cos x) (3) 2 ∂x ∂y ∂z
G ρ = −eρ l 0 2πε 0 G = eρ
ρl 0 4πε 0 ρ
⎧ ρ 1⎫ ⎪ ⎪ − ⎬ ⎨ 2 2 2 2 ρ⎪ ⎪[ L / 2 + ρ + ( L / 2) ] ρ + ( L / 2) ⎩ ⎭ z'
ρ 2 + ( L / 2) 2
3.2 点电荷 q1 = q 位于 P 1 ( − a, 0, 0) ，另一点电荷 q2 = −2q 位于 P 2 ( a, 0, 0) ，求空间的零电位面。解：两个点电荷 + q 和 −2q 在空间产生的电位 ⎤ q 1 ⎡ 2q ϕ ( x, y , z ) = − ⎢ ⎥ 2 2 2 2 2 2 4 πε 0 ⎢ ( ) ( ) ⎥ x a y z x a y z + + + − + + ⎣ ⎦ 1 2 − =0 令 ϕ ( x, y, z ) = 0 ，则有 2 2 2 2 ( x + a) + y + z ( x − a) + y 2 + z 2

电磁场与电磁波课后习题及答案三章习题解答

(3)r * cos( nJ圆柱坐标；
(4)r cos'球坐标；
:;(2)利用直接积分法计算线电荷平分面上任意点的电场E，并用E中核对。
(1)建立如题3.8图所示坐标系。根据电位的积分表达式，线电荷平分面上任意点
3.8
点的电位解电位为
L2
(r,0)
X-24兀e0Jr2+z"2
'仝in(z、.r2z2)
4-；°
:?iodz'
_L2
，io I」2(L2)2L2in
a的圆柱体，
(r)=0
Ja-
「(r)二A(r)cos
Lr
(1)求圆柱内、外的电场强度；
(2)这个圆柱是什么材料制成的？表面有电荷分布吗？试求之。
解(1)由E，可得到r::a时，E0
2
r a时，E_--e^ — [ A(^ —)cos]-e^—[A(r_rrr /'
2 2oo
-erA(1RcoseA(12)sin
「EgS= 9，可求得大、小圆柱中的正、负电荷在点P产生
3.4半径为a的球中充满密度:(r)的体电荷，已知电位移分布为
Dr二亏Aa4
(r-a)
L
1
解：由
r d r
故在
r d r
54
在
r dr
3.5一个半径为a薄导体球壳内表面涂覆了一薄层绝缘膜，球内充满总电荷量为Q为的体
电荷，球壳上又另充有电荷量Q。已知球内部的电场为E=er（r.；：a）4，设球内介质为真空。计
解由于两圆柱面间的电荷不是轴对称分布，不能直接用高斯定律求解。但可把半径为a的
小圆柱面内看作同时具有体密度分别为二订的两种电荷分布，这样在半径为b的整个圆柱体内具

电磁场与电磁波第三章答案

1当0?r时i?应为有限值因此柱内电位为?????1cossinmmmmimbmar???xa?0?yxee?0?习题图322252当??r时圆柱对电场的影响可以忽略若取坐标原点00作为电位参考点注意电位参考点的选择对于电场强度的计算没有影响则柱外无限远处电位为??cos00rexero??????可见o?仅与r和?cos有关因此柱外电位的通解为???cos1cos10drreo???3在圆柱表面上ar?电位应该连续即io???求得柱内电位的通解为??cos1rbi?4在圆柱表面上电通密度应该连续即ararrroi?????????????0由此求得02001ead???????00012eb??????所以当ar?时??????cos2000reri???当ar?时????????cos1cos02000earrero?????已知1???????????????rrreee求得当ar?时0000002sincos2eexri???????????????eeere当ar?时????????????????????????????????????1sin1cos20002000raeraero????????????eere26323若无限长的导体圆柱腔的内半径为a腔壁被纵向地分裂成两部分各部分的电位如习题图323所示试求腔内外的电位分布
x x x 2 ( y h) 2 x 2 ( y h) 2 e x ( y h) ( y h) x 2 ( y h) 2 x 2 ( y h) 2 e y
电场能量密度为
h 2 ( x 4 y 4 h 4 2x 2 h 2 2x 2 y 2 2 y 2 h 2 ) 1 w r E2 l 2 2 r [ x 2 ( y h ) 2 ] 2 [ x 2 ( y h) 2 ] 2

电磁场与电磁波(第4版)第3章部分习题参考解答

cos
x)
=
−e− y
cos
x
+
e− y
cos
x
=
0
所以函数 e− y cos x 是 y > 0 空间中可能的电位解；
(3)
∂ (e− 2 sin x cos x) + ∂ (e− 2 sin x cos x) + ∂ (e− 2 sin x cos x)
∂x2
∂y2
∂z 2
= −4e− 2 sin x cos x + 2e− 2 sin x cos x ≠ 0 所以函数 e− 2 sin x cos x 不是 y > 0 空间中的电位解；
+
(L /
2)2
+
L
/
2
⎤ ⎥
2πε0 ⎢⎣
ρ
⎥⎦
=
G −eρ
ρl0 2πε 0
d dρ
[ln(
ρ 2 + (L / 2)2 + L / 2) − ln ρ]
=
G −eρ
ρl0 2πε 0
⎧⎪ ⎨ ⎪⎩[L / 2 +
ρ ρ 2 + (L / 2)2 ]
ρ2
+ (L / 2)2
−
1 ⎫⎪
ρ
⎬ ⎪⎭
=
L/2
ρl0ρdz '
0 2πε0 (ρ 2 + z '2 )3/ 2
=
G eρ
ρl 0 2πε 0 ρ
⎛ ⎜⎜⎝
=
G eρ
ρl 0 4πε 0 ρ
由
G E
=
−∇ϕ
求
G E
，有

电磁场与电磁波第三章习题及参考答案

第3章习题3-1 半径为的薄圆盘上电荷面密度为s ρ，绕其圆弧轴线以角频率旋转形成电流，求电流面密度。

解：圆盘以角频率旋转，圆盘上半径为r 处的速度为r ω，因此电流面密度为ϕωρρˆr v J s s s ==3-2 在铜中，每立方米体积中大约有28105.8⨯个自由电子。

如果铜线的横截面为210cm ，电流为A 1500。

计算 1）电流密度；2）电子的平均漂移速度；解：1）电流密度m A S I J /105.11010150064⨯=⨯==- 2) 电子的平均漂移速度 v J ρ=，3102819/1036.1105.8106.1m C eN ⨯=⨯⨯⨯==-ρs m J v /101.11036.1105.14106-⨯=⨯⨯==ρ 3-3 一宽度为cm 30传输带上电荷均匀分布，以速度s m /20匀速运动，形成的电流，对应的电流强度为A μ50，计算传输带上的电荷面密度。

解：电流面密度为m A L I J S /7.1663.050μ===因为 v J S S ρ= 所以 2/33.8207.166m C v J S S μρ=== 3-4 如果ρ是运动电荷密度，U是运动电荷的平均运动速度，证明：0=∂∂+∇⋅+⋅∇tU U ρρρ证：如果ρ是运动电荷密度，U是运动电荷的平均运动速度，则电流密度为U J ρ=代入电荷守恒定律tJ ∂∂-=⋅∇ρ得0=∂∂+∇⋅+⋅∇t U U ρρρ3-5 由m S /1012.17⨯=σ的铁制作的圆锥台，高为m 2，两端面的半径分别为cm 10和cm 12。

求两端面之间的电阻。

解：用两种方法（1）如题图3.5所示⎰⎰==2122)(tan zz lz dzS dl R ασπσ)11()(tan 1212z z -=ασπ 01.0202.0tan ==α题3.5图m r z .1001.0/1.0tan /11===α，m r z 1201.0/12.0tan /22===αΩ⨯=-⨯⨯⨯=-=--647212107.4)121101(101012.11)11()(tan 1πασπz z R （2）设流过的电流为I ，电流密度为2rI S I J π==电场强度为 2r IJ E πσσ== 电压为 dz z IEdz V z z z z ⎰⎰==21212)tan (σαπ ⎰==2122)(tan zz zdz I V R απσΩ⨯=-6107.4 3-6 在两种媒质分界面上，媒质1的参数为2,/10011==r m S εσ，电流密度的大小为2/50m A ，方向和界面法向的夹角为030；媒质2的参数为4,/1022==r m S εσ。

电磁学(赵凯华)答案[第3章电磁感应]

1 一根长直导线载有 5.0A 直流电流, 旁边有一个与它共面的矩形线圈l=20cm,a=10cm,b=20cm;线圈共有N=1000 匝,以v=3.0m/s 的速度离开直导线试求线圈中的感应电动势的大小与方向。

解: ABCD, 已知,如图所2. 如图所示,无限长直导线中的电流为I,在它附近有一边长为2a的正方形线圈,可绕其中心轴以匀角速度旋转,转轴与长直导线的距离为b。

试求线圈中的感应电动势面的长方形线圈 ABCD ，长为 l ，宽为（）。

试求：（1）穿过回路 ABCD 的磁通量；（ 2）回路 ABCD 中的感应电动势3. 如图所示，一无限长的直导线中通有交变电流，它旁边有一个与其共解4. 一无限长直导线，通电流为I。

在它旁边放有一矩形金属框，边长分别为a、b，电阻为R，如图所示。

当线圈绕轴转过180o时，试求流过线框截面的感应电量。

解:5. 如图所示为具有相同轴线的两个导线回路，小线圈在大线圈上面x 处，已知大、小线圈半径分别为R、r，且x>> R，故当大线圈中有电流I流动时，小线圈所围面积内（）的磁场可近似视为均匀的。

设大小线圈在同轴情况下，其间距x 以匀速变化。

试求：（1）穿过小线圈的磁通量和x 之间的关系；（2）当x=NR 时（N 为一正数），小线圈内产生的感应电动势；（3）若v>0 ，小线圈内的感应电流的方向。

解:6. 如图所示，在均匀磁场 B 中放一很长的良导体线框，其电阻可忽略。

今在此线框上横跨一长度为l 、质量为m、电阻为R 的导体棒，并让其以初速度运动起来，忽略棒与线框之间的摩擦，试求棒的运动规律。

解:7. 如图所示，在电阻为零，相距为l 的两条平行金属导轨上，平行放置两条质量为m 电阻为R/2 的匀质金属棒AB、CD，他们与导线相垂直，且能沿导轨做无摩擦的滑动。

整个装置水平地置于方向垂直向下的匀强磁场中，磁感应强度为B。

若不考虑感应电流的影响，今对AB 施加一恒力F，使其从静止开始运动起来。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1 第三章作业题解答 3．4．1解答：

Pxydle

Rα

P++

图为均匀介质圆板的正视图，因圆板被均匀极化，故只有在介质圆板边缘上有极化面电荷，弧长为dl，厚度为h的面元面积为dShdlhRd，在α处的极化面电荷密度为

ˆcos

nPeP



根据对称性，极化电荷在圆板中心产生的电场强度只存在y分量，位于α处的极化电荷在圆板中心产生的电场强度的y分量为 2222coscoscosdSPhdlPhddEkkkRRR



全部极化面电荷在圆板中心产生的电场强度大小为 22000

cos44PhPhEdRR

将电场强度写为矢量：

04PhER

 2

3．4．5解答：（1）根据电容器的定义并代入数据，得

10001.810FSCl

（2）金属板内壁的自由电荷（绝对值）为 70005.410CqCU

（3）放入电介质后，电压降至310VU时电容C为 1005.410FqCU

（4）两板间的原电场强度大小为 50

0310V/mUEl

（5）放入电介质后的电场强度大小 510V/mUEl

（6）电介质与金属板交界面上的极化电荷的绝对值为q，因极化电荷与自由电荷反号，有

0EEE

而 7000()3.610CqSESEES （7）电介质的相对介电常数为

03rCC 3

（D、E、P的方向均垂直于介质平板平面） 3．5．3解答：

ldSA

Bεr

介质板用“2”标记，其余空气空间用“1”标记，单位矢ne方向为由高电势指向低电势，设极板上的自由电荷面密度是0 作一圆柱面，使其一个底面1S位于极板内部，另一底面2S位于两极板之间， 1S=2S=S，对该圆柱面应用有介质时的高斯定理，SqSdD



其中 0021侧面SDSdDSdDSdDSdDSSS Sq00

得到 0D 4

则空气中neDE0001 ；介质中 nrreDE0002 UtdEtE)(12

，即 Utdtr)(0000

解得 rrtdtU)(00 （1）介质中场强： nreE002nretdtU)( 介质中电位移：neD0nrretdtU)(0 介质中极化强度： 20)1(EPrnrretdtU)()1(0 （2）Sq00rrtdtSU)(0 （3）空气中场强：neE002nrretdtU)( （4）rrtdtSUqC)(00 5

3．5．9解答： L

εr

（1）以r12()RrR为半径，作一与导线同轴的长度为L的圆柱面，对该圆柱面应用有介质时的高斯定理，SqSdD0 其中 rLDSdDSdDS2侧面 Lq00 得到 0ˆ()2rDrer 电场强度为 00ˆ()2rrErer



极化强度矢量为 00(1)ˆ2rr

PEer

（2）两极的电势差U为 21

002

001ln22RRrr

drR

UrR

(3) 在半径1R与2R处，介质表面的极化电荷面密度分别为 6

10112)1()()('ReRPrrr







； 20222)1()('ReRPrrr

3．7．1解答：有玻璃板时，电容器电容为

0rSCd

将玻璃板移开后，电容器电容为 0SCd

（1）电容器一直与直流电源相接时，电压U不变。未抽出玻璃板时电容器的能量为

212WCU

抽出玻璃板后电容器的能量为 212WCU

二者之比 115rWCWC



（2）用直流电源给电容器充电后，先断开电源再抽出玻璃板，电荷量不变，

故 2222QQWWCC， 7

二者之比 5rWCWC 3．7．2解答：过介质中一点作一半径为r的同心球面作为高斯面，应用有介质时的高斯定理，SqSdD0

其中 24rDSdDS 00qq 得到 02ˆ4rqDer ，02ˆ

4rqEer



电介质内任一点的能量密度为: 42203221r

qEDw



下面求总静电场能量：取半径为r、厚度为dr的薄球壳，其体积为4dVdrr2，其中的静电场能量为：wdVdWdrrqdrrrq220242208432

则总静电场能量为：RqdrrqWR8820220

; 8

第四章作业题解答 4．4．5解答：

ABε1ICR1

ε2

求 ABU，ACU，CBU 解：由全电路欧姆定律得：

12122IRRR

（安）方向如图

由含源电路欧姆定律： 116230ABUIR （伏）

222421100IRIR（伏）

842IRUAC （伏）

11222316108IRIR（伏）

2210218CBUIR （伏）

1124368IRIR

（伏）

4．5．1解答：已知： 22（伏），R1=1.5（欧），R3=2（欧） I2=1（安），求电阻R2和电流I1，I3。 9

ε1ε2

R1R2

回路I回路II

解：各支路电流正方向如图，对节点B： 0132III ①

选图中I、II两个独立回路，绕行方向如图所示。对于回路I：

33111RIRI ②

对回路II：

33222RIRI ③

代入数据，联立求解上述三方程得： I1=4（安），I3=－3（安），R2=4（欧）结果说明：I3的真实方向与选定方向相反。 4．5．3解答： I1

A B2Ω2Ω1Ω

2Ω3Ω

12V 1Ω

10V 1Ω

8V 1ΩC

1）对照附图，令1231212V10V8VRR内内，，， 10

1ΩR内3，123452Ω1Ω3Ω2Ω2ΩRRRRR，，，，。

对外环回路取逆时针绕行方向，电流为 13145210.44AIRRRRRR内内3

设右端节点为C点，则

1211()10.2VACUIRRR内

因为 210V

所以 0.2VABACBCUUU =-= （2）选定流过1的电流1I正方向由右至左，流过2的电流2I与流过3



的电流3I正方向由左至右，两个网孔闭合电路的绕行方向为逆时针方向，列出节点方程和回路方程

123121212312()()IIIIRRRIRR内内

23233453()()IRRIRRR内2内

联立解得：10.46IA

深大电磁学第三章及第四章作业题解答

电磁场与电磁波：第三章作业答案

电磁场与电磁波课后习题及答案四章习题解答

电磁学(赵凯华,陈熙谋第三版)第三章 习题解答

电磁场与电磁波课后习题及答案三章习题解答

电磁场与电磁波（第4版）第3章部分习题参考解答

电磁场与电磁波课后习题及答案三章习题解答

电磁场与电磁波 第三章答案

电磁场与电磁波(第4版)第3章部分习题参考解答

电磁场与电磁波第三章习题及参考答案

电磁学(赵凯华)答案[第3章电磁感应]

电磁学(赵凯华,陈熙谋第三版)第三章习题解答

电磁场与电磁波第三章答案