最小生成树算法
数据结构(Java版)图2(最小生成树)

最小生成树举例
A
50 60 52 65 50
C
45 42 30 50
A
C
45
B
40
D
G
B
40 50
D
42 30
G
E
70
F
E
F
(a) 无向带权连通图G
(b) 无向带权图G 的最小生成树T
从最小生成树的定义可知,构造n个顶点的无向带权连 通图的最小生成树,必须满足如下三个条件: ① 必须包含n个顶点。 ② 有且仅有n-1条边。 ③ 没有回路。
)
将ej边加入到tree中;
}
实践项目
设计一个程序实现Prim和Kruskal算法.
表5-1 lowcost[ ]数组数据变化情况 表5-2 closest[ ]数组数据变化情况
扫描次数
closest[0]
closest[1]
closest[2]
closest[3]
closest[4]
closest[5]
求最小生成树算法
普里姆算法(Prim) (从点着手)
适合于求边稠密的最小生成树 适合于求边稀疏的最小生成树
克鲁斯卡尔算法(Kruskal)(从边着手)
普里姆算法(Prim)思想
1.
2.
3.
4.
令集合U={u0}(即从顶点u0开始构造最小生 成树),集合T={}。 从所有顶点u∈U和顶点v∈V-U的边权中选择最 小权值的边(u,v),将顶点v加入到集合U中,边 (u,v)加入到集合T中。 如此重复下去,直到U=V时则最小生成树构造完 毕。 此时集合U就是最小生成树的顶点集合,集合T 就是最小生成树的边集。
Boruvka算法求最小生成树
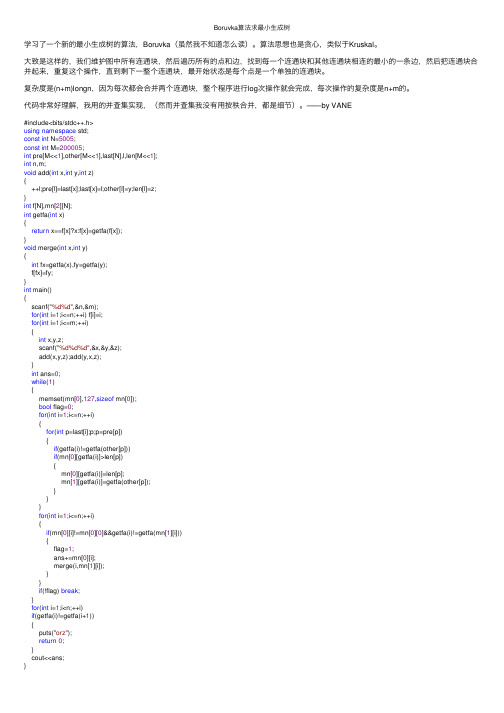
Boruvka算法求最⼩⽣成树学习了⼀个新的最⼩⽣成树的算法,Boruvka(虽然我不知道怎么读)。
算法思想也是贪⼼,类似于Kruskal。
⼤致是这样的,我们维护图中所有连通块,然后遍历所有的点和边,找到每⼀个连通块和其他连通块相连的最⼩的⼀条边,然后把连通块合并起来,重复这个操作,直到剩下⼀整个连通块,最开始状态是每个点是⼀个单独的连通块。
复杂度是(n+m)longn,因为每次都会合并两个连通块,整个程序进⾏log次操作就会完成,每次操作的复杂度是n+m的。
代码⾮常好理解,我⽤的并查集实现,(然⽽并查集我没有⽤按秩合并,都是细节)。
——by VANE#include<bits/stdc++.h>using namespace std;const int N=5005;const int M=200005;int pre[M<<1],other[M<<1],last[N],l,len[M<<1];int n,m;void add(int x,int y,int z){++l;pre[l]=last[x];last[x]=l;other[l]=y;len[l]=z;}int f[N],mn[2][N];int getfa(int x){return x==f[x]?x:f[x]=getfa(f[x]);}void merge(int x,int y){int fx=getfa(x),fy=getfa(y);f[fx]=fy;}int main(){scanf("%d%d",&n,&m);for(int i=1;i<=n;++i) f[i]=i;for(int i=1;i<=m;++i){int x,y,z;scanf("%d%d%d",&x,&y,&z);add(x,y,z);add(y,x,z);}int ans=0;while(1){memset(mn[0],127,sizeof mn[0]);bool flag=0;for(int i=1;i<=n;++i){for(int p=last[i];p;p=pre[p]){if(getfa(i)!=getfa(other[p]))if(mn[0][getfa(i)]>len[p]){mn[0][getfa(i)]=len[p];mn[1][getfa(i)]=getfa(other[p]);}}}for(int i=1;i<=n;++i){if(mn[0][i]!=mn[0][0]&&getfa(i)!=getfa(mn[1][i])){flag=1;ans+=mn[0][i];merge(i,mn[1][i]);}}if(!flag) break;}for(int i=1;i<n;++i)if(getfa(i)!=getfa(i+1)){puts("orz");return0;}cout<<ans;}。
最小生成树的Prim算法以及Kruskal算法的证明

最⼩⽣成树的Prim算法以及Kruskal算法的证明Prime算法的思路:从任何⼀个顶点开始,将这个顶点作为最⼩⽣成树的⼦树,通过逐步为该⼦树添加边直到所有的顶点都在树中为⽌。
其中添加边的策略是每次选择外界到该⼦树的最短的边添加到树中(前提是⽆回路)。
Prime算法的正确性证明:引理1:对于连通图中的顶点vi,与它相连的所有边中的最短边⼀定是属于最⼩⽣成树的。
引理2:证明:假设最⼩⽣成树已经建成;(vi, vj)是连接到顶点vi的最短边,在最⼩⽣成树中取出vi,断开连接到vi的边,则⽣成树被拆分成1、顶点vi2、顶点vj所在的连通分量(单独⼀个顶点也看作⼀个独⽴的连通分量)3、其余若⼲个连通分量(个数⼤于等于0)三个部分现在要重建⽣成树,就要重新连接之前被断开的各边虽然不知道之前被断开的都是哪⼏条边,但是可以通过这样⼀个简单的策略来重建连接:将vi分别以最⼩的成本逐个连接到这若⼲个互相分离的连通分量;具体来说,就是要分别遍历顶点vi到某个连通分量中的所有顶点的连接,然后选择其中最短的边来连接vi和该连通分量;⽽要将vi连接到vj所在的连通分量,显然通过边(vi, vj)连接的成本最低,所以边(vi, vj)必然属于最⼩⽣成树(如果连接到vi的最短边不⽌⼀条,只要任意挑选其中的⼀条(vi, vj)即可,以上的证明对于这种情况同样适⽤)。
这样我们就为原来只有⼀个顶点vi的⼦树添加了⼀个新的顶点vj及新边(vi, vj);接下来只要将这棵新⼦树作为⼀个连通⼦图,并且⽤这个连通⼦图替换顶点vi重复以上的分析,迭代地为⼦树逐个地添加新顶点和新边即可。
Kruskal算法:通过从⼩到⼤遍历边集,每次尝试为最⼩⽣成树加⼊当前最短的边,加⼊成功的条件是该边不会在当前已构建的图中造成回路,当加⼊的边的数⽬达到n-1,遍历结束。
Kruskal算法的正确性证明:Kruskal算法每次为当前的图添加⼀条不会造成回路的新边,其本质是逐步地连接当前彼此分散的各个连通分量(单个顶点也算作⼀个连通分量),⽽连接的策略是每次只⽤最⼩的成本连接任意两个连通分量。
PRIM算法求最小生成树

xx学院《数据结构与算法》课程设计报告书课程设计题目 PRIM算法求最小生成树院系名称计算机科学与技术系专业(班级)姓名(学号)指导教师完成时间一、问题分析和任务定义在该部分中主要包括两个方面:问题分析和任务定义;1 问题分析本次课程设计是通过PRIM(普里姆)算法,实现通过任意给定网和起点,将该网所对应的所有生成树求解出来。
在实现该本设计功能之前,必须弄清以下三个问题:1.1 关于图、网的一些基本概念1.1.1 图图G由两个集合V和E组成,记为G=(V,E),其中V是顶点的有穷非空集合,E是V中顶点偶对的有穷集,这些顶点偶对称为边。
通常,V(G)和E(G)分别表示图G的顶点集合和边集合。
E(G)也可以为空集。
则图G只有顶点而没有边。
1.1.2 无向图对于一个图G,若边集E(G)为无向边的集合,则称该图为无向图。
1.1.3 子图设有两个图G=(V,E)G’=(V’,),若V’是V的子集,即V’⊆V ,且E’是E的子集,即E’⊆E,称G’是G的子图。
1.1.4 连通图若图G中任意两个顶点都连通,则称G为连通图。
1.1.5 权和网在一个图中,每条边可以标上具有某种含义的数值,该数值称为该边的权。
把边上带权的图称为网。
如图1所示。
1.2 理解生成树和最小生成树之间的区别和联系1.2.1 生成树在一个连通图G中,如果取它的全部顶点和一部分边构成一个子图G’,即:V(G’)= V(G)和E(G’)⊆E(G),若边集E(G’)中的边既将图中的所有顶点连通又不形成回路,则称子图G’是原图G的一棵生成树。
1.2.2 最小生成树图的生成树不是唯一的,把具有权最小的生成树称为图G的最小生成树,即生成树中每条边上的权值之和达到最小。
如图1所示。
图1.网转化为最小生成树1.3 理解PRIM(普里姆)算法的基本思想1.3.1 PRIM算法(普里姆算法)的基本思想假设G =(V,E)是一个具有n个顶点的连通网,T=(U,TE)是G的最小生成树,其中U是T的顶点集,TE是T的边集,U和TE的初值均为空集。
信息学奥赛一本通 第4章 第6节 最小生成树(C++版) ppt课件

5
71
4
min[3]=w[2][3]=1; min[5]=w[2][5]=2;
第三次循环是找到min[3]最小的蓝点3。将3变为白点,接着枚举与3相连的所有 蓝点4、5,修改它们与白点相连的最小边权。
1
2 4
22 16
5
3
7
1
4
min[4]=w[3][4]=1; 由于min[5]=2 < w[3][5]=6;所 以不修改min[5]的值。
2
1
2
12
8
10
9
5
6
3
1个集合{ {1,2,3,4,5} } 生成树中有4条边{ <1,2> ,<4,5>,<3,5>,<2,5>}
3
74
ppt课件
16
Kruskal算法
算法结束,最小生成树权值为19。 通过上面的模拟能够看到,Kruskal算法每次都选择一条最小的,且能合并两 个不同集合的边,一张n个点的图总共选取n-1次边。因为每次我们选的都是最小的 边,所以最后的生成树一定是最小生成树。每次我们选的边都能够合并两个集合, 最后n个点一定会合并成一个集合。通过这样的贪心策略,Kruskal算法就能得到一 棵有n-1条边,连接着n个点的最小生成树。 Kruskal算法的时间复杂度为O(E*logE),E为边数。
第一行: 农场的个数,N(3<=N<=100)。
第二行..结 尾
后来的行包含了一个N*N的矩阵,表示每个农场之间的距离。理论 上,他们是N行,每行由N个用空格分隔的数组成,实际上,他们 限制在80个字符,因此,某些行会紧接着另一些行。当然,对角 线将会是0,因为不会有线路从第i个农场到它本身。
最小生成树问题

2.1 最小生成树
树T(V,E)的性质:
E 树的边数等于其顶点数减“1”,即 V 1 ; 树的任意两个顶点之间恰有一条初级链相连接; 在树中任意去掉一条边后,便得到一个不连通的 图; 在树中任意两个顶点之间添加一条新边,所得新 图恰有一个初级圈。
例如,图 6.4.1 给出的 G1 和 G2 是树,但 G3 和 G4 则不是树。
44
44 69
结果显示于图
求最小生成树的 Prim 算法
Prim 算法的直观描述 假设 T0 是赋权图 G 的最小生成树。任选一 个顶点将其涂红,其余顶点为白点;在一个端 点为红色,另一个端点为白色的边中,找一条 权最小的边涂红,把该边的白端点也涂成红色; 如此,每次将一条边和一个顶点涂成红色,直 到所有顶点都成红色为止。最终的红色边便构 成最小生成树 T0 的边集合。
在求最小生成树的有效算法中,最著名的两个是 Kruskal(克罗斯克尔)算法和 Prim(普瑞姆)算法, 其迭代过程都是基于贪婪法来设计的。 1.求最小生成树的 Kruskal 算法
Kruskal 算法的直观描述 假设 T0 是赋权图 G 的最小生成树,T0 中的边和 顶点均涂成红色,初始时 G 中的边均为白色。 ① 将所有顶点涂成红色; ② 在白色边中挑选一条权值最小的边,使其与红 色边不形成圈,将该白色边涂红; ③ 重复②直到有 n1 条红色边,这 n1 条红色边 便构成最小生成树 T0 的边集合。
最小生成树算法
一个简单连通图只要不是树,其生成树就不唯 一,而且非常多。一般地,n 个顶点地完全图,其 不同地生成树个数为 nn2。因而,寻求一个给定赋 权图的最小生成树,一般是不能用穷举法的。例如, 30 个顶点的完全图有 3028个生成树,3028 有 42 位, 即使用最现代的计算机,在我们的有生之年也是无 法穷举的。所以,穷举法求最小生成树是无效的算 法,必须寻求有效的算法。
matlab 普里姆算法
matlab 普里姆算法普里姆算法是一种最小生成树算法,用于求解给定图的最小生成树。
该算法基于贪心策略,每次选择当前已选中的点集到未选中的顶点集中距离最近的一条边,将该边所连接的点加入到已选中的点集中。
在实现普里姆算法时,我们需要使用一个优先队列用于存储当前已选中的点集到未选中的顶点集中的边,以及每个顶点到已选中的点集中最小距离。
在每次选取最小距离的边时,我们将该边所连接的点加入到已选中的点集中,并将该点与未选中的点集中的所有点之间的距离加入到优先队列中,同时更新已选中的点集到未选中的顶点集中的最小距离。
该过程重复进行,直到所有的顶点都已经被加入到已选中点集中,最终得到的图就是原图的最小生成树。
下面是使用matlab实现普里姆算法的示例代码:function MST = prim_algorithm(graph)% graph为邻接矩阵,MST为最小生成树的邻接矩阵表示n = size(graph, 1); % 获取图中节点数key = Inf(1,n); % 存储每个顶点与已选中点集的最小距离mst = zeros(n, n); % 存储最小生成树的邻接矩阵表示visited = false(1,n); % 存储每个顶点是否已加入到已选中点集中pq = PriorityQueue(n); % 创建优先队列start = 1; % 从任意一个顶点开始寻找最小生成树key(start) = 0; % 起始点距离已选中点集的最小距离为0pq.insert(start, 0); % 将起始点加入到优先队列中while ~pq.isempty() % 当优先队列非空时进行迭代[u, cost] = pq.deleteMin(); % 选取距离已选中点集最近的边visited(u) = true; % 将选中的顶点加入到已选中点集中if u ~= start % 将当前边加入到最小生成树的邻接矩阵中mst(parent(u), u) = cost;mst(u, parent(u)) = cost;endfor v = 1:n % 更新与已选点集中每个顶点的最小距离if ~visited(v) && graph(u,v) < key(v)parent(v) = u;key(v) = graph(u,v);if pq.contains(v)pq.updatePriority(v, key(v));elsepq.insert(v, key(v));endendendendMST = mst;end该代码中借助matlab的优先队列类PriorityQueue实现了优先队列的功能,其中包括了队列插入、队列删除、队列是否为空、队列中是否包含某元素以及队列中某元素优先级的更新等方法。
克鲁斯卡尔算法构造最小生成树的过程
克鲁斯卡尔算法构造最小生成树的过程好嘞,今天咱们来聊聊克鲁斯卡尔算法,这个家伙可是构造最小生成树的一把好手。
想象一下,你有一大堆城市,它们之间都有些路,你想用最短的钱和时间把这些路全连起来,这个问题就像是给你一根绳子,让你拼命省着点儿往城市间拉。
你得把所有的路都列出来,然后按照路的长度从短到长来排队。
这样,你就能优先考虑最短的路,节省成本。
比如说,你有一条短短的小路,连接着两个城市,你肯定先铺这条,因为这样最省事,也最省力气。
克鲁斯卡尔算法就是这么个操作,先从最短的路开始连,每连一条路,看看会不会形成环。
形成环的话,就要放弃这条路,换一条次短的,直到你把所有的城市都连起来,但不会形成回路为止。
这样一来,你手里就有了一张最小生成树的地图,这可不是说拿个树枝拼凑的,而是用最合理的方法把所有城市间的联系都搞定了。
有人说这算法像个抠门的人一样,总是要省着点儿花,可这不是省小气,这是精打细算,让每一块钱都花在该花的地方上。
克鲁斯卡尔就像是个精明的理财顾问,给你规划一套最划算的路线,别看他一本正经的,其实心里也有点小聪明,一眼就看出哪条路最值得铺。
想象一下,你手里的路条子越来越多,每一条都是一种选择,你要选对的,不然一不小心可能会给城市之间搞出个乱七八糟的环。
克鲁斯卡尔就像是个懂得捡便宜货的老江湖,他眼光独到,总能一眼看出哪些路最适合先连。
不过,也别以为这算法只能玩玩路,其实它背后的原理,就是避免你贪心,拼命把所有的路都连起来,然后却陷入无限循环。
克鲁斯卡尔就是要让你学会放下那些不合算的选择,每一步都谨慎小心,毕竟谁不想把路走顺当了呢?所以啊,克鲁斯卡尔可不是什么复杂的大师傅,他就是个用心良苦的小算盘,帮你在城市间的小路上玩出了个省时省力的好办法。
他的原则就是小路先连,尽量不要重复造轮子,这样才能保证你在城市之间的行走路线最有效率。
克鲁斯卡尔不仅是个算法,更像是个精明的小商贩,每一分每一毫都能算得清清楚楚,让你的路线规划不但省心,还省力。
最小生成树
对于图G=(V,E)的每一条e∈E, 赋予相应的权数 f(e),得到一个网络图,记为N=(V,E,F),
设T=(为T的权,N中权数最小的 生成树称为N的最小生成树。 许多实际问题,如在若干个城市之间建造铁路网、 输电网或通信网等,都可归纳为寻求连通赋权图 的最小生成树问题。 下面介绍两种求最小生成树的方法:
例1 求下图所示的最小生成树。
v2 e1 v1 e2 e6 v4 e 7 v3
v5
解:按各边的权的不减次序为:
e1 e 2 e3 e7 e6 e 4 e5 e8
所以,首先取 e1 , e2 ,尔后再取 e7 和 e6 , 则构成最小生成树 .
二、破圈法 破圈法就是在图中任取一个圈,从圈中去 掉权最大的边,将这个圈破掉。重复这个 过程,直到图中没有圈为止,保留下的边 组成的图即为最小生成树。 例2 同例1。 解:在圈v2v2v3中,去掉权最大的边e2或e3; 在圈v2v3v4中,去掉权最大的边e4; 在圈v3v4v5中,去掉权最大的边e5; 在圈中v2v3v5,去掉权最大的边e8;
在剩下的图中,已没有圈,于是得到最小生成树, 如下图:
v2 e1 v1 e2 e6 v4 v3 e7
v5
例3 求下图的最小生成树。
C1 1 B1 3 5 A 4 B2 6 5 8 7 6 C4 C3 3 3 4 D3 8 3 C2 8 D2 4 E A
4 3 B2 C4 4 D3 C3 3
B 2 A 3 5 J 2 2 H 5 G 1 F 2 1 S 3 1 4 C 3 4 1 4 E
5
D 2
A 2
B
1
C D 1 2 E
1 S 2 H
数据结构之最小生成树Prim算法
数据结构之最⼩⽣成树Prim算法普⾥姆算法介绍 普⾥姆(Prim)算法,是⽤来求加权连通图的最⼩⽣成树算法 基本思想:对于图G⽽⾔,V是所有顶点的集合;现在,设置两个新的集合U和T,其中U⽤于存放G的最⼩⽣成树中的顶点,T存放G的最⼩⽣成树中的边。
从所有uЄU,vЄ(V-U) (V-U表⽰出去U的所有顶点)的边中选取权值最⼩的边(u, v),将顶点v加⼊集合U中,将边(u, v)加⼊集合T中,如此不断重复,直到U=V为⽌,最⼩⽣成树构造完毕,这时集合T中包含了最⼩⽣成树中的所有边。
代码实现1. 思想逻辑 (1)以⽆向图的某个顶点(A)出发,计算所有点到该点的权重值,若⽆连接取最⼤权重值#define INF (~(0x1<<31)) (2)找到与该顶点最⼩权重值的顶点(B),再以B为顶点计算所有点到改点的权重值,依次更新之前的权重值,注意权重值为0或⼩于当前权重值的不更新,因为1是⼀当找到最⼩权重值的顶点时,将权重值设为了0,2是会出现⽆连接的情况。
(3)将上述过程⼀次循环,并得到最⼩⽣成树。
2. Prim算法// Prim最⼩⽣成树void Prim(int nStart){int i = 0;int nIndex=0; // prim最⼩树的索引,即prims数组的索引char cPrims[MAX]; // prim最⼩树的结果数组int weights[MAX]; // 顶点间边的权值cPrims[nIndex++] = m_mVexs[nStart].data;// 初始化"顶点的权值数组",// 将每个顶点的权值初始化为"第start个顶点"到"该顶点"的权值。
for (i = 0; i < m_nVexNum; i++){weights[i] = GetWeight(nStart, i);}for (i = 0; i < m_nVexNum; i ++){if (nStart == i){continue;}int min = INF;int nMinWeightIndex = 0;for (int k = 0; k < m_nVexNum; k ++){if (weights[k]!= 0 && weights[k] < min){min = weights[k];nMinWeightIndex = k;}}// 找到下⼀个最⼩权重值索引cPrims[nIndex++] = m_mVexs[nMinWeightIndex].data;// 以找到的顶点更新其他点到该点的权重值weights[nMinWeightIndex]=0;int nNewWeight = 0;for (int ii = 0; ii < m_nVexNum; ii++){nNewWeight = GetWeight(nMinWeightIndex, ii);// 该位置需要特别注意if (0 != weights[ii] && weights[ii] > nNewWeight){weights[ii] = nNewWeight;}}for (i = 1; i < nIndex; i ++){int min = INF;int nVexsIndex = GetVIndex(cPrims[i]);for (int kk = 0; kk < i; kk ++){int nNextVexsIndex = GetVIndex(cPrims[kk]);int nWeight = GetWeight(nVexsIndex, nNextVexsIndex);if (nWeight < min){min = nWeight;}}nSum += min;}// 打印最⼩⽣成树cout << "PRIM(" << m_mVexs[nStart].data <<")=" << nSum << ": ";for (i = 0; i < nIndex; i++)cout << cPrims[i] << "";cout << endl;}3. 全部实现#include "stdio.h"#include <iostream>using namespace std;#define MAX 100#define INF (~(0x1<<31)) // 最⼤值(即0X7FFFFFFF)class EData{public:EData(char start, char end, int weight) : nStart(start), nEnd(end), nWeight(weight){} char nStart;char nEnd;int nWeight;};// 边struct ENode{int nVindex; // 该边所指的顶点的位置int nWeight; // 边的权重ENode *pNext; // 指向下⼀个边的指针};struct VNode{char data; // 顶点信息ENode *pFirstEdge; // 指向第⼀条依附该顶点的边};// ⽆向邻接表class listUDG{public:listUDG(){};listUDG(char *vexs, int vlen, EData **pEData, int elen){m_nVexNum = vlen;m_nEdgNum = elen;// 初始化"邻接表"的顶点for (int i = 0; i < vlen; i ++){m_mVexs[i].data = vexs[i];m_mVexs[i].pFirstEdge = NULL;}char c1,c2;int p1,p2;ENode *node1, *node2;// 初始化"邻接表"的边for (int j = 0; j < elen; j ++){// 读取边的起始顶点和结束顶点p1 = GetVIndex(c1);p2 = GetVIndex(c2);node1 = new ENode();node1->nVindex = p2;node1->nWeight = pEData[j]->nWeight;if (m_mVexs[p1].pFirstEdge == NULL){m_mVexs[p1].pFirstEdge = node1;}else{LinkLast(m_mVexs[p1].pFirstEdge, node1);}node2 = new ENode();node2->nVindex = p1;node2->nWeight = pEData[j]->nWeight;if (m_mVexs[p2].pFirstEdge == NULL){m_mVexs[p2].pFirstEdge = node2;}else{LinkLast(m_mVexs[p2].pFirstEdge, node2);}}}~listUDG(){ENode *pENode = NULL;ENode *pTemp = NULL;for (int i = 0; i < m_nVexNum; i ++){pENode = m_mVexs[i].pFirstEdge;if (pENode != NULL){pTemp = pENode;pENode = pENode->pNext;delete pTemp;}delete pENode;}}void PrintUDG(){ENode *pTempNode = NULL;cout << "邻接⽆向表:" << endl;for (int i = 0; i < m_nVexNum; i ++){cout << "顶点:" << GetVIndex(m_mVexs[i].data)<< "-" << m_mVexs[i].data<< "->"; pTempNode = m_mVexs[i].pFirstEdge;while (pTempNode){cout <<pTempNode->nVindex << "->";pTempNode = pTempNode->pNext;}cout << endl;}}// Prim最⼩⽣成树void Prim(int nStart){int i = 0;int nIndex=0; // prim最⼩树的索引,即prims数组的索引char cPrims[MAX]; // prim最⼩树的结果数组int weights[MAX]; // 顶点间边的权值cPrims[nIndex++] = m_mVexs[nStart].data;// 初始化"顶点的权值数组",// 将每个顶点的权值初始化为"第start个顶点"到"该顶点"的权值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最小生成树算法
最小生成树算法是图论中的重要算法之一,用于找到一个连通图的最小生成树。
最小生成树是图中所有节点相连的一棵树,并且边权重的总和最小。
1. 概述
最小生成树算法有多种实现方式,其中最常用的两种是Prim算法和Kruskal算法。
这两种算法都基于贪心算法的思想,通过每一步选择边的方式来构建最小生成树。
2. Prim算法
Prim算法是基于节点的思想。
算法首先选择一个起始节点,然后寻找与该节点相连的边中权重最小的边,并将该边加入生成树中。
然后继续选择下一个节点,重复上述步骤,直到所有的节点都被访问过。
3. Kruskal算法
Kruskal算法是基于边的思想。
算法首先将所有的边按照权重进行排序,然后依次选择权重最小的边。
如果选择该边不会形成环路,则将该边加入生成树中。
直到生成树中包含了所有的节点或者边已经用完。
4. 最小生成树的应用
最小生成树算法在实际应用中有广泛的应用,如网络设计、电力传输、电路布局等。
通过构建最小生成树,可以在保证通信或者输电能
力的基础上,降低网络或者电力的建设和维护成本。
5. 算法复杂度分析
Prim算法和Kruskal算法的时间复杂度都为O(ElogE),其中E为边
的数量。
这是因为在算法中需要对边进行排序操作,排序的时间复杂
度为O(ElogE)。
另外,Prim算法使用了优先队列来选择最小权重的边,优先队列的插入和删除操作的时间复杂度为O(logE),一共需要进行E
次操作。
6. 算法优化
在实际应用中,当图的规模很大时,最小生成树算法可能会面临时
间和空间的限制。
针对这个问题,可以采用一些优化策略来提升算法
的效率。
例如,可以使用并查集来判断是否形成环路,从而提高Kruskal算法的速度。
同时,可以使用其他数据结构来替代优先队列,
以减少空间开销。
总结:
最小生成树算法是解决连通图的重要算法之一,通过选择边的方式
构建最小生成树。
Prim算法和Kruskal算法是两种常用的实现方式。
最小生成树算法在实际应用中有广泛的应用,可以降低网络和电力的建
设成本。
此外,还可以根据实际情况采取优化策略来提升算法的效率。
