量纲分析和相似原理
第2章 相似原理与量纲分析

(Re)p = (Re)m
这表明,原型与模型的雷诺数相等,两流动的黏滞力相似。
(2)弗汝德准则
考虑原型与模型之间重力与惯性力的关系 FIp FGp FIp FIm = = 或 FGp FGm FGm FIm 根据两个力的特征量表示 FI ρl 2 v 2 v 2 = = = Fr 3 FG gl ρgl v2 称为弗汝德数(Froude Number)。 无量纲数 Fr = gl 于是原型与模型重力与惯性力之比可表示为
(1)几何相似(geometric similarity)
几何相似—模型与原型流场的几何形状相似,即相应线 段的长度成比例、夹角相等,即
Hale Waihona Puke lp1 lm1=lp 2 lm 2
=…=
= lr = λ−1 = cons tan t θ = θ p m lm
lp
式中 lr 称为长度比尺(length scale ratio),λ则 2 称为模型比尺。 Ap lp Ar = = 2 = lr2 面积比尺 Am lm 体积比尺
FVp FVm = FGp FGm = FPp FPm = FIp FIm = cons tan t
或
FVr = FGr = FPr = FIr
2.1.2 相似准则 (similarity criteria) 几何相似是流动相似的基础,而动力相似则是流动相似 的保证。模型与原型动力相似的条件为两流动相似准数相等, 这样一个条件称为相似准则(similarity criterion)。 由于不同流动条件下有不同力的作用,因此也就存在着 不同力的相似准数,以及不同的相似准则。
原型流量
Qp = vp (Bp − bp )hp = 2.3 × (90 − 4.3)× 8.2 = 1616 m 3 / s
相似原理与量纲分析
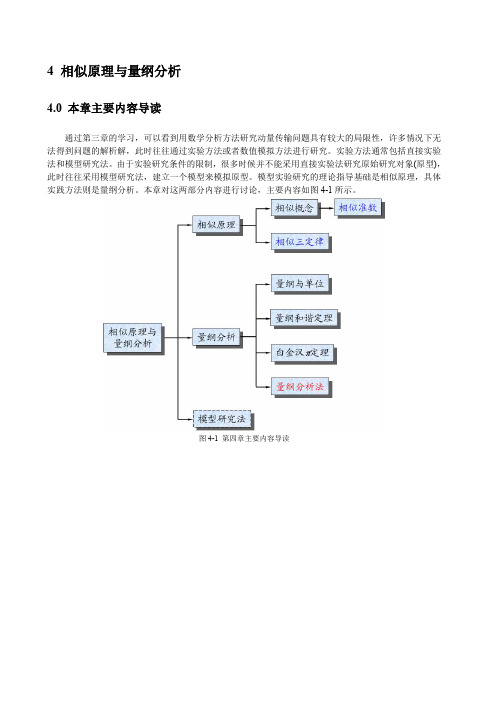
4 相似原理与量纲分析4.0 本章主要内容导读通过第三章的学习,可以看到用数学分析方法研究动量传输问题具有较大的局限性,许多情况下无法得到问题的解析解,此时往往通过实验方法或者数值模拟方法进行研究。
实验方法通常包括直接实验法和模型研究法。
由于实验研究条件的限制,很多时候并不能采用直接实验法研究原始研究对象(原型),此时往往采用模型研究法,建立一个模型来模拟原型。
模型实验研究的理论指导基础是相似原理,具体实践方法则是量纲分析。
本章对这两部分内容进行讨论,主要内容如图4-1所示。
图4-1 第四章主要内容导读4.1 相似原理4.1.1相似的基本概念遵循同一物理方程的现象称为同类现象。
如果两个同类现象对应物理量成比例(在对应的时空点,各标量物理量的大小成比例,各向量物理量大小成比例、方向相同),称这两个现象为相似现象。
对于动量传输问题,模型(model)与原型(prototype)之间必须满足如下相似条件才能成为相似现象(图4-2):(1)几何相似。
几何相似又称为空间相似,要求模型与原型外形完全一样;对应线段成比例;对应夹角相等;有粗糙度时粗糙度相似;(2)运动相似。
要求模型与原型对应流线几何相似;对应点速度大小成比例,方向相同;(3)动力相似。
又称为受力相似,要求模型与原型的两个对应流场受同种外力作用;对应点上对应作用力成比例。
上述三类相似中,几何相似是运动相似和动力相似的前提与依据,动力相似是决定二个流动相似的主导因素,运动相似则是几何相似和动力相似的表现。
相似的流动一定是同时满足几何相似、运动相似和动力相似的流动。
完全的几何相似一般并不容易达到。
例如,采用小尺寸模型模拟原型时,除非能够将模型表面加工得比原型光滑得多,否则无法按照原型的表面粗糙度成比例缩小而加工出模型的表面粗糙度;在研究沉淀物的传输时,不能将河床上的物质按比例缩小成粉末,因为细微的粉末之间有内聚力,无法模拟砂粒的特性;在研究河流流动时,水平方向的尺寸远大于垂直方向的尺寸,受实验空间的限制必须对水平方向采用较大比例尺进行缩小,如果将同样的比例尺用于垂直方向,有可能产生太浅的流动,导致毛细作用影响明显,而且河床的斜率太小会使流动保持层流。
量纲分析与相似原理

上一页 下一页 返回
下一页 返回
9.2 量纲分析
• 由量纲一致性原理可知,上式两侧的量纲是相同的,即 • 由伯努利方程可知,gh与V 2 /2有相同的量纲,于是给式(9−12)两
侧同除以 ,得
• 则上式两侧都应该是量纲为1 的。等式右侧的m 的量纲M 在变量g 和 h 中都未出现( g 和h的量纲只包含L 和T),因此m 不可能与g 和h 组成一个量纲为1 的组合量,应从右侧的变量中删去;
上一页
返回
9.2 量纲分析
• 在前面一节讨论了量纲一致性原理,或量纲齐次性原理、量纲和谐原 理。量纲一致性原理要求,凡是正确反映客观规律的物理方程,其各 项的量纲必须是一致的。从量纲一致性原理可以得到一个重要推论: 一个正确反映客观规律的物理方程必然可以写成量纲为1 的形式。
• 在前面一节中讨论过自由落体运动,现在假设我们并不清楚物体在自 由降落过程中距离与落地速度及重力加速度之间的函数关系。设物体 的释放高度为h ,物体落地速度为V ,从物理常识出发,V 应该与物 体的质量m 、重力加速度g 和h 有关,即
第九章 量纲分析与相似原理
• 9.1 量纲与单位 • 9.2 量纲分析 • 9.3 泊金汉Π 定理 • 9.4 相似原理 • 9.5 模型实验
第九章 量纲分析与相似原理

m
mp mm
pVp mVm
3l
✓ 力的比尺:
F
Pp Pm
Fp Fm
Gp Gm
Ip Im
mpap mmam
ma
l22v
❖ 力学相似:所有的计算结果均列于(P199)表动如果力学相似,则必
然存在着许许多多的比例尺),判断流动动力相似时作用 力的比例尺满足的约束关系称为相似准则。
v
1
l
1 15
v
vp vm
vm
vp v
1015 150m / s
[例9.1] 已知溢流坝的过流量QP=1000m3/s,若用长度比尺λl =60的模型(介质相同)进行实验研究,试求模型的流量Qm 。
如m、cm、mm等同属于长度类,用L表示;小时、分、秒 等同属于时间类,用T表示;公斤、克等同属于质量类,用 M表示。
§9.1 流体相似原理
解决 流体 力学 问题 的 方法
数学 分析
实验 研究
探索未知的流体流动规律 大型水工、机械模型实验
以相似原理为基础
一、力学相似
表征 流动 过程 的物 理量
描述几何形状的
v2 g l p 2v
式(9.2)
lv
设计模型时,所选择的三个基本比例尺如能满足以上三个制
约关系,则模型流动与实物流动是完全力学相似。但这是有困难
的,因为,如前所述单位质量力的比例尺 ,则g 1
1
v2 g l
v l2 模型可大可小,但流体运动黏
lv
3
l2
度的比例尺要保持一致很难。
l v
✓
加速度比尺: a
ap am
vp vm
tp tm
v t
相似性原理和量纲分析

∆p υ l k = f , , 2 v ρ vd d d
∆p kl = f Re, 2 v ρ dd
kl l v2 ∆p = f Re, ρv 2 = λ ρ dd d 2 k λ = f Re, d
(2)雷利法 有关物理量少于5个
FT + FG + FP + FE + …… + FI = 0
动力相似→对应点 上的力的封闭多边 形相似
动力相似是运动相似的保证
2.相似准则 常选惯性力为特征力,将其它作用力与惯性力相比, 组成一些准则,由这些准则得到的准则数(准数) 在相似流动中应该是相等的 (1)雷诺准则——粘性力是主要的力
FTP FIP = FTm FIm
l pυ m
(3)改变压强(30at),温度不变 等温过程p∝ρ,且μ相同
ρvl Re = ⇒ pvl µ
p p v p l p = p m vm l m
20 × 1 vm = v p = 300 × = 200km / h lm Pm 1 × 30 lp pp
例3:溢水堰模型,λl=20,测得模型流量为300L/s,水 的推力为300N,求实际流量和推力 解:溢水堰受到的主要作用力是重力,用佛劳德准则
f (q1 , q2 , q3 , q4 ) = 0
3个基本量,只有一个π项
小结:变量的选取——对物理过程有一定程度 的理解是非常重要FTm
dv FT = µA → µlv = ρυlv dy
FI = ma → ρl 2 v 2
v pl p
υp
=
vm l m
υm
无量纲数
Re =
vl
υ
雷诺数——粘性力的相似准数
四章相似原理与量纲分析ppt课件

但Fr准则要求 Cu CL
二者不能同时满足
而Re准则要求 Cu 1 / CL
解决的办法是采用不同的流体进行实验,同时满足Fr和Re准则
则有: 则:
Cu2 1 和
CgCL
Cu2 CgCL
CL2Cu2 C2
CLCu 1 C
(Cg 1)
C
C
3/ L
2
§4-3相似原理的应用
p m
CL3/ 2
m
L:1 1 3 1 1 0
1 2
T: 1 2 0
1 1
M: 1 0
1 0
1
V
2bg
bg V2
§4-7 量纲分析法之二 ----π定律
2 L1T 1M 0 2 L1T 0M 0 2 L3T 0M 1 2 L1T 1M 1
L:2 2 3 2 1 0
2 1
C
p
m
雷诺数:Re
uL
Re p Re m
雷诺数反映了惯性力与粘性力之比。
§4-2相似准则
三、佛汝德相似准则(重力相似准则)
CG
Gp Gm
M pgp Mmgm
pVp g p mVm gm
CCL3Cg
CG CF 重力与惯性力之比值为同一常数
则: CCL3Cg CCL2Cu2
得:
Cu2 1 也可写成
由量纲和谐原则得:
M 0 1 2
L
1 31 2 3
1 1
2 1
T 1 2
3 1
:
代入原函数:
Vc
K 1d 1
K
d
K Vcd Vcd
即:
Re
Vc d
§4-7 量纲分析法之二 ----π定律
4相似原理和量纲分析
§4.2 量纲分析与定理
影响某种流动现象的物理量可以有很多。当这些物理量间不能 用微分方程表示时,通过量纲分析确定出有关相似准则间的定性 关系。再通过实验进一步确定其定量关系。
定理
如果一个物理过程涉及到 n个物理量和r个基本量纲,则这个
物理过程可以由n个物理量组成的n-r个无量纲量(相似准则数i)
解:这是物体绕流,应该主要考虑粘性力相似和压力相似。
由雷诺数相等: lu lu (空气的粘度不变)
Kl
l l
u u
62.5 3600 5 45000
由欧拉数相等: p p
或
u 2 u2
p
u
2
p
u
R
pA
u
2 pA
u
2
R
A
u
2
l
2
R
R
500
u
u R u l
§4.2 量纲分析与定理
第四章 相似原理和量纲分析
§7.1 相似原理与模型实验 §7.2 量纲分析与π定理
§4.1 相似原理与模型实验
一、流动相似的概念
(1)如何把特定条件下的实验结果推广到其它流动中?
(2)如何将实物(或原型)缩小或放大制成模型,并通过 模型的实验结果推知原型中的流动?
(3)要使两流动现象相似,必须满足力学相似条件,即 几何相似、运动相似和动力相似。
3
v d 3 3 3
4
p
v d 4 4 4
其中,待定系数 , , 由量纲的一致性原则确定。
§4.2 量纲分析与定理
1
l d
2
d
3
vd
1 Re
无量纲准则方程为:
l 1 p F1( d , d , Re , v2 ) 0
量纲分析与相似原理
9.1 量纲与单位
• 如密度的量纲可写为dimρ ,用基本量纲表示为: • 20 世纪80 年代以前习惯用长度、时间和力作为基本量纲,简称FLT
制(F 表示力的量纲),而将质量作为导出量纲。依据牛顿第二定律, 力等于质量乘以加速度,因此 • FLT 制现已被MLT 制所取代。
上一页 下一页 返回
下一页 返回
9.2 量纲分析
• 由量纲一致性原理可知,上式两侧的量纲是相同的,即 • 由伯努利方程可知,gh与V 2 /2有相同的量纲,于是给式(9−12)两
侧同除以 ,得
• 则上式两侧都应该是量纲为1 的。等式右侧的m 的量纲M 在变量g 和 h 中都未出现( g 和h的量纲只包含L 和T),因此m 不可能与g 和h 组成一个量纲为1 的组合量,应从右侧的变量中删去;
上一页
返回
9.3 泊金汉Π定理
• 设一个流动过程涉及n 个变量v1 , v 2 , v3 ,···, vn ,其中 v2 , v3 ,···, vn 是相互独立的自变量,它们是实验中可以控制的量,实 验目的是依次改变其中的一个变量而保持其他变量不变,从而确定它
们各自对变量 v1 的影响; v1 是实验中待确定或测量的量,它是自 变量的函数,称为因变量。如在上节提到的圆球在黏性流体内运动的
量纲是LT−1;ρ和g 分别是密度和重力加速度,它们的量纲分别是 ML−3 和LT−2。读者容易验证方程左右两侧及每一项的量纲都是L。 • 有时方程中会出现常数,如自由落体运动方程可表示为
上一页 下一页 返回
9.1 量纲与单位
• 对上式做量纲检查可知,若要满足量纲一致性原理,则式中的常数 4.904 的量纲必须是LT-2。通常自由落体运动方程写为
相似原理与量纲分析
一个物理现象往往包含许多影响因素,这些影响因 素并非彼此孤立,其间关系由描述该现象的微分方程 规定。各物理量的相似倍数之间必定存在特定的制约 关系——准数(相似准则)。 物理相似:影响物理现象的所有物理量场分别相似的总 和。 必须是同类现象才能相似; 受描述现象的微分方程式的制约,物理量场的相似倍 数间有特定的制约关系——准数 ; 物理量的时间性和空间性——对应瞬间、对应空间点 。
17
前面三个问题的答案 (1)实验时测量各相似准数中包含的全 部物理量; (2)将实验结果整理成准数关联式; (3)实验结果可以推广应用到与模型相 似的系统。
设计模型实验时,为使实验设备与实际设备中的现象 相似,必须保证模型与原型现象的定解条件相似,且 同名的已定准数值相等。
18
1.3.6 三种传递过程的类比分析
第一章 流体力基础
——相似理论和量纲分析
西安建筑科技大学 粉体工程研究所
1
1.3.5 相似理论和量纲分析
• • • • • • 引言 物理相似的基本概念 量纲分析 相似准数 量纲分析优点 相似原理
2
引言
实验既是发展理论的依据又是检验理论的准绳, 解决科技问题往往离不开实验手段的配合。 流体力学中的实验主要有两种: a、工程性的模型实验。目的在于预测即将建造 的大型机械或水工结构上的流动情况; b、探索性的观察实验。目的在于寻找未知的流 动规律,指导这些实验的理论基础就是相似原理和 量纲分析。
du 1 2 ρ ρFb P μ u μ u d 3
能量传递
de q k 2 P T- u d de 2 ρ k T-P u μφ q d
质量传递
第五章量纲分析与相似原理
第五章量纲分析与相似原理在长期的生产实践中,人们总结出两种方法去研究、解决各种工程流体力学问题。
一种是数学分析方法,通过求解描述流动过程的微分方程式,获得各量之间的规律性关系。
另一种是实验方法,通过实验获取流体的流动规律。
然而,能够用数学分析方法求解的流体力学问题是有限的。
在许多情况下,流体流动的现象很复杂,往往难以用微分方程式加以描述;而且即使能够建立微分方程式,由于不能确定初始条件和边界条件,也难以求解。
所以日前大量的流体力学问题只能用实验方法求解。
本章介绍的量纲分析(Dimensional analysis)和相似原理(law of similarity)就是指导实验的理论。
§5-1量纲分析当某一流动过程尚不能用微分方程描述时,量纲分析法是确定物理量间关系的有效方法。
一. 量纲分析的基本知识“量纲”(或“因次”)是用以度量物理量单位的种类的。
以小时、分、秒为例,它们是不同的时间测量单位,但这些单位都属于同一时间种类。
若将这些属于同一种类的单位用[t]表示,则[t]就是上述时间单位的“量纲”。
因此,量纲是代表被测物理量单位种类的一种符号,从符号可以看出它们的属性。
例如[t]表示时间量纲,[L]—表示长度量纲。
SI 制中的基本量纲:dim m = M , dim l = L , dim t = T 物理量大小类别导出量纲工程单位制国际单位制英制单位制量纲基本量纲量纲幂次式§5-1量纲分析导出量纲可用三个基本量纲的指数乘积形式表示。
例如B 为任一物理量,其量纲可用下式表示:[][]a b cB L M t上式称为量纲公式,式中a 、b 、c 可正、负、整数、分数,它取决于物理量的定义和本质。
例如密度的量纲是,动力黏度的量纲是。
流体力学中常用量的量纲见下表。
3[][]ML ρ-=11[][]ML t μ--=导出量物理方程量纲速度V力F压强p密度ρ动力黏度µ运动黏度dlV dt=22d lF ma mdt==dFp dA=dmdvρ=FdVAdlμ=μνρ=1[][]V Lt-=2[][]F MLt-=12[][]p ML t--=11[][]ML tμ--=3[][]MLρ-=21[][]L tν-=在上式中,若a、b、c三个数中有一个不为零,则表明该物理量B是有量纲的量,当“a、b、c”全部为零时,则表明物理量B是无量纲的量,或称无量纲数(Non-dimensional number)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
,可作为基本量。
问题
1. 速度v,长度l,重力加速度g的量纲1的集合是: A. B. C. D. 2. 速度v,密度ρ,压强p的量纲1的集合是: A. B. C. D. 3. 速度v,长度l,时间t的量纲1的集合是: D. A. B. C. 4. 压强△p,密度ρ,长度l,流量Q的量纲的集合是: A. B. C. D.
i x x x xi
x y z 1 2 3
i 1,2,n m
(4)确定量纲一π参数:由量纲和谐原理解联立指数
方程,求出各π项的指数x,y,z,从而定出各量纲一
π参数。
(5)写出描述现象的关系式φ(π1,π2,……,πn-m)=0 ,
解π参数。
设变量共5个,其中x1、x2、x3为三个基本量(m=3), 则x1、x2、x3可与余下的x4,x5组合成2个(n-m=2) 量纲一π1、π2。
三 物理方程量纲的一致性
量纲和谐原理(theory of dimensional omogeneity): 凡是正确反映客观规律的物理方程,其各项的量纲都 必须是一致的,即只有方程两边量纲相同,方程才能 成立。 物理方程中各项物理量的量纲之间存在的规律性: 1.物理方程中各项的量纲应相同。 2.任一有量纲的物理方程可以改写为无量纲项组 成的方程而不会改变物理过程的规律性。 3.物理方程中各物理量之间的规律性以及相应各 量纲之间的规律性,不会因所选择的基本量纲不同而 发生改变。
应该指出:量纲分析并没有也不可能给出流 动问题的最终解,它只提供了这个解的基本 结构,函数的数值关系还有待于实验研究。
§4-3 流动相似性原理
采用模型试验和理论分析相结合的方式是解决问题 的有效途径之一,在把模型中的实测资料引用到原型中 产生下述问题: (1) 如何设计模型才能使模型和原型中的流动相似? (2) 如何把模型中观测的流动现象和数据换算到原型 中去? 相似原理提供了解决这两个问题的理论基础。
代入上式,关于指数有如下关系
1 x 2 y 3 z 0 1 x 2 y 3 z 0 x y z 0 2 3 1
1 2 3 由线性代数知,当 D 1 2 3 0 ,有非零解,则可 1 2 3
1 1
1
3 1
2
1
2
2
2
3
3
3
4
4
4
L : 1 1 3 1 2 0 解得: 1 T : 1 1 0 M: 1 0
L : 2 2 3 2 1 0 2 T : 2 2 0 M: 2 1 0
代入前面π公式得:
1 V 1d 1 0
Vd
2 V 2 d 0 1p
l 3 d l k 4 d d
p V 2
1 Re
据π定理有:
1 p l k f 2 1 , 2 , 3 , 4 f 2 Re , V 2 , d , d 改写为 p l k F , , Re 2 V d d
组成量纲一的量,不独立,不可作为基本量。
1 2 3 当 D 1 2 3 0 ,无非零解,则不能组成量纲一的 1 2 3
量,独立,可作为基本量。
如长度L、速度V、密度ρ三个物理量满足:
1 2 3 D 1 2 3 0 1 2 3
一、几何相似
几何相似是指原型与模型保持几何形状和几何尺 寸相似,也就是原型和模型的任何一个相应线性长度 保持一定的比例关系。
l
式中 l 为长度比尺。
面积比尺 体积比尺
A
Ap Am
lp lm
2 2
lp lm
l
3 3
2
V Vp Vm源自lp lm l
3
二、运动相似 运动相似是指原型与模型两个流动中任何对应质 点的迹线是几何相似的,而且任何对应质点流过相应 线段所需的时间又是具有同一比例的。或者说两个流 动的速度场(或加速度场)是几何相似的。 设时间比尺: t p t 则速度比尺 加速度比尺
√ 如理想流体的伯努利方程:
p1 V p2 V Z1 Z2 g 2 g g 2 g
各项量纲均为L,上式可改写为无量纲的方程:
2 1
2 2
p1 p2 V V 1 0 g z1 z2 2 g z1 z2
2 1 2 2
§4-2 量纲分析法
量纲和谐原理最重要的用途在于能确定方程式中 物理量的指数,从而找到物理量间的函数关系,以建 立合理的方程式。这种利用量纲和谐原理探求物理量 之间的函数关系称为量纲分析法。 • 依据:量纲和谐原理 • 方法:瑞利法:适用于单项指数形式。 π定理:适用于普遍性的问题。
几何学量纲:α≠0,
分类 动力学量纲:γ≠0
β=0,
γ=0,
运动学量纲:β≠0,γ=0
二、量纲一的量
基本量和导出量可以组合成量纲为1的量,称 为量纲一的量,即α=0,β=0,γ=0。 特点: (1)无单位,它的大小与所选单位无关; (2)量纲表示式中的指数均为零。 几个互相独立,不能结合成量纲一的量称为基 本量。如长度L、流速v和密度ρ就可以作为基本量。
一 瑞利法
计算步骤: 1. 确定与所研究的物理现象有关的n个物理量; 2. 写出各物理量之间的指数乘积的形式,如: FD=kDx Uyρz μa 3. 根据量纲和谐原理,即等式两端的量纲应该相 同,确定物理量的指数x,y,z,a ,代入指数方程式即得 各物理量之间的关系式。 应用范围:一般情况下,要求相关变量未知数n小 于等于4~5个。
dim d L dimV LT
1 , 2 , 3 , 4,即 无量纲数:
1
dim ML
3
余下的4个量 , p, l , k ,分别与V , d , 相乘组成4个
1 V d 2 V d p 3 V d l 4 V d k
第4章
量纲分析和相似原理
解决流体力学问题时仅靠三大基本方程是远远不够的, 还需要借助其它科学试验手段。在研究某些流体运动规律 过程中量纲分析常常可给予很大的帮助。
§4-1 量纲分析的概念和原理
一、量纲(dimension) 量纲是指物理量的属性(类别),也叫因次。 物理量的量纲可分为基本量纲(fundamental dimension) 和导出量纲(derived dimension)两类。长度[L]、时间[T]、 质量[M]这三个量纲属于基本量纲;可用基本量纲推导出 来的量纲属于导出量纲。如:流速的量纲[L/T]。
由实验测得k 2300 , Vc d
2300 , Re c 2300
二、π定理
布金汉π定理:对于某个物理现象,如果存在n个变 量互为函数关系:F(q1,q2,q3,……,qn)=0 而在这些变量中含有m个基本量,则可组合这些变量成 (n-m)个量纲一的量的函数关系:
φ(π1, π 2, π 3,……, π n-m)=0
或
p l k F , , Re 2 V d d k 2 l p V F , , Re d d
由实验知压差与管长成正比,因此:
k l V p , Re d d 2
2
量纲分析法的优点:适用未知物理方程的流动。 缺点:选准物理量较难,物理意 义不明确。
tm
lp / tp
l u um lm / tm t
up
a
ap am
lp / tp lm / t m
2 2
2 l u 2 l t
三、动力相似 原型和模型流动中任何对应点上作用着同名的 力,各同名力相互平行且具有同一比值。
基本量的判别
设三个物理量A、B、C,能够作为基本量的条件是 AxByCz不是量纲一的量,即
(dim A) (dim B) (dim C) L T M 的非零解不存在
x y z 0 0 0
设dimA L1 T 1 M1 , dimB L2 T 2 M 2 , dimC L3 T 3 M 3
1 x1 x2 x3 x4
2 2 2
1
1
2
2 x1 x2 x3 x5
所求的物理方程为
f 2 1 , 2 0
[例]:有压管流中的压强损失。 根据实验,压强损失与流速V,管长 l ,管径d,管壁 粗糙度k,流体运动粘滞系数υ ,密度ρ有关,即试用 π定理法求该物理方程。 p f l , d , k ,, ,V 解: 这7个量中,基本物理量有3个,令管径、平均 流速、密度为基本量,量纲依次为
某个物理量A的量纲表示为dimA,如速度量纲表
示为dimu=LT-1 ,加速度量纲dima=LT-2,密度量 纲dimρ=ML-3,力的量纲dimF=dim(ma)=MLT-2 , 压强的量纲dim p=dim (F/A)= MLT-2 /L2=ML-1 T-2 对于任何物理量的量纲
dim q L T M
3 1 1
LT M L L
0 x
1
3 y
M L T M
y
z
z
z
LT 1 M 0 Lx 3 y z T z M y z x 3y z 1 z 1 x 1 y 1
yz 0 z 1 k 1 1 Vc kd d Vc d Vc d 改写为 k k Re c k
1 1 1 2 2 2 3 3 3 4 4 4
将各量的量纲代入,写出各公式:
1 LT
对每一个π写出量纲和谐方程式组:
L ML L T 1 1 3 L ML ML1T 2 1 2 LT 1 3 L ML L 1 3 LT 1 3 L ML L 1 4 LT
