线性规划软件
LINGO应用教程
第十章 LINGOLingo 软件是求解线性规划、非线性规划的数学软件,也可用于一些线性和非线性方程组的求解等。
Lingo 实际上也是最优化问题的一种建模语言,包括许多常用的数学函数供使用者建立优化模型时调用,并可以接受与其他数据文件交换数据。
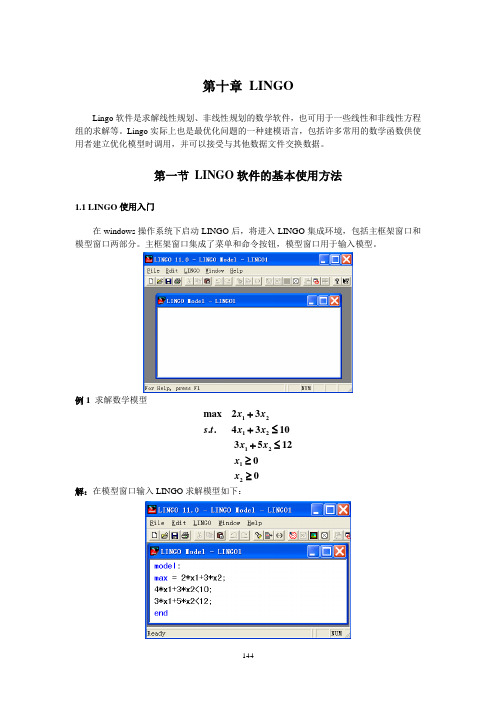
第一节 LINGO 软件的基本使用方法1.1 LINGO 使用入门在windows 操作系统下启动LINGO 后,将进入LINGO 集成环境,包括主框架窗口和模型窗口两部分。
主框架窗口集成了菜单和命令按钮,模型窗口用于输入模型。
例1 求解数学模型12121212max 23..4310351200x x s t x x x x x x ++≤+≤≥≥解:在模型窗口输入LINGO 求解模型如下:输入模型后选择菜单LINGO|Solve 或者按工具栏的,LINGO开始编译模型,如有语法错误将返回一个错误的消息并指明错误出现的位置;如果通过编译,LINGO将激活Solver运算器寻求模型的最优解,首先出现Solver Status状态窗口显示模型求解的运算状态信息:状态窗口显示的信息含义如下:“Global optimal solution found”表示得到全局最优解。
“Objective value: 7.454545”表示最优目标值为7.454545。
“Total solver iterations:2” 表示迭代2次得到结果。
“V alue”给出最优解中各变量的值:x1=1.272727,x2=1.636364。
Reduced Cost 值列出最优单纯形表中判别数所在行的变量的系数,表示当变量有微小变动时,目标函数的变化率。
其中基变量的reduced cost值应为0,对于非基变量xj,相应的reduced cost值表示当某个变量xj 增加一个单位时目标函数减少的量( max型问题)。
本例中此值均为0。
SLACK OR SURPLUS值给出约束条件的松驰变量或剩余变量的值。
线性规划Lindo软件-整数规划

定制化不足
对于特定领域的整数规划问题, 可能需要针对具体问题对软件进 行定制化开发。
未来研究的方向与展望
算法改进
随着计算技术的发展,未来可以进一步优化 Lindo软件的算法,提高求解速度和精度。
扩展应用领域
随着整数规划问题的多样化,未来可以进一步拓展 Lindo软件的应用领域,如金融、物流、能源等领 域。
整数规划的求解方法
分支定界法
通过不断分割可行解空间和排除不可行解空 间来逼近最优解。
割平面法
通过逐步构建整数解来逼近最优解,适用于 小规模问题。
回溯法
通过添加割平面来缩小可行解空间,最终找 到最优解。
Lindo软件求解法
使用Lindo软件进行整数规划求解,具有高效 、稳定、易操作等优点。
04
使用Lindo软件进行整数规划
在求解结果查看界面中,可以查看问题的最优解、最优值、变量取值等信 息。
可以使用软件提供的图表功能,绘制变量取值与目标函数之间的关系图, 以便更好地理解问题的解。
05
案例分析
案例一:简单的整数规划问题
问题描述
01
考虑一个简单的整数规划问题,目标是最小化目标函数,同时
满足一系列线性约束条件。
解决方案
• 易用性:用户界面友好,操作简单,无需复杂的编程知识 即可使用。
Lindo软件在整数规划中的优势与限制
依赖性
Lindo软件的功能和性能高度依赖 于计算机硬件配置,高性能计算 机是求解大规模问题的必要条件。
模型限制
对于某些特殊类型的整数规划问 题,如非凸或非线性问题,Lindo 软件的求解效果可能有限。
在约束条件设置界面中,根据问题数据设置相 应的约束条件,如“less than”、“equal to”或“greater than”。
LINGO软件简介

L INGO 软件简介LIN GO 软件就是一个处理优化问题得专门软件,它尤其擅长求解线性规划、非线性规划、整数规划等问题.一个简单示例有如下一个混合非线性规划问题:。
L IN GO 程序(模型): ﻩ ﻩmax =98*x1+277*x2-x1^2—0、3*x1*x2-2*x2^2+150*x3;x1+2*x2+2*x3〈=100; x1<=2*x 2;gin (x 1);gin (x2);! Ling o默认变量非负(注意:bin (x)表示x 就是0—1变量;gin (x )表示x 就是整数变量;bnd (L,x,U)表示限制L ≤x ≤U;free (x)表示取消对x 得符号限制,即可正、可负。
)ﻩ结果:Gl obal opti mal s ol utio n foun d、Objec tive va lue: 9561、200 Ex tended s olve r ste ps : 0 T ot al solver iterations : 45 Va ri ab le Value Redu ced Cost X1 6、000000 -76、70000X2 31、00000 -151、2000X3 16、00000 -150、0000R ow Slack or Su rpl us Dua l P rice1 9561、200 1、0000002 0、000000 0、0000003 56、00000 0、000000———————— 非常简单!在LINGO 中使用集合ﻩ为了方便地表示大规模得规划问题,减少模型、数据表示得复杂程度,L INGO 引进了“集合”得用法,实现了变量、系数得数组化(下标)表示。
ﻩ例如:对⎪⎪⎩⎪⎪⎨⎧==-++-==≤++∑=.,,;10)0(;4,3,2,1),()())()1()(;4,3,2,1,20)(..)}(20)(450)(400{min4,3,2,1均非负INV OP RP INV I I DEM I OP I RP I INV I INV I I RP t s I INV I OP I RP I求解程序:model :sets:ﻩmark/1,2,3,4/:dem,rp,op,inv;!也可以vmark/1、、4/:dem,rp,o p,inv;ﻩendsetsmin=sum(mark:400*rp+450*op+20*inv);!也可以mark(I):400*rp(I)+450*op(I)+20*inv(I);for(mark(I):rp(I)<40);for(mark(I)|I#gt#1:inv(I)=inv(I—1)+rp(I)+op(I)—dem(I));inv(1)=10+rp(1)+op(1)-dem(1);data:ﻩdem=40,60,75,35;enddataend上面程序在model…end之间有(1)集合定义、(2)数据输入与(3)其她三部分内容。
线性规划问题的Lingo求解

Lingo中参数设置与调整
01
参数设置
02
调整策略
Lingo允许用户设置求解器的参数, 如求解方法、迭代次数、收敛精度等 。这些参数可以通过`@option`进行 设置。
如果求解过程中遇到问题,如无解、 解不唯一等,可以通过调整参数或修 改模型来尝试解决。常见的调整策略 包括放松约束条件、改变目标函数权 重等。
02
比较不同方案
03
验证求解结果
如果存在多个可行解,需要对不 同方案进行比较,选择最优方案。
可以通过将求解结果代入原问题 进行验证,确保求解结果的正确 性和合理性。
感谢您的观看
THANKS
问题,后面跟随线性表达式。
02 03
约束条件表示
约束条件使用`subject to`或简写为`s.t.`来引入,后面列出所有约束条 件,每个约束条件以线性表达式和关系运算符(如`<=`, `>=`, `=`, `<`, `>`)表示。
非负约束
默认情况下,Lingo中的变量是非负的,如果变量可以为负,需要使用 `@free`进行声明。
问题的解通常出现在约束条件的边界上 。
变量通常是连续的。
特点 目标函数和约束条件都是线性的。
线性规划问题应用场景
生产计划
确定各种产品的最优生产量, 以最大化利润或最小化成本。
资源分配
在有限资源下,如何最优地分 配给不同的项目或任务。
运输问题
如何最低成本地将物品从一个 地点运输到另一个地点。
金融投资
03
求解结果
通过Lingo求解,得到使得总加工时间最短的生产计划安 排。
运输问题优化案例
问题描述
某物流公司需要将一批货物从A地运往B地,可以选择不同的运输方式和路径,每种方式和路径的运输时间和成本不 同。公司需要在满足货物送达时间要求的前提下,选择最优的运输方式和路径,使得总成本最低。
LINGO9.0培训教程

相较于其他非线性规划软件,Lingo9.0在算法优化方面更 加出色,能够更快地找到最优解。
适用范围
相较于专门针对非线性规划问题的软件,Lingo9.0的适用 范围更广,既可以处理线性规划问题,也能处理一些非线 性规划问题。
与其他整数规划软件的比较
整数规划能力
Lingo9.0在处理整数规划问题时,具有较高的求解精度和速度,能 够提供更精确的解决方案。
灵活性
相较于其他专门针对整数规划问题的软件,Lingo9.0更加灵活,不 仅适用于整数规划问题,还能处理一些混合整数规划问题。
扩展性
Lingo9.0具有良好的扩展性,可以与其他软件和编程语言集成,方便 用优解。
多目标规划问题
多目标规划问题概述
01
多目标规划是解决具有多个相互冲突的目标函数的优
化问题。
多目标规划问题实例
02 例如,一个城市需要制定交通规划,目标是最大化交
通便利性、减少交通拥堵和降低环境污染。
Lingo9.0求解多目标规划问题
03
使用Lingo9.0软件,可以建立多目标规划模型,并使
随着技术的发展,Lingo9.0不断更新迭代,成为一款功能强大、用户友好的优化求 解器。
Lingo9.0在学术界和工业界都得到了广泛的应用,为决策者提供有效的解决方案。
Lingo9.0的主要特点和功能
01
02
03
04
支持线性规划、整数规 划、二次规划和网络优 化等多种优化问题。
内置丰富的算法库,能 够快速求解大规模问题。
建模常见问题
总结词
建模常见问题主要包括模 型建立错误、模型无法导 出等。
模型建立错误
请检查您的模型是否符合 Lingo9.0的语法规则,并 确保所有参数和变量都已 正确设置。
excel线性规划

excel线性规划Excel线性规划是指利用Excel软件来解决线性规划问题。
线性规划问题是最经典的优化问题之一,主要是在一定约束条件下,找出使某个目标函数取得最优值的决策变量取值。
Excel提供了Solver插件,可以用于求解线性规划问题。
首先,我们需要建立起线性规划问题的模型。
假设我们有m个决策变量x1、x2、...、xm,需要找到这些决策变量的取值,使得目标函数Z(x1、x2、...、xm)取得最优值。
同时,还有n个约束条件,即使得一些函数关系式(一般为等式或不等式)满足。
线性规划模型可以表示为如下形式:目标函数:Z = c1x1 + c2x2 + ... + cmxm + d约束条件:A11x1 + A12x2 + ... + A1mxm <= b1A21x1 + A22x2 + ... + A2mxm <= b2...An1x1 + An2x2 + ... + Anmxm <= bn然后,我们可以通过Excel的Solver插件来求解线性规划问题。
具体步骤如下:1. 打开Excel软件,在工具栏中选择“数据”菜单,点击“求解器”按钮。
2. 在弹出的Solver对话框中,选择“线性规划”作为求解的方法。
3. 在“目标单元格”栏中输入目标函数的单元格地址。
若目标函数是在单元格C1中,则输入$C$1。
4. 在“变量单元格”栏中输入决策变量的单元格范围。
若决策变量是在范围B1:B5中,则输入$B$1:$B$5。
5. 在“约束条件”栏中,点击“添加”按钮,逐个输入约束条件。
每个约束条件包括“约束单元格”、“约束类型”和“约束值”三项。
若第一个约束条件是在单元格D1中,约束类型为“<=”,约束值为10,则输入$D$1<=10。
6. 在“求解方法”下拉菜单中,选择求解的方法。
常用的有“规划求解法”和“单纯形法”。
7. 点击“确定”按钮开始求解。
Solver会根据给定的目标函数和约束条件,寻找使目标函数取得最优值的决策变量取值。
应用Excel软件求解线性规划问题

使用变量xij代表第i种原料用于生产第j种产品的数量(桶)
1
i=1, 2, 3分别代表催化裂化汽油、异戊烷和直馏汽油
2
j=1, 2, 3分别代表80#、100#汽油和燃料油
3
物料平衡约束
4
物料平衡约束
蒸汽压限制
01
辛烷值限制
02
变量非负约束
03
各类约束
Excel求解步骤
打开Excel,建立新工作表,输入公式
应用软件求解线性规划问题
添加副标题
202X
1.1 Excel的规划求解工具
Excel软件提供了求解一般规模数学规划问题的“规划求解”工具 该工具具有界面友好、操作简单、与Excel无缝集成等优点 可用于化学化工常见中、小规模线性规划、非线性规划、整数规划问题的求解
Excel提供的规划求解工具对模型规模有一定限制:求解模型的决策变量数不超过200个。当“规划求解选项”对话框中的“采用线性模型”复选框处于选中状态时,对约束条件的数量没有限制;而对于非线性问题,每个可变单元格除了变量的范围和整数限制外,还可以有最多达100个约束条件
Excel结果分析-3
整数规划的运行结果
由于工程实际问题中存在各种不确定性,因此线性规划模型中的系数C、aji、bj等均可能偏离原来的计算值,因此决策者必须掌握这些系数改变时对原最优解的影响,也就是必须进行线性规划的灵敏度分析。
可以应用Excel方便地实现
线性规划的灵敏度分析
The End
Excel求解步骤-1
打开规划求解窗口
Excel求解步骤-2
设置目标单元格 设置可变单元格 约束的输入
Excel求解步骤-3
设置规划求解选项
lingo介绍.ppt

约束条件复杂的情况
数学表述:
Σi VOLUMEij = DEMANDj, for all j in VENDORS
Lingo表述:
@FOR( VENDORS( J): @SUM( WAREHOUSES( I): VOLUME( I, J)) = DEMAND( J));
@FOR( DAYS( I): @GIN( START( I)));
DATA: REQUIRED = 20 12 18 16 19 14 12;
ENDDATA
MIN = @SUM( DAYS( I): START( I));
@FOR( DAYS( J): @SUM( DAYS( I) | I #LE# 5: START( @WRAP( J - I + 1, 7))) >= REQUIRED( J)
DATA: X = 1 2 3; Y = 4 5 6;
ENDDATA
Looping Function
@FOR The most powerful of the set looping functions, @FOR is used to generate constraints over members of a set.
Some Example
SETS:
DAYS / MON TUE WED THU FRI SAT SUN/: REQUIRED, START; ENDSETS
DATA: REQUIRED = 20 16 13 16 19 14 12;
ENDDATA
MIN = @SUM( DAYS( I): START( I));
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线性规划软件
线性规划是一种数学优化方法,用于解决一类线性约束条件下的最优化问题。
线性规划软件则是用于求解这类问题的工具。
本文将介绍线性规划软件的基本原理、常见应用场景以及优缺点。
线性规划软件的基本原理是利用线性规划模型的特殊结构进行求解,主要包括以下几个步骤:
1. 建立数学模型:根据具体问题,将决策变量、目标函数以及约束条件转化为线性关系式,构建线性规划模型。
2. 求解算法:线性规划问题的求解算法主要有两种,分别是单纯形法和内点法。
单纯形法通过沿着可行解空间的单纯形路径搜索最优解,而内点法则通过求解一系列对数障碍问题逼近最优解。
3. 数据输入和参数设置:用户需要输入问题相关的数据,包括目标函数系数、约束条件等,并设置一些计算参数,如求解算法的选择、精度要求等。
4. 求解结果分析:线性规划软件可以输出最优解的数值结果,如最优目标函数值、决策变量取值等。
用户可以对结果进行进一步分析,评估方案的有效性。
线性规划软件在实际应用中具有广泛的应用场景。
其中,最典型的是生产计划、运输调度和资源分配等问题。
例如,一家工
厂需要确定每个生产批次的生产量,以使得总生产成本最小;一个物流公司需要优化配送路径,以降低运输成本。
线性规划软件可以根据具体的约束条件和目标函数,自动分析求解问题,帮助用户得到最优解决方案。
线性规划软件的优点主要有以下几个方面:
1. 自动化计算:线性规划软件可以通过输入问题相关的数据和约束条件,自动运行求解算法,并输出最优解决方案的数值结果。
大大减少了手工计算的工作量和错误的可能性。
2. 快速求解:线性规划问题具有一定的数学性质,可以利用数值方法进行求解。
线性规划软件通常使用高效的求解算法,可以在较短的时间内得到最优解。
3. 灵活性和可扩展性:线性规划软件可以根据具体问题的需求进行参数设置,用户可以根据实际情况灵活调整算法和求解策略。
此外,线性规划软件还可以扩展到更复杂的问题领域,如整数规划、混合整数规划等。
然而,线性规划软件也存在一些局限性和缺点:
1. 问题复杂性:线性规划软件只适用于满足线性关系的优化问题,对于非线性或具有复杂结构的问题无法求解。
2. 模型建立困难:线性规划软件需要用户将实际问题转化为数学模型,并将模型中的各项参数输入软件中,这一过程对用户提出了一定的需求。
对于非专业人士来说,模型构建和参数设
置可能具有一定的难度。
综上所述,线性规划软件在解决优化问题中发挥了重要作用,具有自动化计算、快速求解和可扩展性的优点。
然而,用户需要了解问题的数学模型和参数设置方法,才能充分利用线性规划软件的优势。
