导数的概念及其几何意义-人教A版高中数学选择性必修第二册优秀课件
合集下载
5.1.2导数的概念及其几何意义(上课课件)

/人A数学/ 选择性必修 第二册
返回导航 上页 下页
1.导数的几何意义就是切线的斜率,因此比较导数大小的问题可以用 数形结合思想来解决.
曲线在某点处的切线斜率的大小反映了曲线在相应点处的变化情况, 由切线的倾斜程度,可以判断出曲线升降的快慢.
/人A数学/ 选择性必修 第二册
返回导航 上页 下页
4.(1)某家电制造集团为尽快实现家电下乡提出四种运 输方案,据预测,这四种方案均能在规定时间T内完成预期的运输任务 Q0,各种方案的运输总量Q与时间t的函数关系如下所示.在这四种方 案中,运输效率(单位时间内的运输量)逐步提高的是( B )
/人A数学/ 选择性必修 第二册
返回导航 上页 下页
2.f(x)在x=x0处的导数、曲线f(x)在x=x0附近的升降情况、点(x0,f(x0))处切 线的斜率与点(x0,f(x0))处切线的倾斜角的关系如表所示.
f(x)在 x=x0 处的导数
f′(x0)>0 f′(x0)<0 f′(x0)=0
曲线f(x)在x =x0附近的 升降情况
/人A数学/ 选择性必修 第二册
返回导航 上页 下页
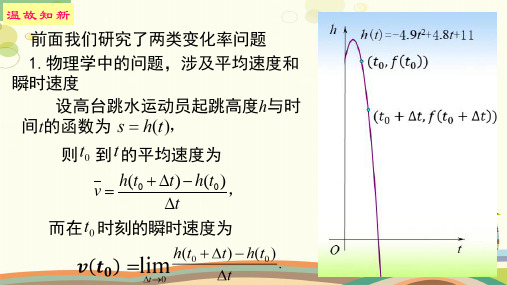
[刻画曲线h(t)在上述 三个时刻附近的变化情况. (1)当t=t0时,曲线h(t)在t=t0处的切线l0平行于t轴,h′(t0)=0. 这时,在t=t0附近曲线比较平坦,几乎没有升降. (2)当t=t1时,曲线h(t)在t=t1处的切线l1的斜率h′(t1)<0. 这时,在t=t1附近曲线下降,即函数h(t)在t=t1附近单调递减.
/人A数学/ 选择性必修 第二册
返回导航 上页 下页
(2)已知函数f1(x),f2(x),f3(x),f4(x),它们在平面直角坐标系中的图象 如图所示,则f1′(x0),f2′(x0),f3′(x0),f4′(x0)的大小关系是( A ) A.f1′(x0)>f2′(x0)>f3′(x0)>f4′(x0) B.f1′(x0)>f3′(x0)>f2′(x0)>f4′(x0) C.f4′(x0)>f1′(x0)>f3′(x0)>f2′(x0) D.f1′(x0)>f3′(x0)>f4′(x0)>f2′(x0)
5-1导数的概念及其意义课件-高二下学期数学人教A版(2019)选择性必修第二册

v(2) lim y lim (t 6) 6
x x0
x0
在第2 h 附近,汽车的速度 每秒大约增加 2m / s
在第6 h 附近,汽车的速度 每秒大约减少 6m / s
练习
设f (x) x ,求f (1)
解:f (1) lim f (1 x) f (1)
x0
x
(1 x) 1
lim
x0
记为 lim h(1 t) h(1) 5
t 0
t
当时间间隔 | t | 无限趋近于0 时,平均速度v 就无限趋近于t 1 时的瞬时速度。
因此,运动员在t 1 s 时的瞬时速度v(1) 5 m / s
思考 在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h ( 单位:m)
与起跳后的时间t(单位:s)存在函数关系
在第2 h 时,原油温度的瞬时变化率是 f (2)
y f (2 x) f (2)
x
x
在第6 h 时,原油温度的瞬时变化率是f (6)
y f (6 x) f ()
x
x
(2 x)2 7(2 x) 15 (22 7 2 15) x
4x x2 7x x 3 x
f (2) lim y lim (x 3) 3
t 0
t 0
质点A 在t 2.7 s 时的瞬时速度为10.8 m / s
3.设函数f (x) x2 1 ,求 (1)当自变量x 由1 变到1.1 时,函数的平均变化率
(2) 函数在x 1 处的导数
解:(1) f (1.1) f (1) (1.1)2 1 (12 1) 2.1
4.8 9.8t0)
4.8 9.8t0
lim x 0
x0
新教材人教a版选择性必修第二册512第2课时导数的几何意义课件

1.若曲线y=h(x)在点P(a,h(a))处的切线方程为2x+y +1=0,B
则( ) A.h′(a)=0 B.h′(a)<0 C.h′(a)>0 D.h′(a)的符号不确定 【解析】 由2x+y+1=0,得y=-2x-1, 由导数的几何意义可知h′(a)=-2<0.
2.已知曲线 f(x)=12 x2+x 的一条切线的斜率是 3,则该切点的
曲线 y=1x 在点2,12 处的切线方程是__x_+__4_y_-__4_=__0___.
【解析】 曲线在点2,12 处的切线的斜率
为 k= lim Δx→0
2+1Δx-12
Δx
= lim Δx→0
-1 2(2+Δx)
=-14
,
由直线的点斜式方程可得切线方程
为 y-12 =-14 (x-2),即 x+4y-4=0.
所以 y0=2×14 2 +1=98 ,所以切点坐标为14,98 .
(2)设直线 y=3x+b 与曲线 y=x3 的切点为 P(x0,y0),
由 y=x3 得 y′=Δlixm→0
Δy Δx
=Δlixm→0
(x0+Δx)3-x30 Δx
=Δlixm→0 [3x20 +3x0Δx+(Δx)2]=3x20 ,
=(x30
-x0)-(x0-1) x0-1
=x02 +x0-1,又由导数的几何意义知
k=f′(x0)=Δlixm→0
f(x0+Δx)-f(x0) Δx
= lim Δx→0
(x0+Δx)3-2(x0+Δx)-(x30 -2x0) Δx
=3x20 -2,所以 x20 +x0-1=3x20 -2,所以 2x20 -x0-1=0,
【拓展】 过点(1,-1)且与曲线y=x3-2x相切的 直线方程 A
高中数学人教A版选择性必修第二册导数的概念及其几何意义完整版课件
的值叫做 y f (x) 在 x x0 处的导数(也称瞬时变化率),
记作 f ' (x0 ) 或 y'|xx0 ,即
:
f
'
(
x0
)
lim
x0
导数的几何意义
y x
f
lim f (x0 x) f (x0
x0
x
'(x0)是函数 y f (x)在
). x
x0
处切线的斜率
典型例题 根据导数定义求函数在某一点处的导数
无限逼近(极限) ★ 答案表示形式具有一致性吗?
平均变化率的极限
4
瞬时变化率的极限
概念生成
1.平均变化率
f(x0+Δx)-f(x0)
fx0+Δx-fx0 Δx
概念生成
2.导数
即
当x 0时,平均变化率 y 有极限,则称 y f (x)在 x
y
x x
无限接近一个确定的值, x0 处可导,并把这个确定
需要对原油进行冷却和加热。已知在第xh时,原油的温 度(单位:。C)为y f (x) x2 7x 15(0 x 8).计算第2h时 与第6h时,原油温度的瞬时变化率,并说明它们的意义.
解 在第2h和第6h时,原油温度的瞬时变化率就是f '2
和 f ' 6.
根据导数的定义, y f 2 x f 2
)
A.f ′(x0) B.2f ′(x0) C.-2f ′(x0) D.0
(2)求函数 y=3x2 在 x=1 处的导数.
解: y f (1 x) f (1)
x
x
f (1) lim y lim ( 1 ) x0 x x0 1 x
典 型 例 题 导数的应用
新教材人教A版高中数学选择性必修第二册5.1导数的概念及其意义 精品教学课件

(2)×.函数y=f(x)从x1到x2的平均变化率
y f(x2) f(x1)公式中Δx与Δy
x
x2 x1
可能同号,也可能异号.
(3)×.物体在某一时刻t的瞬时速度是当Δt➝0时,平均速度的极限.
2.某物体的位移公式为s=s(t),从t0到t0+Δt这段时间内下列理解正确的 是( )
A.(t0+Δt)-t0称为函数值增量 B.t0称为函数值增量 C.Δs=s(t0+Δt)-s(t0)称为函数值增量 D. s 称为函数值增量
x0
x
= lim([ x)2+3x x0
20.+3x
0
x
]=3x
2 0
因为k=3,所以3x20=3,得x0=1或x0=-1,
所以y0=1或y0=-1.
所以点P的坐标为(-1,-1)或(1,1).
2.在抛物线y=x2上求一点P,使在该点处的切线垂直于直线2x-6y+5=0.
【解析】设点P的坐标为(x0,y0),
(2)函数y=f(x)从x1到x2的平均变化率
y x
f(x2) f(x1)公式中Δx与Δy同号.
x2 x1
()
(3)物体在某一时刻t的瞬时速度即在[t,t+Δt]上,当Δt较小时的平均速度.
()
提示:(1)×.在平均变化率的定义中,自变量x在x0处的变化量Δx可以是正数,
也可以是负数,但不能为0.
5.1 导数的概念及其意义
5.1.1 变化率问题 5.1.2 导数的概念及其几何意义 P40
1.瞬时速度 我们把物体在_某__一__时__刻__的速度称为瞬时速度. 【思考】
物体在时间段 1,1 t 的平均速度与在时刻t=1的瞬时速度有什么关系?
数学人教A版选择性必修第二册5.1.2导数的概念课件

∴当 Δx→0 时,f(x0+Δx)2-Δxf(x0-Δx)必趋于 f′(x0)=k,
∴ lim x0
f(x0+Δx)2-Δxf(x0-Δx)=k,
∴ lim x0
f(x0+Δx)Δ-xf(x0-Δx)=2k.
规律方法 由导数的定义可知,若函数 y=f(x)在 x=x0 处可导,则 f′(x)=
[思考] 1.导数或瞬时变化率可以反应函数变化的什么特征?
提示 导数或瞬时变化率可以反应函数在某一点处变化的快慢程度. 2.函数的平均变化率与瞬时变化率有什么区分和联系? 提示 (1)平均变化率与瞬时变化率的区分:平均变化率刻画函数值在区间[x1,x2] 上变化的快慢,瞬时变化率刻画函数值在x=x0处变化的快慢. (2)平均变化率与瞬时变化率的联系:当 Δx 趋于 0 时,平均变化率ΔΔyx趋于一个常数, 这个常数为函数在 x=x0 处的瞬时变化率,它是一个固定值.
2
= lxim 0 Δx[
(Δx)2+2Δx (Δx)2+2Δx+2+
= lim 2] x0
Δx+2 (Δx)2+2Δx+2+
= 2
22.
规律方法 求一个函数 y=f(x)在 x=x0 处的导数的步骤如下: (1)求函数值的变化量 Δy=f(x0+Δx)-f(x0); (2)求平均变化率ΔΔxy=f(x0+ΔxΔ)x -f(x0);
又f′(1)=3,∴a=3. 答案 3
4.已知函数 f(x)= x,则 f′(1)=________.
解析
f′(1)=
f(1+Δx)-f(1) Δx
= lim x0
1+Δx-1 Δx
= lim x0
1+1Δx+1=12.
答案
1 2
5.若 lim x0
高二数学课件(人教A版选择性必修第二册)5.1.2导数的概念及其几何意义(2课时)
l
数 = ()在 = 0 附近的变化情况.那么导数 ’ (0 )的几何意义是什么?
l
思考1:观察函数 = ()的图象,平均变化率
∆
∆
=
(0 +∆)−(0 )
∆
∆
∆→0 ∆
’ (0 ) =
表示什么?瞬时变化率
(0 +∆)−(0 )
表示什么?
=
(0 +∆)−(0 )
叫做函数∆=新知探索源自如果当∆∆∆
→l 0时,平均变化率 无限趋近于一个确定的值,即 有极限,则称
∆
∆
= ()在 = 0 处可导,并把这个确定的值叫做
= ()在 = 0 处的导数(也
l
称为瞬时变化率),记作 ’ (0 )或 ’ |=0 ,即 ’ (0 )
瞬时变化率(精确到0.1).
解:血管中某一时刻药物浓度的瞬时变化率,就是药物浓度()在此时刻的导数,
从图象上看,它表示曲线()在此点处的切线的斜率.
例析
l
l
如图,画出曲线上某点处的切线,利用网格估计这条切线的斜率,可以得到此
时药物浓度瞬时变化率的近似值.
作 = 0.8处的切线,并在切线上取两点,如(0.7,0.91),(1.0,0.48),则该切线的
l
l
对原油进行冷却和加热.已知在 ℎ 第时,原油的温度(单位:
℃)为 = () = 2 − 7 + 15(0 ≤ ≤ 8).计算第2 ℎ与第
6 ℎ时,原油温度的瞬时变化率,并说明它们的意义.
同理可得 ’ (6) = 5.
在第2 ℎ和第6 ℎ时,原油温度的瞬时变化率分别为−3℃/ℎ和5℃/ℎ.说明在第
这样,当变化时, = ’ ()就是的函数,我们称它为 = ()的导函数
数 = ()在 = 0 附近的变化情况.那么导数 ’ (0 )的几何意义是什么?
l
思考1:观察函数 = ()的图象,平均变化率
∆
∆
=
(0 +∆)−(0 )
∆
∆
∆→0 ∆
’ (0 ) =
表示什么?瞬时变化率
(0 +∆)−(0 )
表示什么?
=
(0 +∆)−(0 )
叫做函数∆=新知探索源自如果当∆∆∆
→l 0时,平均变化率 无限趋近于一个确定的值,即 有极限,则称
∆
∆
= ()在 = 0 处可导,并把这个确定的值叫做
= ()在 = 0 处的导数(也
l
称为瞬时变化率),记作 ’ (0 )或 ’ |=0 ,即 ’ (0 )
瞬时变化率(精确到0.1).
解:血管中某一时刻药物浓度的瞬时变化率,就是药物浓度()在此时刻的导数,
从图象上看,它表示曲线()在此点处的切线的斜率.
例析
l
l
如图,画出曲线上某点处的切线,利用网格估计这条切线的斜率,可以得到此
时药物浓度瞬时变化率的近似值.
作 = 0.8处的切线,并在切线上取两点,如(0.7,0.91),(1.0,0.48),则该切线的
l
l
对原油进行冷却和加热.已知在 ℎ 第时,原油的温度(单位:
℃)为 = () = 2 − 7 + 15(0 ≤ ≤ 8).计算第2 ℎ与第
6 ℎ时,原油温度的瞬时变化率,并说明它们的意义.
同理可得 ’ (6) = 5.
在第2 ℎ和第6 ℎ时,原油温度的瞬时变化率分别为−3℃/ℎ和5℃/ℎ.说明在第
这样,当变化时, = ’ ()就是的函数,我们称它为 = ()的导函数
人教版高二下期数学选择性必修第二册-5.1.2 导数的概念及其几何意义(第2课时)【课件】
要点 3 导函数
从求函数 y=f(x)在 x=x0 处导数的过程可以看出,当 x=x0 时,f′(x0)是一个 唯一确定的数.这样,当 x 变化时,y=f′(x)就是 x 的函数,我们称它为 y=f(x)
的___导__函_数____ (简称导数).y=f(x)的导函数记作__f′(_x_) ___或___y_′ __,即 f′(x)=y
要点 2 函数的单调性与导数的关系 若 f′(x0)=0,则函数在 x=x0 处切线的斜率 k=__0___; 若 f′(x0)>0,则函数在 x=x0 处切线的斜率 k__>__0,且函数在 x=x0 附近 _单__调_递__增_且 f′(x0)越大,说明函数图象变化得越快; 若 f′(x0)<0,则函数在 x=x0 处切线的斜率 k_<__0,且函数在 x=x0 附近 ___单_调__递_减____,且|f′(x0)|越大,说明函数图象变化得越快.
f(x+Δx)-f(x) Δx
=
lim
Δx→0
(x+ΔΔxx)2-x2=Δlixm→0 (2x+Δx)=2x.
设点 P(x0,y0)是满足条件的点.
(1)因为点 P 处的切线与直线 y=4x-5 平行,所以 2x0=4,解得 x0=2,所以
y0=4,即满足条件的点的坐标为 P(2,4).
(2)因为点 P 处的切线与直线 2x-6y+5=0 垂直,且直线 2x-6y+5=0 的斜 率为13,所以 2x0·13=-1,解得 x0=-32,所以 y0=94,即满足条件的点的坐标为 P-32,94.
如果函数 y=f(x)在区间(a,b)内的每一点处都有导数,我们就说这个函数在
区间(a,b)上是可导函数.
课时学案
题型一 已知点在曲线上的切线问题
人教版高中数学选择性必修第二册5.1.2导数的概念及其几何意义【教学课件】
1 . 曲 线 y = x2 - 2x + 3 在 点 A( - 1,6) 处 的 切 线 方 程 是
________________.
4x+y-2=0 解析:由导数的定义知 y′|x=-1
= lim Δx→0
-1+Δx2-2-1+Δx+3--12+2×-1-3 Δx
=-4,
∴所求切线方程为 y-6=-4(x+1),
(2)函数 y=f(x)在 x=x0 处的导数 f′(x0)就是切线 P0T 的斜率 k0,
即 k0=lim Δx→0
fx0+ΔΔxx-fx0=f′(x0).
3.导数的概念
当 x 变化时,y=f′(x)就是 x 的函数,我们称它为 y=f(x)的导函
数(简称导数).y=f(x)的导函数有时也记作 y′,即 f′(x)=y′=
得 f′(1)=lim Δx→0
1+ΔΔxx-1=Δlixm→0
1+1Δx+1=12,
∴f(x)在点(1,1)处的切线方程为 y-1=21(x-1).
即 x-2y+1=0.
探究题 2 抛物线 y=x2在点 P 处的切线与直线 4x-y+2=0 平行,
求点 P 的坐标及切线方程.
解:设点 P 的坐标为(x0,y0),
4.已知函数 f(x)=lg(x+1),则 f′(2)的几何意义是
函数 f(x)=lg(x+1)的图象在点(2,lg 3)处切线的斜率. 5.曲线 y=3x2-4x 在点(1,-1)处的切线方程为________.
y=2x-3
解析:k=f′(1)= lim Δx→0
31+Δx2-41+Δx-3×12-4×1 Δx
[(Δx)2-3Δx+3]=3,
所以切线的斜率为 3.
由点斜式可得切线方程为 y-1=3(x+1),即 3x-y+4=0.
5.1.2 导数的概念及其意义课件(第一课时)-高二下学期数学人教A版(2019)选择性必修第二册
问题1中运动员在t=1时的瞬时速度为v(1)就是函数h(t)在t=1处的
导数h′(1),即
v(1) h(1) lim h(1 t) h(1) 5.
t 0
t
问题2中抛物线f(x)=x2在点P0(1, 1)处的切线P0T的斜率k0就是函 数f(x)=x2在x=1处的导数f′(1),即
k0
f (1)
lim f ( x0 x) f ( x0 )
x0
x
是一个常数,你能说出这个常数的意义吗?
结合“高台跳水运动员的速度”和“抛物线的切线的斜率”两个问题思考.
类似地,运用上述思想我们可以定义函数y=f(x)的平均变化率和 瞬时变化率:
1. 平均变化率
对于函数y=f(x),设自变量x从x0变化到x0+∆x,相应地,函数值y
巩固练习
练习.比较函数 f(x)=2x 与 g(x)=12x-1 在区间[a-1,a](a<0)上的 平均变化率的大小.
解:f(x)=2x 在区间[a-1,a](a<0)上的平均变化率为 faa--fa-a-11=2a-2a-1=2a-1;
g(x)=12x-1 在区间[a-1,a](a<0)上的平均变化率为 gaa--ga-a-11=12a-1-121a-1-1=12.
导数(瞬时变化率)为负,体现了下降的变化趋势. f (6) 5 表示在第 6 h 时,原油温度的瞬时变化率为 5℃/h, 这说明在第 6 h 附近,原油温度大约以 5℃/h的速率上升.
导数(瞬时变化率)为正,体现了上升的变化趋势.
巩固练习
练习.一 辆汽车在公路上沿直线变速行驶,假设t s时汽车的速度(单位: m/s) 为y v(t) t 2 6t 60,求汽车在第2 s与第6 s时的瞬时加速度,并说明它 们的意义. 解:在第2 s和6 s时,汽车的瞬时加速度就是v′(2)和 v′(6).
