电磁场与电磁波课件7.2 波的极化
合集下载
电磁场与电磁波PPT优秀版

利用无线电波传递信号,要求发射的无线电波随信号而改变。
要横向波外 或c发纵.射波从无,或经线二电者过波的,调振混荡合制电波路的必高须具频有如振下荡特点中:第一“,要检有 ”出调制信号的过程,叫做检波。检波
机械波只能在介质中传播,而电磁波可以在真空中传播,说法C
是 是正确的。 调制 的逆过程,也叫做
飞机降落过程中,当接收到λ1和λ2的信号都保持最强时,表明
调幅 ,经过调幅以后发射出去的无线电波叫做 调幅波 。使高频 振荡的频率随 信号强弱 而改变叫做调频,经过调频以后发射出 去的无线电波叫做 调频波 。
(2)无线电波的接收
相同 时,激 相同 时,激
从经过调制的高频振荡中“检”出调制信号的过程,叫做检波。
2-2 我国成功研发的反隐身先进米波雷达堪称隐身飞机的克星,它标
(5)电磁振荡的周期T=⑩ 2π LC ,频率f=
1
2电场在周围空间产生 磁场 ,变化 的磁场在周围空间产生 电场 ;均匀变化的电场(磁场)在周围空间 产生 恒定 的磁场(电场),非均匀变化的电场(磁场)在周围空间产 生 变化 的磁场(电场)。 (2)振荡的电场(磁场)在周围空间产生 周期性变化 的磁场(电 场)。 (3)电磁场:变化的电场在周围空间产生磁场,变化的磁场在周围空间产 生电场,变化的电场和磁场成为一个完整的整体,这就是 电磁场
C.波长、频率和波速间的关系,即v=λf,对机械波和电磁波都适用
答案 A 机械波的传播需要介质,而电磁波的传播不需要介质,所以选 项A说法不正确。干涉、衍射是波特有的现象,选项D说法正确。波能 传递能量,v=λf对机械波和电磁波都适用,故选项B、C说法都正确。
3.(多选)下列关于电磁波的说法中正确的是 (AC )
1-1 下列关于电磁波的说法正确的是 ( A )
电磁场与电磁波平面电磁波PPT精选文档

2
6.1.1 波动方程的解
在无源的理想介质中,由第5章我们知道,时谐电磁场 满足复数形式的波动方程 2Ek2E0
其中 k
对于均匀平面波,假设场量仅与坐标变量z有关,与x、
y无关,即
E E 0 x y
方程化简为
d2E k2E 0 d z2
解得
EE0ejk zE0 'ejk z
3
其中
E
0
其定义为
z 20lg Exm
Ex
z ln E xm
Ex
(dB) (Np)
波的振幅不断衰减的物理原因是由于电导率引起的焦
耳热损耗,有一部分电磁能量转换成了热能 。
26
(2)导电媒质中的相速为 vp
称为相位常数(phase constant),即单位长度上的
相移量。与理想介质中的波数k具有相同的意义。
得 ( j) 2 2 2 2 j 2 ( 1 j )
上式两边虚、实部分别相等,可得
2 1( )2 1
2
2
1( )2+ 1
2
24
为讨论方便起见,假设电场只有x方向分量,因
而电磁波的解为
E x E xe m j x e z E xe m z e j z j x
H yE xe m jxe zE xe m zejz jx
00
vp / f 是电磁波的波长 ,k称为波数(wave-number)
或相位常数(phase constant),表示单位长度内的相位变化。
2f 2
k
vp vp
14
x
E
O
z
y H
图6-1 理想介质中均匀平面波的传播
15
(4)均匀平面波传输的平均功率流密度 矢量可由式(6-7)和(6-8)得到
6.1.1 波动方程的解
在无源的理想介质中,由第5章我们知道,时谐电磁场 满足复数形式的波动方程 2Ek2E0
其中 k
对于均匀平面波,假设场量仅与坐标变量z有关,与x、
y无关,即
E E 0 x y
方程化简为
d2E k2E 0 d z2
解得
EE0ejk zE0 'ejk z
3
其中
E
0
其定义为
z 20lg Exm
Ex
z ln E xm
Ex
(dB) (Np)
波的振幅不断衰减的物理原因是由于电导率引起的焦
耳热损耗,有一部分电磁能量转换成了热能 。
26
(2)导电媒质中的相速为 vp
称为相位常数(phase constant),即单位长度上的
相移量。与理想介质中的波数k具有相同的意义。
得 ( j) 2 2 2 2 j 2 ( 1 j )
上式两边虚、实部分别相等,可得
2 1( )2 1
2
2
1( )2+ 1
2
24
为讨论方便起见,假设电场只有x方向分量,因
而电磁波的解为
E x E xe m j x e z E xe m z e j z j x
H yE xe m jxe zE xe m zejz jx
00
vp / f 是电磁波的波长 ,k称为波数(wave-number)
或相位常数(phase constant),表示单位长度内的相位变化。
2f 2
k
vp vp
14
x
E
O
z
y H
图6-1 理想介质中均匀平面波的传播
15
(4)均匀平面波传输的平均功率流密度 矢量可由式(6-7)和(6-8)得到
电磁场与电磁波 PPT

合成波得平均能流密度矢量
S1av
1 2
Re[E1(r )
H1 (r )]
1 2
Re[ex E1y (r )H1z (r )
பைடு நூலகம்
ez E1y (r )H1x (r )]
eexx
24EEimim
11
ssinini isisnin2 (2k(1kz1czocsosi) i
)
例6、4、1 当垂直极化得平面波以角度i 由空气向无限大得理
电磁场与电磁波
因此得到,产生全反射得条件为:
电磁波由稠密媒质入射到稀疏媒质中,即ε1 >ε2
入射角不小于c arcsin 2 1 , c 称为全反射的临界角。
对全反射得进一步讨论
θ i <θc 时,不产生全反射
θ i =θc 时, sint
1 2
sin c
1
t 90o
// 1
2
1 c
arcsin
0 4 0
6
可见入射角θi=π/ 3大于临界角θc=π/ 6 ,此时发生全反射。
入射得圆极化波可以分解成平行极化与垂直极化得两个线极 化波,虽然两个线极化波得反射系数得大小此时都为1,但它们得相 位差不等于±π/ 2,因此反射波就是椭圆极化波。
例6、3、1 下图为光纤得剖面示意图,如果要求光波从空气进 入光纤芯线后,在芯线与包层得分界面上发生全反射,从一端传至另 一端,确定入射角得最大值。
透射波沿分界面方向传播,没有沿z方向传播得功率,并且反射功 率密度将等于入射功率密度。
θ i >θc 时,
sint
1 2
sin i
1
// 1
ktz k2 cost k2 1 sin 2 t
电磁场与电磁波幻灯片

6.在经典物理学发展史中,出现过四个里程碑式的人物:伽利 略,牛顿,法拉第和麦克斯韦。爱因斯坦认为他们同样伟大, 你如何理解?查找相关的资料,写一篇报告。
2.结论:电磁波具有运动能量,以及与其他 物质相互作用的属性,都是物质的性质。电 磁波具有物质一般性质的同时,也具有特殊 的性质。
(四):麦克斯韦电磁场理论的意义
❖ 1.电磁场理论的建立,经历了“实践―― 理论――实践”这一科学发展的过程是物 理学发展史上的典型案例。
2.麦克斯韦的电磁场理论,实现了从经典 物理学向现代物理学的重大转折。
3.学生讨论与交流:从电磁波的特点出 发,你认为电磁场是客观存在的吗?
❖ 根据电磁波的特点中的第(5)点可知, 电磁场本身就是一种特殊形态的物质, 无需借助其他物质来传播
三:电磁场的物质性
❖ 1.几种特殊电磁波的例子:
(1)微波炉是利用电磁波进行加热食物。说明电磁场具有能量。
(2)俄国物理学家列别捷夫测量除光对被照射的物体有压力。
个电场是由变化的磁场引起的。 ―――――变化的磁场周围产生电
场是一种普遍存在的现象。
3.学生讨论与交流:变化的磁场 产生的电场与我们熟悉的静电场
有何不同?
❖ 静电场的电场线是由正电荷出发,终止于负 电荷,是不闭合的。而变化的磁场产生的电 场没有起点也没有终点,是闭合的“旋涡电 场”
4.提出:变化的电场能否也产生磁场?
6.麦克斯韦电磁场理论的基本思想:
❖ (1)均匀变化的磁场(或电场)产生稳定的电场(或磁场)
(2)非均匀变化的磁场(或电场)产生变化的电场(或磁场)。
(3)按三角函数规律变化的振荡磁场(或电场)产生同频 率的三角函数规律变化的振荡电场(或磁场)
Hale Waihona Puke (4)变化的磁场产生电场,变化的电场产生磁场,变化的 电场和磁场总是相互联系,形成一个不可分离的统一场,这 就是电磁场
2.结论:电磁波具有运动能量,以及与其他 物质相互作用的属性,都是物质的性质。电 磁波具有物质一般性质的同时,也具有特殊 的性质。
(四):麦克斯韦电磁场理论的意义
❖ 1.电磁场理论的建立,经历了“实践―― 理论――实践”这一科学发展的过程是物 理学发展史上的典型案例。
2.麦克斯韦的电磁场理论,实现了从经典 物理学向现代物理学的重大转折。
3.学生讨论与交流:从电磁波的特点出 发,你认为电磁场是客观存在的吗?
❖ 根据电磁波的特点中的第(5)点可知, 电磁场本身就是一种特殊形态的物质, 无需借助其他物质来传播
三:电磁场的物质性
❖ 1.几种特殊电磁波的例子:
(1)微波炉是利用电磁波进行加热食物。说明电磁场具有能量。
(2)俄国物理学家列别捷夫测量除光对被照射的物体有压力。
个电场是由变化的磁场引起的。 ―――――变化的磁场周围产生电
场是一种普遍存在的现象。
3.学生讨论与交流:变化的磁场 产生的电场与我们熟悉的静电场
有何不同?
❖ 静电场的电场线是由正电荷出发,终止于负 电荷,是不闭合的。而变化的磁场产生的电 场没有起点也没有终点,是闭合的“旋涡电 场”
4.提出:变化的电场能否也产生磁场?
6.麦克斯韦电磁场理论的基本思想:
❖ (1)均匀变化的磁场(或电场)产生稳定的电场(或磁场)
(2)非均匀变化的磁场(或电场)产生变化的电场(或磁场)。
(3)按三角函数规律变化的振荡磁场(或电场)产生同频 率的三角函数规律变化的振荡电场(或磁场)
Hale Waihona Puke (4)变化的磁场产生电场,变化的电场产生磁场,变化的 电场和磁场总是相互联系,形成一个不可分离的统一场,这 就是电磁场
电磁波的极化

坐标轴 吻合
其余情况均为椭圆极化波。
例 6-7 判断下列平面电磁波的极化形式:
jkz (1) E E0 (ex jey )e jkz (2) E E0 ( jex 2 jey )e jky (3) E E0 (ex 3 jez )e 4 j 20πz (4) E (ex jey )10 e
6.3.2 极化形式
1. 线极化 (1)若Ex、Ey相位相同,即 x y 0
Ex Exm cos t kz 0
设初相位为0
Ey Eym cos t kz 0 Ey Eym cos t kz
y
Ex Exm cos t kz
在z=0的等相位面上
Ex Exm cos t
Ey Eym cos t
Ey x
0
Ex
合成电磁波场强的大小为
2 2 2 2 E Ex E y Exm E ym cos t
合场强的方向用E与x轴的夹角表示
arctg
Ey Ex arctg Eym Exm =常数>0
Ex Exm cos t Em cos t
合成电磁波场强的大小为
Ey Eym sin t Em sin t
2 E Ex2 E y Em =常数
y
t
E
Ey
0 Ex
x
合场强的方向与x轴的夹角为
Ex 由此可见,合场强的模为一定值,方向以角速度ω逆时针旋转,故
arctg
2
x y
可见,合场强 E 的矢端轨迹仍为一椭圆,只是长短轴不再与坐标轴 吻合。
其余情况均为椭圆极化波。
例 6-7 判断下列平面电磁波的极化形式:
jkz (1) E E0 (ex jey )e jkz (2) E E0 ( jex 2 jey )e jky (3) E E0 (ex 3 jez )e 4 j 20πz (4) E (ex jey )10 e
6.3.2 极化形式
1. 线极化 (1)若Ex、Ey相位相同,即 x y 0
Ex Exm cos t kz 0
设初相位为0
Ey Eym cos t kz 0 Ey Eym cos t kz
y
Ex Exm cos t kz
在z=0的等相位面上
Ex Exm cos t
Ey Eym cos t
Ey x
0
Ex
合成电磁波场强的大小为
2 2 2 2 E Ex E y Exm E ym cos t
合场强的方向用E与x轴的夹角表示
arctg
Ey Ex arctg Eym Exm =常数>0
Ex Exm cos t Em cos t
合成电磁波场强的大小为
Ey Eym sin t Em sin t
2 E Ex2 E y Em =常数
y
t
E
Ey
0 Ex
x
合场强的方向与x轴的夹角为
Ex 由此可见,合场强的模为一定值,方向以角速度ω逆时针旋转,故
arctg
2
x y
可见,合场强 E 的矢端轨迹仍为一椭圆,只是长短轴不再与坐标轴 吻合。
第七章 导行电磁波 电磁场与电磁波 课件 谢处方
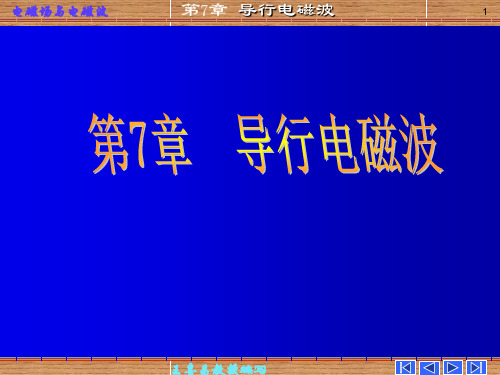
k
2 cmn
m 2 n 2 k k ( ) ( ) a b
2 xm 2 yn
截止波数只与波导 的结构尺寸有关。
王喜昌教授编写
电磁场与电磁波
第7章 导行电磁波
z
13
所以TM波的场分布
m n Ez ( x, y, z ) Ez ( x, y)e E0 sin( x)sin( y)e z a b E m m n E x ( x, y , z ) 2 z 2 Em cos( x)sin( y)e z kc x kc a a b
平行双导线是最简单的TEM波传输线,随着工作频率的升高, 其辐射损耗急剧增加,故双导线仅用于米波和分米波的低频段。
同轴线没有电磁辐射,工作频带很宽。
王喜昌教授编写
电磁场与电磁波
第7章 导行电磁波
4
2、波导管
矩形波导
圆波导
波导是用金属管制作的导 波系统,电磁波在管内传播, 损耗很小,主要用于 3GHz 一 30GHz 的频率范围。
m 2 n 2 ( ) ( ) a b
kcmn 2
y b x a o z
m n H z ( x, y) H m cos( x) cos( y) a b
kcmn ( m 2 n 2 ) ( ) a b
王喜昌教授编写
m 0,2, 1 3 , n 0,2, 1 3 ,
电磁场与电磁波
第7章 导行电磁波
15
所以TE波的场分布
m n H z ( x, y, z ) H m cos( x) cos( y)e z a b m m n H x ( x, y , z ) 2 H 0 sin( x) cos( y )e z kc a a b
垂直极化波
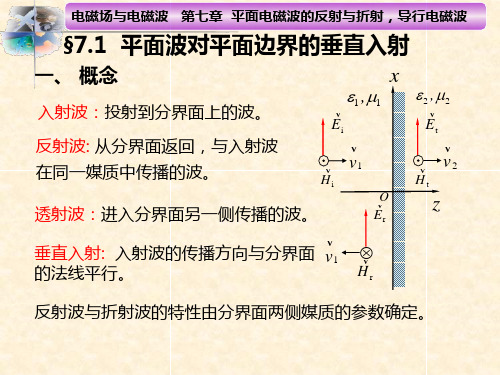
E1 xˆEi0e jk1z
H1
yˆ
Ei0
1
e
jk1z
透射波为: E1 xˆEi0Te jk1z
H1
yˆ
Ei0
1
Te jk1z
电磁场与电磁波 第七章 平面电磁波的反射与折射,导行电磁波
①区中任一点的合成电场强度和磁场强度可表为
E1 xˆEi 0 (e jk1z e jk1z )
,
v Ei
v vv
Hi
Hr
1
1
(zˆ) Er
yˆ
Er0
1
e jk1z
O v
z
Er
k1
11
2 1
,1
1 1
在介质空E间内xˆ任(E一i0e点 j的k1z 电 E场r0:e jk1z )
v v v
Hr
边界条件:理想导体表面上电场强度切向分量为零。
z0 时
Ei0 Er0 0
Er0 Ei0
yˆ
Et0
2
e jk2z
根据边界条件: 在 z 0 处有:
x
1 ,1
v Ei
v v v1
Hi vO Er
v v1 v
Hr
2 ,2
v Et
v v v2
Ht
z
E1t E2t
H1t H2t
电磁场与电磁波 第七章 平面电磁波的反射与折射,导行电磁波
则:
Ei0 Er0 Et0
Ei0 Er0 Et0
H1
yˆ
Ei0
1
(e jk1z
e jk1z )
②区中任一点的电场强度和磁场强度分别为
E2 Et xˆTE i 0e jk2z
电磁场与电磁波

电磁波的极化状态取决于Ex和Ey的振幅Exm、Eym和相位差 φ=φy-φx 对于沿+ z 方向传播的均匀平面波:
线极化:φ=0、± 。 φ=0,在1、3象限;φ=± ,在2、4象限。
圆极化:φ=± /2,Exm=Eym 。 取“+”,左旋圆极化;取“-”,右旋圆极化。
椭圆极化:其它情况。 0 < φ < ,左旋;- < φ<0,右旋 。
决于该时刻的电流和电荷分布,而是取决于比
y
t 较早的时刻
的电流或电荷分
布。时间
正好是电磁波以速度
从源点 传到场点 所需的时间。
电偶极子的电磁场:
z
P
qr
lO
y
x
远区场(辐射场):
辐射功率 辐射电阻
远区场的特点:
(1)远区场是横电磁波,电场、磁场和传播方向相互垂直; (2)远区电场和磁场的相位相同; (3)电场振幅与磁场振幅之比等于媒质的本征阻抗,即
电场波腹点( 的最大值的位置)
(n = 0 ,1,2,3, …) (n = 0,1,2,3,…)
两相邻波节点之间任意两点 的电场同相。同一波节点两 侧的电场反相。
在时间上有π/ 2 的相移。
在空间上错开λ/ 4,电 场的波腹(节)点正好是磁场 的波节(腹)点。
坡印廷矢量的平均值为零,不 发生能量传输过程,仅在两个 波节间进行电场能量和磁场能 的交换。
相位常数 相速 波导波长
波阻抗
结论: 当工作频率 f 大于截止频率fcmn 时,矩形波导中可以传 播相应的TEmn 模式和TMmn
模式的电磁波; 当工作频率 f 小 于或等于截止频率fcmn时,矩形波导中不能传播相 应的TEmn 模式
和TMmn 模式的电磁波。
线极化:φ=0、± 。 φ=0,在1、3象限;φ=± ,在2、4象限。
圆极化:φ=± /2,Exm=Eym 。 取“+”,左旋圆极化;取“-”,右旋圆极化。
椭圆极化:其它情况。 0 < φ < ,左旋;- < φ<0,右旋 。
决于该时刻的电流和电荷分布,而是取决于比
y
t 较早的时刻
的电流或电荷分
布。时间
正好是电磁波以速度
从源点 传到场点 所需的时间。
电偶极子的电磁场:
z
P
qr
lO
y
x
远区场(辐射场):
辐射功率 辐射电阻
远区场的特点:
(1)远区场是横电磁波,电场、磁场和传播方向相互垂直; (2)远区电场和磁场的相位相同; (3)电场振幅与磁场振幅之比等于媒质的本征阻抗,即
电场波腹点( 的最大值的位置)
(n = 0 ,1,2,3, …) (n = 0,1,2,3,…)
两相邻波节点之间任意两点 的电场同相。同一波节点两 侧的电场反相。
在时间上有π/ 2 的相移。
在空间上错开λ/ 4,电 场的波腹(节)点正好是磁场 的波节(腹)点。
坡印廷矢量的平均值为零,不 发生能量传输过程,仅在两个 波节间进行电场能量和磁场能 的交换。
相位常数 相速 波导波长
波阻抗
结论: 当工作频率 f 大于截止频率fcmn 时,矩形波导中可以传 播相应的TEmn 模式和TMmn
模式的电磁波; 当工作频率 f 小 于或等于截止频率fcmn时,矩形波导中不能传播相 应的TEmn 模式
和TMmn 模式的电磁波。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
右旋圆极化波: 右旋圆极化波:若φy - φx=-π/2,则电场矢端的旋转方向与 , 电磁波传播方向成右手螺旋关系, 电磁波传播方向成右手螺旋关系,称为右旋圆极化波
y Ey o E x
α
Ex
右旋圆极化波
若以右手的四指随E的矢端运动 若以右手的四指随 的矢端运动,姆指就指出了波的传播方 右手的四指随 的矢端运动, 表示的圆极化波称为右旋圆极化波 右旋圆极化波。 向,表示的圆极化波称为右旋圆极化波。
2Exm E ym cosϕ
2 2 Exm − E ym
椭圆极化的平面波
合成电场的矢量箭头在一椭圆轨迹上旋转, 合成电场的矢量箭头在一椭圆轨迹上旋转,因此我们称这种极 化的波为椭圆极化波。 化的波为椭圆极化波。
图 椭圆极化波
的相位超前y的相位 当θ>0时,x的相位超前 的相位, 它逆时针方向旋转称之为右旋椭圆极化波; 时 的相位超前 的相位, 它逆时针方向旋转称之为右旋椭圆极化波; 的相位超前x的相位 当θ <0, y的相位超前 的相位, 它顺时针方向旋转,成为左旋椭圆极化波。 , 的相位超前 的相位, 它顺时针方向旋转,成为左旋椭圆极化波。
2 r r r E 1 + E 2 = 2 a x E m cos( ω t − β z )
ϕ x = 0,ϕ y = −
π
r r 而 E = a x E 0 cos( ω t − β z )
∴
Em
1 = E0 2
分解完毕
例: 试证明等幅的左旋圆极化波及右旋圆极化波合成一个线 极化波 证明:设电磁波是沿方向z传播的, 证明:设电磁波是沿方向z传播的,则左旋圆极化波和右旋圆 极化波分别可表示为
合成波电场大小随时间变化,但矢端轨迹在与x轴为的直线 合成波电场大小随时间变化,但矢端轨迹在与x轴为的直线 大小随时间变化 上。
φx − φy = 0
φ x − φ y = ±π
(2) 圆极化 令 ϕ y − ϕx = m
π
2
Exm = Eym = Em ,
得
E y = Em cos(ωt m ) = ± Em sin(ωt ) 2
r v v E = ax Em sin(ωt − kz ) + a y Em cos(ωt − kz )
解:(1) Exm = E ym , ) (2) Exm = E ym , )
φx = − 、φ y = 0, ∆φ =
2
π φx = 0、φ y = − , ∆φ = −
2
π
π
2 π
2
左旋圆极化波 右旋圆极化波
Exm = E ym , φ = − π 、φ = − π , ∆φ = 0 (3) ) x y
4
4
线极化波 左旋椭圆极化波
(4) Exm ≠ E ym , )
π π φx = − 、φ y = 0, ∆φ = −
2
2
• P255 • 例7-4和例7-5
右旋圆极化波: 右旋圆极化波: 左旋圆极化波: 左旋圆极化波:
r r (a x − ja y ) E0 e j (ωt − kz )
r r (a x + ja y ) E0 e j (ωt −kz )
将两波相加得: 将两波相加 r r r r r r j (ωt − kz ) j (ωt − kz ) E = (a x − ja y ) E 0 e + ( a x + ja y ) E 0 e = a x (2 E0 )e j (ωt − kz ) 因此,该迭加波为一个线极化波 因此,该迭加波为一个线极化波。
圆极化: 圆极化:∆φ = ±π /2,Exm = Eym;
±π
,在2、4象限
右旋圆极化, 左旋圆极 取 “ - ” , 右旋圆极化 , 取 “ + ” , 左旋 圆极 化 椭圆极化:其它情况; 椭圆极化:其它情况;∆φ < 0,右旋,∆φ > 0,左旋 ,右旋, ,
r r 例:将 x 方向的直线极化波 E = a x E 0 cos( ω t − β z )
合成后
π
常数
2 2 E = E x + E y = Em
α = arctan[± tan(ωt )] = ± (ωt )
特点:合成波电场的大小不随时间改变, 方向却随时间变 特点:合成波电场的大小不随时间改变,但方向却随时间变 大小不随时间改变 化,电场的矢端在一个圆上并以角速度ω 旋转。这 电场的矢端在一个圆上并以角速度 旋转。 种极化方式称之为圆极化。 种极化方式称之为圆极化。 圆极化
说明下列均匀平面波的极化方式。 例 说明下列均匀平面波的极化方式。 (1) (2) (3) (4)
r v v E = ax Em e − jkz − a y jEm e− jkz r v π v π E = ax Em sin(ωt − kz + ) + a y Em cos(ωt − kz − ) 4 4 r v v E = ax Em sin(ωt − kz ) + a y 2 Em cos(ωt − kz )
合成电场
E
是圆极化波。
r r r π E1 = ax Em cos(ωt − βz ) + a y Em cos(ωt − βz − ) 2 π
右旋
2 r r r π E2 = ax Em cos(ωt − βz ) + a y Em cos(ωt − βz + ) 2
左旋 则
ϕ x = 0,ϕ y =
(1) 线极化
取z=0
Ex = Exm cos(ωt − ϕx ) , Ey = Eym cos(ωt − ϕy )
ϕ
y
−ϕ
x
= 0或 ± π
Ex = Exm cosωt , Ey = Eym cosωt
合成后
2 2 2 2 E = E x + E y = E xm + E ym cos ω t E arctg ym = const (φx − φy = 0) Exm Ey α = arctg = Eym Ex −arctg = const (φx − φy = ±π ) Exm
右旋椭圆极化波 图 右旋椭圆极化波
合成波极化的小结 电磁波的极化状态取决于E 的振幅E 电磁波的极化状态取决于 x和Ey的振幅 xm、Eym和相位差
∆φ= φy - φx =
对于沿 方向传播的均匀平面波: 对于沿+ z 方向传播的均匀平面波: 线极化: ∆φ = 0、±π ; 线极化:
∆φ = 0,在1、3象限,∆φ = 象限,
令
ϕx = 0,ϕy = θ
得
Ex = Exm cosωt , Ey = Eym cos (ωt −θ )
y
上式中消去t 得
2 Ex E y E + 2 − cos θ = sin 2 θ E E ym Exm E ym
可以证明, 可以证明,椭圆的长轴与 x 轴的夹角为
2 x 2 xm
2 Ey
x
tan2θ =
正余弦的转换
sin(-a)=-sin(a) cos(-a)=cos(a) sin(π/2-a)=cos(a) cos(π/2-a)=sin(a) sin(π/2+a)=cos(a) cos(π/2+a)=-sin(a) sin(π-a)=sin(a) cos(π-a)=-cos(a) sin(π+a)=-sin(a) cos(π+a)=-cos(a)
7.2 平面波的极化
波的极化 在给定空间点或面上,电场强度矢量的取向随时间变化的特性。 在给定空间点或面上,电场强度矢量的取向随时间变化的特性。 空间点或面上 强度矢量的取向随时间变化的特性 极化的分类 一般情况下, +z方向传播的均匀平面波, 一般情况下,沿+z方向传播的均匀平面波,其中 方向传播的均匀平面波
分解为两个振幅相等但旋转方向相反的圆极化 波的叠加形式。
解:圆极化波的定义:
E x 与 E y 的振幅相等,且 相位差为 ± π 时, 当 r 2
r r r π 设 E1 = ax Em cos(ωt − βz ) + a y Em cos(ωt − βz − ) 2 r r r π E2 = ax Em cos(ωt − βz ) + a y Em cos(ωt − : 左旋圆极化波:若φy - φx =π/2,则电场矢端的旋转方向与 , 电磁波传播方向成左手螺旋关系, 电磁波传播方向成左手螺旋关系,称为左旋圆极化波
y Ex o Ey
α
x E
左旋圆极化波
(3) 椭圆极化 若 Ex和 Ey 振幅、相位都不相同。则合成波为椭圆极化波。 振幅、相位都不相同。则合成波为椭圆极化波。
E x = E xm cos(ωt − kz + φ x ) ,
E y = E ym cos(ωt − kz + φ y )
Ey = Eym cos(ωt − kz + φy ) 电磁波的极化状态取决于E 电磁波的极化状态取决于 x和Ey的振幅之间和相位之间的关 分为:线极化、圆极化、椭圆极化。 系,分为:线极化、圆极化、椭圆极化。
