小波去噪和小波包去噪的对比
小波去噪

di =
������ =0
dt + σ zi (������ = 1, … , ������ − 1)
Hale Waihona Puke 然后将上式的关系进行转换一下: yi = di − di −1 ,y0=d0 这等价于下式非白噪声 yi = xi + σ (zi − zi −1 ) 重建中根据下式按小波分解级别来选择阈值 t j,n = 2 ln ������ ∗ 2σ ������ ∗ 2(������ −������ )/2 (������ = j0 , … , ������)
频域内分辨率高时,时间域内分辨率低;在频率域内分辨率低时,在 时间域内分辨率高,有自动变焦的功能) ,因此它能有效区分信号中 的突变部分和噪声,从而实现信号的去噪。 运用小波分析进行去噪处理一般有三种方法, 第一种为强制去噪 处理,即把小波分解结构中的高频系数全部变为 0,即把高频部分全 部滤除掉,然后再对信号进行重构处理。该法比较简单,重构后的信 号也比较平滑,但容易丢失信号的有用成分。另外还有默认阈值去噪 处理和给定阈值去噪处理。图 12.2 为利用以上三种方法对污染信号 进行去噪处理的波形图。从图中可以看出,应用强制去噪处理后的信 号比较光滑,但它很有可能丢失了信号中的一些有用成分;默认阈值 去噪和给定阈值去噪这两种方法在实际中应用得更为广泛一些。 小波去噪 1、 小波去噪原理 在去噪领域,利用小波变换进行去噪以及重构是一个热门课题。 小波去噪取得成功的主要原因如下: (1)低熵性。小波系数的稀疏分 布,使图像变换后的熵降低。 (2)多分辨性。由于采用多分辨率的方 法,所以它能非常好的刻画信号的非平稳特征,如断点、边缘等,可 在不同分辨率下根据信号和噪声分布的特点去噪。 (3)选择基底的灵 活性。小波变换可灵活悬着不同的小波基,如单小波,多小波,小波 包等。下面简要说明其去噪的基本原理,我们重点讨论一维信号的情 况,对于二维图像信号也同样适用。 小波变换是线性的,先分析小波如何去除加性噪声。
小波去噪和小波包去噪的对比

小波去噪和小波包去噪的对比问题 1:试生成一个含噪声信号,利用 matlab 中的小波去噪和小波 包去噪函数去除噪声,比较两者的性能差异程序如下:clcclear all load noisdopp x=noisdopp; subplot(311) plot(x);title(' 原始信号的波形图 ') axis tight;[thr,sorh,keepapp]=ddencmp('den','wv',x); xwd=wden(x,'rigrsure','s','one',4,'sym4'); subplot(312) plot(xwd) title(' 小波降噪信号 ') axis tight [thr1,sorh1,keepapp1,crit]=ddencmp('den','wp',x); xwpd=wpdencmp(x,'h',4,'sym4','sure',thr1,1);subplot(313) plot(xwpd) title(' 小波包降噪信号 ') axis tight 运行结果如下:区别:小波变换在低信噪比情况下的去噪效果较好,小波包分解去噪后信号更 加的平滑;小波分解主要是针对细节成分全置 0 或者给定软(硬)阈值去噪, 容易丢失信号中的有用信息。
问题 2:研究小波包分解树中各节点的重构系数,给出其频谱分布, 讨论波包分解的频带划分程序如下:clcclear allload noisdopp; s=noisdopp;wpt=wpdec(s,3,'sym1');100 200300400 500 600 700小波降噪信号800900 1000100 200 300 400 500 600 700 800 900 10005 0 -5原始信号的波形图5 0 -5小波包降噪信号plot(wpt);r20=wprcoef(wpt,[2 0]);subplot(621)plot(r20)title('r20')subplot(623)hua_fft(r20,10000,1)title('r20 的FFT')r21=wprcoef(wpt,[2 1]);subplot(622)plot(r21)title('r21')subplot(624) hua_fft(r21,10000,1) title('r21 的FFT') r22=wprcoef(wpt,[2 2]); subplot(625)plot(r22)title('r22')subplot(627) hua_fft(r22,10000,1) title('r22 的FFT') r23=wprcoef(wpt,[2 3]); subplot(626)plot(r23)title('r23')subplot(628) hua_fft(r23,10000,1) title('r23 的FFT') r10=wprcoef(wpt,[1 0]); subplot(629)plot(r10)title('r10')subplot(6,2,11)hua_fft(r10,10000,1) title('r10 的FFT') r11=wprcoef(wpt,[1 1]); subplot(6,2,10) plot(r11) title('r11') subplot(6,2,12) hua_fft(r11,10000,1) title('r11 的FFT') 程序运行结果如下:10 8 6 4 2 0 -2 -4 -6 -8 -10Tree Decomposition data for node: (0) or (0,0).200 400 600 800 1000问题 3:生成最优树结构,给出其熵值程序如下:clc clear all load noisdopp; x=noisdopp; wpt=wpdec(x,3,'sym4'); wpt=wpsplt(wpt,[3 0]); plot(wpt) bt=besttree(wpt); plot(bt) ent=read(wpt,'ent',allnodes(wpt)) T=entrupd(bt,'shannon'); ent=read(wpt,'ent',allnodes(bt))10 8 6 4 2 0 -2 -4 -6-8 -10图 1 小波包树10 8 6 4 2 0-2 -4 -6 -8-10图2 最优小波包树Tree Decompositiondata for node: 0 or (0,0).200 400 600 800 1000Tree Decompositiondata for node: (0) or (0,0).200 400 600 800 1000表1 小波包树中各节点的熵值表最优小波包树中各节点的熵值。
小波图像去噪及matlab分析
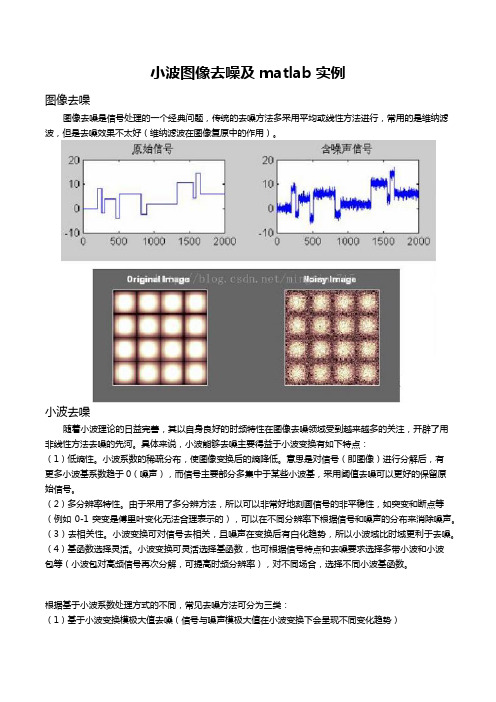
小波图像去噪及matlab实例图像去噪图像去噪是信号处理的一个经典问题,传统的去噪方法多采用平均或线性方法进行,常用的是维纳滤波,但是去噪效果不太好(维纳滤波在图像复原中的作用)。
小波去噪随着小波理论的日益完善,其以自身良好的时频特性在图像去噪领域受到越来越多的关注,开辟了用非线性方法去噪的先河。
具体来说,小波能够去噪主要得益于小波变换有如下特点:(1)低熵性。
小波系数的稀疏分布,使图像变换后的熵降低。
意思是对信号(即图像)进行分解后,有更多小波基系数趋于0(噪声),而信号主要部分多集中于某些小波基,采用阈值去噪可以更好的保留原始信号。
(2)多分辨率特性。
由于采用了多分辨方法,所以可以非常好地刻画信号的非平稳性,如突变和断点等(例如0-1突变是傅里叶变化无法合理表示的),可以在不同分辨率下根据信号和噪声的分布来消除噪声。
(3)去相关性。
小波变换可对信号去相关,且噪声在变换后有白化趋势,所以小波域比时域更利于去噪。
(4)基函数选择灵活。
小波变换可灵活选择基函数,也可根据信号特点和去噪要求选择多带小波和小波包等(小波包对高频信号再次分解,可提高时频分辨率),对不同场合,选择不同小波基函数。
根据基于小波系数处理方式的不同,常见去噪方法可分为三类:(1)基于小波变换模极大值去噪(信号与噪声模极大值在小波变换下会呈现不同变化趋势)(2)基于相邻尺度小波系数相关性去噪(噪声在小波变换的各尺度间无明显相关性,信号则相反)(3)基于小波变换阈值去噪小波阈值去噪是一种简单而实用的方法,应用广泛,因此重点介绍。
阈值函数选择阈值处理函数分为软阈值和硬阈值,设w是小波系数的大小,wλ是施加阈值后小波系数大小,λ为阈值。
(1)硬阈值当小波系数的绝对值小于给定阈值时,令其为0,而大于阈值时,保持其不变,即:(2)软阈值当小波系数的绝对值小于给定阈值时,令其为0,大于阈值时,令其都减去阈值,即:如下图,分别是原始信号,硬阈值处理结果,软阈值处理结果。
如何使用小波变换进行信号去噪处理

如何使用小波变换进行信号去噪处理信号去噪是信号处理领域中的一个重要问题,而小波变换是一种常用的信号去噪方法。
本文将介绍小波变换的原理和应用,以及如何使用小波变换进行信号去噪处理。
一、小波变换的原理小波变换是一种时频分析方法,它可以将信号分解成不同频率和时间尺度的成分。
与傅里叶变换相比,小波变换具有更好的时域分辨率和频域分辨率。
小波变换的基本思想是通过选择不同的小波函数,将信号分解成不同尺度的波形,并通过对这些波形的加权叠加来重构信号。
二、小波变换的应用小波变换在信号处理中有着广泛的应用,其中之一就是信号去噪处理。
信号中的噪声会影响信号的质量和准确性,因此去除噪声是信号处理的重要任务之一。
小波变换可以通过将信号分解为不同尺度的波形,利用小波系数的特性来区分信号和噪声,并通过滤波的方式去除噪声。
三、小波变换的步骤使用小波变换进行信号去噪处理的一般步骤如下:1. 选择合适的小波函数:不同的小波函数适用于不同类型的信号。
选择合适的小波函数可以提高去噪效果。
2. 对信号进行小波分解:将信号分解成不同尺度的小波系数。
3. 去除噪声:通过对小波系数进行阈值处理,将小于一定阈值的小波系数置零,从而去除噪声成分。
4. 重构信号:将去噪后的小波系数进行逆变换,得到去噪后的信号。
四、小波阈值去噪方法小波阈值去噪是小波变换中常用的去噪方法之一。
它的基本思想是通过设置一个阈值,将小于该阈值的小波系数置零,从而去除噪声。
常用的阈值去噪方法有软阈值和硬阈值。
软阈值将小于阈值的小波系数按照一定比例进行缩小,而硬阈值将小于阈值的小波系数直接置零。
软阈值可以更好地保留信号的平滑性,而硬阈值可以更好地保留信号的尖锐性。
五、小波变换的优缺点小波变换作为一种信号处理方法,具有以下优点:1. 可以提供更好的时域分辨率和频域分辨率,能够更准确地描述信号的时频特性。
2. 可以通过选择不同的小波函数适用于不同类型的信号,提高去噪效果。
3. 可以通过调整阈值的大小来控制去噪的程度,灵活性较高。
小波理论及小波滤波去噪方法

要点二
详细描述
小波硬阈值去噪法是小波阈值去噪法的一种,通过对小波 系数应用硬阈值函数进行处理,能够有效地去除噪声。硬 阈值函数的特点是在阈值处将小波系数分为两部分,保留 大于阈值的系数,置小于阈值的系数为零,具有简单易行 的优点。然而,硬阈值函数在处理过程中存在不连续性, 可能会引入新的噪声或信号失真。
通过软阈值函数处理小波系数,实现去噪的小波去噪方法。
详细描述
小波软阈值去噪法是在小波阈值去噪法的基础上发展而来的,通过对小波系数应用软阈值函数进行处理,能够更 好地保留信号的细节信息,提高去噪效果。软阈值函数的特点是在阈值处平滑过渡,避免了硬阈值函数的不连续 性。
小波硬阈值去噪法
要点一
总结词
通过硬阈值函数处理小波系数,实现去噪的小波去噪方法 。
03
小波滤波去噪的优缺点
优点
多尺度分析
小波变换能够同时提供信号在 时间和频率域的信息,允许在
多个尺度上分析信号。
去噪效果好
小波变换具有很好的局部化特 性,能够有效地将信号和噪声 在不同尺度上分离,从而实现 去噪。
自适应性
小波变换能够根据信号的特性 自适应地选择合适的小波基和 分解尺度,以更好地适应信号 的特性。
小波理论及小波滤波去噪 方法
• 小波理论概述 • 小波滤波去噪方法 • 小波滤波去噪的优缺点 • 小波滤波去噪的改进方法 • 小波滤波去噪的实例分析
01
小波理论概述
小波的定义与特性
小波是一种特殊的函数,具有局部性和波动性, 能够在时间和频率两个维度上进行分析。
小波具有可伸缩性,能够适应不同的频率分析需 求。
实例一:图像去噪
总结词
图像去噪是小波滤波去噪方法的重要应用之一,通过小波变换对图像进行多尺度分析, 有效去除噪声,提高图像质量。
小波变换去噪基础知识整理

1.小波变换的概念小波(Wavelet)这一术语,顾名思义,“小波”就是小的波形。
所谓“小”是指它具有衰减性;而称之为“波”则是指它的波动性,其振幅正负相间的震荡形式。
与Fourier变换相比,小波变换是时间(空间)频率的局部化分析,它通过伸缩平移运算对信号(函数)逐步进行多尺度细化,最终达到高频处时间细分,低频处频率细分,能自动适应时频信号分析的要求,从而可聚焦到信号的任意细节,解决了Fourier变换的困难问题,成为继Fourier变换以来在科学方法上的重大突破。
有人把小波变换称为“数学显微镜”。
2.小波有哪几种形式?常用的有哪几种?具体用哪种,为什么?有几种定义小波(或者小波族)的方法:缩放滤波器:小波完全通过缩放滤波器g——一个低通有限脉冲响应(FIR)长度为2N和为1的滤波器——来定义。
在双正交小波的情况,分解和重建的滤波器分别定义。
高通滤波器的分析作为低通的QMF来计算,而重建滤波器为分解的时间反转。
例如Daubechies和Symlet 小波。
缩放函数:小波由时域中的小波函数(即母小波)和缩放函数(也称为父小波)来定义。
小波函数实际上是带通滤波器,每一级缩放将带宽减半。
这产生了一个问题,如果要覆盖整个谱需要无穷多的级。
缩放函数滤掉变换的最低级并保证整个谱被覆盖到。
对于有紧支撑的小波,可以视为有限长,并等价于缩放滤波器g。
例如Meyer小波。
小波函数:小波只有时域表示,作为小波函数。
例如墨西哥帽小波。
3.小波变换分类小波变换分成两个大类:离散小波变换(DWT) 和连续小波转换(CWT)。
两者的主要区别在于,连续变换在所有可能的缩放和平移上操作,而离散变换采用所有缩放和平移值的特定子集。
DWT用于信号编码而CWT用于信号分析。
所以,DWT通常用于工程和计算机科学而CWT经常用于科学研究。
4.小波变换的优点从图像处理的角度看,小波变换存在以下几个优点:(1)小波分解可以覆盖整个频域(提供了一个数学上完备的描述)(2)小波变换通过选取合适的滤波器,可以极大的减小或去除所提取得不同特征之间的相关性(3)小波变换具有“变焦”特性,在低频段可用高频率分辨率和低时间分辨率(宽分析窗口),在高频段,可用低频率分辨率和高时间分辨率(窄分析窗口)(4)小波变换实现上有快速算法(Mallat小波分解算法)另:1) 低熵性变化后的熵很低;2) 多分辨率特性边缘、尖峰、断点等;方法, 所以可以很好地刻画信号的非平稳特性3) 去相关性域更利于去噪;4) 选基灵活性: 由于小波变换可以灵活选择基底, 也可以根据信号特性和去噪要求选择多带小波、小波包、平移不变小波等。
基于小波变换的脉搏信号去噪方法研究

基于小波变换的脉搏信号去噪方法研究下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!基于小波变换的脉搏信号去噪方法研究1. 引言脉搏信号作为医学诊断中重要的生理信号之一,其精确的提取和分析对于诊断疾病具有重要意义。
小波变换的硬阈值与软阈值去噪技术比较

小波变换的硬阈值与软阈值去噪技术比较引言在数字信号处理领域,噪声是一个常见的问题,它会影响到信号的质量和可靠性。
因此,信号去噪技术一直是研究的热点之一。
小波变换是一种常用的信号分析工具,它在去噪领域有着广泛的应用。
其中,硬阈值和软阈值是两种常用的小波去噪方法。
本文将对这两种方法进行比较,并分析其优缺点。
1. 硬阈值去噪技术硬阈值去噪技术是一种基于小波变换的去噪方法。
其基本思想是将小波变换系数与一个给定的阈值进行比较,如果小波系数的绝对值小于阈值,则将其置为零,否则保留原值。
这种方法能够有效地去除信号中的噪声,但同时也会对信号的细节部分造成一定的损失。
硬阈值去噪技术的优点是简单易实现,计算速度快,适用于噪声较强的信号。
然而,由于其对信号细节的损失,可能会导致信号失真。
2. 软阈值去噪技术软阈值去噪技术是另一种基于小波变换的去噪方法。
与硬阈值不同的是,软阈值对小波系数的处理方式是将小波系数的绝对值减去一个给定的阈值,并保留正值。
这种方法能够更好地保留信号的细节信息,减少信号的失真。
软阈值去噪技术的优点是能够提供更好的去噪效果,适用于噪声较弱的信号。
然而,软阈值去噪技术的计算复杂度较高,需要更多的计算资源。
3. 硬阈值与软阈值的比较硬阈值和软阈值是两种常用的小波去噪方法,它们各有优缺点。
硬阈值去噪技术适用于噪声较强的信号,能够快速去除噪声,但可能会对信号的细节造成一定的损失。
软阈值去噪技术适用于噪声较弱的信号,能够更好地保留信号的细节信息,但计算复杂度较高。
因此,在选择使用哪种方法时,需要根据具体的应用场景和信号特点进行权衡。
4. 应用案例为了更好地说明硬阈值和软阈值的应用,我们以图像去噪为例进行分析。
在图像处理中,噪声往往会导致图像的模糊和失真。
通过对图像进行小波变换,并应用硬阈值或软阈值去噪技术,可以有效地去除图像中的噪声,并保留图像的细节信息。
在实际应用中,可以根据图像的噪声水平和需要保留的细节信息来选择合适的去噪方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
