初中数学练习题拔尖习题
部编数学八年级下册二次根式专项提升训练(重难点培优)【拔尖特训】2023年培优【人教版】含答案

【拔尖特训】2022-2023学年八年级数学下册尖子生培优必刷题【人教版】专题16.1专项提升训练(重难点培优)班级:___________________ 姓名:_________________ 得分:_______________注意事项:本试卷满分120分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2022秋•南湖区校级期中)要使二次根式有意义,x的值可以是( )A.4B.2C.1D.0【分析】根据二次根式有意义的条件可得x﹣3≥0,再解即可.【解答】解:要使二次根式有意义,则x﹣3≥0,解得:x≥3,故x的值可以是4.故选:A.2.(2022秋•北碚区校级期中)要使式子有意义,则a的取值范围是( )A.a≠0B.a≥﹣2C.a>﹣2且a≠0D.a≥﹣2且a≠0【分析】根据分子的被开方数不能为负数,分母不能为零,可得答案.【解答】解:由题意得,a+2≥0且a≠0,即a≥﹣2且a≠0,故选:D.3.(2022秋•惠山区期中)下列各式中,一定是二次根式的是( )A.B.C.D.【分析】根据二次根式的定义进行判断.【解答】解:A.被开方数为负数,不是二次根式,故此选项不合题意;B.根指数是3,不是二次根式,故此选项不合题意;C.a﹣1的值不确定,被开方数的符号也不确定,不能确定是二次根式,故此选项不合题意;D.被开方数恒为正数,是二次根式,故此选项符合题意.4.(2022秋•奉贤区期中)使二次根式有意义的x的取值范围是( )A.B.C.D.【分析】根据二次根式的被开方数是非负数、分母不为0列出不等式,解不等式得到答案.【解答】解:由题意得:2x﹣1>0,解得:x>,故选:B.5.(2022秋•南湖区校级期中)已知y=++4,y x的平方根是( )A.16B.8C.±4D.±2【分析】根据二次根式有意义的条件可得,据此可得x的值,进而得出y的值,再代入所求式子计算即可.【解答】解:∵y=++4,∴,解得x=2,∴y=4,∴y x=42=16.∴y x的平方根是±4.故选:C.6.(2022秋•通州区期中)已知n是一个正整数,且是整数,那么n的最小值是( )A.6B.36C.3D.2【分析】先把=2,从而判断出6n是完全平方数,所以得出答案正整数n的最小值是6.【解答】解:=2,则6n是完全平方数,∴正整数n的最小值是6,故选:A.7.(2022秋•新蔡县校级月考)已知x、y为实数,且y=+1,则x+y的值是( )A.2022B.2023C.2024D.2025【分析】根据二次根式有意义的条件:被开方数是非负数求出x的值,代入求得y的值,代入代数式求【解答】解:∵x﹣2023≥0,2023﹣x≥0,∴x﹣2023=0,∴x=2023,∴y=1,∴x+y=2023+1=2024,故选:C.8.(2022春•东平县期中)已知a满足|2018﹣a|+=a,则a﹣20182=( )A.0B.1C.2018D.2019【分析】根据二次根式的被开方数是非负数求出a的取值范围,化简绝对值即可得出答案.【解答】解:根据题意得:a﹣2019≥0,∴a≥2019,∴原式可变形为:a﹣2018+=a,∴=2018,∴a﹣2019=20182,∴a﹣20182=2019.故选:D.9.已知a为实数,若在实数范围内有意义,那么等于( )A.a B.﹣a C.﹣1D.0【分析】根据非负数的性质与被开方数大于等于0列式计算即可得解.【解答】解:根据非负数的性质a2≥0,所以,﹣a2≤0,又∵﹣a2≥0,∴﹣a2=0,∴=0.故选:D.10.(2022春•荣昌区校级期末)若二次根式有意义,且关于分式方程﹣3=有正整数解,则符合条件的整数m的和是( )A.5B.3C.﹣2D.0【分析】根据二次根式有意义,可得m≤4,解出关于x的分式方程﹣3=的解为x=,解为正整数解,进而确定m的取值范围,注意增根时m的值除外,再根据m为整数,确定m的所有可能的整数值,求和即可.【解答】解:去分母得,2﹣3(x﹣1)=﹣m,解得x=,∵关于x的分式方程﹣3=有正整数解,∴>0,∴m>﹣5,又∵x=1是增根,当x=1时,=1,即m=﹣2∴m≠﹣2,∵有意义,∴4﹣m≥0,∴m≤4,因此﹣5<m≤4且m≠﹣2,∵m为整数且关于x的分式方程﹣3=有正整数解,∴m可以为1,4,其和为5.故选:A.二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上11.(2022秋•南安市期中)若二次根式在实数范围内有意义,则x的取值范围是 x≤4 .【分析】根据二次根式的被开方数是非负数列出不等式,解不等式得到答案.【解答】解:由题意得:12﹣3x≥0,解得x≤4,故答案为:x≤4.12.(2022秋•罗湖区校级期中)若在实数范围内有意义,则x的取值范围是 x<4 .【分析】根据二次根式有意义的条件和分母不为0,即可求出x的取值范围.【解答】解:根据题意得:4﹣x>0,故答案为:x<4.13.(2022秋•海曙区校级期中)若,则x y= .【分析】直接利用二次根式有意义的条件得出x,y的值,进而代入得出答案.【解答】解:∵,∴2x﹣3≥0且3﹣2x≥0,解得:x=,则y=2,则x y=()2=.故答案为:.14.(2022秋•卧龙区校级月考)若y=+﹣3,则点P(x,y)在第 四 象限.【分析】根据二次根式的被开方数是非负数,求出x的值,进而得到y的值,再根据点的坐标特征解答即可.【解答】解:根据题意,得x﹣4≥0且4﹣x≥0,.所以x=4.所以y=﹣3.所以P(4,﹣3),位于第四象限.故答案为:四.15.(2022春•东莞市校级期中)若是整数,则满足条件的最小正整数n的值为 6 .【分析】24=22×6,所以要想能开平方,必须再乘一个6.【解答】解:=2,∵是整数,∴满足条件的最小正整数n=6.故答案为:6.16.(2022春•东平县期中)已知y=++2022,则x2+y﹣3的值为 2023 .【分析】根据二次根式有意义的条件得到x2=4,进而求出y的值,代入代数式求值即可.【解答】解:根据题意得:x2﹣4≥0,4﹣x2≥0,∴y=2022,∴原式=4+2022﹣3=2023.故答案为:2023.17.(2022•沙坪坝区校级开学)已知a,b分别为等腰三角形的两条边长,且a,b满足,则该三角形的周长为 10 .【分析】根据题意求出a、b的值,根据等腰三角形的三边关系确定三角形的边长,求出此三角形的周长.【解答】解:由题意得,a﹣2≥0,2﹣a≥0,解得a≥2,a≤2,∴a=2,则b=4,∵2+2=4,∴2、2、4不能组成三角形,∴该三角形的三边分别为2、4、4,∴此三角形的周长为2+4+4=10.18.(2021春•南通期中)实数a、b在数轴上对应点的位置如图所示,,b为整数,则a+b= ﹣2 .【分析】通过识图可得a<b<,从而利用二次根式的性质进行化简.【解答】解:∵a<b<,∵|b﹣2|=b﹣2,∵a+4≥0,b﹣2≥0,∴b≥2,∵b<,∴2≤b<,b为整数,∴b=2,将b=2代入|b﹣2|=b﹣2,∴a+b=﹣4+2=﹣2,故答案为:﹣2.三、解答题(本大题共6小题,共66分.解答时应写出文字说明、证明过程或演算步骤)19.(2021春•新泰市期中)(1)已知2a﹣1的平方根是±3,3a+b﹣1的平方根是±4,求a+2b的平方根;(2)若x,y都是实数,且y=+8,求x+3y的立方根.【分析】(1)根据平方根的定义求出a、b的值,然后代入a+2b即可求出答案.(2)根据二次根式有意义的条件可求出x与y的值,然后代入原式即可求出答案.【解答】解:(1)由题意可知:2a﹣1=9,3a+b﹣1=16,∴a=5,b=2,∴a+2b=5+4=9,∴9的平方根是±3,即a+2b的平方根为±3.(2)由题意可知:,∴x=3,∴y=8,∴x+3y=3+24=27,∴27的立方根是3,即x+3y的立方根是320.(2019秋•松北区期末)已知a,b分别为等腰三角形的两条边长,且a,b满足b=4++3,求此三角形的周长.【分析】根据题意求出a、b的值,根据三角形的三边关系确定三角形的边长,求出此三角形的周长.【解答】解:由题意得,3a﹣6≥0,2﹣a≥0,解得,a≥2,a≤2,则a=2,则b=4,∵2+2=4,∴2、2、4不能组成三角形,∴此三角形的周长为2+4+4=10.21.(2022秋•济南期中)已知实数a,b,c满足:.(1)a= ﹣3 ;b= 5 ;c= 2 ;(2)求﹣b﹣3a+2c的平方根.【分析】(1)根据二次根式有意义的条件求得b=5,再根据绝对值以及算术平方根的非负性求得a与c.(2)将(1)中a、b与c的值代入,再求得﹣b﹣3a+2c的平方根.【解答】解:(1)由题意得,b﹣5≥0,5﹣b≥0.∴b=5.∴|a+3|+=0.∵|a+3|≥0,,∴a+3=0,c﹣2=0.∴a=﹣3,c=2.故答案为:﹣3;5;2.(2)由(1)得,a=﹣3,b=5,c=2.∴﹣b﹣3a+2c=﹣5+9+4=8.∴﹣b﹣3a+2c的平方根是±=.22.(2022秋•锦江区校级月考)(1)若m﹣2=+,求n m的值;(2)已知有理数a,b,c在数轴上对应位置如图所示:①用“<”或“>”填空:a+c < 0,b﹣c > 0;②化简:|a+c|﹣+.【分析】(1)利用二次根式有意义的条件得到n﹣3≥0且3﹣n≥0,则n=3,所以m﹣2=0,则m=2,然后利用乘方的意义计算n m;(2)①利用数轴表示数的方法进行判断;②根据二次根式的性质和立方根的定义得到原式|=|a+c|﹣|b﹣c|+b+c,再利用①中的结论去绝对值,然后取括号合并即可.【解答】解:(1)根据题意得n﹣3≥0且3﹣n≥0,解得n=3,∴m﹣2=0,解得m=2,∴n m=32=9;(2)①a+c<0,b﹣c>0;故答案为:<,>;②|a+c|﹣+=|a+c|﹣|b﹣c|+b+c=﹣(a+c)﹣(b﹣c)+b+c=﹣a﹣c﹣b+c+b+c=﹣a+c.23.(2022春•定远县期末)在学习了算术平方根和二次根式等内容后,我们知道以下的结论:结论①:若实数a≥0时,=a;结论②:对于任意实数a,=|a|.请根据上面的结论,对下列问题进行探索:(1)若m<2,化简:+|m﹣3|.(2)若=4,|b|=8,且ab>0,求a+b的值.(3)若A=+|1﹣m|有意义,化简A.【分析】(1)先根据二次根式的性质和绝对值进行计算,再算加减即可;(2)先根据二次根式的性质和绝对值求出a、b的值,再求出a+b的值即可;(3)根据二次根式的性质得出m﹣2≥0,求出m≥2,再进行化简即可.【解答】解:(1)分为两种情况:①当m≤﹣3时,+|m﹣3|.=|m+3|+|m﹣3|=﹣m﹣3﹣m+3=﹣2m,②当﹣3<m<2时,+|m﹣3|=|m+3|+|m﹣3|=m+3+3﹣m=6;(2)∵,∴|a|=4,∴a=±4,∵|b|=8,∴b=±8,∵ab>0,∴a=4,b=8或a=﹣4,b=﹣8,当a=4,b=8时,则a+b=4+8=12,当a=﹣4,b=﹣8时,则a+b=﹣4﹣8=﹣12,∴a+b=±12;(3)∵有意义,∴m﹣2≥0,∴m≥2,∴1﹣m<0,∴A=m﹣2+m﹣1=2m﹣3.24.(2022春•天门校级月考)二次根式的双重非负性是指被开方数a≥0,其化简的结果≥0,利用的双重非负性解决以下问题:(1)已知=0,则a+b的值为 ﹣2 ;(2)若x,y为实数,且x2=+9,求x+y的值;(3)已知实数m,n(n≠0)满足|2m﹣4|+|n+2|++4=2m,求m+n的值.【分析】(1)利用非负数的性质,可求a,b的值,从而求得a+b的值为﹣2;(2)利用二次根式有意义的条件,可得y值,进而求x值,最终得x+y的值;(3)是上两个题目的综合运用,利用(1)(2)可出得m+n的值.【解答】解:(1)∵,且,∴a﹣1=0,且3+b=0,∴a=1,b=﹣3,∴a+b=﹣2.(2)∵,∴y﹣5≥0且5﹣y≥0,∴y≥5且y≤5,∴y=5,∴x2=9,∴x=±3,当x=3时,x+y=3+5=8;当x=﹣3时,x+y=﹣3+5=2.(3)∵|2m﹣4|+|n+2|++4=2m,∴(m﹣3)n2≥0,∴m≥3,∴2m﹣4>0,∴|2m﹣4|+|n+2|++4=2m2m﹣4+|n+2|++4=2m∴|n+2|+=0,∵|n+2|≥0,≥0,∴n+2=0,(m﹣3)n2=0,∴n=﹣2,m=3,∴m+n=3﹣2=1.。
浙教版数学八年级下册八下第五章 特殊平行四边形 拔尖训练(含答案)
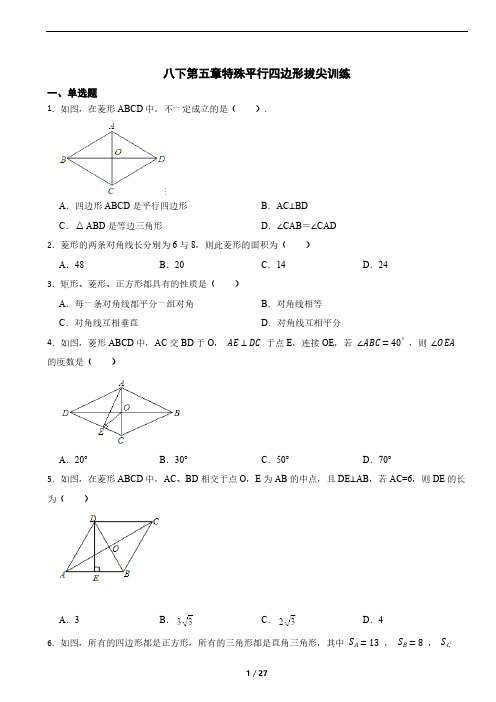
八下第五章特殊平行四边形拔尖训练一、单选题1.如图,在菱形ABCD中,不一定成立的是( ).A.四边形ABCD是平行四边形B.AC⊥BDC.△ABD是等边三角形D.∠CAB=∠CAD2.菱形的两条对角线长分别为6与8,则此菱形的面积为( )A.48B.20C.14D.243.矩形、菱形、正方形都具有的性质是( )A.每一条对角线都平分一组对角B.对角线相等C.对角线互相垂直D.对角线互相平分4.如图,菱形ABCD中,AC交BD于O,AE⊥DC于点E,连接OE,若∠ABC=40°,则∠OEA 的度数是( )A.20°B.30°C.50°D.70°5.如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,若AC=6,则DE的长为( )A.3B.C.D.46.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中S A=13,S B=8,S C=10,S D=5,则S=( )A.25B.36C.32D.407.如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )A.23B.43C.4D.68.如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( ).A.8B.3C.4D.329.如图,P是正方形ABCD的对角线BD上任意一点,PE⊥AB于点E,PF⊥AD于点F,连接EF.有下列结论:①CP=EF;②CP⊥EF;③△CPD一定是等腰三角形;④∠PFE=∠BCP;⑤PD=2AE.其中,正确结论的序号是( )A.①②③④B.②③④⑤C.①②④⑤D.①③④⑤10.如图,正方形ABCD的边长为2cm,正方形CEFG的边长为1cm,若正方形CEFG绕点C旋转,则点F 到点A的距离最小值为( )A.3B.22C.32D.2二、填空题11.菱形定义:一组 相等的平行四边形叫菱形.12.如图,矩形ABCD中,AB=4,AD=6.在边AD上取一点E,使BE=BC,过点C作CF⊥BE,垂足为点F,则BF的长为 .13.如图是一幅赵爽弦图,利用此图可以证明勾股定理.现连接BE,发现AB=BE,若DE=1,则正方形ABCD的面积为 .14.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则△AEF的周长= cm.15.如图,大正方形ABCD中,AB=3,小正方形AEFG中,AE=3,在小正方形绕A点旋转的过程中,当C,F,G三点共线时,线段CF的长为 .16.如图,在边长为2的正方形ABCD中,点E,F分别为AD,CD边上的动点(不与端点重合),连接BE,BF,分别交对角线AC于点P,Q.点E,F在运动过程中,始终保持∠EBF=45°,连接EF,PF,PD.下列结论:①PB=PD;②∠EFD=2∠FBC;③PQ=PA+CQ;④△BPF为等腰直角三角形;⑤若过点B作BH⊥EF,垂足为H,连接DH,则DH的最小值为22−2,其中所有正确结论的序号是 .三、作图题17.图1,图2,图3,图4是四张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,A,C两点都在格点上,连结AC,请完成下列作图:(1)以AC为对角线在图1中作一个正方形,且正方形各顶点均在格点上.(2)以AC为对角线在图2中作一个矩形,使得矩形面积为6,且矩形各顶点均在格点上.(3)以AC为对角线在图3和图4中分别作出一个面积为8的平行四边形(不含矩形),且平行四边形顶点在格点上.四、综合题18.如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.(1)求∠2、∠3的度数;(2)求长方形纸片ABCD的面积S.19.如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.(1)求证:AE=DF;(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.20.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E、F.(1)求证:四边形AECF是菱形;(2)当BE=3,AF=5时,求AC的长.21.如图,AC是平行四边形ABCD的对角线,∠BAC=∠DAC.(1)求证:AB=BC;(2)若AB=4,AC=4 3,求平行四边形ABCD的面积.22.如图,在菱形ABCD中,AB=10,S菱形ABCD=60,点E从点B出发在边BC上向终点C运动.过点E作边BC的垂线,交菱形其它的边于点F,在EF的右侧作矩形EFGH.(1)如图1,点G在AC上.①求证:FA=FG;②若点G是AC的中点,求证:BF=FG;(2)若EF=FG,当EF过AC中点时,求AG的长.23.已知:在边长为4的正方形ABCD中,点P为对角线BD上一点,且BP=32.将三角板的直角顶点与点P重合,一条直角边与直线BC交于点E,另一条直角边与射线BA交于点F(点F 不与点B重合),将三角板绕点P旋转.(1)如图,当点E、F在线段BC、AB上时,求证:PE=PF;(2)当∠FPB=30°时,求△BEP的面积;(3)当△BEP为等腰三角形时,求线段BF的长.五、实践探究题24.如图,点E为正方形ABCD内一动点,∠AEB=90°.过点B作BG⊥BE,且BG=BE,连接CG,DE.(1)求证:∠EAB=∠GCB;(2)延长AE交CG于点F,求证:EF=BE;(3)在(2)的条件下,若点E在运动过程中,存在四边形CFBE为平行四边形,试探究此时DE、CD满足的数量关系.答案解析部分1.【答案】C【解析】【解答】菱形是特殊的平行四边形,故A正确,根据菱形的性质:对角线互相平分且平分对角得B、D正确,所以选C.【分析】此题主要考查菱形的基本性质:菱形的对角线互相垂直平分,且每一条对角线平分一组对角;以及和平行四边形的联系.2.【答案】D【解析】【解答】6×8÷2=24故答案为:D.【分析】根据S菱形等于两对角线乘积的一半可求解.3.【答案】D【解析】【解答】解:矩形、菱形、正方形都具有的性质是:对角线互相平分,故答案为:D.【分析】根据矩形、菱形、正方形的性质判断求解即可。
初二数学拔高练习题推荐

初二数学拔高练习题推荐数学作为一门基础学科,对于中学生的学习非常重要。
通过不断的练习和提高,可以帮助学生更好地理解和掌握数学知识。
在初二阶段,为了能够更好地拔高自己的数学水平,以下是一些数学拔高练习题的推荐。
1. 代数方程练习题1.1 解方程:求解2x + 5 = 17的解。
1.2 模型应用:某图书馆现有图书n本,已借出了8本,还剩下的图书比已借出的图书的3倍多5本,请问图书馆共有多少本图书?1.3 字母代数:如果ab = 12,且a + b = 7,求a和b的值。
2. 几何运算练习题2.1 曲线长度:计算抛物线y = x^2在区间[0, 2]上的弧长。
2.2 三角形相似:已知两个三角形的两角分别相等,另一角对应边的比为3:4,判断这两个三角形是否相似。
3. 概率与统计练习题3.1 概率计算:有5个白球和3个黑球放在一个盒子里,从中随机摸出2个球,求摸出的两个球颜色相同的概率。
3.2 统计分析:在班级的一次数学测验中,40名学生的得分情况如下:60分及以下10人,60-70分15人,70分以上15人,请根据这个数据回答以下问题:- 60分及以下的学生占总人数的百分之几?- 70分以上的学生占总人数的百分之几?- 平均分是多少?4. 数列与函数练习题4.1 等差数列:已知某数列的前四项分别是-5、-2、1、4,请写出该数列的通项公式。
4.2 函数应用:已知函数f(x) = 2x^2 + 3x - 2,请计算f(-1)的值。
5. 实际问题应用练习题5.1 比例问题:某地区有3000名中学生,其中男生占总数的35%,女生占其余的65%,计算男生和女生的人数各是多少。
5.2 利息问题:小明存入银行1000元,年利率为4%,存款时间为3年,请计算存款到期后的总金额。
通过解答以上的练习题,可以帮助初二学生更好地巩固和提高数学知识。
同时,还可以培养学生的思维能力、逻辑思维和问题解决能力。
建议学生在课余时间,结合教材和学校作业,进行这些拔高练习题的练习。
部编数学八年级下册勾股定理专项提升训练(重难点培优)【拔尖特训】2023年培优含答案

【拔尖特训】2022-2023学年八年级数学下册尖子生培优必刷题【人教版】专题17.1勾股定理专项提升训练(重难点培优)班级:___________________ 姓名:_________________ 得分:_______________注意事项:本试卷满分120分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2022春•忻城县期中)在Rt△ABC中,∠C=90°,且AB=10,BC=6,则AC等于( )A.12B.8C.4D.2【分析】由勾股定理可直接得出结果.【解答】解:由勾股定理得:AC==8,故选:B.2.(2022春•黔西南州期末)如图,在△ABC中,∠B=90°,AC=,则AB2+BC2的值是( )A.2B.3C.2D.4【分析】由勾股定理可直接得出结果.【解答】解:由勾股定理得:AB2+BC2=AC2,即AB,故选:A.3.(2022秋•溧水区期中)在△ABC中,∠C=90°,∠A,∠B,∠C的对应边分别是a,b,c,则下列式子成立的是( )A.a2+b2=c2B.a2+c2=b2C.a2﹣b2=c2D.b2+c2=a2【分析】根据勾股定理进行解答即可.【解答】解:∵∠C=90°,∠A,∠B、∠C的对应边分别是a、b、c,∴a2+b2=c2.故选:A.4.(2022秋•西安月考)如图,三个正方形围成一个直角三角形,图中的数据是它们的面积,则正方形A的面积为( )A.72B.64C.60D.54【分析】根据勾股定理和正方形面积的公式直接可得答案.【解答】解:由勾股定理得,图形A的面积为100﹣36=64,故选:B.5.(2022春•合川区校级期中)平面直角坐标系内,点P(1,)到原点的距离是( )A.B.2C.+1D.4【分析】直接利用两点间的距离公式可得答案.【解答】解:由两点间距离公式得,OP=,故选:B.6.(2022春•中宁县期末)如图,在△ABC中,AB=AC=4,∠B=15°,CD是腰AB上的高,则CD的长( )A.4B.2C.1D.【分析】根据三角形外角的性质得∠DAC=30°,再利用含30°角的直角三角形的性质可得CD的长.【解答】解:∵AB=AC,∠B=15°,∴∠ACB=∠B=15°,∴∠DAC=30°,∵CD是腰AB上的高,∴CD⊥AB,∴CD=AC=2,故选:B.7.(2022春•普陀区校级期末)如图所示,以数轴上的单位长度线段为边作一个正方形,以表示数1的点为圆心、正方形的对角线长为半径画弧,交数轴于点A,则点A表示的数是( )A.﹣B.1﹣C.﹣1+D.﹣1﹣【分析】利用勾股定理求出正方形的对角线长,从而得出答案.【解答】解:∵正方形的边长为1,∴对角线长为=,∴点A表示的数是1﹣,故选:B.8.(2022春•兰山区期末)如图,边长为1的正方形网格图中,点A,B都在格点上,若,则BC 的长为( )A.B.C.D.【分析】根据勾股定理求得AB的长度,然后根据线段的和差即可得到结论.【解答】解:∵AB==2,,∴BC=AB=AC=2﹣=,故选:C.9.(2022秋•高新区校级月考)如图,Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD平分∠CAB,交BC于D,DE⊥AB于E,则CD等于( )A.2cm B.3cm C.4cm D.5cm【分析】首先利用勾股定理求出AB,然后利用角平分线的性质得到CD=DE,在Rt△DEB中,利用勾股定理建立方程求解即可.【解答】解:∵AD是∠CAB的平分线,DE⊥AB,∠C=90°,∴CD=DE,在Rt△ACD和Rt△AED中,,∴Rt△ACD≌Rt△AED(HL),∴AC=AE=6cm,∵AC=6cm,BC=8cm,∴AB==10cm,∴BE=AB﹣AE=10﹣6=4(cm),设DE=xcm,则CD=xcm,BD=(8﹣x)cm,在Rt△DEB中,BD2=DE2+BE2,∴(8﹣x)2=x2+42,∴x=DE=3.故选:B.10.(2022秋•海曙区期中)勾股定理是人类最伟大的科学发现之一,在我国算术《周髀算经》中早有记载.如图以直角三角形纸片的各边分别向外作正三角形纸片,再把较小的两张正三角形纸片按如图的方式放置在最大正三角形纸片内.若已知图中阴影部分的面积,则可知( )A.直角三角形纸片的面积B.最大正三角形纸片的面积C.最大正三角形与直角三角形的纸片面积和D.较小两个正三角形纸片重叠部分的面积【分析】设三个正三角形面积分别为S1,S2,S3,(不妨设S1>S2>S3),由勾股定理和三角形面积可得S1=S2+S3,再由面积和差关系即可求解.【解答】解:如图,设三个正三角形面积分别为S1,S2,S3,(不妨设S1>S2>S3),两个小正三角形的重叠部分的面积为S4,∵△ABC是直角三角形,∠ACB=90°,∴AB2=AC2+BC2,∵S1=AB2,S2=AC2,S3=BC2,∴S2+S3=AC2+BC2=(AC2+BC2)=AB2,∴S1=S2+S3,∴S=S1﹣(S2+S3﹣S4)=S1﹣S2﹣S3+S4=S4,阴影故选:D.二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上11.(2022秋•溧阳市期中)若直角三角形两直角边长分别为9和40,则斜边长为 41 .【分析】利用勾股定理直接计算即可.【解答】解:由勾股定理得,斜边==41.故答案为:41.12.(2022秋•天桥区校级月考)在如图所示的方格纸中,建立直角坐标系,点A表示(3,4),则OA= 5 .【分析】根据勾股定理直接计算即可.【解答】解:由勾股定理得,OA==5,故答案为:5.13.(2022秋•临沭县校级月考)在△ABC中,BC=6,BC边上的高AD=4,且BD=2,则△ACD的面积为 8或16 .【分析】根据题意得出CD的长度,再利用三角形面积公式求出△ACD的面积即可.【解答】解:根据题意,分以下两种情况:①如图:∵BC=6,AD=4,BD=2,∴CD=BC﹣BD=6﹣2=4,=CD•AD==8,∴S△ACD②如图:∵BC=6,AD=4,BD=2,∴CD=BD+BC=8,=CD•AD=8×4=16,∴S△ACD故答案为:8或16.14.(2022春•中山市期末)平面直角坐标系中有两点A(m,﹣1),B(3,4),当m取任意实数时,线段AB长度的最小值为 5 .【分析】根据垂线段最短即可解决问题.【解答】解:∵A(m,﹣1),∴点A在直线y=﹣1上,要使AB最小,根据“垂线段最短”,可知:过B作直线y=﹣1的垂线,垂足为即为A,∴AB最小为5.故答案为:5.15.(2022秋•建邺区校级期中)如图,△ABC中,∠C=90°,AC=4,BC=3,若CH是△ABC的高线,则CH= .【分析】先根据勾股定理求出AB的长,再由三角形的面积公式即可得出结论.【解答】解:∵Rt△ABC中,AC=4,BC=3,∴AB===5.∵CH是△ABC的高线,∴AB•CH=AC•BC,即5CH=4×3,解得CH=.故答案为:.16.(2022秋•秦淮区期中)如图,在Rt△ABC中,∠ACB=90°,AB=4cm,分别以AC,BC为边作正方形,面积分别记为S1,S2,则S1+S2= 16 cm2.【分析】在直角三角形ABC中,利用勾股定理求出AC2+BC2的值,根据S1,S2分别表示正方形面积,求出S1+S2的值即可.【解答】解:在Rt△ABC中,∠ACB=90°,AB=4cm,由勾股定理得:AC2+BC2=AB2=16,则S1+S2=AC2+BC2=16(cm2),故答案为:16.17.(2022秋•云岩区月考)如图,在Rt△ABC中,∠ABC=90°,AC=5,BC=,分别以△ABC的三边为直径画半圆,则两个月形图案(阴影部分)的面积之和是 5 .【分析】由勾股定理得AB2+BC2=AC2,AB=2,设以AB、BC、AC为直径的半圆分别为①、②、③,则S①+S②=S③,而S阴影=S①+S②+S△ABC﹣S③=S△ABC,即可解决问题.【解答】解:∵∠ABC=90°,∴AB2+BC2=AC2,AB===2,设以AB、BC、AC为直径的半圆分别为①、②、③,∴S①=π×()2=AB2,同理:S②=BC2,S③=AC2,∴S①+S②=(AB2+BC2)=AC2=S③,=S①+S②+S△ABC﹣S③=S△ABC=AB•BC=×2×=5,∴S阴影即两个月形图案(阴影部分)的面积之和是5,故答案为:5.18.(2022秋•仁寿县校级月考)如图,已知在Rt△ABC中,∠ACB=90°,AC=8,BC=16,D是AC上的一点,CD=3,点P从B点出发沿射线BC方向以每秒2个单位的速度向右运动.设点P的运动时间为t.过点D作DE⊥AP于点E.在点P的运动过程中,当t为 5或11 时,能使DE=CD?【分析】根据动点运动的不同位置利用勾股定理即可求解.【解答】解:①点P在线段BC上时,过点D作DE⊥AP于E,如图1所示:则∠AED=∠PED=90°,∴∠PED=∠ACB=90°,∴PD平分∠APC,∴∠EPD=∠CPD,又∵PD=PD,∴△PDE≌△PDC(AAS),∴ED=CD=3,PE=PC=16﹣2t,∴AD=AC﹣CD=8﹣3=5,∴AE=4,∴AP=AE+PE=4+16﹣2t=20﹣2t,在Rt△APC中,由勾股定理得:82+(16﹣2t)2=(20﹣2t)2,解得:t=5;②点P在线段BC的延长线上时,过点D作DE⊥AP于E,如图2所示:同①得:△PDE≌△PDC(AAS),∴ED=CD=3,PE=PC=2t﹣16,∴AD=AC﹣CD=8﹣3=5,∴AE=4,∴AP=AE+PE=4+2t﹣16=2t﹣12,在Rt△APC中,由勾股定理得:82+(2t﹣16)2=(2t﹣12)2,解得:t=11.综上所述,在点P的运动过程中,当t的值为5或11时,能使DE=CD.三、解答题(本大题共6小题,共66分.解答时应写出文字说明、证明过程或演算步骤)19.(2022秋•温州期中)如图,在△ABC中,AB=AC,AD平分∠BAC,已知BC=10,AD=12,求AC 的长.【分析】根据等腰三角形的性质和勾股定理即可得到结论.【解答】解:∵AB=AC,AD平分∠BAC,∴AD⊥BC,BD=CD=BC=5,∵AD=12,∴AC===13,故AC的长为13.20.(2022秋•玉林期中)如图,在△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,求线段CD的长.【分析】由于∠C=90°,∠ABC=60°,可以得到∠A=30°,又由BD平分∠ABC,可以推出∠CBD=∠ABD=∠A=30°,BD=AD=6,再利用“30°角所对的直角边等于斜边的一半”即可求出结果.【解答】解:∵∠C=90°,∠ABC=60°,∴∠A=30°,∵BD平分∠ABC,∴∠CBD=∠ABD=∠A=30°,∴BD=AD=6,∴CD=BD=6×=3.故线段CD的长为3.21.(2022秋•碑林区校级期中)在△ABC中,AB=13,BC=14,AC=15,AD为BC边上的高,求AD的长.【分析】由题意知,BD+DC=14,设BD=x,则CD=14﹣x,在直角△ABD中,AB是斜边,根据勾股定理AB2=AD2+BD2,在直角△ACD中,根据勾股定理AC2=AD2+CD2,列出方程组即可计算x的值,即可求得AD的长度.【解答】解:∵BC=14,且BC=BD+DC,设BD=x,则DC=14﹣x,则在直角△ABD中,AB2=AD2+BD2,即132=AD2+x2,在直角△ACD中,AC2=AD2+CD2,即152=AD2+(14﹣x)2,整理计算得x=5,即AD=12.22.(2022秋•苏州期中)如图1,将长为2a+3,宽为2a的矩形分割成四个全等的直角三角形,拼成如图2所示的“赵爽弦图”,得到大小两个正方形.(1)用关于a的代数式表示图2中小正方形的边长;(2)已知图2中小正方形面积为36,求大正方形的面积?【分析】(1)观察图形,用直角三角形较长的直角边减去较短的直角边即可;(2)根据正方形的面积=边长的平方列出代数式,把a=3代入求值即可.【解答】解:(1)∵直角三角形较短的直角边=×2a=a,较长的直角边=2a+3,∴小正方形的边长=2a+3﹣a=a+3;(2)小正方形的面积=(a+3)2=36,∴a=3(负值舍去),∴大正方形的面积=92+32=90.23.(2022春•巢湖市校级期中)学习勾股定理之后,同学们发现证明勾股定理有很多方法.某同学提出了一种证明勾股定理的方法:如图1点B是正方形ACDE边CD上一点,连接AB,得到直角三角形ACB,三边分别为a,b,c,将△ACB裁剪拼接至△AEF位置,如图2所示,该同学用图1、图2的面积不变证明了勾股定理.请你写出该方法证明勾股定理的过程.【分析】连接BF,由图1可得正方形ACDE的面积为b2,由图2可得四边形ABDF的面积为三角形ABF 与三角形BDF面积之和,再利用正方形ACDE的面积与四边形ABDF的面积相等即可证明.【解答】证明:如图,连接BF,∵AC=b,∴正方形ACDE的面积为b2,∵CD=DE=AC=b,BC=a,EF=BC=a,∴BD=CD﹣BC=b﹣a,DF=DE+EF=a+b,∵∠CAE=90°,∴∠BAC+∠BAE=90°,∵∠BAC=∠EAF,∴∠EAF+∠BAE=90°,∴△BAE为等腰直角三角形,∴四边形ABDF的面积为:c2+(b﹣a)(a+b)=c2+(b2﹣a2),∵正方形ACDE的面积与四边形ABDF的面积相等,∴b2=c2+(b2﹣a2),∴b2=c2+b2﹣a2,∴a2+b2=c2,∴a2+b2=c2.24.(2022秋•大丰区期中)如图,在Rt△ABC中,∠ACB=90°,AB=10cm,AC:BC=3:4,动点P从B出发沿射线BC以1cm/s的速度运动,设运动时间为t(s).(1)求BC边的长.(2)当△ABP为等腰三角形时,求t的值.【分析】(1)利用勾股定理求解BC的长即可;(2)分3种情况讨论:当AP=BP时,当AB=BP时,当AB=AP时,分别计算可求解.【解答】解:(1)∵AC:BC=3:4,∴设AC=3xcm,BC=4xcm,在Rt△ABC中,∠ACB=90°,∴AB==5x=10cm,∴x=2,∴BC=8cm;(2)由(1)知,BC=8cm,AC=6cm,当AP=BP时,如图1,则AP=t,PC=BC﹣BP=8﹣t,在Rt△ACP中,AC2+CP2=AP2,∴62+(8﹣t)2=t2,解得t=;当AB=BP时,如图2,则BP=t=10;当AB=AP时,如图3,则BP=2BC;∴t=2×8=16,综上,t的值为或10或16.。
初中数学一元一次方程应用题类型及拔尖试题

初中数学一元一次方程应用题类型及拔尖试题工程类型应用题类型:工作量=工作效率×工作时间1.相遇类型:S快 + S慢 = S总2.追击类型:S快 - S慢 = S初3.顺风(水)类型:顺风(水)速度=静风(水)速度+风(水)速度4.逆风(水)类型:逆风(水)速度=静风(水)速度-风(水)速度5.环形跑道类型:同向:S快 + S慢 = C反向:S快 - S慢 = C6.计算利息类型:本息和=本金+利息=本金+本金×利率×期数7.利润类型:利润=利润率×成本8.一元一次方程类型9.形积变化类型10.劳力调配类型11.储蓄类型12.配套类型13.方案类型:弄清配套的比例,列方程组,求正整数解14.数字类型:数字=位上的数字乘以进率解应用题步骤:1.审清题意2.设未知数3.列方程4.解方程5.验证答案6.写出答语工程问题:1.工作总量=工作效率×工作时间2.经常在题目中未给出工作总量时,设工作总量为单位1.即完成某项任务的各工作量的和=总工作量=1.例1:一项工程,甲单独做要10天完成,乙单独做要15天完成,两人合做4天后,剩下的部分由乙单独做,还需要几天完成?解:设还需要x天完成,依题意,得(1/10+1/15)×4+x=1,解得x=5.例2:某工作,甲单独干需用15小时完成,乙单独干需用12小时完成,若甲先干1小时、乙又单独干4小时,剩下的工作两人合作,问:再用几小时可全部完成任务?解:设甲、乙两个龙头齐开x小时。
由已知得,甲每小时灌池子的2,乙每小时灌池子的3.列方程:2×0.5+(2+3)x=3,解得x=1(小时)。
例3:某工厂计划26小时生产一批零件,后因每小时多生产5件,用24小时,不但完成了任务,而且还比原计划多生产了60件,问原计划生产多少零件?解:设原计划生产x件,由已知得(26+x/24)×24=x+60,解得x=780.例4:某工程,甲单独完成需20天,乙单独完成需12天,甲乙合干6天后,再由乙继续完成,乙再做几天可以完成全部工程?解:1-6/20-12=x/12,解得x=2.4.已知甲和乙合作一项工程,甲独立完成需要25天,乙独立完成需要20天。
拔尖数学练习题

拔尖数学练习题在数学学习过程中,练习题是提高学生数学能力的重要途径之一。
本文将为您提供一些拔尖数学练习题,帮助您深入理解数学知识并提高解题能力。
一、代数与方程1. 计算以下方程的解:a) 2x + 5 = 13b) 3(x + 4) = 33c) 5(x - 6) + 2 = 322. 简化并求解以下方程:a) 3(2x - 5) + 4(x + 2) = 32 - xb) (2x + 3)(x - 4) = 0c) x^2 - 5x + 6 = 0二、几何与三角学1. 在直角三角形ABC中,AB = 3 cm,BC = 4 cm。
求AC的长度。
2. 在等腰三角形ABC中,AB = AC = 5 cm,角BAC的度数为36°。
求角ABC的度数。
3. 已知三角形ABC的边长分别为AB = 6 cm,BC = 8 cm,AC = 10 cm。
判断该三角形是什么类型的三角形,并说明理由。
三、函数与图像1. 已知函数f(x) = 2x^2 - 3x + 5,求f(2)的值。
2. 函数g(x)的图像经过点(3,8)和(-1,-2)。
求该函数的表达式,并画出其图像。
四、概率与统计1. 在一副扑克牌中,从中随机抽取2张牌。
求抽到的两张牌都是红心的概率。
2. 甲、乙两个人掷骰子,甲掷得6的概率为1/6,乙掷得6的概率为1/4。
如果两人同时掷骰子,求至少有一个人掷得6的概率。
五、数学推理与证明1. 数列{an}满足递推关系式an = 3an-1 - 2,其中a1 = 2。
求该数列的通项公式。
2. 证明勾股定理:对于直角三角形ABC,设AC为斜边,AB和BC 为两条直角边,满足AB^2 + BC^2 = AC^2。
六、应用题1. 甲、乙两人共同摘了若干个苹果,甲摘了总数的1/3,乙摘了20个,甲和乙摘的苹果总数的2/5是奇数个。
求摘了多少个苹果。
2. 一列火车以50 km/h的速度行驶了2小时后,因故停下来。
初中数学全年级拔高题150练习(附答案解析)

中点之间的距离是( )
A.3cm
B.4cm
C.5cm
D.无法计算
15.规定
a b
c d
=ad-bc,若
2 3
x
x 1 = 3
,则 x=(
)
A.-5
B.-4
C.0.8
D.1
二、填空题
16.化简 2 x 3 x 4 ______________
17.在体育课的跳远比赛中,以 5.00 米为标准,若小东跳出了 5.22 米,可记做+
2
4
5
你规定的新运算 a⊕b=
(用 a,b 的一个代数式表示).
三、解答题 31.计算:
(1)
1 2
-
5 9
7 12
-36
(2)
23
4 9
2 3
2
(3)
14பைடு நூலகம்
1 5
4
(1)3
32.计算
5
6
2a
a
3
1
33.先化简,再求值:
1 4
(-4x2+2x-8)-(
1 2
x-1),其中
x=
1 2
.
34.解方程:
7.如图,有一个正方体纸巾盒,它的平面展开图不可能的是( )
A.
B.
C.
D.
8.厦深铁路起点厦门北站,终点深圳北站.汕尾鲘门站、深圳坪山站在其沿线上,
它们之间有惠东站、惠州南站,那么在鲘门站和坪山站之间需准备火车票的种数为
(任何两站之间,往返两种车票)( )
A.8 种
B.10 种
C.12 种
D.14 种
(1) 6 2 x 3 x ;(2)1 3x 5 1 5x .
苏科版七年级数学下第八章《幂的运算》拔尖训练(有答案)

七下第八章《幂的运算》拔尖训练学校:___________姓名:___________班级:___________考号:___________一、选择题1. 计算(−2)100+(−2)99的结果是( )A. 2B. −2C. −299D. 2992. 若a x =3,a y =2,则a 2x+y 等于( )A. 6B. 7C. 8D. 183. 下列运算正确的是( )A. (3xy 2)2=6x 2y 4B. 2x −1=12xC. (−x)7÷(−x 2)=x 5D. 3x 3+2x 2=5x 5 4. 若(a +b)9=−1,(a −b)10=1,则a 19+b 19的值是( )A. 2B. 0C. −1D. 0或−1 5. 给出下列算式①(−3pq)2=6pq ,②−2−2=14,③(x 3)4×(−x 2)3=x 18 , ④a 5÷a 5=0 , ⑤(x −y )2=x 2−y 2,⑥(a +2b )2=a 2+2ab +4b 2,⑦−(a −b )4÷(b −a )3=a −b ,其中运算正确的有( )A. 0个B. 1个C. 2个D. 3个 6. 如果a =355,b =444,c =533,那么a 、b 、c 的大小关系是( )A. a >b >cB. c >b >aC. b >a >cD. b >c >a 7. (−23)2007⋅(−32)2008的计算结果是( )A. 23B. −23C. 32D. −32 8. 若a =999999,b =119990,则下列结论正确是( ) A. a <bB. a =bC. a >bD. ab =1 9. 若m 、n 为正整数且3m ×3n =81,则m 、n 的值可能有( )A. 7组B. 6组C. 5组D. 3组二、填空题10.若3n=2,3m=5,则33m+2n−1=________;11.若=________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学练习题拔尖习题
1. 某商品原价为120元,现以打8折出售,求售价。
解析:
打8折意味着折扣是80%,即原价的80%。
售价 = 原价 ×折扣
= 120 × 80%
= 120 × 0.8
= 96元
答案:96元
2. 一个矩形的长是2倍于宽,若矩形的面积为60平方单位,求其长和宽。
解析:
设矩形的宽为x单位,则矩形的长为2x单位。
矩形的面积 = 长 ×宽
= 2x × x
= 2x²
根据题意,2x² = 60,解方程得到x = 5。
因此,矩形的宽为5单位,长为2 × 5 = 10单位。
答案:宽为5单位,长为10单位
3. 已知一个等差数列的首项是5,公差是3,求这个数列的第10项。
解析:
等差数列的通项公式为:an = a1 + (n-1)d,
其中,an表示第n项,a1表示首项,d表示公差。
代入已知条件,an = 5 + (10-1)3,
计算得到an = 5 + 27 = 32。
答案:第10项为32。
4. 某班有35名学生,男生和女生人数之比为4:3,求男生和女生的
人数分别是多少?
解析:
假设男生人数为4x,女生人数为3x,则男生和女生人数之和为7x。
根据题意,7x = 35,解方程得到x = 5。
因此,男生人数为4x = 4 × 5 = 20,女生人数为3x = 3 × 5 = 15。
答案:男生人数为20,女生人数为15。
5. 如图所示,ABCD为一个平行四边形,AB的长为8cm,BC的长
为5cm,求BD的长。
解析:
由平行四边形的性质可知,AB与CD平行且长度相等,BC与AD 平行且长度相等。
因此,BD与AC平行且长度相等。
根据题意,AC = AB = 8cm,BC = 5cm。
根据三角形ACB,可使用勾股定理求得AC的长:AC² = AB² + BC²= 8² + 5² = 89,即AC = √89。
由于BD与AC平行,且BC = AD,所以BD的长度也为√89cm。
答案:BD的长为√89cm。
6. 若a:b = 3:4,且a + b = 35,求a和b的值。
解析:
根据题意,可以设a的倍数为3x,b的倍数为4x。
由于a + b = 35,则3x + 4x = 35,解方程可得到x = 5。
因此,a = 3x = 3 × 5 = 15,b = 4x = 4 × 5 = 20。
答案:a的值为15,b的值为20。
7. 一件商品的原价为65元,现在以每件打85折出售。
小明买了3件,小红买了2件,他们分别支付了多少钱?
解析:
商品的折扣为85%,即原价的85%。
小明购买了3件商品,小红购买了2件商品。
小明支付的金额 = 原价 ×折扣 ×数量
= 65 × 85% × 3
= 65 × 0.85 × 3
= 165.75元
小红支付的金额 = 原价 ×折扣 ×数量
= 65 × 85% × 2
= 65 × 0.85 × 2
= 110.5元
答案:小明支付了165.75元,小红支付了110.5元。
8. 若a:b = 2:5,b:c = 3:4,求a:b:c的值。
解析:
根据已知条件,可以设a的倍数为2x,b的倍数为5x,c的倍数为
4y。
由于b:c = 3:4,则5x:4y = 3:4,解方程可得到y = 5/3x。
代入a:b = 2:5的条件,可以得到a:5x = 2:5,解方程可得到a = 2x/5。
因此,a:b:c的值为2x/5:5x:4y = 2/5:5:4(5/3) = 6:25:20。
答案:a:b:c的值为6:25:20。
通过以上习题的练习,我们可以加深对初中数学知识点的理解,并提高解题的能力。
希望同学们能够继续努力,取得更好的成绩!。
