高考物理计算题复习《天体密度和质量的计算》(解析版)
专题5.2 天体质量和密度的估算(解析版)-3年高考2年模拟1年原创备战2020高考精品系列之物理

专题5.2天体质量和密度的估算【考纲解读与考频分析】利用万有引力等于重力可以估算地球质量,若测量出绕天体运行卫星的周期和轨道半径可以估算天体的质量,若知道天体的半径,可以估算出天体的密度。
高考有关天体质量和密度的估算考查频率较高。
【高频考点定位】:天体质量和密度的估算考点一:天体质量和密度的估算【3年真题链接】1.(2018高考理综II ·16)2018年2月,我国500m 口径射电望远镜(天眼)发现毫秒脉冲星“J0318+0253”,其自转周期T =5.19ms ,假设星体为质量均匀分布的球体,已知万有引力常量为11226.6710N m /kg -⨯⋅。
以周期T 稳定自转的星体的密度最小值约为()A .93510kg /m ⨯B .123510kg /m⨯C .153510kg /m ⨯D .183510kg /m⨯【参考答案】C【命题意图】本题考查万有引力定律、牛顿运动定律、密度及其相关的知识点。
【解题思路】设脉冲星质量为M ,半径为R 。
选取脉冲星赤道上一质元,设质量为m ,由万有引力定律和牛顿第二定律可得G2Mm R =mR (2T π)2,星体最小密度ρ=M/V ,星球体积V=43πR 3,联立解得:ρ=23GTπ,代入数据得ρ=5×1015kg/m ,选项C 正确。
2.(2018高考全国理综I ).2017年,人类第一次直接探测到来自双中子星合并的引力波。
根据科学家们复原的过程,在两颗中子星合并前约100s 时,它们相距约400km ,绕二者连线上的某点每秒转动12圈,将两颗中子星都看作是质量均匀分布的球体,由这些数据、万有引力常量并利用牛顿力学知识,可以估算出这一时刻两颗中子星()A.质量之积B.质量之和C.速率之和D.各自的自转角速度【参考答案】BC【命题意图】本题考查天体运动、万有引力定律、牛顿运动定律及其相关的知识点。
【解题思路】双中子星做匀速圆周运动的频率f=12Hz(周期T=1/12s),由万有引力等于向心力,可得,G122m mr=m1r1(2πf)2,G122m mr=m2r2(2πf)2,r1+r2=r=40km,联立解得:(m1+m2)=(2πf)2Gr3,选项B正确A错误;由v1=ωr1=2πf r1,v2=ωr2=2πf r2,联立解得:v1+v2=2πf r,选项C正确;不能得出各自自转的角速度,选项D错误。
高中物理天体密度与质量求解问题

高中物理万有引力天体密度与质量的求解(1)利用天体表面的重力加速度g 和天体半径R .由于G Mm R 2=mg ,故天体质量M =gR 2G ,天体密度ρ=M V =M 43πR 3=3g4πGR .(2)通过观察卫星绕天体做匀速圆周运动的周期T 和轨道半径r .①由万有引力等于向心力,即G Mm r 2=m 4π2T 2r ,得出中心天体质量M =4π2r 3GT 2;②若已知天体半径R ,则天体的平均密度ρ=M V =M 43πR 3=3πr 3GT 2R3.例题:1、2013年12月14日21时许,嫦娥三号携带“玉兔”探测器在月球虹湾成功软着陆,在实施软着陆过程中,嫦娥三号离月球表面4m 高时最后一次悬停,确认着陆点。
若总质量为M 的嫦娥三号在最后一次悬停时,反推力发动机对其提供的反推力为F ,已知引力常量为G ,月球半径为R ,则月球的质量为()A.FR 2MGB.FR MGC.MG FRD.MG FR 2【解析】在月球表面附近:Mg =G M 月MR2,嫦娥三号悬停时,F =Mg ,由以上两式解得:M 月=FR 2MG ,选项A 对。
【答案】A2、嫦娥五号探测器由轨道器、返回器、着陆器等多个部分组成。
探测器预计在2017年由长征五号运载火箭在中国文昌卫星发射中心发射升空,自动完成月面样品采集,并从月球起飞,返回地球,带回约2kg 月球样品。
某同学从网上得到一些信息,如表格中的数据所示,请根据题意,判断地球和月球的密度之比为()月球半径R 0月球表面处的重力加速度g 0地球和月球的半径之比RR 0=4地球表面和月球表面的重力加速度之比g g 0=6A.23B.32C .4D .6【解析】利用题给信息,对地球,有G Mm R 2=mg ,得M =gR 2G ,又V =43πR 3,得地球的密度ρ=M V =3g 4G πR ;对月球,有G M 0m R 20=mg 0,得M 0=g 0R 20G ,又V 0=43πR 30,得月球的密度ρ0=M 0V 0=3g 04G πR 0,则地球的密度与月球的密度之比ρρ0=32,故B 正确。
届高考物理二轮复习力与曲线运动专项练习(4):计算中心天体质量密度问题(含解析)
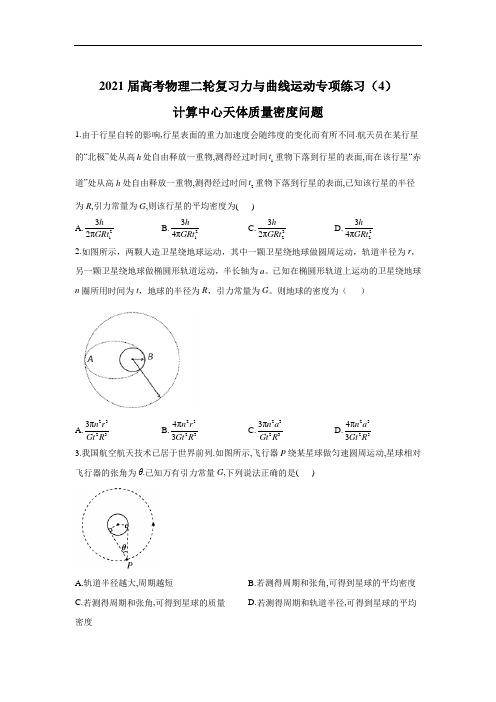
2021届高考物理二轮复习力与曲线运动专项练习(4)计算中心天体质量密度问题1.由于行星自转的影响,行星表面的重力加速度会随纬度的变化而有所不同.航天员在某行星的“北极”处从高h 处自由释放一重物,测得经过时间1t 重物下落到行星的表面,而在该行星“赤道”处从高h 处自由释放一重物,测得经过时间2t 重物下落到行星的表面,已知该行星的半径为R ,引力常量为G ,则该行星的平均密度为( ) A.2132πhGRtB.2134πhGRtC.2232πhGRt D.2234πhGRt 2.如图所示,两颗人造卫星绕地球运动,其中一颗卫星绕地球做圆周运动,轨道半径为r ,另一颗卫星绕地球做椭圆形轨道运动,半长轴为a 。
已知在椭圆形轨道上运动的卫星绕地球n 圈所用时间为t ,地球的半径为R ,引力常量为G 。
则地球的密度为( )A.23233πn r Gt R B.23234π3n r Gt R C.23233πn a Gt R D.23234π3n a Gt R 3.我国航空航天技术已居于世界前列.如图所示,飞行器P 绕某星球做匀速圆周运动,星球相对飞行器的张角为θ.已知万有引力常量G ,下列说法正确的是( )A.轨道半径越大,周期越短B.若测得周期和张角,可得到星球的平均密度C.若测得周期和张角,可得到星球的质量D.若测得周期和轨道半径,可得到星球的平均密度4.假如宇航员乘坐宇宙飞船到达某一行星,在该行星“北极”距“地面”高h 处无初速度释放一个小球,经时间t 落至“地面”.已知该行星的半径为R 、自转周期为T ,引力常量为G ,不计一切阻力.则下列说法正确的是( ) A.该行星的第一宇宙速度为2πRTB.该行星的平均密度为232πhGtC.如果该行星存在一颗同步卫星,D.宇宙飞船绕该行星做圆周运动的周期不小于π 5.科学家发现了一颗距离地球14光年的“另一个地球”沃尔夫,它是迄今为止在太阳系外发现的距离地球最近的宜居星球.沃尔夫的质量为地球的4倍,它围绕红矮星运行的周期为18天.设想从地球发射一颗科学探测卫星围绕沃尔夫表面运行.已知引力常量为G ,天体的环绕运动可看作匀速圆周运动.则下列说法正确的是( ) A.从地球发射该探测卫星的速度应该小于第三宇宙速度 B.根据沃尔夫围绕红矮星运行的周期可求出红矮星的密度C.若已知围绕沃尔夫表面运行的探测卫星的周期和地球的质量,可近似求出沃尔夫的半径D.沃尔夫绕红矮星公转和地球绕太阳公转的轨道半径的三次方的比值等于218()3656.习近平主席在2018年新年贺词中提到,科技创新、重大工程建设捷报频传,“慧眼”卫星遨游太空。
2020高考备考物理重难点《天体运动与人造航天器》(附答案解析版)

重难点05 天体运动与人造航天器【知识梳理】考点一 天体质量和密度的计算1.解决天体(卫星)运动问题的基本思路(1)天体运动的向心力来源于天体之间的万有引力,即ma r mv r T m r m rMm G ====2222)2(πω(2)在中心天体表面或附近运动时,万有引力近似等于重力,即2R MmG mg =(g 表示天体表面的重力加速度).(2)利用此关系可求行星表面重力加速度、轨道处重力加速度: 在行星表面重力加速度:2R Mm Gmg =,所以2R MG g = 在离地面高为h 的轨道处重力加速度:2)(h R Mm G g m +=',得2)(h R MG g +=' 2.天体质量和密度的计算(1)利用天体表面的重力加速度g 和天体半径R .由于2R Mm G mg =,故天体质量GgR M 2=天体密度:GRgV M πρ43==(2)通过观察卫星绕天体做匀速圆周运动的周期T 和轨道半径r .①由万有引力等于向心力,即r T m rMm G 22)2(π=,得出中心天体质量2324GT r M π=;②若已知天体半径R ,则天体的平均密度3233RGT r V M πρ== ③若天体的卫星在天体表面附近环绕天体运动,可认为其轨道半径r 等于天体半径R ,则天体密度23GTV M πρ==.可见,只要测出卫星环绕天体表面运动的周期T ,就可估算出中心天体的密度. 【重点归纳】 1.黄金代换公式(1)在研究卫星的问题中,若已知中心天体表面的重力加速度g 时,常运用GM =gR 2作为桥梁,可以把“地上”和“天上”联系起来.由于这种代换的作用很大,此式通常称为黄金代换公式. 2. 估算天体问题应注意三点(1)天体质量估算中常有隐含条件,如地球的自转周期为24 h ,公转周期为365天等. (2)注意黄金代换式GM =gR 2的应用. (3)注意密度公式23GTπρ=的理解和应用. 考点二 卫星运行参量的比较与运算 1.卫星的动力学规律由万有引力提供向心力,ma r mv r T m r m rMm G ====2222)2(πω2.卫星的各物理量随轨道半径变化的规律r GM v =;3r GM =ω;GMr T 32π=;2r GM a = (1)卫星的a 、v 、ω、T 是相互联系的,如果一个量发生变化,其它量也随之发生变化;这些量与卫星的质量无关,它们由轨道半径和中心天体的质量共同决定.(2)卫星的能量与轨道半径的关系:同一颗卫星,轨道半径越大,动能越小,势能越大,机械能越大.3.极地卫星和近地卫星(1)极地卫星运行时每圈都经过南北两极,由于地球自转,极地卫星可以实现全球覆盖. (2)近地卫星是在地球表面附近环绕地球做匀速圆周运动的卫星,其运行的轨道半径可近似认为等于地球的半径,其运行线速度约为7.9 km/s. (3)两种卫星的轨道平面一定通过地球的球心. 【重点归纳】1.利用万有引力定律解决卫星运动的一般思路 (1)一个模型天体(包括卫星)的运动可简化为质点的匀速圆周运动模型. (2)两组公式卫星运动的向心力来源于万有引力:ma r mv r T m r m rMm G ====2222)2(πω在中心天体表面或附近运动时,万有引力近似等于重力,即:2R MmGmg = (g 为星体表面处的重2.卫星的线速度、角速度、周期与轨道半径的关系⎪⎪⎩⎪⎪⎨⎧⇒⇒⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫====减小增大减小减小增大时当半径a T v r r GM a GM r T r GM r GM v ωπω2332 考点三 宇宙速度 卫星变轨问题的分析1.第一宇宙速度v 1=7.9 km/s ,既是发射卫星的最小发射速度,也是卫星绕地球运行的最大环绕速度.2.第一宇宙速度的两种求法:(1)r mv r Mm G 212=,所以r GMv =1 (2)rmv mg 21=,所以gR v =1.3.第二、第三宇宙速度也都是指发射速度.4.当卫星由于某种原因速度突然改变时(开启或关闭发动机或空气阻力作用),万有引力不再等于向心力,卫星将变轨运行:(1)当卫星的速度突然增加时,r mv rMm G 22<,即万有引力不足以提供向心力,卫星将做离心运动,脱离原来的圆轨道,轨道半径变大,当卫星进入新的轨道稳定运行时由rGMv =可知其运行速度比原轨道时减小.(2)当卫星的速度突然减小时,r mv rMm G 22>,即万有引力大于所需要的向心力,卫星将做近心运动,脱离原来的圆轨道,轨道半径变小,当卫星进入新的轨道稳定运行时由rGMv =可知其运行速度比原轨道时增大.卫星的发射和回收就是利用这一原理.1.处理卫星变轨问题的思路和方法(1)要增大卫星的轨道半径,必须加速;(2)当轨道半径增大时,卫星的机械能随之增大.2.卫星变轨问题的判断:(1)卫星的速度变大时,做离心运动,重新稳定时,轨道半径变大.(2)卫星的速度变小时,做近心运动,重新稳定时,轨道半径变小.(3)圆轨道与椭圆轨道相切时,切点处外面的轨道上的速度大,向心加速度相同.3.特别提醒:“三个不同”(1)两种周期——自转周期和公转周期的不同(2)两种速度——环绕速度与发射速度的不同,最大环绕速度等于最小发射速度(3)两个半径——天体半径R和卫星轨道半径r的不同【限时检测】(建议用时:30分钟)1.(2019·新课标全国Ⅰ卷)在星球M上将一轻弹簧竖直固定在水平桌面上,把物体P轻放在弹簧上端,P由静止向下运动,物体的加速度a与弹簧的压缩量x间的关系如图中实线所示。
2023届浙江高三物理高考复习专题模型精讲精练第23讲 应用万有引力定律估算天体质量和密度(解析版)

第23讲 应用万有引力定律估算天体质量和密度1.(2021·全国)卡文迪许用扭秤实验测定了引力常量,以实验验证了万有引力定律的正确性。
应用引力常量还可以计算出地球的质量,卡文迪许也因此被称为“能称出地球质量的人”。
已知引力常量G =6.67×10﹣11N •m 2/kg 2,地面上的重力加速度g =9.8m/s 2,地球半径R =6.4×106m ,则地球质量约为( ) A .6×1018kg B .6×1020 kgC .6×1022 kgD .6×1024 kg【解答】解:根据公式GMm R 2=mg 可得M =gR 2G =9.8×(6.4×106)26.67×10−11kg =6×1024kg ,故ABC 错误,D 正确。
故选:D 。
2.(2021·乙卷)科学家对银河系中心附近的恒星S2进行了多年的持续观测,给出1994年到2002年间S2的位置如图所示。
科学家认为S2的运动轨迹是半长轴约为1000AU (太阳到地球的距离为1AU )的椭圆,银河系中心可能存在超大质量黑洞。
这项研究工作获得了2020年诺贝尔物理学奖。
若认为S2所受的作用力主要为该大质量黑洞的引力,设太阳的质量为M ,可以推测出该黑洞质量约为( )A .4×104MB .4×106MC .4×108MD .4×1010M【解答】解:设地球的质量为m ,地球到太阳的距离为r =1AU ,地球的公转周期为T =1年; 由万有引力提供向心力可得:GMm r 2=mr4π2T 2,解得:M =4π2r 3GT2; 对于S2受到黑洞的作用,椭圆轨迹半长轴R =1000AU ,根据图中数据结合图象可以得到S2运动的半周期T′2=(2002﹣1994)年=8年,则周期为T ′=16年,根据开普勒第三定律结合万有引力公式可以得出:M 黑=4π2R 3GT′2,其中R 为S 2的轨迹半长轴,因此有:M 黑=R 3T 2r 3T′2M ,代入数据解得:M黑≈4×106M ,故B 正确,ACD 错误。
人教版高中物理必修第二册《7.3 万有引力理论的成就》练习题(解析版)

7.3 万有引力理论的成就【三大题型】【人教版2019】【题型1 天体的质量和密度的计算】 ................................................................................................................... 1 【题型2 天体运动的分析与计算】 ....................................................................................................................... 3 【题型3 天体自转的相关问题】 (4)知识点1:天体的质量和密度的计算 1.天体质量的计算(1)“自力更生法”:若已知天体(如地球)的半径R 和表面的重力加速度g ,根据物体的重力近似等于天体对物体的引力,得mg =G Mm R 2,解得天体质量为M =gR 2G ,因g 、R 是天体自身的参量,故称“自力更生法”.(2)“借助外援法”:借助绕中心天体做圆周运动的行星或卫星计算中心天体的质量,常见的情况: G Mm r 2=m ⎝⎛⎭⎫2πT 2r ⇒M =4π2r 3GT 2,已知绕行天体的r 和T 可以求M .2.天体密度的计算若天体的半径为R ,则天体的密度ρ=M43πR 3,将M =4π2r 3GT 2代入上式可得ρ=3πr 3GT 2R 3.特殊情况,当卫星环绕天体表面运动时,其轨道半径r 可认为等于天体半径R ,则ρ=3πGT2.注意:(1)计算天体的质量的方法不仅适用于地球,也适用于其他任何星体.要明确计算出的是中心天体的质量.(2)要注意R 、r 的区分.一般地R 指中心天体的半径,r 指行星或卫星的轨道半径.若绕“近地”轨道运行,则有R =r .知识点2:天体运动的分析与计算1.基本思路:一般行星或卫星的运动可看作匀速圆周运动,所需向心力由中心天体对它的万有引力提供.2.常用关系(1)G Mm r 2=ma 向=m v 2r =mω2r =m 4π2T2r(2)mg =G MmR 2(物体在天体表面时受到的万有引力等于物体重力),整理可得:gR 2=GM ,该公式通常被称为黄金代换式.3.四个重要结论:设质量为m 的天体绕另一质量为M 的中心天体做半径为r 的匀速圆周运动. (1)由G Mm r 2=m v 2r 得v =GMr,r 越大,v 越小. (2)由G Mmr2=mω2r 得ω=GMr 3,r 越大,ω越小. (3)由G Mm r2=m ⎝⎛⎭⎫2πT 2r 得T =2πr 3GM,r 越大,T 越大. (4)由G Mm r 2=ma 向得a 向=GMr 2,r 越大,a 向越小.以上结论可总结为“一定四定,越远越慢”.【题型1 天体的质量和密度的计算】【例1】2021年4月,我国自主研发的空间站“天和”核心舱成功发射并入轨运行,若核心舱绕地球的运行可视为匀速圆周运动,已知引力常量,由下列物理量能计算出地球质量的是( ) A .核心舱的质量和绕地半径 B .核心舱的质量和绕地周期 C .核心舱的绕地角速度和绕地周期 D .核心舱的绕地线速度和绕地半径【变式1-1】木星的卫星中,木卫一、木卫二、木卫三做圆周运动的周期之比为1:2:4。
高考物理复习---《天体质量和密度的计算》考点归纳PPT课件
③若卫星绕天体表面运行,可认为轨道半径 r 等于天体半径 R,则天体密度 ρ=G3Tπ2,故只要 测出卫星环绕天体表面运动的周期 T,就可估算出中心天体的密度.
高考物理复习---《天体质量和密度的计算》考点归纳PPT 课件
应用万有引力定律估算天体的质量、密度 (1)利用天体表面重力加速度 已知天体表面的重力加速度g和天体半径R.
①由G
Mm R2
=mg,得天体质量M=.gGR2
②天体密度. ρ=MV=43πMR3=4π3GgR
(2)利用运行天体 测出卫星绕中心天体做匀速圆周运动的半径r和周期T.
B.5×1012 kg/m3
C.5×1015 kg/m3
D.5×1018 kg/m3
答案 C 解析 脉冲星自转,边缘物体 m 恰对球体无压力时万有引力提供向心力,则有 GMr2m=mr4Tπ22, 又知 M=ρ·43πr3 整理得密度 ρ=G3Tπ2=6.67×10-311××3.51.419×10-32 kg/m3≈5.2×1015 kg/m3.
GMR1火2 m=m(2Tπ)2R1 结合两个公式可解得:M 火=4gπR2R221T3M2 ,故 A 对.
(2020·广东广雅中学模拟)宇航员在月球表面将一片羽毛和一个铁锤从同一高度由静止同时释 放,二者几乎同时落地.若羽毛和铁锤是从高度为 h 处下落,经时间 t 落到月球表面.已知 引力常量为 G,月球的半径为 R.求:(不考虑月球自转的影响) (1)月球表面的自由落体加速度大小 g 月; (2)月球的质量 M; (3)月球的密度 ρ.
星前贴近火星表面运行一周用时为T,已知火星的半径为R1,地球的半径为R2,地球的质量 为M,地球表面的重力加速度为g,引力常量为G,则火星的质量为( )
专题07 天体的质量和密度的估算-2019高考物理一轮复习专题详解(解析版)
知识回顾1.牢记两个基本关系式(1)利用F 万=F 向,有GMm r 2=m v 2r =mω2r =m 4π2T 2r =ma .(2)在星球表面附近有GMmR 2=mg 星.2.明确三个常见误区(1)天体质量和密度的估算是指中心天体而非环绕天体的质量和密度的估算. (2)注意区分轨道半径r 和中心天体的半径R . (3)在考虑自转问题时,只有两极才有GMmR 2=mg .规律方法估算中心天体质量和密度的两条思路(1)利用天体表面的重力加速度和天体半径估算由G Mm R 2=mg 得M =gR 2G ,再由ρ=M V ,V =43πR 3得ρ=3g 4G πR.(2)已知天体做匀速圆周运动的轨道半径和周期,由G Mm r 2=m 4π2T 2r 得M =4π2r 3GT 2,再结合ρ=M V ,V =43πR 3得ρ=3πr 3GT 2R 3――→天体表面ρ=3πGT2.典例分析【例1】 假设地球可视为重量均匀分布的球体.已知地球表面重力加速度在两极的大小为g 0,在赤道的大小为g ;地球自转的周期为T ,引力常量为G .地球的密度为( )A.3πg 0-g GT 2g 0 B.3πg 0GT 2g 0-g C.3πGT 2 D.3πg 0GT 2g 【答案】 B【例2】 宇宙中有两颗相距无限远的恒星s 1、s 2,半径均为R 0.图分别是两颗恒星周围行星的公转周期T 2与公转半径r 3的图象,则( )A .恒星s 1的质量大于恒星s 2的质量B .恒星s 1的密度小于恒星s 2的密度C .恒星s 1的第一宇宙速度大于恒星s 2的第一宇宙速度D .距两恒星表面高度相同的行星,s 1的行星向心加速度较大 【答案】 B专题练习1.(多选)通过观测冥王星的卫星,可以推算出冥王星的质量.假设卫星绕冥王星做匀速圆周运动,除了引力常量外,至少还需要两个物理量才能计算出冥王星的质量.这两个物理量可以是( )A .卫星的速度和角速度B .卫星的质量和轨道半径C .卫星的质量和角速度D .卫星的运行周期和轨道半径 【答案】:AD【解析】知道卫星的速度和角速度,由v =ωr 可求得卫星的轨道半径,根据G Mm r 2=m v 2r ,即可求得冥王星的质量,选项A 正确;根据G Mm r 2=m 2πT 2r ,知道卫星的运行周期和轨道半径,可求得冥王星的质量,选项D 正确;求冥王星的质量,不需要知道卫星的质量,选项B 、C 错误.2.假设地球是一半径为R 、质量分布均匀的球体.一矿井深度为d .已知质量分布均匀的球壳对壳内物体的引力为零,矿井底部和地面处的重力加速度大小之比为( )A .1-d RB .1+dRC.R -d R 2D.R R -d2【答案】:A【解析:】根据万有引力与重力相等可得,在地面处有: G m ·43πR 3ρR 2=mg ,在矿井底部有:Gm ·43R -d 3ρR -d2=mg ′,所以g ′g =R -d R =1-d R.故选项A 正确.学科&网3.有一个质量为M ,半径为R ,密度均匀的大球体.从中挖去一个半径为R2的小球体,并在空腔中心放置一质量为m 的质点,则大球体的剩余部分对该质点的万有引力大小为(已知质量分布均匀的球壳对壳内物体的引力为零)( )A .G MmR 2 B .0C .4G Mm R 2D .G Mm 2R 2【答案】:D4.(2017年河北重点中学联考)假设地球是一半径为R 、质量分布均匀的球体.已知质量分布均匀的球壳对壳内物体的引力为零,不考虑地球自转的影响,则距离地球球心为r 处的重力加速度大小g 与r 的关系图象可能为( )【答案】:A5.已知月球半径为R ,飞船在距月球表面高度为R 的圆轨道上飞行,周期为T .引力常量为G ,下列说法正确的是( )A .月球第一宇宙速度为4πR TB .月球表面重力加速度为8π2T 2RC .月球密度为3πGT 2D .月球质量为32π2R 3GT 2【答案】:D【解析】:由题意知,飞船运行的速度为v =4πR T ,小于月球的第一宇宙速度,所以A 错误;根据G Mm 4R 2=m 4π2T 2·2R ,又GM =gR 2,联立解得g =32π2R T 2,M =32π2R 3GT 2,所以B 错误,D 正确;再根据M =32π2R 3GT 2=ρ43πR 3,解得ρ=24πGT2,C 错误.6.(2017年湖北八校三月模拟)据英国《每日邮报》报道,科学家发现了一颗距离地球仅14光年的“另一个地球”——沃尔夫(Wolf)1061c.沃尔夫1061c 的质量为地球的4倍,围绕红矮星沃尔夫1061运行的周期为5天,它是迄今为止在太阳系外发现的距离最近的宜居星球.设想从地球发射一颗科学探测卫星围绕沃尔夫1061c 表面运行.已知万有引力常量为G ,天体的环绕运动可看作匀速圆周运动.则下列说法正确的是( )A .从地球发射该卫星的速度应该小于第三宇宙速度B .卫星绕行星沃尔夫1061c 运行的周期与该卫星的密度有关C .沃尔夫1061c 和地球公转轨道半径的三次方之比等于⎝⎛⎭⎫53652D .若已知探测卫星的周期和地球的质量,可近似求出沃尔夫1061c 的半径 【答案】:D7.(多选)在研究发现太阳与行星间的引力规律过程中,下列说法正确的是( ) A .研究思路是根据行星的受力情况去探究行星的运动情况 B .引用了公式F =mv 2r,这个关系式实际上是牛顿第二定律C .由太阳对行星的引力表达式推出行星对太阳的引力表达式,采用的论证方法是等效法D .在开普勒第三定律r 3T 2=k 和引力公式F =G Mmr 2中,常数k 和G 与太阳和行星均无关【答案】 BC【解析】研究思路是根据行星的运动情况去探究行星的受力情况,A 项错误.公式F =mv 2r 实际上是牛顿第二定律的表达式.由太阳对行星的引力表达式推出行星对太阳的引力表达式,采用的论证方法是等效法.常数k 与太阳有关,G 与太阳和行星均无关,B 、C 两项正确.8.(多选)已知下面的哪组数据,可以算出地球的质量M(引力常量G 为已知)( ) A .月球绕地球运动的周期T 1及月球到地球中心的距离R 1 B .地球绕太阳运行周期T 2及地球到太阳中心的距离R 2 C .人造卫星在地面附近的运行速度v 3和运行周期T 3D .地球绕太阳运行的速度v 4及地球到太阳中心的距离R 4 【答案】AC9.(2017·山东泰安市质检)(多选)我国计划在2017年发射“嫦娥四号”,层次、更加全面的科学探测月球地貌、资源等方面的信息,完善月球档案资料.已知月球的半径为R ,月球表面的重力加速度为g ,引力常量为G ,嫦娥四号离月球中心的距离为r ,绕月周期为T.根据以上信息可求出( )A .“嫦娥四号”绕月运行的速度 r 2g RB .“嫦娥四号”绕月运行的速度为R 2g rC .月球的平均密度为3πGT 2D .月球的平均密度为3πr 3GT 2R 3【答案】 BD【解析】月球表面任意一物体重力等于万有引力G MmR 2=mg ,则有GM =R 2g ,“嫦娥四号”绕月运行时,万有引力提供向心力:G Mm r 2=m v 2r,解得v =GMr,联立解得gR 2r,故A 项错误,B 项正确;“嫦娥四号”绕月运行时,根据万有引力提供向心力,有G Mm r 2=m 4π2T 2r ,解得M =4π2r 3GT 2,月球的平均密度为ρ=MV =4π2r 3GT 24π3R 3=3πr 3GT 2R3,故C 项错误,D 项正确;所以B 、D 项正确,A 、C 项错误. 10.(2017·山东泰安市质检)(多选)密度均匀的球形行星对其周围物体的万有引力使物体产生的加速度用a 表示,物体到行星表面的距离用h 表示.a 随h 变化的图像如图所示.图中a 、h 1、a 2、h 2及万有引力常量G 均为已知.根据以上数据可以计算出( )A .该行星的半径B .该行星的质量C .该行星的自转周期D .该行星同步卫星离行星表面的高度 【答案】 ABC 项,由题目以及相关的公式的物理量都与该行星转动的自转周期无关,所以不能求出该行星的自转周期,C 项错误;D 项,由于不能求出该行星的自转周期,所以也不能求出该行星同步卫星离行星表面的高度,D 项错误;故选A 、B 两项.11.(2017·山西模拟)2016年8月16日,我国将世界首颗量子卫星发射升空,轨道距离地面高度为h.我国“蛟龙号”载人潜水器执行科考任务时下潜深度为d.把地球看做质量分布均匀的球体,且质量分布均匀的球壳对壳内物体的引力为零.若地球半径为R ,“蛟龙号”所在处与“量子卫星”所处的加速度之比为( )A.(R -d )2(R +h )2B.R -dR +hC.(R -d )(R +h )2R 3D.(R -d )(R +h )R 2【答案】 C【解析】令地球的密度为ρ,则在地球表面,重力和地球的万有引力大小相等,有g =GMR 2,由于地球的质量为:M =43πR 3ρ,所以重力加速度的表达式可写成:g =43πG ρR.根据题意有,质量分布均匀的球壳对壳内物体的引力为零,固在深度为d 的地球内部,受到地球的万有引力即为半径等于(R -d)的球体在其表面产生的万有引力,故重力加速度g ′=43πG ρ(R -d).所以有g ′g =R -dR. 根据万有引力提供向心力GMm (R +h )2=ma ,量子卫星的加速度a =GM(R +h )2,所以a g =R 2(R +h )2,所以g ′a =(R -d )(R +h )2R 3,故C 项正确,A 、B 、D 项错误.学科&网12.宇航员在地球表面以一定初速度竖直上抛一小球,经过时间t 小球落回原地.若他在某星球表面以相同的初速度竖直上抛同一小球,需经过时间5t 小球落回原处.已知该星球的半径与地球半径之比为R 星∶R 地=1∶4,地球表面重力加速度为g ,设该星球表面附近的重力加速度为g ′,空气阻力不计.则( )A .g ′∶g =5∶1B .g ′∶g =5∶2C .M 星∶M 地=1∶20D .M 星∶M 地=1∶80【答案】 D13.(2017·宝鸡一模)宇航员在某星球上为了探测其自转周期做了如下实验:在该星球两极点,用弹簧秤测得质量为M 的砝码所受重力为F ,在赤道测得该砝码所受重力为F ′.他还发现探测器绕该星球表面做匀速圆周运动的周期为T.假设该星球可视为质量分布均匀的球体,则其自转周期为( )A .T F ′FB .TF F ′ C .TF -F ′FD .T FF -F ′【答案】 D【解析】设星球及探测器质量分别为m 、m ′在该星球两极点,用弹簧秤测得质量为M 的砝码所受重力为F ,则有GMmR 2=F ,在赤道测得该砝码所受重力为F ′,则有GMmR 2-F ′=M 4π2T 自2R ,探测器绕该星球表面做匀速圆周运动的周期为T ,则有G mm ′R 2=m ′R 4π2T 2;联立两式解得T 自=TFF -F ′.故D 项正确,A 、B 、C 三项错误.14.(2017·湖南省二模)一宇航员到达半径为R 、密度均匀的某星球表面,做如下实验:用不可伸长的轻绳拴一质量为m 的小球,上端固定在O 点,如图甲所示,在最低点给小球某一初速度,使其绕O 点在竖直面内做圆周运动,测得绳的拉力F 大小随时间t 的变化规律如图乙所示.F 1=7F 2,设R 、m 、引力常量G 以及F 1为已知量,忽略各种阻力.以下说法正确的是( )A .该星球表面的重力加速度为7F 17mB .卫星绕该星球的第一宇宙速度为Gm RC .星球的密度为3F 128πGmRD .小球过最高点的最小速度为0 【答案 】CF 1=7F 2,所以该星球表面的重力加速度为F 17m ,故A 项错误.根据万有引力提供向心力,得GMm R 2=m v 2R ,卫星绕该星球的第一宇宙速度为v =GM R ,故B 项错误.在星球表面,万有引力近似等于重力GMmR2=mg⑤由④⑤解得M =F 1R 27Gm ,星球的密度ρ=M 43πR 3=3F 128πGmR ,C 项正确;小球在最高点受重力和绳子拉力,根据牛顿运动定律,得F 2+mg =m v 22R ≥mg所以小球在最高点的最小速度v 2≥gR ,故D 项错误.15.(2017·广西模拟)为了方便研究物体与地球间的万有引力问题,通常将地球视为质量分布均匀的球体.已知地球的质量为M ,半径为R ,引力常量为G ,不考虑空气阻力的影响.(1)求北极点的重力加速度的大小;(2)若“天宫二号”绕地球运动的轨道可视为圆周,其轨道距地面的高度为h ,求“天宫二号”绕地球运行的周期和速率;(3)若已知地球质量M =6.0×1024 kg ,地球半径R =6 400 km ,其自转周期T =24 h ,引力常量G =6.67×10-11N ·m 2/kg 2.在赤道处地面有一质量为m 的物体A ,用W 0表示物体A 在赤道处地面上所受的重力,F 0表示其在赤道处地面上所受的万有引力.请求出F 0-W 0F 0的值(结果保留1位有效数字),并以此为依据说明在处理万有引力和重力的关系时,为什么经常可以忽略地球自转的影响.【答案】 (1)GMR2 (2)2π(R +h )3GMGMR +h(3)见解析 【解析】(1)设北极点的重力加速度为g 0,则有m 0g 0=G Mm 0R 2解得g 0=GMR2(3)物体A 在赤道处地面上所受的万有引力F 0=GMmR 2对于物体A 在赤道处地面上随地球运动的过程,设其所受地面的支持力为N ,根据牛顿第二定律,有F 0-N =m 4π2T2R物体A 此时所受重力的大小为:W 0=N =G MmR 2-m 4π2T 2R所以F 0-W 0F 0=m 4π2T 2R G MmR2代入数据,解得F 0-W 0F 0=3×10-3.这一计算结果说明,由于地球自转对地球赤道外地面上静止的物体所受重力与所受地球引力大小差别的影响很小,所以通常情况下可以忽略地球自转造成的地球引力与重力大小的区别.16.如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P 点沿水平方向以初速度v 0抛出一个小球,测得小球经时间t 落到斜坡上另一点Q ,斜面的倾角为α,已知该星球半径为R ,万有引力常量为G ,求:(1)该星球表面的重力加速度;(2)该星球的密度;(3)该星球的第一宇宙速度v ;(4)人造卫星绕该星球表面做匀速圆周运动的最小周期T.【答案】 (1)2v 0tan αt (2)3v 0tan α2πRtG(3)2v 0Rtan αt (4)2πR t 2v 0Rtan α【解析】(1)由平抛运动的知识得tan α=12gt 2v 0t ,则g =2v0tan αt ;17.(2017年广东珠海模拟)某火星探测实验室进行电子计算机模拟实验,结果为探测器在靠近火星表面轨道做圆周运动的周期是T ,探测器着陆过程中,第一次接触火星表面后,以v 0的初速度竖直反弹上升,经t 时间再次返回火星表面,设这一过程只受火星的重力作用,且重力近似不变.已知引力常量为G ,试求:(1)火星的密度;(2)火星的半径.【答案】ρ=M V =4π2R 3GT 243πR 3=3πGT 2. ;R =v 0T 22π2t .(2)探测器在火星表面的万有引力近似等于重力,有G mM R 2=mg ′,③ 根据题意有探测器在火星表面反弹后做竖直上抛运动,根据竖直上抛运动落回抛出点的时间t =2v 0g ′得火星表面的重力加速度g ′=2v 0t,④ 将②④代入③得R =v 0T 22π2t.学科&网 18.由于地球自转的影响,地球表面的重力加速度会随纬度的变化而有所不同.已知地球表面两极处的重力加速度大小为g 0,在赤道处的重力加速度大小为g ,地球自转的周期为T ,引力常量为G .假设地球可视为质量均匀分布的球体.求:(1)质量为m 的物体在地球北极所受地球对它的万有引力的大小;(2)地球的半径;(3)地球的密度.【解析】:(1)质量为m 的物体在两极所受地球的引力等于其所受的重力,即F =mg 0.(2)设地球的质量为M ,半径为R ,在赤道处随地球做圆周运动物体的质量为m .物体在赤道处随地球自转做圆周运动的周期等于地球自转的周期,轨道半径等于地球半径.根据万有引力定律和牛顿第二定律有GMm R 2-mg =m 4π2T 2R ;在赤道的物体所受地球的引力等于其在两极所受的重力即GMm R 2=mg 0,解得 R =g 0-g T 24π2. (3)因为G Mm R 2=mg 0,所以 M =g 0R 2G .又因地球的体积V =43πR 3,所以ρ=M V =3πg 0GT 2g 0-g.。
2021届高三物理二轮复习常考模型微专题复习—天体质量和密度计算专题(含解析)
天体质量和密度计算专题一、单选题1.我国首个月球探测计划“嫦娥工程”分三个阶段实施,大约用十年左右时间完成,假设“嫦娥四号”探测器在距月球表面高度为6R的圆形轨道I上做匀速圆周运动,运行周期为T,到达轨道的A点时点火变轨进入椭圆轨道II,到达轨道的近月点B时,再次点火进入近月轨道III绕月做匀速圆周运动,如图所示,已知月球半径为R,重力加速度约为16g,引力常量为G,则下列说法正确的是A. 月球的质量可表示为343π2R3GT2B. 在轨道II上B点速率等于√16gRC. “嫦娥四号”探测器在椭圆轨道II上的周期小于轨道I上的周期D. “嫦娥四号”探测器在轨道I上的机械能小于轨道II上的机械能2.假设宇宙中有两颗相距无限远的行星A和B,半径分别为R A和R B两颗行星周围卫星的轨道半径的三次方(r3)与运行周期的平方(T2)的关系如图所示,T0为卫星环绕行星表面运行的周期。
则()A. 行星A的质量小于行星B的质量B. 行星A的密度小于行星B的密度C. 行星A的第一宇宙速度等于行星B的第一宇宙速度D. 当两行星的卫星轨道半径相同时,行星A的卫星向心加速度大于行星B的卫星向心加速度3.2019年6月25日2时09分,我国在西昌卫星发射中心用长征三号乙运载火箭,成功发射第46颗北斗导航卫星。
目前已有46颗卫星在轨运行,其每一颗卫星运动的周期会因轨道半径的不同而不同,根据测得的不同卫星做圆周运动的半径r与周期T作出如图所示的图像,则可求得地球密度为________。
(已知引力常量为G,地球的半径为R)()A. 3πaGR3b B. GR3b3πaC. 3πbGR3aD. GR3a3πb4.某高中的航天兴趣小组查询相关资料获取到以下信息:①忽略地球自转时,距地心距离r处的引力场强度a随r变化的曲线如图所示,R为地球的半径,在0~R范围内是过原点的直线,在R~∞范围内是遵从“平方反比”的曲线,即在此区间内,引力场强度a与距地心距离r的平方成反比,引力场某点的强度等于质点在该点受到的万有引力除以质点的质量;②轨道高度ℎ=R处有一卫星A绕地球做匀速圆周运动的周期为T;③引力常量G。
高考物理3年高考2年模拟1年原创专题5.2天体质量和密度的估算含解析
专题5.2 天体质量和密度的估算【考纲解读与考频分析】利用万有引力等于重力可以估算地球质量,若测量出绕天体运行卫星的周期和轨道半径可以估算天体的质量,若知道天体的半径,可以估算出天体的密度。
高考有关天体质量和密度的估算考查频率较高。
【高频考点定位】:天体质量和密度的估算考点一:天体质量和密度的估算【3年真题链接】1.(2018高考理综II·16)2018年2月,我国500 m口径射电望远镜(天眼)发现毫秒脉冲星“J0318+0253”,其自转周期T=5.19 ms,假设星体为质量均匀分布的球体,已知万有引力常量为。
以周期T稳定自转的星体的密度最小值约为()A. B.C. D.【参考答案】C【命题意图】本题考查万有引力定律、牛顿运动定律、密度及其相关的知识点。
【解题思路】设脉冲星质量为M,半径为R。
选取脉冲星赤道上一质元,设质量为m,由万有引力定律和牛顿第二定律可得G=mR()2,星体最小密度ρ=M/V,星球体积V=πR3,联立解得:ρ=,代入数据得ρ=5×1015kg/m,选项C正确。
2.(2018高考全国理综I).2017年,人类第一次直接探测到来自双中子星合并的引力波。
根据科学家们复原的过程,在两颗中子星合并前约100 s时,它们相距约400 km,绕二者连线上的某点每秒转动12圈,将两颗中子星都看作是质量均匀分布的球体,由这些数据、万有引力常量并利用牛顿力学知识,可以估算出这一时刻两颗中子星()A.质量之积 B.质量之和 C.速率之和 D.各自的自转角速度【参考答案】BC【命题意图】本题考查天体运动、万有引力定律、牛顿运动定律及其相关的知识点。
【解题思路】双中子星做匀速圆周运动的频率f=12Hz(周期T=1/12s),由万有引力等于向心力,可得,G=m1r1(2πf)2,G=m2r2(2πf)2,r1+ r2=r=40km,联立解得:(m1+m2)=(2πf)2Gr3,选项B正确A错误;由v1=ωr1=2πf r1,v2=ωr2=2πf r2,联立解得:v1+ v2=2πf r,选项C正确;不能得出各自自转的角速度,选项D错误。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《天体密度和质量的计算》一、计算题1.如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点沿水平方向以初速度抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为,已知该星球半径为R,万有引力常量为G,求:该星球表面的重力加速度;该星球的密度;人造卫星绕该星球表面做匀速圆周运动的周期T2.如图所示,火箭栽着宇宙探测器飞向某行星,火箭内平台上还放有测试仪器火箭从地面起飞时,以加速度竖直向上做匀加速直线运动为地面附近的重力加速度,已知地球半径为R.到某一高度时,测试仪器对平台的压力是刚起飞时压力的,求此时火箭离地面的高度h.探测器与箭体分离后,进入行星表面附近的预定轨道,进行一系列科学实验和测量,若测得探测器环绕该行星运动的周期为,试问:该行星的平均密度为多少?假定行星为球体,且已知万有引力恒量为3.飞船沿半径为R的圆周绕地球运动,其周期为T,如果飞船要返回地面,可在轨道上的某一点A处,将速率降低到适当数值,从而使飞船沿着以地心为焦点的特殊椭圆轨道运动,椭圆和地球表面在B点相切,如图所示,如果地球半径为,万有引力常量G已知,求地球的密度飞船由A点到B点所需的时间。
4.我国月球探测计划嫦娥工程已经启动,“嫦娥1号”探月卫星也已发射。
设想嫦娥1号登月飞船贴近月球表面做匀速圆周运动,飞船发射的月球车在月球软着陆后,自动机器人在月球表面上沿竖直方向以初速度抛出一个小球,测得小球经时间t 落回抛出点,已知该月球半径为R,万有引力常量为G,月球质量分布均匀。
求:月球表面的重力加速度;月球的密度;月球的第一宇宙速度。
5.宇航员在月球表面完成下面的实验:在一固定的竖直光滑圆轨道内部有一质量为m的小球可视为质点,如图所示当在最高点给小球一瞬间的速度v时,刚好能使小球在竖直平面内做完整的圆周运动。
已知圆弧的轨道半径为r,月球的半径为R,引力常量为求:若在月球表面上发射一颗环月卫星,所需最小发射速度为多大?月球的平均密度为多大?轨道半径为2R的环月卫星周期为多大?6.已知某星球半径为R,若宇航员随登陆舱登陆该星球后,在此星球表面某处以速度竖直向上抛出一个小球,小球能上升的最大高度为,不考虑星球自转的影响,引力常量为。
求星球表面的自由落体加速度和该星球的质量;在登陆前,宇宙飞船绕该星球做匀速圆周运动,运行轨道距离星球表面高度为h,求卫星的运行周期T.7.宇航员站在一星球表面上高h处,以初速度沿水平方向抛出一个小球,小球落地时的水平位移为已知该星球的半径为R,不计星球自转,万有引力常量为G,求:该星球表面的重力加速度;该星球的质量;该星球的第一宇宙速度。
8.如图所示,“嫦娥三号”探测器在月球上着陆的最后阶段为:当探测器下降到距离月球表面高度为h时,探测器速度竖直向下,大小为v,此时关闭发动机,探测器仅在重力月球对探测器的重力作用下落到月面已知从关闭发动机到探测器着地时间为t,月球半径为R且,引力常量为G,忽略月球自转影响,则:月球表面附近重力加速度g的大小;月球的质量M.9.一航天仪器在地面上重为,被宇航员带到月球表面上时重为已知月球半径为R,引力常量为G,地球表面的重力加速度大小为,求:月球的密度;月球的第一宇宙速度和近月卫星贴近月球表面的周期.10.宇航员站在星球表面,从高h处以初速度水平抛出一个小球,小球落到星球表面时,与抛出点的水平距离是x,已知该星球的半径为R,引力常量为G,求该星球的质量M.11.2016年8月16日,我国科学家自主研制的世界首颗量子科学实验卫星“墨子号”成功发射,并进入预定圆轨道.已知“墨子号”卫星的质量为m,轨道离地面的高度为h,绕地球运行的周期为T,地球半径为R,引力常量为求:“墨子号”卫星的向心力大小;地球的质量;第一宇宙速度.12.物体在地球上不同纬度处随地球自转所需向心力的大小不同,故同一个物体在地球上不同纬度处重力大小不同,在地球赤道上的物体受到的重力与其在地球两极点受到的重力大小之比约为299:300,因此我们通常忽略两者的差异,可认为两者相等.而有些星球,却不能忽略.假如某星球因为自转原因,一物体在赤道上的重力与其在该星球两极点受到的重力大小之比为5:6,已知该星球的半径为R,求绕该星球运动的同步卫星的轨道半径r;若已知该星球赤道上的重力加速度大小为g,万有引力常量为G,求该星球的密度.13.某行星的自转周期为T,用弹簧测力计在该行星的“赤道”和“两极”处测同一物体的重力,弹簧测力计在赤道上的读数比在两极上的读数小引力常量为G,行星视为球体.求行星的平均密度;设想该行星自转角速度加快到某一值时,在“赤道”上的物体会“飘”起来,求此时的自转周期.14.中国计划在2017年实现返回式月球软着陆器对月球进行科学探测,宇航员在月球上着陆后,将一个小球从距月球表面高度h处自由释放,测得小球从静止落到月球上的时间为t,不计阻力.已知月球半径为R,万有引力常量为求:月球的质量月;如果要在月球上发射一颗绕月球运行的卫星,所需的最小发射速度;当着陆器绕距月球表面高H的轨道上运动时,着陆器环绕月球运动的周期.15.“嫦娥一号”卫星在距月球表面高度为h处做匀速圆周运动的周期为T,已知月球半径为R,引力常量为球的体积公式,其中R为球的半径求:月球的质量M;月球的密度;月球表面的重力加速度g.16.科学家观测到某一卫星环绕月球做匀速圆周运动,卫星距月球表面的高度为己知月球半径为R,月球质量为M,引力常量为G,忽略月球自转影响.求:月球表面的重力加速度g;该卫星绕月球运行时速度v;该卫星环绕月球运行的周期T.17.宇航员在地球表面以一定初速度竖直上抛一小球,经过时间t小球落回原处;若它在某星球表面以相同的初速度竖直上抛同一小球,需经过时间小球落回原处.取地球表面重力加速度,空气阻力不计,忽略星体和地球的自转求该星球表面附近的重力加速;已知该星球的半径与地球半径之比为星:地:2,求该星球的质量与地球质量之比星:地.18.一颗“北斗”导航卫星在距地球表面高度为h的轨道上做匀速圆周运动,已知地球半径为R,引力常量为G,地球表面的重力加速度为求:地球的质量M;地球的第一宇宙速度;该“北斗”导航卫星做匀速圆周运动的周期T.19.“嫦娥一号”的成功发射,为实现中华民族几千年的奔月梦想迈出了重要的一部,假设“嫦娥一号”在月球的近地轨道上做匀速圆周运动,绕行周期为T,月球的半径为R,万有引力常量为G。
求月球的质量M;求月球表面的重力加速度g。
20.我国已经进入全面的天空活动中,2016年10月19日,神舟十一号载人飞船与天宫二号空间实验室成功实现自动交会对接,再次引起人们对月球的关注.我国发射的“嫦娥三号”探月卫星在环月圆轨道绕行n圈所用时间为t,如图所示.已知月球半径为R,月球表面处重力加速度为月,引力常量为试求:月球的质量M;月球的第一宇宙速度;“嫦娥三号”卫星离月球表面高度h.21.已知地球的半径为R,地球表面的重力加速度为g,引力常量为G,求地球的平均密度;假设“神舟七号”飞船进入预定轨道后绕地球做匀速圆周运动,运行的周期是T,求飞船绕地球飞行时离地面的高度h.22.10年10月1日,我国“嫦娥二号”探月卫星成功发射。
“嫦娥二号”卫星开始绕地球做椭圆轨道运动,经过若干次变轨、制动后,最终使它绕月球在一个圆轨道上运行。
设“嫦娥二号”距月球表面的高度为h,绕月圆周运动的周期为T。
已知月球半径为R,引力常量为G。
求:月球的质量M;月球表面的重力加速度g;若发射一颗绕月球表面做匀速圆周运动的飞船,则其绕月运行的线速度应为多大。
23.宇航员到达某行星上,一小球从高为h处自由下落,落到星球表面时速度为,设行星的半径为R、引力常量为G,求:该行星表面的重力加速度大小;该行星的质量。
24.天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星.双星系统在银河系中很普遍.利用双星系统中两颗恒星的运动特征可以推算出它们的总质量.已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动,周期均为T,两颗恒星之间的距离为r试推算这个双星系统的总质量引力常量为研究发现,双星系统演化过程中,两星的总质量、距离和周期均可能发生变化.若某双星系统中两星经过一段时间的演化后,两星总质量变为原来的k倍,两星间距变为原来的n倍,则此时双星做圆周运动的周期变为原来的多少倍?25.一颗卫星以轨道半径r绕地球做匀速圆周运动,已知引力常量为G,地球半径R,地球表面的重力加速度g,求:地球的质量M;该卫星绕地球运动的线速度大小v。
26.火星探测飞行器发送回的信息表明,探测器关闭发动机后,在离火星表面为h的高度沿圆轨道运行过程中,测得周期为T,已知火星半径为R,引力常量为G.求火星的密度.求火星表面的重力加速度.27.卡文迪许利用微小量放大法由实验测出了万有引力常量G的数值,因为由G的数值及其它已知量,就可以计算出地球的质量,卡文迪许也因此被誉为第一个“称量”地球的人.若在某次实验中,卡文迪许测出质量分别为、相距为r的两个小球之间引力的大小为F,求万有引力常量G;若已知地球半径为R,地球表面重力加速度为g,万有引力常量为G,忽略地球自转的影响,请推导出地球质量M.28.在月球表面上沿竖直方向以初速度抛出一个小球,测得小球经时间t落回抛出点,已知该月球半径为R,万有引力常量为G,月球质量分布均匀。
求:月球的密度;月球的第一宇宙速度。
答案和解析1.【答案】解:设该星球表现的重力加速度为g,根据平抛运动规律:水平方向:竖直方向:平抛位移与水平方向的夹角的正切值得;在星球表面有:,该星球的密度:解得;由,可得,又,所以;绕星球表面运行的卫星具有最小的周期,即:该星球表面的重力加速度为;该星球的密度为;人造卫星绕该星球表面做匀速圆周运动的周期T为。
【解析】根据平抛运动规律列出水平方向和竖直方向的位移等式,结合几何关系求出重力加速度。
忽略地球自转的影响,根据万有引力等于重力列出等式。
根据密度公式求解。
该星球的近地卫星的向心力由万有引力提供,该星球表面物体所受重力等于万有引力,联立方程即可求出该星球的第一宇宙速度v。
处理平抛运动的思路就是分解。
重力加速度g是天体运动研究和天体表面宏观物体运动研究联系的物理量。
2.【答案】解:火箭刚起飞时,以测试仪为研究对象,受地球引力、平台的支持力,有:根据牛顿第三定律,起飞时测试仪器对平台的压力大小为.设火箭离地高为h时,平台对测试仪器的支持力为,则有:,其中G为万有引力恒量,M为地球质量.在地面附近,有:则:于是得到:设行星质量为M,行星平均密度为,又有:得:.答到某一高度时,测试仪器对平台的压力是刚起飞时压力的,此时火箭离地面的高度h为.探测器与箭体分离后,进入行星表面附近的预定轨道,进行一系列科学实验和测量,若测得探测器环绕该行星运动的周期为,则该行星的平均密度为.【解析】以测试仪器为研究对象,根据牛顿第二定律求出某一高度处的重力加速度,再由重力等于万有引力,代入数据求解火箭离地面的高度.现根据万有引力提供向心力,求出行星的质量,再根据密度的定义式,计算密度.本题中称为黄金代换式,反映了重力加速度与高度的关系,可根据重力与万有引力推导出来的.3.【答案】解:设地球质量为M,飞船质量为m,飞船沿半径为R的圆周绕地球运动,其周期为T,由牛顿第二定律得:,地球质量:,解得地球的密度为:;根据题意得椭圆轨道的半长轴根据开普勒第三定律得:,因为,解得:则飞船由A点到B点的运动时间为:。
