单缝的夫琅禾费衍射PPT课件
合集下载
实验18 单缝和双缝衍射的光强分布ppt

物理实验教学示范中心
10
杭州电子科技大学
实验内容
物理实验教学示范中心
1.测量夫琅禾费单缝衍射光强分布: (1)按图6安放实验仪器。
打开激光器和检流 计开关预热30分钟。 调节激光器使激光 束垂直照射于狭缝 平面上。
11
杭州电子科技大学
物理实验教学示范中心
(2)调节狭缝支架,使屏上衍射图样清晰、对称、 最亮且条纹间距适当。方法是用光电探头测±1级 次极大的光电流是否相等,若不相等,可调节狭缝 位置。 (3)测量光强分布。转动一维光强测量装置的手 轮,使光电探头逐点扫描,每隔0.2mm(或0.5mm) 记录一次光电流,并注意记录极大值和极小值。 (4)作光强分布曲线。在坐标纸上作出相对光电 流i/i0(即相对光强I/I0)与位置X的关系曲线,并与 理论结果进行比较。
4
杭州电子科技大学
物理实验教学示范中心
单缝夫琅禾费衍射及其衍射图阵如图1所示 当使用氦氖激光器作为光源及屏缝间距 D远大于狭缝宽度a时,凸透镜l1和l2可以 省略,如图2所示。
杭州电子科技大学
物理实验教学示范中心
由理论计算可得,垂直入射于单缝平面的平 行光经单缝衍射后光强分布的规律为
I
I0
sin 2 2
物理实验教学示范中心
2
物理实验教学示范中心
实验目的 1、通过对夫朗禾费单缝和双缝衍射的光
强分布曲线的制作,加深对光的衍射 现象和理论的理解。 2、学习光强分布的光电测量方法。 3、测量单缝宽度。
3
杭州电子科技大学
实验原理
物理实验教学示范中心
衍射是波动光学的重要特征之一。衍射通常 分为两类:一类是满足衍射屏离光源或接收屏的 距离为有限远的衍射,称为菲涅耳衍射;另一类 是满足衍射屏与光源和接收屏的距离都是无限远 的衍射,也就是照射到衍射屏上的入射光和离开 衍射屏的衍射光都是平行光的衍射,称为夫琅和 费衍射。
《高中物理光学课件-夫琅禾费衍射》

夫琅禾费衍射形成的图案通常是明暗交替的条纹,通过解析这些图案可以获取被衍射物体的信息。这种图案解 析技术在光学测量和成像中具有广泛应用。
同轴圆眼和夫琅禾费衍射
同轴圆眼是一种特殊的夫琅禾费衍射器,其结构能够实现对光波的高效控制。 同轴圆眼在光学成像和光学测量中有重要的应用。
衍射在日常生活中的应用
夫琅禾费衍射在日常生活中有许多应用,例如手机屏幕的显示技术、传感器的测量原理以及激光器的构造等。
夫琅禾费衍射的研究历史
夫琅禾费衍射的研究可以追溯到19世纪。这一时期,夫琅禾费和菲涅尔等物 理学家做出了重要的贡献,推动了衍射现象的理论和实验探索。
著名物理学家夫琅禾费和菲涅 尔的贡献
夫琅禾费和菲涅尔是夫琅禾费衍射理论的奠基人。他们的工作深刻地影响了 光学领域的发展,并为后来的研究提供了重要的理论基础。
ห้องสมุดไป่ตู้
衍射的量化分析-信噪比、分辨率等
夫琅禾费衍射可以通过信噪比、分辨率等参数进行量化分析。这些参数可以帮助我们评估衍射效果的好坏,从 而优化光学系统的设计。
衍射的影响因素-光源、裂缝、衍射板等
夫琅禾费衍射的效果受到多种因素的影响,包括光源的强度、裂缝的形状和大小,以及衍射板的特性等。理解 这些影响因素对于设计和优化衍射器件至关重要。
衍射在光学技术中的应用-光学传感、光学 测量、光学显示
夫琅禾费衍射在光学技术领域有广泛的应用。它被用于光学传感、光学测量和光学显示等领域,为这些技术的 发展提供了基础和创新。
衍射与光学成像技术的关系
衍射是光学成像技术中重要的一个环节。通过控制衍射现象,可以实现高分辨率的光学成像,进一步推动光学 成像技术的进步。
光阑和衍射器
光阑和衍射器是控制光波衍射的重要工具。光阑用于限制光波传播的范围,而衍射器则通过控制光波的传播路 径来实现特定的衍射效果。
同轴圆眼和夫琅禾费衍射
同轴圆眼是一种特殊的夫琅禾费衍射器,其结构能够实现对光波的高效控制。 同轴圆眼在光学成像和光学测量中有重要的应用。
衍射在日常生活中的应用
夫琅禾费衍射在日常生活中有许多应用,例如手机屏幕的显示技术、传感器的测量原理以及激光器的构造等。
夫琅禾费衍射的研究历史
夫琅禾费衍射的研究可以追溯到19世纪。这一时期,夫琅禾费和菲涅尔等物 理学家做出了重要的贡献,推动了衍射现象的理论和实验探索。
著名物理学家夫琅禾费和菲涅 尔的贡献
夫琅禾费和菲涅尔是夫琅禾费衍射理论的奠基人。他们的工作深刻地影响了 光学领域的发展,并为后来的研究提供了重要的理论基础。
ห้องสมุดไป่ตู้
衍射的量化分析-信噪比、分辨率等
夫琅禾费衍射可以通过信噪比、分辨率等参数进行量化分析。这些参数可以帮助我们评估衍射效果的好坏,从 而优化光学系统的设计。
衍射的影响因素-光源、裂缝、衍射板等
夫琅禾费衍射的效果受到多种因素的影响,包括光源的强度、裂缝的形状和大小,以及衍射板的特性等。理解 这些影响因素对于设计和优化衍射器件至关重要。
衍射在光学技术中的应用-光学传感、光学 测量、光学显示
夫琅禾费衍射在光学技术领域有广泛的应用。它被用于光学传感、光学测量和光学显示等领域,为这些技术的 发展提供了基础和创新。
衍射与光学成像技术的关系
衍射是光学成像技术中重要的一个环节。通过控制衍射现象,可以实现高分辨率的光学成像,进一步推动光学 成像技术的进步。
光阑和衍射器
光阑和衍射器是控制光波衍射的重要工具。光阑用于限制光波传播的范围,而衍射器则通过控制光波的传播路 径来实现特定的衍射效果。
单缝的夫琅禾费衍射
同学们好
缝平面
透镜L2
透镜L1
A
S
*
a
Bδ f
f
观察屏
·p
0
§17-9 单缝的夫琅禾费衍射
一. 装置
O
*
f
A
BC
P·x
0 f
缝宽a:其上每一点均为子波源发出衍射光
衍射角θ:衍射光线与波面法线夹角
P:
0
0
θ=0衍射光线汇集于L2的焦点 δ=0 中央明纹中心
θ≠0衍射光线汇集于L2的焦平面上某点P δ≠0 P处光强可由菲涅耳公式计算
零
三级 暗纹
二级 一级 中央明纹 暗纹 暗纹
一级 明纹
二级 明纹
3
2
a
a
a
0
3 a 2a
sin
5 2a
2
2
2
22
2
暗纹公式中k=0,δ=0,为中央明纹中心,
不是暗纹
明纹公式中可k=0, δ=λ/2,仍在中央明纹区不 是明纹中心
(3暗纹和中央明纹位置精确其他明纹位置只 是 近似
1 I / I0 相对光强曲线
屏幕
讨论:
(1单缝衍射明暗纹条件是否与双缝干涉明暗纹条 件矛盾
双缝干涉 单缝衍射
明纹条件
k
(2k1)
2
暗纹条件 (2k1) k
max
2
条纹级次 k 0 、 1 、 2 、 k1 、 2 、
不矛盾单缝衍射δ不是两两相干光线的光程差而 是衍射角为θ的一束光线的最大光程差
(2单缝衍射明暗纹条件中 k 值为什么不能取
衍射屏 透镜
观测屏 x2
角宽度为:
λ
x1 Δx
缝平面
透镜L2
透镜L1
A
S
*
a
Bδ f
f
观察屏
·p
0
§17-9 单缝的夫琅禾费衍射
一. 装置
O
*
f
A
BC
P·x
0 f
缝宽a:其上每一点均为子波源发出衍射光
衍射角θ:衍射光线与波面法线夹角
P:
0
0
θ=0衍射光线汇集于L2的焦点 δ=0 中央明纹中心
θ≠0衍射光线汇集于L2的焦平面上某点P δ≠0 P处光强可由菲涅耳公式计算
零
三级 暗纹
二级 一级 中央明纹 暗纹 暗纹
一级 明纹
二级 明纹
3
2
a
a
a
0
3 a 2a
sin
5 2a
2
2
2
22
2
暗纹公式中k=0,δ=0,为中央明纹中心,
不是暗纹
明纹公式中可k=0, δ=λ/2,仍在中央明纹区不 是明纹中心
(3暗纹和中央明纹位置精确其他明纹位置只 是 近似
1 I / I0 相对光强曲线
屏幕
讨论:
(1单缝衍射明暗纹条件是否与双缝干涉明暗纹条 件矛盾
双缝干涉 单缝衍射
明纹条件
k
(2k1)
2
暗纹条件 (2k1) k
max
2
条纹级次 k 0 、 1 、 2 、 k1 、 2 、
不矛盾单缝衍射δ不是两两相干光线的光程差而 是衍射角为θ的一束光线的最大光程差
(2单缝衍射明暗纹条件中 k 值为什么不能取
衍射屏 透镜
观测屏 x2
角宽度为:
λ
x1 Δx
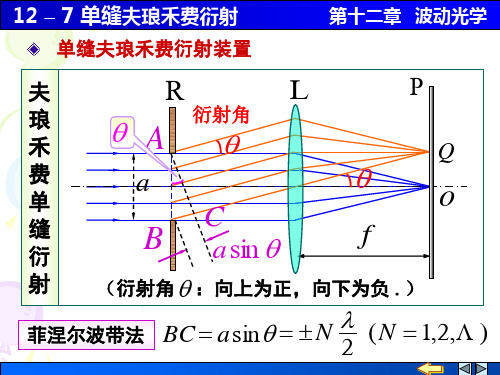
12-07 单缝夫琅禾费衍射
o
a
2
a
3
a
sin
12 – 7 单缝夫琅禾费衍射
S
L1 R
L2
a
第十二章 波动光学
Px
f
x
O
I 当 较小时,sin
x f tan f
3
a
2
a
a
o
a
2
a
3
a
sin
3
a
f
2
a
f
a
f
a
f
2
a
f
3
a
f
x
12 – 7 单缝夫琅禾费衍射
第十二章 波动光学
a sin 2k k 干涉相消(暗纹)
发射的微波波长是18mm ,则在它监视范围内的公路长 度大约是多少?
解 将雷达天线输出口看成是发出衍射波的单缝, 衍射波能量主要集中在中央明纹范围内.
d 15m
15 a 0.10m
12 – 7 单缝夫琅禾费衍射
第十二章 波动光学
s1
s s2
1 15
2
d 15m
a 0.10m
根据暗纹条件 a sin , arcsin 10.37
a
s2 s s1 d (cot2 cot1)
d[cot(15 ) cot(15 )] 153m
解 AD BC
a(sin sin)
由暗纹条件
a(sin sin) k
(k 1,2,3, )
A
a
D
C
B
arcsin(
k
a
sin )
12 – 7 单缝夫琅禾费衍射
第十二章 波动光学
例3 如图,一雷达位于路边 15m 处,它的射束与
6.7 夫琅禾费单缝衍射和矩孔衍射

这些次波都可认为是球面次波,各自向前传播。
4
A0 dx dE0 cos t b
首先对其中传播方向与原入射方向成角(称为衍 射角)的所有各次波进行研究。 屏幕
dx
S
F1
x
r
r0
x
0
x sin
M点与B点到达P点的光程差为 2 x sin 相位差为:
B
'B
M
2. 衍射光强分布公式:
为了计算衍射场中任一点P 的强度,设平行光束垂直 于缝的平面入射,波面与缝平面重合。 按惠更斯—菲涅耳原理,把缝内的波面分割为许多等 宽的窄条dx,从每一条窄带发出的次波的振幅正比于窄 带的宽度dx,设光波的初相位为0,缝宽为b,A0为整个 狭缝所发出的次波在=0 的方向上的合振幅,狭缝单 位宽度发出次波的振幅为A0 /b。而宽度为dx窄带所发出 的次波的振幅为A0 dx /b,则振动表达式为
y f tan1 50cm 0.03rad 1.5cm
所以中央亮纹中心的宽度为
y 2 y 2 1.5cm=3cm
20
本节结束
物理科学与信息工程学院 21
P
F '2
x sin
物理科学与信息工程学院 5
则M点的次波到达P点的光振动的表达式为:
A0 dx 2 dE cos t x sin b
或
A0 dx dE e b
2 i x sin t
2
其复振幅为
~ A0 dx dE e b
2
-称为单缝衍 射因子
dI d sin 2 u A0 ( 2 )0 u du du u (1) 主最大(中央亮纹中心)位置:
单缝衍射 ppt课件

PPT课件
26
单缝衍射
第20章 光的衍射
单缝宽度变化,中央明纹宽度如何变化?
PPT课件
27
单缝衍射
第20章 光的衍射
入射波长变化,衍射效应如何变化 ?
越大, 越大,衍射效应越明显.
1
PPT课件
28
单缝衍射
第20章 光的衍射
PPT课件
29
单缝衍射
单缝上下移动
R
A
a
B
第20章 光的衍射
Lf
P
PPT课件
39
单缝衍射
第20章 光的衍射
例 设有一单色平面波斜射到宽度为 b 的单缝
上(如图),求各级暗纹的衍射角 .
解 Δ AD BC
b(sin sin)
由暗纹条件
b(sin sin) k
(k 1,2,3,)
A
b
D
C
B
arcsin( k sin)
b
PPT课件
40
单缝衍射
第20章 光的衍射
例2 如图,一雷达位于路边 15m 处,它的射束与
公路成15角. 假如发射天线的输出口宽度 b 0.10m,
发射的微波波长是18mm ,则在它监视范围内的公路长 度大约是多少?
提示 将雷达天线输出口看成是发出衍射波的单缝, 衍射波能量主要集中在中央明纹范围内.
15
d 15m
b 0.10m
PPT课件
对应位置为___暗___条纹,此时单缝的波 阵面可分为____1_0__个半波带。
若将缝宽缩小一半,则此位置将变为
_明___条纹
PPT课件
19
单缝衍射
练习2:
第20章 光的衍射
夫琅禾费单缝衍射
当 = 2 时,可将缝分成四个“半波带”,
它们发的光在 P 处两两相消,又形成暗纹……
菲涅耳半波带的数目决定于 bsin
P•
•
•
2
f
对应沿方向衍射
的平行光狭缝,波 阵面可分半波带数
k
b sin
2
1、k 由 b、、 确定。
2、k 不一定是整数。
三、单缝衍射明暗条纹条件
由半波带法可得明暗纹条件为:
a sin1
0 21
1 sin1
中央明纹
1
a
k 1
k2
0
2
a
上式为中央明纹角宽度
中央明纹线宽度
x
x0
2 x1
2
ftg 0
2
f 0
2 f
a
xk
k2
x0
2 f
a
(a, )
其他明纹宽度
0 2 1
f
k 1 O中明央纹
a sin k k
tg k
xk f
tg k sin k
xk
k
f
a
f xk a
0.017 0.047
0.047 0.017
-2( /a) -( /a) 0 /a 2( /a) sin
中央极大值对应的明条纹称 中央明纹。 中央极大值两侧的其他明条纹称 次极大。
明纹暗纹的图示
sin Δ x / f
中央亮纹的半角宽
1
x
f
(1)明纹宽度
中央明纹:两个一级暗纹间的距离,
为1
1
级暗纹对应的衍射角
xkk
条纹散开了 b
光通量减少,
清晰度变差。
分析与讨论:
12-8单缝的夫琅禾费衍射
f
x0
2f
tan 1
2 f 12f来自aaB. 次极大
x
f
a
1 2
x0
前提仍然是很小
上页 下页 返回 退出
缝宽变化对条纹的影响
由
x
f
a
1 2
x0
知,缝宽越小,条纹宽度越宽
I
0
sin
当 a 时,
当 a 时,0
x ,此时屏幕呈一片明亮;
,x此时0屏幕上只显出单
一的明条纹单缝的几何光学像。
∴几何光学是波动光学在/a0时的极限情形
b
b
b
3 f 2 f f
bbb
f 2 f 3 f x
b
上页
下页b
返回
退b 出
衍射图样 衍射图样中各级条纹的相对光强如图所示.
1 I / I0 相对光强曲线
0.017 0.047
0.047 0.017
-2( /a) -( /a) 0 /a 2( /a) sin
中央极大值对应的明条纹称 中央明纹。 中央极大值两侧的其他明条纹称 次极大。 中央极大值两侧的各极小值称暗纹。
(P处干涉相消形成暗纹)
上页 下页 返回 退出
2.明暗纹条件
由半波带法可得明暗纹条件为:
a sin 2k k 1,2,3,L ——暗纹
2
a sin 2k 1 k 1,2,3,L
2
——明纹(中心)
asin 0
——中央明纹(中心)
上述暗纹和中央明纹(中心)的位置是准确的,其余 明纹中心的实际位置较上稍有偏离。
上页 下页 返回 退出
明纹宽度
A. 中央明纹
当 a 时 , 1 级暗纹对应的衍射角
单缝的夫琅禾费衍射
a si n k , k 1 ,2 ,3 … ——暗纹
a s i n (2 k 1 ), k 1 ,2 ,3 … 2 ——明纹(中心)
asin 0
——中央明纹(中心)
上述暗纹和中央明纹(中心)的位置是准确的,其余明 纹中心的实际位置较上稍有偏离。
单缝的夫琅禾费衍射
3.3 衍射图样
衍射图样中各级条纹的相对光强如图所示.
x1 2x0f
a
知
x
波长越长,条纹宽度越宽。
单缝的夫琅禾费衍射
例题17-8 水银灯发出的波长为546nm的绿色平行 光,垂直入射于宽0.437mm的单缝,缝后放置一焦 距为40cm的透镜,试求在透镜焦面上出现的衍射条 纹中央明纹的宽度。
解 两个第一级暗纹中心间的距离即为中央明 纹宽度,对第一级暗条纹(k=1)求出其衍射角
1 I / I0 相对光强曲线
0.017 0.047
0.047 0.017
Hale Waihona Puke -2( /a) -( /a) 0 /a 2( /a) sin
中央极大值对应的明条纹称 中央明纹。
中央极大值两侧的其他明条纹称 次极大。
中央极大值两侧的各极小值称暗纹。
单缝的夫琅禾费衍射
(1)明纹宽度
A. 中央明纹
当 a时 ,1 级暗纹对应的衍射角
单缝的夫琅禾费衍射
(2) 缝宽变化对条纹的影响
由
x12x0f
a
知,缝宽越小,条纹宽度越宽
I
0
sin
当 a 时, x,此时屏幕呈一片明亮;
当 a 时,0
此x 时屏0, 幕上只显出单
一的明条纹 单缝的几何光学像。
∴几何光学是波动光学在/a0时的极限情形
光学之夫琅禾费单缝衍射的强度和条纹
完整版课件ppt
7
{范例7.5} 夫琅禾费单缝衍射的强度和条纹
BCkasink2k2
A aθ
F O
(k = 1,2,3,…)
C
缝长 B λ/2
f
可见:AB间最大光差等于入射光半 波长的偶数倍时,也就是单缝被分 割成偶数个半波带时(最少2个),
k =1,2,3,…的条纹分 别称为第一级暗条纹, 第二级暗条纹,第三级
根据相邻半波带干涉相消的原则, 暗条纹,…,式中的正
几何路程不同,却有相同的光程。
从而干涉互相加强。
单缝中心O处出现一条与单完缝整版平课件行pp的t 亮条纹,即中央明条纹。1
{范例7.5} 夫琅禾费单缝衍射的强度和条纹
波长为λ的单色光,平行通过宽度为a的单缝,产生的衍射称为
夫琅禾费单缝衍射。(1)说明半波带理论,分析衍射明暗条纹的
分布规律。在什么地方光强最大? 单缝 L
由于Δφ很小,所以sinΔφ = Δφ,因此
A
A0
sin u u
单缝 L A
y F
其中A0 = nΔA,u = πasinθ/λ。
θ
O
F点的 光强为
I
I
0
(
sinu u
)2
其中I0
=
A02。
aB
C Δδ
当θ→0时,u→0,因此I→I0。I0是最大光强,称为主极大。
单缝衍射中间的明纹是中央明纹,主极大是明纹中心的光强。
y
如图所示,设δ = asinθ,
A
F
θ称为衍射角,δ是BF与AF之 间的光程差,代表AB之间所
aθ
O
有点光源的最大光程差。
C
用与AC平行的平面将BC分割成 缝长 B λ/2
