实验三 用matlab求极限和导数

实验三 用matlab 求极限和导数
1.求极限、导数的MATLAB 命令
MATLAB 中主要用limit,diff 分别求函数的极限与导数。
可以用help limit, help diff 查阅有关这些命令的详细信息
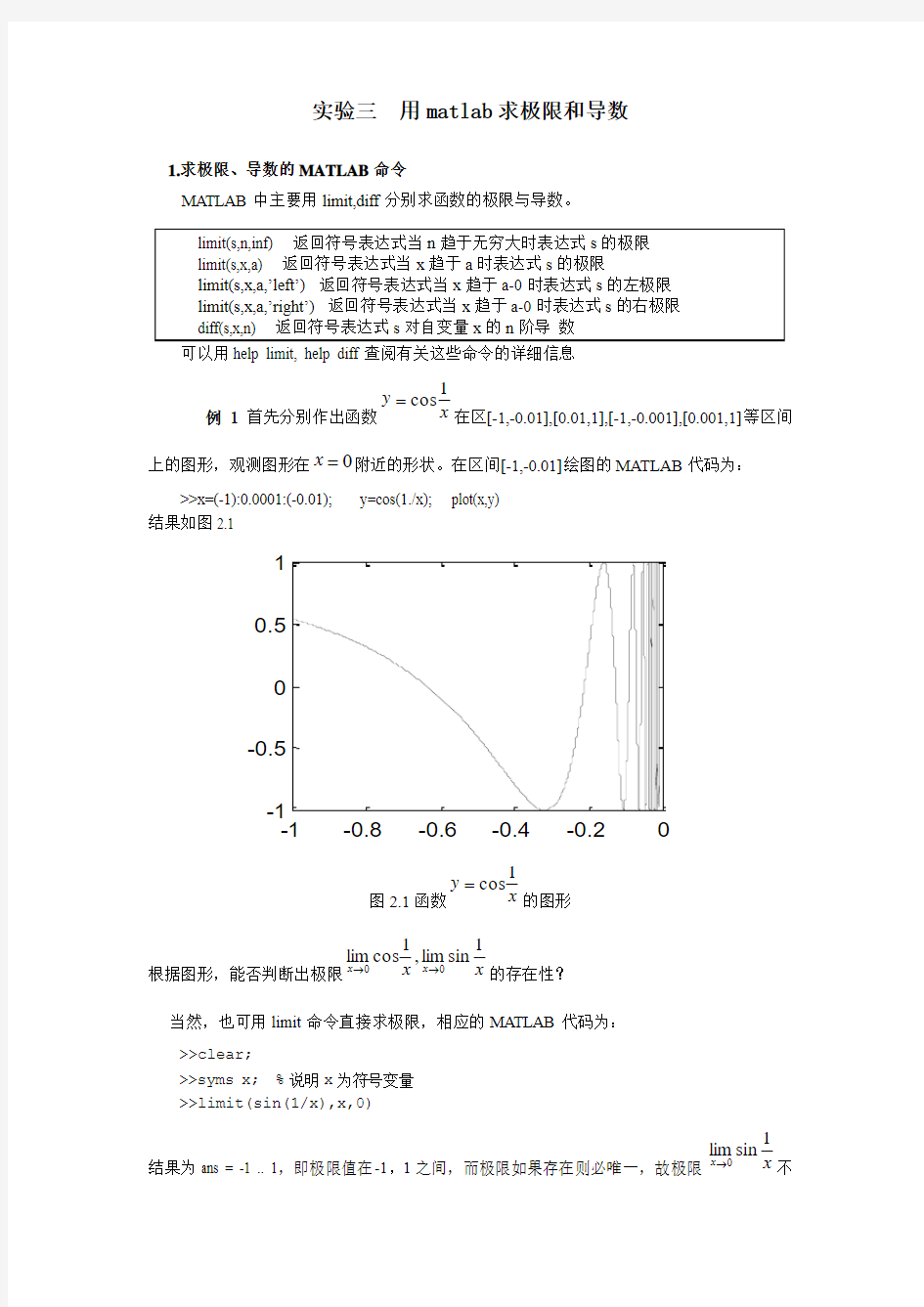
例1首先分别作出函数
x y 1
cos
=在区[-1,-0.01],[0.01,1],[-1,-0.001],[0.001,1]等区间
上的图形,观测图形在0=x 附近的形状。在区间[-1,-0.01]绘图的MA TLAB 代码为: >>x=(-1):0.0001:(-0.01); y=cos(1./x); plot(x,y) 结果如图2.1
图2.1函数
x y 1
cos
=的图形
根据图形,能否判断出极限x x x x 1
sin
lim ,1cos lim 00
→→的存在性? 当然,也可用limit 命令直接求极限,相应的MATLAB 代码为:
>>clear;
>>syms x; %说明x 为符号变量
>>limit(sin(1/x),x,0)
结果为ans = -1 .. 1,即极限值在-1,1之间,而极限如果存在则必唯一,故极限x x 1sin
lim 0
→不
存在,同样,极限x x 1
cos
lim 0
→也不存在。 例2 首先分别作出函数
x x
y sin =
在区间[-1,-0.01],[0.01,1],[-1,-0.001],[0.001,1]等区间上
的图形,观测图形在0=x 附近的形状。在区间[-1,-0.01]绘图的MA TLAB 代码为: >>x=(-1):0.0001:(-0.01); y=sin(x)./x; plot(x,y) 结果如图2.2
图2.2 函数
x x
y sin =
的图形
根据图形,能否判断出极限1
sin lim
0=→x x
x 的正确性?
当然,也可用limit 命令直接求极限,相应的MATLAB 代码为:
>>clear; >>syms x;
>>limit(sin(x)/x,x,0) 结果为ans =1.
例3 观测当n 趋于无穷大时,数列n n n a )11(+=和1
)1
1(++=n n n A 的变化趋势。例如,
当100,,2,1 =n 时,计算
n
n A a ,的MATLAB 代码为:
>>for n=1:100, a(n)=(1+1/n)^n;,A(n)=(1+1/n)^n ;, end
在同一坐标系中,画出下面三个函数的图形:
e
y x
y x y x x =+=+=+,
)1
1(,
)1
1(1
观测当x 增大时图形的走向。例如,在区间[10,400]绘制图形的MA TLAB 代码为
>>x=10:0.1:400;
>>y1=exp(x.*log(1+1./x)); y2=exp((x+2).*log(1+1./x)); y3=2.71828; >>plot(x,y1,'-.',x,y2,':',x,y3,'-'); %’-.’表示绘出的图形是点线,’-’是实
线
结果如图2.3,其中点线表示1)11(++=x x y 的图形,虚点线表示
x
x y )1
1(+=的图形。
图2.3
通过观测可以看到,当n 增大时,n n n a )11(+=递增,1
)11(++=n n n A 递减。随着n 的
无穷增大,
n
a 和
n
A 无限接近,趋于共同的极限 71828.2=e .当然,也可用limit 命令直
接求极限,相应的MATLAB 代码为:
>>clear; >>syms n;
>>limit((1+1/n)^n,n,inf)
结果为ans =exp(1)。
例4已知
2
()f x ax bx c =++,求()f x 的微分. >> f=sym('a*x^2+b*x+c') %定义函数表达式
f =a*x^2+b*x+c
>> diff(f) %对默认变量x 求一阶微分 ans =2*a*x+b
>> diff(f,'a') %对符号变量a 求一阶微分 ans =x^2
>> diff(f,'x',2) %对符号变量x 求二阶微分 ans =2*a
>> diff(f,3) %对默认变量x 求三阶微分 ans =0
例5 先求函数363+-=x x y ,然后在同一坐标系里作出函数
363
+-=x x y 及
其导函数
6
3
'2-
=x
y的图形。
函数求导相应的MA TLAB代码为:
>>clear;
>>syms x;
>>diff(x^3-6*x+3,x,1)
结果为ans =3*x^2-6
函数绘图相应的MA TLAB代码为:
>>x=-4:0.1:4; y1=x.^3-6*x+3; y2=3*x.^2-6;
>>plot(x,y1,x,y2,’:’)
结果如图2.4,其中实线是
3
6
3+
-
=x
x
y的图形,点线是6
3
'2-
=x
y的图形。
图2.4 函数及其导数
这里画的是区间[-4,4]上的图形,也可以选别的区间试试。
习题16-3
1.求下列各极限
(1)
n
n n
)
1
1(
lim-
∞
→(2)
n n
n
n3
lim3+
∞
→(3)
)
1
2
2
(
lim n
n
n
n
+
+
-
+
∞
→
(4)
)
1
1
1
2
(
lim
2
1-
-
-
→x
x
x(5)
x
x
x
2
cot
lim
→(6
)
)
3
(
lim2x
x
x
x
-
+
∞
→
(7)
x
x x
m
)
(cos
lim
∞
→(
8)1
11
lim()
1
x
x x e
-
→
-
-(9)0
1
lim
x
x
+
→
2.求下列函数的导数
(1)
1)
y=
(2)
sin ln
y x x x
=
(3)
sin
x
y e x
-
=(4)
y=
专题8极限与函数的导数的题型与方法
专题八 极限与函数的导数的题型与方法 【考点审视】 极限与导数作为初等数学与高等数学的衔接点,新课程卷每年必考,主要考查极限与导数的求法及简单应用。纵观近年来的全国卷与各省市的试卷,试题呈“一小一大”的布局,“小题”在选择、填空题中出现时,都属容易题;“大题”在解答题中出现时,极限通常与其它数学内容联系而构成组合题,主要考查极限思想与方法的灵活应用能力;导数的考查常给出一个含参的函数或应用建模,通过求导、分析函数的单调性与最值,考查“数形结合”、“分类讨论”等数学思想方法的综合运用能力。从2004年各地的高考试卷看,考生在备考时,应从下列考点夯实基础,做到以不变应万变: (1)从数列或函数的变化趋势了解极限概念,理解三个基本极限: 1)c c c n (lim =∞ →是常数),2)01 lim =∞→n n ,3)∞→n lim )1|(|0<=q q n . (2)明确极限四则运算法则的适用条件与范围,会求某些数列和函数的极限。 (3)了解函数连续的意义,理解闭区间上连续函数有最大值和最小值。 (4)了解导数的概念,掌握函数在一点处的导数定义,理解导函数的概念。 (5)熟记八个基本导数公式,掌握求导的四则运算法则,理解复合函数的求导法则,会求简单函数的导数。 (6)掌握导数的几何意义与物理意义,理解可导函数的单调性、极值与导数的关系,强化用导数解决实际问题的能力。 【疑难点拨】:1,极限的四则运算法则,只有当两数列或两函数各自都有极限时才能适用。对 00、∞ ∞ 、∞-∞、∞?0型的函数或数列的极限,一般要先变形或化简再运用法则求极限。例如(2004年辽宁,14)π ππ --→x x x x cos )(lim = 【分析】这是 00 型,需因式分解将分母中的零因子消去,故π ππ--→x x x x cos )(lim =x x x cos )(lim ππ +→=π2-。 2,极限的运算法则仅可以推广到有限个数列或函数,对于无穷项的和或积必须 先求和或积再求极限;商的极限法则,必须分母的极限不为零时才适用。例如: (2004年广东,4)-+++-+∞→131211( lim n n n n …+1 2112+-++n n n n )的值为…( ) (A )-1 (B )0 (C )2 1 (D )1 【分析】这是求无穷项的和,应先求前n 2项的和再求极限
导数和极限精辟总结(全)
导数和导数的极限 函数 )(x f 在 0x 点的左导数定义为 )(0x f -'x x f x x f x ?-?+=-→?)()(lim 000 。 函数 )(x f 在 0x 点的右导数定义为 )(0x f +'x x f x x f x ?-?+=+→?)()(lim 000 。 函数 )(x f 在 0x 点导数的左极限定义为 )0(0-'x f )(lim 0 0x f x x '=-→ 。 函数 )(x f 在 0x 点导数的右极限定义为 )0(0+'x f )(lim 0 0x f x x '=+→ 。 在很多情况下,导数的左极限 )(lim 0 0x f x x '-→ 往往就是左导数 )(0x f -' ,导数的右极限 )(lim 00x f x x '+→ 往往就是右导数 )(0x f +' 。 例如,函数 ?????≥<=1 11)(2x x x x x f 。 在 1=x 点的左导数为 )1(-'f 1111lim )1()1(lim 00-=?-?+=?-?+=-→?-→?x x x f x f x x ;导数的左极限为 )(lim 01x f x '-→1)1(lim )1(lim 20101-=-='=-→-→x x x x ,两者是一样的。 在 1=x 点的右导数为 21)1(lim )1()1(lim )1(200=?-?+=?-?+='+→?+→?+x x x f x f f x x ;导数的右极限为 )(lim 01x f x '+→2)2(lim )(lim 0 1201=='=+→+→x x x x ,两者也是一样的。 但有时候,导数的左极限 )(lim 0 0x f x x '-→ 并不等于左导数 )(0x f -' ,导数的右极限 )(lim 00x f x x '+→ 并不等于右导数 )(0x f +' 。
极限和导数
一、极限 极限是考研数学每年必考的内容,在客观题和主观题中都有可能会涉及到平均每年直接考查所占的分值在10分左右,而事实上,由于这一部分内容的基础性,每年间接考查或与其他章节结合出题的比重也很大。极限的计算是核心考点,考题所占比重最大。熟练掌握求解极限的方法是得高分的关键。考研教育\网 极限的计算常用方法:四则运算、洛必达法则、等价无穷小代换、两个重要极限、利用泰勒公式求极限、夹逼定理、利用定积分求极限、单调有界收敛定理、利用连续性求极限等方法。 四则运算、洛必达法则、等价无穷小代换、两个重要极限是常用方法,在基础阶段的学习中是重点,考生应该已经非常熟悉,进入强化复习阶段这些内容还应继续练习达到熟练的程度;在强化复习阶段考生会遇到一些较为复杂的极限计算,此时运用泰勒公式代替洛必达法则来求极限会简化计算,熟记一些常见的麦克劳林公式往往可以达到事半功倍之效;夹逼定理、利用定积分定义常常用来计算某些和式的极限,如果最大的分母和最小的分母相除的极限等于1,则使用夹逼定理进行计算,如果最大的分母和最小的分母相除的极限不等于1,则凑成定积分的定义的形式进行计算;单调有界收敛定理可用来证明数列极限存在,并求递归数列的极限。 与极限计算相关知识点包括: 1、连续、间断点以及间断点的分类:判断间断点类型的基础是求函数在间断点处的左、右极限,分段函数的连续性问题关键是分界点处的连续性,或按定义考察,或分别考察左、右连续性; 2、可导和可微,分段函数在分段点处的导数或可导性,一律通过导数的定义直接计算或检验,存在的定义是极限存在,求极限时往往会用到推广之后的导数定义式; 3、渐近线(水平、垂直、斜渐近线); 4、多元函数微分学,二重极限的讨论计算难度较大,多考察证明极限不存在。 二、导数 求导与求微分每年直接考查的知识所占分值平均在10分到13分左右。常考题型:(1)利用定义计算导数或讨论函数可导性;(2)导数与微分的计算(包括高阶导数);(3)切线与法线;(4)对单调性与凹凸性的考查;(5)求函数极值与拐点;(6)对函数及其导数相关性质的考查。 对于导数与微分,首先对于它们的定义要给予足够的重视,按定义求导在分段函数求导 中是特别重要的。应该熟练掌握可导、可微与连续性的关系。求导计算中常用的方法是四则运算法则和复合函数求导法则,一元函数微分法则中最重要的是复合函数求导法及相应的一阶微分形式不变性,利用求导的四则运算法则与复合函数求导法可求初等函数的任意阶导数。幂指函数求导法、隐函数求导法、参数式求导法、反函数求导法及变限积分求导法等都是复合函数求导法的应用。 导数计算中需要掌握的常见类型有以下几种: 1、基本函数类型的求导; 2、复合函数求导; 3、隐函数求导,对于隐函数求导,不要刻意记忆公式,记住计算方法即可,计算的时候要注意结合各种求导法则;
高等数学习题及解答(极限-连续与导数)
高等数学习题库 淮南联合大学基础部 2008年10月
第一章 映射,极限,连续 习题一 集合与实数集 基本能力层次: 1: 已知:A ={x|1≤x ≤2}∪{x|5≤x ≤6}∪{3},B={y|2≤y ≤3} 求:在直角坐标系内画出 A ×B 解:如图所示A ×B ={(x,y )| ,x A y B ∈∈ }. 2: 证明:∵ P 为正整数,∴p =2n 或p =2n+1,当p =2n+1时,p 2=4n 2+4n+1,不能被2整除,故p =2n 。即结论成立。 基本理论层次: 习题二 函数、数列与函数极限 基本能力层次 1: 解: 2: 证明:由得cxy ay ax b -=+即 ay b x cy a += -,所以 ()x f y = 所以命题成立
3: (1)2 2x y -= (2)lg(sin )y x = (3 []y x = (4)0,01,0x y x ≥?? =??取N =[1 ω ],则当n>N 时,就有 11|1|n n n ω--=<有定义变知1lim 1n n n →∞-=成立 5:求下列数列的极限 (1)lim 3n n n →∞ (2)222 3 12lim n n n →∞+++ (3) (4)lim n 解:(1) 233n n n n <,又 2lim 03n n x →∞=,所以 0lim 03n n n →∞≤≤ , 故:lim 3n n n →∞=0 (2)由于 222 3 312(1)(21)111 (1)(2)6n n n n n n n n n ++ +++= =++ 又因为:1111 lim (1)(2)63 n n n n →∞++=,所以:2223121 lim 3 n n n →∞+++ (3)因为: 所以: (4) 因为:111n n ≤+,并且1 lim(1)1n n →∞+=, 故由夹逼原理得 1n =
导数极限知识总结
导数极限知识总结——仅作了解切忌深究 一.洛必达法则是什么(鄙人觉得高中数学神器) 洛必达法则是在一定条件下通过分子分母分别求导再求极限来确定未定式值的方法。 在导数问题的3)问中通常会出现形似 的式子,而一般会出现求其导数,极值,甚至是某一点极限的问题,洛必达法则就是解决这一类而且不能用普通导数解决的问题。 引入:试求 试求 x x x x x sin sin lim +-∞→ 显而易见,这两个极限在以往的算法中一个是 式,一个则是∞ ∞ ,无法求导,这时就需要用到高端大气上 档次的洛必达法则了。 1.使用条件 定理1 若函数)(x f 与函数)(x g 满足下列条件: (1)在a 的某去心邻域)(x v 内可导,且0)('≠x g (2)0)(lim 0 =+→x f a x 0)(lim 0 =+→x g a x (3)A x g x f a x =+→)(')('lim 0 则A x g x f x g x f a x a x ==+→+→) (') ('lim )()(lim 00(包括A 为无穷大的情形) 定理2 若函数)(x f 和)(x g 满足下列条件 (1)在a 的某去心邻域)(x v 内可导,且0)('≠x g (2)∞=+→)(lim 0 x f a x ∞=+→)(lim 0 x g a x (3) A x g x f a x =+→)(')('lim 则A x g x f x g x f a x a x ==+→+→) (') ('lim )()(lim 00(包括A 为无穷大的情形) 此外法则所述极限过程对下述六类极限过程均适用: -∞→+∞→∞→→→→- + x x x x x x x x x ,,,,,000。 简而言之,当满足 或 ∞ ∞的不定式时,A x g x f x g x f a x a x ==+→+→) (')('lim )() (lim 0000 PS :一次求导不行仍未不定式,则多次求导 于是上面的两个式子可以这样解 例一. = = = 例二.1)sin sin (lim cos 1cos 1lim sin sin lim -=-=+-=+-∞→∞→∞→x x x x x x x x x x x (此为错解)
导数在求极限中的应用
引言 极限是研究变量的变化趋势的基本工具。在高等数学中许多基本概念和研究问题的方法都和极限密切相关,如函数的连续、导数、定积分和无穷级数等都是建立在极限的基本之上的。极限的思想和方法产生某些实际问题的精确解,并且对数学在实际中的应用也有着重要的作用。因此研究生考试往往把求极限问题作为考核的一个重点,而在不同的函数类型条件下所采用的求极限的技巧是各不相同的,因此大家要学会判断极限的类型,熟练和灵活的掌握各种技巧的应用。 本文主要介绍了导数在求极限中的基本应用,包括导数定义法,L’Hospital 法则,Taylor展式法及微分中值定理在求极限中的应用。旨在让大家掌握各种导数方法适用的函数类型,要注意的事项及它的一些推广结论。达到能灵活运用导数方法去求解一些极限问题以使问题简单化的目的。 1
2 第1章 导数在求极限中的基本应用 1.1 导数定义法 这种极限求法主要针对所给的极限不易求,但是函数满足导数定义的形式且能够确定的变化趋向的极限易求出时,可以用此法比较方便的求出极限. 定义 若函数()y f x =在其定义域中的一点0x 处极限 0000()()lim lim x x f x x f x y x x ?→?→+?-?=?? 存在,则称在0x 处可导,称此极限值为()f x 在0x 处的导数,记为0()f x '.显然,()f x 在0x 处的导数还有如下的等价定义形式: 000 ()() ()lim x x f x f x f x x x →-'=-. 下面通过两个例子让大家逐步领悟导数定义法的内涵 例1 求极限tan sin 0 lim sin b x b x x x αα+-→-. 解 由于 tan sin tan sin tan sin tan sin sin b x b x b x b b b x x x x x x αααααα+-+----= + . 所以,tan sin tan sin 0 tan lim lim lim sin tan sin sin b x b x b x b b b x x x x x x x x x αααααα+-+-→→→---=+ ln ln 2ln b b b αααααα=+=. 例2 (本题选自《数学分析中的典型问题与方法》裴礼文.第二版.) 设(0)f k '=,试证00()() lim a b f b f a k b a - + →→-=-. 证明 (希望把极限式写成导数定义中的形式)
极限与导数
第十四章 极限与导数 一、基础知识 1.极限定义:(1)若数列{u n }满足,对任意给定的正数ε,总存在正数m ,当n>m 且n ∈N 时,恒有|u n -A|<ε成立(A 为常数),则称A 为数列u n 当n 趋向于无穷大时的极限,记为 )(lim ),(lim x f x f x x -∞ →+∞ →,另外)(lim 0 x f x x +→=A 表示x 大于x 0且趋向于x 0时f(x)极限为A ,称右 极限。类似地)(lim 0 x f x x -→表示x 小于x 0且趋向于x 0时f(x)的左极限。 2.极限的四则运算:如果0 lim x x →f(x)=a, 0 lim x x →g(x)=b ,那么0 lim x x →[f(x)±g(x)]=a ±b, lim x x →[f(x)?g(x)]=ab, 0 lim x x →).0()()(≠=b b a x g x f 3.连续:如果函数f(x)在x=x 0处有定义,且0 lim x x →f(x)存在,并且0 lim x x →f(x)=f(x 0),则称f(x)在x=x 0处连续。 4.最大值最小值定理:如果f(x)是闭区间[a,b]上的连续函数,那么f(x)在[a,b]上有最大值和最小值。 5.导数:若函数f(x)在x0附近有定义,当自变量x 在x 0处取得一个增量Δx 时(Δx 充分小),因变量y 也随之取得增量Δy(Δy=f(x 0+Δx)-f(x 0)).若x y x ??→?0lim 存在,则称f(x)在x 0 处可导,此极限值称为f(x)在点x 0处的导数(或变化率),记作'f (x 0)或0'x x y =或 x dx dy , 即0 00) ()(lim )('0 x x x f x f x f x x --=→。由定义知f(x)在点x 0连续是f(x)在x 0可导的必要条件。 若f(x)在区间I 上有定义,且在每一点可导,则称它在此敬意上可导。导数的几何意义是:f(x)在点x 0处导数'f (x 0)等于曲线y=f(x)在点P(x 0,f(x 0))处切线的斜率。 6.几个常用函数的导数:(1))'(c =0(c 为常数);(2)1 )'(-=a a ax x (a 为任意常数);(3) ;cos )'(sin x x =(4)x x sin )'(cos -=;(5)a a a x x ln )'(=;(6)x x e e =)'(;(7))'(log x a x x a log 1= ;(8).1 )'(ln x x = 7.导数的运算法则:若u(x),v(x)在x 处可导,且u(x)≠0,则 (1))(')(')]'()([x v x u x v x u ±=±;(2))(')()()(')]'()([x v x u x v x u x v x u +=;(3) )(')]'([x u c x cu ?=(c 为常数);(4) )()(']')(1[2x u x u x u -=;(5)) () ()(')(')(]')()([2x u x v x u x v x u x u x u -=。
求极限的方法总结
学号:0 学年论文 求极限的方法总结 Method of Limit 学院理学院专业班级 学生指导教师(职称) 完成时间年月日至年月日
摘要 极限的概念是高等数学中最重要、最基本的概念之一。许多重要的概念如连续、导数、定积分、无穷级数的和及广义积分等都是用极限来定义的。因此掌握好求极限的方法对学好高等数学是十分重要的。但求极限的方法因题而异,变化多端,有时甚至感到变幻莫测无从下手,通过通过归纳和总结,我们罗列出一些常用的求法。本文主要对了数学分析中求极限的方法进行一定的总结,以供参考。 关键词:极限洛必达法则泰勒展开式定积分无穷小量微分中值定理
Abstract The concept of limit is the most important mathematics,one of the most basic important concepts such as continuity,derivative,definite integral,infinite series and generalized integrals and are defined by the mater the methods the Limit learn mathematics integrals and are defined by the limit varies by title,varied,anf sometimes even impossible to start very unpredictable,and summarized through the adoption,we set out the requirements of some commonly used this paper,the mathematical analysis of the method of seeking a certain limit a summary for reference. Keyword:Limit Hospital's Rule Taylor expansion Definite integral Infinitesimal Mean Value Theorem
经济数学基础微分学之第2章 极限、导数与微分
第一单元 极限的概念及其运算 第一节 极限的概念 一、学习目标 极限是微积分学中的重要概念,微积分中的许多重要概念都是由极限定义的.学习了这一节课,要使我们了解极限、左、右极限和无穷小量的概念. 并且能够利用函数图形和极限定义去求简单函数的极限. 二、内容讲解 1.极限的概念1 数列的极限: ①数列:一般地,按一定规律排列的一串数1x ,2x ,…,n x ,…称为数列,简记为{}n x 。其中的第n 项n x 称为该数列的通项。 ②数列的极限:给定数列{}n x ,如果当n 无限增大时,n x 无限地趋近某个固定的常数A ,则称当n 趋于无穷时,数列{}n x 以A 为极限。记为A x n n =∞ →lim 2.极限的概念2 研究函数是利用极限的方法来进行;极限是一个变量在变化过程中的变化趋势。 例1 圆的周长的求法.早在公元263年,古代数学家刘徽用圆内接正四边形、正五边形、正八边形、正十六边形……等的边长近似圆的周长,显然随着边数的增加,正多边形的边长将无限趋近圆的周长. 例2 讨论当+∞→x 时,x 1 的变化趋势. 例3 讨论一个定长的棒,每天截去一半,随着天数的增加,棒长的变化趋势.“一尺之棰,日截其半,万世不竭”——庄子?天下 定义2.1——函数的极限
设函数)(x f 在点0x 的邻域(点0x 可以除外)内有定义,如果当x 无限趋于0x (但0x x ≠) 时,)(x f 无限趋近于某个常数A ,则称x 趋于0x 时,)(x f 以A 为极限,记为A x f x x =→)(lim 0或 A x f →)()(0x x →;若自变量x 趋于0x 时,函数)(x f 没有一个固定的变化趋势,则称函数) (x f 在 x 处没有极限. 在理解极限定义时要注意两个细节: 1.0x x →时(0x x ≠), 2. ?? ?→<→>→000 00)()(x x x x x x x x (包括这两种情况) 考虑函数x y =,依照极限的定义,不能考虑0→x 的极限.因为x y =在0
函数极限与导数高中数学基础知识与典型例题
知识网 数学归纳法、数列的极限与运算1.数学归纳法: (1)由特殊事例得出一般结论的归纳推理方法,通常叫做归纳法. 归纳法包含不完全归纳法和完全归纳法. ①不完全归纳法:根据事物的部分(而不是全部)特殊事例得出一般结论的推理方法. ②完全归纳法: 根据事物的所有特殊事例得出一般结论的推理方法 数学归纳法常与不完全归纳法结合起来使用,用不完全归纳法发现规律, 用数学归纳法证明结论. (2)数学归纳法步骤: ①验证当n取第一个 n时结论 () P n成立; ②由假设当n k =( , k N k n + ∈≥)时,结论() P k成立,证明当1 n k =+时,结论(1) P k+成立; 根据①②对一切自然数 n n ≥时,() P n都成立. 2.数列的极限 (1)数列的极限定义:如果当项数n无限增大时,无穷数列{}n a的项n a无限地趋近于某个常数a(即 n a a -无限地接近于),那么就说数列 {} n a以a为极限,或者说a是数列{} n a的极限.记为 lim n n a a →∞ =或当n→∞时, n a a →. (2)数列极限的运算法则: 如果{}n a、{}n b的极限存在,且lim,lim n n n n a a b b →∞→∞ ==, 那么lim() n n n a b a b →∞ ±=±;lim(); n n n a b a b →∞ ?=?lim(0) n n n a a b b b →∞ =≠ 特别地,如果C是常数,那么lim()lim lim n n n n n C a C a Ca →∞→∞→∞ ?=?=. ⑶几个常用极限: ①lim n C C →∞ =(C 为常数)②lim0 n a n →∞ = k (,a k 均为常数且N* ∈ k) ③ (1) 1 lim0(1) (1或1) 不存在 n n q q q q q ④首项为 1 a,公比为q(1 q<)的无穷等比数列的各项和为lim 1 n n a S q →∞ = - . 注:⑴并不是每一个无穷数列都有极限. ⑵四则运算法则可推广到任意有限个极限的情况,但不能推广到无限个情况. 数 学 归 纳 法 、数 列 的 极 限 与 运 算 例 1. 某个命题与正整数有关,若当) (* N k k n∈ =时该命题成立,那么可推得当 = n1 + k时该命题也成立,现已知当5 = n时该命题不成立,那么可推得() (A)当6 = n时,该命题不成立(B)当6 = n时,该命题成立 (C)当4 = n时,该命题成立(D)当4 = n时,该命题不成立 例2.用数学归纳法证明:“)1 ( 1 1 1 2 1 2≠ - - = + + + + + +a a a a a a n n ”在验证1 = n时,左端 计算所得的项为 ( ) (A)1 (B)a + 1 (C)2 1a a+ + (D)3 2 1a a a+ + + 例3.2 2 21 lim 2 n n n →∞ - + 等于( ) (A)2 (B)-2 (C)- 2 1 (D) 2 1 例4. 等差数列中,若 n n S Lim ∞ → 存在,则这样的数列( ) (A)有且仅有一个(B)有无数多个 (C)有一个或无穷多个(D)不存在 例5.lim(1) n n n n →∞ +-等于( ) (A) 1 3 (B)0 (C) 1 2 (D)不存在 例6.若2 012 (2)n n n x a a x a x a x +=++++, 12 n n A a a a =+++,则2 lim 83 n n n A A →∞ - = + ( ) (A) 3 1 -(B) 11 1(C) 4 1(D) 8 1 - 例7. 在二项式(13)n x +和(25)n x+的展开式中,各项系数之和记为,, n n a b n是正整 数,则 2 lim 34 n n n n n a b a b →∞ - - =. 例8. 已知无穷等比数列{}n a的首项N a∈ 1 ,公比为q,且 n n a a a S N q + + + = ∈ 2 1 , 1, 且3 lim= ∞ → n n S,则= + 2 1 a a_____ . 例9. 已知数列{ n a}前n项和1 1 (1) n n n S ba b =-+- + , 其中b是与n无关的常数,且0 <b<1,若lim n n S →∞ =存在,则lim n n S →∞ =________. 例10.若数列{ n a}的通项21 n a n =-,设数列{ n b}的通项 1 1 n n b a =+,又记 n T是数 列{ n b}的前n项的积. (Ⅰ)求 1 T, 2 T, 3 T的值;(Ⅱ)试比较 n T与 1+ n a的大小,并证明你的结论. 例 1.D 2.C 例 3.A 例 4.A例 5.C将分子局部有理化,原式 =11 lim lim 2 11 11 n n n n n n →∞→∞ == ++ ++ 例6.A例7. 1 2 例8. 3 8 例9.1 例10(见后面)
matlab求积分极限导数
一.计算下列极限: 1. x e e x x x sin lim 0-→- 解:y=sym(‘(exp(x)-exp(-x))/sin(x)’); y1=limit(y) 结果:y1=2 2. n n m m a x a x a x --→lim 解:syms x a m n y=(x^m-a^m)/(x^n-a^n); y1=limit(y,x,a) 结果:y1=n a m a n m 3. n x x x 21lim ??? ??+∞→ 解:syms x n y=((1+x)/x)^(2*n); y1=limit(y,x,inf) 结果:y1=1 4. 111lim --→x x e 解:y=exp(1/(x-1)); y1=limit(y,x,1,‘left ’) 结果:y1= 0 5. 111lim -+→x x e 解:y=exp(1/(x-1)); y1=limit(y,x,1,‘right ’) 结果:y1= ∞ 二.创建表达式 f=2x+4, g=4x^2+5x-2, 并计算 (1) f+g; (2) f-g; (3) f ×g; (4) f /g; (5) f [g(x)]; (6) 求 g 的反函数。 解:syms x f=2*x+4;
g=4*x^2+5*x-2; 结果:(1) f+g= 7*x+2+4*x^2 (2)f-g= -3*x+6-4*x^2 (3)f*g= (2*x+4)*(4*x^2+5*x-2) (4)f/g= (2*x+4)/(4*x^2+5*x-2) (5) f [g(x)]=compose(f,g)=8*x^2+10*x (6)clear syms x g=4*x^2+5*x-2; g1= finverse(g) 结果:g1= ()2116578 185x ++- 三.计算下列导数 (1))1ln(2x x e e y ++= 解:syms x y=log(exp(x)+sqrt(1+exp(2*x))); z=diff(y,x); simple(z) 结果:z=exp(x)/(exp(2*x) + 1)^(1/2) z=()21 21+x x e e (2)x e y 1sin 2-= 解: syms x y=exp(-(sin(1/x))^2); z=diff(y,x); simple(z) 结果:z=(exp(cos(2/x)/2 - 1/2)*sin(2/x))/x^2 z=2 21)2cos()2sin(*x x e x - (3) 212arcsin t t y += 解: syms t y=asin(2*t/(1+t^2)); z=diff(y,t); simple(z) 结果:z=-(2*t^2 - 2)/((t^2 + 1)^2*((t^2 - 1)^2/(t^2 + 1)^2)^(1/2))
高中数学教案:极限与导数函数极限的运算法则
函数极限的运算法则(4月30日) 教学目标:掌握函数极限的运算法则,并会求简单的函数的极限 教学重点:运用函数极限的运算法则求极限 教学难点:函数极限法则的运用 教学过程: 一、引入: 一些简单函数可从变化趋势找出它们的极限,如o x x x x x x o ==→∞→lim ,01lim .若求极限的函数比较复杂,就要分析已知函数是由哪些简单函数经过怎样的运算结合而成的,已知函数的极限与这些简单函数的极限有什么关系,这样就能把复杂函数的极限计算转化为简单函数的极限的计算. 二 、新课讲授 限,分别等于这两个函数的极限的和、差、积、商(作为除数的函数的极限不能为0). 说明:当C 是常数,n 是正整数时,)(lim )]([lim x f C x Cf o o x x x x →→= n x x n x x x f x f o o )](lim [)]([lim →→= 这些法则对于∞→x 的情况仍然适用. 三 典例剖析 例1 求)3(lim 2 2x x x +→
例2 求1 12lim 231++-→x x x x 例3 求4 16lim 24--→x x x 分析:当4→x 时,分母的极限是0,不能直接运用上面的极限运用法则.注意函数 4 162--=x x y 在定义域4≠x 内,可以将分子、分母约去公因式4-x 后变成4+x ,由此即可求出函数的极限. 例4 求1 33lim 22++-∞→x x x x 分析:当∞→x 时,分子、分母都没有极限,不能直接运用上面的商的极限运算法则.如果分子、分母都除以2 x ,所得到的分子、分母都有极限,就可以用商的极限运用法则计算。 总结:),(lim ,lim *N k x x C C k o k x x x x o o ∈==→→ )(01lim ,lim *N k x C C k x x ∈==∞→∞→
用导数极限法解一类求参数取值范围的高考题
用导数—极限法解一类求参数取值范围的高考题 虽说在现行高中数学教材中没有给出极限的定义(只是在导数的定义中使用了极限符号),但在教材中从多方位多角度的渗透了极限思想:在研究双曲线的渐近线、求2的近似值、二分法求方程近似解、幂指对函数增长速度的快慢、介绍无理数指数幂的意义以及在统计中研究密度曲线等等都渗透了极限思想. 在即将出台的高中数学课标及教材中均会给出极限的定义,所以这里先由函数极限的δ-ε定义给出函数极限的保号性的相关结论,再给出该结论在求解函数问题中的应用. 函数极限的δ-ε定义 若存在实数b ,0,0εδ?>?>,当0x a δ<-<时,()f x b ε-<,则当x a →时,函数()f x 存在极限,且极限是b ,记作lim ()x a f x b →=. 由该定义,还可得 函数极限的保号性 (1)①若0)(lim >=→b x f a x ,则 {}0)(,,,0>≠+<<-∈?>?x f a t a t a t x 且δδδ; ②若0)(lim >=+ →b x f a x ,则0)(),,(,0>+∈?>?x f a a x δδ; ③若0)(lim >=- →b x f a x ,则0)(),,(,0>-∈?>?x f a a x δδ. (2)①若0)(lim <=→b x f a x ,则{} 0)(,,,0<≠+<<-∈?>?x f a t a t a t x 且δδδ; ②若0)(lim <=+ →b x f a x ,则0)(),,(,0<+∈?>?x f a a x δδ; ③若0)(lim <=- →b x f a x ,则0)(),,(,0<-∈?>?x f a a x δδ. 题1 设函数)1ln()1()(++=x x x f .若对所有的0≥x ,都有ax x f ≥)(成立,求实数a 的取值范围. (答案:]1,(-∞.) 题2设函数x x x f --=e e )(,若对所有的0≥x ,都有ax x f ≥)(,求实数a 的取值范围. (答案:]2,(-∞.) 题3设函数x x x f cos 2sin )(+= ,若对所有的0≥x ,都有ax x f ≤)(,求实数a 的取值范围.(答案:?? ????+∞,31.) 题4设函数2)1e ()(ax x x f x --=,若当0≥x 时,都有0)(≥x f ,求a 的取值范围.(答
考研数学极限与导数复习方法
考研数学极限与导数复习方法 我们在进行考研数学的备考复习时,需要掌握好极限与导数的复习方法。小编为大家精心准备了考研数学极限与导数复习秘诀,欢迎大家前来阅读。 考研数学极限与导数复习技巧 极限 极限是考研数学每年必考的内容,在客观题和主观题中都有可能会涉及到平均每年直接考查所占的分值在10分左右,而事实上,由于这一部分内容的基础性,每年间接考查或与其他章节结合出题的比重也很大。极限的计算是核心考点,考题所占比重最大。熟练掌握求解极限的方法是得高分的关键。 极限的计算常用方法:四则运算、洛必达法则、等价无穷小代换、两个重要极限、利用泰勒公式求极 限、夹逼定理、利用定积分求极限、单调有界收敛定理、利用连续性求极限等方法。 四则运算、洛必达法则、等价无穷小代换、两个重要极限是常用方法,在基础阶段的学习中是重点,考生应该已经非常熟悉,进入强化复习阶段这些内容还应继续练习达到熟练
的程度;在强化复习阶段考生会遇到一些较为复杂的极限计算,此时运用泰勒公式代替洛必达法则来求极限会简化计算,熟记一些常见的麦克劳林公式往往可以达到事半功倍之效;夹逼定理、利用定积分定义常常用来计算某些和式的极限,如果最大的分母和最小的分母相除的极限等于1,则使用夹逼定理进行 计算,如果最大的分母和最小的分母相除的极限不等于1,则 凑成定积分的定义的形式进行计算;单调有界收敛定理可用来 证明数列极限存在,并求递归数列的极限。 与极限计算相关知识点包括:1、连续、间断点以及 间断点的分类:判断间断点类型的基础是求函数在间断点处的左、右极限,分段函数的连续性问题关键是分界点处的连续性,或按定义考察,或分别考察左、右连续性;2、可导和可微,分段函数在分段点处的导数或可导性,一律通过导数的定义直接计算或检验,存在的定义是极限存在,求极限时往往会用到推广之后的导数定义式;3、渐近线(水平、垂直、斜渐近线);4、多元函数微分学,二重极限的讨论计算难度较大,多考察证明极限不存在。 导数 求导与求微分每年直接考查的知识所占分值平均在 10分到13分左右。常考题型:(1)利用定义计算导数或讨论 函数可导性;(2)导数与微分的计算(包括高阶导数);(3)切线与法线;(4)对单调性与凹凸性的考查;(5)求函数极值与拐点;(6)对函数及其导数相关性质的考查。
高中数学 极限与导数【讲义】
极限与导数 一、基础知识 1.极限定义:(1)若数列{u n }满足,对任意给定的正数ε,总存在正数m ,当n>m 且n ∈N 时,恒有|u n -A|< ε成立(A 为常数),则称A 为数列u n 当n 趋向于无穷大时的极限,记为)(lim ),(lim x f x f x x -∞ →+∞ →,另外)(lim 0 x f x x + →=A 表示x 大于x 0且趋向于x 0时f(x)极限为A ,称右极限。类似地)(lim 0 x f x x - →表示x 小于x 0且趋向于x 0时f(x)的左极限。 2.极限的四则运算:如果0 lim x x →f(x)=a, 0 lim x x →g(x)=b ,那么0 lim x x →[f(x)±g(x)]=a ±b, 0 lim x x →[f(x)?g(x)]=ab, lim x x →).0()()(≠=b b a x g x f 3.连续:如果函数f(x)在x=x 0处有定义,且0 lim x x →f(x)存在,并且0 lim x x →f(x)=f(x 0),则称f(x)在x=x 0处连续。 4.最大值最小值定理:如果f(x)是闭区间[a,b]上的连续函数,那么f(x)在[a,b]上有最大值和最小值。 5.导数:若函数f(x)在x0附近有定义,当自变量x 在x 0处取得一个增量Δx 时(Δx 充分小),因变量y 也随之取得增量Δy(Δy=f(x 0+Δx)-f(x 0)).若x y x ??→?0lim 存在,则称f(x)在x 0处可导,此极限值称为f(x)在 点x 0处的导数(或变化率),记作'f (x 0)或0'x x y =或 x dx dy ,即0 00) ()(lim )('0 x x x f x f x f x x --=→。由定义知 f(x)在点x 0连续是f(x)在x 0可导的必要条件。若f(x)在区间I 上有定义,且在每一点可导,则称它在此敬意上可导。导数的几何意义是:f(x)在点x 0处导数'f (x 0)等于曲线y=f(x)在点P(x 0,f(x 0))处切线的斜率。 6.几个常用函数的导数:(1))'(c =0(c 为常数);(2)1)'(-=a a ax x (a 为任意常数);(3) ;cos )'(sin x x =(4)x x sin )'(cos -=;(5)a a a x x ln )'(=;(6)x x e e =)'(;(7))'(log x a x x a log 1 =;(8).1 )'(ln x x = 7.导数的运算法则:若u(x),v(x)在x 处可导,且u(x)≠0,则 (1))(')(')]'()([x v x u x v x u ±=±;(2))(')()()(')]'()([x v x u x v x u x v x u +=;(3))(')]'([x u c x cu ?=(c 为常数);(4))()(']')(1[ 2x u x u x u -=;(5)) () ()(')(')(]')()([2x u x v x u x v x u x u x u -=。 8.复合函数求导法:设函数y=f(u),u=?(x),已知?(x)在x 处可导,f(u)在对应的点u(u=?(x))处可导,则复合函数y=f[?(x)]在点x 处可导,且(f[?(x)])'=)(')](['x x f ??. 9.导数与函数的性质:(1)若f(x)在区间I 上可导,则f(x)在I 上连续;(2)若对一切x ∈(a,b)有0)('>x f ,则f(x)在(a,b)单调递增;(3)若对一切x ∈(a,b)有0)(' 实验五 用matlab 求二元函数的极值 1.计算二元函数的极值 对于二元函数的极值问题,根据二元函数极值的必要和充分条件,可分为以下几个步骤: 步骤1.定义二元函数),(y x f z =. 步骤2.求解方程组0),(,0),(==y x f y x f y x ,得到驻点. 步骤3.对于每一个驻点),(00y x ,求出二阶偏导数 22222,,.z z z A B C x x y y ???===???? 步骤4. 对于每一个驻点),(00y x ,计算判别式2B AC -,如果02>-B AC ,则该驻点是 极值点,当0>A 为极小值, 0>clear; syms x y; >>z=x^4-8*x*y+2*y^2-3; >>diff(z,x) >>diff(z,y) 结果为 ans =4*x^3-8*y ans =-8*x+4*y实验五 用matlab求二元函数的极值
