高二数学线性规划试题
高二数学线性规划练习题

2.(2009安徽卷理)若不等式组⎪⎩⎪⎨⎧≤+≥+≥43430y x y x x 所表示的平面区域被直线34+=kx y 分为面积相等的两部分,则k 的值是 ( )(A )37 (B ) 73 (C )34 (D )43 [解析]:不等式表示的平面区域如图所示阴影部分△ABC由⎩⎨⎧=+=+4343y x y x 得)1,1(A ,又)34,0(),4,0(C B ∴341)344(21=⨯-⨯=∆ABC S ,设kx y =与43=+y x 的交点为D , 则由3221==∆∆ABC BCD S S 知:25,21=∴=D D y x ,37,342125=+⨯=∴k k .选A 。
4.(2006·黄冈模拟)原点O 和点P (1,1)在直线0=-+a y x 的两侧,则a 的取值范围是( )A. 20><a a 或B. 20==a a 或C. 20<<aD. 20≤≤a 10.(2009山东卷理)设x ,y 满足约束条件⎪⎩⎪⎨⎧≥≥≥+-≤--0,002063y x y x y x ,若目标函数z=ax+by (a>0,b>0)的最大值为12,则b a 32+的最小值为( ). A.625 B.38 C.311 D. 4 不等式表示的平面区域如图所示阴影部分,当直线ax+by= z (a>0,b>0)过直线x-y+2=0与直线3x-y-6=0的交点(4,6)时,目标函数z=ax+by (a>0,b>0)取得最大12,即4a+6b=12,即2a+3b=6, 而23a b +=2323131325()()26666a b b a a ba b ++=++≥+=,故选A. 11.在平面直角坐标系中,若不等式组⎪⎩⎪⎨⎧≥+-≤-≥-+010101y ax x y x (a 为常数)所表示的平面区域内的面积等于2,则a 的值为( )A. -5B. 1C. 2D. 317. 已知⎪⎩⎪⎨⎧≤--≥-+≥+-0520402y x y x y x ,求:(1)42-+=y x z 的最大值;(2)251022+-+=y y x z 的最小值;(3)112++=x y z 的范围。
高中数学高二试题解析高二数学专题简单线性规划问题高

简单线性规划问题(二)复习旧知:一线性规划的步骤:根据课本87页例子填写下列空白:1在坐标内作图。
2将 化为 。
这是一条斜率为 截距为 直线。
当截距 ,z 最 。
3由图可见,当直线 经过可行域上点M 时,截距 .,z最 。
4解方程组⎩⎨⎧,得M( , ) 5 z= =二根据上例指出约束条件,目标函数,可行域,可行解,最优解。
教学目标:重点:通过各种情况分析来掌握线性规划的一般方法。
难点:一族直线平移过程中与可行域的交点情况分析。
问题探讨:在上述例子中,最后条件;(1)若生产一件甲产品获利1万元,若生产一件乙产品获利4万元,采用哪种方式利润最大?(2)若生产一件甲产品获利1万元,若生产一件乙产品获利2万元,采用哪种方式利润最大?(3)若目标函数为z=x —y ,那么Z 的取值范围为?总结:在一族直线的移动过程中,直线开始与可行域开始相交时,可能是 可能是 也可能是 直线最后与可行域开始相交时,可能 是 可能 也可能是 。
1所以最优解可能是 可能是 也可能是2此时截距 ,z 最 。
3原来线性规划的步骤可改为:(1)(2)(3)(4)把上图中的交点坐标分别代入目标函数,比较结果,得出结论:使用这种方法来解决上节复习旧知中的最后两道题。
知识拓展:已知平面区域如图,z=mx+y(m)0)在平面区域内取得最大值的最优解有无数多个,则m 的值为( )边界直线的交点:A(1,1),B(5,3),C(1,22/5)练习:1(2006年安徽卷)如果实数x y 、满足条件101010x y y x y -+≥⎧⎪+≥⎨⎪++≤⎩,那么2x y -的最大值为( )A .2B .1C .2-D .3-2(2006年湖北卷)已知平面区域D 由以()3,1A 、()2,5B 、()1,3C 为顶点的三角形内部和边界组成.若在区域D 上有无穷多个点()y x ,可使目标函数my x z +=取得最小值,则=m(C )A. 2-B. 1-C. 1D. 43(2005湖南卷)已知点P (x ,y )在不等式组⎪⎩⎪⎨⎧≥-+≤-≤-022,01,02y x y x 表示的平面区域上运动,则z =x -y 的取值范围是 ( C )A .[-2,-1]B .[-2,1]C .[-1,2]D .[1,2]。
高二数学简单线性规划单元测试.doc

高二数学简单线性规划单元测试x y 2 0,1. 设变量 x, y 满足约束条件 x5 y 100, 则目标函数 z 3x 4 y 的最大值和最x y80,小值 分别为( ) A .3,-11 B . -3 ,-11 C .11, -3 D . 11,3 2. 不等式 ( x -y +1)( x + 2y - 1) ≤ 0 在坐标平面内表示的区域 ( 用阴影部分表 示 ) 为( )y ≥ ,13. 已知实数, 满足y ≤2x -1,如果目标函数z=-y 的最小值为- ,x yx +y ≤ mx1.则实数 m 为()A .7B. 5C.4D .34. 若实数 x 、y 满足xy 1 0,则 y的取值范围为( )x0 x A .(0,1)B .(0,1)C .(1,+ ∞)D . 1,→ → ,O 为坐标 原点,动 点 P x , y 满足条件5. 向量 OA =(1,0) , OB =(1,1) ( )→ →0< OP ·OA < ,1 则点 P 的变化范围用阴影部分表示为 ()→ →0< OP ·OB < ,2x - y +5≥06. 若不等式组 y ≥ a 表示的平面区域是一个三角形,则 a 的取值范0≤ x ≤2 围为( ) A .a <5B. a ≥7 C .5≤ a <7 D . a< 5 或 a ≥7x +y ≥2,7. 已知 O 是坐标原点,点 A -1,1) ,若点 M x ,y为平面区域x ≤1,上(()y ≤2→ →)的一个动点,则 OA ·OM 的取值范围为 (A .[ -1,0]B .[0,1] C. [0,2] D .[ -1,2]8. 某运输公司有 12 名驾驶员和 19 名工人,有 8 辆载重量为 10 吨的甲型卡车和7 辆载重量为 6 吨的乙型卡车.某天需运往 A地至少 72 吨的货物,派用的每辆车需满载且只运送一次. 派用的每辆甲型卡车需配 2 名工人,运送一次可得利润 450 元;派用的每辆乙型卡车需配 1 名工人,运送一次可得利润 350 元.该公司 合理计划当天派用两类卡车的车辆数,可得最大利润 z=( ) A .4650 元 B .4700 元 C .4900 元 D .5000 元x y 19. 若 x ,y 满足约束条件x y1 ,目标函数 z ax2 y 仅在点( 1,0)处取2x y 2得最小值,则 a 的取值范围为( )A .( 1,2 )B .( 4 ,2 )C .(4,0]D . ( 2,4)x ≥0410. 若不等式组 x +3y ≥4, 所表示的平面区域被直线y =kx + 分为面积x + y ≤4 33相等的两部分,则 k 的值为 ( )7 3 4 3 A .3B. 7C.3D.4x1,11. 已知点 P(x, y) 的坐标满足条件y2, 那么 x 2 y 2 的取值范围为2xy 2 0,________.x 4 y 312. 已知变量 x, y 满足 3x5y 25 ,设 z ax y(a0) , 若当 z 取得最大值时对x 1应的点有无数个,则 a 的值为.x -y < ,3 013. 已知 A(3 , 3) ,O 是原点,点 P( x ,y) 的坐标满足 x - 3y +2<0,则y ≥0,→ →OA ·OP→ 的取值范围为 ________.| OP|x ≤ 0,14. 若 A 为不等式组 y ≥ 0,表示的平面区域, 则 a 从 -2 连续变化到 1 时,动y x ≤ 2直线 x y a 扫过 A 中的那部分区域的面积为 .15. 实系数一元二次方程 x 2+ ax +2b =0 有两个根,一个根在区间 (0,1) 内,另一个根在区间 (1,2) 内,求:(1) 点 ( a ,b) 对应的平面区域;b -2(2) a -1的取值范围;(3)( a -1) 2+( b -2) 2 的取值范围.16. 某公司计划 2012 年在甲、乙两个电视台做总时间不超过 300 分钟的广告,广告总费用不超过9 万元,甲、乙电视台的广告收费标准分别为500 元/ 分钟和200元/ 分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为 0.3 万元和 0.2 万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?17.(2011 安徽理)在数 1 和 100 之间插入n个实数,使得这 n 2 个数构成递增的等比数列,将这n 2 个数的乘积记作Tn,再令anlg Tn,n≥1.{ a }(Ⅱ)设b n tan a n gtan a n 1,求数列{b n}的前n项和S n.18.( 2011 山东理)等比数列an中,a1, a2,a3分别是下表第一、二、三行中的某一个数,且a1, a2,a3 中的任何两个数不在下表的同一列.第一列第二列第三列第一行 3 2 10 第二行 6 4 14 第三行9 8 18(Ⅰ)求数列an的通项公式;(Ⅱ)若数列bn 满足:bnan( 1)ln an ,求数列{bn}的前n项和Sn .高二数学简单线性规划单元测试参考答案ACBCA CCCBA11. [ 4,5]512. 3513. [ -3,3) 14.7.415. 实系数一元二次方程 x 2+ ax +2b =0 有两个根,一个根在区间 (0,1) 内,另一个根在区间 (1,2) 内,求:(1) 点 ( a ,b) 对应的平面区域;b -2(2) a -1的取值范围;(3)( a -1) 2+( b -2) 2 的取值范围. 和上的几何意义是:函数 y = 解:方程 x 2+ax + b = 0 的两根在区间(0,1) (1,2) f x =x 2+ ax + b 2 和 的图象与 x轴的两个交点的横坐标分别在区间(0,1) (1,2) ( ) 2内, f b ,0 >0,>0由此可得不等式组 f 1 <0, 所以 a +2b +1<0,f 2 >0,a +b +2>0.a +b + =2 1 ,解得 A( -3,1) .由a +b + =2由 a + b + 2= 0,解得B -1.b = 0( 2,0) .( 4, 1) .(8,17)a +b + =21C - 1,0) .由,解得(b = 0(1) 在如图所示的 aOb 坐标平面内,满足约束条件的点 ( a , b) 对应的平面区域为△ ABC( 不包括边界 ) .b -2(2) a -1的几何意义是点 ( a ,b) 和点 D(1,2) 连线的斜率.2-1 1 2-0因为 k AD =1+3=4,k CD =1+1=1,b-2由图可知 k AD<a-1<k CD.1 b-2b-2 1所以4<a-1<1,即a-1∈( 4,1) .(3)因为 ( a- 1) 2+( b-2) 2表示区域内的点 ( a,b) 与定点 (1,2) 之间的距离的平方,2 + 2 + 2 2 + 2 +- 2 所以a其最小值为 CD=(1 1) 2 =,最大值为 AD=(1 3) (2 1) =17.8 ( -1) 2+ ( b-2) 2∈(8,17) .16.某公司计划2012年在甲、乙两个电视台做总时间不超过300 分钟的广告,广告总费用不超过9 万元,甲、乙电视台的广告收费标准分别为500 元/ 分钟和200元/ 分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为 0.3 万元和 0.2 万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?【解】设公司在甲电视台和乙电视台做广告的时间分别为x 分钟和 y 分钟,总收x y ≤ 300,益为 z 元,由题意得500x 200y ≤ 90000,x ≥ 0, y ≥ 0.目标函数为 z 3000 x 2000 y .x y ≤ 300,二元一次不等式组等价于5x 2 y ≤ 900,x ≥ 0,y ≥ 0.作出二元一次不等式组所表示的平面区域,即可行域.如图:作直线 l :3000 x 2000 y 0 ,即 3x 2 y 0 .平移直线 l ,从图中可知,当直线 l 过M点时,目标函数取得最大值.y500 400300x y300,联立解得 x 100, y200 .5x 2 y900.l 200 M点 M 的坐标为 (100,200) .100z max 3000 x 2000 y 700000 (元)答:该公司在甲电视台做100 分钟广告,在乙电视台做0 100 200 300x 200 分钟广告,公司的收益最大,最大收益是70 万元.17.(2011 安徽理)在数 1 和 100 之间插入n个实数,使得这n 2个数构成递增的等比数列,将这n 2个数的乘积记作T n,再令a n lg T n, n≥1.(Ⅰ)求数列{ an}的通项公式;(Ⅱ)设bntan angtan an 1,求数列{bn}的前n项和Sn .解:( I )设 l 1 ,l 2 ,,l n 2 构成等比数列,其中 t11,t n 2100, 则T n t 1 t 2t n 1 tn 2 , ①T n t n 1 t n 2t 2 t 1 ,②①×②并利用 t 1tn3 it 1tn 210 2 (1 in 2), 得T n 2 (t 1t n 2 ) (t 2t n 1 ) (t n 1t 2 ) (t n 2 t 1 ) 102 (n 2 ) , a nlg T n n 2, n 1.(II )由题意和( I )中计算结果,知bntan(n 2) tan(n 3), n 1.tan1 tan(( k 1) k )tan(k 1) tan k ,另一方面,利用1 tan( k 1) tan ktan(k 1) tan k tan(k 1) tan k 1.tan1得n n 2所以S nb k tan(k 1) tan kk 1k 3n 2( tan(k1) tan k 1) k 3tan1 tan(n 3) tan 3 n.tan118. ( 2011 山东理) 等比数列an中,a 1, a 2,a3分别是下表第一、二、三行中的某一个数,且a 1, a 2,a3中的任何两个数不在下表的同一列.第一列 第二列第三列 第一行 3 2 10第二行 6 4 14 第三行 9818(Ⅰ)求数列 a n的通项公式;(Ⅱ)若数列b n满足:b nan( 1) ln an,求数列{b n }的前 n 项和Sn.解:(I )当 a 13时,不合题意;当a 1 2时,当且仅当a 26, a 318时,符合题意;当a 110时,不合题意。
高二数学专项练习:简单的线性规划问题检测试题-精选学习文档

高二数学专项练习:简单的线性规划问题检测试题查字典数学网为大家提供高二数学专项练习:简单的线性规划问题检测试题一文,供大家参考使用:高二数学专项练习:简单的线性规划问题检测试题1.目标函数z=4x+y,将其看成直线方程时,z的几何意义是()A.该直线的截距B.该直线的纵截距C.该直线的横截距D.该直线的纵截距的相反数解析:选B.把z=4x+y变形为y=-4x+z,则此方程为直线方程的斜截式,所以z为该直线的纵截距.2.若x0,y0,且x+y1,则z=x-y的最大值为()A.-1 B.1C.2 D.-2答案:B3.若实数x、y满足x+y-20,x4,y5,则s=x+y的最大值为________.解析:可行域如图所示,作直线y=-x,当平移直线y=-x至点A处时,s=x+y取得最大值,即smax=4+5=9.答案:94.已知实数x、y满足y-2x.x3(1)求不等式组表示的平面区域的面积;(2)若目标函数为z=x-2y,求z的最小值.解:画出满足不等式组的可行域如图所示:(1)易求点A、B的坐标为:A(3,6),B(3,-6),所以三角形OAB的面积为:S△OAB=12123=18.(2)目标函数化为:y=12x-z2,画直线y=12x及其平行线,当此直线经过A时,-z2的值最大,z的值最小,易求A 点坐标为(3,6),所以,z的最小值为3-26=-9.一、选择题1.z=x-y在2x-y+10x-2y-10 x+y1的线性约束条件下,取得最大值的可行解为()A.(0,1) B.(-1,-1)C.(1,0) D.(12,12)解析:选C.可以验证这四个点均是可行解,当x=0,y=1时,z=-1;当x=-1,y=-1时,z=0;当x=1,y=0时,z=1;当x=12,y=12时,z=0.排除A,B,D. 2.(2019年高考浙江卷)若实数x,y满足不等式组x+3y-30,2x-y-30,x-y+10,则x+y的最大值为()A.9 B.157C.1 D.715解析:选A.画出可行域如图:令z=x+y,可变为y=-x+z,作出目标函数线,平移目标函数线,显然过点A时z最大.由2x-y-3=0,x-y+1=0,得A(4,5),zmax=4+5=9. 3.在△ABC中,三顶点分别为A(2,4),B(-1,2),C(1,0),点P(x,y)在△ABC内部及其边界上运动,则m=y-x的取值范围为()A.[1,3] B.[-3,1]C.[-1,3] D.[-3,-1]解析:选C.直线m=y-x的斜率k1=1kAB=23,且k1=1<kAC=4,直线经过C时m最小,为-1,经过B时m最大,为3.4.已知点P(x,y)在不等式组x-20y-10x+2y-20表示的平面区域内运动,则z=x-y的取值范围是()A.[-2,-1] B.[-2,1]C.[-1,2] D.[1,2]解析:选C.先画出满足约束条件的可行域,如图阴影部分,∵z=x-y,y=x-z.由图知截距-z的范围为[-2,1],z的范围为[-1,2].5.设动点坐标(x,y)满足?x-y+1??x+y-4?0,x3,y1.则x2+y2的最小值为()A.5B.10C.172 D.10解析:选D.画出不等式组所对应的平面区域,由图可知当x =3,y=1时,x2+y2的最小值为10.6.(2009年高考四川卷)某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨、B原料2吨;生产每吨乙产品要用A原料1吨、B原料3吨.销售每吨甲产品可获得利润5万元、每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A原料不超过13吨、B原料不超过18吨,那么该企业可获得的最大利润是() w w w .x k b 1.c o m A.12万元 B.20万元C.25万元 D.27万元解析:选D.设生产甲产品x吨、乙产品y吨,则获得的利润为z=5x+3y.由题意得x0,y0,3x+y13,2x+3y18,可行域如图阴影所示.由图可知当x、y在A点取值时,z取得最大值,此时x=3,y=4,z=53+34=27(万元).二、填空题7.点P(x,y)满足条件0101,y-x12则P点坐标为________时,z=4-2x+y取最大值________.解析:可行域如图所示,新课标第一网当y-2x最大时,z最大,此时直线y-2x=z1,过点A(0,1),(z1)max=1,故当点P的坐标为(0,1)时z=4-2x+y取得最大值5.答案:(0,1)58.已知点P(x,y)满足条件xx2x+y+k0(k为常数),若x +3y的最大值为8,则k=________.解析:作出可行域如图所示:作直线l0∶x+3y=0,平移l0知当l0过点A时,x+3y最大,由于A点坐标为(-k3,-k3).-k3-k=8,从而k=-6.答案:-69.(2019年高考陕西卷)铁矿石A和B的含铁率a,,冶炼每万吨铁矿石的CO2的排放量b及每万吨铁矿石的价格c如下表:a b/万吨 c/百万元A 50% 1 3B 70% 0.5 6某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为________(百万元).解析:设购买A、B两种铁矿石分别为x万吨、y万吨,购买铁矿石的费用为z百万元,则z=3x+6y.由题意可得约束条件为12x+710y1.9,x+12y2,x0,y0. 作出可行域如图所示:由图可知,目标函数z=3x+6y在点A(1,2)处取得最小值,zmin=31+62=15答案:15三、解答题10.设z=2y-2x+4,式中x,y满足条件01022y-x1,求z的最大值和最小值.解:作出不等式组01022y-x1的可行域(如图所示).令t=2y-2x则z=t+4.将t=2y-2x变形得直线l∶y=x+t2.则其与y=x平行,平移直线l时t的值随直线l的上移而增大,故当直线l经过可行域上的点A时,t最大,z最大;当直线l经过可行域上的点B时,t最小,z最小.zmax=22-20+4=8,zmin=21-21+4=4.11.已知实数x、y满足约束条件x-ay-102x+y1(aR),目标函数z=x+3y只有当x=1y=0时取得最大值,求a的取值范围.解:直线x-ay-1=0过定点(1,0),画出区域2x+y0,x1,让直线x-ay-1=0绕着(1, 0)旋转得到不等式所表示的平面区域.平移直线x+3y=0,观察图象知必须使直线x-ay -1=0的斜率1a>0才满足要求,故a>0.12.某家具厂有方木料90 m3 ,五合板600 m2,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1 m3,五合板2 m2;生产每个书橱需要方木料0.2 m3,五合板1 m2,出售一张方桌可获利润80元;出售一个书橱可获利润120元.(1)如果只安排生产方桌,可获利润多少?(2)如果只安排生产书橱,可获利润多少?(3)怎样安排生产可使所获利润最大?解:由题意可画表格如下:方木料(m3) 五合板(m2) 利润(元)书桌(个) 0.1 2 80书橱(个) 0.2 1 120(1)设只生产书桌x张,可获利润z元,则0.1x600xN*?x300xN*?x300,xN*.目标函数为z=80x.所以当x=300时,zmax=80300=24000(元),即如果只安排生产书桌,最多可生产300张书桌,获得利润24000元.(2)设只生产书橱y个,可获利润z元,则0.2y901?y600yN*?y600yN*?y450,yN*.目标函数为z=120y.所以当y=450时,zmax=120450=54000(元),即如果只安排生产书橱,最多可生产450个书橱,获得利润54000元.(3)设生产书桌x张,书橱y个,利润总额为z元,则0.1x+0.2y902x+y0,x0,xN?x+2y900,2x+y600,x0,y0,且xN,yN.目标函数为z= 80x+120y.在直角坐标平面内作出上面不等式组所表示的平面区域,即可行域(图略).作直线l∶80x+120y=0,即直线l∶2x+3y=0(图略).把直线l向右上方平移,当直线经过可行域上的直线x+2y =900,2x+y=600的交点时,此时z=80x+120y取得最大值.由x+2y=9002x+y=600解得交点的坐标为(100,400).所以当x=100,y=400时,zmax=80100+120400=56000(元).因此,生产书桌100张,书橱400个,可使所获利润最大.以上就是高二数学专项练习:简单的线性规划问题检测试题的所有内容,希望对大家有所帮助!。
高二数学上简单的线性规划问题练习测试题

高二数学上简单的线性规划问题练习测试题1、设变量y x ,满足约束条件⎪⎩⎪⎨⎧≤-+≥+-≥+0320302y x y x x ,则目标函数y x z 6+=的最大值为( )A.3B.4C.18D.402、某服装制造商有210m 的面布料,210m 的羊毛料和26m 的丝绸料,做一条裤子需要21m 的棉布料,22m的羊毛料和21m 的丝绸料,做一条裙子需要21m 的棉布料,21m 的羊毛料和21m 的丝绸料,做一条裤子的纯收益是20元,一条裙子的纯收益是40元,为了使收益达到最大,若生产裤子x 条,裙子y 条,利润为z ,则生产这两种服装所满足的数学关系式与目标函数分别为( )A.y x z Ny x y x y x y x 4020,,610210+=⎪⎪⎩⎪⎪⎨⎧∈≤+≤+≤+ B.y x z Ny x y x y x y x 4020,,610210+=⎪⎪⎩⎪⎪⎨⎧∈≤+≥+≥+ C.y x z y x y x y x 4020,610210+=⎪⎩⎪⎨⎧≤+≤+≤+D.y x z Ny x y x y x y x 2040,,610210+=⎪⎪⎩⎪⎪⎨⎧∈≤+≤+≤+ 3、设变量y x ,满足约束条件⎪⎩⎪⎨⎧-≥-≤+≥+144222y x y x y x ,则目标函数y x z -=3的取值范围是( )A.]6,23[-B.]1,23[-- C.]6,1[- D.]23,6[-4、某学校用800元购买B A ,两种教学用品,A 种用品每件100元,B 种用品每件160元,两种用品至少各买一件,要使剩下的钱最少,B A ,两种用品应各买的件数为( )A.4,2B.3,3C.2,4D.不确定5、设y x ,满足约束条件⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+00625y x y x y x ,使目标函数y x z 86+=取得最大值的点的坐标是( ) A.)4,1( B.)5,0( C.)0,5( D.)0,3(6、设y x ,满足约束条件⎪⎩⎪⎨⎧≤-+≥≤+-07102y x x y x ,则x y 的取值范围是( )A.]6,59[B.),6[]59,(+∞-∞C.]6,3(D.),6[]3,(+∞-∞ 7、已知⎪⎩⎪⎨⎧≤--≥+-≥022011y x y x x ,若y ax z +=的最小值是2,则a 的值为( )A.1B.2C.3D.48、已知实数y x ,满足条件⎪⎩⎪⎨⎧≤+-≤≥012210y x y x ,若目标函数)0(≠-=m y mx z 取得最大值时的最优解有无穷多个,则实数m 的值为( )A.1B.21C.21- D.1- 9、若y x ,满足约束条件⎪⎩⎪⎨⎧≤≥+≥+-3005x y x y x ,则目标函数y x z 42+=的最小值为10、设关于y x ,的不等式组⎪⎩⎪⎨⎧>+<->+-00012m y m x y x 表示的平面区域内存在点),(00y x P 满足:-0x220=y ,则实数m 的取值范围是11、已知线性目标函数y x z +=在线性约束条件⎪⎩⎪⎨⎧≤≤-≤-+a y y x y x 0203下取得最大值时,最优解有且只有一个,则实数a 的取值范围是 12、如果实数y x ,满足⎪⎩⎪⎨⎧≤≥-+≥-30402x y x y x ,则x y 的取值范围是 ,xy y x z 22+=的最大值为 13、关于x 的方程022=++b ax x的两根分别在区间)1,0(与)2,1(内,求12--a b 的取值范围.14、若y x ,满足约束条件⎪⎩⎪⎨⎧≤--≥-≥+2211y x y x y x .(1)求目标函数2121+-=y x z 的最值; (2)若目标函数y ax z 2+=仅在)0,1(处取得最小值,求a 的取值范围.高二数学上简单的线性规划问题②练习测试题1、已知变量y x ,满足约束条件⎪⎩⎪⎨⎧≥+≤-≤+0111x y x y x ,则目标函数y x z 2+=的最小值为( )A.3B.1C.5-D.6-2、已知点)2,5(),1,1(),,(00C B y x A .如果可行域是ABC ∆边界及其内部,目标函数+=ax zby 在点B 处取得最小值3,在点C 处取最大值12,则下列关系一定成立的是( )A.1200>+by axB.300<+by axC.1200≤+by axD.300≤+by ax3、在平面直角坐标系中,),(y x M 为不等式组⎪⎩⎪⎨⎧≤-+≥-+≥--083012022y x y x y x 所表示的区域上的一个动点,则直线OM 斜率的最小值为( )A.2B.1C.31- D.21- 4、配置B A ,两种药剂都需要甲、乙两种原料,一剂A 药需要甲2千克,乙5千克,售价100元,一剂B 药需要甲5千克,乙4千克,售价200元.现有原料甲kg 20,原料乙kg 25,那么可以获得的最大销售额为( )A.600元B.700元C.800元D.900元5、已知y x ,满足⎪⎩⎪⎨⎧≥+-≤--≥-+052053052y x y x y x ,则++2)1(x2)1(+y 的最小值为( )A.13B.13C.564 D.558 6、定义⎩⎨⎧<≥=b a b b a a b a ,,},max{,设实数y x ,满足约束条件⎩⎨⎧≤≤2||2||y x ,则-+=x y x z 3,4m ax{ }y 的取值范围是( )A.]10,8[-B.]10,7[-C.]8,6[-D.]8,7[-7、设平面点集}0)1)((|),{(≥--=xy x y y x A , }1)1()1(|),{(22≤-+-=y x y x B ,那么B A 所表示的平面图形的面积为( )A.π43B.π53C.π74D.2π。
高二数学简单线性规划测试卷
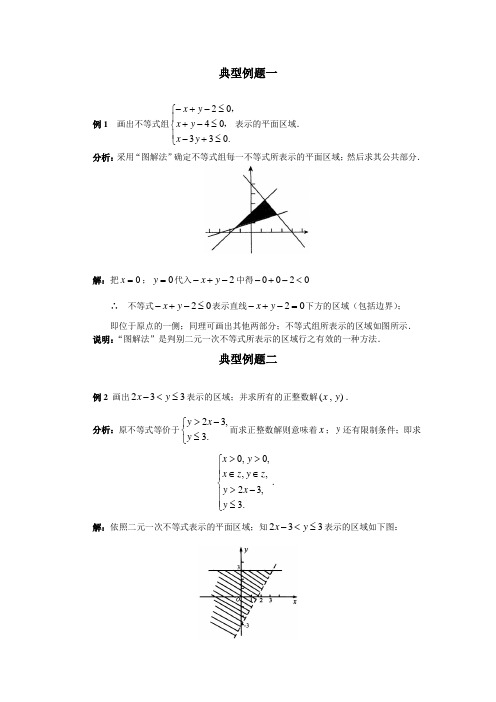
典型例题一例1 画出不等式组⎪⎩⎪⎨⎧≤+-≤-+≤-+-.0330402y x y x y x ,,表示的平面区域.分析:采用“图解法”确定不等式组每一不等式所表示的平面区域;然后求其公共部分.解:把0=x ;0=y 代入2-+-y x 中得0200<-+-∴ 不等式02≤-+-y x 表示直线02=-+-y x 下方的区域(包括边界); 即位于原点的一侧;同理可画出其他两部分;不等式组所表示的区域如图所示. 说明:“图解法”是判别二元一次不等式所表示的区域行之有效的一种方法.典型例题二例2 画出332≤<-y x 表示的区域;并求所有的正整数解),(y x .分析:原不等式等价于⎩⎨⎧≤->.3,32y x y 而求正整数解则意味着x ;y 还有限制条件;即求⎪⎪⎩⎪⎪⎨⎧≤->∈∈>>.3,32,,,0,0y x y z y z x y x . 解:依照二元一次不等式表示的平面区域;知332≤<-y x 表示的区域如下图:对于332≤<-y x 的正整数解;先画出不等式组.⎪⎪⎩⎪⎪⎨⎧≤->∈∈>>.3,32,,,0,0y x y z y z x y x 所表示的平面区域;如图所示.容易求得;在其区域内的整数解为)1,1(、)2,1(、)3,1(、)2,2(、)3,2(. 说明:这类题可以将平面直角坐标系用网络线画出来;然后在不等式组所表示的平面区域内找出符合题设要求的整数点来.典型例题三例3 求不等式组⎪⎩⎪⎨⎧+-≤-+≥111x y x y 所表示的平面区域的面积.分析:本题的关键是能够将不等式组所表示的平面区域作出来;判断其形状进而求出其面积.而要将平面区域作出来的关键又是能够对不等式组中的两个不等式进行化简和变形;如何变形?需对绝对值加以讨论.解:不等式11-+≥x y 可化为)1(-≥≥x x y 或)1(2-<--≥x x y ; 不等式1+-≤x y 可化为)0(1≥+-≤x x y 或)0(1<+≤x x y . 在平面直角坐标系内作出四条射线)1(-≥=x x y AB :; )1(2-<--=x x y AC : )0(1≥+-=x x y DE :;)0(1<+=x x y DF :则不等式组所表示的平面区域如图由于AB 与AC 、DE 与DF 互相垂直; 所以平面区域是一个矩形.根据两条平行线之间的距离公式可得矩形的两条边的长度分别为22和223.所以其面积为23.典型例题四例1 若x 、y 满足条件⎪⎩⎪⎨⎧≤+-≥+-≤-+.0104010230122y x y x y x ,,求y x z 2+=的最大值和最小值.分析:画出可行域;平移直线找最优解.解:作出约束条件所表示的平面区域;即可行域;如图所示.作直线z y x l =+2:;即z x y 2121+-=;它表示斜率为21-;纵截距为2z的平行直线系;当它在可行域内滑动时;由图可知;直线l 过点时;z 取得最大值;当l 过点B 时;z 取得最小值.∴ 18822max =⨯+=z ∴ 2222min =⨯+-=z说明:解决线性规划问题;首先应明确可行域;再将线性目标函数作平移取得最值.典型例题五例5 用不等式表示以)4,1(A ;)0,3(-B ;)2,2(--C 为顶点的三角形内部的平面区域.分析:首先要将三点中的任意两点所确定的直线方程写出来;然后结合图形考虑三角形内部区域应怎样表示。
高二数学同步测试(6)—线性规划

)3,5(A)522,1(Cy高二数学同步测试(6)—线性规划一、选择题(本大题共10小题,每小题5分,共50分)1.不在3x+ 2y < 6 表示的平面区域内的一个点是()A.(0,0)B.(1,1)C.(0,2)D.(2,0)2.已知点(3 ,1)和点(-4 ,6)在直线3x–2y + m = 0 的两侧,则()A.m<-7或m>24 B.-7<m<24C.m=-7或m=24 D.-7≤m≤243.若⎩⎨⎧≥+≤≤2,22yxyx,则目标函数z = x + 2 y 的取值范围是()A.[2 ,6] B.[2,5] C.[3,6] D.[3,5]4.不等式⎩⎨⎧≤≤≥++-3))(5(xyxyx表示的平面区域是一个()A.三角形B.直角三角形C.梯形D.矩形5.在△ABC中,三顶点坐标为A(2 ,4),B(-1,2),C(1 ,0 ),点P(x,y)在△ABC内部及边界运动,则z= x– y 的最大值和最小值分别是()A.3,1 B.-1,-3 C.1,-3 D.3,-16.在直角坐标系中,满足不等式x2-y2≥0 的点(x,y)的集合(用阴影部分来表示)的是()A B C D7.不等式3<+yx表示的平面区域内的整点个数为()A.13个B.10个C.14个D.17个8.不等式3|2|<++myx表示的平面区域包含点)0,0(和点),1,1(-则m的取值范围是()A.32<<-m B.60<<m C.63<<-m D.30<<m9.已知平面区域如右图所示,)0(>+=mymxz在平面区域内取得最大值的最优解有无数多个,则m的值为()A.207B.207-C .21D .不存在10.如图所示,表示阴影部分的二元一次不等式组是( )A .232600y x y x ≥-⎧⎪-+>⎨⎪<⎩B .232600y x y x >-⎧⎪-+≥⎨⎪≤⎩C .232600y x y x >-⎧⎪-+>⎨⎪≤⎩D .232600y x y x >-⎧⎪-+<⎨⎪<⎩二、填空题(本题共4小题,每小题6分,共24分)11.已知x ,y 满足约束条件 35≤≥+≥+-x y x y x ,则y x z -=4的最小值为______________.12.已知约束条件2828,x y x y x N y N +++≤⎧⎪+≤⎨⎪∈∈⎩,目标函数z=3x+y ,某学生求得x =38, y=38时,z max =323,这显然不合要求,正确答案应为x = ; y= ; z max = .13.某电脑用户计划用不超过500元的资金购买单价分别为60元,70元的单片软件和盒装磁盘,根据需要软件至少买3件,磁盘至少买2盒,则不同的选购方式共有______________种.14.已知x ,y 满足⎪⎩⎪⎨⎧≥-+≥≥≤-+0320,1052y x y x y x ,则xy的最大值为___________,最小值为____________.三、解答题(本大题共6题,共76分)15.由12+≤≤≤x y x y 及围成的几何图形的面积是多少?(12分)16.已知),2,0(∈a 当a 为何值时,直线422:422:2221+=+-=-a y a x l a y ax l 与及坐标轴围成的平面区域的面积最小?(12分)17.有两种农作物(大米和小麦),可用轮船和飞机两种方式运输,每天每艘轮船和每架飞机运输效果如下:在一天内如何安排才能合理完成运输2000吨小麦和1500吨大米的任务?(12分)18.设422+-=x y z ,式中变量y x ,满足条件⎪⎩⎪⎨⎧≥-≤≤≤≤122010x y y x ,求z 的最小值和最大值.(12分)19.某家俱公司生产甲、乙两种型号的组合柜,每种柜的制造白坯时间、油漆时间及有关数(14分)20.某运输公司接受了向抗洪抢险地区每天至少送180t支援物资的任务.该公司有8辆载重为6t的A型卡车与4辆载重为10t的B型卡车,有10名驾驶员;每辆卡车每天往返的次数为A型卡车4次,B型卡车3次;每辆卡车每天往返的成本费A型车为320元,B 型车为504元.请你们为该公司安排一下应该如何调配车辆,才能使公司所花的成本费最低?若只调配A型或B型卡车,所花的成本费分别是多少?(14分)参考答案一.选择题(本大题共10小题,每小题5分,共50分)01=`二.填空题(本大题共4小题,每小题6分,共24分)11. 5.12- 12.3,2,11 13. 7 14. 2,0 三、解答题(本大题共6题,共76分)15.(12分)[解析]:如下图由12+≤≤≤x y x y 及围成的几何图形就是其阴影部分,且312212421=⋅⋅-⋅⋅=S .16.(),2,2(211A )2,0(),0,42,a C aB y x --(轴分别为交 ),2,2()2(22:222A l x a y l 恒过∴--=-)42,0(),0,2,22a C a D y x ++(轴分别为交, 02,04220>-<-∴<<a aa ,由题意知21l l 与及坐标轴围成的平面区域为ACOD , ,415)21(42)4(21)42)(2(2122222+-=+-=⋅+-++=-=∴∆∆a a a a a aa S S S ECA EOD ACOD 415)(21min ==∴ACOD S a 时,当. 17.(12分)[解析]:设轮船为x 艘、飞机为y 架,则可得⎪⎩⎪⎨⎧∈≥≥+≥+8,,0,30254036N y x y x y x y x ,目标函数z=x +y ,作出可行域,利用图解法可得点A (320,0)可使目标函数z=x +y 最小,但它不是整点,调整为B (7,0).答:在一天内可派轮船718.(12分)[解析]: 作出满足不等式⎪⎩⎪⎨⎧≥-≤≤≤≤122010x y y x作直线,22:1t x y l =-.840222)2,0(max =+⨯-⨯=z A l 时,经过当 .441212)1,1(min =+⨯-⨯=z B l 时,经过当19.(14分)[解析]:设x ,y 分别为甲、乙二种柜的日产量,可将此题归纳为求如下线性目标函数Z=20x +24y 的最大值.其中线性约束条件为 0,06448120126≥≥≤+≤+y x y x y x ,由图及下表Z max =272 答:该公司安排甲、乙二种柜的日产量分别为4台和8台可获最大利润272元. 20.(14分)解:设每天调出A 型车x 辆、B 型车y 辆,公 司所花的成本为z 元,则⎪⎪⎪⎩⎪⎪⎪⎨⎧∈≥⋅+⋅≤+∈≤≤∈≤≤N y x y x y x N y y N x x ,1803104610,40,80目标函数z=320x +504y , 作出可行域(如上图),作L :320x +504y=0, 可行域内的点E 点(7.5,0)可使Z 最小,但不是整数点,最近的整点是(8,0)即只调配A 型卡车,所花最低成本费z=320×8=2560(元); 若只调配B 型卡车,则y 无允许值,即无法调配车辆.(x ,y ) Z=20x+24y (0,10) 240 (0,0) 0 (8,0) 160(4,8) 272A 型车B 型车 物资限制 载重(t ) 6 10 共180 车辆数 8 4 出车次数 4 3 每车每天运输成本(元)320504x +y=104 3 21 4 5 6 7 84x +5y=30。
高中数学线性规划练习题(含详细解答)

x0 7.若 x, y 满足约束条件: x 2 y 3 ;则 x y 的取值范围为 _____ . 2 x y 3
8.约束条件
2 x y 4 ,则目标函数 z=3x-y 的取值范围是 4 x y 1 3 ,6] 2
B.[
A. [
第 5 页 共 11 页
X 2Y 12 2 X Y 12 由已知, 得 Z=300X+400Y, 且 , 画可行域如图所示, X 0 Y 0 3 z 目标函数 Z=300X+400Y 可变形为 Y= x 4 400
这是随 Z 变化的一族平行直线,解方程组
2 2
C
6
D
4 4
( )
12.若实数 x、y 满足 A.(0,1)
x y 1 0 y , 则 的取值范围是 x x0
B. 0,1 C.(1,+ )
D. 1,
c ln b ≥ a c ln c ,则 b, c 满足: 5c 3a ≤ b ≤ 4c a , 13. 已知正数 a ,
A.20 B.35 C.45 D.55
x y 1 0 3.若 x, y 满足约束条件 x y 3 0 ,则 z 3x y 的最小值为 x 3y 3 0
4. 设函数 f ( x )
。
ln x, x 0 , D 是由 x 轴和曲线 y f ( x ) 及该曲线在点 (1, 0) 处的切线所围成的封 2 x 1, x 0
x y 50, 1.2 x 0.9 y 54, 线性约束条件为 x 0, y 0.
x y 50, 4 x 3 y 180, 即 x 0, y 0.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二数学线性规划试题
1.若实数满足则的最大值为;
【答案】9
【解析】先在平面直角坐标系中画出实数的可行解范围,将目标函数化为,在直角坐标系中作出函数的图像,考虑到前的符号是“”,所以将函数的图像向上平移至可行解范围的最上顶点,此时函数的图像在轴上的截距为所求的最大值(另解:可将可
行解范围的最上顶点的坐标代入目标函数可得解).如下图所示.
【考点】简单线性规划问题.
2.设变量满足约束条件,则目标函数的取值范围是()A.B.C.D.
【答案】A
【解析】由约束条件在直角坐标系中画出目标函数的可行域,如图所包围的阴影部分(包括边界):
因为,所以,故选A.
【考点】简单线性规划问题(用平面区域表示二元一次不等式组)
3.已知实数x,y满足条件,则z=x+3y的最小值是()
A.B.C.12D.-12
【答案】B
【解析】画出不等式表示的平面区域,作直线,将平移过点时取得最小值.
【考点】线性规划求最值.
4.已知平面区域如图,,,,在平面区域内取得最大值时的最优解有无数多个,则.
【答案】.
【解析】由得,故是直线的纵截距,因此当直线向上平移时增加,要使得最优解有无数个,从图可知必有直线平移到与直线AC
重合,因此,.
【考点】线性规划.
5.设,满足若目标函数的最大值为14,则
()
A.1B.2C.23D.
【答案】B
【解析】根据题意作出可行域
如图所示,目标函数z=ax+y(a>0)最大值为14,即目标函数z=ax+y(a>0)在3x-y-6≤0与x-y+2≥0的交点M(4,6)处,目标函数z最大值为14,所以4a+6=14,所以a=2.
故选B
【考点】本试题主要是考查了线性规划区域的最优解的问题。
研究二元一次目标函数的最大值问题。
点评:解决这类问题的核心就是准确作图,表示出目标区域,并利用直线的截距的平移得到过哪个点时,得到最优解的问题。
6.设满足则()
A.有最小值2,最大值3B.有最小值2,无最大值
C.有最大值3,无最小值D.既无最小值,也无最大值
【答案】B
【解析】作出不等式表示的可行域可知当直线z=x+y经过直线2x+y=4与直线x-2y=2的交点(2,0)时,z取得最小值2.无最大值.
7.某投资人打算投资甲、乙两个项目. 根据预测,甲、乙项目可能的最大盈利率分别为100﹪和
50﹪,可能的最大亏损分别为30﹪和10﹪. 投资人计划投资金额不超过10万元,要求确保可能
的资金亏损不超过1.8万元. 问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?【答案】投资人用4万元投资甲项目、6万元投资乙项目,才能在确保亏损不超过1.8 万元的前
提下,使可能的盈利最大
【解析】先设投资人分别用x万元、y万元投资甲、乙两个项目得到x,y满足的约束条件为,目标函数,再作出不等式组表示的可行域,找出最优解,求出z的最大值.
解:设投资人分别用x万元、y万元投资甲、乙两个项目,由题意:,目标函数,上述不等式组表示的平面区域如图所示,
阴影部分(含边界)即可行域.作直线,并作平行于直线的一组直线,与可行域相交,其中有一条直线经过可行域上的点M,且与直线的距离最大,其中M点是直线
和直线的交点,解方程组得,此时
(万元),,当时,最得最大值.
答:投资人用4万元投资甲项目、6万元投资乙项目,才能在确保亏损不超过1.8 万元的前提下,使可能的盈利最大.
8.已知, 则的最大值是 .
【答案】10
【解析】作出不等组表示的可行域,当直线经过直线x+y=3与直线x-y=1的交点(2,1)时,z取得最大值10.
9.某工厂计划生产A.B两种涂料,生产A种涂料1t需要甲种原料
1t.乙种原料2t,可获利润3千元;生产B种涂料1t需要甲种原料2t,乙种原料1t,
可获利润2千元,又知该工厂甲种原料的用量不超过400t,乙种原料的用量不超过500t,
问如何安排生产才能获得最大利润?(注:t表示重量单位“吨”)
【答案】应分别生产A、B两种涂料各200t、100t才能获得最大利润
【解析】本试题主要是考查了线性规划的最优解问题在实际生活中的运用。
根据已知设出变量设应分别生产A、B两种涂料、,总利润为Z千元,那么得到x,y的关系式,以及总利润的表达式,进而结合平移法得到最值。
解:设应分别生产A、B两种涂料、,总利润为Z千元…………1分
则线性约束条件是:
目标函数………………6分
作出可行域,如图所示
………………8分
平移可知,当直线
经过点A时,纵截距最大,则取得最大值。
由得即A(200,100)
此时千元………………11分
答:应分别生产A、B两种涂料各200t、100t才能获得最大利润。
…………12分
10.设变量x,y满足约束条件,则z=2x+y的最大值为
A.—2B.4C.6D.8
【答案】C
【解析】不等式组表示的平面区域如图所示
当直线过点B(3,0)的时候,z取得最大值6
11.已知变量x,y满足约束条件,则z=3x+y的最大值为
【答案】11;
【解析】解:因为变量x,y满足约束条件,则过点(3,2)点时,目标函数z=3x+y的最大值为11.
12.设变量满足约束条件,则目标函数的最大值为()
A.2B.3C.4D.5
【答案】D
【解析】因为变量满足约束条件,利用作图可知目标函数过点(1,0)最大为5,选D.
13.在约束条件下,当时,目标函数的最大值的变化范围是()A.[7,8]B.C.[6,8]D.[7,15]
【答案】A
【解析】解:由
x+y=s
y+2x=4 ⇒ x=4-s, y=2s-4
交点为A(0,2),B(4-s,2s-4),
C(0,s),C'(0,4),
当3≤s<4时可行域是四边形OABC,此时,7≤z≤8
当4≤s≤5时可行域是△OAC'此时,zmax=8
故选A.
14.(本题满分12分)设不等式组表示的平面区域为D。
(1)在直角坐标系中画出平面区域D
(2)若直线分平面区域D为面积相等的两部分,求k得值。
【答案】(1)略(2)7/3
【解析】(1)根据直线定界,特殊点定域的原则画出可行域,不注意边界是虚线还是实线。
(2)先把总面积求出来,然后可据一侧的面积等于总面积的一半求解即可。
15.、满足约束条件:,则的最小值是
【答案】
【解析】略
16.已知二次函数、的两个零点分别在与内,则
的取值范围是()
A.B.C.D.
【答案】D
【解析】由题意得,即 ,画出可行域如图,不包含边界,
的几何意义为:可行域内的点到点(-1,2)的距离的平方,故取值范围是.
【考点】一元二次方程根的分布及线性规划
17.已知点和点在直线的两侧,则的取值范围是()
A.B.C.D.
【答案】C
【解析】由题意知,即。
【考点】二元一次不等式表示的平面区域。
18.已知点(3,1)和(-4,6)在直线的两侧,则的取值范围是
A.B.
C.D.
【答案】C
【解析】点(3,1),(-4,6)在直线的两侧,所以,即,所以
【考点】平面区域点的性质
19.设变量x,y满足约束条件,则目标函数的最大值是()
A.4B.2C.1D.
【答案】C
【解析】先画出二元一次不等式组所表示的平面区域,在可行域内平移基准线,得到最优解,
取得最大值为.
【考点】线性规划;
20.设满足约束条件,则的最大值为()
A.5B.3C.7D.-8
【答案】C
【解析】根据题意,作出可行域与目标函数基准直线;将直线化为,当直线向右上方平移时,直线在轴上的截距变大,当直线经过
时,有最大值,即.
【考点】线性规划.。
