等腰三角形前四节导学案
等腰三角形的判定导学案

___.
例 2、求证:如果三角形一个外角的平分线平行于三角形的一边,那么这 个三角形是等腰三角形 已知:∠CAE 是△ABC 的一个外角,∠1=∠2,AD//BC, 求证:AB=AC.
E A 1 2
D
B
C
例 3(自学课本例 3,小组交流) 思考:已知底边和底边上的高,你能用尺规作图方法作出这个等腰三角形 吗?
A
C
D
B
E
【当堂训练】
2
鸡西市第十九中学初三数学组
1、如图, ∠A=36°,∠DBC=36°, ∠C=72°.分别计算∠1,∠2 的度数, 并说明图中有哪些等腰三角形
A
D 1 2 B C
2、如图,AC 和 BD 相交于点 O,且 AB//DC,OA=OB.求证:OC=OD
D C
O
A
B
3. 如图,C 表示灯塔,轮船从 A 处出发以每小时 15 海里的速度向 正北(AN 方向)航行,2 时后到达 B 处,测得 C 在 A 的北偏西 40° 方向,并在 B 的北偏西 80°方向,求 B 处到灯塔 C 的距离.
八年级上
【复习检测】 1、等腰三角形的两边长分别为 6,8,则周长为 2、等腰三角形的周长为 14,其中一边长为 6,则另两边长分别为 3、等腰三角形的一个角为 70°,则另外两个角的度数是 4、等腰三角形的一个角为 120°,则另外两个角的度数是 5、如图,在⊿ABC 中,AB=AC (1) (2) (3) 若 AD 平分∠BAC,那么_________ 、____________
D
C
A
E
B
4鸡西市第十九中学初三来自学组鸡西市第十九中学学案
班级 姓名
学科 时间 学习 目标 重点 难点
等腰三角形 第四课时 导学案

1.1 等腰三角形(四)一、学习准备:1、等边三角形的三个角都 ,并且每个角都等于 .2、已知:∠ABC,∠ACB 的平分线相交于F,过F 作DE ∥(1) 找出图中的等腰三角形(2) BD,CE,DE 之间存在着怎样的关系? (3) 证明以上的结论。
二、学习目标:1、掌握等边三角形的判定定理及推论。
2、能利用所学定理解决简单的实际问题。
三、学习提示:阅读P10~12完成下列任务: 1,合作探究:(1).一个等腰三角形满足什么条件时便成为等边三角形?(2).你认为有一个角等于60°等腰三角形是等边三角形吗?你能证明你的结论吗?把你的思路与小组成员进行交流一下。
要求画出图形,写出已知、求证、然后再证明得到定理: .2、练习:证明:三个角都相等的三角形是等边三角形.3. 自主探究:用两个含30°的三角尺,你能拼成一个怎样的三角形?能拼出一个等边三角形吗?说说你的理由.由此你能想到,在直角三角形中,30°角所对的直角三角形与斜边有怎样的大小关系?能证明你的结论吗?如图,在△ABC 中,∠ACB =90°,∠A =30°,则∠B =60°。
延长BC 至D ,使CD =BC ,连接AD得到定理 .(1) (2)D图 1-74、练习:求证:等腰三角形的底角为15°,那么腰上的高是腰长的一半。
已知:如图1-8,在△ABC 中,已知AB =AC ,∠ABC =15°,CD 是腰AB 上的高, 求证:CD=21四、学习小结:你有哪些收获? 五、夯实基础:(1).等腰三角形的顶角为150°,腰长为10cm ,则这个三角形的面积为_______. (2).若等腰三角形一腰上的高线平分这腰,则这个三角形是______三角形;若等腰三角形底边上的高等于一腰上的高,则这个三角形是____三角形. (3).在△ABC 中,AB =AC ,∠A =60°,则△ABC 是 三角形. (4)、已知:如图,在△ABC 中,∠ACB = 90°,∠A=30°,CD ⊥AB 于D. 求证:BD=41AB六、能力提升1、如图,P 是等边三角形ABC 内的一点,连结PA 、PB 、PC ,•以BP 为边作∠PBQ=60°,且BP=BQ ,连结CQ .(1)观察并猜想AP 与CQ 之间的大小关系,并证明你的结论. (2)若PA:PB:PC=3:4:5,连结PQ ,试判断△PQC 的形状,并说明理由.作业:P9习题1.3---1、2、4 【评价反思】 :图1-8DB。
等腰三角形的性质 导学案
等腰三角形的性质 导学案
日期: 第 页 姓名:
一、等腰三角形的性质
1、性质引入
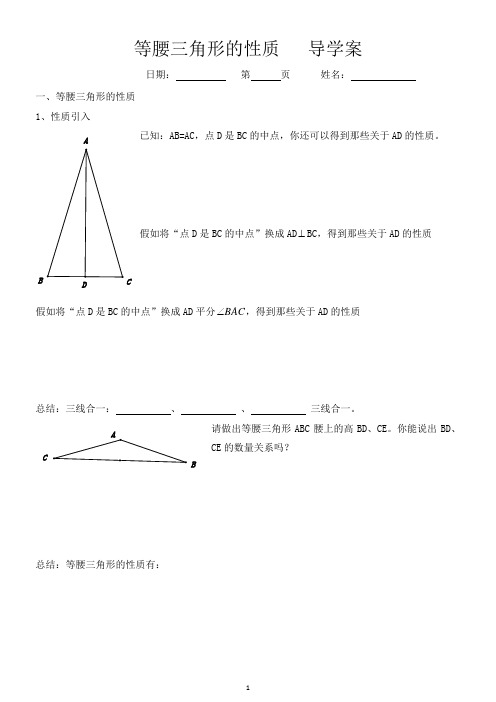
已知:AB=AC ,点D 是BC 的中点,你还可以得到那些关于AD 的性质。
假如将“点D 是BC 的中点”换成AD ⊥BC ,得到那些关于AD 的性质
假如将“点D 是BC 的中点”换成AD 平分BAC ∠,得到那些关于AD 的性质
总结:三线合一: 、 、 三线合一。
请做出等腰三角形ABC 腰上的高BD 、CE 。
你能说出BD 、CE 的数量关系吗?
总结:等腰三角形的性质有:
B C
A C B
二、等腰直角三角形的性质
1、性质推导
已知:等腰Rt ABC ∆中,AD 是斜边上的高,
请说出图中相等的角:
相等的线段:
三、应用
1、已知:如图,△ABC 是等腰三角形,AB=AC ,∠1=∠2.求证:OA 平分∠BAC .
2、如图,在等腰直角△ABC 中,AD 为斜边上的高,以D 为端点任作两条互相垂直的射线与两腰相交于E 、F ,连接EF 与AD 相交于G ,则∠AED 与∠AGF 的关系为( )
下,上述结论是否成立?若成立,请
给予
证明
;若不成立,DEF S ∆、CEF S ∆、ABC S ∆又有怎样的数量关系?请写出你的猜想,不需证明.
C B A。
《等腰三角形》导学案设计(孙冬梅)

《等腰三角形》导学案设计在几何画板中,教师拖动一个顶点,让学生观察底两角的大小关系.伴的互相补充,基本上都得到所有性质定理.当然,在教学过程中,教师应注意小组的巡视,提醒学生思考多种证明思路,思考不同的辅助线之间的关系从而得到“三线合一”.第三环节:明晰结论和证明过程活动内容:1.利用不同的方法来证明等腰三角形的两个底角相等.2.思考:等腰三角形顶角的平分线、底边上的中线、底边上的高有什么关系?1.让两至三个学生板演证明,其余学生在练习本上证明.2.各小组通过课件汇总各小组的结果以及具体证明方法,3.每一个小组找一人为代表展示本组的学习成果.大部分学生都能写出正确的证明的过程,并且思路清析,且能够通过多种不同的方法来证明同一个命题,但一部分写出的过程思路不清,且步骤混乱.学生都能总结出等腰三角形三线合一的性质.第四环节:随堂练习巩固新知如图,在△ABD中,C是BD上的一点,且AC⊥BD,AC=BC=CD,(1)求证:△ABD是等1.独立探究写出完整的证明过程.2.同桌活动,互检互评,交流对证明一个几何题1.求证:等边三角形三个内角都相等并且每个内角都等于60°.腰三角形;(2)求∠BAD的度数.的心得.3.小组内交流,然后以小组为单位,推选一名学生把完整的证明过程写到板上.4.全班同学共同订正不完整的地方.2.如图:在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且2AE=BD,DF⊥AB于F.求证:CD=DF.(图形见课件)第五环节:课堂小结1.师总结本课学习内容.2.布置课后学习内容.谈自己本节课的收获.板书设计等腰三角形1.两角及其中一角的对边对应相等的两个三角形全等.(AAS)2.等腰三角形的两个底角相等;3.等腰三角形顶角的平分线、底边中线、底边上高三条线重合;4.等边三角形三个内角都相等并且每个内角都等于60°.。
1.1等腰三角形的性质和判定导学案

1.1 等腰三角形的性质和判定
班级 姓名 学号 完成时间45分钟
等腰三角形的性质:
①等腰三角形的 角相等.(简称“ ”)
②等腰三角形的 、 、 互相重合.(简称“ ”) ③等腰三角形是 对称图形,它的对称轴是: .
练习:
1.若等腰三角形的周长为12,一边长为5,那么另两边长分别为 .
2.若等腰三角形有两边长为2和5,那么周长为 .
3.若等腰三角形有一个外角等于50°,那么另两个角为 .
4.若等腰三角形有一个角等于120°,那么另两个角为 .
★5.若等腰三角形一腰上的高与另一腰的夹角等于30°,那么这个等腰三角形的顶角为 . ★6.若等腰三角形的周长等于12cm ,那么腰长x 的取值范围是 .
7.如图在△ABC 中,AB =AC ,∠A=50°,BD 为∠ABC 的平分线,则∠BDC=_ ____°.
8.如图在△ABC 中,AB =AC ,D 为AC 边上一点,且BD =BC =AD .•则∠A 等于 ( )
A .30° B.36° C.45° D.72°
9.已知:如图,AB=AC .CE=BD ,求证:GE=GD ;
10.如图,在△ABC 中,点O 在AC 上,过点O 作MN ∥BC ,CE
MN 分别交于E 、F ,求证:OE=OF.
第9题图
第7题图 第8题图
11.在平面直角坐标系xOy中,已知点P(2,2),点Q在y轴上,△PQO是等腰三角形,
则满足条件的点Q共有______个.
12.如图,等腰三角形ABC中,AB=AC,一腰上的中线BD•将这个等腰三角形周长分成15和6两部分,
求这个三角形的腰长及底边长.。
等腰三角形性质

《等腰三角形性质》导学案班级____ 姓名________ 小组___ 评价____学习目标:1.等腰三角形的概念.2.等腰三角形的性质.3.等腰三角形的概念及性质的应用.教学重点难点1.等腰三角形的概念及性质.2.等腰三角形性质的应用.【使用说明与学法指导】1.用15分钟左右的时间,阅读探究课本P125--128 的基础知识,自主高效预习,提升自己的阅读理解能力;2.独立完成学案中设计的例题及练习题,注意解题方法的选择。
一、基础知识回顾:1、两个图形关于某直线对称,那么它们的对应边_________,对应角_________,对应点连线被对称轴__________。
2、全等三角形的对应边__________,对应角_________。
二、导学:1.等腰三角形的定义:有两条边__________的三角形叫等腰三角形符号表示:∵在△ABC中,____________________∴△ABC是____________________2. 性质:(1)等腰三角形的两底角相等(简写成“等边对等角”).几何语言:∵在△ABC中,__________. (已知).∴__________(__________)(2)等腰三角形的____________、底边上的_______、底边上的_________互相_________ (简写成“等腰三角形的三线________”)几何语言:①∵AB=AC,AD平分∠BAC (已知). ②∵AB=AC,_____________ (已知).∴AD⊥BC且AD平分BC(三线合一)∴_______________________________∴∠ADB=∠ADC=900, BD=CD ∴_______________________________③∵AB=AC,_____________ (已知).∴_________________________________∴_________________________________三、质疑探究——质疑解疑、合作探究已知:在△ABC 中,AB = AC ,且BD = BC = AD , 求∠ A 的度数。
等腰三角形 导学案
1.4、等腰三角形
Xx市初中教师:
课型
学习
目标
1.经历探索等腰三角形性质的过程,掌握等腰三角形的轴对称性及其相关性质,进一步体验轴对称的特征,发展空间观念.
2.经历探索等边三角形轴对称性和内角性质的过程,掌握这个性质。
学习过程
师生活动
学习笔记
一、复习回顾:
1、什么叫一条角平分线?
2、角平分线的性质是什么?
请你在下面写出等腰三角形的性质:
三、交流与发现:
任意画一个等边三角形ABC
(1)等边三角形是轴对称图形吗?找出它的对称轴.
(2)你能发现它的哪些性质?
学习笔记
师生活动
总结如下:
等边三角形是___对称图形.
等边三角形每个角的平分线和这个角的对边上的中线、高线重合(三线合一),它们所在的直线都是等边三角形的对称轴.等边三角形共有__条对称轴.
2、等腰三角形两边的长分别为2cm和5cm,则这个三角形的周长是()
A. 9cmB. 12cm
C. 9cm或12cmD.在9cm与12cm之间
师生活动
学习笔记
3、如图,等腰△ABC中,AD⊥BC于D,已知DC=2cm,AB=3cm,则△ABC的周长为___________。
4、已知:等腰三角形的一个角是80°,则它的另外两个角是。
A. 36°B. 32°ቤተ መጻሕፍቲ ባይዱ. 64°D. 72°
3、等腰三角形的对称轴是___________。
4、有一角是60°的等腰三角形是_____________,它有_____________条对称轴。
分别找出如图所示中各个图形的对称轴。
练习二、
1、等腰三角形一腰上的高与底边所成的角等于()
初中数学最新版《等腰三角形的判定 》精品导学案(2022年版)
$13.3.1等腰三角形〔二〕导学案$13.3.1等腰三角形〔二〕导学案$13.3.1等腰三角形〔二〕导学案$13.3.1等腰三角形〔二〕导学案$13.3.1等腰三角形〔二〕导学案五、课堂小测〔约5分钟〕:如图,AD ∥BC ,BD 平分∠ABC . 求证:AB=AD .第4课时 “斜边、直角边〞DCAB1.理解并掌握三角形全等的判定方法——“斜边、直角边〞.(重点)2.经历探究“斜边、直角边〞判定方法的过程,能运用“斜边、直角边〞判定方法解决有关问题.(难点)一、情境导入舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.(1)你能帮他想个方法吗?(2)如果他只带了一个卷尺,能完成这个任务吗?工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的〞,你相信他的结论吗?二、合作探究探究点一:应用“斜边、直角边〞判定三角形全等如图,∠A =∠D =90°,E 、F 在线段BC 上,DE 与AF 交于点O ,且AB=CD ,BE =CF .求证:Rt △ABF ≌Rt △DCE .解析:由题意可得△ABF 与△DCE 都为直角三角形,由BE =CF 可得BF =CE ,然后运用“HL 〞即可判定Rt △ABF 与Rt △DCE 全等.证明:∵BE =CF ,∴BE +EF =CF +EF ,即BF =CE .∵∠A =∠D =90°,∴△ABF与△DCE 都为直角三角形.在Rt △ABF 和Rt △DCE 中,∵⎩⎪⎨⎪⎧BF =CE ,AB =CD ,∴Rt △ABF ≌Rt △DCE (HL).方法总结:利用“HL 〞判定三角形全等,首先要判定这两个三角形是直角三角形,然后找出对应的斜边和直角边相等即可.探究点二:“斜边、直角边〞判定三角形全等的运用 【类型一】 利用“HL 〞判定线段相等如图,AD ,AF 分别是两个钝角△ABC 和△ABE 的高,如果AD =AF ,AC =AE .求证:BC =BE .解析:根据“HL 〞证Rt △ADC ≌Rt △AFE ,得CD =EF ,再根据“HL 〞证Rt △ABD ≌Rt △ABF ,得BD =BF ,最后证明BC =BE .证明:∵AD ,AF 分别是两个钝角△ABC 和△ABE 的高,且AD =AF ,AC =AE ,∴Rt △ADC ≌Rt △AFE (HL).∴CD =EF .∵AD =AF ,AB =AB ,∴Rt △ABD ≌Rt △ABF (HL).∴BD =BF .∴BD -CD =BF -EF .即BC =BE .方法总结:证明线段相等可通过证明三角形全等解决,作为“HL 〞公理就是直角三角形独有的判定方法.所以直角三角形的判定方法最多,使用时应该抓住“直角〞这个隐含的条件.【类型二】 利用“HL 〞判定角相等或线段平行如图,AB ⊥BC ,AD ⊥DC ,AB =AD ,求证:∠1=∠2.解析:要证角相等,可先证明全等.即证Rt △ABC ≌Rt △ADC ,进而得出角相等.证明:∵AB ⊥BC ,AD ⊥DC ,∴∠B =∠D =90°,∴△ABC 与△ACD 为直角三角形.在Rt △ABC 和Rt △ADC 中,∵⎩⎪⎨⎪⎧AB =AD ,AC =AC ,∴Rt △ABC ≌Rt △ADC (HL),∴∠1=∠2.方法总结:证明角相等可通过证明三角形全等解决.【类型三】 利用“HL 〞解决动点问题如图,有一直角三角形ABC ,∠C =90°,AC =10cm ,BC =5cm ,一条线段PQ =AB ,P 、Q 两点分别在AC 上和过A 点且垂直于AC 的射线AQ 上运动,问P 点运动到AC 上什么位置时△ABC 才能和△APQ 全等?解析:此题要分情况讨论:(1)Rt △APQ ≌Rt △CBA ,此时AP =BC =5cm ,可据此求出P 点的位置.(2)Rt △QAP ≌Rt △BCA ,此时AP =AC ,P 、C 重合.解:根据三角形全等的判定方法HL 可知:(1)当P 运动到AP =BC 时,∵∠C =∠QAP =90°.在Rt △ABC 与Rt △QPA 中,∵⎩⎪⎨⎪⎧AP =BC ,PQ =AB ,∴Rt △ABC ≌Rt △QPA (HL),∴AP =BC =5cm ;(2)当P 运动到与C 点重合时,AP =AC .在Rt △ABC 与Rt △QPA 中,∵⎩⎪⎨⎪⎧AP =AC ,PQ =AB ,∴Rt △QAP ≌Rt △BCA (HL),∴AP =AC =10cm ,∴当AP =5cm 或10cm 时,△ABC 才能和△APQ 全等.方法总结:判定三角形全等的关键是找对应边和对应角,由于此题没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.【类型四】 综合运用全等三角形的判定方法判定直角三角形全等如图,CD ⊥AB 于D 点,BE ⊥AC 于E 点,BE ,CD 交于O 点,且AO 平分∠BAC .求证:OB =OC .解析:BE ⊥AC ,CD ⊥AB 可推出∠ADC =∠BDC =∠AEB =∠CEB =90°,由AO 平分∠BAC 可知∠1=∠2,然后根据AAS 证得△AOD ≌△AOE ,根据ASA 证得△BOD ≌△COE ,即可证得OB =OC .证明:∵BE ⊥AC ,CD ⊥AB ,∴∠ADC =∠BDC =∠AEB =∠CEB =90°.∵AO 平分∠BAC ,∴∠1=∠2.在△AOD 和△AOE 中,∵⎩⎪⎨⎪⎧∠ADC =∠AEB ,∠1=∠2,OA =OA ,∴△AOD ≌△AOE (AAS).∴OD =OE .在△BOD 和△COE 中,∵⎩⎪⎨⎪⎧∠BDC =∠CEB ,OD =OE ,∠BOD =∠COE ,∴△BOD ≌△COE (ASA).∴OB =OC .方法总结:判定直角三角形全等的方法除“HL 〞外,还有:SSS 、SAS 、ASA 、AAS.三、板书设计“斜边、直角边〞1.斜边、直角边:斜边和一条直角边分别相等的两个直角三角形全等.简记为“斜边、直角边〞或“HL〞.2.方法归纳:(1)证明两个直角三角形全等的常用方法是“HL〞,除此之外,还可以选用“SAS〞“ASA〞“AAS〞以及“SSS〞.(2)寻找未知的等边或等角时,常考虑转移到其他三角形中,利用三角形全等来进行证明.本节课的教学主要通过分组讨论、操作探究以及合作交流等方式来进行.在探究直角三角形全等的判定方法——“斜边、直角边〞时,要让学生进行合作交流.在寻找未知的等边或等角时,常考虑将其转移到其他三角形中,利用三角形全等来进行证明.此外,还要注重通过适量的练习稳固所学的新知识.。
13.3 等腰三角形导学案
第六课时 13.3.1等腰三角形(1)【学习目标】1、了解等腰三角形的概念,掌握等腰三角形的性质; 2、会运用等腰三角形的概念及性质解决相关问题。
【学习重点】等腰三角形性质的探索及应用【学习难点】等腰三角形性质的应用 一、学前准备1、下列图形不一定是轴对称图形的是( ) A 、圆 B 、长方形 C 、线段D 、三角形2、怎样的三角形是轴对称图形?答:3、有两边相等的三角形叫 ,相等的两边叫 ,另一边叫 ; 两腰的夹角叫,腰和底边的夹角叫 4、如图,在△ABC 中,AB=AC ,标出各部分名称 5、用一张长方形的纸剪一个等腰三角形。
二、探索思考 (一)1、操作、实践: 将你剪得等腰三角形,照图折叠,找出其中重合的线段和角,填入右表:2、根据上表你能得出哪些结论?并将你的结论与同学交流。
3、请用学过的知识证明以上结论。
(二)归纳:等腰三角形的性质:(1)等腰三角形的 。
(简写成“ ”) 符号语言:如图1∵ ∴(2)等腰三角形的 、 、 相互重合(简写成“ ”)符号语言①:如图2∵ , ∴ 符号语言②:如图2∵ , ∴ 符号语言③:如图2∵ , ∴ 练习1、填空:(1)等腰三角形一个底角为70°,它的顶角为 . (2)等腰三角形一个角为70°,它的另外两个角为三、典例分析例2:如图所示,在△ABC 中,AB=AC ,点D 在AC 上,且BD=BC=AD ,求△ABC 各角的度数.例2:如图3,在△ABC 中,AB=AC ,点D 、E 在BC 上,且AD=AE.,求证:BD=CE四、当堂反馈1、(1) 等腰三角形的一边长为3cm ,另一边长为4cm,则它的周长是 ; (2) 等腰三角形的一边长为3cm ,另一边长为8cm,则它的周长是 。
2、在△ABC 中,AB =AC ,(1)如果∠A =70°,则∠C =_______,∠B =_______ (2)如果∠A =90°,则∠B =_______,∠C =________ (3)如果有一个角等于120°,则其余两个角分别是 度 (4)如果有一个角等于55°,则其余两个角分别是 度3、如图(3)所示,△ABC 是等腰直角三角形(AB =AC ,∠BAC =90°),AD 是底边BC 上的高, 标出∠B 、∠C 、∠BAD 、∠DAC 的度数,图中有哪些相等线段?4、如图,在△ABC 中,AB =AD =DC ,∠BAD =26°,求∠B 和∠C 的度数.五、学习反思(请你对照学习目标,谈一下这节课的收获及困惑。
广东省梅州市五华县八年级数学上册 12.3.1《等腰三角形》导学案2(无答案) 新人教版
用心 爱心 专心1一、学习目标:1、 掌握等腰三角形的判定方法,并能灵活运用解决实际问题;2、 通过独立思考,交流讨论,发展推理能力和运用数学知识解决实际问题的能力;3、 极度热情,高度责任,享受学习的快乐; 二、重点难点学习重点:等腰三角形的判定方法学习难点:等腰三角形的判定和性质的区别,等腰三角形的判定的应用。
使用说明:先由学生自学课本51页练习以后至53页练习,经历自主探索总结的过程,然后独立认真完成学案,用红笔标记出疑点与盲点,以备上课时展示和质疑。
三、合作探究(同学合作,教师引导)1、复习回顾:等腰三角形的性质,平行线的性质,三角形全等的判定2、用直尺和量角器画△ABC ,使∠B=∠C ,再用刻度尺量一量线段AB 、AC 的长,你有什么发现?猜想:如果一个三角形有两个角相等,那么这两个角所对的边也想等。
3、 你能验证2中的猜想吗? 已知:如图 在△ABC 中,∠B=∠C 求证:AB=AC等腰三角形的判定方法:如果一个三角形有两个角相等,那么这两个角所对的边也想等(简写成:等角对等边”)。
4、 等腰三角形的性质与判定有什么区别和联系?区别: 联系: 四、精讲精练例1.如图,AC 和BD 相交于点O ,且AB ∥DC ,OC=OD , 求证:OA=OB例 2.求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。
精练:1.如图,在△ABC 中,AB=AC ,∠B=36O,D 、E 是BC 上的两点, 且∠ADE=∠AED=2∠BAD ,则图中的等腰三角形共有( )个。
ED ABCDOA.3个B.4个C.5个D.6个2.如图,△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作EF∥BC,交AB于点E,交AC于点F求证:EF=EB+FC.五、课堂小结:等腰三角形的判定方法:如果一个三角形有两个角相等,那么这两个角所对的边也想等(简写成:等角对等边)六、作业 P53 1 3教学反思:AC BFE O用心爱心专心 2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章三角形的证明等腰三角形导学案(1)主备人审核人班级:姓名:学习目标:1、认知目标:经历“探索——发现——猜想——归纳”的过程,能用语言表述等腰三角形的性质。
2、能力目标:掌握等腰三角形的性质,能灵活地运用它们进行论证。
提高数学思维能力和解决问题能力。
学习重点和难点:重点是等腰三角形性质;难点是等腰三角形性质的灵活运用。
导学过程:一、预习导学:1、什么样的三角形是等腰三角形?2、画一个等腰三角形并标识出等腰三角形的腰、底边、顶角、底角。
二、自主探索:1.实验与探究:如图,用纸剪一个等腰三角形ABC,将三角形对折,使它的两腰AB与AC重合,记折痕与底边BC的交点为D,把纸展平后铺平。
思考下面的问题:(1)等腰三角形ABC是轴对称图形吗?(2)∠BAD与∠CAD相等吗?为什么?(3)∠B与∠C相等吗?为什么?(4)折痕所在的直线AD与底边BC有什么位置关系?(5)线段BD与CD 线段相等吗?(6)你能总结一下折痕所在的直线AD具有的性质吗?2.总结等腰三角形的性质:等腰三角形是_________图形,_______是对称轴,有条对称轴;等腰三角形的两个底角________,简称“______________________________”。
等腰三角形顶角的平分线_____________________________相互重合,简称“三线合一”。
三、课堂合作研讨1.证明等腰三角形两个底角相等。
已知:如图,⊿ABC中,AB=AC.求证:∠B = ∠C. 2、已知:如图3,⊿ABC中,AB=AC,∠BAC=120°,点D、E是底边上两点,且BD=AD,CE=AE.求∠DAE的度数。
作业1、已知:如图,在△ABC中,AB=AC。
(1)∵AD⊥BC,∴∠ =∠,= 。
(2)∵AD是底边上的中线∴⊥,∠ = ∠(3)∵AD是顶角的平分线,∴⊥, =2.如图:房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC,求顶架上∠B、∠C、∠BAD、∠CAD的度数。
3、已知等腰三角形的腰长比底边多2cm,并且它的周长为16cm.求这个等腰三角形的边长.4、已知一个等腰三角形两内角的度数之比为1:4 ,则这个等腰三角形顶角的度数为多少?5、如图:点D、E在△ABC的边BC上,AB=AC,AD=AE,求证:BD=CEA BCA 12 12图8 图9 B DA CE AB C DE图10图14第2课时 1.等腰三角形导学案第二课时主备人 审核人 班级: 姓名: 学习目标:1、 了解等边三角形的性质和判定方法。
2、 会用等边三角形得相关性质解决简单的实际问题。
学习重点:了解等边三角形的性质和判定方法。
学习难点:了解等边三角形的性质和判定方法。
学习过程: 1、前置准备: (1)、等腰三角形的性质是什么?(2)、等腰三角形的一个内角为700,则顶角为 。
(3)、等腰三角形的一个外角为1000,则其顶角为 。
2、自主学习: (1)、在等腰三角形中作出一些相等的线段(角平分线、中线、高),你能发现其中一些相等的线段吗?你能证明你的结论吗? (2)、等腰三角形的两底的角平分线相等吗?怎样证明。
已知: 求证: 证明:得出定理: 。
问题:等腰三角形两条腰上的中线相等吗?高呢?还有其他的结论吗?请你证明它们,并与同伴交流。
一、自学课本5 -6页内容后完成下列各题:1.等边三角形的概念:三边都 的三角形叫做等边三角形,它是特殊的 三角形,也叫 .2.等边三角形的性质:等边三角形的内角都 ,且等于 度;反过来,三个内角都等于 度的三角形一定是等边三角形.等边三角形是 图形,等边三角形每条边上的 、 和所对角的都三线合一,它们所在的直线都是等边三角形的 . 【例1】已知,如图3,延长ABC △的各边,使得BF AC =,AE CD AB ==,顺次连接D E F ,,,得到DEF △为等边三角形.说明下列结论成立的理由. (1)AEF CDE △≌△;(2)ABC △为等边三角形. 作业1. 如图5, 等边△ABC,延长BC 至D,使AC=CD,连结AD,则∠BAD 的度数是……( ) A.80° B.90° C.100°D.110°2. 如图6,正△ABC 的两条角平分线BD 和CE 交于点I ,则∠BIC 等于………( )A .60°B .90°C .120°D .150°3.下列三角形:①有两个角等于60°;②有一个角等于60°的等腰三角形;•③三个外角(每个顶点处各取一个外角)都相等的三角形;•④一腰上的中线也是这条腰上的高的等 腰三角形.其中是等边三角形的有…………………………………………………………( ) A .①②③ B .①②④ C .①③ D .①②③④4. 如图7,ABC ∆是等边三角形,CBD ∠=90°,BD=BC , 则1∠的度数是________.5.如图8,将一等边三角形剪去一个角后,∠1+∠2= .6.如图9,在等边△ABC 中,D 、E 分别是AB 、AC 上的点, 且AD =CE ,则∠BCD +∠CBE =______度.7. 如图10,△ABC 是等边三角形,DE ∥BC ,交AB 、AC 于D 、E .则△ADE 是等边三角形.试说明理由.8. 如图14,△ABC 是一个等边三角形,点D 、E 分别在AB 、AC 上,F 是BE 和CD 的交点,已知∠BFC =120°.则AD =CE .请说明理由.等腰三角形第三课时导学案图3A B C DE FA FBC E 主备人 审核人 班级: 姓名: 学习目标:1、经历“探索——发现——猜想——证明”的过程,能够用综合法证明等腰三角形的有关性质定理和判定定理.2、能够灵活运用公理和等腰三角形有关性质、判定定理进行相关题目的证明,进一步发展推理能力. 学习重点:探索并证明等腰三角形的性质、判定的过程. 学习难点:用文字语言叙述的几何命题的证明及辅助线的添加. 学习过程:一.学前准备:回想一下,我们探索过的等腰三角形的性质? 性质1: ;性质2: . 二、自主学习,合作探究:前面已经证明了等腰三角形的两个底角相等。
反过来,有两个角相等的三角形是等腰三角形吗?1、如图:在△ABC 中,∠B=∠C ,求证:AB=AC. 反证法例题用反证法证明:一个三角形中不能有两个是直角 三、自我小结:等腰三角形的判定方法:如果有一个三角形有两个角相等, 那么这两个角所对的边 ,简写成 。
作业1.如上图,在△ABC 中BC=AC ,CD ⊥AB ,DE ∥BC ,试说明△ADE 和△CED 都是等腰三角形。
2.如图,点D 在AC 上,点E 在AB 上,且AB=AC ,BC=BD=BE ,AE=DE ,求∠A 的度数。
3,已知AB=AC ,D 是AB 上一点,DE ⊥BC 于E ,ED 的延长线交CA 的延长线于F ,说明△ADF 是等腰三角形的理由。
4、已知:如图2,在△ABC 中,AB=AC ,D 是AB 的中点,E 是AC 的中点,DF ⊥BC ,EG ⊥BC ,垂足分别是点F ,G 。
求证:DF=EG 。
5、已知,如图3,点D ,E 分别在AB ,AC 上,AB=AC ,DE ∥BC 。
求证:BD=CE 。
D C BA图1E D C B A EC图3CA BD E 图2 C A B F GD EC A B等腰三角形导学案第四课时主备人 审核人 班级 姓名学习目标:1、掌握含30°角的直角三角形的性质。
2、会用含30°角的直角三角形的性质解决简单的实际问题。
教学重点、难点:重点:含30°角的直角三角形的性质;几何问题的代数解法。
难点:理解含30°角的直角三角形的性质的理论依据。
导学过程:一、合作探究: 自己动手操作,用两个含30°角的三角尺摆一摆,猜一猜,证一证。
用含30°角的直角三角尺摆出了如下两个三角形.1、其中,图(1)中ΔABC 是 三角形,为什么?2、图(1)中,根据等腰三角形“三线合一”的性质,可得BD=DC=12.即BD=12,所以可得出在Rt △ABD 中,∠BAD=30°,它所对的边 是斜边 的 .定理:在直角三角形中,如果一个锐角等于30°,•那么 。
已知:如图,在Rt △ABC 中,∠C=90°,∠BAC=30°.求证:BC=12AB .DC AB分析:从三角尺的摆拼过程中得到启发,延长BC 至D ,使CD=BC ,连接AD . 证明:二、展示 例5:右图是屋架设计图的一部分,点D 是斜梁AB 的中点,立柱BC 、DE 垂直于横梁AC ,AB=7.4m ,∠A=30°,立柱BD 、DE 要多长? 作业 判断:1、等边三角形的对称轴只有一条 ( )2、等腰三角形的底角可以是直角 ( )3、等腰三角形的中线是它的对称轴( )4、等腰三角形的中线是它的对称轴( ) 仔细做一做:1、等腰三角形的顶角与底角的比为3︰1,则三个角的度数为_______2、等边三角形有_________条对称轴3. 如果一个三角形的一个内角的平分线垂直于对边,那么它是______三角形。
4.在等边△ABC 所在的平面内求一点P ,使△PAB 、△PBC 、△PAC 都是等腰三角形,具有这样性质的点P 有____________个。
5.等腰三角形一腰上的高等于该三角形某一条边的长度的一半,则其顶角等于( )A .30°B .30°或150°C .120°或150°D .30°或120°或150°6.如图:∠BCD=90,DC 是边BD 的一半,AC 是BD 边上的中线,求∠CAD 的度数。
7、已知:如图,在△ABC 中,AB=AC=2a ,∠ABC=∠ACB=15°,CD 是腰AB 上的高.求:CD 的长.8已知:如图,△ABC 中,BC ⊥AC,DE ⊥AC ,点D 是AB 的中点,∠A=300,DE=1.8,求AB 的长D CAEB DCABDCAB。
