北师大版九年级上期相似三角形单元检测卷
2022-2023学年北师大版九年级数学上册《4-4探索三角形相似的条件》同步达标测试题(附答案)

2022-2023学年北师大版九年级数学上册《4.4探索三角形相似的条件》同步达标测试题(附答案)一.选择题(共12小题,满分48分)1.图形中,每个小网格均为正方形网格,带阴影部分的三角形中与如图△A1B1C1相似的是()A.B.C.D.2.如图,在△ABC中,D,E两点分别在BC,AC上,且AD平分∠BAC,若∠ABE=∠C,BE与AD相交于点F,则图中与△ABD相似的是()A.△ABC B.△ABF C.△BFD D.△AEF3.如图,在△ABC中,点D、E分别在AB、AC边上,DE与BC不平行,那么下列条件中,不能判断△ADE∽△ACB的是()A.∠ADE=∠C B.∠AED=∠B C.=D.=4.已知△ABC三边长是,,2,与△ABC相似的三角形三边长可能是()A.1,,B.1,,C.1,,D.1,,5.如图,D是△ABC边AB上一点,添加一个条件后,仍然不能使△ACD∽△ABC的是()A.∠ACB=∠ADC B.∠ACD=∠ABC C.D.6.已知Rt△ABC中,∠C=90°,∠A≠∠B,点P是边AC上一点(不与A、C重合),过P点的一条直线与△ABC的边相交,所构成的三角形与原三角形相似,这样的直线有()条.A.1B.2C.3D.47.如图,△ABC中,点D、E分别在AB、AC边上,则下列条件中,不一定能使△AED∽△ABC的是()A.∠2=∠B B.∠1=∠C C.D.8.如图:点D在△ABC的边AB上,连接CD,下列条件:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=AD•AB;④AB•CD=AC•BC.其中能判定△ACD∽△ABC的共有()A.1个B.2个C.3个D.4个9.如图,在△ABC中,点D、E分别在边AB、AC上,则在下列四个条件中:①∠AED=∠B;②DE∥BC;③;④AD•BC=DE•AC,能满足△ADE∽△ACB的条件有()A.1个B.2个C.3个D.4个10.如图,在△ABC中,AB=AC=8,BC=6,点P从点B出发以1个单位/s的速度向点A运动,同时点Q从点C出发以2个单位/s的速度向点B运动.当以B,P,Q为顶点的三角形与△ABC相似时,运动时间为()A.s B.s C.s或s D.以上均不对11.如图,在△ABC中,点D、E分别在边AB、AC上,则在下列五个条件中:①∠AED=∠B;②DE∥BC;③=;④AD•BC=DE•AC;⑤∠ADE=∠C,能满足△ADE∽△ACB的条件有()A.1个B.2个C.3个D.4个12.如图,正方形ABCD中,F为AB上一点,E是BC延长线上一点,且AF=EC,连接EF,DE,DF,M是FE中点,连接MC,设FE与DC相交于点N.则4个结论:①DN =DG;②△BFG∽△EDG∽△BDE;③CM垂直BD;④若MC=,则BF=2;正确的结论有()个A.4B.3C.2D.1二.填空题(共4小题,满分20分)13.如图,∠B=∠D,请你添加一个条件,使得△ABC∽△ADE,这个条件可以是.14.如图,在边长为4的正方形ABCD中,点E、F分别是BC、CD的中点,DE、AF交于点G,AF的中点为H,连接BG、DH.给出下列结论:①AF⊥DE;②DG=;③HD∥BG;④△ABG∽△DHF.其中正确的结论有.(请填上所有正确结论的序号)15.如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件:,可以使得△FDB与△ADE 相似.(只需写出一个)16.如图,在△ABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC =∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC与△ACB相似的条件是(只填序号).三.解答题(共8小题,满分52分)17.已知:如图,点C,D在线段AB上,△PCD是等边三角形,且AC=1,CD=2,DB =4.求证:△ACP∽△PDB.18.如图,已知∠1=∠2,∠AED=∠C,求证:△ABC∽△ADE.19.如图,AB•AE=AD•AC,且∠1=∠2,求证:△ABC∽△ADE.20.如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.求证:△ABE∽△ACD.21.如图,在△ABC中,BD平分∠ABC,交AC于点D,点E是AB上一点,连接DE,BD2=BC•BE.证明:△BCD∽△BDE.22.如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向B以2cm/s的速度移动,点Q从点B开始沿BC向C点以4cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒钟△PBQ与△ABC相似?23.如图,已知AD•AC=AB•AE.求证:△ADE∽△ABC.24.如图,在△ABC中,AB=AC=1,BC=,在AC边上截取AD=BC,连接BD.(1)通过计算,判断AD2与AC•CD的大小关系;(2)求∠ABD的度数.参考答案一.选择题(共12小题,满分48分)1.解:因为△A1B1C1中有一个角是135°,选项中,有135°角的三角形只有B,且满足两边成比例夹角相等,故选:B.2.解:在△ABE与△ACB中,∠ABE=∠C,∠BAE=∠CAB,∴△ABE∽△ACB,∴∠AEB=∠ABC,∵AD平分∠BAC,∴∠BAD=∠EAF,∴△ABD∽△AEF.故选:D.3.解:∵∠DAE=∠CAB,∴当∠ADE=∠C时,△ADE∽△ACB;当∠AED=∠B时,△ADE∽△ACB;当=时,△ADE∽△ACB.故选:C.4.解:∵△ABC三边长是,,2,∴△ABC三边长的比为:2:=1::,∴△ABC相似的三角形三边长可能是1,,,故选:A.5.解:A、当∠ACB=∠ADC时,再由∠A=∠A,可得出△ACD∽△ABC,故此选项不合题意;B、当∠ACD=∠ABC时,再由∠A=∠A,可得出△ACD∽△ABC,故此选项不合题意;C、当=时,再由∠A=∠A,可得出△ACD∽△ABC,故此选项不合题意;D、当=时,无法得出△ACD∽△ABC,故此选项符合题意;故选:D.6.解:如图,过点P作AB的平行线,或作BC的平行线,或作AB的垂线,或作∠CPD=∠B,共4条直线,故选:D.7.解:∠A=∠A,A、若添加∠2=∠B,可利用两角法判定△AED∽△ABC,故本选项错误;B、若添加∠1=∠C,可利用两角法判定△AED∽△ABC,故本选项错误;C、若添加=,可利用两边及其夹角法判定△AED∽△ABC,故本选项错误;D、若添加=,不能判定△AED∽△ABC,故本选项正确;故选:D.8.解:①∠A=∠A,∠ACD=∠B,∴△ACD∽△ABC,②∵∠A=∠A,∠ADC=∠ACB,∴△ACD∽△ABC,③∵AC2=AD•AB,∴,∵∠A=∠A,∴△ACD∽△ABC,④条件不符合,不能判定△ACD∽△ABC,故选:C.9.解:①∠B=∠AED,∠A=∠A,则可判断△ADE∽△ACB,故①符合题意;②DE∥BC,则△ADE∽△ABC,故②不符合题意,③,且夹角∠A=∠A,能确定△ADE∽△ACB,故③符合题意;④由AD•BC=DE•AC可得=,此时不确定∠ADE=∠ACB,故不能确定△ADE∽△ACB,故④不符合题意,故选:B.10.解:设运动时间为t秒.BP=t,CQ=2t,BQ=BC﹣CQ=6﹣2t,当△BAC∽△BPQ,=,即=,解得t=;当△BCA∽△BPQ,=,即=,解得t=,综上所述,当以B,P,Q为顶点的三角形与△ABC相似时,运动时间为s或s,故选:C.11.解:①∠B=∠AED,∠A=∠A,则可判断△ADE∽△ACB,故①符合题意;②DE∥BC,则△ADE∽△ABC,故②不符合题意,③,且夹角∠A=∠A,能确定△ADE∽△ACB,故③符合题意;④由AD•BC=DE•AC可得,此时不确定∠ADE=∠ACB,故不能确定△ADE∽△ACB;故④不符合题意,⑤∠ADE=∠C,∠A=∠A,则可判断△ADE∽△ACB,故⑤符合题意;故选:C.12.解:正方形ABCD中,AD=CD,在△ADF和△CDE中,,∴△ADF≌△CDE(SAS),∴∠ADF=∠CDE,DE=DF,∴∠EDF=∠FDC+∠CDE=∠FDC+∠ADF=∠ADC=90°,∴∠DEF=45°,∵∠DGN=45°+∠FDG,∠DNG=45°+∠CDE,∠FDG≠∠CDE,而∠FDG与∠CDE不一定相等,∴∠DGN与∠DNG不一定相等,故判断出①错误;∵△DEF是等腰直角三角形,∵∠ABD=∠DEF=45°,∠BGF=∠EGD(对顶角相等),∴△BFG∽△EDG,∵∠DBE=∠DEF=45°,∠BDE=∠EDG,∴△EDG∽△BDE,∴△BFG∽△EDG∽△BDE,故②正确;连接BM、DM.∵△AFD≌△CED,∴∠FDA=∠EDC,DF=DE,∴∠FDE=∠ADC=90°,∵M是EF的中点,∴MD=EF,∵BM=EF,∴MD=MB,在△DCM与△BCM中,,∴△DCM≌△BCM(SSS),∴∠BCM=∠DCM,∴CM在正方形ABCD的角平分线AC上,∴MC垂直平分BD;故③正确;过点M作MH⊥BC于H,则∠MCH=45°,∵MC=,∴MH==1,∵M是EF的中点,BF⊥BC,MH⊥BC,∴MH是△BEF的中位线,∴BF=2MH=2,故④正确;综上所述,正确的结论有②③④.故选:B.二.填空题(共4小题,满分20分)13.解:∵∠B=∠D,∴添加∠C=∠E或∠BAC=∠DAE或∠BAD=∠CAE或=,可证△ABC∽△ADE.故答案为:∠C=∠E或∠BAC=∠DAE或∠BAD=∠CAE或=.14.解:∵四边形ABCD为正方形,∴∠ADC=∠BCD=90°,AD=CD,∵E和F分别为BC和CD中点,∴DF=EC=2,∴△ADF≌△DCE(SAS),∴∠AFD=∠DEC,∠F AD=∠EDC,∵∠EDC+∠DEC=90°,∴∠EDC+∠AFD=90°,∴∠DGF=90°,即DE⊥AF,故①正确;∵AD=4,DF=CD=2,∴AF=,∴DG=AD×DF÷AF=,故②错误;∵H为AF中点,∴HD=HF=AF=,∴∠HDF=∠HFD,∵AB∥DC,∴∠HDF=∠HFD=∠BAG,∵AG==,AB=4,∴,∴△ABG∽△DHF,故④正确;∴∠ABG=∠DHF,而AB≠AG,则∠ABG和∠AGB不相等,故∠AGB≠∠DHF,故HD与BG不平行,故③错误;故答案为:①④.15.解:DF∥AC,或∠BFD=∠A.理由:∵∠A=∠A,==,∴△ADE∽△ACB,∴①当DF∥AC时,△BDF∽△BAC,∴△BDF∽△EAD.②当∠BFD=∠A时,∵∠B=∠AED,∴△FBD∽△AED.故答案为DF∥AC,或∠BFD=∠A.16.解:前三项正确,因为他们分别符合有两组角对应相等的两个三角形相似;两组对应边的比相等且相应的夹角相等的两个三角形相似.故相似的条件是①,②,③.三.解答题(共8小题,满分52分)17.证明:∵△PCD是等边三角形,∴∠PCD=∠PDC=60°,PC=CD=PD=2,∴∠PCA=∠PDB=120°,∵AC=1,BD=4,∴,=,∴=,∴△ACP∽△PDB.18.证明:∵∠1=∠2,∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠BAC,∵∠AED=∠C,∴△ABC∽△ADE.19.证明:如图,∵AB•AE=AD•AC,∴=.又∵∠1=∠2,∴∠2+∠BAE=∠1+∠BAE,即∠BAC=∠DAE,∴△ABC∽△ADE.20.解:∵∠BAC=∠BDC,∠AOB=∠DOC,∴∠ABE=∠ACD又∵∠BAC=∠DAE∴∠BAC+∠EAC=∠DAE+∠EAC∴∠DAC=∠EAB∴△ABE∽△ACD.21.证明:∵BD平分∠ABC,∴∠DBE=∠CBD.∵BD2=BC•BE,∴,∴△BCD∽△BDE.22.解:设在开始运动后第x秒,△BPQ与△BAC相似,由题意得:AP=2xcm,PB=(8﹣2x)cm,BQ=4x,分两种情况考虑:当∠BPQ=∠C,∠B=∠B时,△PBQ∽△CBA,∴,即解得:x=0.8,当x=0.8秒时,△BPQ与△BAC相似;当∠BPQ=∠A,∠B=∠B时,△BPQ∽△BAC,∴,即,解得:x=2,当x=2秒时,△BPQ与△BAC相似.综上,当x=0.8秒或2秒时,△BPQ与△BAC相似.23.证明:∵AD•AC=AE•AB,∴=在△ABC与△ADE中∵=,∠A=∠A,∴△ABC∽△ADE.24.解:(1)∵AD=BC,BC=,∴AD=,DC=1﹣=.∴AD2==,AC•CD=1×=.∴AD2=AC•CD.(2)∵AD=BC,AD2=AC•CD,∴BC2=AC•CD,即.又∵∠C=∠C,∴△BCD∽△ACB.∴,∠DBC=∠A.∴DB=CB=AD.∴∠A=∠ABD,∠C=∠BDC.设∠A=x,则∠ABD=x,∠DBC=x,∠C=2x.∵∠A+∠ABC+∠C=180°,∴x+2x+2x=180°.解得:x=36°.∴∠ABD=36°.。
(常考题)北师大版初中数学九年级数学上册第四单元《图形相似》测试卷(含答案解析)(3)
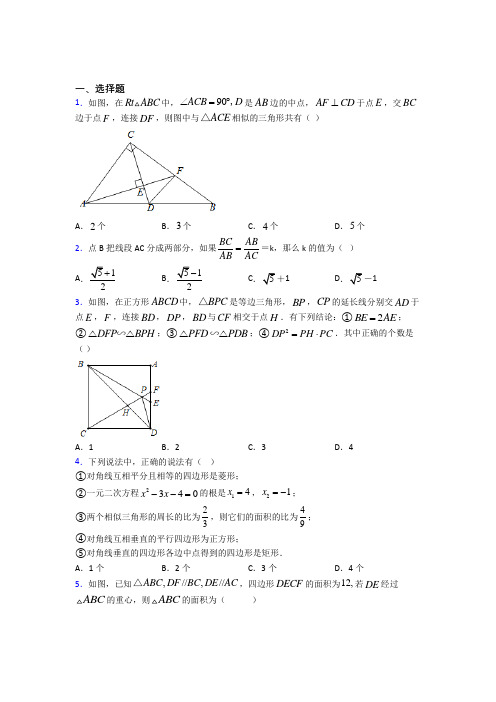
一、选择题1.如图,在Rt ABC 中,90ACB D ∠=︒,是AB 边的中点,AF CD ⊥于点E ,交BC 边于点F ,连接DF ,则图中与ACE △相似的三角形共有( )A .2个B .3个C .4个D .5个2.点B 把线段AC 分成两部分,如果BC AB AB AC ==k ,那么k 的值为( ) A .51+ B .51- C .5+1 D .5-1 3.如图,在正方形ABCD 中,BPC △是等边三角形,BP ,CP 的延长线分别交AD 于点E ,F ,连接BD ,DP ,BD 与CF 相交于点H .有下列结论:①2BE AE =;②DFP BPH ∽△△;③PFD PDB ∽△△;④2DP PH PC =⋅.其中正确的个数是( )A .1B .2C .3D .44.下列说法中,正确的说法有( )①对角线互相平分且相等的四边形是菱形;②一元二次方程2340x x --=的根是14x =,21x =-;③两个相似三角形的周长的比为23,则它们的面积的比为49; ④对角线互相垂直的平行四边形为正方形;⑤对角线垂直的四边形各边中点得到的四边形是矩形. A .1个 B .2个 C .3个 D .4个5.如图,已知,//,//ABC DF BC DE AC △,四边形DECF 的面积为12,若DE 经过ABC 的重心,则ABC 的面积为( )A .25B .26C .27D .286.点B 是线段AC 的黄金分割点,且AB <BC .若AC=4,则BC 的长为( ) A .252+ B .252- C .512- D .51- 7.如图,在正方形ABCD 中,BPC △是等边三角形,BP 、CP 的延长线分别交AD 于点E 、F ,连接BD 、DP ,BD 与CF 相交于点H ,给出下列结论:①2BE AE =;②DFP BPH ∽△△;③PFD PDB ∽△△;④2DP PH PC =⋅.其中正确的是( )A .①②③B .①③④C .②③④D .①②④ 8.如图,点D 、E 、F 分别是ABC 的边AB 、AC 、BC 上的点,若//DE BC ,//EF AB ,则下列比例式一定成立的是( )A .EF FC AD BF =B .AD DE DB BC = C .BF EF BC AD = D .EF DE AB BC = 9.如图,点A 在线段BD 上,在BD 的同侧作等腰直角三角形ABC 和等腰直角三角形ADE (ABC ∠和AED ∠是直角),连接,BE CD 交于点,P CD 与AE 边交于点M ,对于下列结论:①BAE CAD △△,②45BPC ∠=︒,③MP MD MA ME ⋅=⋅,④22CB CP CM =⋅,其中正确的个数为( )A.1个B.2个C.3个D.4个10.如图,梯形ABCD中,AC交BD于点O,已知AD∥BC,AD=2,BC=4,S△AOD=1,则梯形ABCD的面积为()A.9 B.8 C.7 D.611.如图,在正方形ABCD中,4AB=,M是边BC的中点,连接AM,按以下步骤作图:①以点D为圆心,适当的长度为半径作弧,交线段AM于E,F两点;②分别以点E,F为圆心,大于12EF的长为半径作弧,两弧交于点G;③连接DG,交AM于点P,则DP的长为()A.3 B.453C.352D.85512.如图,在ABC中,点D、E、F分别在AB、AC、BC上,DE∥BC,DF∥AC.下列比例式中,正确的是()A.AD DEBD BC=B.DF DEAC BC=C.AD DEAB BC=D.AE BFEC FC=二、填空题13.已知35ab=,则aa b+的值为______.14.如图,点P是ABC的重心,过P作AB的平行线DE,分别交AC于点D、交BC于点E;作//DF BC,交AB于点F,若ABC的面积为36,则四边形BEDF的面积为________.15.如图所示是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的半径为0.8m ,桌面距离地面1m ,若灯泡距离地面3m ,则地面上阴影部分的面积为_________m 2(结果保留)π.16.如图1,是2002年发行的中国纪念邮票,其图案是三国时期吴国数学家赵爽在注释《周髀算经》中所给勾股定理的证明.同学们在探索勾股定理时还出现了许多利用正方形证明勾股定理的方法,如图2,正方形ABCD 是由四个全等的直角三角形和一个正方形EFGH 拼成;正方形EFGH 是由与上述四个直角三角形全等的三角形和正方形IJKL 拼成;正方形ABCD ,EFGH ,IJKL 的面积分别为S 1,S 2,S 3,分别连结AK ,BL ,CI ,DJ 并延长构成四边形MNOP ,它的面积为m .①请用等式表示S 1,S 2,S 3之间的数量关系为:_____;②m =_____(用含S 1,S 3的代数式表示m ).17.如图,在平行四边形ABCD 中,点E 在BC 边上,且:2:1CE BE =,AC 与DE 相交于点F ;若9AFD S =,则CFE S =___________.18.如图,ABC 中,10AB AC ==,16BC =.P 为边BC 上的一个动点,点D 在边AC 上,且始终保持APD B ∠=∠,若PCD 为直角三角形,则线段BP 的长为__________.19.如图,在ABC 中,////DE FG BC ,ADE 的面积=梯形DFGE 的面积=梯形FBCG 的面积,则DE BC的值为______.20.如图,在矩形纸片ABCD 中,将AB 沿BM 翻折,使点A 落在BC 上的点N 处,BM 为折痕,连接MN ;再将CD 沿CE 翻折,使点D 恰好落在MN 上的点F 处,CE 为折痕,连接EF 并延长交BM 于点P ,若AD =8,AB =5,则线段PE 的长等于____.三、解答题21.如图,在ABC 中,AB AC =,AD BC ⊥,垂足为点D ,以AD 为对角线作正方形AEDF ,DE 交AB 于点M ,DF 交AC 于点N ,连结EF ,EF 分别交AB ,AD 、AC 于点G 、点O 、点H .(1)求FDC ∠的度数;(2)若60BAC ︒∠=,4AB =,求NC ;(3)设HF kHE =,AEH △和四边形EDNH 的面积分别为1S 和2S ,求21S S 的最大值. 22.在边长为1的正方形ABCD 中,E 是AB 的中点,CF DE ⊥,F 为垂足.求CF 的长.23.体验:如图1,在四边形ABCD 中,AB ∥CD ,∠B =90°,点M 在BC 边上,当∠AMD =90°时,可知△ABM △MCD (不要求证明).探究:如图2,在四边形ABCD 中,点M 在BC 上,当∠B =∠C =∠AMD 时,求证:△ABM ∽△MCD .拓展:如图3,在△ABC 中,点M 是边BC 的中点,点D 、E 分别在边AB 、AC 上.若∠B =∠C =∠DME =45°,BC =82,CE =6,求DE 的长.24.如图,已知四边形ABCD 是矩形,点E 在BA 的延长线上,,AE AD EC =与BD 相交于点,G 与AD 相交于点,F AF AB =.(1)求证:BD EC ⊥;(2)求:AD AB 的值;(3)连接AG ,求证:2EG DG AG -=.25.(1)如图1,矩形ABCD 中,点M 在BC 上,连接AM ,作AMN AMB ∠=∠,点N 在直线AD 上,MN 交CD 于点E .请找出图1中的一个等腰三角形,并证明结论.(2)如图2,矩形ABCD 中,3AB =,2BC =,点M 为BC 中点,连接AM ,作AME AMB ∠=∠,ME 交于点E ,求CE 的长.26.如图,在平面直角坐标系中,已知ΔABC 三个顶点的坐标分别是A(-4,2),B(-3,1),C(-1,2).(1)请画出ΔABC 关于x 轴对称的ΔA 1B 1C 1;(2)以点O 为位似中心,相似比为1:2,在y 轴右侧,画出ΔA 1B 1C 1放大后的ΔA 2B 2C 2;【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】利用直角三角形斜边上的高线模型,可判断有2个三角形与ACE △相似,利用直角三角形斜边上的中线等于斜边的一半,传递一组等角,得到第3个三角形.【详解】∵∠EAC=∠CAF ,∠AEC=∠ACF ,∴△ACE ∽△AFC ;∵∠EAC+∠AFC=90°,∠ECF+∠AFC=90°,∴∠EAC=∠ECF ,∵∠AEC=∠CEF ,∴△ACE ∽△CFE ;∵90ACB D ∠=︒,是AB 边的中点,∴DC=DB ,∴∠ECF=∠EAC=∠B ,∵∠AEC=∠BCA ,∴△ACE ∽△BAC ;共有3个,故选B.【点睛】本题考查了直角三角形的相似,熟练运用三角形相似的判定定理是解题的关键. 2.B解析:B【分析】设AC=1,由题意得AB=k ,BC=2k ,由AC=AB+ BC=1得到关于k 的一元二次方程,解方程即可.【详解】设AC=1, ∵BC AB AB AC==k ,且0k >, ∴AB=k ,BC=2k ,∵AC=AB+ BC=1,∴21k k +=,即210k k +-=,∵1a =,1b =,1c =-,()224141150b ac =-=-⨯⨯-=>,∴k =负值舍去),∴12k =, 故选:B .【点睛】本题考查了比例线段,公式法解一元二次方程,由比例线段得到一元二次方程是解题的关键.3.C解析:C【分析】利用直角三角形30度角的性质即可解决①;证明∠FDP=∠PBD ,根据∠DFP=∠BPC ,∠FDP=∠PBD 即可判断②;通过计算证明∠PFD≠∠PDB ,即可判断③;证明△DPH ∽△CPD 即可判断④.【详解】解:∵△BPC 是等边三角形,∴BP=PC=BC ,∠PBC=∠PCB=∠BPC=60°,在正方形ABCD 中,∵AB=BC=CD ,∠A=∠ADC=∠BCD=90°∴∠ABE=∠DCF=30°,∴BE=2AE ;故①正确;∵PC=CD ,∠PCD=30°,∴∠PDC=75°,∴∠FDP=15°,∵∠DBA=45°,∴∠PBD=15°,∴∠FDP=∠PBD ,∵∠DFP=∠BPC=60°,∴△DFP ∽△BPH ;故②正确;∵∠FDP=∠PBD=15°,∠ADB=45°,∴∠PDB=30°,而∠DFP=60°,∴∠PFD≠∠PDB ,∴△PFD 与△PDB 不会相似;故③错误;∵∠PDH=∠PCD=30°,∠DPH=∠DPC ,∴△DPH ∽△CPD , ∴DP PH PC DP=, ∴DP 2=PH•PC ,故④正确;故选:C .【点睛】本题考查的正方形的性质,等边三角形的性质以及相似三角形的判定和性质,解答此题的关键是熟练掌握性质和定理.4.C解析:C【分析】根据矩形的判定定理、一元二次方程的解法、【详解】解:①对角线互相平分且相等的四边形是矩形,故①错误;②一元二次方程x 2-3x -4=0(x -4)(x +1)=0x -4=0或x =1=0x 1=4,x 2=-1,故②正确;③两个相似三角形的周长的比为23,则它们的面积的比为22()349=,故③正确; ④对角线相等且互相垂直的平行四边形为正方形,故④错误;⑤对角线垂直的四边形各边中点得到的四边形是矩形,说法正确.故选:C【点睛】 本题考查的是命题的真假判断,掌握矩形的判定定理、一元二次方程的解法、中点四边形的性质、矩形、菱形和正方形的判断是解题的关键.5.C解析:C【分析】设重心为G ,则2BG GH =,根据三角形相似的判定与性质可得49BDE ABC S S =,19ADF ABC S S =,列出方程组并求解即可.【详解】 解:∵DE 经过ABC 的重心,设重心为G ,则2BG GH =,∵//,//DF BC DE AC ,∴△BDE ∽△BAC ,△ADF ∽△ABC , ∴23DE BG BD AC BH AB ===, ∴13AD AB =, ∴49BDE ABC S S =,19ADF ABC S S =, ∴45BDE ADF DECF S S S =+,18ADF BDE DECF SS S =+, ∴41251128BDE ADF ADF BEDS S S S ⎧=⎪+⎪⎨⎪=⎪+⎩, 解得12BDE S =,3ADF S =,∴27△ABC S =,故选:C .【点睛】本题考查重心的性质、相似三角形的判定与性质,得到面积的比例关系是解题的关键. 6.B解析:B【分析】根据黄金分割的定义可得出较长的线段BC=512AC ,将AC=4代入即可得出BC 的长度. 【详解】解:∵点B 是线段AC 的黄金分割点,且AB <BC ,∴BC=512AC , ∵AC=4,∴BC=252.故选:B .【点睛】本题考查了黄金分割的定义:把线段AB 分成两条线段AC 和BC (AC >BC ),且使AC 是AB 和BC 的比例中项(即AB :AC=AC :BC ),叫做把线段AB 黄金分割,点C 叫做线段AB的黄金分割点.其中AB≈0.618AB ,并且线段AB 的黄金分割点有两个. 7.D解析:D【分析】由正方形ABCD ,与BPC △是等边三角形的性质求解,求解30,EBA ∠=︒ 从而可判断①;证明60,PFE BPC ∠=∠=︒ =15,PBH PDF ∠=∠︒ 可判断②;由15,30,15,60,PBD BDP PDF PFD ∠=︒∠=︒∠=︒∠=︒ 可判断③; 证明30,PDH PCD ∠=︒=∠ 再证明,PDH PCD ∽ 可得,DP PH PC PD=从而可判断 ④. 【详解】 解: 正方形ABCD , 90,,ABC A BCD ADC CB CD AB ∴∠=∠=∠=∠=︒==BPC △是等边三角形,60,PBC PCB BPC ∴∠=︒=∠=∠906030,EBA ∴∠=︒-︒=︒2,BE AE ∴= 故①符合题意;正方形ABCD ,//,45,AD BC CBD ∴∠=︒60,PFE PCB ∴∠=∠=︒60,PFE BPC ∴∠=∠=︒BPC △是等边三角形,,PC BC CD ∴==而906030,PCD ∠=︒-︒=︒()11803075,2CDP ∴∠=︒-︒=︒ 907515,PDF ∴∠=︒-︒=︒由60,45,PBC CBD ∠=︒∠=︒15,PBH ∴∠=︒,PBH PDF ∴∠=∠,BPH DFP ∴∽ 故②符合题意;15,30,15,60,PBD BDP PDF PFD ∠=︒∠=︒∠=︒∠=︒,PFD BPD ∴不相似,故③不符合题意;正方形ABCD ,45CDB ∴∠=︒,90451530,PDH PCD ∴∠=︒-︒-︒=︒=∠,DPH CPD ∠=∠,PDH PCD ∴∽,DP PH PC PD∴= ∴ 2DP PH PC =⋅,故④符合题意,综上:符合题意的有:①②④.故选:.D【点睛】本题考查的是等边三角形的性质,含30的直角三角形的性质,正方形的性质,相似三角形的判定与性质,掌握以上知识是解题的关键.8.A解析:A【分析】 根据平行可得EC FC AE BF =,EC BD AE DA =,再根据平行四边形的性质得EF=BD 即可. 【详解】解:∵//EF AB , ∴EC FC AE BF= ∵//DE BC , ∴EC BD AE DA =, ∴FC BD BF DA= ∵//DE BC ,//EF AB ,∴四边形BFED 是平行四边形,∴EF=BD, ∴EF FC AD BF=, 故选:A .【点睛】 本题考查了平行线分线段成比例定理,解题关键是根据平行线列出恰当的比例式,再结合平行四边形性质进行推理.9.D解析:D【分析】①由等腰Rt ABC 和等腰Rt ADE △三边份数关系可证;②根据相似三角形的性质即可得到结论;③通过等积式倒推可知,证明PME AMD △△∽即可;④22CB 转化为2AC ,证明ACP ∽△MCA,问题可证;【详解】 由已知得:2,2AC AB AD AE ==AC AD AB AE∴= BAC EAD ∠=∠BAE CAD ∴∠=∠BAE CAD ∴∽ 所以①正确;如图:设BE 与AC 相交于点O则AOB POC ∠=∠BAE CAD ∽45ABE ACD BPC BAC ∴∠=∠∴∠=∠=︒所以②正确;BAE CAD ∽BEA CDA ∴∠=∠PME AMD ∠=∠PME AMD ∴∽MP ME MA MD∴= MP MD MA ME ⋅=⋅∴所以③正确;由③MP MD MA ME ⋅=⋅,PMA DME ∠=∠PMA EMD ∴△∽90APD AED ∴∠=∠=︒18090CAE BAC EAD ∠=︒-∠-∠=︒CAP CMA ∴∽2AC CP CM ∴=⋅2AC =22CB CP CM ∴=⋅所以④正确故选:D.【点睛】本题考查了相似三角形的性质和判断,在等积式和比例式的证明中应注意应用倒推的方法寻找相似三角形进行证明,进而得到答案.10.A解析:A【分析】先根据AD ∥BC ,得到△AOD ∽△COB ,从而得出△COB 的面积,再根据△AOB 与△COB 等高,从而得出△AOB 的面积,同理得出△DOC 的面积即可得出梯形ABCD 的面积.【详解】解:∵AD ∥BC ,∴△AOD ∽△COB∵AD =2,BC =4,∴12AD BC = ∴114AOD COB COB S S S == ∴COB S △ =4∵△AOB 与△COB 等高,又∵12AO CO = ∴142AOB AOB COB S S S == ∴AOB S =2同理,DOC S =2∴ABCD S 梯形=AOD COB AOB DOC SS S S +++ =1+4+2+2=9.故选:A .【点睛】 本题主要考查了相似三角形的性质,解题的关键是熟练掌握相似三角形的面积比等于相似比的平方.11.D解析:D【分析】连接GE ,GF ,DE ,DF ,由题意可证△DEG ≌△DFG(SSS),得到∠EDP=∠FDP 再证△DEP ≌△DFP(SAS),得到∠DPE=∠DPF ,从而可证△APD ∽△MBA ,根据勾股定理求出AM ,由对应边成比例,可以得到DP 的长.【详解】解:由尺规作图可知,DP AM ⊥∴∠DPE=∠DPF=90°又∵AD ∥BC∴∠DAM=∠BMA 且∠MBA=90°=∠APD∴△APD ∽△MBA ,∵正方形ABCD 中,AB=4 ,M 是边BC 的中点,∴BM=12BC=2且== 又△APD ∽△MBA , ∴AD DP AM AB= ∴4DP =∴5= 故选:D【点睛】本题考查了全等三角形的性质和判定,相似三角形的性质与判定以及勾股定理的运用,解题的关键是根据题意灵活运用全等三角形性质和判定,相似三角形的性质与判定,结合勾股定理,求出线段的长.12.C解析:C【分析】利用平行线分线段成比例以及相似三角形的性质一一判断即可.【详解】解: ∵DE ∥BC ,∴ADE ABC △△∽, ∴AD DE AB BC=,故选项A 错误,选项C 正确, ∵DF ∥AC , ∴BDF BAC △∽△, ∴BD DF AB AC=,∴DF DE AC BC≠,故选项B 错误, ∵DE ∥BC ,DF ∥AC , ∴AD AE BD EC =,AD FC BD BF =, ∴AE FC EC BF=,故选项D 错误, ∴故选:C .【点睛】本题考查了相似三角形的判定和性质,平行线分线段成比例定理等知识,解题的关键是掌握相关知识点并能准确判断对应的比例线段.二、填空题13.【分析】根据比例的性质求解即可;【详解】∵设∴;故答案是【点睛】本题主要考查了比例的性质准确计算是解题的关键 解析:38【分析】根据比例的性质求解即可;【详解】 ∵35a b =, 设3a k =,5b k =, ∴33358a k ab k k ==++; 故答案是38. 【点睛】本题主要考查了比例的性质,准确计算是解题的关键.14.16【分析】延长CP 交AB 于G 由CP :PG=2:1推出CE :BC=2:3AD :AC=1:3由△CED ∽△CBA △AFD ∽△ABC 推出S △CED=×S △ABC=16S △AFD=×S △ABC=4由此即可解析:16【分析】延长CP 交AB 于G .由CP :PG =2:1,推出CE :BC =2:3,AD :AC =1:3,由△CED ∽△CBA ,△AFD ∽△ABC ,推出S △CED =49×S △ABC =16,S △AFD =19×S △ABC =4,由此即可解决问题.【详解】解:如图,延长CP 交AB 于G .∵点P 是△ABC 的重心,∴CP :PG =2:1,∵DE ∥AB ,∴CE :BE =2:1,AD :CD =1:2,∴CE :CB =2:3,AD :AC =1:3,∵ED ∥AB ,DF ∥BC ,∴△CED ∽△CBA ,△AFD ∽△ABC ,∴S △CED =49×S △ABC =16,S △AFD =19×S △ABC =4, ∴S 平行四边形BEDF =S △ABC -S △CED -S △AFD =36-16-4=16,故答案为:16.【点睛】本题考查了三角形重心的性质,平行线分线段成比例定理,相似三角形的判定与性质,难度适中.准确作出辅助线是解题的关键.15.44π【分析】证明△OBQ ∽△OAP 根据相似三角形的性质求出AP 根据圆的面积公式计算得到答案【详解】解:如图由题意得OB=08mOQ=OP-PQ=3-1=2(m )BQ ∥AP ∴△OBQ ∽△OAP ∴即解解析:44π【分析】证明△OBQ ∽△OAP ,根据相似三角形的性质求出AP ,根据圆的面积公式计算,得到答案.【详解】解:如图,由题意得,OB=0.8m ,OQ=OP-PQ=3-1=2(m ),BQ ∥AP ,∴△OBQ ∽△OAP ,∴BQ OQ AP OP =,即0.823AP =,解得,AP=1.2(m ),则地面上阴影部分的面积=π×1.22=1.44π(m 2),故答案为:1.44π.【点睛】本题考查的是相似三角形的应用,掌握相似三角形的判定定理和性质定理是解题的关键. 16.【分析】设四个全等的直角三角形的较短的直角边为较长的直角边为斜边为则再表示正方形ABCD 的面积为:正方形EFGH 的面积为:正方形IJKL 的面积为:可得;由轴对称的性质可得:由正方形EFGH 的性质可得解析:2132S S S =+13132.S S S S + 【分析】设四个全等的直角三角形的较短的直角边为,a 较长的直角边为,b 斜边为,c 则222,a b c += 再表示正方形ABCD 的面积为:()21,S a b =+ 正方形EFGH 的面积为:2222,S c a b ==+ 正方形IJKL 的面积为:()23,S b a =- 可得2132S S S =+;由轴对称的性质可得:,AK HE ⊥ 由正方形EFGH 的性质可得:,HE EF ⊥ 可得//,AK EF 同理://,BL GF 证明90KML ∠=︒, 同理:90LNI JOI JPK ∠=∠=∠=︒,再证明,MKL PJK ≌ 同理:,PJK OIJ NLI ≌≌ 可得四边形MNOP 是正方形,再证明,MLK KEH ∽ 可得,ML MK LK KE KH EH ==求解22MN = 可得()()22222,b a b a m MN a b +-==+ 从而可得答案.【详解】解:设四个全等的直角三角形的较短的直角边为,a 较长的直角边为,b 斜边为,c 则222,a b c += ∴ 正方形ABCD 的面积为:()21,S a b =+正方形EFGH 的面积为:2222,S c a b ==+ 正方形IJKL 的面积为:()23,S b a =- ()()2222222,2,a b a ab b b a a ab b +=++-=-+()()()22222,a b a b b a ∴+=++-2132.S S S ∴=+由轴对称的性质可得:,AK HE ⊥ 由正方形EFGH 的性质可得:,HE EF ⊥//,AK EF ∴同理://,BL GF由正方形EFGH 可得://,HE GF//,BM HE ∴ ,BM AK ⊥90KML ∴∠=︒,同理:90LNI JOI JPK ∠=∠=∠=︒, ∴ 四边形MNOP 是矩形,正方形IJKL ,,90KL KJ LKJ ∴=∠=︒,90,MKL PKJ MKL MLK ∴∠+∠=︒=∠+∠ ,PKJ MLK ∴∠=∠,MKL PJK ∴≌同理:,PJK OIJ NLI ≌≌∴ 四边形MNOP 是正方形,由//,BM HE,MLK HEK ∴∠=∠90,LMK EKH ∠=︒=∠,MLK KEH ∴∽,ML MK LK KE KH EH∴== ,,AE b BE a ==ML MK b a ∴==,b b a a b a ML MK LN --∴===22b b a a b a MN --∴==()()222222222,b a b a b a m MN a b a b +-⎛⎫-∴===⎪++⎝⎭正方形ABCD 的面积为:()21,S a b =+正方形EFGH 的面积为:2222,S c a b ==+ 正方形IJKL 的面积为:()23,S b a =- ()131213132.12S S S S m S S S S ∴==++故答案为:2132S S S =+,13132.S S S S +【点睛】本题考查的是全等三角形的判定与性质,勾股定理的应用,矩形的判定,正方形的判定与性质,相似三角形的判定与性质,完全平方公式的运用,分式的运算,掌握以上知识是解题的关键.17.4【分析】由于四边形ABCD是平行四边形所以得到BC//ADBC=AD而CE:BE=2:1由此即可得到△AFD∽△CFE它们的相似比为3:2最后利用相似三角形的性质即可求解【详解】解:∵四边形ABC解析:4【分析】由于四边形ABCD是平行四边形,所以得到BC//AD、BC=AD,而CE:BE=2:1,由此即可得到△AFD∽△CFE,它们的相似比为3:2,最后利用相似三角形的性质即可求解.【详解】解:∵四边形ABCD是平行四边形,∴BC//AD、BC=AD,∴△AFD∽△CFE,∵CE:BE=2:1,∴CE:BC=2:3,∴AD:CE =3:2,∴S△AFD:S△EFC=(32)2=94,∵S△AFD=9,∴S△EFC=4.故答案为:4.【点睛】此题主要考查了平行四边形的性质,相似三角形的判定与性质,解题是证明△AFD∽△CFE,然后利用其性质即可求解.18.8或【分析】因为∠C为定角DP为动点所以△PCD为直角三角形有两种情况:∠PDC=90°时△PCD为直角三角形如详解图根据等腰三角形三线合一的性质求出BP的长;当∠DPC=90°时△PCD为直角三角解析:8或25 2【分析】因为∠C为定角,D、P为动点,所以△PCD为直角三角形有两种情况:①∠PDC=90°时,△PCD为直角三角形,如详解图,根据等腰三角形三线合一的性质求出BP的长;②当∠DPC=90°时,△PCD为直角三角形,如详解图,作AF BC,根据△BFA∽△BAP求出BP的长.【详解】分两种情况:①∠PDC=90°时,△PCD 为直角三角形,如图:∵AB=AC∴∠B=∠C∵∠APD=∠B∴∠APD=∠C∵90C DPC ∠+∠=︒∴90APD DPC ∠+∠=︒AP BC ∴⊥∴点P 为BC 中点 ∴12BP BC = 16BC =11682BP ∴=⨯= ②当∠DPC=90°时,△PCD 为直角三角形,如图,作AF BC ⊥,10,16AB AC BC ===,AF BC ⊥90AFB ∴∠=︒∴点F 为BC 中点1116822BF BC ∴==⨯= ∵∠APD=∠B ,∠DPC=9090APB APD ∴∠+∠=∠︒90APB B ∴∠+∠=︒90BAP ∴∠=︒BFA BAP ∴△∽△AB BF BP AB∴= 10810BP ∴= 252BP ∴=故答案为:8或252. 【点睛】 本题考查了等腰三角形,相似三角形的性质和判定,同时还运用了分类讨论的思想,利用相似三角形对应边成比例求线段长是解题关键.19.【分析】由平行线可得△ADE ∽△AFG ∽△ABC 进而利用相似三角形面积比等于对应边的平方比即可得出结论【详解】解:∵S △ADE =S 梯形DFGE =S 梯形FBCG ∵DE ∥FG ∥BC ∴△ADE ∽△AFG ∽【分析】由平行线可得△ADE ∽△AFG ∽△ABC ,进而利用相似三角形面积比等于对应边的平方比,即可得出结论.【详解】解:∵S △ADE =S 梯形DFGE =S 梯形FBCG ,∵DE ∥FG ∥BC ,∴△ADE ∽△AFG ∽△ABC , ∴13ADE ABC S S ∆=, 由于相似三角形的面积比等于对应边长的平方比,∴DE : BC=13.故答案为:3. 【点睛】本题主要考查了相似三角形的判定及性质以及三角形面积比与对应边长之间的关系,能够熟练掌握并运用. 20.【分析】根据折叠可得四边形ABNM 是正方形CD=CF=5∠D=∠CFE=90°ED=EF 可求出三角形FNC 的三边为345在中由勾股定理可以求出三边的长通过作辅助线可证可得三边的比为3:4:5设FG= 解析:203根据折叠可得四边形ABNM 是正方形,CD=CF=5,∠D=∠CFE=90°,ED=EF ,可求出三角形FNC 的三边为3,4,5,在Rt MEF 中,由勾股定理可以求出三边的长,通过作辅助线,可证FNC PGF ∽,可得PFG △三边的比为3:4:5,设FG=3m ,则PG=4m ,PF=5m ,通过PG=HN ,列方程解方程,进而求出PF 的长,从而可求PE 的长.【详解】解:过点P 作PG ⊥FN ,PH ⊥BN ,垂足为G 、H ,由折叠得:四边形ABNM 是正方形,AB=BN=NM=MA=5, CD=CF=5,∠D=∠CFE=90°,ED=EF , ∴NC=MD=8-5=3,在Rt FNC 中,22534FN =-=,∴MF=5-4=1,在Rt MEF 中,设EF=x ,则ME=3-x ,由勾股定理得, ()22213x x +-=, 解得:53x =, ∵∠CFN+∠PFG=90°,∠PFG+∠FPG=90°,∴∠CFN=∠FPG ,又∵∠FGP=∠CNF=90°∴FNC PGF ∽,∴FG :PG :PF=NC :FN :FC=3:4:5,设FG=3m ,则PG=4m ,PF=5m ,四边形ABNM 是正方形,45MBN BPH ∴∠=︒=∠,∴GN=PH=BH=4-3m ,HN=5-(4-3m )=1+3m=PG=4m ,解得:m=1,∴PF=5m=5,∴PE=PF+FE=5205=33+, 故答案为:203.本题考查的是轴对称的性质,矩形,正方形的性质,勾股定理的应用,三角形相似的判定与性质,掌握以上知识是解题的关键.三、解答题21.(1)45°;(2)2-;(3)54 【分析】(1)根据三线合一得到∠ADC ,再根据正方形的性质得到∠ADF ,相减可得结果;(2)当60BAC ∠=︒时,ABC ∆为正三角形.设OH a =,则OA OE OF ==,求得1)EH a =,1)HF a =-,根据相似三角形的性质得到AH EH NH FH ==,12OH OA DC AD ==,得到2CD a =,再证明HNF CND △∽△,得到NH ,根据4AC AH NH NC =++=,可求出NC ;(3)设2EH m =,则2FH km =求得1(1)2OA EF k m ==+,得到21(1)S k m =+,于是得到结论.【详解】解:(1)∵AB =AC ,AD ⊥BC ,∴∠ADC =90°,∵四边形AEDF 为正方形,∴∠ADF =45°,∴∠FDC =90°-45°=45°;(2)当60BAC ∠=︒时,ABC ∆为正三角形. AD EF ⊥30OAH ∴∠=︒∴AO OH=设OH a =,则OA OE OF ===,1)EH a ∴=+,1)HF a =,//AE FN ,AEH NFH ∴△∽△,∴AH EH NH FH ==,则AH , //EF BC ,AOH ADC ∴△∽△, ∴12OH OA DC AD ==,2CD a ∴=,//EF BC ,∴HNF CND △∽△,∴NH FH NC CD ==,∴NH =, ∵AC AH NH NC =++1122NC NC NC ++=4,解得:2NC =; (3)设2EH m =,则2FH km =,1(1)2OA EF k m ==+, 21(1)S k m ∴=+,由(2)得,AEH NFH ∆∆∽,2221(1)HNF S k S k k m ∆∴==+,而222(1)EDF S OA k m ∆==+,2222222(1)(1)(1)(1)EDF HNF S S S k m k k m k k k m ∆∆∴=-=+-+=-+++, ∴2211S k k S =-++, ∴当12k =时,21S S 的最大值为54. 【点睛】本题考查了相似三角形的判定和性质,等腰三角形的性质,正方形的性质,正确的识别图形是解题的关键.22【分析】利用正方形是性质和平行线的性质可得∠CDF =∠DEA ,∠CFD =∠A ,则可利用相似三角形的判定证明△ADE ∽△FCD ,根据相似三角形的性质可得比例式,结合勾股定理即可求解CF 的长.【详解】解:∵四边形ABCD 是正方形,∴∠A =90°,AB ∥CD .∴∠CDF =∠DEA .又CF ⊥DE ,∴∠CFD =90°,即∠CFD =∠A .∴△FCD ∽△ADE .∴CF CD AD DE=. ∴CD AD CF DE ⋅=. ∵AD =CD =1,E 是AB 的中点,∴AE =12.∴由勾股定理得DE 2==.∴CF . 【点睛】本题主要考查了相似三角形的判定与性质,根据正方形的性质正确证明△ADE ∽△FCD 是解题的关键23.体验:∽;探究:△ABM ∽△MCD ;拓展:DE =103【分析】体验:根据同角的余角相等得到∠BAM=∠DMC ,根据平行线的性质得到∠C=∠B=90°,根据两角相等的两个三角形相似证明结论;探究:根据三角形的外角性质、相似三角形的判定定理证明;拓展:根据相似三角形的性质求出BD ,根据等腰直角三角形的性质求出AD ,根据勾股定理计算,得到答案.【详解】解:体验:∵∠AMD =90°,∴∠AMB +∠DMC =90°,∵∠B =90°,∴∠AMB +∠BAM =90°,∴∠BAM =∠DMC ,∵AB ∥CD ,∠B =90°,∴∠C =∠B =90°,∴△ABM ∽△MCD ,故答案为:∽;探究:∵∠AMC =∠BAM +∠B ,∠AMC =∠AMD +∠CMD ,∴∠BAM +∠B =∠AMD +∠CMD .∵∠B =∠AMD ,∴∠BAM =∠CMD ,∵∠B =∠C ,∴△ABM ∽△MCD ;拓展:同探究的方法得出,△BDM ∽△CME ,∴BD CM =BM CE, ∵点M 是边BC 的中点,∴BM =CM =,∵CE =6,∴=6, 解得,BD =163, ∵∠B =∠C =45°,∴∠A =180°﹣∠B ﹣∠C =90°,∴AC =AB BC =8, ∴AD =AB ﹣BD =8﹣163=83,AE =AC ﹣CE =2,在Rt △ADE 中,DE 103. 【点睛】 本题考查的是相似三角形的判定与性质、勾股定理、三角形内角和定理以及三角形外角性质,解本题的关键是判断出△ABM ∽△MCD .24.(1)见解析;(2;(3)见解析 【分析】(1)由矩形的性质及已知证得△EAF ≌△DAB ,则有∠E=∠ADB ,进而证得∠EGB=90º即可证得结论;(2)设,AD a AB b ==,利用矩形性质知AF ∥BC ,得,AEF BEC △∽△再根据相似三角形的性质得到,a b 的方程,变形整理即可;(3)在EF 上截取EM=DG ,进而证明△EMA ≌△DGA ,得到∠EAM=∠DAG ,AM=AG ,则证得△MAG 为等腰直角三角形,即可得证结论.【详解】 ()1证明:四边形ABCD 是矩形,点E 在BA 的延长线上, 90EAF DAB ∴∠=∠=︒, 又,AE AD AF AB ==,()AEF ADB SAS ∴△≌△,1E ∴∠=,21290E ∴∠+∠=∠+∠=︒,90EGB ∴∠=︒,故BD EC ⊥.()2在矩形ABCD 中,,//AD BC AD BC =,AEF BEC ∴△∽△, AF AE BC BE ∴=, 设,AD a AB b ==,则b a a a b =+, 得220a ba b --=,∴22415b b b a b ±+-±==(负值舍去), 51a b +∴= :AD AB ∴的值为51+; ()3如图,在线段EG 上取点M ,使得EM DG =,在AEM ∆与ADG ∆中,,1,AE AD E EM DG =∠=∠=,()AEM ADG SAS ∴△≌△,,34AM AG ∴=∠=∠,535490MAG ∴∠=∠+∠=∠+∠=︒,2MG AG ∴=,2EG DG EG EM MG AG ∴-=-==.【点睛】本题主要考查了矩形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、直角定义、相似三角形的判定与性质、解一元二次方程等知识,涉及知识面广,解答的关键是认真审题,提取相关信息,利用截长补短等解题方法确定解题思路,进而推理、探究、发现和计算.25.(1)AMN ,证明见解析;(2)34【分析】(1)根据矩形的性质和平行线的性质证明即可;(2)作NH AM ⊥于H ,证明NAH AMB ∆∆∽,根据相似三角形的性质得到212AN BM AM =,根据相似三角形的性质即可得到结论. 【详解】 解:(1)AMN ∆是等腰三角形,证明:四边形ABCD 是矩形,//AD BC ∴,NAM BMA ∴∠=∠,又AMN AMB ∠=∠,AMN NAM ∴∠=∠,AN MN ∴=,即AMN ∆是等腰三角形;(2)如图,延长AD 和ME ,交于点N ,作NH AM ⊥于H , AN MN =,NH AM ⊥,12AH AM ∴=, 90NHA ABM ∠=∠=︒,AMN AMB ∠=∠,NAH AMB ∴∆∆∽,∴AN AH AM BM=, 212AN BM AH AM AM ∴==, M 为BC 中点,112BM CM BC ∴===, 2223110AM =+=,5AN ,523DN ∴=-=,设DE x =,则3CE x =-,//AN BC ,∴DN DE CM CE =,即313x x=-, 解得,94x =,即94DE =, 34CE ∴=.【点睛】本题考查的是相似三角形的判定和性质、勾股定理的应用以及等腰三角形的性质和矩形的性质,掌握相似三角形的判定定理和性质定理是解题的关键,注意方程思想的正确运用.26.(1)见解析;(2)见解析【分析】(1)利用关于x轴对称点的性质:横坐标相等,纵坐标互为相反数,可以求出1A、1B、C,进而可画出图形;1(2)利用位似图形的性质得出对应点的位置,即可画出图形.【详解】解:(1)如图所示:ΔA1B1C1即为所求;(2)如图所示,ΔA2B2C2即为所求.【点睛】本题考查关于对称轴对称的点的性质以及位似的性质,掌握相关性质是解题的关键.。
2020年北师大版九年级数学上学期第4章 图形的相似 单元检测卷(含答案)

北师版九年级数学上册 第四章图形的相似测试卷题号 一 二 三 总分 得分第Ⅰ卷(选择题)一、选择题(共10小题,3*10=30)1.如果mn =ab ,那么下列比例式中错误的是( ) A.a m =n b B.a n =m b C.m a =n b D.m a =b n2.如图,△ABC ∽△DEF ,相似比为12,若BC =1,则EF 的长是( )A .1B .2C .3D .43.如图,在△ABC 中,∠ACB =90°,CD ⊥AB ,DE ⊥BC ,那么与△ABC 相似的三角形的个数有( ) A .1个 B .2个C .3个D .4个4.如图,在△ABC 中,D ,E 分别为AB ,AC 边上的点,DE ∥BC ,BE 与CD 相交于点F ,则下列结论一定正确的是( ) A.AD AB =AE AC B.DF FC =AE EC C.AD DB =DE BC D.DF BF =EF FC5.某人要在报纸上刊登广告,一块10cm×5cm 的矩形版面要付广告费180元,他要把该版面的边长都扩大为原来的3倍,在每平方厘米版面广告费相同的情况下,他应付广告费( ) A .540元 B .1080元 C .1620元 D .1800元6.如图,点E ,F 的坐标分别为E(-4,2),F(-1,-1),以原点O 为位似中心,按相似比12把△EFO 缩小,则E 点的对应点E′的坐标为( ) A .(2,1) B .(12,12) C .(2,-1) D .(2,-12)7.“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( ) A .1.25尺 B .57.5尺 C .6.25尺 D .56.5尺8.如图,点D 在△ABC 的边AC 上,要判定△ADB 与△ABC 相似,添加一个条件,不正确的是( ) A .∠ABD =∠C B .∠ADB =∠ABC C.AB BD =CB CD D.AD AB =AB AC9.如图,在△ABC 中,A 、B 两个顶点在x 轴的上方,点C 的坐标是(-1,0).以点C 为位似中心,在x 轴的下方作△ABC 的位似图形△A′B′C ,并把△ABC 的边长放大到原来的2倍.设点B 的对应点B′的横坐标是a ,则点B 的横坐标是( ) A .-12a B .-12(a +1) C .-12(a -1) D .-12(a +3)10.如图所示的是一张等腰三角形纸片,底边长18 cm ,底边上的高长18 cm ,现沿底边依次由下往上裁剪宽度均为3 cm 的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( ) A .第4张 B .第5张 C .第6张 D .第7张第Ⅱ卷(非选择题)二.填空题(共8小题,3*8=24)11.若x ∶y =1∶2,则x -yx +y=__________.12. 如图,已知AB ∥CD ,若AB CD =14,则OAOC=__________.13.如图,AE ,BD 交于点C ,BA ⊥AE 于点A ,ED ⊥BD 于点D ,若AC =4,AB =3,CD =2,则CE =__________.14.如图,测量小玻璃管口径的量具ABC ,AB 的长为10 cm ,AC 被分为60等份.如果小玻璃管口DE 正好对着量具上20等份处(DE ∥AB),那么小玻璃管口径DE 是__________m.15.如图,在平面直角坐标系中,△ABC 的顶点坐标分别为(4,0),(8,2),(6,4).已知△A 1B 1C 1的两个顶点的坐标为(1,3),(2,5).若△ABC 与△A 1B 1C 1位似,则△A 1B 1C 1的第三个顶点的坐标为______________.16如图,E 为▱ABCD 的边AB 延长线上的一点,且BE ∶AB =2∶3,连接DE 交BC 于点F ,则CF ∶AD =____________.17.如图,在▱ABCD 中,点E 是边BC 上的黄金分割点,且BE >CE ,AE 与BD 相交于点F ,那么BF ∶FD 的值为________________.18.“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD 长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A 点,则FH=____________里.三.解答题(共7小题,46分)19.(6分)如图,l1∥l2∥l3,AB=3,AD=2,DE=4,EF=7.5,求BC,BE的长.20. (6分) 如图,一油桶高1 m,桶内有油,一根木棒长1.2 m,从桶盖的小口处斜插入桶内,一端插到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长为0.48 m,求桶内油面的高度h′.21. (6分)如图,▱ABCD中,AE∶EB=2∶3,DE交AC于点F.(1)求证:△AEF∽△CDF;(2)求△AEF与△CDF周长之比;22.(6分)九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,如图所示,已知标杆高度CD=3 m,标杆与旗杆的水平距离BD=15 m,人的眼睛与地面的高度EF=1.6 m,人与标杆CD的水平距离DF=2 m,则旗杆AB的高度.23.(6分)如图,在△ABC中,AD是BC边上的高,点G在AD上,过G作BC的平行线分别与AB,AC交于P,Q两点,过点P作PE⊥BC于点E,过点Q作QF⊥BC于点F,设AD=80,BC=120,当四边形PEFQ为正方形时,试求出正方形的边长.24.(8分)如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F.(1)求证:四边形ABCD是正方形;(2)当AE=2EF时,判断FG与EF有何数量关系?并证明你的结论.25.(8分)晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长.(结果精确到0.01米)参考答案 1-5 CBDAC 6-10CBCDB 11. -1312. 1413. 5214.20315. (3,4)或(0,4) 16. 3∶5 17.5-1218. 1.0519. 解:∵l 1∥l 2∥l 3,∴FB BE =AB BC =ADDE ,即BF BE =3BC =24,∴BC =6,BF =12BE , ∴EF =12BE +BE =7.5,∴BE =520. 解:∵CD ∥BE ,∴△ACD ∽△ABE , ∴AC AB =ADAE ,∴1.2-0.481.2=1-h′1, ∴h′=0.4 m答:桶内油面的高度是0.4 m.21. 解:(1)证明:∵四边形ABCD 是平行四边形,∴DC ∥AB , ∴∠CDF =∠FEA ,∠DCA =∠FAE ,∴△AEF ∽△CDF (2)∵四边形ABCD 是平行四边形,∴DC =AB. 又∵AE ∶EB =2∶3,∴可设AE =2λ,则BE =3λ,DC =5λ. ∵△AEF ∽△CDF ,∴C △AEF C △CDF =AE DC =2λ5λ=2522. 解:∵CD ⊥FB ,∴AB ⊥FB ,∴CD ∥AB , ∴△CGE ∽△AHE ,∴CG AH =EG EH, 即:CD -EF AH =FD FD +BD ,∴3-1.6AH =22+15, ∴AH =11.9,∴AB =AH +HB =AH +EF =11.9+1.6=13.5(m) 答:旗杆AB 的高度是13.5m.23. 解:设正方形的边长为x ,则PQ =PE =x. ∵AD ⊥BC ,∴∠ADB =90°.∵PQ ∥BC ,∴∠AGP =90°,∴AG ⊥PQ.又∵PQ ∥BC ,PE ⊥BC ,∴GD =PE =x ,AG =AD -GD =80-x. ∵PQ ∥BC ,∴△APQ ∽△ABC ,∴PQ BC =AG AD ,∴x 120=80-x 80, 解得x =48,答:正方形的边长为4824. (1)证明:易证△ABE ≌△CBE ,∴AB =BC ,∴四边形ABCD 是正方形 (2)解:当AE =2EF 时,FG =3EF.证明如下:∵四边形ABCD 是正方形,∴AB ∥CD ,AD ∥BC ,∴△ABE ∽△FDE ,△ADE ∽△GBE. ∵AE =2EF ,∴BE ∶DE =AE ∶EF =2.∴BG ∶AD =BE ∶DE =2,即BG =2AD. ∵BC =AD ,∴CG =AD.易证△ADF ∽△GCF ,∴FG =AF ,即FG =AF =AE +EF =3EF 25. 解:由题意得:∠CAD =∠MND =90°,∠CDA =∠MDN ,∴△CAD ∽△MND , ∴CA MN =AD ND ,∴1.6MN =1×0.8(5+1)×0.8, ∴MN =9.6,又∵∠EBF =∠MNF =90°,∠EFB =∠MFN , ∴△EFB ∽△MFN , ∴EB MN =BF NF ,∴EB 9.6=2×0.8(2+9)×0.8, ∴EB≈1.75,答:小军身高约为1.75米1、老吾老以及人之老,幼吾幼以及人之幼。
(常考题)北师大版初中数学九年级数学上册第四单元《图形相似》检测题(有答案解析)(3)

一、选择题1.如图,在Rt ABC 中,90ACB D ∠=︒,是AB 边的中点,AF CD ⊥于点E ,交BC 边于点F ,连接DF ,则图中与ACE △相似的三角形共有( )A .2个B .3个C .4个D .5个2.如图,在菱形ABCD 中,10BC =,点E 在BD 上,F 为AD 的中点,FE BD ⊥,垂足为E ,4EF =,则BD 长为( )A .8B .10C .12D .163.在ABC 中,10AB AC ==,72ABC ∠=︒,ABC ∠的角平分线交AC 于点D ,则CD 的长为( )A .5B .555-C .1555-D .551- 4.如图,ABC 中,AD BC ⊥于点D ,下列条件中不.能判定ABC 是直角三角形的是( )A .B DAC ∠=∠B .90B DAC ∠+∠=︒ C .2AB BD BC =⋅ D .2AC CD BC =⋅5.如图,ABC 的两个顶点B 、C 均在第一象限,以点()0,1A 为位似中心,在y 轴左侧作ABC 的位似图形ADE ,ABC 与ADE 的位似比为1:2若点C 的纵坐标是m ,则其对应点E 的纵坐标是( )A .32m -+B .23m +C .()23m -+D .23m -+ 6.已知ABC 的三边长是2,6,2,则与ABC 相似的三角形的三边长可能是( )A .1,2,3B .1,3, 22C .1,3,6D .1,3,3 7.古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G 将一线段MN 分为两线段MG 、GN ,使得其中较长的一段MG 是全长MN 与较短的一段GN 的比例中项,即满足512MG GN MN MG -==,后人把51-这个数称为“黄金分割数”,把点G 称为线段MN 的“黄金分割点”.如图,在△ABC 中,已知AB =AC =3,BC =4,若点D 是边BC 边上的一个“黄金分割点”,则△ADC 的面积为( )A .55B .355C .205-D .1045-8.点B 是线段AC 的黄金分割点,且AB <BC .若AC=4,则BC 的长为( ) A .252 B .252 C 51- D 51 9.已知30MAN ∠=︒,点B 在射线AM 上,按以下步骤作图:①分别以A ,B 为圆心,大于12AB 的长为半径画弧,两弧相交于P ,Q 两点; ②作直线PQ ,交射线AN 于点C ,连接BC ;③以B 为圆心,BA 长为半径画弧,交射线AN 于点D .根据以上作图过程及所作图形,下列结论中错误的是( )A .60BCD ∠=︒B .2AB AD AC = C .4ABD CBA ∠=∠ D .23AD AB =10.如图,正方形ABCD 中,E ,F 分别在边AD ,CD 上,AF ,BE 相相交于点G ,若3AE ED =,DF CF =,则BG GE的值是( )A .73B .83C .2D .7411.如图,在ABC 中,D 、E 分别是AB 、BC 边上的点,连接DE 并延长,与AC 的延长线交于点F ,且3AD BD =,2EF DE =,若2CF =,则AF 的长为( )A .5B .6C .7D .812.如图,D ,E 分别是ABC 的边AB 、BC 上的点,//DE AC ,若:1:2BDE CDE S S =,则:DOE AEC S S 的值为( )A .16B .19C .112D .116二、填空题13.如图,在ABC 中,,D E 分别为,AB AC 边上的中点,则ABC 与ADE 的周长的比值是_____.14.已知35a b =,则a a b+的值为______. 15.如图,在ABC 中,90ACB ∠=︒,30A ∠=︒,3BC =.点D 是AB 上一动点,以DC 为斜边向右侧作等腰直角三角形CDE ,使90CED ∠=︒,连接BE . (1)若点E 恰好落在AB 上,则AD 的值为______;(2)线段BE 的最小值为______.16.如图,正方形ABCD 的边长为4,点E 为CD 中点,点F 为BC 边上一点,且CF=1,连接AF ,EG ⊥AF 交BC 于点G ,则BG=________.17.如图,小静在横格纸上画了两条线段AB ,CD ,点A ,D 在同一条格线上,点B ,C 在同一条格线上,AB 与CD 的交点也在格线上,横格纸的横线平行且相邻横线间的距离相等,若4=AD ,则BC =______.18.如图,在平行四边形ABCD 中,E 是BC 上一点,BE :EC =1:2,AE 与BD 相交于F ,则S △ADF :S △EBF =_____.19.已知35y x =,那么x y x y -=+________. 20.如图,在等腰ABC 中,AB AC =,点P 在BA 的延长线上,14PA AB =,点D 在BC 边上,PD PC =,则CD BC的值是_____.三、解答题21.体验:如图1,在四边形ABCD 中,AB ∥CD ,∠B =90°,点M 在BC 边上,当∠AMD =90°时,可知△ABM △MCD (不要求证明).探究:如图2,在四边形ABCD 中,点M 在BC 上,当∠B =∠C =∠AMD 时,求证:△ABM ∽△MCD .拓展:如图3,在△ABC 中,点M 是边BC 的中点,点D 、E 分别在边AB 、AC 上.若∠B =∠C =∠DME =45°,BC =82,CE =6,求DE 的长.22.如图,小明想测量河对岸建筑物AB 的高度,在地面上C 处放置了一块平面镜,然后从C 点向后退了2.4米至D 处,小明的眼睛E 恰好看到了镜中建筑物A 的像,在D 处做好标记,将平面镜移至D 处,小明再次从D 点后退2.52米至F 处,眼睛G 恰好又看到了建筑物顶端A 的像,已知小明眼睛距地面的高度ED ,GF 均为1.6米,求建筑物AB 的高度.(注:图中的左侧α,β为入射角,右侧的α,β为反射角)23.如图1,边长为4的正方形ABCD 与边长为a (1<a <4)的正方形CFEG 的顶点C 重合,点E 在对角线AC 上.问题发现:(1)如图1,AE 与BF 的数量关系为 .类比探究:(2)如图2,将正方形CFEG 绕点C 旋转α度(0<α<30),请问(1)中的结论是否仍成立?若成立,写出证明过程;若不成立,请说明理由.拓展延伸:(3)若点F 为BC 的中点,在正方形CFEG 的旋转过程中,当点A ,F ,G 在一条直线上时,求线段AG 的长度.24.如图,已知90EOF ∠=︒,A 是EOF ∠内部的一点,过点A 作AB OF ⊥,垂足为点B ,6cm AB =,8cm OB =,动点M ,N 同时从O 点出发,点M 以1.5cm /秒的速度沿OF 方向运动,点N 以2cm /秒的速度沿OE 方向运动,MN 与OA 交于点C ,连接AM ,当点M 到达点B 时,点N 随之停止运动.设运动时间为t 秒(0)t >. (1)当2t =秒时,MON △与ABO 是否相似?请说明理由;(2)在运动过程中,试判断MN 与OA 的位置关系,并说明理由.(3)连接AN ,在运动过程中,是否存在某一时刻t ,使得2AMN ABON SS =四边形?若存在,请求出此时t 的值;若不存在,请说明理由.25.(1)如图1,矩形ABCD 中,点M 在BC 上,连接AM ,作AMN AMB ∠=∠,点N 在直线AD 上,MN 交CD 于点E .请找出图1中的一个等腰三角形,并证明结论.(2)如图2,矩形ABCD 中,3AB =,2BC =,点M 为BC 中点,连接AM ,作AME AMB ∠=∠,ME 交于点E ,求CE 的长.26.如图,在ABC 中,点D ,E 分别在AB ,AC 的边上,//,6,3,4DE BC AD DB AE ===,求AC 的长.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】利用直角三角形斜边上的高线模型,可判断有2个三角形与ACE △相似,利用直角三角形斜边上的中线等于斜边的一半,传递一组等角,得到第3个三角形.【详解】∵∠EAC=∠CAF ,∠AEC=∠ACF ,∴△ACE ∽△AFC ;∵∠EAC+∠AFC=90°,∠ECF+∠AFC=90°,∴∠EAC=∠ECF ,∵∠AEC=∠CEF ,∴△ACE ∽△CFE ;∵90ACB D ∠=︒,是AB 边的中点,∴DC=DB ,∴∠ECF=∠EAC=∠B ,∵∠AEC=∠BCA ,∴△ACE ∽△BAC ;共有3个,故选B.【点睛】本题考查了直角三角形的相似,熟练运用三角形相似的判定定理是解题的关键. 2.C解析:C【分析】连接AC ,交BD 于点O ,由菱形性质,可得AC BD ⊥,且BD=2OB ,由勾股定理求得3DE =,由90DEF DOA ∠=∠=︒,FDE ADO ∠=∠,可证得DEF DAO ∆∆,由此DF DE DA DO=,即可求得DO=6,从而BD=2OD=12. 【详解】如图:连接AC ,交BD 于点O ,在菱形ABCD 中,则AC BD ⊥,且BD=2OB ,10BC =,点E 在BD 上,F 为AD 的中点,∴AD=10, DF=5, ∴2222543DE DF EF =-=-=,FE BD ⊥,AC BD ⊥,∴90DEF DOA ∠=∠=︒,FDE ADO ∠=∠,DEF DAO ∴∆∆,DF DE DA DO ∴=,即5310DO=, ∴DO=6,∴BD=2OD=12,故选:C【点睛】 此题考查了勾股定理、菱形的性质,相似三角形的判定和性质等知识点,正确作出辅助线是解答此题的关键.3.C解析:C【分析】证明△ABC ∽△BCD ,得到AB BC BC CD=,设CD=x ,表示出BC ,代入得到方程,解之即可. 【详解】解:如图,∵AB=AC ,∠ABC=72°,∴∠C=72°,∴∠A=180°-2×72°=36°,∵BD 平分∠ABC ,∴∠ABD=∠CBD=36°,∴AD=BD ,∠BDC=72°,∴BC=BD ,在△ABC 和△BCD 中,∠A=∠CBD ,∠ABC=∠C ,∴△ABC ∽△BCD ,∴AB BC BC CD =, 设CD=x ,则BD=AD=BC=10-x ,∴101010x x x-=-, 解得:x=1555+(舍)或1555-,故选C .【点睛】本题考查了等腰三角形的判定和性质,相似三角形的判定和性质,解题的关键是根据已知条件证明出△ABC ∽△BCD .4.B解析:B【分析】根据已知对各个条件进行分析,从而得到答案.【详解】解:A.能,∵AD ⊥BC ,∴∠B+∠BAD=90°,∵∠B=∠DAC ,∴∠BAC=∠BAD+∠DAC=∠BAD+∠B=90°;∴△ABC 是直角三角形;B.不能,∵AD ⊥BC ,∴∠B+∠BAD=90°,∵∠B+∠DAC=90°,∴∠BAD=∠DAC ,∴△ABD ≌△ACD (ASA ),∴AB=AC ,∴△ABC 是等腰三角形,∴无法证明△ABC 是直角三角形;C.能,∵2AB BD BC =⋅∴AB BC BD AB= ∵∠B=∠B∴△CBA ∽△ABD ,∴∠ADB=∠BAC ,∵AD ⊥BC ,∴∠ADB=∠ADC=90°,∴∠BAC=90°∴△ABC 是直角三角形;D.能,∵2AC CD BC =⋅, ∴AC BC CD AC= ∵∠C=∠C ∴△CBA ∽△CAD ,∴∠ADC=∠BAC=90°∴△ABC 是直角三角形.故选:B【点睛】此题考查了相似三角形的判定与性质、直角三角形的判定与性质.此题难度适中,解题的关键是注意数形结合思想的应用,注意相似三角形的判定与性质的应用.5.D解析:D【分析】设点C 的纵坐标为m ,然后表示出AC 、EA 的纵坐标的距离,再根据位似比列式计算即可;【详解】设点C 的纵坐标为m ,则A 、C 间的纵坐标的长度为()1m -,∵△ABC 放大到原来的2倍得到△ADE ,∴E 、A 间的纵坐标的长度为()21m -,∴点E 的纵坐标为()()2112323m mm ⎡⎤---=--=-+⎣⎦;故答案选D .【点睛】 本题主要考查了位似变换,坐标与图形的性质,准确分析计算是解题的关键.6.A解析:A【分析】根据相似三角形的判定定理即可得到结论.【详解】解:∵△ABC 三边长是2,6,2, ∴△ABC 三边长的比为2:2:6=1:2:3,∴△ABC 相似的三角形三边长可能是1:2:3,故选:A .【点睛】本题考查了相似三角形的判定,熟练掌握相似三角形的判定定理是解题的关键. 7.A解析:A【分析】作AF ⊥BC ,根据等腰三角形ABC 的性质求出AF 的长,再根据黄金分割点的定义求出CD 的长度,利用三角形面积公式即可解题.【详解】解:过点A 作AF ⊥BC ,∵AB=AC ,∴BF=12BC=2, 在Rt ABF ,AF=2222325AB BF -=-=,∵D 是边BC 的两个“黄金分割”点,∴512CD BC -=即5142CD -=, 解得CD=252-,∴12ADC C AF S D ⨯⨯==()125252⨯-⨯=55-, 故选:A .【点睛】本题考查了“黄金分割比”的定义、等腰三角形的性质、勾股定理的应用以及三角形的面积公式,求出DC 和AF 的长是解题的关键.8.B解析:B【分析】根据黄金分割的定义可得出较长的线段BC=12AC ,将AC=4代入即可得出BC 的长度. 【详解】 解:∵点B 是线段AC 的黄金分割点,且AB <BC ,∴AC , ∵AC=4,∴BC=2.故选:B .【点睛】本题考查了黄金分割的定义:把线段AB 分成两条线段AC 和BC (AC >BC ),且使AC 是AB 和BC 的比例中项(即AB :AC=AC :BC ),叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点.其中AB≈0.618AB ,并且线段AB 的黄金分割点有两个. 9.D解析:D【分析】根据垂直平分线的性质、等腰三角形的性质及判定,相似三角形的判定一一判断即可.【详解】由作图可知,PQ 垂直平分AB ,AB=BD∵PQ 垂直平分AB ,∴AC =BC ,∴∠MAN =∠CBA ,∵∠MAN =30,∴∠DCB =∠MAN +∠CBA =60︒,故选项 A 正确;AB BD =MAN ADB ∴∠=∠∠MAN =∠CBA ,ADB CBA ∴∠=∠ACB ABD ∴△∽△2AC AB AB ADAB AC AD ∴=∴=⋅ 故选项B 正确;ABD 为等腰三角形,且两底角均为301803030120ABD ∴∠=︒-︒-︒=︒30MAN CBA ∠=∠=︒4ABD CBA ∴∠=∠故选项C 正确;如图:过点B 作BF AD ⊥在ABF 中,30A ∠=︒3AB AF ∴=223AD AFAB AF =∴= 33AB AD AD ∴=∴= 故选项D 错误;故选:D .【点睛】本题考查作图﹣复杂作图,线段的垂直平分线的性质,等腰三角形的性质及判定、相似三角形的判定等知识,解题的关键是熟练掌握基本知识.10.B解析:B【分析】如图,延长BC 、AF ,交于点H ,由正方形的性质及DF =CF 判定△ADF ≌△HCF (AAS ),从而可得CH =AD ;由AE =3ED ,可设DE =x ,从而可用x 表示出正方形的边长;然后由AD ∥BC 判定△AEG ∽△HBG ,从而可得比例式,化简比例式即可得到答案.【详解】解:如图,延长BC 、AF ,交于点H ,∵AE =3ED ,∴设DE =x ,则AE =3x ,∵四边形ABCD 是正方形,∴AD =BC =4x ,AD ∥BC ,∴∠DAF =∠CHF ,∠D =∠FCH ,∴在△ADF 和△HCF 中,DAF CHF D FCHDF CF ∠∠⎧⎪∠∠⎨⎪⎩=== , ∴△ADF ≌△HCF (AAS ),∴CH =AD =4x ,∴BH =BC +CH =8x ,∵AD ∥BC ,∴△AEG ∽△HBG , ∴8833BH x GE AE BG x === . 故选:B .【点睛】 本题考查了正方形的性质、全等三角形的判定与性质及相似三角形的判定与性质等知识点,正确作出辅助线并熟练掌握相关性质及定理是解题的关键.11.B解析:B【分析】过点F 作//FG AB ,通过证明BED GEF ∽△△可得2FG BD =再证明FCG ACB ∽△△可得AC 的长度,即可求解.【详解】如图,过点F 作//FG AB ,交BC 延长线于点G ,则由平行易知BED GEF ∽△△,因此12BD DE FG EF ==, 即2FG BD =由平行易知FCG ACB ∽△△,因此FG CF AB AC = ∵3AD BD =,∴4AB AD BD BD =+=, ∴2142FG BD AB BD ==, ∴12CF AC =, 即212AC =, ∴4AC =,∴6AF AC CF =+=. 故答案选:B .【点睛】 本题主要考查了利用三角形相似的性质求解线段的长度的问题,正确做出辅助线并证明三角形相似是解决本题的关键. 12.C解析:C【分析】先根据等高三角形的面积证明BE :1EC =:2,进而可得BE :1BC =:3;根据DE//AC 可得DOE △∽COA ,BDE ∽BAC ,得到13DE BE EO AC BC OA ===,根据相似三角形的性质得到DOE S △:21()9AOC DE S AC ==,再根据等高三角形的面积计算得到AOC S :39412AEC S ==即可得答案. 【详解】 ∵BDE S △:1CDE S =:2,BDE 和CDE △等高,∴BE :1EC =:2;∴BE :1BC =:3;∵//DE AC ,DOE ∴△∽COA ,BDE ∽BAC ,13DE BE EO AC BC OA ∴===, ∴34AO AE =,DOE S △:21()9AOC DE S AC ==, ∵AOC △和AEC 等高,∴AOC S :39412AEC AO S AE ===, ∴:1DOE AEC S S =:12.故选:C .【点睛】本题主要考查了相似三角形的判定与性质,根据平行得出两组相似三角形并熟练掌握相似三角形的面积比等于相似比的平方是解题关键.二、填空题13.2【分析】根据三角形中位线的定义及性质可得DE ∥BCDE =BC 再利用相似三角形的判定及性质即可求出答案【详解】解:∵分别为边上的中点∴DE 是△ABC 的中位线∴DE ∥BCDE =BC ∴△ADE ∽△ABC解析:2【分析】根据三角形中位线的定义及性质可得DE ∥BC ,DE =12BC ,再利用相似三角形的判定及性质即可求出答案.【详解】解:∵D 、E 分别为AB 、AC 边上的中点,∴DE 是△ABC 的中位线,∴DE ∥BC ,DE =12BC , ∴△ADE ∽△ABC , ∴12DE BC =, ∴2ABC ADE C BC C DE ==, ∴ABC 与ADE 的周长的比值是2,故答案为:2.【点睛】 本题考查了相似三角形的判定与性质,解题的关键是熟练运用相似三角形的性质与判定求解三角形的周长比.14.【分析】根据比例的性质求解即可;【详解】∵设∴;故答案是【点睛】本题主要考查了比例的性质准确计算是解题的关键 解析:38 【分析】 根据比例的性质求解即可; 【详解】 ∵35a b =, 设3a k =,5b k =, ∴33358a k ab k k ==++; 故答案是38. 【点睛】本题主要考查了比例的性质,准确计算是解题的关键.15.【分析】(1)根据含30°的直角三角形的性质可得AB=6BE=CE=再根据等腰直角三角形的性质得出CE=DE=最后依据AD=AB-BE-ED 得出结果;(2)以BC 为直角边向左构造以∠CBH 为直角的等解析:933- 324【分析】(1)根据含30°的直角三角形的性质可得AB=6,BE=32,CE=33,再根据等腰直角三角形的性质得出CE=DE=33,最后依据AD=AB-BE-ED 得出结果; (2)以BC 为直角边向左构造以∠CBH 为直角的等腰直角三角形BCH ,先证明△CDH ∽△CEB ,得出2DH BE=,当DH 取最小值时,BE 边为最小值,当DH ⊥AB 时,DH 最小,即图中的D H ',根据含30°的直角三角形的性质可得出结论.【详解】(1)如图所示:∵∠ACB=90°,∠A=30°,BC=3,∴AB=6,BE=32,CE=33, ∵△CDE 为等腰直角三角形,∴CE=DE=33, ∴AD=6-32-33=933-; (2)以BC 为直角边向左构造以∠CBH 为直角的等腰直角三角形BCH ,∵△CDE 为等腰直角三角形,∴∠DCE=∠HCB=45°,∠DCH=∠HCB ,∵2CD CH CE CB==, ∴△CDH ∽△CEB , ∴2DH BE=, ∴当DH 取最小值时,BE 边为最小值,当DH ⊥AB 时,DH 最小,即图中的D H ',∵∠A=30°,∠ACB=90°∴∠ABC=60°∵∠CBH=90°∴D BH '∠=30°∵BH=BC=3∴32D H '= ∴32=42BE =最小值, 故答案为933-,324.【点睛】本题考查了相似三角形的判定和性质,含30°的直角三角形的性质,等腰三角形的性质,解题的关键是证明△CDH ∽△CEB .16.【分析】证明△ECG △FBA 利用相似三角形的性质求解即可【详解】设EG 交AF 于点Q ∵EG ⊥AF ∴∠FQG=90∴∠QFG+∠QGF=90在正方形ABCD 中∠B=∠C=90∴∠QAB+∠AFB=90∴ 解析:43【分析】证明△ECG ~△FBA ,利用相似三角形的性质求解即可.【详解】设EG 交AF 于点Q ,∵EG ⊥AF ,∴∠FQG=90︒,∴∠QFG+∠QGF =90︒,在正方形ABCD 中,∠B=∠C =90︒,∴∠QAB+∠AFB =90︒,∴∠QGF =∠FAB ,在△ECG 和△FBA 中,∠B=∠C =90︒,∠QGF =∠FAB ,∴△ECG ~△FBA(两组对应角相等的三角形是相似三角形),∴EC CG BF AB =, ∴EC CF FG BF AB+=, ∵E 是CD 的中点,∴122CE CD ==, ∵CF=1,∴BF=3,∴2134FG +=, 解得:FG=53,∴43BG BF FG =-=, 故答案为:43. 【点睛】 本题考查了正方形的性质,相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形,利用相似三角形的性质解决问题. 17.6【分析】过点O 作OE ⊥AD 于点EOF ⊥CB 于点F 则EOF 三点共线根据平行线分线段成比例可得代入计算即可解答【详解】解:如图过点O 作OE ⊥AD 于点EOF ⊥CB 于点F 则EOF 三点共线∵横格纸的横线平行解析:6【分析】过点O 作OE ⊥AD 于点E ,OF ⊥CB 于点F ,则E 、O 、F 三点共线,根据平行线分线段成比例可得AD OE BC OF=,代入计算即可解答. 【详解】解:如图,过点O 作OE ⊥AD 于点E ,OF ⊥CB 于点F ,则E 、O 、F 三点共线,∵横格纸的横线平行且相邻横线间的距离相等,∴AD OE BC OF =, 即423BC =, ∴CD=6.故答案为:6.【点睛】本题主要考查平行线分线段成比例,掌握平行线分线段所得线段对应成比例是解题的关键.18.【分析】根据相似三角形面积比等于相似比的平方即可求【详解】解:在平行四边形ABCD 中AD ∥BCAD=BC ∵BE :EC =1:2∴BE:AD=1:3∵AD ∥BC ∴△BEF ∽△DAF ∴S △ADF :S △EB解析:【分析】根据相似三角形面积比等于相似比的平方即可求.【详解】解:在平行四边形ABCD中,AD∥BC,AD=BC,∵BE:EC=1:2,∴BE:AD=1:3,∵AD∥BC,∴△BEF∽△DAF,∴S△ADF:S△EBF=9,故答案为:9.【点睛】本题考查相似三角形的判定与性质,解题关键是熟练运用平行线可得三角形相似,面积比是相似比的平方等知识.19.【分析】由可得设则x=5ky=3k;然后代入计算即可【详解】解:∵∴设则x=5ky=3k∴故填:【点睛】本题主要考查了代数式求值根据比例的性质得到x=5ky=3k成为解答本题的关键解析:1 4【分析】由35yx=可得,53yx=,设531=yx k=,则x=5k,y=3k;然后代入x yx y-+计算即可.【详解】解:∵35 yx=∴53y x=设531=yx k=,则x=5k,y=3k∴531534x y k kx y k k--==++.故填:14.【点睛】本题主要考查了代数式求值,根据比例的性质得到x=5k,y=3k成为解答本题的关键.20.【分析】过点P作交DC延长线于点E根据等腰三角形判定与性质平行线的性质可证再证可得再利用平行线分线段成比例得结合线段的等量关系及比例的性质即可得到结论【详解】如图:过点P作交DC延长线于点E在和中故解析:3 4【分析】过点P 作//PE AC 交DC 延长线于点E ,根据等腰三角形判定与性质,平行线的性质可证PB PE =,再证PDB △PCE ≌△,可得BD CE =,再利用平行线分线段成比例得PACE AB BC=,结合线段的等量关系及比例的性质即可得到结论. 【详解】如图:过点P 作//PE AC 交DC 延长线于点E ,AB AC B ACB=∴∠=∠ //AC PEACB EB EPB PE PC PDPDC PCDBPD EPC ∴∠=∠∴∠=∠∴==∴∠=∠∴∠=∠∴在PCE 和PDB △中PC PD EPC BPD PE PB =⎧⎪∠=∠⎨⎪=⎩ PCE PDB ∴△≌△BD CE ∴= //AC PEPA CE AB BC∴= 14PA AB = 14CE BC ∴= 14BD BC ∴= 34CD BC ∴=故答案为:34.【点睛】本题考查了等腰三角形的判定与性质,平行线分线段成比例,以及全等三角形的判定,解题关键是正确作出辅助线,列出比例式.三、解答题21.体验:∽;探究:△ABM∽△MCD;拓展:DE=10 3【分析】体验:根据同角的余角相等得到∠BAM=∠DMC,根据平行线的性质得到∠C=∠B=90°,根据两角相等的两个三角形相似证明结论;探究:根据三角形的外角性质、相似三角形的判定定理证明;拓展:根据相似三角形的性质求出BD,根据等腰直角三角形的性质求出AD,根据勾股定理计算,得到答案.【详解】解:体验:∵∠AMD=90°,∴∠AMB+∠DMC=90°,∵∠B=90°,∴∠AMB+∠BAM=90°,∴∠BAM=∠DMC,∵AB∥CD,∠B=90°,∴∠C=∠B=90°,∴△ABM∽△MCD,故答案为:∽;探究:∵∠AMC=∠BAM+∠B,∠AMC=∠AMD+∠CMD,∴∠BAM+∠B=∠AMD+∠CMD.∵∠B=∠AMD,∴∠BAM=∠CMD,∵∠B=∠C,∴△ABM∽△MCD;拓展:同探究的方法得出,△BDM∽△CME,∴BDCM =BMCE,∵点M是边BC的中点,∴BM=CM=,∵CE=6,∴,解得,BD =163, ∵∠B =∠C =45°,∴∠A =180°﹣∠B ﹣∠C =90°,∴AC =AB =2BC =8, ∴AD =AB ﹣BD =8﹣163=83,AE =AC ﹣CE =2,在Rt △ADE 中,DE 103. 【点睛】 本题考查的是相似三角形的判定与性质、勾股定理、三角形内角和定理以及三角形外角性质,解本题的关键是判断出△ABM ∽△MCD .22.32米【分析】易得△ABC ∽△EDC 以及△ABD ∽△GFD ,根据相似三角形的性质得到关于x 和y 的方程组,求解即可.【详解】解:设AB 为xm ,BC 为ym ,根据题意知,△ABC ∽△EDC ,有1.62.4x y =①. △ABD ∽△GFD ,有 1.62.4 2.52x y =+②. 联立①②,得x =32.答:建筑物AB 的高度为32m .【点睛】本题考查相似三角形的实际应用,掌握相似三角形的性质是解题的关键.23.(1)BF ,(2)成立,理由见解析;(3【分析】(1)证出AB ∥EF ,由平行线分线段成比例定理得出AE CE BF CF ==(2)证明△ACE ∽△BCF ,得出AE AC BF CB==,即可的结论; (3)分两种情况,连接CE 交GF 于H ,由正方形的性质得出AB=BC=4,,GH=HF=HE=HC ,得出CF=12BC=2,,由勾股定理求出AH ==【详解】解:(1)AE=2BF ,理由如下: ∵四边形ABCD 和四边形CFEG 是正方形, ∴∠B=∠CFE=90°,∠FCE=∠BCA=45°,CE=2CF ,CE ⊥GF ,∴AB ∥EF , ∴2AE CE BF CF ==, ∴AE=2BF ;故答案为:AE=2BF ; (2)上述结论还成立,理由如下:连接CE ,如图2所示:∵∠FCE=∠BCA=45°,∴∠BCF=∠ACE=45°-∠ACF ,在Rt △CEG 和Rt △CBA 中,CE=2CF ,CA=2CB ,∴2CE CA CF CB==, ∴△ACE ∽△BCF , ∴2AE AC BF CB==, ∴AE=2BF ;(3)分两种情况:①如图3所示:连接CE 交GF 于H ,∵四边形ABCD 和四边形CFEG 是正方形,∴AB=BC=4,22,2CF ,HF=HE=HC ,∵点F 为BC 的中点,∴CF=12BC=2,2,2∴2222(42)(2)30AH AC HC =-=-=, ∴302AG AH HG =+=+;②如图4所示:连接CE 交GF 于H ,同①得:2, ∴2222(42)(2)30AH AC HC =-=-=,∴302AG AH HG =-=故AG 302302【点睛】本题是四边形综合题目,考查了正方形的性质、旋转的性质、平行线分线段成比例定理、相似三角形的判定与性质、勾股定理等知识;熟练掌握正方形的性质,证明三角形相似是解题的关键.24.(1)∽MON ABO △△,见解析;(2)MN OA ⊥,见解析;(3)存在,3t =或83t = 【分析】解:(1)由2t =,求得3cm OM =,4cm ON =,由6cm AB =,8cm OB =,计算比值OM AB =12ON OB =,由夹角相等90MON ABM ∠=∠=︒,可证∽MON ABO △△; (2) 由15OM t =.,2ON t =.6AB =,8OB =.可得OM ON AB OB=.可证Rt MON Rt ABO ∽△△.由性质MNO AOB ∠=∠.由90ONM NMO ∠+∠=︒,可得90AOB NMO ∠+∠=︒,经计算∠OCM=90°即可; (3)如图,连接AN ,由15OM t =.,2ON t =,求出815BM t =-.,求出232NOM S t =△,9242ABM S t =-△,824ABON S t =+梯形由12AMN ABON S S =四边形△,知余下部分面积12NOM ABM ABON S S S +=梯形△△,构造方程()239124824222t t t +-=+,解之即可.【详解】解:(1)∵2t =,∴3cm OM =,4cm ON =,∵6cm AB =,8cm OB =, ∴3162OM AB ==,4182ON OB ==, ∴OM AB =ON OB, ∵90MON ABM ∠=∠=︒,∴∽MON ABO △△;(2)MN OA ⊥在运动过程中,15OM t =.,2ON t =.∵6AB =,8OB =. ∴4OM ON t AB OB ==. 又∵90MON ABO ∠=∠=︒, ∴Rt MON Rt ABO ∽△△.∴MNO AOB ∠=∠.∵90ONM NMO ∠+∠=︒,∴90AOB NMO ∠+∠=︒,∴∠OCM=90°,∴MN OA ⊥;(3)如图,连接AN ,∵15OM t =.,2ON t =,∴815BM t =-., ∴2113152222NOM S OM ON t t t =⋅=⨯⨯=.△, ()1981562422ABM S t t =⨯-⨯=-.△, ()12688242ABON S t t =+⨯=+梯形, ∵12AMN ABONS S =四边形△, ∴12NOM ABM ABON S S S +=梯形△△, ∴()239124824222t t t +-=+, 即231712022t t -+=, 解得3t =或83t =.∴当3t =或83t =时,12AMN ABON S S =四边形△.【点睛】本题考查三角形相似判定与性质,抓住三角形ANM 面积的2倍=四边形ABON 面积构造t 的方程是解题关键.25.(1)AMN ,证明见解析;(2)34 【分析】(1)根据矩形的性质和平行线的性质证明即可;(2)作NH AM ⊥于H ,证明NAH AMB ∆∆∽,根据相似三角形的性质得到212AN BM AM =,根据相似三角形的性质即可得到结论. 【详解】 解:(1)AMN ∆是等腰三角形,证明:四边形ABCD 是矩形,//AD BC ∴,NAM BMA ∴∠=∠,又AMN AMB ∠=∠,AMN NAM ∴∠=∠,AN MN ∴=,即AMN ∆是等腰三角形;(2)如图,延长AD 和ME ,交于点N ,作NH AM ⊥于H ,AN MN =,NH AM ⊥,12AH AM ∴=, 90NHA ABM ∠=∠=︒,AMN AMB ∠=∠, NAH AMB ∴∆∆∽,∴AN AH AM BM=, 212AN BM AH AM AM ∴==, M 为BC 中点,112BM CM BC ∴===, 2223110AM =+=,5AN ,523DN ∴=-=,设DE x =,则3CE x =-,//AN BC ,∴DN DE CM CE =,即313x x=-, 解得,94x =,即94DE =, 34CE ∴=.【点睛】本题考查的是相似三角形的判定和性质、勾股定理的应用以及等腰三角形的性质和矩形的性质,掌握相似三角形的判定定理和性质定理是解题的关键,注意方程思想的正确运用. 26.【分析】根据平行线分线段成比例定理,列出比例式求解即可得到答案.【详解】解:∵DE BC ∥,∴AD AE BD EC=. ∵6AD =,3DB =,4AE =, ∴643EC=. ∴2EC =.∴6AC AE EC =+=.【点睛】此题考查了平行线分线段成比例定理的运用,熟练利用平行线分线段成比例定理是解题关键.。
相似三角形常考综合题精练(11大题型)(原卷版)—2024-2025学年九年级数学上册(北师大版)

相似三角形常考综合题精练(11大题型)本讲目录链接题型01比例线段的应用题型02黄金分割题型03平行线分线段成比例定理题型04相似多边形的性质题型05相似三角形的性质与判定题型06相似三角形的实际应用题型07图形的位似题型08旋转背景下的相似三角形的性质与判定题型09折叠背景下的相似三角形的性质与判定题型10动点背景下的相似三角形的性质与判定题型11相似三角形的综合问题题型01比例线段的应用1.定义一个运算()()1212121212,,,,0n n n n nx x x H x x x y y y y y y y y y +++=+++¹+++L L L L L ,下列说法正确的有( )个①()1,231H =;②若()()24,41,21H x H x ---=-,则=1x -或2;③()()()()22217511,212,413,6110,20264H H H H ++++=L ;④若()()()(),,,,,,,,H a b c d H b a c d H c a b d H d a b c ===,则1c d a b +=+.A .1B .2C .3D .42.已知代数式x A y z =+,y B x z=+,z C x y =+,下列结论中,正确的个数是( )①若::1:2:3x y z =,则::2:5:10A B C =;②若A B C a ===,则一次函数1y ax =-的图像必过第一、三、四象限;③若x ,y ,z 均为正整数,且x y z <<,则A B C <<;④若1y =,2z =-,且x为方程21m =的一个实数根,则22182023y A B C +=+.A .1B .2C .3D .43.如图,已知在ABC V 中,点D F 分别为边AB BC AC 、、上的点,且AE BF CD 、、相交于点G ,如果2014AG BG CG GE GF GD ++=,那么AG BG CG GE GF GD ××的值为 .4.已知代数式x A y z =+,y B x z=+,z C x y =+,下列结论中,正确的个数是( )①若::1:2:3x y z =,则::2:5:10A B C =;②若()0A B C a a ===¹,则一次函数1y ax =-的图象必定经过第一、三、四象限;③若x ,y ,z 为正整数,且x y z <<,则A B C <<;④若1y =,2z =-,且x为方程21m =的一个实根,则2211A B +与82023C+的值相等;⑤若222x y zx yzxy yz zx z-+-=+++,222y z xy zxxy yz zx x-+-=+++()()()A AB B BC C C A-+-+-的值为28.A.1B.2C.3D.4题型02黄金分割5.我们把宽与长的比等于黄金比的矩形称为黄金矩形.如图,在黄金矩形ABCD()AB BC<中,ABCÐ的平分线交AD边于点E,EF BC^于点F,则下列结论错误的是()A.AE DEAD AE=B.CF BFBF BC=C.AE BEBE BC=D.DE ABEF BC=6.在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连接BE,延长DA至F,使得EF BE=,以AF为边作正方形AFGH,则点H 即是线段AB的黄金分割点.若20AD=,记正方形AFGH的面积为1S,矩形BCIH的面积为2S,则1S与2S 的和为.7.如图①,点C把线段AB分成两部分()AC BC>,若AC BCAB AC=,那么称点C为线段AB的黄金分割点.类似的,可以定义“黄金分割线”:直线l把一个面积为S的图形分成面积为1S和2S的两部分12()S S>,如果121S SS S=,那么称直线l为该图形的黄金分割线.(1)如图②,在ABC V 中,若点D 是线段AB 的黄金分割点()BD AD >,线段CD 所在直线是ABC V 的黄金分割线吗?为什么?(2)在(1)的条件下,如图③,过点C 作一条直线交BD 边于点E ,过点D 作DF EC ∥交ABC V 的一边于点F ,连接EF ,交CD 于点G ,回答问题.①CFG S V ______EDG S △(填“>”“<”或“=”).②EF 是ABC V 的黄金分割线吗?为什么?8.(1)在图①中按下列步骤作图:第一步:过点C 画CD AC ^,使12CD AC =;第二步:连接AD ,以点D 为圆心,DC 的长为半径画弧,交AD 于点E ;第三步:以点A 为圆心,AE 的长为半径画弧,交AC 于点B .(2)在所画图中,点B 是线段AC 的黄金分割点吗?为什么?(3)如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请你在图②中以线段AB 为腰,用直尺和圆规,作一个黄金三角形ABC .(不写作法,保留作图痕迹)9.请阅读下列材料,并完成相应的任务:公元前300著.黄金分割(goldensection )是指把一条线段分割为两部分,使较大部分与全长的比值等于较小部分与较大部分的比值.如图①,在线段AD 上找一个点C ,C 把AD 分为AC 和CD 两段,其中AC 是较小的一段,如果::AC CD CD AD =,那么称线段AD 被C 点黄金分割,点C 叫做线段AD 的黄金分割点,AC 与CD 的比值叫做黄金分割数.为简单起见,设1,AD CD x ==,则1AC x =-.∵::AC CD CD AD =,∴……任务:(1)请根据上面的部分解题过程,求黄金分割数.(2)如图②,采用如下方法可以得到黄金分割点:①设AB 是已知线段,过点B 作BD AB ^且使12BD AB =;②连接DA ,在DA 上截取DE DB =;③在AB 上截取AC AE =;则点C 即为线段AB 黄金分割点.你能说说其中的道理吗?(3)已知线段1AB =,点C ,D 是线段AB 上的两个黄金分割点,则线段CD 的长是 .10.材料一:北师大版数学教材九年级上册第四章,对“黄金分割比”的定义如下:“如图 ,点C 把线段AB 分成两条线段AC 和BC ,如果AC AB =BC AC ,那么称线段AB被点C 黄金分割,点C 叫做线段AB 的黄金分割点,AC AB .”根据定义不难发现,在线段AB 另有一点D 把线段AB 分成两条线段AD 和BD ,满足BD AB =AD BD ,所以点D 也是线段AB 的黄金分割点.材料二:对于实数:a 1<a 2<a 3<a 4,如果满足(a 3﹣a 1)2=(a 4﹣a 3)(a 4﹣a 1),(a 4﹣a 2)2=(a 2﹣a 1)(a 4﹣a 1)则称a 3为a 1,a 4的黄金数,a 2为a 1,a 4的白银数.请根据以上材料,回答下列问题(1)如图,若AB =4,点C 和点D 是线段AB 的黄金分割点,则AC = ,CD = .(2)实数0<a <b <1,且b 为0,1的黄金数,a 为0,1的白银数,求b ﹣a 的值.(3)实数k <n <m <t ,t =2|k |,m ,n 分别为k ,t 的黄金数和白银数,求m n 的值.11.根据以下素材,探索完成任务.题型03平行线分线段成比例定理12.如图,在正方形中,分别以点A 和为圆心,以大于的长为半径作弧,两弧相交于点和ABCD B 12AB E,作直线,再以点A 为圆心,以的长为半径作弧交直线于点(点在正方形内部),连接并延长交于点.若,则正方形的边长为( )AB .CD13.如图是一张矩形纸片,点为AD 中点,点在上,把该纸片沿折叠,点,的对应点分别为,,与相交于点,的延长线过点.若,则.14.如图,、,、分别是和的中点,过的直线依次交、、、于点、、、,求证:.15.如图,,点在上,过点作的平行线,与的平分线交于点,为的中点,点在上,(不与点重合),连接,将线段绕点顺时针旋转,得到线段,连接.F EF AD EFG G ABCD DG BC K 2BK =ABCD 1521ABCD E F BC EF A B A ¢B ¢A E ¢BC G B A ¢¢C 23BF GC =AD AB =AB CD ∥AD CE F G AC FD G AB AD CD CE M N P Q 2PQ PN +=OPQ a Ð=A PQ A PO OPQ ÐB M PB C PM P M ,AC AC A 180a °-AD BD(1)①直接写出线段与之间的数量关系;②用等式表示线段,,之间的数量关系,并证明;(2)连接并延长,分别交,于点,过点作的垂线,交于点.依题意补全图形,用等式表示线段,,之间的数量关系.16.四边形的两条对角线,相交于点O ,.(1)如图1,已知.①求证:;②若,求的值;(2)如图2,若,,,求的值.题型04相似多边形的性质17.如图,已知在矩形 中,,,点 从点 出发,沿 方向以每秒 个单位的速度向点 运动,点 从点 出发,沿射线 以每秒 个单位的速度运动,当点 运动AP AB BD BM MC DC AB PO E F ,M OP DC N CF CN NE ABCD AC BD 90BAD Ð=°AC CD =ACD BAC Ð=Ð225OC OA =OB OD 90BCD Ð=°AB AD =3CD BC =AC BDABCD AB 2=BC 6=E D DA 1A F B AB 3E到点 时,, 两点停止运动.连接 ,过点 作 ,垂足为 ,连接 ,交 于点 ,交 于点 ,连接 .给出下列结论:① ;② ;③ ;④ 的值为定值.上述结论中正确的个数为 ( )个.A.B .C .D .18.已知E、F 、G 、H 各点分别在四边形的、、、边上(如图).(1)当时,求证:(2)当上述条件中比值为3,4,…,n 时(为自然数),那么与之比是多少?19.如图1,矩形ODEF 的一边落在矩形ABCO 的一边上,并且矩形ODEF ∽矩形ABCO ,其相似比为1:4,矩形ABCO 的边AB =4,BC (1)求矩形ODEF 的面积;(2)将图1中的矩形ODEF 绕点O 逆时针旋转一周,连接EC 、EA ,ACE 的面积是否存在最大值或最小A E F BD E EH BD ^H EF BD G BC M CF CDE CBF V V ∽DBC EFC ÐÐ=DE HG AB EH=GH 1234ABCD AB BC CD DA 2AE BF CG DH EB FC GD HA ====59EFGH ABCDS S =四边形四边形n EFGH S 四边形ABCD S 四边形V值?若存在,求出最大值或最小值;若不存在,请说明理由.20,则称这条直线为该矩形的黄金线.例如图所示的矩形中,直线,分别交、于点、,且,显然直线是矩形的黄金线.(1)如图,在矩形中,,.请在图中画出矩形的其中一条黄金线,其中在边上,在边上,并标注出线段的长度;(2)将正方形纸片按图所示的方式折叠.如图所示,按上述方法折叠所得到的折痕是否为正方形的黄金线?请说明理由.ABCD EF BC^AD BC E F AE AB =EF ABCD ABCD 2AB = 3AD =ABCD MN M AD N BC AM GH ABCD(3)在矩形中,,,已知矩形的黄金线恰好将矩形分割成两个黄金矩形,则______(只要求直接写出其中三个答案).21.阅读下列材料,完成任务:自相似图形定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD 中,点E 、F 、G 、H 分别是AB 、BC 、CD 、DA 边的中点,连接EG ,HF 交于点O ,易知分割成的四个四边形AEOH 、EBFO 、OFCG 、HOGD 均为正方形,且与原正方形相似,故正方形是自相似图形.任务:(1)如图1中正方形ABCD 分割成的四个小正方形中,每个正方形与原正方形的相似比为________;(2)如图2,已知△ABC 中,∠ACB=90°,AC=4,BC=3,小明发现△ABC 也是“自相似图形”,他的思路是:过点C 作CD ⊥AB 于点D ,则CD 将△ABC 分割成2个与它自己相似的小直角三角形.已知△ACD ∽△ABC ,则△ACD 与△ABC 的相似比为________;(3)现有一个矩形ABCD 是自相似图形,其中长AD=a ,宽AB=b (a >b ).请从下列A 、B 两题中任选一条作答.A :①如图3﹣1,若将矩形ABCD 纵向分割成两个全等矩形,且与原矩形都相似,则a=________(用含b 的式子表示);ABCD 1AB =AD a =ABCD EF ABCD a=②如图3﹣2若将矩形ABCD 纵向分割成n 个全等矩形,且与原矩形都相似,则a=________(用含n ,b 的式子表示);B :①如图4﹣1,若将矩形ABCD 先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a=________(用含b 的式子表示);②如图4﹣2,若将矩形ABCD 先纵向分割出m 个全等矩形,再将剩余的部分横向分割成n 个全等矩形,且分割得到的矩形与原矩形都相似,则a=________(用含m ,n ,b 的式子表示).题型05相似三角形的性质与判定22.如图,在中,,以为边向三角形外作正方形,作于点,交对角线于点,连接.要求的周长,只需知道( )A .的长B .的长C .的长D .的长23.如图,,,,点E 在边上运动(不与端点重合),边始终过点A ,交于点G 是等腰三角形时,的面积是( ).A .8或B .8C.D .6或 24.由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.将小正方形对角线双向延长,分别交边AB ,和边的延长线于点,.若大正方形与小正方形的面积之比为,,则大正方形的边长为 .Rt ABC △90ACB Ð=°AB ABDE EF BC ^F AD G BG BFG V AC BC BF FG ABC DEF ≌△△5AB AC ==6BC EF ==BC DE EF AC AEG AEG △625108625108625107ABCD EF BC G H 5GH =25.如图,在正方形中,为边上的两个三等分点,点关于的对称点为,的延长线交于点.(1)求证:;(2)求的大小;(3)求证:.26.如图1,四边形是正方形,点E 在边的延长线上,点F 在边上,且,连接交于点P ,连接交于Q ,连接.(1)求证:;(2)连接,如图2,①若的长;②若,则 .27.平移图形是解答几何题目时一种重要的添加辅助线策略.如图①,在正方形中,E 、F 、G 分别是、、上的点,于点Q .求证:.小鹿在分析解题思路时想到了两种平移法:方法一:平移线段使点F 与点B 重合,构造全等三角形;ABCD E F ,AB A DE A ¢AA ¢BC G DE A F ¢∥GA B ¢Ð2A C A B ¢¢=ABCD BC AB AF CE =EF DC AC EF DE DF 、EQ FQ =BQ AQ DP ×=BQ FP FD =PE PQ=ABCD BC AB CD FG AE ^=AE FG FG方法二:平移线段使点B 与F 重合,构造全等三角形;【尝试应用】(1)请按照小鹿的思路,选择其中一种方法进行证明;(2)如图②,点E 、F 、G 、H 分别是矩形边、、、上的点,且,若,,求的值;【拓展探究】(3)如图③,点E 、F 分别是平行四边形边、上的点,连接、交于点G ,若,求证:.28.如图,,,.(1)如图1,不添加辅助线,请写出图中所有相似三角形;(2)如图2,若点E 落在边上,求证:;(3)如图3,若点H ,I ,J 分别为,AB ,AD 中点,判断与的数量关系及夹角度数(锐角).题型06相似三角形的实际应用29.将一本高为(即)的词典放入高(AB )为的收纳盒中(如图1).恰好能盖上盒盖时,测得底部F 离收纳盒最左端B 处,若此时将词典无滑动向右倒,书角的对应点恰为CD 中点.BC ABCD AB CD AD BC EF GH ^3AB =4BC =EF GHABCD AB AD CF DE 180B EGC Ð+Ð=°DE AD CF CD=90BAC AED ÐÐ==°AB AC =EA ED =BC 2222AD EF BF EF =+×BC IJ HE 17cm 17cm EF =16cm 8cm H H ¢(1)收纳盒的长 ;(2)现将若干本同样的词典放入此有盖的收纳盒中,如图2放置,则最多有本书可与边BC 有公共点.30.【问题探究】(1)如图①,在中,,,,将绕点逆时针旋转到的位置,点的对应点落在上,则的长为 ;(2)如图②,在矩形中,,,点是矩形的对称中心,点在边上,且,点是边上的动点,连接与,求的最大值;【问题解决】(3)有一块三角形草地,其示意图如图③所示,,,是一条小道(宽度不计),点是的中点,点在内,、两点之间的距离为,.市政府为丰富市民的业余生活,计划将部分草地改建,在、上分别找点、,在、处栽种梧桐树,,连接、,在.根据规划,现要沿线段修建一段文化长廊(宽度不计),为容纳更多的市民在文化长廊内活动,要求文化长廊的长度尽可能的长,当文化长廊的长最大时,请求出此时点的位置(即的长).31.BC =Rt ABC △90BAC Ð=°4AB=AC =ABC V C DEC V A D BC BD ABCD 2AB =6AD =O ABCD E AD 2AE =F BC EF OF EF OF -ABC 24cm AB BC ==90ABC Ð=°DE D BC E ABC V B E 13cm DE BC ^BC BA M N M N BM BN =EM EN EP EM =PN PN PN NBN32.在光学中,由实际光线会聚成的像,称为实像,而光线能会聚的是因为折射.图中,凸透镜的焦距为f ,主光轴,A ,B ,C ,D 都在l 上,其中O 是光心,,蜡烛(蜡烛可移动,EF l EF ^2OB OD f ==PQ l ^且),光线,其折射光线与另一条经过光心的光线相交于点()即为蜡烛在光屏上所成的实像.图中所有点都在同一平面内.记物高为h ,像高为,物距,像距为v .(1)若,,, .(2)求证.(3)当f 一定时,画出v 与u 之间的函数图象,并结合图象描述v 是怎么随着u 的变化而变化的?33.阅读理解:如图1,在△ABC 中,当DE ∥BC 时可以得到三组成比例线段:① ;② ;③ .反之,当对应线段成比例时也可以推出DE ∥BC .理解运用:三角形的内接四边形是指顶点在三角形各边上的四边形.(1)如图2,已知矩形DEFG 是△ABC 的一个内接矩形,将矩形DEFG 沿CB 方向向左平移得矩形PBQH ,其中顶点D 、E 、F 、G 的对应点分别为P 、B 、Q 、H ,在图2中画出平移后的图形;(2)在(1)所得的图形中,连接CH 并延长交BP 的延长线于点R ,连接AR .求证:AR ∥BC ;(3)如图3,某小区有一块三角形空地,已知△ABC 空地的边AB =400米,BC =600米,∠ABC =45°;准备在△ABC 内建一个内接矩形广场DEFG (点E 、F 在边BC 上,点D 、G 分别在边AB 和AC 上),三角形其余部分进行植被绿化,按要求欲使矩形DEFG 的对角线EG 最短,请在备用图中画出使对角线EG 最短距离(不要求证明).34.阅读理解:如图1,AD 是△ABC 的高,点E 、F 分别在AB 和AC 边上,且EF BC ,可以得到以下结论:.OQ f >PG l ∥GC PP ¢P ¢P Q l ¢¢^()PQ ()P Q ¢¢h ¢()OQ ()OQ ¢10cm f =10cm h =15cm u ==v cm 111u v f+=()u f >AD AE DE AB AC BC ==AD AE BD CE =BD CE AB AC=//AH EF AD BC=拓展应用:(1)如图2,在△ABC中,BC=3,BC边上的高为4,在△ABC内放一个正方形EFGM,使其一边GM在BC 上,点E、F分别在AB、AC上,则正方形EFGM的边长是多少?(2)某葡萄酒庄欲在展厅的一面墙上,布置一个腰长为100cm,底边长为160cm的等腰三角形展台.现需将展台用隔板沿平行于底边,每间隔10cm分隔出一排,再将每一排尽可能多的分隔成若干个无盖正方体格子,要求每个正方体格子内放置一瓶葡萄酒.平面设计图如图3所示,将底边BC的长度看作是0排隔板的长度.①在分隔的过程中发现,当正方体间的隔板厚度忽略不计时,每排的隔板长度(单位:厘米)随着排数(单位:排)的变化而变化.请完成下表:排数/排0123…隔板长度/厘米160__________________…若用n表示排数,y表示每排的隔板长度,试求出y与n的关系式;②在①的条件下,请直接写出该展台最多可以摆放多少瓶葡萄酒?35.阅读以下文字并解答问题:在“测量物体的高度”活动中,某数学兴趣小组的3名同学选择了测量学校里的三棵树的高度,在同一时刻的阳光下,他们分别做了以下工作:小芳:测得一根长为1米的竹竿的影长为0.8米,甲树的影长为4.08米(如1图).小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如2图),墙壁上的影长为1.2米,落在地面上的影长为2.4米.小明:测得丙树落在地面上的影长为2.4米,落在坡面上影长为3.2米(如3图).身高是1.6米的小明站在坡面上,影子也都落坡面上,小芳测得他的影长为2米.(1)在横线上直接填写甲树的高度为______米,乙树的高度为________米﹔(2)请求出丙树的高度.36.【问题背景】人教版九年级下册教材第58页第11题:如图1,一块材料的形状是锐角三角形,边,高.把它加工成正方形零件,使正方形的一边在上,其余两个顶点分别在上,这个正方形零件的边长是多少?【提出问题】在满足正方形的一边在三角形的一边上,其余两个顶点分别在另外两边上的条件下,能否在上面的材料上,加工一个面积更大的正方形?如何用直角尺(只能画直角)和圆规画出这个正方形?【分析问题】小敏认为,由于正方形的一边在三角形的一边上,这样就存在三种可能.在已知三边长度的情况下,可以通过计算,分别求出三个正方形的边长,然后比较三条边长的大小,进而知道面积最大的正方形;也可以结合当前所学的位似,分别画出满足条件的正方形,再利用圆规比较三个正方形的边长的大小,即可解决问题.【解决问题】为了简化探索过程,小敏取边长分别为的三个等腰三角形(其中为腰)木块进行研究.如图2,正方形的顶点分别在上,边在上.如图3,正方形的顶点分别在上,边在上.请你完成下面两个问题:(1)通过计算,比较这两个正方形的边长的大小;(2)在图4中,用直角尺(只能画直角)和圆规画出面积最大的正方形,使其一边在三角形的一边上,其ABC 120mm BC =80mm AD =BC AB AC,556cm cm cm ,,AB AC ,EFGH E H ,AB AC ,FG BC MNPQ M N ,AB BC ,PQ AC余两个顶点分别在另外两边上(保留画图痕迹).【学以致用】定义:由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.小敏类比上面的研究方法,又提出下面问题:在如图5所示的扇形中,能否用直角尺和圆规画出一个正方形,使其两个顶点在弧上,另外两个顶点在半径上?你认为可以吗?如果可以、在图中画出符合条件的正方形(保留画图痕迹);如果不可以,说明理由.题型07图形的位似37.如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.A ,B ,C 三点是格点,点P 在上,仅用无刻度的直尺在给定网格中完成画图.(1)在图(1)中,将线段沿的方向平移,使点B 与点C 重合,画出平移后的线段;再将绕的中点顺时针旋转,得到,画出线段;(2)在图(2)中,连接,将以C为位似中心缩小为原来的得到,画出;88´BC AB BC CD PC AC 180°GA GA AP APC △12EFC V EFC V(3)在图(3)中,在上画一点M ,在AB 上画一点N ,使得最小.38.(1)在正方形方格纸中,我们把顶点都在“格点”上的三角形称为“格点三角形”,如图,△ABC 是一个格点三角形,点A 的坐标为(-2,2).①△ABC 的面积为______;②在所给的方格纸中,请你以原点O 为位似中心,将△ABC 缩小为原来的一半;(仅用直尺完成作图)③在(2)中,若P (a ,b )为线段AC 上的任一点,则缩小后点P 的对应点P 1的坐标为______.(2)按要求作图,不要求写作法,但要保留作图痕迹:我们知道,三角形具有性质:三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高所在直线相交于一点.请运用上述性质,只用直尺(不带刻度)作图.AC PM PN+①如图1,在平行四边形ABCD 中,E 为CD 的中点,作BC 的中点F .②如图2,在由小正方形组成的4×3的网格中,△ABC 的顶点都在小正方形的顶点上,作△ABC 的高AH .39.如图①,在中,,,点D 是上一点,且.动点F 从点C 出发沿方向以每秒2个单位长度的速度向经点B 运动,以为边构造等腰直角三角形,其中F 为直角顶点,且点E 与点B 位于线段两侧.设点F 的运动时间为t (秒).AI(1)求线段的长度;(2)当点E 落在的中位线上时,求出t 的值:(3)连接,则线段的最小值是______.(4)如图②.以点B 为位似中心,将缩小后得到,且.连接,当与的某条边平行时,直接写出t 的值.题型08旋转背景下的相似三角形的性质与判定40.定义:如果将一个三角形绕着它的一个角的顶点旋转后,使这个角的一边与另一边重叠,再将所旋转后的三角形进行相似缩放,使重叠的两条边相互重合,我们称这样的图形变换为三角形转似,这个三角形的顶点称为转似中心,所得的三角形称为原三角形的转似三角形.如图,在中,,是以点为转似中心的顺时针的一个转似三角形,那么以点A 为转似中心的逆时针的另一个转似三角形 (点分别与对应),其中边的长为Rt ABC △9AB =12BC =AB 2AD BD =CB DF DEFDF AC Rt ABC △CE CE DEF V D E F ¢¢¢△3DF D F ¢¢=E C ¢E C ¢Rt DEF △ABC V 465AB AC BC ===,,AB C ¢¢△ABC V A AB C ¢¢¢¢△B C ¢¢¢¢,B C 、B C ¢¢¢¢41.在矩形中,点是对角线、的交点,直角的顶点与重合,、分别与、边相交于、,连接,(为常数).(1)发现问题:如图1,若,猜想:________;(2)类比探究:如图2,,探究线段,之间的数量关系,并说明理由;(3)拓展运用:如图3,在(2)的条件下,若,的长.42.综合与实践.问题情境:综合与实践课上,同学们开展了以“图形的旋转”为主题的数学活动.实践操作:如图1,将等腰Rt △AEF 绕正方形ABCD 的顶点A 逆时针方向旋转,其中∠AEF =90,EA =EF ,连接CF ,点H 为CF 的中点,连接HD ,HE ,DE ,得到△DHE .应用探究:(1)勤奋组:如图2,当点E 恰好落在正方形ABCD 的对角线AC 上时,判断△DHE 的形状,并说明理由;(2)善思组:如图3,当点E 恰好落在正方形ABCD 的边AB 上时,(1)中的结论还成立吗?请说明理由;深入探究:(3)创新小组:ABCD O AC BD EPF ÐP O OE OF AB BC E F EF BC k AB =×k 1k =OE OF=1k ¹OE OF FO FC =k OD =EF发现若连接BE ,在旋转Rt △AEF 的过程中,为定值,请你直接写出其值 .43.数学课上,有这样一道探究题.如图,已知中,AB =AC =m ,BC =n ,,点P 为平面内不与点A 、C 重合的任意一点,将线段CP 绕点P 顺时针旋转a ,得线段PD ,E 、F 分别是CB 、CD 的中点,设直线AP 与直线EF 相交所成的较小角为β,探究的值和的度数与m 、n 、α的关系,请你参与学习小组的探究过程,并完成以下任务:(1)填空:【问题发现】小明研究了时,如图1,求出了___________,___________;小红研究了时,如图2,求出了___________,___________;【类比探究】他们又共同研究了α=120°时,如图3,也求出了;【归纳总结】最后他们终于共同探究得出规律:__________(用含m 、n 的式子表示);___________ (用含α的式子表示).(2)求出时的值和的度数.BE CFABC V ()0180BAC a a Ð=°<<°EF AP b 60a =°EF PA =b =90a =°EF PA =b =EF PA EF PA =b =120a =°EF PAb44.在学习完《图形的旋转》后,数学小组的同学们展开了新的探究.(1)【问题初探】如图1,在中,点D 在边上,交于点E .绕点A 逆时针旋转得到(点D 的对应点为点,点E 的对应点为点),连接,,得到和,如图2,数学小组的同学们发现.请你帮助他们证明这一发现.(2)【问题应用】如图3,中,,,,M ,N 分别为边与的中点.绕点C 旋转,点M 的对应点为点E ,点N F ,直线与直线交于点G .①如图4,当点E 落在线段AF 上时,求证:;②当点A ,E ,F 三点在同一条直线上时,直接写出的长.(3)【问题拓展】如图5,在(2)条件下,连接,取中点K ,取中点H ,请直接写出的最大值为___________.题型09折叠背景下的相似三角形的性质与判定45.在边长为4的正方形中,E 是边上一动点(不与端点重合),将沿翻折,点A 落在点H 处,直线交于点F ,连接,,分别与AC 交于点P 、Q ,连接,.则以下结论中正确的有________ (写出所有正确结论的序号).①;②;③;④为等腰直角三角形;⑤若连接,则的最小值为.ABC V AB DE BC ∥AC ADE V AD E ¢¢△D ¢E ¢BD ¢CE ¢ABD ¢△ACE ¢V ABD ACE ¢¢△∽△Rt ABC V 90ACB Ð=°6AC =8BC =AC BC CMN V EF BC 90BFE Ð=°BG AF AF EB HK ABCD AD ABE V BE EH CD BF BE BF PD PF =PB PD 2EFD FBC Ð=ÐPQ AP QC =+BPF △DHDH 446.如图,正方形的边长为6,点P 是边上的动点,将沿折叠得到,射线与边和射线的延长线交于F ,E 点.(1)如图①,若四边形是平行四边形,求证:;(2)如图②,当时,求的长;(3)如图③,当时,求的面积.47.如图①,在中,,动点D 从点C 出发沿以每秒5个单位长度的速度向终点A 从点A 出发沿以每秒3个单位长度的速度向终点B 运动.设点D 运动的时间是t 秒.过点D 作于点F ,连结.(1) , ;(用含t 的代数式表示)(2)当四边形是菱形时,t 的值为 ;ABCD BC ABP V AP APB ¢V AB ¢DCBC APED DF EF =DF 2CF =BP FB CF ¢=DFE △Rt ABC △90159ABC AC AB Ð=°==,,CA AB ()03t <<DF BC ^DE EF、AE =AD =AEFD(3)当垂直于的一边时,求t 的值;(4)如图②,将沿翻折,点A 的对应点为点,直接写出点在外部时t 的取值范围.48.在矩形中,点E ,F 分别在边AD ,上,将矩形沿折叠,使点A 的对应点P 落在边CD 上,点B 的对应点为点G ,交于点H .(1)如图1,求证:;(2)如图2,当P 为CD 的中点,,时,求的长;(3)如图3,连接,当P ,H 分别为CD ,的中点时,探究与AB 的数量关系,并说明理由.49.(1)【动手操作】如图1,将正方形沿直线折叠,使点的对应点M 始终落在边上(点M 不与点A ,D 重合),点C 落在点N 处,与交于点P ,折痕分别与边,交于点,,连接.求证:;(2)【问题探究】在图1中,若正方形的边长为,当点运动到的中点时,求的长;(3)【拓展延伸】如图2,若把(1)【动手操作】中的正方形改成矩形,且,其中,其他条件不变,若,直接写出折痕的长度的取值范围是______.(用含m 的式子表示)题型10动点背景下的相似三角形的性质与判定50.如图,在矩形中,厘米,厘米.点沿AB 边从开始向点以厘米/秒的速度移动;同时点沿边从点开始向点以厘米/秒速度移动,用(秒)表示移动的时间().DE ABC V DEA △DE A ¢A ¢ABC V ABCD BC ABCD EF PGBC DEP CPH △∽△2AB =3AD =GH BG BC BG ABCD EF B AD MN CD AB CD E F BM BM EF=ABCD 3P CD MD ABCD ABCD AB mAD =1m ³2AD =EF ABCD 12AB =6BC =P A B 2Q DA D A 1t 06t ££。
北师大版九年级数学上册相似三角形判定定理的证明测试题

4.5 相似三角形判定定理的证明一、选择题1.下列语句正确的是( )A.在 △ABC 和△A′B′C′中,∠B=∠B′=90°,∠A=30°,∠C′=60°, 则⊿ABC 和⊿A′B′C′不相似;B.在⊿ABC 和⊿A′B′C′中,AB=5,BC=7,AC=8,A′C ′=16,B′C′=14,A′B ′=10, 则⊿ABC ∽⊿A′B′C′;C.两个全等三角形不一定相似;D.所有的菱形都相似2.如图,在正三角形ABC 中,D 、E 分别在AC 、AB 上,且AC AD =31,AE =BE ,则有( )A.△AED ∽△BEDB.△AED ∽△CBDC.△AED ∽△ABDD.△BAD ∽△BCD( 3题 ) (4题)3.已知:如图,∠ADE =∠ACD =∠ABC ,图中相似三角形共有( ) A.1对 B.2对 C.3对 D.4对4.三角形三边之比为3:5:7,与它相似的三角形的最长边为21cm,则其余两边之和为( ) A.32cm B.24cm C.18cm D.16cm5.可以判定∆ABC ∽'''C B A ∆,的条件是 ( ) A.∠A=∠'C =∠'BB.''''C A B A AC AB =,且∠A=∠'C C.''''C A ACB A AB =且∠A=∠'BD.以上条件都不对 二、填空题6. 已知一个三角形三边长是6cm ,7.5cm ,9cm ,另一个三角形的三边是8cm ,10cm ,12cm ,则这两个三角形 (填相似或不相似)7. 如图,平行四边形ABCD 中,M 是BC 的中点,且AM=9,BD=12,AD=10,则该平行四边形的面积是_____________8.四边形ABCD ∽四边形A ,B ,C ,D , ∠A=70度,∠B ,=108度,∠C ,=92度 则∠D=_______9.在平行四边形ABCD 中,AB=10,AD=6,E 是AD 的中点,在AB 上取一点F ,使⊿CBF ∽⊿CDE ,则BF 的长三、计算题10.已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.求证:⊿ADQ∽⊿QCP.11. ⊿AB C中,AD、CE 是中线, ∠BAD=∠BCE,请猜想⊿ABC的形状,并证明.AED CB参考答案一、选择题1.B2.B3.C4.B5.D 二、填空题6.相似7.728.∠D=9009.1.8三、10.证明(主要步骤)有正方形性质及已知得PC=BC=CD ,DQ=CD ,即:DQ:PC=2:1QC:AD=2:1 加上直角相等可证相似。
九年级数学上册第四章《图形的相似》测试卷-北师大版(含答案)
九年级数学上册第四章《图形的相似》测试卷-北师大版(含答案)(满分120分)一、选择题(每题3分,共30分)1.若两个相似三角形的面积之比为4 :9,则它们对应角的平分线之比为()A. 49B.32C.23D.622.下列各组线段中,能成比例的是()A. 1c m,3c m,4c m,6c m,B. 1c m,3c m,4c m,12c m,C. 1c m,2c m,3c m,4c m,D. 2c m,3c m,4c m,5c m,3.下列说法中,正确的是()A.相似三角形都是全等三角形B.所有的矩形都相似C.所有的等腰三角形都相似D.所有的等腰直角三角形都相似4.如图,DE// BC ,A D = 2BD,下列结论错误的是()A. A E=2CEB. BC=2DEC. DE:BC=2:3D. C△A D E:C△ABC=2 :35.在比例尺1:10000的地图上,相距2C m的两地的实际距离是()A.200c mB.200 d mC.200 mD.200 km6.如图,l//l2//l3,两条直线与这三条平行线分别交于点A,B,C和D,E,F,已知32ABBC=,则DEDF的值为()A. 32B.23.C.25D.357.下列四个三角形,与左图中的三角形相似的是()8.△ABC与△DEF相似,且相似比是23.,反之,△DEF与△ABC的相似比是()A. 23. B.32C.25D.499.如图,由下列条件不能判定△ABC与△A D E相似的是()A. AE ACAD AB= B.∠B=∠A D EC. AE DEAC BC= D.∠C=∠A E D10.小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为()A.10米B.12米C.15米D.22.5米二、填空题(每题4分,共28分)。
11.若1a+b,2ab b==则_____________。
北师大版九年级数学上册《相似三角形》压轴练习题(附答案)
北师大版九年级数学上册《相似三角形》压轴练习题(附答案)一综合题1.在如图的方格纸中△OAB的顶点坐标分别为O(0,0),A(−2,−1),B(−1,−3)△O1A1B1与△OAB是关于点P为位似中心的位似图形.( 1 )在图中标出位似中心P的位置并直接写出点P的坐标为.( 2 )以原点O为位似中心在位似中心的同侧画出△OAB的一个位似△OA2B2使它与△OAB的位似比为2:1;( 3 )△OAB的内部一点M的坐标为(a,b)直接写出点M在△OA2B2中的对应点M2的坐标为.2.(2022九上·济南期末)如图1 长宽均为3cm 高为8cm的长方体容器放置在水平桌面上里面盛有水水面高为6cm 绕底面一棱进行旋转倾斜后水面恰好触到容器口边缘图2是此时的示意图将这个情景转化成几何图形如图3所示.(1)利用图1 图2所示水的体积相等求DE的长;(2)求水面高度CF.3.(2022九上·济南期末)如图点F是平行四边形ABCD的边AD上的一点直线CF交线段BA的延长线于点E.(1)求证:△AEF∽△DCF;(2)若AF:DF=1:2,AE=√2①求AB的长;②求△EBC的面积.4.(2022九上·济南期末)如图直线y=k1x+b与双曲线y=k2x交于A B两点已知点A的横坐标为−3点B的纵坐标为−3直线AB与x轴交于点C 与y轴交于点D(0,−2),tan∠AOC=13.(1)求双曲线和直线AB的解析式;(2)若点P是第二象限内反比例函数图象上的一点△OCP的面积是△ODB的面积的3倍求点P的坐标.(3)若点E在x轴的负半轴上是否存在以点E C D为顶点构成的三角形与△ODB相似?若存在求出点E的坐标;若不存在请说明理由.5.如图AD、BE是ΔABC的高连接DE.(1)求证:ΔACD∽ΔBCE;(2)若点D是BC的中点CE=3,BE=4求AB的长.6.(2022九上·平阴期中)如图在直角三角形ABC中直角边AC=3cm,BC=4cm.设P Q分别为AB BC上的动点在点P自点A沿AB方向向B作匀速移动的同时点Q自点B沿BC方向向点C作匀速移动它们移动的速度均为每秒1cm 当Q点到达C点时P点就停止移动.设P Q移动的时间t 秒.(1)当t为何值时△PBQ是以∠B为顶角的等腰三角形?(2)△PBQ能否与直角三角形ABC相似?若能求t的值;若不能说明理由.7.(2022九上·济南期中)(1)[问题背景]如图①已知△ABC∽△ADE求证:△ABD∽△ACE.(2)[尝试应用]如图②在△ABC和△ADE中∠BAC=∠DAE=90°,∠ABC=∠ADE=30°,AC与DE相交于点F 点D在BC边上ADBD=√3.①填空:AEBD=;②求DFCF的值.8.(2022九上·章丘期中)如图在正方形ABCD外取一点E 连接DE AE CE过点D作DE的垂线交AE于点P 交AB于点Q DE=DP=1,PC=2√5.(1)求证:①△APD≌△CED;②求∠AEC的大小;(2)求正方形ABCD的面积;(3)求线段PQ的长.9.如图Rt△ABC,∠C=90°,AC=10cm,BC=8cm.点P从点C出发以2cm/s的速度沿CA向点A匀速运动同时点Q从点B出发以1cm/s的速度沿BC向点C匀速运动设点P Q运动时间为t 当一个点到达终点时另一个点随之停止.(1)求经过几秒后△PCQ的面积等于16cm2?(2)经过几秒△PCQ与△ABC相似?(3)①是否存在t 使得△PCQ的面积等于20cm2?若存在请求出t的值若不存在请说明理由;②设四边形APQB的面积为S 请直接写出....S的最大值或最小值.10.(2022九上·济南期中)小明和几位同学做手的影子游戏时发现对于同一物体影子的大小与光源到物体的距离有关.因此他们认为:可以借助物体的影子长度计算光源到物体的位置.于是他们做了以下尝试.(1)如图1 垂直于地面放置的正方形框架ABCD边长AB为30cm在其上方点P处有一灯泡在灯泡的照射下正方形框架的横向影子A′B D′C的长度和为6cm.那么灯泡离地面的高度PM为多少.(2)不改变图1中灯泡的高度将两个边长为30cm的正方形框架按图2摆放请计算此时横向影子A′B D′C的长度和为多少?11.(2022九上·长清期中)如图一路灯AB与墙OP相距20米当身高CD=1.6米的小亮在离墙17米的D 处时影长DG为1米.(1)求路灯B的高度;(2)若点P为路灯请画出小亮位于N处时在路灯P下的影子NF(用粗线段表示出来)12.(2022九上·长清期中)如图△ABC的三边长分别为a b c(a>b>c)△A1B1C1的三边长分别为a1、b1、c1.已知△ABC∽△A1B1C1相似比为k(k>1).(1)若c=a1=2a=5求c1的值.(2)若c=a1求证:a=kc;(3)若c=a1试给出符合条件的一对△ABC和△A1B1C1使得a b c和a1、b1、c1都是正整数;(4)若b=a1,c=b1是否存在△ABC和△A1B1C1使得k=2?并请说明理由.13.(2021九上·槐荫期中)在平面直角坐标系中∽ABC的顶点坐标分别为A(0 2)B(1 3)C (2 1).(1)以点O为位似中心在给定的网格中画出∽A'B'C' 使∽A'B'C'与∽ABC位似且相似比为2;(2)求出∽A'B'C'的面积.14.(2021九上·槐荫期中)请阅读以下材料并完成相应的问题:角平分线分线段成比例定理如图1 在∽ABC中AD平分∽BAC 则ABAC=BDCD.下面是这个定理的部分证明过程.证明:如图2 过点C作CE∥DA.交BA的延长线于点E.…(1)任务:请按照上面的证明思路写出该证明过程的剩余部分;(2)如图3 已知Rt∽ABC中AB=3 BC=4 ∽ABC=90° AD平分∽BAC 求∽ABD的周长.15.已知点E在∽ABC内∠ABC=∠EBD=α∽ACB=∽EDB=60° ∽AEB=150° ∽BEC=90°.(1)当α=60°时(如图1)①判断∽ABC的形状并说明理由;②求证:AEBD=tan∠CED;(2)当α=90°时(如图2)②的结论还成立吗?若成立说明理由;若不成立求出AEBD的比值.16.(2021九上·商河期末)如图已知点C D在线段AB上且AC=4 BD=9 ∽PCD是边长为6的等边三角形.(1)求证:∽PAC∽∽BPD;(2)求∽APB的度数.17.在△ABC中AB=AC,∠BAC=90°点D E分别是AC,BC的中点点P是射线ED上一点连接AP将线段PA绕点P顺时针旋转90°得到线段PM连接AM,CM.(1)问题发现如图(1)当点P与点D重合时线段CM与PE的数量关系是∠ACM=.(2)探究证明当点P在射线ED上运动时(不与点E重合)(1)中结论是否一定成立?请仅就图(2)中的情形给出证明.(3)问题解决若AC=√2+√6连接PC当△PCM是等边三角形时直接写出PE的长度.18.(2022九上·章丘期中)如图1四边形ABCD和四边形AMPN有公共顶点A(1)如图2 若四边形ABCD和四边形AMPN都是正方形当正方形AMPN绕点A逆时针旋转α角(0°<α<180°)时BM和DN的数量关系是位置关系是;(2)如图3 若四边形ABCD和四边形AMPN都是矩形且ABAD=AMAN=1√3判断BM和DN的数量关系和位置关系并说明理由;(3)在(2)的条件下若AB=2AM=1矩形AMPN绕点A逆时针旋转α角(0°<α<180°)当MN∥AB时求线段DN的长.19.(2022九上·济南期中)如图在平面直角坐标系中C(8,0)B(0,6)是矩形ABOC的两个顶点点D是线段AB上的一个动点(不与A、B重合) 双曲线y=kx(k>0)经过点D 与矩形ABOC的边AC相交于点E.(1)如图①当点D为AB中点时k的值为点E的坐标为;(2)如图②当点D在线段AB上的任意位置时(不与A、B重合) 连接BC、DE求证:BC∥DE;(3)是否存在反比例函数上不同于点D的一点F 满足:△ODF为直角三角形∠ODF=90°且tan∠DOF=13若存在请直接写出满足以上条件时点D的横坐标若不存在请说明理由.20.(2022九上·济南期中)如图①已知在正方形ABCD中点E是边BC的中点以BE为斜边构造等腰直角△BEF将△BEF绕点B在平面内作逆时针旋转.(1)如图②当∠EBC=30°时若CG=√2则BG=;AG=;(2)如图③延长BE与AC、DC分别相交于点G、N延长BF与AC、AD分别相交于点H、M求证:△AMH∽△CGN;(3)如图④连接CE、DE请直接写出当√2DE+4CE取得最小值时∠ECB的正切值.21.如图RtΔABC中∠C=90°AB=10BC=6D是AB的中点动点P从点A出发沿线段AC以每秒2个单位长度的速度向终点C运动设点P的运动时间为t秒.(1)当t为多少秒时以点A D P为顶点的三角形与ΔABC相似?(2)若ΔAPD为钝角三角形请直接写出t的取值的范围.22.(2022九上·历城期中)如图:(1)【问题初探】如图1 ΔABC中∠BAC=90°AB=AC点D是BC上一点连接AD以AD为一边作ΔADE使∠DAE=90°AD=AE连接BE BE与CD的数量关系位置关系.(2)【类比再探】如图2 ΔABC中∠BAC=90°AB=AC点M是AB上一点点D是BC上一点连接MD以MD 为一边作ΔMDE使∠DME=90°MD=ME连接BE求∠EBD的度数.(3)【方法迁移】如图3 RtΔABC中∠BAC=90°∠ACB=30°BC=6点M是AB中点点D是BC上一点且BD=1连接MD以MD为一边作ΔMDE使∠DME=90°MD=√3ME连接BE求BE的长.23.在∽ABC中∽ACB=90° ∽BAC=60° 点D在斜边AB上且满足BD=13AB 将线段DB绕点D逆时针旋转至DE 记旋转角为α 连接AE BE 以AE为斜边在其一侧作直角三角形AEF 且∽AFE=90° ∽EAF=60° 连接CF.(1)如图1 当α=180°时请直接写出线段BE与线段CF的数量关系;(2)当0°<α<180°时①如图2 (1)中线段BE与线段CF的数量关系是否仍然成立?诸说明理由;②如图3 当B E F三点共线时连接CE 判断∽CEF的形状并证明.24.如图(1)问题如图1 在四边形ABCD中点P为AB上一点当∠DPC=∠A=∠B=90°时求证:AD⋅BC= AP⋅BP.(2)探究若将90°角改为锐角或钝角(如图2)其他条件不变上述结论还成立吗?说明理由.(3)应用如图3 在△ABC中AB=2√2∠B=45°以点A为直角顶点作等腰Rt△ADE.点D在BC上点E在AC上点F在BC上且∠EFD=45°若CE=√5求CD的长.25.如图(1)如图1 正方形ABCD与调研直角∽AEF有公共顶点A ∽EAF=90° 连接BE DF 将∽AEF绕点A旋转在旋转过程中直线BE DF相交所成的角为β 则BEDF=;β=;(2)如图2 矩形ABCD与Rt∽AEF有公共顶点A ∽EAF=90° 且AD=2AB AF=2AE 连接BE DF 将Rt∽AEF绕点A旋转在旋转过程中直线BE DF相交所成的角为β 请求出BEDF的值及β的度数并结合图2进行说明;(3)若平行四边形ABCD与∽AEF有公共顶点A 且∽BAD=∽EAF=α(0°<α<180°) AD=kAB AF=kAE(k≠0) 将∽AEF绕点A旋转在旋转过程中直线BE DF相交所成的锐角的度数为β则:①BEDF=;②请直接写出α和β之间的关系式.26.(2021九上·槐荫期末)在平面直角坐标系中 已知OA =10cm OB =5cm 点P 从点O 开始沿OA 边向点A 以2cm/s 的速度移动;点Q 从点B 开始沿BO 边向点O 以1cm/s 的速度移动.如果P Q 同时出发 用t (s )表示移动的时间(0≤t≤5)(1)用含t 的代数式表示:线段PO = cm ;OQ = cm .(2)当t 为何值时∽POQ 的面积为6cm 2?(3)当∽POQ 与∽AOB 相似时 求出t 的值.27.如图(1)感知:数学课上 老师给出了一个模型:如图1 ∠BAD =∠ACB =∠AED =90° 由∠1+∠2+∠BAD =180° ∠2+∠D +∠AED =180° 可得∠1=∠D ;又因为ACB =∠AED =90° 可得△ABC ∽△DAE 进而得到BC AC= .我们把这个模型称为“一线三等角”模型.(2)应用:实战组受此模型的启发 将三等角变为非直角 如图2 在△ABC 中 AB =AC =10 BC =12 点P 是BC 边上的一个动点(不与B C 重合) 点D 是AC 边上的一个动点 且∠APD =∠B .①求证:△ABP ∽△PCD ;②当点P 为BC 中点时 求CD 的长;(3)拓展:在(2)的条件下如图2 当△APD 为等腰三角形时 请直接写出BP 的长.28.如图1 在Rt∽ABC 中 ∽BAC=90° ∽ACB=60° AC=2 点A 1 B 1为边AC BC 的中点 连接A 1B 1 将∽A 1B 1C 绕点C 逆时针旋转α(0°≤α≤360°).(1)如图1 当α=0°时BB1AA1=BB1AA1所在直线相交所成的较小夹角的度数为;(2)将∽A1B1C绕点C逆时针旋转至图2所示位置时(1)中结论是否仍然成立?若成立请给出证明;若不成立请说明理由;(3)当∽A1B1C绕点C逆时针旋转过程中①请直接写出∽ABA1面积的最大值;②当A1B1B三点共线时请直接写出线段BB1的长.答案解析部分1.【答案】解:∽如图 点P 为所作;故答案为:(−5,−1);∽如图 △OA 2B 2为所作;∽(2a ,2b).2.【答案】(1)解:如图所示设DE=xcm 则AD=(8-x )cm根据题意得:12(8-x+8)×3×3=3×3×6 解得:x=4 ∴DE=4(cm )(2)解:∵∽E=90° DE=4 CE=3∴CD=5∵∽BCE=∽DCF=90°∴∽DCE+∽DCB=∽BCF+∽DCB∴∽DCE=∽BCF∵∽DEC=∽BFC=90°∴∽CDE∽∽CBF∴CE CF =CD CB 即3CF =58∴CF=245(cm )答:CF 的高是245cm 3.【答案】(1)证明:∵平行四边形ABCD 中 AB ∥CD∴AE ∥CD∴∠E =∠FCD ∠EAF =∠D∴△AEF ∽△DCF .(2)解:①∵△AEF ∽△DCF∴AE DC =AF DF∵AF :DF =1:2∴CD =2√2∵四边形ABCD 是平行四边形ABCD∴AB =CD =2√2.②∵四边形ABCD 是平行四边形ABCD∴AD ∥BC∴△EAF ∽△EBC∴S △EAF S △EBC =(EA EB )2=(√2√2+2√2)2=19 ∵S △AEF =23∴△EBC 的面积为6.4.【答案】(1)解:如图 过点A 作AF∽x 轴于点F∵tan∠AOC =13=AF OF 且点A 的横坐标为-3 ∴OF =3∴AF =1∴A(−3,1)∵双曲线y =k 2x过A 点 ∴1=k 2−3解得 k =−3 ∴双曲线的解析式为y =−3x将A(−3,1) D(0,−2)代入直线y =k 1x +b 得{1=−3k 1+b −2=b 解得{k 1=−1b =−2∴直线AB 的解析式为:y =−x −2(2)解:如图 连接OB PO PC当y =−x −2=0时∴C(−2,0)∴OC =2∵D(0,−2)∴OD =2∵点B 的纵坐标为−3∴−3=−x −2∴x =1∴B(1,−3)∵△OCP 的面积是△ODB 的面积的3倍∴12⋅OC ⋅y P =3⋅12⋅OD ⋅x B即12×2⋅y P=3×12×2×1解得yP=3即y=−3x=3∴x=−1∴P(−1,3)(3)解:由(2)得OC=OD∴∠OCD=∠ODC∴∠ECD=∠ODB∵D(0,−2)B(1,−3)BD=√12+(−3+2)2=√2∴ΔECD与△ODB相似有两种情况讨论如下:①△ODB∼△ECD∴OD CE=BDCD即2CE=√22√2∴CE=4∴E(−6,0)②△ODB∼△DCE∴OD CD=BDCE即22√2=√2CE∴CE=2∴E(−4,0)综上点E的坐标为(−6,0)或(−4,0).5.【答案】(1)证明:∵AD BE是ΔABC的高∴∠ADC=∠BEC=90°∵∠C=∠C∴ΔACD∽ΔBCE;(2)解:∵点D是BC的中点AD⊥BC∴AB=AC在RtΔBEC中∵CE=3BE=4∴BC=√CE2+BE2=√32+42=5∴CD=12BC=52∵ΔACD ∽ΔBCE∴AD CD =BE EC∴AD =4×523103∴AC =√AD 2+CD 2=√(103)2+(52)2=256∴AB =AC =256. 6.【答案】(1)解:∵直角边AC =3cm BC =4cm∴由勾股定理可得 AB =√AC 2+BC 2=√32+42=5∴AP =t BP =5−t BQ =t∵△PBQ 是以∠B 为顶角的等腰三角形∴BP=BQ 即5-t=t 解得t =52秒 ∴当t =52秒 △PBQ 是以∠B 为顶角的等腰三角形; (2)解:能.理由:当∽PBQ∽∽ABC 时BQ BC =BP AB 即t 4=5−t 5 解得:t =209秒; 当∽PBQ∽∽CBA 时 BQ AB =BP BC 即t 5=5−t 4 解得:t =259秒 ∴当t =209或259秒时 △PBQ 与直角三角形ABC 相似. 7.【答案】(1)证明:∵△ABC ∽△ADE∴∠BAC =∠DAE AB AD =AC AE∴∠BAC −∠CAD =∠DAE −∠CAD即∠BAD =∠CAE∴△ABD ∽△ACE ;(2)解:①1②连接CE ∵∠BAC =∠DAE =90°,∠ABC =∠ADE ∴△BAC ∽△CAE ∴AB AD =AC AE ∴AB AC =AD AE∵∠BAD =∠CAE =90°−∠CAD ∴△BAD ∽△CAE ∴∠ABC =∠ACE ∴∠ADE =∠ACE ∵∠AFD =∠EFC ∴△AFD ∽△EFC ∴DF CF =AD CE由①得AD =√3AE ,AD =√3BD ∴BD CE =AD AE =√3 ∴BD =√3CE ∴AD =√3×√3CE =3CE ∴AD CE =3∴DFCF=ADCE=3.8.【答案】(1)解:①∵DP⊥DE∴∠PDE=∠PDC+∠CDE=90°∵在正方形ABCD中∴∠ADC=∠ADP+∠PDC=90°AD=CD∴∠CDE=∠ADP在△APD和△CED中{AD=CD ∠ADP=∠CDE PD=DE∴△APD≌△CED;②∵△APD≌△CED∴∠APD=∠CED又∵∠APD=∠PDE+∠DEP∠CED=∠CEA+∠DEP∴∠AEC=90°(2)解:过点C作CF⊥DE交DE延长线于点F∵DE=DP=1∠PDE=90°∴PE=√DP2+DE2=√2∴∠DPE=∠DEP=45°∵∠CEA=90°∴∠CEF=45°∵∠EFC=90°∴∠FCE=45°∴∠CEF=∠FCE在Rt△PCE中CE=√PC2−PE2=√20−2=3√2∴CF=EF=√22CE=3∴在Rt △CDF 中 CD 2=CF 2+DF 2=32+(1+3)2=25 ∴正方形ABCD 的面积为:CD 2=25.(3)解:∵△APD ≌△CED∴∠ADQ =∠CDF∵∠DAQ =∠DFC∴△DAQ ∽△DFC∴DQ DC =DA DF∵DA =DC∴DQ =DC 2DF=DC 2DE +EF =251+3=254 ∴PQ =DQ −DP =254−1=214. 9.【答案】(1)解:由题意知 PC =2tcm BQ =tcm ∵AC =10cm BC =8cm∴CQ =(8−t)cm 0<t ≤5∵△PCQ 的面积等于16cm 2∴12PC ·CQ =16 ∴12×2t ·(8−t)=16 即(t −4)2=0 ∴t 1=t 2=4即经过4秒后 △PCQ 的面积等于16cm 2(2)解:∵∠ACB =∠PCQ =90°∴①当△PCQ ∽△ACB 时∴2t 10=8−t 8解得:t =4013; ②当△PCQ ∽△BCA 时∴2t 8=8−t 10 解得:t =167; 由①②可得:当经过4013秒或167秒△PCQ 与△ABC 相似. (3)①不存在 理由:假设存在t 使得△PCQ 的面积等于20cm 2∴12PC·CQ=20∴12×2t·(8−t)=20∴t2−8t+20=0而Δ=64−4×1×20=−16<0∴此方程无实数根∴不存在t 使得△PCQ的面积等于20cm2②S的最小值是24cm210.【答案】(1)解:∵AD∥A′D′∴∠PAD=∠PA′D′,∠PDA=∠PD′A′.∴△PAD∽△PA′D′.∴ADA′D′=PNPM∴3036=PM−30PM解得PM=180;∴灯泡离地面的高度PM为180cm;(2)解:设横向影子A′B D′C的长度和为xcm 同理可得△PAD∽△PA′D′.∴ADA′D′=PNPM即6060+x=150180解得:x=12cm∴横向影子A′B D′C的长度和为12cm.11.【答案】(1)解:∵AB⊥BO CD⊥BO ∴∠ABG=∠CDG∵∠CGD=∠AGB∴△ABG∽△CDG∴BGDG=ABCD∵OB=20米OD=17米DG=1米∴BD=OB−OD=20−17=3米BG=BD+DG=3+1=4米∴41=AB1.6解得:AB=6.4.∴路灯高6.4米.(2)解:如图所示:12.【答案】(1)解:∵△ABC∽△A1B1C1c=a1=2a=5∴aa1=cc1即:52=2c1解得:c1=45;(2)证明:∵△ABC∽△A1B1C1相似比为k(k>1)∴aa1=k∴a=ka1又∵c=a1∴a=kc.(3)解:取a=8,b=6,c=4同时取a1=4,b1=3,c1=2此时aa1=bb1=cc1=2∴△ABC∽△A1B1C1且c=a1(4)解:不存在这样的△ABC和△A1B1C1理由如下:假设存在则a=2a1,b=2b1,c=2c1.又∵b=a1c=b1∴a=2a1=2b=4b1=4c∴b=2c∴b+c=2c+c<4c=a与三角形的三边关系b+c>a不符∴不存在△ABC和△A1B1C1使得k=2.13.【答案】(1)解:如图∽A'B'C'为所作;(2)解:∽A'B'C'的面积=4×4﹣12×2×4﹣12×2×2﹣12×2×4=6. 14.【答案】(1)证明:如图2 过C 作CE ∥DA .交BA 的延长线于E ∵CE ∥AD∴BD CD =BA EA∽2=∽ACE ∽1=∽E ∵∽1=∽2∴∽ACE =∽E∴AE =AC∴AB AC =BD CD. (2)解:如图3 ∵AB =3 BC =4 ∽ABC =90°∴AC =√BC 2+AB 2=√42+32=5∵AD 平分∽BAC∴AC AB =CD BD 即53=CD BD∴BD =38BC =38×4=32∴AD =√BD 2+AB 2=√(32)2+32=32√5 ∴∽ABD 的周长=32+3+32√5=9+3√52. 15.【答案】(1)解:①判断:∽ABC 是等边三角形.理由如下: ∵∽ABC=∽ACB=60°∴∽BAC=180°-∽ABC-∽ACB=60°=∽ABC=∽ACB∴∽ABC 是等边三角形.②∽EBD 也是等边三角形 理由如下:如图1 连接DC则AB=BC BE=BD ∽ABE=60°-∽EBC=∽CBD ∴∽ABE∽∽CBD∴AE=CD ∽AEB=∽CDB=150°∴∽EDC=150°-∽BDE=90°∴在Rt∽EDC中tan∠CED=CDED=AEBD.(2)解:如图2:连接DC∵∽ABC=∽EBD=90° ∽ACB=∽EDB=60°∴∽ABC∽∽EBD∴ABEB=BCBD即ABBC=EBBD又∵∽ABE=90°-∽EBC=∽CBD∴∽ABE∽∽CBD∴∽AEB=∽CDB=150°∴∽EDC=150°-∽BDE=90° ∽CED=∽BEC-∽BED=90°-(90°-∽BDE)=60°设BD=x在Rt∽EBD中DE=2x BE=√3x在Rt∽EDC中CD=DE×tan60°=2√3x∴AE=CD·BEBD=2√3x⋅√3xx=6x=6BD即BDAE=16.16.【答案】(1)证明:∵等边∽PCD的边长为6∴PC=PD=6 ∽PCD=∽PDC=60°又∵AC=4 BD=9∴PCBD=69=23=46=ACPD∵等边∽PCD中∽PCD=∽PDC=60°∴∽PCA=∽PDB=120°∴∽ACP∽∽PDB;(2)解:∵∽ACP∽∽PDB∴∽APC=∽PBD∵∽PDB=120°∴∽DPB+∽DBP=60°∴∽APC+∽BPD=60°∴∽APB=∽CPD+∽APC+∽BPD=120°.17.【答案】(1)(1)CM=√2PE;45(2)解:结论成立证明如下:如图(2)中连接AE.∵AB=AC,BE=EC∴AE平分∠BAC∴∠CAE=12∠BAC=45°∵DE∥AB∴∠ADE=180°−∠BAC=90°∵AD=DC∴AE=√2AD∵AM=√2AP∴ACAE=AMAP∵∠PAM=∠CAE=45°∴∠CAM=∠EAP∴△CAM∽△EAP∴CMPE=AMAP=√2∠ACM=∠AED=45°∴CM=√2PE.(3)解:√2或2√2+√618.【答案】(1)相等;垂直(2)解:数量关系:DN=√3BM位置关系:BM⊥DN.理由如下:如图:∵四边形ABCD和四边形AMPN都是矩形∴∠BAD=∠MAN=90°∴∠BAD−∠MAD=∠MAN−∠MAD∴∠BAM=∠DAN∵ABAD=AMAN=1√3∴△ADN∽△ABM∴BMDN=ABAD=√3∴DN=√3BM.延长BM交AD于点O 交DN于点H∵△ADN∽△ABM∴∠ABM=∠AND又∵∠AOB=∠DOH∴∠OHD=∠OAB=90°即BM⊥DN.(3)解:∵AB=2AM=1ABAD=AMAN=1√3∴AN=√3分类讨论:连结MN.①如图:当MN位于AB上方时在Rt△MAN中由勾股定理得MN=√AN2+AM2=√(√3)2+12=2∴AB=MN又∵MN∥AB∴四边形ABMN是平行四边形∴BM=AN=√3∵DN=√3BM∴DN=3.②如图:当MN位于AB下方时连结BN同理可得四边形ABNM是平行四边形∴BN=AM=1BN∥AM∴∠ANB=∠MAN=90°又∠ANP=90°∴B N P在一条直线上∴∠BPM=90°∴BP=BN+NP=2MP=AN=√3∴在Rt△BPM中BM=√BP2+MP2=√7∵DN =√3BM∴DN =√21.综上所述 DN 的长为3或√21.19.【答案】(1)24;(8 3)(2)证明:设点D 的横坐标为m∴点D 的坐标为(m ,6)∴k =6m∴反比例函数的解析式为:y =6m x点E 的坐标为(8,3m 4)∴AD =8−m ,AE =AC −CE =6−3m 4=3(8−m)4∴AB AC =86=43,AD AE =43∴AB AC =AD AE即AD AB =AE AC∴BC ∥DE ;(3)存在 点D 的横坐标为√37+1或√37−120.【答案】(1)2;√6(2)证明:∵∠EBF =∠ACB =45°∴∠CGN =45°+∠CBN =∠MBC∵AD ∥BC∴∠AMH =∠MBC∴∠AMH =∠CGN∵∠MAH =∠GCN =45°∴△AMH ∽△CGN ;(3)1721.【答案】(1)解:在RtΔABC 中 ∠C =90° AB =10 BC =6∴AC =√AB 2−BC 2=√102−62=8∵ D 是AB 的中点∴AD =12AB =5∵动点P 从点A 出发 沿线段AC 以每秒2个单位长度的速度向终点C 运动设点P 的运动时间为t 秒∴AP =2t 0≤t ≤4若以点A D P 为顶点的三角形与ΔABC 相似 而∠A =∠A 分两种情况:①当∠APD =∠C =90°时 ΔAPD ∽ΔACB 如图1∴AP AC =AD AB 即2t 8=510解得t =2;②当∠ADP =∠C =90°时 ΔADP ∽ΔACB 如图2∴AP AB =AD AC 即2t 10=58解得t =258;故当t 为2或258秒时 以点A D P 为顶点的三角形与ΔABC 相似 (2)解:由(1)知:当t =2时 ∠APD =90° 当t =258时 ∠ADP =90° 而∠A 是锐角∴当0<t <2时 ∠APD 为钝角 ΔAPD 为钝角三角形; 当258<t ≤4时 ∠ADP 为钝角 ΔAPD 为钝角三角形; 故若ΔAPD 为钝角三角形 则t 的取值的范围是0<t <2或258<t ≤4.22.【答案】(1)BE=CD ;BE∽CD(2)解:过点M 作MF ∥AC 交BC 于点F 如图2所示∴∠BMF =∠A =90° ∠MFB =∠C =45°∴MB=MF∵∠DME=∠BMF=90°∴∠BME=∠FMD又∵ME=MD,MB=MF∴ΔMBE≌ΔMFD(SAS)∴∠MBE=∠MFD=45°∴∠EBD=∠MBE+∠MBF=90°故∠EBD=90°(3)解:取BC中点G 连接MG如图3所示∵点M是AB中点∴MG为ΔABC的中位线∴MG∥AC∴BMG=90°,∠MGB=30°∴BM=12BG=14BC=32MG=32√3DG=3−1=2∴BM MG=√3又MD=√3ME∴ME MD=√3∴MEMD=BMMG又∵∠EMD=∠BMG=90°∴∠EMB=∠DMG∴ΔMEB∽ΔMDG∴BEDG=BMMG=√3∴BE =√33×2=2√33故BE 的长为2√33. 23.【答案】(1)解:BE =2CF 理由如下: ∵∽ACB =90° ∽BAC =60°∴∽ABC =30°∴AC =12AB ∵BD =13AB 将线段DB 绕点D 逆时针旋转至DE ∴BD =DE =13AB BE =23AB ∴AE =13AB ∵∽AFE =90° ∽EAF =60°∴∽AEF =30°∴AF =12AE =16AB ∴CF =AC ﹣AF =13AB ∴BE =2CF ;(2)解:①结论仍然成立 理由如下: ∵∽BAC =∽EAF =60°∴∽BAE =∽CAF又∵AC AB =12=AF AE∴∽ABE∽∽ACF∴CF BE =AF AE =12∴BE =2CF ;②∽CEF 是等边三角形 理由如下: ∵B E F 三点共线∴∽AEB+∽AEF =180°∴∽AEB =150°∵∽ABE∽∽ACF∴∽AEB =∽AFC =150°∴∽EFC =150°﹣90°=60°如图3 过点D作DH∽BE于H∵BD=DE DH∽BE∴BH=HE∵BE=2CF∴BH=HE=CF∵DH∽BE AF∽BE∴DH∥AF∴BHHF=BDAD=12∴HF=2BH∴EF=HE=BH∴EF=CF∴∽EFC是等边三角形.24.【答案】(1)证明:如题图1∵∽DPC=∽A=∽B=90°∴∽ADP+∽APD=90° ∽BPC+∽APD = 90°∴∽ADP = ∽BPC∴∽ADP∽∽BPC∴ADBP=APBC∴AD⋅BC = AP⋅BP(2)解:结论仍然成立理由如下∵∠BPD=∠DPC+∠BPC又∵∠BPD=∠A+∠ADP∴∠DPC+∠BPC=∠A+∠ADP∵∠DPC=∠A设∠DPC=∠A=α∴∠BPC=∠ADP∴△ADP∽△BPC∴ADBP=APBC∴AD⋅BC = AP⋅BP(3)解:∵∠EFD=45°∴∠B=∠ADE=45°∴∠BAD=∠EDF∴△ABD∽△DFE∴ABDF=ADDE∵△ADE是等腰直角三角形∴DE=√2AD∵AB=2√2∴DF=4∵∠EFD=45°,∠ADE=45°∴∠EFC=∠DEC=135°∴△EFC∽△DEC∴FCEC=ECCD∵EC=√5CD=DF+FC=4+FC∴EC2=FC⋅CD=FC⋅(4+FC)=5∴FC=1∴CD=5.25.【答案】(1)1;90°(2)解:如图2 延长DF交EB于点H∵AD=2AB AF=2AE∴ADAB=AFAE=2∵∽BAD=∽EAF=90°∴∽FAD=∽EAB∴∽FAD∽∽EAB∴DF BE =AF AE =2∴DF=2BE∵∽FAD∽∽EAB∴∽AFD=∽AEB∵∽AFD+∽AFH=180°∴∽AEH+∽AFH=180°∵∽EAF=90°∴∽EHF=180°-90°=90°∴DF∽BE∴BE DF =12 β=90°;(3)1k ;α+β=180°26.【答案】(1)2t ;(5﹣t )(2)解:由(1)知 OP=2t cm OQ=(5-t )cm ∵∽POQ 的面积为6cm 2∴6=12×2t×(5-t )∴t=2或3∴当t=2或3时 三角形POQ 的面积为6cm 2; (3)解:∵∽POQ 与∽AOB 相似 ∽POQ=∽AOB=90° ∴∽POQ∽∽AOB 或∽POQ∽∽BOA∴OP OA =OQ OB 或OP OB =OQ OA当OP OA =OQ OB 则2t 10=5−t 5∴t=52;当OP OB =OQ OA 时 则2t 5=5−t 10∴t=1∴当t=52或1时 ∽POQ 与∽AOB 相似. 27.【答案】(1)AE DE(2)解:①∵∽APC=∽B+∽BAP ∽APC=∽APD+∽CPD ∽APD=∽B∴∽BAP=∽CPD∵AB=AC∴∽B=∽C∴∽ABP∽∽PCD ;②BC=12 点P 为BC 中点 ∴BP=PC=6·∵∽ABP∽∽PCD∴AB PC =BP CD 即106=6CD解得:CD=3.6;(3)解:BP 的长为2或113. 28.【答案】(1)2;60°(2)解:(1)中结论仍然成立 证明:延长AA 1 BB 1相交于点D 如图2由旋转知 ∽ACA 1=∽BCB 1 A 1C=1 B 1C=2∵AC=2 BC=4∴AC A 1C =2 BC B 1C =2 ∴AC A 1C =BC B 1C ∴∽ACA 1∽∽BCB 1∴BB 1AA 1=BC AC =2 ∽CAA 1=∽CBB 1 ∴∽ABD+∽BAD=∽ABC+∽CBB 1+∽BAC-∽CAA 1 =∽ABC+∽BAC=30°+90°=120°∴∽D=180°-(∽ABD+∽BAD )=60°; (3)解:①∽ABA 1面积的最大值=12×2√3×3=3√3; ②线段BB 1的长为√15+√3或√15−√3.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
DA
C
120°
ED
CB
A
C
A
B
八年级相似三角形单元检测卷
A卷(100分,时间60分钟)
一、 选择题 (每题3分,共30分)
1.在比例尺为1:500000的地图上,A、B两个城市之间的距离为6㎝,那A、B两个城市之
间的实际距离是( )
A.30 km B. 3km C. 300 km D. 3000km
2.下列各组线段(单位:㎝)中 ,四条线段成比例的是( )
A.1、3、4、6 B.2、3、6、9 C. 3、5、9、12 D. 3、4、5、6
3.已知△ABC∽△DEF,则下列等式正确的是( )
A.ABEFDEAC B.ABBCDEEF
C.BCDFACEF D.ACDFBCDF
4.ABC△中,DEBC∥,且23ADDB,4DEcm,则
BC
( )
A.14cm B.12cm
C.10cm D.8cm
5.某天同时同地,甲同学测得2m的测竿在地面上的影长为1.6m,乙同学测得国旗旗杆在
地面上的影长为9.6m,则国旗旗杆的高度为( )m
A. 10 B. 12 C. 13 D. 15
6.五边形ABCDE∽五边形EDCBA,且最长边分别为AB=10㎝和BA=8㎝,如果五
边形ABCDE的周长为35㎝,则五边形EDCBA的周长为( )㎝
A.28㎝ B. 24㎝ C. 56㎝ D. 30㎝
7.下列判断正确的是( )
A.等腰三角形都相似 B.正方形都相似
C.直角三角形形都相似 D.对应角都分别相等的多边形相似
8.如图,在直角△ABC中,∠ACB=900 ,CD⊥AB与点D.则下列结
论错误的是( )
A.AC2=AD·AB B.BC2=BD·AB
C.CD2=AD·BD D.AC2:BC2=AD2:BD2
9. 如图所示,△ABC是等边三角形,∠DAE=120°,
D、B、C、E共线,则图中相似三角形的对数至少为
( )
A.一对 B.二对 C.三对 D.四对
10.1.如图,小正方形的边长均为1,则下列图中的三
角形(阴影部分)与△ABC相似的是( )
A
B
C
D
E
E
D
C
B
A
D
C
B
A
A
B
C
D
二、填空题(每题4分,共20分)
11.若3x-2y=0, 则yx = 。
若a= 2 ,b=3, c= 8 则成比例线段a、b、c、d中的d= .
12. 如图在△ABC中,点D为AB之中点,DE∥BC, △ADE
的面积为S1,四边形DBCE的面积为S2,则S1 :S2=
13. 如图,小明在地面上放置一个平面镜E来测量铁塔AB的高度,
镜子与铁塔的距离EB=20米,镜子与小明的距离ED=2米时,小明
刚好从镜子中看到铁塔顶端点A,已知小明的眼睛距地面的高度
CD=1.5米,则铁塔AB的高度是_________米.
14.如图,在△ABC中,点D为边BC上一点,请你填
写一个条件, ,可 使△ABC∽△DBA。
15.若53fedcba,则fdbeca= ,5232fdbeca= .
三、解答题(16—21题每题7分,22题8分)
16. 若等腰三角形ABC中,AB=AC, ∠A=120°,AD为高,求AD:BC的值。
17. 若532cba,且3a-2b+5c=50,求a,b,c 的值
A
BCDE
