第二章 电阻电路分析11
合集下载
第二章 电阻电路的等效变换
＋
i
＋
… i
＋ －
u
－
K=1，2 ， i
＋ －
u
Reg
u
G1
in Gn
u
－
Geg
分流公式： 分流公式：ik=Gku=Gk/Geg i n=2时，Reg=R1R2/（R1+R2） 时 （ i1=R2/（R1+R2）， 2=R1/（R1+R2）×i ），i （ （ *混联：有串，又有并 混联：有串， 混联 1 R1 R2 R3 R4
对于△ 对于△形，各电阻中电流为：i12=u12/R12 i23=u23/R23 i31=u31/R31 各电阻中电流为：
i ′ =i12-i31=u12/R12-u31/R31 1
i ′2 =u23/R23-u12/R12
i ′3 =u31/R31-u23/R23
i1 + i 2 + i 3 = 0
③
2
2 i31 1 i12
④
2
⑤
i′2
1
1
R2
3
自已补充:R 自已补充 4与1串,R3与2串,然 串 串然 后再并 i2
R4 R3 2
3
i3 2
1
1
2-5
电压源和电流源的串联和并联
＋
1、n个电压源串联：us=∑usk--------等效电压源 、 个电压源串联： 等效电压源 个电压源串联 ＋ － ＋ ○ ○ －○ us1 us2 usn。 。 注：正、负号取 。 。 。 2、n个电流源的并联： 个电流源的并联： 、 个电流源的并联 is1 is=is1+is2+…is=∑isk 。 。
αi
＋ uS － i ＋
i
＋
… i
＋ －
u
－
K=1，2 ， i
＋ －
u
Reg
u
G1
in Gn
u
－
Geg
分流公式： 分流公式：ik=Gku=Gk/Geg i n=2时，Reg=R1R2/（R1+R2） 时 （ i1=R2/（R1+R2）， 2=R1/（R1+R2）×i ），i （ （ *混联：有串，又有并 混联：有串， 混联 1 R1 R2 R3 R4
对于△ 对于△形，各电阻中电流为：i12=u12/R12 i23=u23/R23 i31=u31/R31 各电阻中电流为：
i ′ =i12-i31=u12/R12-u31/R31 1
i ′2 =u23/R23-u12/R12
i ′3 =u31/R31-u23/R23
i1 + i 2 + i 3 = 0
③
2
2 i31 1 i12
④
2
⑤
i′2
1
1
R2
3
自已补充:R 自已补充 4与1串,R3与2串,然 串 串然 后再并 i2
R4 R3 2
3
i3 2
1
1
2-5
电压源和电流源的串联和并联
＋
1、n个电压源串联：us=∑usk--------等效电压源 、 个电压源串联： 等效电压源 个电压源串联 ＋ － ＋ ○ ○ －○ us1 us2 usn。 。 注：正、负号取 。 。 。 2、n个电流源的并联： 个电流源的并联： 、 个电流源的并联 is1 is=is1+is2+…is=∑isk 。 。
αi
＋ uS － i ＋
直流电阻电路
第四节
基尔霍夫定律
在学习电路的时候，经常会用欧姆定律、并联电路 和串联电路的特点去解决一些电路的计算问题。利用它 们去分析一些简单的电路是很方便的，但对于复杂的电 路，如图2-13所示，它们便显得无能为力。为此，下面 来学习一个新的定律，即基尔霍夫定律。
图2-13复杂电路
一、电路的结构 复杂电路的结构可用支路、节点、回路等术语来描述。 电路中的每一个分支被称为支路；3条或3条以上的支路的汇聚点被 称为节点；有一条或多条支路所组成的闭合电路被称为回路。在图 2-14所示的电路中，支路有3条：由R1、E1构成的支路，由R2、E2 构成的支路，由R5构成的支路；节点有2个：a和b；回路有3个：l1， l2，l3。 特别需要注意，c和d并不是节点。
第三节 电阻混联电路
混联电阻电路的分析步骤一般是： （1）化简电路，就是利用电路中的各等电位点画出 等效电路图，或者分别求出串联电阻和并联电阻，从 而得到混联电路的等效电路。 （2）根据欧姆定律，由电路的总的等效电阻和电路 的端电压计算电路中的总电流。 （3）根据电阻串联的分压关系和电阻并联的分流关 系，逐步推算出各支路的电流和电压。
第二章 直流电阻电路
知识目标 直流电路在生产实践中有着广泛的应用。本章主要介绍直流 电路的联接方式，包括串联电路、并联电路和混联电路，以及 简单电路的分析方法，涉及到基尔霍夫定律、支路电流法、电 源的等效变换、叠加定理和戴维南定理等。 学习目标 1.掌握电阻串联、并联、混联电路电压、电流、电阻的特点。 2.掌握利用基尔霍夫电压定律和基尔霍夫电流定律列写电路的 方程。 3.学会利用支路电流法求解电路。 4.了解实际电源的两种电路模型，以及电源的等效变换概念。 5.学会利用叠加定理分析含有两个直流电源的电路。 6.学会灵活运用戴维南定理求解电路。
人教版高二物理选修3-1第二章 2.4串联电路和并联电路--电阻的测量(共22张PPT)
限流式电路的特点:
1.电压不能从零开始调节,调节范围较小.
但电路结构较为简单.
2.电能损耗较小.
2020/6/11
3
二、限流和分压电路的选取
2.分压式
Rx P
AR B
E
s
图中变阻器起分压作用，求待测电阻Rx的 电压可调范围
0~E
分压式电路的特点:
1.电压可以从零开始调节到电源电动势,调节范
围较大. 但电路结构较为复杂.
伏安法
用电压表测出电阻两端的电压U，用电流表 测出通过电阻的电流I，利用部分电路欧姆定律 可以算出电阻的阻值R，
RU I
2020/6/11
6三、电阻的测量来自伏安法测电阻的两种电路
电流表接在电压表两接线柱外侧，
通常叫“外接法”
V
A R
电流表接在电压表两接线柱内侧，
通常叫“内接法”
V
A R
因为电流表、电压表分别有分压、分流作
AV
2020/6/11
s
17
课堂训练
6.在图中,AB间的电压为30V,改变滑动变阻 器触头的位置,可以改变CD间的电压,UCD的变化
范围是( C )
A.0~10V B.0~20V
C.10~20V D.20~30V
A R
R
C
R
V
B
D
2020/6/11
18
课堂训练
7.如图所示R1=6Ω, R2=3Ω R3=4Ω,A、B两 点电压UAB=12V,C1C2的电容分别为2μF和1μF,则 它们带电荷量分别为1.44X10-5C 和 4.8X10-6C .
三、电阻的测量
伏安法测电阻
外接法
误差来源 伏特表的分流
电路分析第2章电路分析方法.ppt
I1=(U2 – U3)/4=(1 – 21)/4= – 5A
I2= –(1/3)U3= – 7A
12A
若选3为参考点，列节点电压方程
节点1 (1/3)U1= – 4 – 12 +Io
节点2 (1/4)U2= 4 – Io 辅助方程 U2 – U1=1
U1 – 3Io = – 48 U1+4Io =15 U1 = – 21V U2= – 20V 12A I1=U2/4= – 20/4= – 5A I2=U1/3= – 21/3= – 7A
令 R11=R1+R4+R5
i1 R1
R2 i2
为第一网孔的自电阻
令 R12= R21 = R5 为一、二两网孔中互电阻
令 R13 =R31 =－R4
+
US1
iA
–
–+ US4
R4
i5
R5
iB
i4 R6 i6 iC
+ –US2
为一、三两网孔中互电阻
令 uS11= uS1-uS4 为第一网孔中电压源电压升的代数和
- G5u1 - G3u2 + (G3 + G4 + G5 )u3 = 0
1. 自电导×节点电位 + 互电导×相邻节点电位 = 流进 该节点的电流源电流代数和。 2. 自电导均为正值，互电导均为负值。
例1 求图示电路中I1及I2。 解：若选1为参考点，列节点电压方程
– 1V+
节点2
U2=1V
节点3 (1/3+1/4)U3 – (1/4) U2=12 U3=21V
名称 放大倍数(增益) 输入电阻 输出电阻
典型值 105-107 106-1013 10-100
＜＜电路原理＞＞系重庆大学电气工程学院教材 第二章课件
3. 戴维宁定理的应用
例1. 求电流I 解： 1. 求开路电压
U oc U s U oc Is 0 R1 R2 U oc R2 (U s R1 I s ) R1 R2
2. 求等效电阻
R1 R2 Req R1 R2
3. 作戴维宁等效电路，求电流 I
U oc R2 (U s R1 I s ) I Req R L R1 R2 R L ( R1 R2 )
R3 R1 R3 R4 R2 R4 U ( )U s ( )I s R2 R4 R1 R3 R1 R3 R2 R4
二. 线性电路的叠加定理
例1. 采用叠加定理重新求解图中的求I和U
＝
＋
1）当Us单独作用时，求I'和U '
1 1 I' ( )U s R1 R3 R2 R4
1 1 1 ( )U 5 x 2 4 2
U 4 V x
2)独立电压源单独作用
U 6 U U x x x 0 2 4 2
U 1.2 V x
3)两个独立源共同作用
U x U U (4 1.2) V 2.8 V x x
U' ( R3 R4 )U s R2 R4 R1 R3
2）当Is单独作用时，求I''和U''
R3 I1 ' ' Is R1 R3
R4 I 2 '' Is R2 R4
R3 R4 I '' I1 '' I 2 '' ( )I R1 R3 R2 R4 s
2. 诺顿定理的应用
电路原理(邱关源)习题解答第二章课件-电阻电路的等效变换练习
第二章 电阻电路的等效变换“等效变换”在电路理论中是很重要的概念，电路等效变换的方法是电路问题分析中经常使用的方法。
所谓两个电路是互为等效的，是指（1）两个结构参数不同的电路再端子上有相同的电压、电流关系，因而可以互相代换；（2）代换的效果是不改变外电路（或电路中未被代换的部分）中的电压、电流和功率。
由此得出电路等效变换的条件是相互代换的两部分电路具有相同的伏安特性。
等效的对象是外接电路（或电路未变化部分）中的电压、电流和功率。
等效变换的目的是简化电路，方便地求出需要求的结果。
深刻地理解“等效变换”的思想，熟练掌握“等效变换”的方法在电路分析中是重要的。
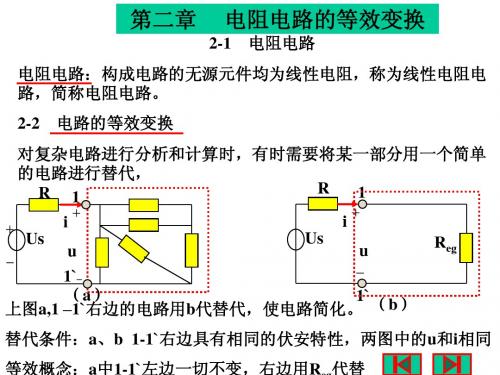
2-1 电路如图所示，已知12100,2,8s u V R k R k ==Ω=Ω。
若：（1）38R k =Ω；（2）处开路）33(R R ∞=；（3）处短路）33(0R R =。
试求以上3种情况下电压2u 和电流23,i i 。
解：（1）2R 和3R 为并联，其等效电阻84R k ==Ω，则总电流 mA R R u i s 3504210011=+=+=分流有 mA i i i 333.86502132==== V i R u 667.666508222=⨯==（2）当∞=3R ，有03=imA u i s 10100212===V i R u 80108222=⨯==（3）03=R ，有0,022==u imA R u i s 50210013===2-2 电路如图所示，其中电阻、电压源和电流源均为已知，且为正值。
求：（1）电压2u 和电流2i ；（2）若电阻1R 增大，对哪些元件的电压、电流有影响？影响如何？解：（1）对于2R 和3R 来说，其余部分的电路可以用电流源s i 等效代换，如题解图（a ）所示。
因此有 32332R R i R i += 32322R R i R R u s+=（2）由于1R 和电流源串接支路对其余电路来说可以等效为一个电流源，如题解图（b ）所示。
第二章 电阻电路的等效变换
注意： 注意： 上的电压； （1）变换后 0是两个元件上的电压； ）变换后u 两个元件上的电压 控制变量所在支路不能动 （2）受控源的控制变量所在支路不能动。 ）受控源的控制变量所在支路不能动。 2. 利用两类约束找关系 利用两类约束 两类约束找关系
1 对回路列KVL： (1 + R 3 + R 4 )i + 2 R 4 u 3 = u S 对回路列 ： 2 受控源的控制量： 受控源的控制量： u 3 = R3 i
2、并联等效电阻 、并联等效电阻
（1）等效条件： ）等效条件： （2）分流公式： ）分流公式：
G
等
=
∑
G
并
Gk ik = G k u = i G等
i1
i2 G2 iS
特殊： 特殊：
G
k
= ∞ ，即 R
k
=
0 ，
i
k
=
i
，
短路处电流 电流源电流 其它电导电流 电流＝ 电流， 电导电流＝ ） （短路处电流＝电流源电流，其它电导电流＝0）
§2－1 引言 －
由时不变线性无源元件、线性受控源和独立电源 时不变线性无源元件 线性受控源和 元件、 组成的电路，称为时不变线性电路，简称线性电 组成的电路，称为时不变线性电路，简称线性电 路。 如果构成电路的无源元件均为线性电阻，则称为 如果构成电路的无源元件均为线性电阻， 构成电路的无源元件均为线性电阻 线性电阻性电路。 线性电阻性电路。电路中电压源的电压或电流源 的电流，可以是直流， 的电流，可以是直流，也可以随时间按某种规律 变化；当电路中的独立电源均为直流电源 直流电源时 变化；当电路中的独立电源均为直流电源时，称 直流电路。 为直流电路。 简单电阻电路的分析与计算 本章为简单电阻电路的分析与计算，着重介绍 本章为简单电阻电路的分析与计算， 等效变换的概念 的概念。 等效变换的概念。
第二章 电阻电路的等效变换
Ib Ic
c
将Y形联接等效变换为∆形联结时 形联接等效变换为∆ 3R 若 Ra=Rb=Rc=RY 时，有Rab=Rbc=Rca= R∆ = 3RY； 将∆形联接等效变换为Y形联结时 形联接等效变换为Y 若 Rab=Rbc=Rca=R∆ 时，有Ra=Rb=Rc=RY =R∆/3
总目录 章目录 返回 上一页 下一页
总目录 章目录 返回 上一页 下一页
+ U –
2.3.2 电阻的并联
I + I1 U – I2 R1 R2 特点: 特点: (1)各电阻联接在两个公共的结点之间； (1)各电阻联接在两个公共的结点之间 各电阻联接在两个公共的结点之间； (2)各电阻两端的电压相同； (2)各电阻两端的电压相同； 各电阻两端的电压相同 (3)等效电阻的倒数等于各电阻倒数之和； (3)等效电阻的倒数等于各电阻倒数之和； 等效电阻的倒数等于各电阻倒数之和 1 1 1 = + Req R1 R2 (4)并联电阻上电流的分配与电阻成反比。 (4)并联电阻上电流的分配与电阻成反比 并联电阻上电流的分配与电阻成反比。 两电阻并联时的分流公式： 两电阻并联时的分流公式： Req
R R ab ca R = a R +R +R ab bc ca R R bc ab R = b R +R +R ab bc ca R R ca bc R = c R +R +R ab bc ca
总目录 章目录 返回 上一页 下一页
Ia a Ra Ib Ic b Rb Rc c 等效变换
Ia
a Rab RbcRca b
第2章 电阻电路的等效变换 章
2.1 引言 2.2 电路的等效变换 2.3 电阻的串联和并联 2.4 电阻星型联结与三角型联结的等效变换 电阻星型联结与三角型联结的等效变换 2.5 电压源、电流源的串联和并联 电压源、 2.6 实际电源的两种模型及其等效变换 实际电源的两种模型及其等效变换 2.7 输入电阻
第二章 等效变换
例2：
求图2-9a电路中电流 I1, I2, I3 , I4。
I
I2 I1
解: 思路
Δ→Y
Req
I
Rb
48 2, 同理, 求得 : Rc 2, Rd 1, Req (1 Rb ) //(5 Rd ) Rc 4 4 48 1 Rb 18 I 3 A, 由分流公式, 可得: I1 I 1A, I 2 I I1 2 A 2 Req 1 Rb 5 Rd U db 5 I1 1 I 2 I3 0.75 A, I 4 I1 I 3 1.75 A 4 4
根据电路的对称性, 可知 c, d, e三点等电位, 故可用导线短接。
8 2 8 2 3 3 2 16 Req [( 2 // 1) 2] //(2 // 1) 2 // 2 8 2 3 3 15 3 3
§2-4电阻的Y－Δ 等效变换
R1, R2, R3 Y(星)形连接 R3, R4, R5 R1, R3, R4 Δ(三角)形连接 R2, R3, R5
②
'' Req R1 Req 6 6 12 ③
15 10 6 ②R R2 R34 15 10
'' eq ' R2 Req
Req R1 R2 //(R3 R4 ) R1
R2 ( R3 R4 ) 15(5 5) 6 12 R2 R3 R4 15 5 5
6 9 54 断开时，Req 2＋4） 3 6) （ //( 3.6 6 9 15
结论：若电路中两点电位相等，则： ①可将这两点短路 ② 可将这两点之间连接的支路断开 对某些对称性电路可采用此方法处理
第二章电路定理及分析方法lqx
2
3
2A 2A
6
1A
4
1 I
2
4
I
1 4A
1A
电路分析 方法
解：
2 2
2
4
I 1
+ 8V -
4
1A
I
1
4A
1A
2
I 2A 1A 4 4 1 3A 2
I 1
2 I 3A 2A 21
电路分析 方法
等效电路
3V
5Ω
3V
3V
2A
3V
(a)
(b)
3V 2A 2A
I 3 I1 I 4 0
I4 I2 I5 0
I1
R1
I2 1
R2 + US2 2 I6 R6
US1 +
I5 I3 I6 0
-
R1 I1 R2 I 2 R4 I 4 US1 US2 0 d R6 I 6 R5 I 5 R2 I 2 US2 0 US3 R3 I 3 R4 I 4 R5 I 5 0
–
(1)应用KCL列(n-1)个结点电流方程 对结点 a： I1 – I2 –IG = 0 对结点 b： I3 – I4 +IG = 0 c 对结点 c： I + I – I = 0 2 4 (2)应用KVL选网孔列回路电压方程 对网孔abda：IG RG – I3 R3 +I1 R1 = 0 对网孔acba：I2 R2 – I4 R4 – IG RG = 0 对网孔bcdb：I4 R4 + I3 R3 = E
§2.2
基本分析方法
一、 支路电流法
未知数：各支路电流